2. 城市与工程安全减灾教育部重点实验室(北京工业大学), 北京 100124;
3. 国网经济技术研究院有限公司,北京 102209;
4. 国网天津市电力公司城东供电分公司, 天津 300151;
5. 河南省交通运输发展集团有限公司, 郑州 450016
2. Key Laboratory of Urban Security and Disaster Engineering (Beijing University of Technology), Ministry of Education, Beijing 100124, China;
3. State Grid Economic and Technology Research Institute, Beijing 102209, China;
4. Chengdong Power Supply Branch, State Grid Tianjin Electric Power Company, Tianjin 300151, China;
5. Henan Transportation Development Group Co., Ltd., Zhengzhou 450016, China
历次震害表明,水电网络作为城市生命线工程的典型代表,一旦在地震以后发生破坏,必将引起严重的后果[1]。城市水网对于保障地震灾后的紧急救援、火场控制具有重要意义,而管网破坏导致的洪水、传染病也是关注的重点[2-3]。电网作为城市基础能源网络,除自身能够提供能源以供生产生活之外,地震之后还凸显了应急转运、医疗救助、通信指挥等重要的功能,更是各基础设施中最重要的网络之一。然而,传统的水网和电网的地震灾害研究通常是以隔离的形式单独分析其中某一个网络的抗灾可靠性或韧性[4-7],忽略一方对另一方的影响,其暗含的假设即一个系统的功能并不依赖于另一系统,显然,仅考虑系统自身功能的耦合性是不够的,还需要考虑系统间的关联性[5, 8]。
深入研究城市水电网络运行功能的物理机制不难发现[6],二者在本质上是具有高度耦合的基础设施系统,电网不同节点的功能状态影响水网节点的功能状态,水网节点的供水能力也将影响电网节点的供电能力,特别是在震后城市的恢复阶段,考虑二者相互影响,合理安排各网络之间的维修顺序,是影响城市恢复速度的关键问题[9]。因此,期望能够建立反映两种基础设施系统功能耦合关系的抗震韧性分析方法,从而不仅可以有效地评估各网络不同部分的抗震韧性,而且能够根据既有的维修资源,合理安排维修任务,实现耦合系统的最优恢复。
1 耦合水电网络抗震韧性分析 1.1 总体框架由于震后水电网络的协同恢复本质上是一个优化问题,该模型的总体思路是建立一个以成本最优为目标函数的优化求解模型,并采用线性规划方法予以求解。通过成本最优以实现系统协同恢复的最低经济成本,在总体上,该模型可以表述为
| $ \begin{gathered} \min _x f(\boldsymbol{x}) \end{gathered} $ | (1) |
| $ \text { Subject to } g_i(\boldsymbol{x})=c_i $ | (2) |
| $ h_j(\boldsymbol{x}) \geqslant d_i $ | (3) |
式中:f(x)为优化的目标函数,与震后管网及电网的状态和维修策略相关,此处采取经济成本最低的方式进行优化分析; x为优化问题的自变量,由于本文采用的是基于网络流的方法,自变量必有网络中抽象的物质流,还应当与节点的功能状态和维修状态有关; gi(x)和hj(x)分别表示自变量应当遵循的条件,包括等式条件和不等式条件,针对本例,自变量的取值范围、节点的功能状态、维修队的工作状态是必然加以约束的变量条件,其他还需根据模型具体分析确定。
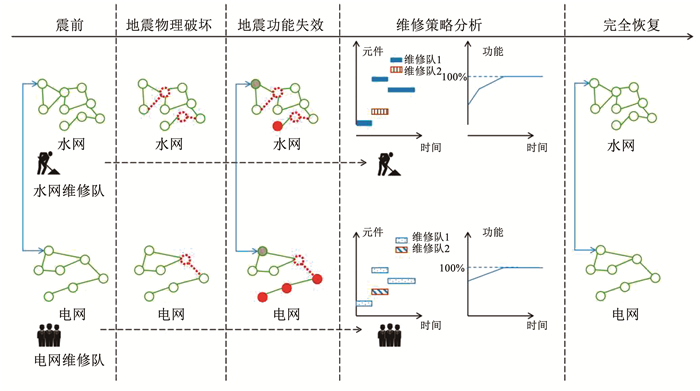
基于上述考虑,对耦合特性的水电网络,建模的思路可以概述为图 1所示的过程。
|
图 1 耦合水电网络抗震韧性分析建模的基本过程 Fig. 1 Basic process of analysis and modeling of seismic resilience of interdependent water and power supply networks |
1) 震前状态,水电网络分别处于正常功能的运行状态,同时,考虑两个网络之间的耦合机制,某一些节点还存在功能依存的关系。另外,考虑耦合网络各自的恢复机制,两个网络还存在各自的维修队。
2) 地震发生以后,由于地震动场的作用,水网和电网首先是一些节点和连接的物理破坏,表现形式为对水网如水厂、加压泵站、水塔、管线等的破坏,对电网则有变压器、架空线路等破坏。为此,对网络的节点和连接,首先有物理状态的变量描述,这一变量可以是0-1双变量,也可以是其他整数变量以对应不同的破坏等级,如0、1、2、3、4分别对应无破坏、微小破坏、中等破坏、严重破坏和彻底破坏。
3) 网络发生地震物理破坏后,会引发网络的功能破坏,有两种基本的表现形式。第一种是网络内物理破坏引发的功能破坏的扩散,如上游节点断电或者断水进而引发下游节点的断电断水。为此,还必须建立描述网络节点和连接功能的自变量,而节点的功能状态在本文中采用网络流方法,功能状态的变化必须依赖网络中网络流的变化,因此,自变量还需包括网络内物质流动计量。第二种表现形式是一方功能的破坏导致耦合网络中一些节点的功能失效,例如,电网供应水厂电力的节点断电破坏,对应的水厂也会受到影响。因此,还必须建立描述两种网络功能依赖的限制条件。
4) 水电网功能状态确定以后,不同网络的维修队伍需指定维修策略对网络进行维修,这也是本文的研究重点。为此,需要建立维修队工作状态的变量,并将维修队施加于网络的节点或连接上,待节点维修完毕,维修队转入下一个节点,此处注意需要确保维修队的连续施工状态。通过求解所建立的优化模型,得到最优的维修策略。同时,为了得到目标函数,还需要将网络内物质运输、节点功能状态、维修队工作状态等转化为单位经济成本,从而建立网络功能、维修队工作与总成本之间的桥梁,最终建立总体优化目标函数。求解优化问题,从而可以得到维修队工作计划安排和水电网络功能状态的恢复曲线,两个网络均恢复到100%表示维修任务的结束。
5) 待维修结束,两个水电网络即恢复到正常状态。
1.2 物理模型令T和K分别表示时间序列和所研究的网络集合(此处K即为水电网络构成的集合),其元素分别为t∈T和k∈K。网络k的节点集合和边集合分别为Vk和Ak,其中,运输的物质为Lk。网络中的节点分为3类,分别是消费节点、传输节点和源点,其节点集合分别表示为Vkl-、Vkl=、Vkl+。地震之后破坏的节点或者边集合分别为
令cijlkt表示在时刻t网络k中运输物质l∈Lk的单位成本,rilkt表示在时间t节点i∈Vk处所需的物质l∈Lk的数量(当rilkt>0时,表示该节点为消费节点; 当rilkt=0时,表示该节点为传输节点; 当rilkt <0时,表示该节点为源点)。对t时刻节点i∈Vk处物质l∈Lk发生剩余或者不足的的情况,其剩余和不足量的单位成本为milk-t和milk+t。uilk和uijlk分别表示节点i∈Vk和边(i, j)∈Ak的承载能力。当节点i∈Vk失效时,其成本为wik。
令
在该模型中,一共有5种决策变量,分别是流变量、松弛变量、失效变量、赋值变量、恢复状态变量。此处,令xijlkt表示在t时刻网络k∈K边(i, j)∈Ak中传输的物质l∈Lk的流变量。非负的松弛变量silk+和silk-表示在网络k∈K中节点i∈Vk处物质l∈Lk的盈余和不足量。失效变量fikt表示t时刻,网络k中节点i∈Vk的失效状态,当出现下述情况其一时,就判断为1(即表示功能失效):1)灾害导致该节点直接破坏而且没有被彻底地维修好; 2)尽管该节点没有发生物理破坏,但是其所需要的物质供应不足; 3)父节点集合
因此,该模型的优化目标函数为
| $ \sum\limits_{t \in T} \sum\limits_{k \in K} \sum\limits_{l \in L^k(i, j) \in A^k} c_{i j}^{l k} x_{i j}^{l k t}+ $ | (4) |
| $ \left.\sum\limits_{t \in T} \sum\limits_{k \in K} \sum\limits_{l \in L^k i \in V k l-\cap V^{k l t}} \sum\limits_{i-l}^{l k t} s_{i-}^{l k t}+m_{i+}^{l k t} s_{i+}^{l k t}\right)+ $ | (5) |
| $\sum\limits_{t \in T} \sum\limits_{k \in K} \sum\limits_{i \in V^k} w_i^k f_i^{k t}+ $ | (6) |
| $ \sum\limits_{k \in K} \sum\limits_{g \in G^k}\left(\sum\limits_{i \in \tilde{V} k} \eta_{g i}^{k t} y_{g i}^{k t}+\sum\limits_{(i, j) \in \tilde{A}^k} \eta_{g i}^{k t} y_{g i}^{k t}\right)+ $ | (7) |
| $ \sum\limits_{t \in T} \sum\limits_{k \in K} \sum\limits_{g \in G^k}\left(\sum\limits_{i \in \tilde{V}^k} \delta_{g i}^{k t} z_{g i}^{k t}+\sum\limits_{(i, j) \in \tilde{A}^k} \delta_{g i}^{k t} z_{g i}^{k t}\right) $ | (8) |
从目标函数不难看出,该目标函数包含5个部分,即物质运输成本、节点物质盈余或者不足成本、节点失效成本、维修队通行成本和所有构件破坏维修成本。在目标函数中,式(4)为在恢复过程中网络总流量运输成本。式(5)计算了节点流量不足或者超出需求时所产生的成本。这两类松弛变量的成本应该足够大,以确保破坏构件的维修处于比较优先的位置。式(6)为节点失效成本。通过调整松弛成本和失效成本的数值,可以确定不同构建维修的优先顺序。显然,对于惩罚或者失效成本更高的节点,在维修过程中会得到更快的维修。式(7)计算了维修队到达各个破坏构件的通行成本。式(8)则衡量了所有破坏构件的维修成本。
因此,该模型就是寻找最优的恢复策略,通过指定每一个维修队对不同破坏构件的维修顺序,以使得总体的恢复成本最小。
该模型相应的限制条件为
| $ \sum\limits_{(i, j) \in A^k} x_{i j}^{l k t}-\sum\limits_{(j, i) \in A^k} x_{i j}^{l k t}=r_i^{l k t}- \\ s_{i+}^{l l t}+s_{i-}^{l l t}, \forall i \in V^{k l+} \cup V^{k l-}, \\ \forall l \in L^k, \forall k \in K, \forall t \in T $ | (9) |
| $\sum\limits_{(i, j) \in A^k} x_{i j}^{l k t}-\sum\limits_{(j, i) \in A^k} x_{i j}^{l k t}=0, \\ \forall i \in V^{k l=}, \forall l \in L^k, \forall k \in K, \\ \forall t \in T $ | (10) |
| $ x_{i j}^{l k t} \leqslant u_{i j}^k, \forall(i, j) \in A^k / \tilde{A}^k, \\ \forall l \in L^k, \forall k \in K, \forall t \in T $ | (11) |
| $ x_{i j}^{l l k} \leqslant u_{i j}^k, \forall(i, j) \in \tilde{A}^k, \forall l \in L^k, \\ \forall k \in K, \forall t \in T $ | (12) |
| $ \sum\limits_{(i, j) \in A^k} x_{i j}^{l k t}, \forall i \in V^k, \forall l \in L^k, \\ \forall k \in K, \forall t \in T $ | (13) |
| $ f_i^{k t} \geqslant 1-z_i^{k t}, \forall i \in \tilde{V}^k, \forall k \in K, \\ \forall t \in T $ | (14) |
| $ M f_i^{k t} \geqslant s_{i-}^{l k t}, \forall l \in L^k, \forall i \in V^{k l-}, \\ \forall k \in K, \forall t \in T $ | (15) |
| $ 1-f_i^{k t} \leqslant \sum\limits_{j \in C_{C i k}^k} \lambda_{i {k}}^{j \hat{k}}\left(1-f_j^{\hat{k}}\right), \\ \forall i \in\left\{n \in V^k \mid C_{i k}^{\hat{k}} \neq 0\right\}, \forall k \in K, \\ \forall t \in T $ | (16) |
| $\sum\limits_{(i, j) \in A^k} x_{i j}^{l k t} \leqslant u_i^k\left(1-f_i^{k t}\right), \forall i \in V^k, \\ \forall l \in L^k, \forall k \in K, \forall t \in T $ | (17) |
| $ z_i^{k\left(t+\delta_{g i}\right)} \geqslant \sum\limits_{g \in G^k} y_{k i}^{k t}, \forall i \in \tilde{V}^k, \\ \forall k \in K, \forall t \in T $ | (18) |
| $ z_i^{k\left(t+\delta_{g i}\right)} \geqslant \sum\limits_{g \in G^k} y_{g i}^{k t}, \forall(i, j) \in \tilde{A}^k, \\ \forall k \in K, \forall t \in T $ | (19) |
| $y_{g i}^{k t} \leqslant p_{g i}^{k t}, \forall g \in G^k, \forall i \in \tilde{V}^k, \\ \forall k \in K, \forall t \in T $ | (20) |
| $y_{g i}^{k t} \leqslant p_{g i}^{k t}, \forall g \in G^k, \forall(i, j) \in \tilde{A}^k, \\ \forall k \in K, \forall t \in T $ | (21) |
| $ y_{g i}^{k(t+1)}+z_{g i}^{k(t+1)} \leqslant y_{g i}^{k t}+z_{g i}^{k t}, \\ \forall g \in G^k, \forall i \in \tilde{V}^k, \forall k \in K, \\ \forall t \in T $ | (22) |
| $ y_{g i}^{k(t+1)}+z_{g i}^{k(t+1)} \leqslant y_{g i}^{k t}+z_{g i}^{k t}, \\ \forall g \in G^k, \forall(i, j) \in \tilde{A}^k, \\ \forall k \in K, \forall t \in T $ | (23) |
| $ z_{g i}^{k(t+1)} \geqslant z_{g i}^{k t}, \forall g \in G^k, \forall i \in \tilde{V}^k, \\ \forall k \in K, \forall t \in T $ | (24) |
| $ z_{g i}^{k(t+1)} \geqslant z_{g i}^{k t}, \forall g \in G^k, \\ \forall(i, j) \in \tilde{A}^k, \\ \forall k \in K, \forall t \in T $ | (25) |
| $ \sum\limits_{g \in G^k} y_{g i}^{k t}+z_{i j}^{k t} \leqslant 1, \forall i \in \tilde{V}^k, \\ \forall k \in K, \forall t \in T $ | (26) |
| $\sum\limits_{g \in G^k} y_{g i}^{k t}+z_{i j}^{k t} \leqslant 1, \forall(i, j) \in \tilde{A}^k, \\ \forall k \in K, \forall t \in T $ | (27) |
| $ \sum\limits_{i \in \tilde{V} k} y_{g i}^{k t}+\sum\limits_{\substack{(i, j) \in \tilde{A}^k}} y_{g i j}^{k t} \leqslant 1, \forall g \in G^k, \\ \forall k \in K, \forall t \in T $ | (28) |
| $ \begin{gathered} \sum\limits_{i \in \tilde{V}^k} y_{g i}^{k t+1}+\sum\limits_{(i, j) \in \tilde{A}^k} y_{g i j}^{k t+1} \leqslant \sum\limits_{(i, j) \in \tilde{A}^k} y_{g i}^{k t}+ \\ \sum\limits_{i \in \tilde{V}^{k t}}^{k t}, \forall g \in G^k, \forall k \in K, \\ \forall t \in T \end{gathered} $ | (29) |
| $ \sum\limits_{t \in T} \sum\limits_{g \in G^k} y_{g i}^{k t}=\delta_{g i}^k, \forall i \in \tilde{V}^k, \\ \forall k \in K $ | (30) |
| $ \sum\limits_{t \in T} \sum\limits_{g \in G^k} y_{g i}^{k t}=\delta_{g i}^k, \forall(i, j) \in \tilde{A}^k, \\ \forall k \in K $ | (31) |
| $ x_{i j}^{l k t} \geqslant 0, \forall(i, j) \in A^k, \forall l \in L^k, \\ \forall k \in K, \forall t \in T $ | (32) |
| $ s_i^{l k+t}, s_i^{l k-t} \geqslant 0, \forall i \in V^{k l+} \cup V^{k l-}, \\ \forall l \in L^k, \forall k \in K, \forall t \in T $ | (33) |
| $f_i^{k t} \in\{0, 1\}, \forall i \in V^k, \forall k \in K, \\ \forall t \in T $ | (34) |
| $y_{g i}^{k t}, z_{g i}^{k t} \in\{0, 1\}, \forall g \in G^k, \\ \forall i \in \tilde{V}^k, \forall k \in K, \forall t \in T $ | (35) |
| $y_{g i}^{k t}, z_{g i}^{k t} \in\{0, 1\}, \forall g \in G^k, \\ \forall(i, j) \in \tilde{A}^k, \forall k \in K, \\ \forall t \in T $ | (36) |
条件(9)和(10)确保在t∈T时刻网络k∈K中节点i∈Vk的流平衡。与松弛变量相关的惩罚成本可以确保对节点尽可能提供所需要的物质。对传输节点i∈Vk=,其总得输入流应该等于该节点总得输出流。条件(11)确保对每一个没有破坏的边,其中的流量不能超过其预先限定的边的承载能力。条件(12)是对破坏边的流量加以限定,以确保直到这条边修复时才允许有流量通过。条件(13)和(14)确保物理破坏的节点直到完全恢复以后,才能够消费物质。在本研究中,对消费节点,只要没有满足所需就是失效的。这一点是通过条件(15)的限定实现的:如果对某一个节点i, 其所需的物质没有满足(即silk-t>0时),失效变量就强制为1。式(15)中的参数M是用来确保节点失效状态变量和该节点与物质相关的松弛变量之间的逻辑一致性。这一变量应该足够大,从而避免人为导致的计算不收敛。条件(16)将父节点的失效传播到子节点之中。因此,通过条件(14)~(16)节点失效的3种状态都被限定了。式(17)确保没有流进入失效的节点之中。例如,对一个供水泵站,即便地震之后水泵等设施并没有震坏,一旦停电该节点的加压功能也即失效。
式(20)和(21)确保了交通系统和其他网络之间的逻辑依赖关系。也就是说,当维修队和破坏构件之间没有路径时,恢复工作就无法进入安排日程。任何维修队在t时刻对破坏的节点/边进行维修,那么相应的维修状态在δ d之后就设定为完成(状态变量z=1, 在t+δ时)。δgik和δgijk为平均的维修所需时间,文献[11]中对该参数有详细的规定。本研究中,假设对同一破坏构件的维修时不可中断,也就是说,维修队不可以移动到其他破坏构件处,直至当前的维修工作完成,这一条件是通过式(22)和(23)的限制实现的。也就是说,如果维修队g在t时刻维修
式(30)和(31)限定所有的破坏构件最终都被修复完成。条件(32)和(33)确保流变量和松弛变量是连续非负的。最终,节点失效变量、维修队工作状态变量、破坏构件(节点/边)的完成状态变量,分别在条件(34)~(36)限定为双变量。
求解上述模型,即可以得到水电网络不同节点的功能状态,考虑不同时间维修情况,即可得到节点在震后随时间变化的恢复情况,同时得到不同维修队的工作情况,进而得到水电网络总体的功能恢复情况。
1.3 方法步骤根据上述物理模型,建立具有功能耦合的城市水电网络抗震韧性分析方法,基本步骤如下:
1) 确定城市场地基本信息,根据采用的地震动场模型生成符合城市场地特征的地震动场[12-13]; 确定城市水电网络的基本信息,主要包括拓扑结构、管线和节点的物理信息等; 确定水电网络的维修资源信息,主要包括维修队的数量和维修效率等。
2) 根据所生成的地震动场,计算网络各个构件的物理状态,确定各个构件(元件)的物理状态。
3) 根据本文所建立的模型,计算得到网络各个节点的功能损失情况,获得各维修队伍的安排策略。
2 算例以杭州市上城区水电网络为例验证这一方法的可行性。该地区共有54个社区,人口约35万,是杭州的中心城区之一,其水网和电网分布如图 2所示。

|
图 2 上城区水电网络分布示意 Fig. 2 Diagram of water and power supply networks in Shangcheng District |
由于本文集中讨论所提出的优化恢复模型的可行性,水网和电网物理破坏状态及其与地震动场之间的关系并不是研究重点,因此,水网和电网的初始地震破坏状态是一组假设的情况。在此基础上进行恢复策略的分析和维修工作的安排。出于快速计算节约时间的目的,仅考虑比较简单的物理破坏和两个维修队进行修复工作的情况,展示本文方法的可行性。
水电系统节点的功能指标选用的是fi取值为0或者1的双变量指标,其定义为
| $f_i=\left\{\begin{array}{l} 0, Q_i \geqslant D_i \\ 1, Q_i<D_i \end{array}\right. $ | (37) |
其中Qi和Di分别为网络中节点i的物质提供量和需求量。对水网或者电网整个系统的功能指标,采用的是网络系统功能百分比Fn,定义为
| $ F_{\mathrm{n}}=\frac{\sum\limits_i f_i}{N_0} \times 100 \% $ | (38) |
其中N0为网络节点的总数量。
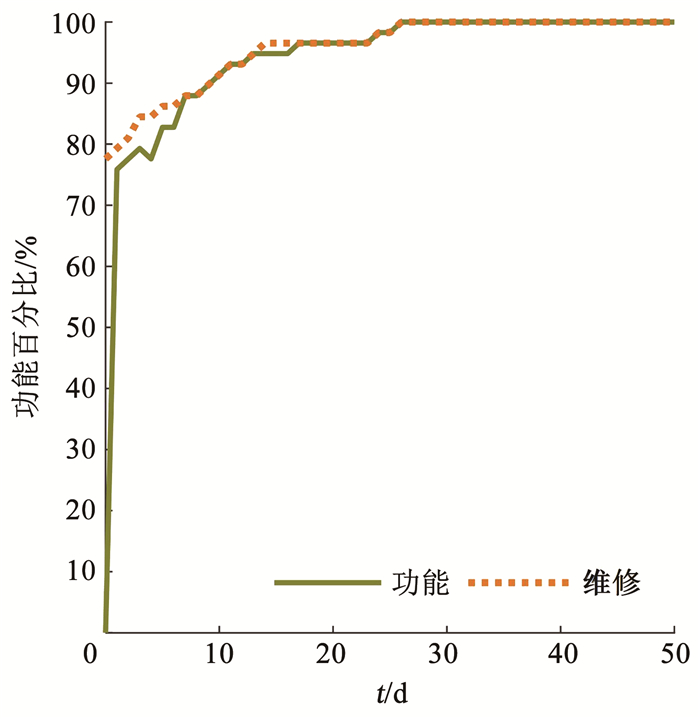
水网系统的功能和维修恢复曲线如图 3所示。可以看出,由于水网源点(5号点)的破坏,在地震发生以后,水网功能为0,即处于彻底失效状态,一旦维修开始以后,由于源点被首先修复,水网的功能即得到迅速提升,在地震后修好的第1天结束时,功能即可恢复到75.86%。随着维修过程的逐渐推进,水网功能逐渐恢复,在地震后的第10、20天,功能指标分别为91.38%、96.55%,并在第26天恢复到100%的功能状态。水网不同节点对应的服务区域震后的恢复顺序如图 4所示。
|
图 3 水网功能和维修恢复曲线 Fig. 3 Function and repair recovery curves of water supply network |

|
图 4 水网恢复过程 Fig. 4 Restoration process of water supply network |
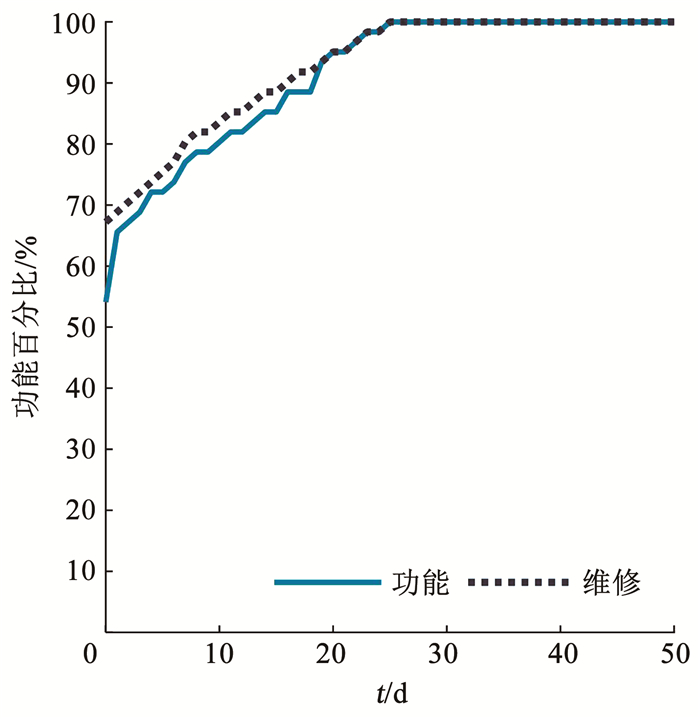
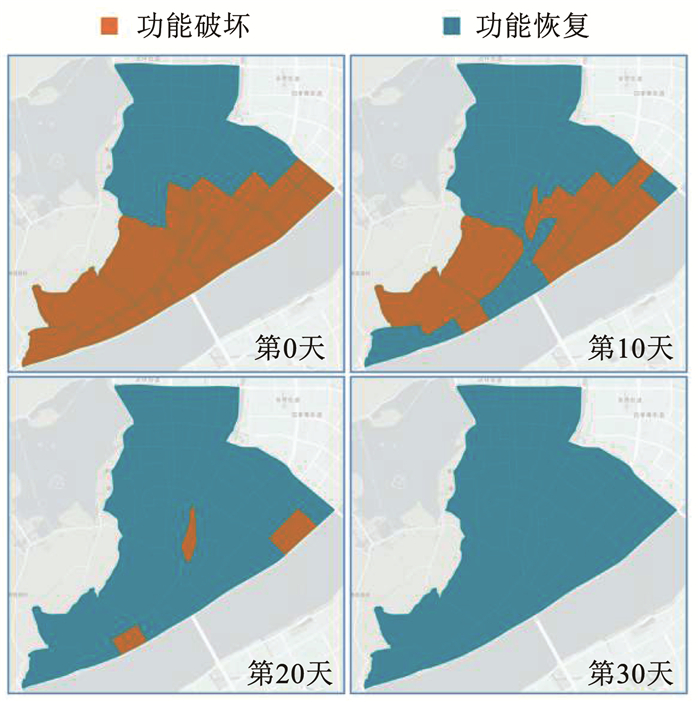
电网系统的维修和功能恢复曲线如图 5所示。可以看出,地震发生后,电网还可以维持54.1%的功能。随着维修过程的进行,电网系统功能逐渐恢复,在地震后的第1、10、20天,功能指标分别为65.57%、80.33%、95.08%,并在第26天恢复到100%。电网不同节点所对应的城市服务区域震后的恢复过程如图 6所示。
|
图 5 电网功能和维修恢复曲线 Fig. 5 Function and repair recovery curves of power grid |
|
图 6 电网恢复过程 Fig. 6 Restoration process of power grid |
水网维修队伍的安排如图 7所示。此处,维修队伍一共有两队,分别是队伍1和队伍2。从图 7可以看出,对于维修队伍1,维修首先从节点15开始,维修1 d后转至节点5,持续2 d后转至节点12,并依次按图 7所示进行维修。而维修队伍2首先从节点9开始维修,维修2 d后跳转到节点8,维修1 d后又到节点6进行维修。
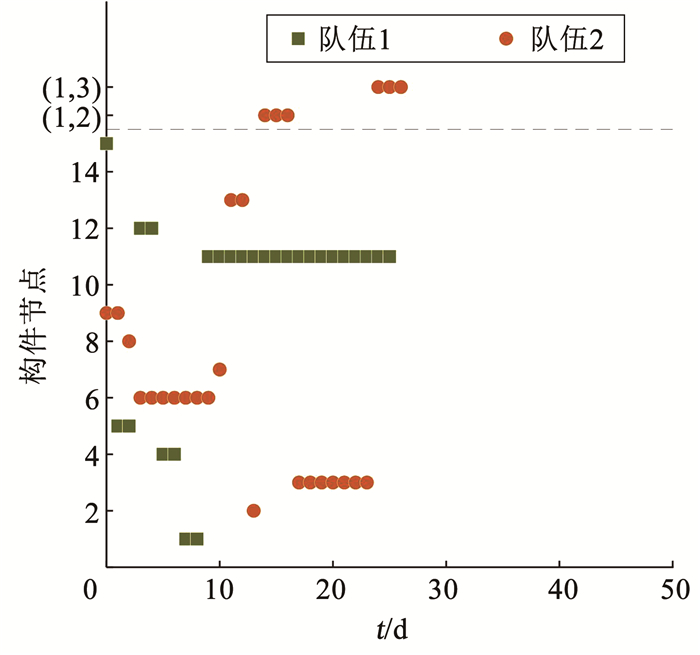
|
图 7 水网维修队伍维修任务安排 Fig. 7 Repair task arrangement of repair teams for water supply network |
电网的维修任务安排如图 8所示,可以看出,维修队伍首先在节点9进行维修,1 d后转至节点30,1 d后又转至节点29,并依次按照图示所叙进行维修任务。对于队伍2,其任务首先开始于节点18,持续7 d后转至节点2,维修1 d后再转至节点14,随后的任务安排依次按图 8所示进行。
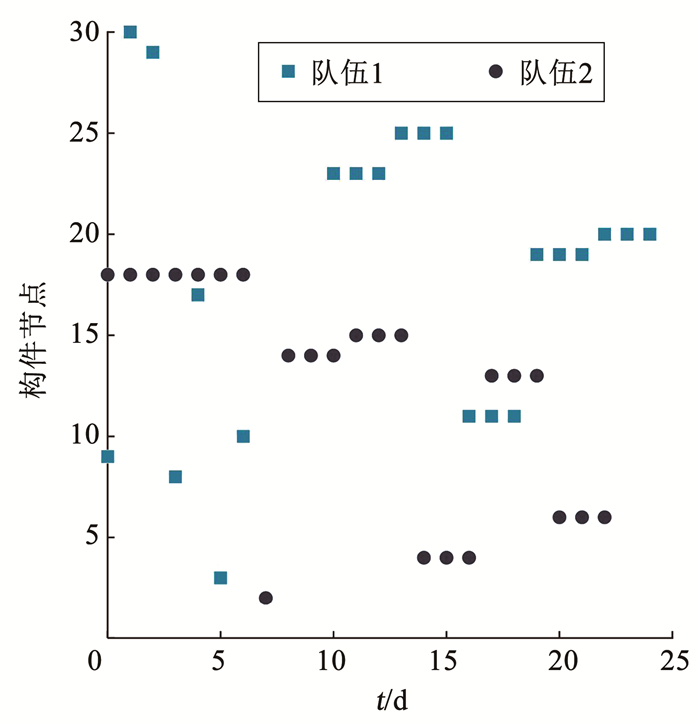
|
图 8 电网维修队伍维修任务安排 Fig. 8 Repair task arrangement of repair teams for power grid |
为进一步探究随机性对水电系统协同恢复的影响,根据生成的情景地震动场和水电网络构件的破坏概率,随机生成具有不同物理状态的样本1 000个,并进行蒙特卡洛模拟分析。
水网多样本维修恢复曲线的上下界和均值、功能恢复曲线的上下边界和均值分别如图 9和10所示。从图 9和10可以看出,由于水网结构物理状态破坏的不确定性,当考虑水电网络的协同恢复时,水网的维修恢复曲线和功能恢复曲线均呈现了显著的离散性,且该离散性是不稳定的,多样本的离散型随灾后时间的变化也呈现显著的变化。
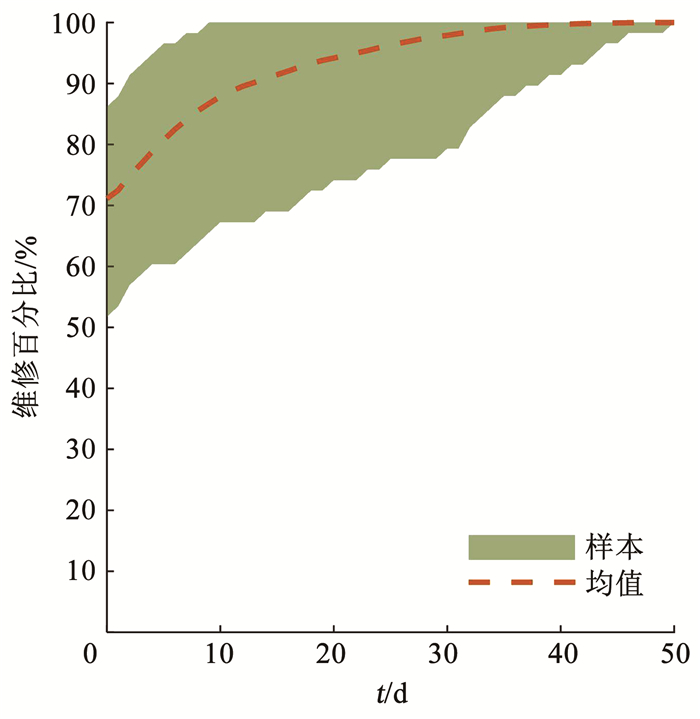
|
图 9 水网维修恢复分析 Fig. 9 Repair restoration analysis of water supply network |
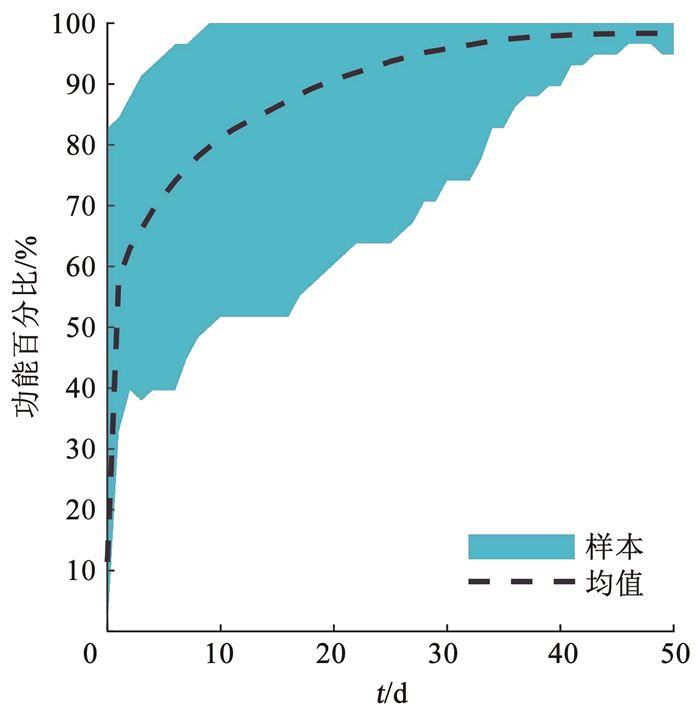
|
图 10 水网功能恢复分析 Fig. 10 Function restoration analysis of water supply network |
从图 9可以看出,灾后第1、10、20、30、40、50天,维修恢复曲线平均恢复了72.15%、87.06%、93.47%、97.56%、99.72%、100%,其标准差则分别为5.86%、5.35%、4.49%、2.97%、1.05%、0;类似地,从图 10可以看出,在灾后第1、10、20、30、40、50天,功能恢复曲线平均恢复了55.60%、78.75%、88.34%、94.19%、96.77%、97.08%,其标准差则分别为9.01%、7.99%、6.83%、4.25%、1.68%、1.26%。另外,从图 9和10中均值曲线的对比不难发现,水网功能总体上呈现了物理修复在前、功能恢复在后的特点,灾后第1、10、20、30、40、50天,后者比前者恢复分别慢16.55%、8.31%、5.13%、3.37%、2.94%、2.92%。
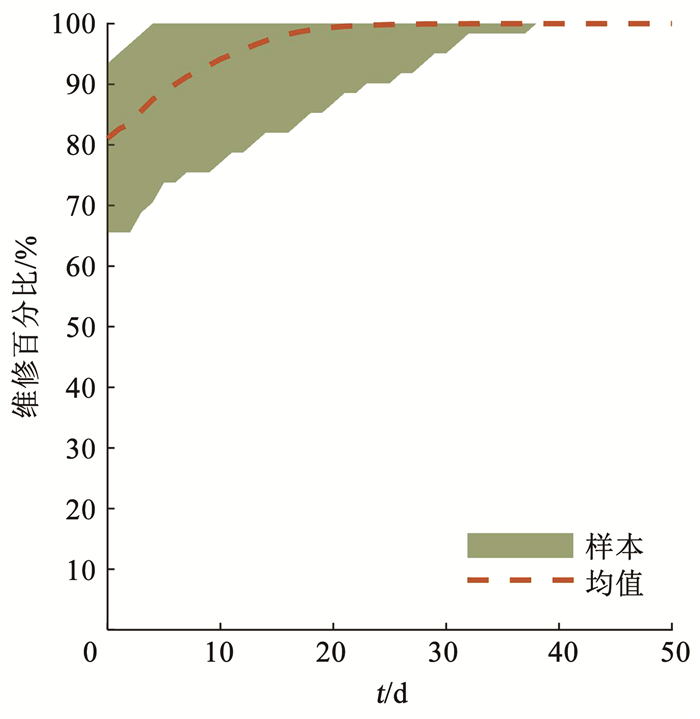
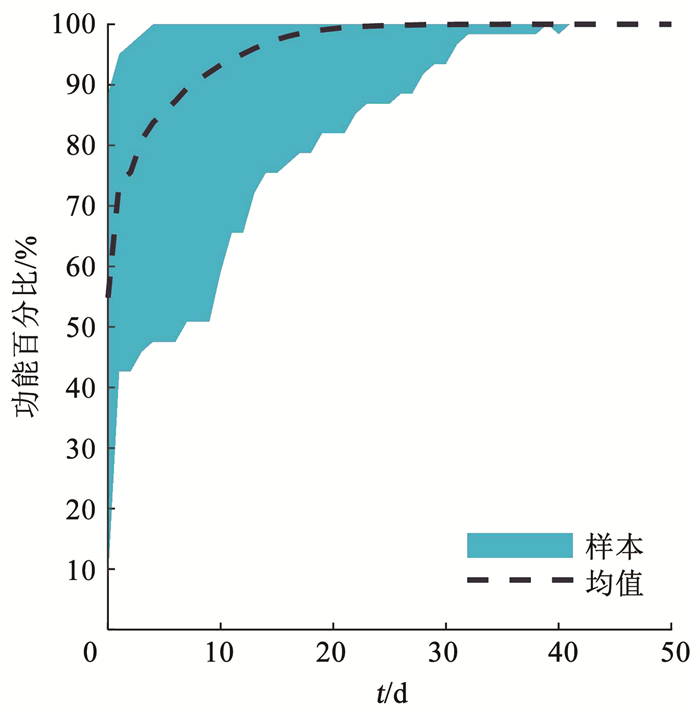
电网多样本维修恢复曲线的上下界和均值、功能恢复曲线的上下边界和均值分别如图 11和12所示。从图 11和12可以看出,电网构件物理状态破坏的不确定性,同样会导致电网的维修恢复曲线和功能恢复曲线产生显著的离散。
|
图 11 电网维修恢复分析 Fig. 11 Repair restoration analysis of power grid |
|
图 12 电网功能恢复分析 Fig. 12 Function restoration analysis of power grid |
从图 11可以看出,灾后第1、10、20、30、40、50天,维修恢复曲线平均恢复了82.46%、93.97%、99.42%、100%、100%、100%,其标准差则分别为4.81%、4.25%、1.62%、0、0、0;类似地,从图 12可以看出,在灾后第1、10、20、30、40、50天,功能恢复曲线平均恢复了72.40%、93.07%、99.34%、99.98%、99.99%、100%,其标准差则分别为8.97%、5.44%、1.89%、0.16%、0.10%、0。与水网类似,电网也呈现了物理恢复在前、功能恢复在后的特点,后者比前者恢复分别慢10.06%、0.90%、0.08%、0.02%、0.01%、0。当然,应该注意到这是一种平均意义的刻画,具体到某一处节点,则可能因为上级节点的破坏而导致功能失效,只要上级节点的功能恢复,则该节点自然也可以恢复。
另外,从水网和电网的恢复分析对比可以发现,从平均意义上来看,电网比水网表现出更快的恢复速度,这一点无论是从维修恢复曲线还是功能恢复曲线的均值中都可以得到验证。从维修恢复曲线来看,在第1、10、20、30、40、50天,电网比水网的恢复分别快10.31%、6.91%、5.96%、2.44%、0.28%、0;而从功能恢复曲线来看,在第1、10、20、30、40、50天,电网比水网的恢复分别快16.80%、14.32%、11.00%、5.79%、3.22%、2.92%。
3 结论基于网络流理论,考虑城市水网和电网之间的相互影响机制,建立了具有功能耦合特性的城市水电网络抗震韧性分析方法,得到如下结论:
1) 通过确定性算例验证了本文方法的可行性。这一方法不仅可以有效评估震后以及恢复过程中水电网络不同部位、不同时间的功能状态,而且实现了维修资源的有效分配,合理安排了维修任务,实现了耦合系统的最优恢复。
2) 由于水电网络构件物理破坏的不确定性,水电网络的恢复过程呈现显著的离散性,且这种离散性呈现随时间变化而变化的特点。
3) 从平均意义上来看,电网比水网表现出了更快的恢复速度,体现出更强的恢复韧性。
| [1] |
于山, 苏幼坡, 刘天适, 等. 唐山大地震救援与恢复重建[M]. 北京: 中国科学技术出版社, 2003. YU Shan, SU Youpo, LIU Tianshi, et al. Rescue and rehabilitation of Tangshan earthquake[M]. Beijing: China Science and Technology Press, 2003. |
| [2] |
LIU W, SUN Q, MIAO H, et al. Nonlinear stochastic seismic analysis of buried pipeline systems[J]. Soil Dynamics and Earthquake Engineering, 2015, 74: 69. DOI:10.1016/j.soildyn.2015.03.017 |
| [3] |
MIAO H, LIU W, LI J. Seismic reliability analysis of water distribution networks on the basis of the probability density evolution method[J]. Structural Safety, 2020, 86: 101960. DOI:10.1016/j.strusafe.2020.101960 |
| [4] |
TODINI E. Looped water distribution networks design using a resilience index based heuristic approach[J]. Urban Water, 2000, 2(2): 115. DOI:10.1016/S1462-0758(00)00049-2 |
| [5] |
OUYANG M, DUEÑAS-OSORIO L, MIN X. A three-stage resilience analysis framework for urban infrastructure systems[J]. Structural Safety, 2012, 36/37(5/6): 23. DOI:10.1016/j.strusafe.2011.12.004 |
| [6] |
缪惠全, 李杰. 基于物理机制的供水管网抗震功能实时动态分析[J]. 地震工程与工程振动, 2018, 28(3): 20. MIAO Huiquan, LI Jie. Real-time dynamic analysis of seismic function of water supply network based on physical mechanism[J]. Earthquake Engineering and Engineering Vibration, 2018, 28(3): 20. DOI:10.6052/j.issn.1000-4750.2021.04.0243 |
| [7] |
缪惠全, 李杰. 基于物理机制的随机地震动场中供水管网抗震功能反应分析[J]. 工程力学, 2021, 39(7): 99. MIAO Huiquan, LI Jie. Seismic response analysis of water supply network in random ground motion field based on physical mechanism[J]. Engineering Mechanics, 2021, 39(7): 99. DOI:10.6052/j.issn.1000-4750.2021.04.0243 |
| [8] |
OUYANG M. Review on modeling and simulation of interdependent critical infrastructure systems[J]. Reliability Engineering and System Safety, 2014, 121(1): 43. DOI:10.1016/j.ress.2013.06.040 |
| [9] |
LIN P, WANG N. Building portfolio fragility functions to support scalable community resilience assessment[J]. Sustainable and Resilient Infrastructure, 2016, 1(3/4): 108. DOI:10.1080/23789689.2016.1254997 |
| [10] |
ZHANG W, WANG N, NICHOLSON C. Resilience-based post-disaster recovery strategies for road-bridge networks[J]. Structure and Infrastructure Engineering, 2017, 13(11): 1404. DOI:10.1080/15732479.2016.1271813 |
| [11] |
FEMA/NIBS. Multi-hazard loss estimation methodology eathquake model (Hazus-MH 2.1)[M]. Washington: FEMA, 2015
|
| [12] |
SHEN J, CHEN J, DING G. Random field model of sequential ground motions[J]. Bulletin of Earthquake Engineering, 2020, 18(11): 5119. DOI:10.1007/s10518-020-00901-4 |
| [13] |
缪惠全, 李杰. 基于物理机制的工程场地地震动相干函数模型[J]. 中国科学: 技术科学, 2018, 48(2): 209. MIAO Huiquan, LI Jie. The coherence function model of ground motion in engineering sites based on physical mechanism[J]. Scientia Sinica: Technologica, 2018, 48(2): 209. DOI:10.1360/N092017-00077 |
 2023, Vol. 55
2023, Vol. 55


