控制坡体地下水位上升,对于滑坡防治具有重要作用[1-4]。目前,最常用的地下水钻孔排水方法为水平排水孔,但由于水平排水孔为开放体系,且倾角小排水流速低,使用过程中易产生淤堵[5-6],长期排水的可靠性差。虹吸排水是一种利用液面高差推动液体流动的排水技术,采用俯倾钻孔更有利于汇集地下水,且抗淤堵能力明显高于水平排水孔,能更好地满足坡体地下水位控制的需要[7-9]。但虹吸排水过程中,溶解于水中的空气会在虹吸管内的低压环境下释放形成气泡,必须采用细管径形成段塞流,保证水流能够把释放的气泡排出虹吸管[10-11],从而确保免维护虹吸排水的长期有效性。大量研究[12-13]表明,选择虹吸管不超过5 mm的管径才能形成稳定的段塞流。不同于粗管径的排水能力具有自然满足边坡排水需要的特性,小于5 mm虹吸管的排水能力低,其排水能力能否有效应对暴雨时地表水入渗导致地下水激增的情况,成为边坡虹吸排水方案设计的基础。
滑坡虹吸排水工程是利用向下倾斜钻孔进入坡体深部,保持地下水位控制点与孔口高差小于10 m,达到滑坡深层地下水的降排要求[7],已在多处滑坡中应用且降排效果良好[14-15]。其中,所用虹吸排水管多为长直管段[16-17],流体大部分能量损失为沿程水头损失,所以,沿程水头损失系数λ的精度决定了流速计算准确性。但是,现有虹吸流速计算的相关研究中,大部分集中在流速计算或低扬程工况等情况[18-21],关于沿程水头损失系数计算研究较少[22-23],且针对特定工况下通过气泡孔隙率的分析方法计算虹吸流速[24],计算值和实测值之间仍存在较大的误差。本文从确定虹吸流速相关参数和沿程水头损失系数λ计算方法出发,旨在提高5 mm及其以下管径虹吸管单管流速的计算精度,为虹吸排水的工程应用提供理论支持。
1 计算参数分析确定 1.1 虹吸管流计算参数分析虹吸是有压管流,常采用水力学中有压管流公式进行求解[25]
| $ v=\sqrt{\frac{2 g H_1}{1+\lambda \frac{l}{d}+\sum \zeta}} $ | (1) |
式中:v为流速,g为重力加速度,H1为水头差,l为虹吸管的长度,d为虹吸管的直径,ζ为局部损失系数,λ为沿程水头损失系数。
有压管流计算公式是基于伯努利方程条件下化简得到的,所以,适用范围和伯努利方程一致。伯努利方程的前提条件是不可压缩连续流,高扬程虹吸存在空气释放与积累的问题,所以,管顶及下水管往往是气液两相流,传统有压管流公式并不适用于虹吸管流计算。如图 1所示虹吸由上水管和下水管两部分组成。虹吸未启动前,假设下水管末端是堵住的,上下水管内充满了水。虹吸启动后,下水管的液体由于重力作用下落,带动虹吸管内液体流动,由于水的抗拉强度为0,在一瞬间dt内上下水管之间拉出了一个微元dr长的真空带,即瞬间液体“断裂”。于是上水管与真空带之间产生压差,推动上水管内液体运动。当上水管内液体以vup流入下水管时,会出现3种情况:1)vup>vdown,上水管及时向下水管“供水”,上下管内为连续流,可用常规伯努利方程求解; 2)vup=vdown,上下管流速相同,由于真空带几乎可忽略不计,上下管内近似看作连续流处理,此时仍可用常规伯努利方程进行求解; 3)vup <vdown,上水管不能及时向下水管补水,导致真空带被“拉长”,即出现了非连续流,此时常规有压管流计算公式不再适用。

|
图 1 虹吸管内流动示意 Fig. 1 Flow diagram in siphon |
对于第3种情况,由于上水管和下水管之间形成真空带,即上下水管中液体为非连续流,伯努利方程不再适用,但上水管仍可看作连续流,可将上水管单独进行分析。理想化计算条件,将管顶处简化为完全真空环境,进水口和管顶处伯努利方程如下:
| $ H_0+\frac{v^2}{2 g}-H_{\text {max }}+\left(\lambda \frac{l_{\text {up }}}{d}+\sum \zeta_{\text {up }}\right) \frac{v^2}{2 g}=0 $ | (2) |
式中:Hmax为当地最大提水高度,lup为上水管长,ζup为上水管局部水头损失系数,H0为虹吸扬程。
局部水头损失系数取值如下[26]:虹吸管进口处ζ=0.5,出口处ζ=1.0,每个弯折处ζ=0.8。
将上水管最大提水高度ΔH=Hmax-H0代入式(2),此时虹吸流速可表示为
| $v_{\text {ир }}=\sqrt{\frac{2 g \varDelta H}{1+\lambda \frac{l_{\mathrm{up}}}{d}+\sum \zeta_{\mathrm{up}}}} $ | (3) |
综合上述3种情况,虹吸流速可表达为[18]
| $ v=\min \left(\sqrt{\frac{2 g \varDelta H}{1+\lambda \frac{l_{\text {up }}}{d}+\sum \zeta_{\text {up }}}}, \sqrt{\frac{2 g H_1}{1+\lambda \frac{l}{d}+\sum \zeta}}\right) $ | (4) |
式(4)是通过分析虹吸流动过程得到,是目前考虑最全面、运算最简便的虹吸流速计算方法。相比传统有压管流公式计算误差大的问题,其采用取两者之间较小值的方法更适合评估不同工况下的虹吸流速。本文采用式(4)进行理论计算。
1.2 沿程水头损失系数λ的确定用式(4)计算沿程水头损失必须先确定λ的大小,而λ与流态和管壁粗糙度等因素有关。流体的流态可根据下临界雷诺数Rec分为层流、过渡流和湍流,雷诺通过大量实验发现下临界雷诺数Rec≈2 100时流态发生动荡[27],选取Rec=2 100作为分段计算λ的标准。下临界雷诺数可由下式计算:
| $ \begin{gathered} R e=\frac{v d}{v} \end{gathered} $ | (5) |
| $ v=\frac{0.01775 \times 10^{-4}}{1+0.0337 t+0.000221 t^2} $ | (6) |
式中:υ为运动黏度,t为水温,Re为雷诺数,v为断面平均流速。
对于层流,λ和雷诺数Re成反比[28],即
| $ \lambda=\frac{64}{R e} $ | (7) |
对于过渡流和湍流,选择巴尔公式计算沿程水头损失系数λ[29]。巴尔公式有以下优点:考虑了管材、管径、雷诺数等影响因素; 显式; 计算简便且适用于编程; 适用于各阻力区。具体公式如下
| $ \frac{1}{\sqrt{\lambda}}=-2 \lg \left(\frac{\varDelta}{3.7 d}+\frac{5.1286}{R e^{0.89}}\right) $ | (8) |
式中Δ为绝对粗糙度,与管材有关。
综上,下列公式将用于λ的计算
| $ \lambda=\left\{\begin{array}{l} \frac{64}{R e}, \operatorname{Re} \leqslant 2100 \\ {\left[\frac{1}{-2 \lg \left(\frac{\varDelta}{3.7 d}+\frac{5.1286}{\operatorname{Re}^{0.89}}\right)}\right]^2, R e>2100} \end{array}\right. $ | (9) |
虹吸流速的计算结果需将式(9)代入式(4)进行迭代运算后产生。
2 物理试验测试与理论计算结果对比 2.1 物理试验测试虹吸物理模型试验为1∶ 1的足尺物理模型试验。图 2为物理试验模型,由上水管、下水管、水桶A、水桶B和补水管组成。虹吸管为聚氨酯(PU)材质,管顶曲率为0.1 m。上水管放置在水桶A中,补水管使水箱A中的水位保持恒定。H0为管顶与进水液面的高差(即扬程),H1为液面进口与出口的高差(即水头差)。待虹吸稳定后,在量杯中收集一定时间的流量计算虹吸的平均流速。为减少收集流量中产生的误差,本次试验收集流量的时间统一为30 min。

|
图 2 虹吸物理模型试验装置 Fig. 2 Experimental device of siphon physical model |
试验选用3、4、5 mm 3种管径,各管径分别在表 1所示方案中进行一轮试验,共开展了75组试验。由于温度和气压会对虹吸流速产生影响,同一管径、同一扬程H0试验在相同工况下进行。表 1为各管径具体试验方案。Lup为上水管长,Ldown为下水管长。
| 表 1 试验工况 Tab. 1 Experimental conditions |
采用不同扬程分组,各组均包含3、4、5 mm 3种管径,试验结果以及依据式(4)的计算结果如图 3~6所示。由于各组试验不能同时进行,计算结果已考虑气压和温度等因素产生的影响。此次试验采用聚氨酯(PU)材料,绝对粗糙度Δ取0.001 5 mm[30]。误差率均以绝对误差率Er表示,即
| $ E_{\mathrm{r}}=\left|\frac{v_{\mathrm{c}}-v_{\mathrm{t}}}{v_{\mathrm{t}}} \times 100\right| $ | (10) |

|
图 3 H0=4.05 m时虹吸流速计算值与试验值 Fig. 3 Comparison of calculated and experimental values of siphon velocity when H0=4.05 m |
|
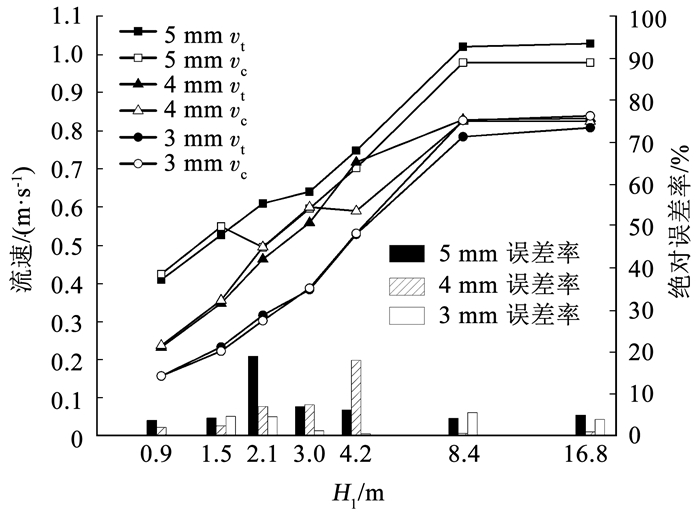
图 4 H0=7.35 m时虹吸流速计算值与试验值 Fig. 4 Comparison of calculated and experimental values of siphon velocity when H0=7.35 m |
|
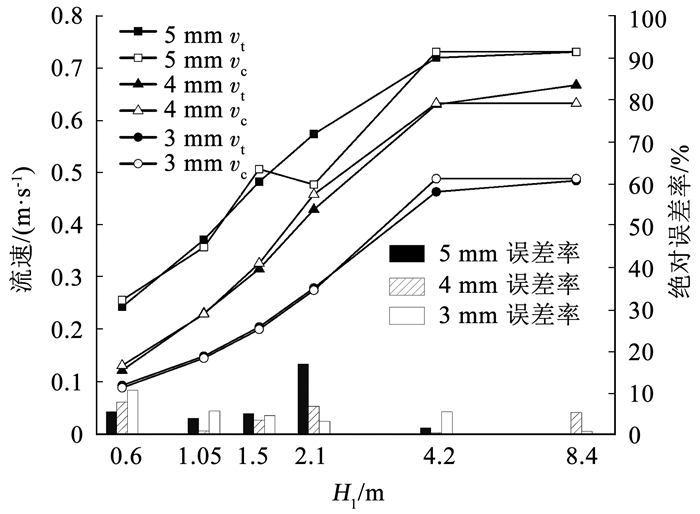
图 5 H0=8.25 m时虹吸流速计算值与试验值 Fig. 5 Comparison of calculated and experimental values of siphon velocity when H0=8.25 m |

|
图 6 H0=9.15 m时虹吸流速计算值与试验值 Fig. 6 Comparison of calculated and experimental values of siphon velocity when H0=9.15 m |
式中:vt代表实测值,vc为修正伯努利方程计算值。
图 3为H0=4.05 m时各管径试验值与计算值。对于3种不同的管径,计算值和试验值契合度较高。除了方案d=4 mm、H1=2.1 m的绝对误差率Er为14.07%,其余方案的绝对误差率Er均在6%以下。而方案d=4 mm、H1=2.1 m的雷诺数为2 544,表明流体的流态位于层流和湍流的过渡段,此时流态混乱,λ不易精确计算。
图 4为H0=7.35 m时各管径试验值与计算值,计算值和试验值的增长趋势基本一致。当高差超过8.4 m时,实测值仍有增长,而计算值已达到稳定。对于d=4 mm、H1=4.2 m和d=5 mm、H1=2.1 m这两组方案,绝对误差率Er分别达到了17.90%和18.96%。值得注意是,此时管内流体雷诺数为2 481和2 503,意味流体处于过渡流,管内流态不稳定,通过巴尔公式计算的沿程阻力比实际环境下的更大。除了上述提及的,其余方案的绝对误差率Er均低于10%。
图 5为H0=8.25 m时各管径试验值与计算值,两者的整体吻合度较高。可以看出,实测流速随着高差的增大而增加,当H1≥4.2 m时,实测值增长幅度缓慢,而计算值已经达到稳定; 当处于过渡流时,例如,方案d=5 mm、H1=2.1 m的绝对误差率Er达到了16.81%。
图 6为H0=9.15 m时各管径试验值与计算值结果和误差率,曲线的变化趋势基本一致。存在的问题如下:1)方案d=5 mm时,H1=3.3、4.2、8.4、16.8 m,绝对误差率Er分别为13.31%、12.91%、12.89%、13.07%。这4个方案雷诺数为2 479~2 491,此时管内为过渡流,计算值小于实测值,意味着基于巴尔公式计算下的阻力比流体在实际环境中受到的更大; 2)对于d=3 mm时H1=0.6、1.2、1.5 m和d=4 mm时H1=0.6、1.2 m这5个方案,误差率Er分别为40%、38%、40%、29%、33%。实测流速值较小,均小于0.2 m/s,引入无量纲雷诺数Re进行分析,这种情况下Re较小(Re < 350),虹吸管内液体的流态为层流。
通过试验对比,巴尔公式结合修正伯努利计算方法将绝大部分方案的计算误差率Er控制在10%以内,说明该方法是合理的; 但是,针对部分方案也出现了较高的误差,主要源自两方面:1) H0=9.15 m条件下,当水头差H1较小时,3、4 mm虹吸管流速较小,计算值明显大于实测值,且最大误差率Er为40.38%。所以,在小管径高扬程低高差情况下,式(4)仍存在不足,需对流速的计算方式进行修正; 2)当虹吸管内液流处于层流与湍流之间的过渡流时,计算值的最大绝对误差率Er达19%,且均为负误差率,这表明通过巴尔公式计算的沿程阻力比实际流体环境中的大。
3 流速计算误差修正方法 3.1 高扬程低水头差流速计算误差原因与修正管壁附近存在一黏性不能忽略的边界层,导致圆管层流断面流速分布不均匀。对于3、4 mm的小管径虹吸管,本身管径较小,其边界层的作用在流速较小时更加明显,导致理论计算值与实测值之间存在一定的误差,需要对式(4)进行修正。
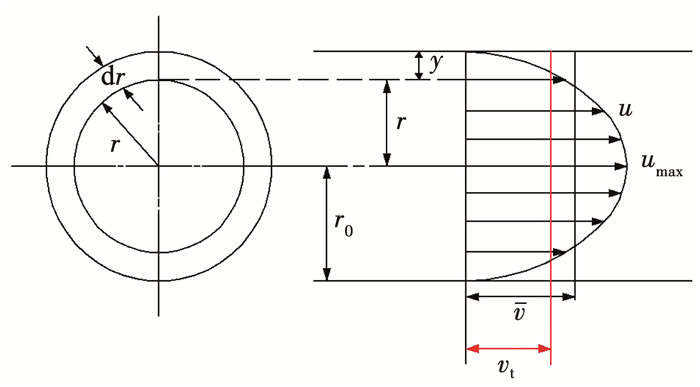
通过分析可知,高误差率方案均为高扬程(H0≥9.15 m)低水头差,实测值均小于计算值,且绝对误差率Er最高达40%,这表明流体流动过程中受到的黏滞作用更明显。圆管层流的流速分布并不均匀,呈以管轴为中心的旋转抛物面分布[26]。简化计算过程,截取二维过流断面,如图 7所示,对整个过流断面进行平均水头损失的计算,推导新的理论计算公式。
|
图 7 层流断面示意 Fig. 7 Schematic diagram of laminar flow section |
圆管层流理论由哈根和泊肃叶提出,二维断面流速分布如下[26]
| $ u=u_{\max }\left(1-\frac{r^2}{r_0^2}\right) $ | (11) |
式中:r为到管轴中心的距离,r0为虹吸管半径,umax为断面最大流速。
| $ u_{\max }=\frac{g J}{4 v} r^2 $ | (12) |
式中:υ为运动黏度,g为重力加速度,J为水力坡降,且最大流速umax位于管轴处。
水力坡降是沿水流方向单位渗透途径上的水头损失,与沿程水头损失和沿程长度有关。在圆管层流中沿程水头损失与平均流速的一次方成正比,即
| $ h_{\mathrm{f}}=\frac{32 \mu l}{\rho g d^2} v $ | (13) |
式中:μ为水的黏滞系数,v为平均流速,l为管长。
将水力坡降
| $ u_{(r)}=\frac{8}{d^2}\left(r_0^2-r^2\right) v $ | (14) |
通过式(14),层流圆管断面不同位置的水头损失hf可表示为
| $ h_{\mathrm{f}(r)}=\frac{32 v l}{g d^2} u_{(r)} $ | (15) |
对不同位置的水头损失进行积分,可得整个断面的平均沿程水头损失,即
| $ \bar{h}_{\mathrm{f}}=\frac{\int\limits_{-r_0}^{r_0} h_{\mathrm{f}(r)} \mathrm{d} r}{2 r} $ | (16) |
将式(14)、(15)代入式(16),可得修正后的流速计算公式,即
| $v_{\mathrm{c}}=\frac{g d^5 \bar{h}_{\mathrm{f}}}{256 v l \int\limits_{-r_0}^{r_0}\left(r_0^2-r^2\right) \mathrm{d} r}=\frac{3 g d^2 \bar{h}_{\mathrm{f}}}{128 v l} $ | (17) |
针对细管径高扬程低水头差条件下边界层作用导致计算方法不适用的问题,提出的式(17)将在后续章节中用于修正计算流速来降低与实测值之间的误差。
3.2 过渡流计算误差修正过渡流的研究一直是流体力学领域的重大难题。当处于过渡流时,管内流态混乱,无法精确计算沿程水头损失系数λ。通过巴尔公式对流速进行迭代运算的计算值小于实测值,表明计算过程中的沿程阻力比管内实际环境中的更大。表 2为8组处于过渡流时的方案,列出各方案计算和实测的流速、雷诺数和沿程水头损失系数。由表 2可知,高误差率方案计算值的雷诺数Rec均处于2 000~2 200,当下临界雷诺数Re≈2 100时,流态由层流逐渐向湍流开始过渡。此时,基于巴尔公式的计算存在一定的误差,考虑在巴尔公式中引入折减系数a对临界雷诺区(2 000≤Rec≤2 200)的方案进行重新迭代计算。
| 表 2 高误差率方案物理参数统计 Tab. 2 Statistics of physical parameters of schemes with high error rates |
由表 2可知,处于临界雷诺区时,计算值的沿程水头损失系数明显大于实测值的沿程水头损失系数,这是由巴尔公式计算的局限性导致的。对两者进行相关性分析,发现λt 与λc的比均在0.7左右,可用下式表示:
| $ \lambda_{\mathrm{t}} \approx 0.71 \lambda_{\mathrm{c}} $ | (18) |
将折减系数a=0.71引入式(8)中,新的经验巴尔公式如下:
| $ \lambda=0.71\left[\frac{1}{-2 \lg \left(\frac{\varDelta}{3.7 d}+\frac{5.1286}{R e^{0.89}}\right)}\right]^2, 2000 \leqslant R e_{\mathrm{c}} \leqslant 2200 $ | (19) |
重新审视计算过程,需对计算值的雷诺数进行判断验证。当2 000≤Rec≤2 200时,在巴尔公式中引入折减系数a进行重新运算。最后,新的计算流程如图 8所示。
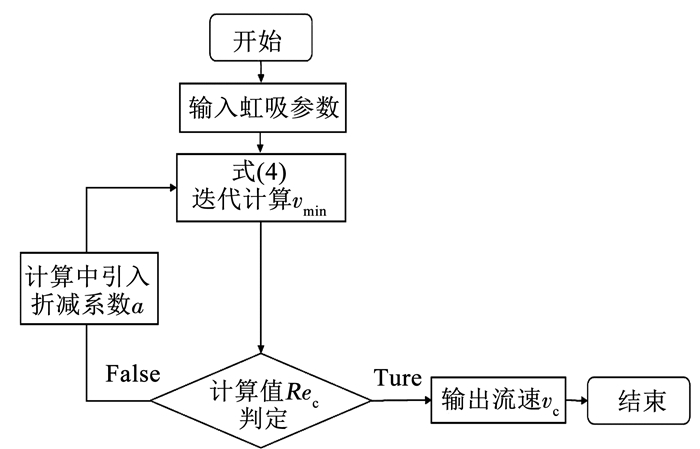
|
图 8 过渡流计算流程 Fig. 8 Transition flow calculation process |
采用提出的修正计算方法,获得各管径在不同扬程下的计算值和实测值,如图 9(a)~(d)所示。表 3为修正前后的绝对误差率对比,高扬程低水头差情况下,整体的绝对误差率Er从29%~40%降低至0~6%,对于过渡流方案的绝对误差率Er均控制在5%以下。结果表明,计算值和实测值之间的吻合程度较高,具有较好的一致性,有效提高了计算精度。

|
图 9 虹吸流速修正计算值与实测值 Fig. 9 Comparison between measured values of siphon velocity and calculated values by correction method |
| 表 3 计算值修正前后误差对比 Tab. 3 Comparison of errors before and after correction of calculated values |
对不同工况下的虹吸流速展开研究,提出流速的修正计算公式,有效提高了细管径(d≤5 mm)虹吸流速的计算精度,主要结论如下:
1) 基于虹吸流动过程的分析,确定了流速计算的参数和适用于虹吸迭代运算的沿程水头损失系数计算公式,并通过物理试验验证了其合理性。
2) 发现高扬程低水头差虹吸流速计算误差较大是由于忽略了管壁边界层作用,进而提出了利用断面平均水头损失反映边界层作用影响的虹吸圆管层流流速计算公式,物理试验表明,公式修正后绝对误差率Er从最大的40%降低到10%以内。
3) 针对过渡流(2 000≤Rec≤2 200),引入折减系数a修正巴尔公式,物理试验表明,该修正公式的绝对误差率Er在6%以内,修正效果良好。
| [1] |
王塞, 邓建辉, 陈菲, 等. "10 · 10"西藏白格滑坡运动特征反演分析[J]. 哈尔滨工业大学学报, 2022, 54(2): 162. WANG Sai, DENG Jianhui, CHEN Fei, et al. Inverse analysis of motion characteristics of "10 · 10" Baige landslide in Tibet[J]. Journal of Harbin Institute of Technology, 2022, 54(2): 162. DOI:10.11918/202009039 |
| [2] |
宋享桦, 谭勇, 张生杰. 暴雨气候下砂土边坡植被护坡模型试验研究[J]. 哈尔滨工业大学学报, 2021, 53(5): 123. SONG Henghua, TAN Yong, ZHANG Shengjie. Experimental study on vegetation slope protection model of sandy slope under rainstorm climate[J]. Journal of Harbin Institute of Technology, 2021, 53(5): 123. DOI:10.11918/201908166 |
| [3] |
WEI Z, WANG D, XU H, et al. Clarifying the effectiveness of drainage tunnels in landslide controls based on high-frequency in-site monitoring[J]. Bulletin of Engineering Geology and the Environment, 2020, 79(7): 3289. DOI:10.1007/s10064-020-01769-z |
| [4] |
TOHARI A, WIBAWA S, KOIZUMI K, et al. Effectiveness of siphon drainage method for landslide stabilization in a tropical volcanic hillslope: a case study of Cibitung Landslide, West Java, Indonesia[J]. Bulletin of Engineering Geology and the Environment, 2021, 80(3): 2101. DOI:10.1007/s10064-020-02093-2 |
| [5] |
ALOI F, PIRONE M, URCIUOLI G. Numerical investigation of small-and medium-diameter drain wells to stabilise deep landslides[J]. Acta Geotechnica, 2019, 14(4): 1065. DOI:10.1007/s11440-018-0688-8 |
| [6] |
许欢, 尚岳全, 徐浩迪, 等. 水平排水孔地下水位线附近淤堵机理分析[J]. 防灾减灾工程学报, 2019, 39(6): 961. XU Huan, SHANG Yuequan, XU Haodi, et al. Analysis of siltation mechanism near the groundwater level of horizontal drainage holes[J]. Journal of Disaster Prevention and Reduction Engineering, 2019, 39(6): 961. DOI:10.13409/j.cnki.jdpme.2019.06.011 |
| [7] |
尚岳全, 蔡岳良, 魏振磊, 等. 滑坡虹吸排水方法[J]. 工程地质学报, 2015, 23(4): 706. SHANG Yuequan, CAI Yueliang, WEI Zhenlei, et al. Siphon drainage method of landslide[J]. Journal of Engineering Geology, 2015, 23(4): 706. DOI:10.13544/j.cnki.jeg.2015.04.018 |
| [8] |
汪磊, 尚岳全, 吕俊俊, 等. 虹吸排水抗淤堵能力模型试验与理论分析[J]. 中南大学学报(自然科学版), 2019, 50(2): 384. WANG Lei, SHANG Yuequan, LV Junjun, et al. Model test and theoretical analysis of anti silting capacity of siphon drainage[J]. Journal of Central South University (Natural Science Edition), 2019, 50(2): 384. DOI:10.11817/j.issn.1672-7207.2019.02.018 |
| [9] |
吴纲, 谢威, 严鑫, 等. 虹吸水流作用下的土柱运动特性及虹吸管道防淤堵措施[J]. 吉林大学学报(地球科学版), 2019, 49(5): 1398. WU Gang, XIE Wei, YAN Xin, et al. Movement characteristics of soil column under siphon flow and anti silting measures of siphon pipeline[J]. Journal of Jilin University (Geoscience Edition), 2019, 49(5): 1398. DOI:10.13278/j.cnki.jjuese.20180138 |
| [10] |
CAI Y, SUN H, SHANG Y, et al. Air accumulation in high-lift siphon hoses under the influence of air dissolution and diffusion[J]. Journal of Zhejiang University: Science A, 2015, 16(9): 760. DOI:10.1631/jzus.A1400358 |
| [11] |
CAI Y, SUN H, SHANG Y, et al. An investigation of flow characteristics in slope siphon drains[J]. Journal of Zhejiang University: Science A, 2014, 15(1): 22. DOI:10.1631/jzus.A1300178 |
| [12] |
孙红月, 熊晓亮, 尚岳全, 等. 边坡虹吸排水管内空气积累原因及应对措施[J]. 吉林大学学报(地球科学版), 2014, 44(1): 278. SUN Hongyue, XIONG Xiaoliang, SHANG Yuequan, et al. Causes of air accumulation in slope siphon drainage pipe and countermeasures[J]. Journal of Jilin University(Geoscience Edition), 2014, 44(1): 278. DOI:10.13278/j.cnki.jjuese.201401205 |
| [13] |
熊晓亮, 孙红月, 张世华, 等. 高扬程虹吸保障条件分析与合理管径选择数值模拟[J]. 吉林大学学报(地球科学版), 2014, 44(5): 1595. XIONG Xiaoliang, SUN Hongyue, ZHANG Shihua, et al. Analysis of high lift siphon support conditions and numerical simulation of reasonable pipe diameter selection[J]. Journal of Jilin University (Geoscience Edition), 2014, 44(5): 1595. DOI:10.13278/j.cnki.jjuese.201405202 |
| [14] |
潘攀. 黑方台滑坡机理及防治对策研究[D]. 杭州: 浙江大学, 2017 PAN Pan. Study on mechanism and control counter measures of Heifangtai landslide[D]. Hangzhou: Zhejiang University, 2017 |
| [15] |
吴显. 虹吸排水方法在横山路滑坡治理中的应用[D]. 杭州: 浙江大学, 2019 WU Xian. Application of siphon drainage method in Hengshan Road landslide treatment[D]. Hangzhou: Zhejiang University, 2019 |
| [16] |
YU Y, SHEN M, SUN H, et al. Robust design of siphon drainage method for stabilizing rainfall-induced landslides[J]. Engineering Geology, 2019, 249: 186. DOI:10.1016/j.enggeo.2019.01.001 |
| [17] |
张永防, 张朝林. 湘黔线K93路堑滑坡虹吸排水工点的试验研究[J]. 路基工程, 1999(4): 26. ZHANG Yongfang, ZHANG Chaolin. Experimental study on siphon drainage construction site of K93 cutting landslide on Hunan Guizhou line[J]. Subgrade Engineering, 1999(4): 26. |
| [18] |
ZHENG J, GUO J, WANG J, et al. Calculation of the flow velocity of a siphon[J]. Physics of Fluids, 2021, 33(1): 17105. DOI:10.1063/5.0036443 |
| [19] |
MEI C, LIANG X, SUN H, et al. High-lift siphon flow velocity in a 4-mm siphon hose[J]. Journal of Zhejiang University: Science A, 2017, 18(6): 487. DOI:10.1631/jzus.A1600428 |
| [20] |
JUMPER W D, STANCHEV B. Towards explaining the water siphon[J]. The Physics Teacher, 2014, 52(8): 474. DOI:10.1119/1.4897583 |
| [21] |
ZHENG J, WANG J, GUO J, et al. A siphon drainage system with variable diameters for landslides: concept, calculation, and validation[J]. Journal of Hydrology, 2021, 597: 126305. DOI:10.1016/j.jhydrol.2021.126305 |
| [22] |
LI P, SEEM J E, LI Y. A new explicit equation for accurate friction factor calculation of smooth pipes[J]. International Journal of Refrigeration, 2011, 34(6): 1535. DOI:10.1016/j.ijrefrig.2011.03.018 |
| [23] |
方玉建, 袁寿其, 赵丽伟, 等. 负压输水光滑管道水力摩擦系数的试验研究[J]. 排灌机械工程学报, 2020, 38(1): 58. FANG Yujian, YUAN Shouqi, ZHAO Liwei, et al. Experimental study on hydraulic friction coefficient of negative pressure water delivery smooth pipeline[J]. Journal of Drainage and Irrigation Mechanical Engineering, 2020, 38(1): 58. DOI:10.3969/j.issn.1674-8530.18.0037 |
| [24] |
SHI S, WANG Y, QI Z, et al. Experimental investigation and new void-fraction calculation method for gas-liquid two-phase flows in vertical downward pipe[J]. Experimental Thermal and Fluid Science, 2021, 121: 110252. DOI:10.1016/j.expthermflusci.2020.110252 |
| [25] |
POTTER A, BARNES F H. The siphon[J]. Physics Education, 1971(6): 362. DOI:10.1088/0031-9120/6/5/005 |
| [26] |
赵振兴, 何建京. 水力学[M]. 2版. 北京: 清华大学出版社, 2010. ZHAO Zhenxing, HE Jianjing. Hydraulics[M]. 2nd ed. Beijing: Tsinghua University Press, 2010. |
| [27] |
MULLIN T. Experimental studies of transition to turbulence in a pipe[J]. Annual Review of Fluid Mechanics, 2011, 43(1): 1. DOI:10.1146/annurev-fluid-122109-160652 |
| [28] |
张俊, 张晓婷. 流体传输中流体阻力和水头损失的计算[J]. 流体传动与控制, 2011(4): 28. ZHANG Jun, ZHANG Xiaoting. Calculation of fluid resistance and head loss in fluid transmission[J]. Fluid Transmission and Control, 2011(4): 28. |
| [29] |
BARR D I H. Discussion of "Accurate explicit equation for friction factor"[J]. Journal of Hydraulics Division, 1977, 103(3): 334. DOI:10.1061/JYCEAJ.0004722 |
| [30] |
COLEBROOK F C. Turbulent flow in pipes with particular reference to the transition region between smooth and rough pipe laws[J]. Journal of the ICE, 1939, 11(4): 133. DOI:10.1680/ijoti.1939.13150 |
 2023, Vol. 55
2023, Vol. 55


