2. 岩土及地下工程教育部重点实验室(同济大学),上海 200092
2. Key Laboratory of Geotechnical and Underground Engineering (Tongji University), Ministry of Education, Shanghai 200092, China
盾构法作为一种机械化和智能化的施工工法,已被广泛地应用于软土地区的地铁、城市综合管廊等隧道工程建设中。在城市盾构隧道的修建和运营中,隧道的结构病害主要有开裂损伤、渗漏水和过大变形3类[1]。其中,过大的隧道横向收敛变形会引起接头张开、管片裂缝以及接头处出现渗漏水现象[2]。因此,预防和监测隧道横向收敛变形对保障隧道结构的安全十分重要。
造成隧道横向收敛变形的可能原因包括地质条件、上部堆载、邻近工程施工及结构病害养护不及时等[3]。理论上,盾构隧道的横向变形主要由管片接头处旋转产生的刚体位移和管片自身的弹塑性变形组成。王如路[4]认为接头转动影响盾构隧道收敛变形的比例更大。Blom[5]认为盾构隧道收敛变形主要来源于相邻管片在纵缝接头处的相对旋转导致的管片刚体位移。Zhang等[6]通过非线性多尺度分析方法对足尺隧道承载力试验进行分析时发现,由转角导致刚体位移引起的收敛变形甚至能占到隧道整体收敛变形的95%。王如路等[7]将管片环作为刚体考虑从收敛变形反推得到的纵缝接头转动量大于数值模拟结果,且误差在30%以内。曾格华[8]通过调整各衬砌块的大小来改变接头的位置,发现环内弯矩重分配,接头转角和管片环收敛变形值相应增大或缩小。谢家冲等[9]认为接头的相对转动主导衬砌的非线性响应。He等[10]认为接头的刚度增加会使轨道、隧道与地面振动响应增强。目前,接头变形引起的刚体位移对隧道总收敛变形的影响规律尚未有统一的认识。
另一方面,盾构隧道横向收敛变形目前常用的监测方法有全站仪量测、巴塞特(Bassett)隧道断面收敛自动量测系统、徕卡(TCA2003)测量机器人、BOTDA分布式光纤传感技术和位移传感器等[11]。相比之下,接头处的监测更加经济、方便且精度更高。因此,若能提出一种简易有效的基于接头转角推算隧道整体收敛变形的方法,评价接头对于隧道总体收敛变形的贡献与变化规律,有助于增强当前对于盾构隧道结构受力变形特性的认识,指导盾构隧道结构的优化设计及加固维护策略的制定。
本文引入接头转动引起隧道收敛变形占总收敛变形的比值作为评估接头转动对隧道收敛变形影响的指标,提出一种基于几何关系递推的针对纵缝接头转动引起盾构隧道横向收敛变形的简易计算方法。首先,通过与Zhang等[6]的多尺度混合分析结果对比验证了该算法的合理性。然后,应用该方法分析足尺管片试验及三维精细化数值模拟中通/错缝拼装、接头位置、衬砌纵向力大小、重复加卸荷等因素对纵缝接头在隧道收敛变形控制中影响的变化规律,从而进一步明确盾构隧道结构受力变形特性及控制接头变形的重要性。
1 简易算法介绍盾构隧道的横向收敛变形主要由接头转动引起的刚体位移和管片弹塑性变形两部分组成,目前尚未有通用的分析接头转动引起衬砌收敛变形的分离计算方法。王如路等[7]根据盾构隧道管片的转动变形特点,提出了一种通过收敛变形反推盾构隧道接头转动的几何计算方法,建立了接头与收敛变形量的对应关系,但该方法只适用于空间对称布置的衬砌。本文基于初始装配角度的几何递推关系,提出一种基于刚体位移假设,用于计算盾构隧道管片因接头转动产生收敛变形的简易算法,分离接头转动和管片弹塑性变形对收敛变形的贡献。
1.1 基本假设主要假设如下:1)盾构隧道管片的材料为均质; 2)管片材料各向同性; 3)管片材料连续; 4)管片在荷载作用下发生的变形相对于自身尺寸可忽略不计; 5)管片在接头处不发生脱离,接头处变形前后,内外侧处于同一平面,接头旋转中心在隧道轴线。
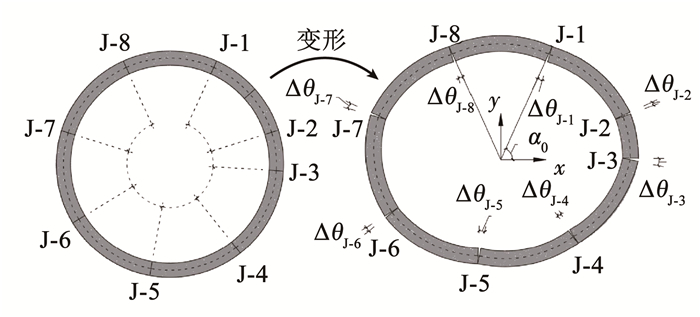
1.2 算法推导假设有一盾构隧道外径为R,内径为r,管片轴线处半径为R′,管片数n=8。隧道变形前后示意如图 1。将接头的旋转中心简化到管片中心半径处,如图 2所示。以内侧张开的转角为正、外侧张开的转角为负,从隧道顶部右侧第一个接头开始沿顺时针方向由式(1)求得各接头转角ΔθJ-i。并根据测量学中的附合导线方位角闭合差的计算原理,按照式(2)对转角进行修正。
| $\begin{gathered} \Delta \theta_{\mathrm{J}-i}^{\prime}=\frac{\delta_{\text {inner }}-\delta_{\text {outer }}}{d} \end{gathered} $ | (1) |
| $ \Delta \theta_{\mathrm{J}-i}=\Delta \theta_{\mathrm{J}-i}^{\prime}-\sum\limits_{k=1}^n \Delta \theta_{\mathrm{J}-k}^{\prime} \frac{\Delta \theta_{\mathrm{J}-i}^{\prime}}{\sum\limits_{k=1}^n\left|\Delta \theta_{\mathrm{J}-k}^{\prime}\right|} $ | (2) |
|
图 1 衬砌变形前后示意 Fig. 1 Diagram of lining before and after deformation |

|
图 2 简化计算的结构示意 Fig. 2 Structure diagram for simplified calculation |
式中:δinner、δouter分别为第i个接头内、外侧张开量(张开为正、闭合为负),Δθ′J-i、ΔθJ-i分别为修正前、后第i接头处的转角。在隧道顶部所在管片的圆心处建立直角坐标系。坐标系的y轴始终朝向初始拱顶位置。隧道顶点所在管片弦长为L1,顺时针方向相邻管片的弦长为L2,L2与x轴正方向的夹角(逆时针)为β1,接头J-1的旋转中心坐标设为J1=(x1, y1), 依次类推。各管片弦长计算公式如下:
| $ L_i=2 R^{\prime} \sin \left(\alpha_i / 2\right) $ | (3) |
各管片弦长方位角βi可通过下式计算:
| $ \begin{gathered} \beta_1=\frac{\pi+\alpha_2}{2}-\alpha_0-\Delta \theta_{\mathrm{J}-1} \end{gathered} $ | (4) |
| $ \beta_i=\frac{\alpha_i+\alpha_{i+1}}{2}+\beta_{i-1}-\Delta \theta_{\mathrm{J}-i}, i \in[2, n] $ | (5) |
根据测量学坐标闭合差的计算原则,接头坐标Jri=(xri, yri)的顺时针递推公式和闭合修正公式分别为
| $ J_{{\rm{r}}1}^\prime = \left( {x_{{\rm{r}}1}^\prime , y_{{\rm{r1}}}^\prime } \right) = (0, 0) $ | (6) |
| $ \begin{array}{l} J_{{\rm{r}i}}^\prime = \left( {x_{{\rm{r}}i}^\prime , y_{{\rm{r}}i}^\prime } \right) = \left( {x_{{\rm{r}}(i - 1)}^\prime + {L_i}\cos {\beta _{{\rm{r}}(i - 1)}}, y_{{\rm{r}}(i - 1)}^\prime } \right) - \\ \left. {{L_i}\sin {\beta _{{\rm{r}}(i - 1)}}} \right), i \in [2, n] \end{array} $ | (7) |
| $\begin{array}{l} {J_{{\rm{r}}i}} = J_{_{{\rm{r}}i}}^\prime + \left( { - x_n^\prime - {L_1}\cos {\beta _n}, - y_n^\prime + } \right.\\ \left. {{L_1}\sin {\beta _n}} \right)\frac{{{L_i}}}{{\sum\limits_{k = 1}^n {{L_i}} }}, i \in [1, n] \end{array} $ | (8) |
同理可得逆时针递推的接头坐标:
| $ J^{\prime}{ }_{1 n}=\left(x^{\prime}{ }_{\mathrm{1n}}, y^{\prime}{ }_{\mathrm{1n}}\right)=\left(-L_1 \cos \beta_{\mathrm{l}n}, L_1 \sin \beta_{\mathrm{l}n}\right) $ | (9) |
| $\begin{gathered} J_{1 i}^{\prime}=\left(x_{1 i}^{\prime}, y_{1 i}^{\prime}\right)=\left(x_{1(i+1)}^{\prime}-L_{1(i+1)} \cos \beta_{1 i}, y_{1(i+1)}^{\prime}+\right. \\ \left.L_{1(i+1)} \sin \beta_{1 i}\right), i \in[2, n-1] \end{gathered} $ | (10) |
| $ \begin{aligned} J_{1 i}= & J_{1 i}^{\prime}+\left(-x_2^{\prime}+L_2 \cos \beta_1, -y_2^{\prime}-\right. \\ & \left.L_2 \sin \beta_1\right) \frac{L_i}{\sum\limits_{k=1}^n L_i}, i \in[1, n] \end{aligned} $ | (11) |
计算可得矫正后第i个接头坐标:
| $ J_i=\left(J_{1 i}+J_{r i}\right) / 2 $ | (12) |
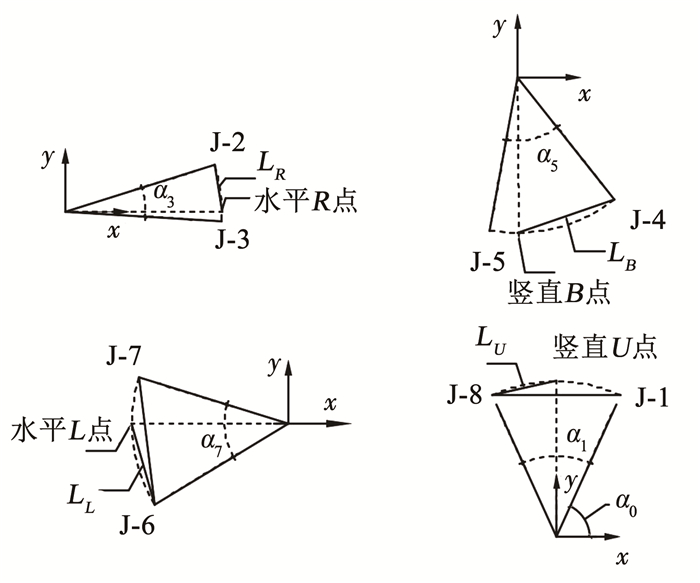
由小变形假设,管片块上质点之间的相对位移忽略不计。根据图 3定义的管片块的水平收敛测点L、R和竖向收敛测点U、B所在管片块的角度位置,作辅助弦(式(13)~(16))、对应方位角(式(17)~(19))以及定位测点坐标(式(21)~(24)),进而计算隧道收敛变形(式(25)、(26))。
| $ \begin{gathered} L_R=2 R^{\prime} \sin \left(\frac{\alpha_0-\alpha_2}{2}\right) \end{gathered} $ | (13) |
| $ L_U=2 R^{\prime} \sin \left(\frac{\alpha_0+\pi / 2-\alpha_2-\alpha_3-\alpha_4}{2}\right) $ | (14) |
| $ L_L=2 R^{\prime} \sin \left(\frac{\alpha_0+\pi-\sum\limits_{k=2}^6 \alpha_k}{2}\right) $ | (15) |
| $ L_B=2 R^{\prime} \sin \left(\frac{\alpha_0+3 \pi / 2-\sum\limits_{k=2}^8 \alpha_k}{2}\right) $ | (16) |
|
图 3 隧道顶部、底部、水平左右端测点示意 Fig. 3 Measuring points at top, bottom, and horizontal left and right waists of tunnel |
辅助弦长对应的方位角:
| $ \begin{gathered} \beta_R=\beta_2-\frac{\sum\limits_{k=2}^3 \alpha_k-\alpha_0}{2} \end{gathered} $ | (17) |
| $ \beta_B=\beta_4-\frac{\sum\limits_{k=2}^5 \alpha_k-\alpha_0-\pi / 2}{2} $ | (18) |
| $ \beta_L=\beta_6-\frac{\sum\limits_{k=2}^7 \alpha_k-\alpha_0-\pi}{2} $ | (19) |
| $\beta_U=\beta_8-\frac{\pi / 2-\alpha_0}{2} $ | (20) |
| $ \begin{aligned} U=\left(x_U, y_U\right)=\left(x_8+L_U \cos \beta_U, y_8-L_U \sin \beta_U\right) \end{aligned} $ | (21) |
| $ B=\left(x_B, y_B\right)=\left(x_4+L_B \cos \beta_B, y_4-L_B \sin \beta_B\right) $ | (22) |
| $L=\left(x_L, y_L\right)=\left(x_6+L_L \cos \beta_L, y_6-L_L \sin \beta_L\right) $ | (23) |
| $R=\left(x_R, y_R\right)=\left(x_2+L_R \cos \beta_R, y_2-L_R \sin \beta_R\right) $ | (24) |
由此可得,竖向收敛ΔV和水平收敛ΔH:
| $ \begin{aligned} \Delta V=y_U-y_B \end{aligned} $ | (25) |
| $ \Delta H=x_R-x_L $ | (26) |
上述方法可计算出衬砌上任意一点的坐标,从而获得管片任意两点间的相对距离。计算收敛变形的最后结果与第一个接头的坐标无关,仅与第一个接头在衬砌圆环上的装配角度α0有关。该方法不局限于管片和接头的数量及其空间布局,从刚体转动的角度出发计算结构在变形后的性态特征,具有一定的普适性,适用于装配式单圆盾构衬砌任意断面的接头影响分析。
1.3 算法验证Liu等[12]对上海地铁某盾构隧道进行足尺模型试验。试验加载的隧道环外径为6.2 m,内径为5.5 m,管片厚度为0.35 mm,宽度为1.2 mm。管片材料为C55级混凝土。一个完整的环包括一个顶部块(F块中心角为16.0°)、两个相邻块(L1和L2块中心角为65.0°)、两个标准块(B1和B2块中心角为65.0°)和一个底部块(D块中心角为84.0°)。相邻管节间采用两个5.8-M30螺栓连接。其加载千斤顶布置及荷载路径如图 4所示。Zhang等[6]通过多尺度混合分析方法分离了接头转动引起的收敛变形和管片变形产生的收敛变形。该试验中各工况荷载数值与接头的转角见文献[6]。

|
图 4 各级荷载工况千斤顶压力 Fig. 4 Jack force under each loading level |
基于足尺试验得到的转角数据和本文提出的简易算法,分离接头转动引起的收敛变形和管片弹塑性变形引起的收敛变形与接头转动引起的收敛变形占比(显著性评价指标),并与试验[12]及Zhang等[6]的计算结果对比,如图 5所示。本文提出的简易算法计算占比结果与Zhang等[6]的多尺度混合分析方法计算结果基本一致。本文所提出的方法与Zhang等[6]的计算结果在前3个加载步略有差异,这可能是因为本文所提出的方法对旋转角度的测量精度依赖性更高,在前3个加载步变形较小的工况下,刚体转动产生变形递推过程中的递推累积误差影响略大。但本文提出的简易算法仅需简单的几何和代数运算无需复杂的数值计算,实用性更强。

|
图 5 简易算法的收敛变形与实测及Zhang等[6]数据对比 Fig. 5 Comparison of convergence deformation obtained by simple algorithm with measured results and predicted data of Zhang et al.[6] |
上海“深隧”盾构隧道是排水调蓄隧道,具有复杂荷载变化工况与受力模式。Liu等[13]开展了单环和三环足尺试验,通过上述简易算法,计算仅在接头影响下的衬砌收敛变形量,与实际试验中测量的收敛变形量对比,可分析在单环(相当于通缝)和错缝三环试验中接头转动在复杂水土荷载工况下对衬砌收敛变形影响的差异。
2.1 试验概况上海“深隧”盾构隧道足尺模型试验包含单环足尺试验和三环足尺试验两部分[13],模拟排水调蓄隧道的作业工况。试验中加载的隧道环由8块预制管片组成,管片外径R=5.15 m,内径r=4.5 m,中心半径R′=4.825 m,环宽L=1.5 m。
由于依托项目为深埋排水调蓄盾构隧道,径向力荷载模拟的工况先从埋深0 m增加至埋深50 m,蓄水压从空管到满隧,再至满管50 m水压状态,然后排水至满隧、再到空管状态,最后按原路径卸载减少模拟埋深,模拟工况示意如图 6所示。

|
图 6 试验设计工况加载流程 Fig. 6 Design loading process of working condition test |
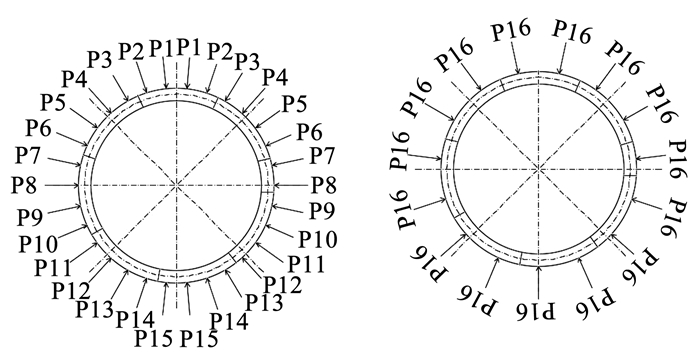
如图 7所示,衬砌的封顶块K圆心角为21°,邻接块L1、L2圆心角为48.25°,标准块B1~B5圆心角为48.5°,单环与三环初始装配角α0=65.75°。试验的径向加载装置包括“外压+内拉”组合的千斤顶试验加载系统模拟水土压力[14-15]。外框架上每隔12°一组共30组沿管片竖直方向对称布置外压千斤顶,由15套系统控制,编号依次为P1~P15;中心圆筒每24°一组内拉千斤顶由1套系统控制,千斤顶荷载编号P16。各加载等级下千斤顶荷载数值可参见Liu等[12]。
|
图 7 足尺试验径向加载示意 Fig. 7 Radial loading diagram of full-scale loading test |
管片变形数据采用两台Leica三维激光扫描仪进行采集,获得收敛变形值。在接头内外安装位移传感器进行监测,张开位移计采用自制角钢安装。基于内外侧的相对位移,通过式(1)计算得到接头处的相对转角。
2.2 单环足尺模型试验结果分析单环试验模型由一个整环组成。通过足尺盾构隧道试验中得到的接头转角代入简易算法,计算接头转角产生的收敛变形, 以及在试验中实际测量的衬砌收敛位移比值随荷载工况变化,结果如图 8所示。

|
图 8 单环足尺试验下的衬砌收敛变形 Fig. 8 Convergence deformation of tunnel lining in single-ring full-scale loading test |
在单环足尺模型试验中,衬砌接头转动引起盾构隧道的水平和竖直直径方向收敛变形,是衬砌的总收敛变形量主要影响因素。收敛变形的变化趋势与接头转角的变化趋势基本一致,但由接头转动产生的刚体位移占比变化趋势在卸荷阶段与收敛变形的变化趋势不同。在埋深增加阶段占比为50%~75%,而后随着内水头的升高进一步增大。
在内水增加和埋深减少阶段,接头转动引起的刚体位移占总收敛变形的比值大于1。这可能是因为:在内水头增加阶段,隧道衬砌的轴力逐渐减小,但弯矩基本不变[16],管片变形产生的轴向弹性变形及由此产生的收敛变形减小,挠曲变形几乎不变; 在埋深减少阶段,管片卸载,前续工况产生的管片自身弹性变形(包括挠曲和轴向变形)同样逐渐恢复。而对于接头来说,无论是内水头增加还是埋深减少的卸载,接头转动变形均较难恢复。事实上,这里还忽略了衬砌沿接头界面的滑移平动刚体位移,即实际工程中可能出现的错台和错缝。由于卸荷作用,衬砌间可能会发生与加载方向相反的滑移平动回位,从而产生与收敛监测位移相反的位移增量。在上述两种情况下,衬砌的收敛变形量可能出现小于转动的刚体位移产生的收敛变形,导致接头转动的收敛变形量比值大于1。
2.3 三环足尺模型试验研究三环试验模型由一个整环和前后两个半环组成。将足尺试验中测得的接头转角代入简易算法计算接头转动引起的收敛变形以及占衬砌收敛变形比,结果如图 9所示。与单环试验不同,三环足尺模型试验中,隧道接头转动引起的收敛变形占比较单环试验有较明显下降,而且虽然接头转动引起收敛变形占比仍然是在卸载阶段大于加载阶段,但接头变形占比对加卸载路径如单环敏感。这是因为错缝拼装下,管片纵向刚度提高、整体性更强,衬砌环间接头及较大的纵向力显著降低了接头转动引起的刚体位移。

|
图 9 三环足尺模型试验收敛变形 Fig. 9 Convergence deformation of tunnel lining in three-ring full-scale loading test |
隧道结构受力变形特性中接头变形的影响受到诸多因素的影响,由于试验条件有限以及足尺试验的成本巨大,无法对所有因素都进行系统分析,而精细化考虑接头的三维数值模型与试验有较好的一致性[17-18]。为进一步验证本文所提出简易算法的有效性,并明确封顶块位置、纵向力等因素对隧道收敛变形中接头转动行为的影响,基于上述上海“深隧”盾构隧道工程,建立深埋排水调蓄隧道衬砌的三维数值模型,按照相同的荷载工况进行隧道受力变形特性的研究。从数值模型中提取每个接头的转动量,利用简易算法计算仅由接头转动导致的收敛变形量,并与数值模型中衬砌总收敛变形量对比,分析不同工况下接头转动对管片环收敛变形的影响。
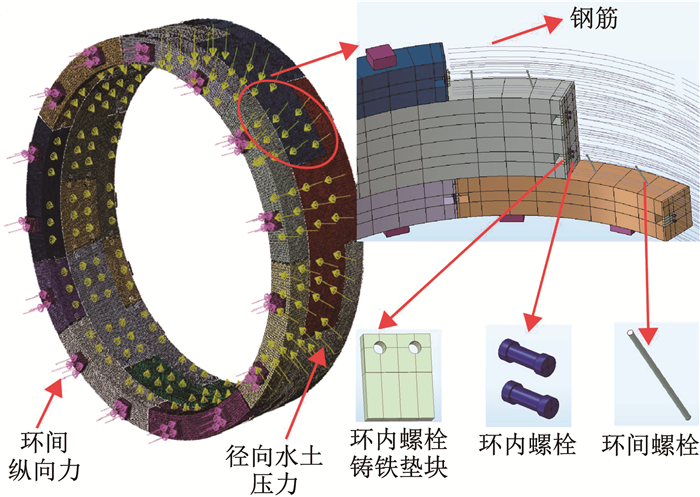
按照足尺试验的尺寸,精细化考虑管片接头、手孔、铸铁件、螺栓等构件的细部构造,以及接头与接头、螺栓与铸铁、衬砌环与衬砌环等构件间的连接相互作用,建立深埋排水调蓄隧道错缝三环(中间一个整环、上下两个半环)衬砌管片三维数值模型,环间错缝角度为23°,总体模型如图 10所示。
|
图 10 有限单元数值仿真模型 Fig. 10 Finite element numerical simulation model |
管片几何参数与2.1节描述一致。管片结构材料为均质C60混凝土,力学特征模拟采用塑性损伤本构模型[19-20]。模型参数参考余志武等[19]的研究成果。钢筋采用双折线弹塑性本构模型,弹性模量为200 GPa,泊松比为0.28,屈服强度为400 MPa,极限屈服强度为540 MPa。块间接头由8.8级M36短直螺栓通过铸铁件连接,环间接头通过8.8级M30长直螺栓连接。块间、环间接头螺栓均采用理想弹塑性本构模型,弹性模量为200 GPa,泊松比为0.28,屈服强度为640 MPa。管片、螺栓、垫块均采用实体单元模拟,单元类型为C3D8R。受力主筋采用桁架单元模拟,单元类型为T3D2。整个模型网格数量共计50万。界面模型通过设置接触面的接触关系进行模拟,面面接触关系在法向上为硬接触,禁止接触面网格相互侵入,切向上为依赖于法向力的摩擦因数,块间和环间接触面摩擦因数为0.2,螺栓和铸铁件摩擦因数为0.2,垫片和管片摩擦因数为0.03,铸铁与管片为绑定约束。
模型的边界条件如图 11所示。模型与足尺试验一致采用卧式加载,约束拱顶和拱底水平位移(ux=0)及两腰处的竖向位移(uy=0)。同时,在模型底部提供纵向力的垫块约束水平、竖向和纵向位移(ux=uy=uz=0),顶部垫块限制水平和竖向位移(ux=uy=0)。

|
图 11 数值模型的边界条件 Fig. 11 Boundary conditions of numerical model |
首先建立与三环足尺试验相同的数值模型,中间环的封顶块位置与图 7一致,相邻环错缝角度为23°,环间纵向力1 000 kN。如图 12所示,数值仿真模型获得的收敛变形与足尺试验监测的变形趋势一致大小接近,能较好地反映结构的受力变形特性,故可以采用该模型分析接头转动引起的隧道收敛变形特征。

|
图 12 仿真模型与足尺试验收敛变形对比 Fig. 12 Comparison between convergence deformation obtained in numerical simulation and in full-scale loading test |
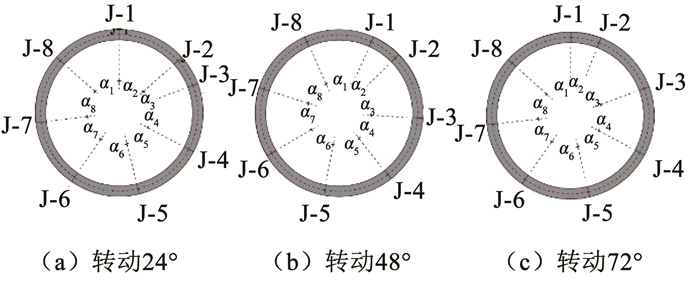
盾构隧道收敛变形与封顶块位置有关。在数值仿真模型中保持上下两半环位置不变,将隧道环封顶块位置逆时针旋转24°、48°、72°改变接头位置,如图 13所示。采用与三环足尺试验相同的加载路径。不同封顶块布局下接头旋转引起的隧道收敛变形与隧道总的收敛变形对比如图 14所示。
|
图 13 中间环接头位置变动工况 Fig. 13 Variation of key block positions of middle full ring |

|
图 14 不同封顶块位置下的收敛变形 Fig. 14 Variation of convergence deformation under different positions of key block |
由图 14可知,当封顶块逆时针转动24°时接头转动引起的水平变形占总水平变形的比例在埋深增加至内水增加阶段逐步从20%上升至40%,接头转动引起的竖向变形占总竖向变形的比例在埋深增加至内水增加阶段逐步从30%上升至60%左右,由于拱顶(最大正弯矩)位置存在竖向接头,接头旋转对于竖向变形的贡献大于接头旋转对水平变形的贡献。此外,在卸荷阶段,接头转动引起变形对整体变形的贡献逐步增大。这时因为隧道管片仍处于弹性阶段,其变形在卸载过程中逐步恢复,而由于块间和环间的摩擦约束作用,接头变形较难恢复,由接头转动导致的收敛变形占比逐步增大。其他两个接头布局工况也有类似的规律,但转动48°工况,拱顶位置无竖向接头,故接头变形对整体水平和竖向变形的贡献较为接近。转动72°工况接头转动对整体变形的贡献大于其他工况,这是因为此时在隧道顶部半环位置也是封顶块,接头密集,降低了环间的约束效应。
数值模拟的结果表明,封顶块的位置不仅会影响结构的整体变形,还会影响纵缝接头在隧道整体收敛变形中的贡献。
3.3 纵向力的影响研究纵向力指沿隧道掘进轴线方向的千斤顶顶推力,其大小影响管片环间摩擦力和接头刚度。在模型中每个纵向加载点设置1、300、600和1 000 kN,分析纵向力对接头引起的刚体转动位移在隧道整体收敛变形贡献的影响。
加载全过程中不同纵向力作用下管片收敛变形如图 15所示,加载全过程中不同纵向力下接头转动对整体竖向和水平收敛变形占比的影响如图 16和17所示。随着纵向力的增加,隧道整体收敛变形逐渐减小,但纵向力对收敛变形随加载工况的变化趋势影响不大。相同荷载等级下,随着纵向力的提高,接头转动引起的刚体位移在隧道总收敛变形中的占比也减小。这是因为纵向力有助于提高相邻环间的摩擦力和接头处的刚度,随着纵向力的增大,隧道环收敛变形接头处的转动受到的约束增大,管片表现出更强的整体性。

|
图 15 不同纵向力模型的衬砌收敛变形 Fig. 15 Convergence deformation of lining with different longitudinal force models |

|
图 16 不同纵向力下接头旋转引起的竖直收敛变形占比 Fig. 16 Ratio of vertical convergence deformation to overall deformation caused by joint rotation under different longitudinal forces |

|
图 17 不同纵向力下接头旋转引起的水平收敛变形占比 Fig. 17 Ratio of horizontal convergence deformation to overall deformation caused by joint rotation under different longitudinal forces |
本文基于纵缝接头初始装配角和几何递推关系提出一种计算接头转动对盾构隧道整体收敛变形贡献的简易算法,并与多尺度混合分析结果进行了对比验证。应用该简易算法对足尺试验和数值模拟结果进行分析,获得了通/错缝拼装、接头位置、衬砌纵向力大小、反复加卸荷等因素对纵缝接头旋转引起的收敛变形在隧道总收敛变形中占比的影响规律。主要结论如下:
1) 本文建立的纵缝接头转动引起收敛变形的简易算法可用于量化纵缝接头转动对衬砌变形的贡献。该算法适用于单圆形装配式衬砌,不受接头数量和空间分布的影响,具有一定的普适性。
2) 通缝拼装下,接头转动引起的收敛变形在管片总变形中占主导地位,采用本文提出的方法可近似估计管片整体收敛变形; 而错缝拼装显著降低了纵缝接头转动对衬砌整体收敛变形的贡献。在排水调蓄隧道中,内水压增大减少了衬砌轴力,从而提高了接头转动影响的占比。
3) 纵缝接头转动对整体收敛变形的贡献受接头位置的影响。接头越靠近弯矩最大处,接头转动对整体收敛变形的影响越大。
4) 卸载过程中由于块间和环间的摩擦约束作用,接头变形较难恢复,由纵缝接头转动导致的收敛变形占比逐步增大。
5) 纵向力的提高使得错缝拼装管片受到的相邻环管片摩擦约束增大,管片的整体性提升,故纵缝接头转动导致的收敛变形占比随纵向力的增加而减小。
6) 未来可结合修正惯用法、梁弹簧模型等方法进行设计方案的优化,或结合运维监测获得的整环收敛变形指导管片加固策略的制定。
| [1] |
王如路. 上海轨道交通隧道结构安全性分析[J]. 地下工程与隧道, 2011(4): 37. WANG Rulu. Structural safety analysis of Shanghai rail transit tunnel[J]. Underground Engineering and Tunnels, 2011(4): 37. DOI:10.13547/j.cnki.dxgcysd.2011.04.011 |
| [2] |
闫静雅, 王如路. 上海软土地铁隧道沉降及横向收敛变形的原因分析及典型特征[J]. 自然灾害学报, 2018, 27(4): 178. YAN Jingya, WANG Rulu. Cause analysis and typical characteristics of settlement and transverse convergence deformation of metro tunnel in soft ground in Shanghai[J]. Journal of Natural Disasters, 2018, 27(4): 178. DOI:10.13577/j.jnd.2018.0424 |
| [3] |
杨波, 谭勇. 土石混合体地层中基坑开挖对邻近既有隧道影响[J]. 哈尔滨工业大学学报, 2021, 53(11): 46. YANG Bo, TAN Yong. Influence of deep excavation on adjacent tunnel in soil-rock mixture[J]. Journal of Harbin Institute of Technology, 2021, 53(11): 46. DOI:10.11918/202005040 |
| [4] |
王如路. 上海软土地铁隧道变形影响因素及变形特征分析[J]. 地下工程与隧道, 2009(1): 1. WANG Rulu. Analysis of influencing factors and deformation characteristics of Shanghai soft soil railway tunnel[J]. Underground Engineering and Tunnels, 2009(1): 1. |
| [5] |
BLOM C. Design philosophy of concrete linings for tunnels in soft soils[M]. Delft: Delft University Press, 2002.
|
| [6] |
ZHANG J, MANG H, LIU X, et al. On a nonlinear hybrid method for multiscale analysis of a bearing-capacity test of a real-scale segmental tunnel ring[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2019, 43(14): 1343. DOI:10.1002/nag.2894 |
| [7] |
王如路, 张冬梅. 超载作用下软土盾构隧道横向变形机理及控制指标研究[J]. 岩土工程学报, 2013, 35(6): 1092. WANG Rulu, ZHANG Dongmei. Mechanism of transverse deformation and assessment index for shield tunnels in soft clay under surface surcharge[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(6): 1092. |
| [8] |
曾格华. 盾构隧道管片环接头布设方案优化研究[J]. 公路, 2019, 64(12): 312. ZENG Gehua. Optimization study on layout scheme of segment ring joint in shield tunnel[J]. Highway, 2019, 64(12): 312. |
| [9] |
谢家冲, 王金昌, 周高云, 等. 土体参数对隧道衬砌与土体共同作用影响分析[J]. 隧道建设(中英文), 2021, 41(增刊1): 247. XIE Jiachong, WANG Jinchang, ZHOU Gaoyun, et al. Influence of soil parameters on response of shield tunnel lining considering soil-structure interaction[J]. Tunnel Construction, 2021, 41(S1): 247. DOI:10.3973/j.issn.2096-4498.2021.S1.031 |
| [10] |
HE C, ZHOU S, DI H, et al. Effect of longitudinal joint on train-induced vibrations from subway shield-driven tunnels in a homogeneous half-space[J]. International Journal of Transportation Science and Technology, 2021, 11(2): 381. DOI:10.1016/j.ijtst.2021.05.001 |
| [11] |
王飞, 黄宏伟, 张冬梅, 等. 基于BOTDA光纤传感技术的盾构隧道变形感知方法[J]. 岩石力学与工程学报, 2013, 32(9): 1901. WANG Fei, HUANG Hongwei, ZHANG Dongmei, et al. Deformation sensing method of shield tunnel based on optical fiber sensing technology of BOTDA[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(9): 1901. DOI:10.3969/j.issn.1000-6915.2013.09.023 |
| [12] |
LIU X, BAI Y, YUAN Y. Experimental investigation of the ultimate bearing capacity of continuously jointed segmental tunnel linings[J]. Structure and Infrastructure Engineering, 2016, 12(10): 1364. DOI:10.1080/15732479.2015.1117115 |
| [13] |
LIU W, ZHANG Z, HUANG X, et al. Design and application of a mechanical loading system for a deeply-buried water-conveying shield tunnel lining test[C]//The Thirty-First KKHTCNN Symposium on Civil Engineering. Kyoto: [s. n.], 2018: 139
|
| [14] |
ZHANG Z, LIU W, ZHUANG Q, et al. A novel testing setup for determining the flexural properties of tunnel segmental joints: development and application[J]. Archives of Civil and Mechanical Engineering, 2019, 19(3): 724. DOI:10.1016/j.acme.2019.02.003 |
| [15] |
刘威, 王祺, 庄欠伟, 等. 深埋排水调蓄盾构隧道管片1∶ 1力学试验系统的研发与应用[J]. 中国公路学报, 2020, 33(2): 103. LIU Wei, WANG Qi, ZHUANG Qianwei, et al. Development and application of a 1∶ 1 mechanical testing system for deeply-buried water storage and sewage shield tunnel[J]. China Journal of Highway and Transport, 2020, 33(2): 103. DOI:10.3969/j.issn.1001-7372.2020.02.010 |
| [16] |
HUANG X, LIU W, ZHANG Z, et al. Exploring the three-dimensional response of a water storage and sewage tunnel based on full-scale loading tests[J]. Tunnelling and Underground Space Technology, 2019, 88: 156. DOI:10.1016/j.tust.2019.03.003 |
| [17] |
JIN Y, DING W, YAN Z, et al. Experimental investigation of the nonlinear behavior of segmental joints in a water-conveyance tunnel[J]. Tunnelling and Underground Space Technology, 2017, 68: 153. DOI:10.1016/j.tust.2017.05.018 |
| [18] |
张力, 封坤, 何川, 等. 盾构隧道管片接头三维精细化数值模拟研究[J]. 隧道建设(中英文), 2020, 40(8): 1169. ZHANG Li, FENG Kun, HE Chuan, et al. Three-dimensional refined simulation of segmental joint of shield tunnel[J]. Tunnel Construction, 2020, 40(8): 1169. DOI:10.3973/j.issn.2096-4498.2020.08.009 |
| [19] |
丁发兴, 余志武, 欧进萍. 混凝土单轴受力损伤本构模型[J]. 长安大学学报(自然科学版), 2008(4): 70. DING Faxing, YU Zhiwu, OU Jinping. Damage constitutive model for concrete under uniaxial stress conditions[J]. Journal of Chang'an University (Natural Science Edition), 2008(4): 70. DOI:10.3321/j.issn:1671-8879.2008.04.016 |
| [20] |
王威, 王冰洁, 罗麒锐, 等. 波纹钢板-混凝土界面黏结滑移性能试验[J]. 哈尔滨工业大学学报, 2022, 54(4): 141. WANG Wei, WANG Bingjie, LUO Qirui, et al. Bond-slip behavior of inter face between corrugated steel plate and concrete[J]. Journal of Harbin Institute of Technology, 2022, 54(4): 141. DOI:10.11918/202109036 |
 2023, Vol. 55
2023, Vol. 55


