2. 地质灾害防治与地质环境保护国家重点实验室(成都理工大学),成都 610059
2. Stake Key Laboratory of Geohazard Prevention and Geoenvironment Protection (Chengdu University of Technology), Chengdu 610059, China
在交通、水利、油气输送和城市管廊等基础设施中存在大量的上埋式涵洞工程,回填土固结沉降差常造成涵洞明显的竖向土压力集中,使得涵顶易发生纵向开裂[1],严重影响涵洞的实际工作性态。众多研究探讨了如何降低涵洞设计荷载以缓解顶部竖向土压力集中,杨锡武等[2]提出高填方涵洞的加筋桥减载法,郑俊杰等[3]建立加筋减载涵洞的力学模型,El Naggar等[4]采用PLAXIS2D讨论土工格栅搭接法的减载有效性,Kang等[5]基于现场实测和数值模拟分析ETI(embedded trench installation)技术的效率。
诱导减载(induced trench installation)是一种降低上埋式涵洞竖向土压力的重要方法,有别于加筋减载法,由于原理简单且实用性好已成为探讨涵洞高效减载途径的热点,包括:1)现场实测与模型试验。顾安全等[6]结合涵洞现场实测提出EPS板诱导减载法,Parker等[7]依据现场测试数据得出诱导减载法是有效可行的,Megui等[8]通过模型试验量测轮胎集料诱导减载涵洞的竖向土压力及分布,邓谦等[9]开展模型试验研究EPS板厚度的诱导减载影响。2)数值模拟。Witthoef等[10]建立FLAC2D数值模型讨论EPS板形状的诱导减载机制,Ni等[11]应用ABAQUS分析轮胎集料诱导减载涵洞的竖向土压力,张业勤等[12]采用FLAC3D模拟诱导减载涵洞和非减载涵洞的竖向土压力。3) 理论分析。王晓谋等[13]假定涵顶回填土应力分布与半无限均质线弹性变形体的应力分布相当,基于弹性理论获得诱导减载涵洞的竖向土压力计算公式;Qin等[14]考虑竖向土压力的水平向非均匀分布,建立诱导减载涵洞的竖向土压力解析解;Chen等[15]结合涵洞-回填土的刚度串联模型,提出诱导减载涵洞竖向土压力及基底压力的计算方法。
上述有关诱导减载涵洞的竖向土压力研究除现场实测外均假定(包括虽未明确但实际采用饱和土理论)回填土处于饱和状态。然而,工程实践中遇到的土体大多处于非饱和状态[16-18],非饱和土与饱和土在力学性能上存在显著差别,且实测数据表明, 基于饱和土理论的诱导减载涵洞竖向土压力计算偏于保守[19]。同时,涵洞上方内土柱与两侧外土柱间的固结沉降差使得非饱和回填土产生土拱效应。应考虑非饱和特性与土拱效应的共同影响,建立适用于非饱和回填土的诱导减载涵洞竖向土压力解答,以完善涵洞设计理论,拓展诱导减载法的应用范围。Fredlund等[20]采用双应力状态变量即净法向应力和基质吸力,基于Mohr-Coulomb准则建立了非饱和土的双应力状态变量强度理论,已在众多岩土问题分析中得到很好的实践和检验[21-23]。
为此,首先,基于非饱和土诱导减载涵洞的力学模型,以圆弧小主应力轨迹描述非饱和回填土拱效应,获得滑移面土压力系数的理论解答,继而由非饱和土的双应力状态变量强度理论确定滑移面摩擦切应力,建立诱导减载涵洞顶部的竖向土压力解析解,结合等沉面高度求解给出应用步骤,最后,与文献现场实测对比进行正确性和适用性验证,并定义减载率分析基质吸力及分布形式、吸力角、减载材料厚度和变形模量等的影响规律。
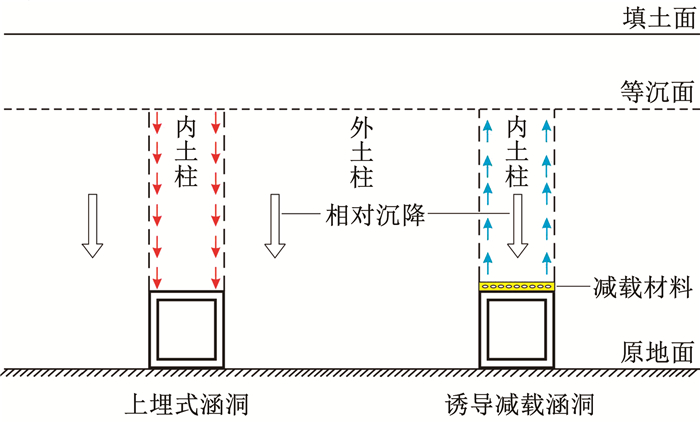
1 基本理论及假定 1.1 诱导减载法由于涵洞刚度远大于周围回填土的刚度,且假设原地基为不变形的刚性体,上埋式涵洞上方内土柱与两侧外土柱存在固结沉降差,并随填土高度的增加不断减小,直到等沉面处沉降相差为零,如图 1所示。
在等沉面高度以下,上埋式涵洞外土柱对内土柱产生向下的滑动摩擦力,呈现涵顶竖向土压力大于上覆土体自重的土拱负效应[24]。诱导减载法是在涵顶敷设足量压缩性强的减载材料(EPS板、轮胎集料、锯末层等),诱导涵顶内土柱沉降量增加而大于两侧外土柱的沉降量,使得外土柱对内土柱产生向上的滑动摩擦力。因此,诱导减载涵洞上方内土柱的自重通过滑动摩擦部分转移给两侧土体,涵顶竖向土压力因土拱正效应而小于上覆土体自重,以改善涵洞受力和降低设计荷载[19]。
减载材料铺设厚度有两方面要求[6]:减载材料压缩变形抵消内/外土柱因回填土自重而形成的沉降差,即消除刚性涵洞在回填土中引起的应力集中;诱导内土柱相对外土柱产生向下的沉降差,并按内土柱减载率计算减载材料铺设厚度。
1.2 力学模型与吸力分布在图 2中,诱导减载涵洞(外包尺寸,圆形取外径)及非饱和回填土处于平面应变状态,且竖直滑移面处非饱和回填土达到极限平衡。应注意的是,图 2为减载材料宽度B与涵洞宽度D相等的常见情形,此时内土柱宽度为减载材料宽度或涵洞宽度。对于工程中不同于此的实际情况,当B>D时内土柱宽度取为涵洞宽度D,当B < D时内土柱宽度取为减载材料宽度B。同时,设由涵顶算起的填土高度为H,等沉面到涵顶的距离即等沉面高度为Hc, 涵洞高度为h,减载材料厚度为t。

|
图 2 诱导减载涵洞力学模型 Fig. 2 Mechanical model of an induced trench installation culvert |
基质吸力及分布形式受降雨入渗、水分蒸发和地表植被等影响,工程应用时常简化为图 2沿深度减少至地下水位Dw处为零的线性分布[25-26]。自填土面算起深度z处的基质吸力(ua-uw)z为
| $ \left(u_{\mathrm{a}}-u_{\mathrm{w}}\right)_z=\left(u_{\mathrm{a}}-u_{\mathrm{w}}\right)_0\left(1-z / D_{\mathrm{w}}\right) $ | (1) |
式中:(ua-uw)0为填土面处的基质吸力即地表吸力。当Dw→∞时,线性吸力分布退化为更为简单的均匀吸力分布。
1.3 非饱和土强度公式相比非饱和土有效应力理论中有效应力参数的复杂性,非饱和土双应力状态变量理论因参数物理意义明确且可由直剪或三轴试验较容易测定而得到广泛应用。Fredlund等[20]基于净法向应力和基质吸力所建立的非饱和土双应力状态变量强度理论及其公式为
| $ \tau_{\mathrm{f}}=c^{\prime}+\left(\sigma-u_{\mathrm{a}}\right) \tan \varphi^{\prime}+\left(u_{\mathrm{a}}-u_{\mathrm{w}}\right) \tan \varphi^{\mathrm{b}} $ | (2) |
式中:τf为抗剪强度,c′为有效黏聚力,φ′为有效内摩擦角,φb为与基质吸力有关的吸力角,ua为孔隙气压力,uw为孔隙水压力,(ua-uw)为基质吸力,σ为总法向应力,(σ-ua)为净法向应力。
设ct=c′+(ua-uw)tan φb为非饱和土的总黏聚力,则式(2)变为
| $ \tau_{\mathrm{f}}=c_{\mathrm{t}}+\left(\sigma-u_{\mathrm{a}}\right) \tan \varphi^{\prime} $ | (3) |
采用圆弧小主应力轨迹描述涵洞上方非饱和回填土的拱效应,以获得考虑土拱效应的滑移面土压力系数表达式,继而根据填土高度与等沉面高度的相对大小,分别建立等沉面存在和不存在时诱导减载涵洞顶部的竖向土压力解析解。
2.1 滑移面土压力系数随着内/外土柱固结产生差异沉降,土拱效应逐渐发挥,薄层单元小主应力的方向发生旋转,直至达到图 3(a)的极限平衡状态,其中(σ1-ua)为大主应力、(σ3-ua)为小主应力。忽略涵洞竖向土压力沿水平向的非线性变化,薄层单元上各点的主应力大小相同,但各点的主应力方向发生了不同程度的旋转。假定所形成的小主应力轨迹为图 3(b)虚线所示的圆弧,其切线代表该薄层单元某点的小主应力方向,大/小主应力相互垂直,且中点处小主应力方向为水平。

|
图 3 薄层单元应力状态及小主应力轨迹 Fig. 3 Stress state of a thin layer element and trajectory of minor principal stress |
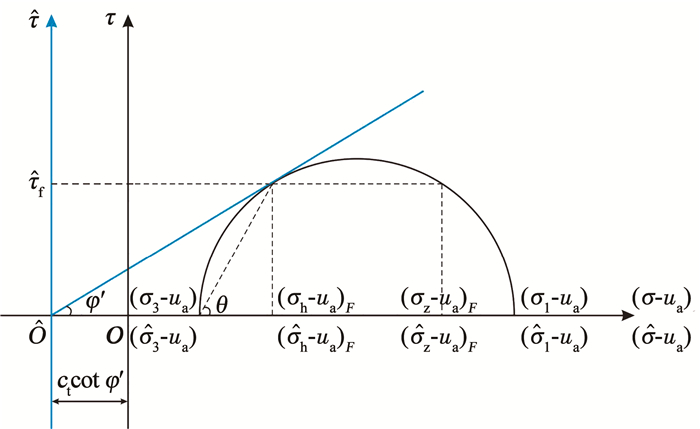
将图 3(a)的纵坐标向左平移ctcot φ′,并绘制等沉面以下深度z处(H-Hc≤z≤H)滑移面点F的Mohr应力圆,如图 4所示,其中,(σh-ua)F、(σz-ua)F分别为旧坐标系下点F的水平应力和竖向应力。
|
图 4 坐标平移后点F的Mohr应力圆 Fig. 4 Mohr stress circle of point F after coordinate translation |
新/旧坐标系满足
| $ \left\{\begin{array}{l} \left(\hat{\sigma}-u_{\mathrm{a}}\right)=\left(\sigma-u_{\mathrm{a}}\right)+c_{\mathrm{t}} \cot \varphi^{\prime} \\ \hat{\tau}=\tau \end{array}\right. $ | (4) |
式中(
在新坐标系下,由图 4中的Mohr应力圆得点F的水平应力(
| $ \left(\hat{\sigma}_{\mathrm{h}}-u_{\mathrm{a}}\right)_F=\left(\hat{\sigma}_1-u_{\mathrm{a}}\right)\left(\cos ^2 \theta+\frac{1}{N} \sin ^2 \theta\right) $ | (5) |
式中:θ为点F的大主应力作用面与水平面的夹角,且θ=45°+φ′/2;N为新坐标系下大主应力(
同理,由图 3(b)中同一薄层单元上点m的Mohr应力圆,拓展得点m的竖向应力(
| $ \left(\hat{\sigma}_{\mathrm{z}}-u_{\mathrm{a}}\right)_m=\left(\hat{\sigma}_1-u_{\mathrm{a}}\right)\left(\sin ^2 \psi+\frac{1}{N} \cos ^2 \psi\right) $ | (6) |
式中:ψ为点m的大主应力作用面与水平面的夹角,且θ≤ψ≤180°-θ。
由式(6)积分出薄层单元的竖向合力,再除以薄层单元宽度B=2Rcos θ(其中,R为圆弧小主应力轨迹的半径),得平均竖向应力(
| $ \left(\hat{\sigma}_{\mathrm{z}}-u_{\mathrm{a}}\right)=\left(\hat{\sigma}_1-u_{\mathrm{a}}\right)\left(1-\frac{N-1}{3 N} \cos ^2 \theta\right) $ | (7) |
滑移面土压力系数为滑移面处水平应力与平均竖向应力的比值[27-28],用以反映滑移面内侧土体的受挤程度。由式(5)和(7)得新坐标系下的滑移面土压力系数
| $ \hat{K}=\frac{\left(\hat{\sigma}_{\mathrm{h}}-u_{\mathrm{a}}\right)_F}{\left(\hat{\sigma}_{\mathrm{z}}-u_{\mathrm{a}}\right)}=\frac{\left(\sigma_{\mathrm{h}}-u_{\mathrm{a}}\right)_F+c_1 \cot \varphi^{\prime}}{\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)+c_{\mathrm{t}} \cot \varphi^{\prime}}=\\ \;\;\;\;\;\frac{N \cos ^2 \theta+\sin ^2 \theta}{N-(N-1) \cos ^2 \theta / 3} $ | (8) |
于是,由式(8)得旧坐标系下滑移面处的水平应力(σh-ua)F为
| $ \left(\sigma_{\mathrm{h}}-u_{\mathrm{a}}\right)_F=\hat{K}\left[\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)+c_{\mathrm{t}} \cot \varphi^{\prime}\right]-c_{\mathrm{t}} \cot \varphi^{\prime} $ | (9) |
将式(9)两边同除以竖向应力(σz-ua)得旧坐标系下滑移面土压力系数K,其大小随着竖向应力(σz-ua)、总黏聚力ct(有效黏聚力c′+吸附黏聚力(ua-uw)tan φb,后者反映土体非饱和特性影响)和有效内摩擦角φ′的变化而变化。
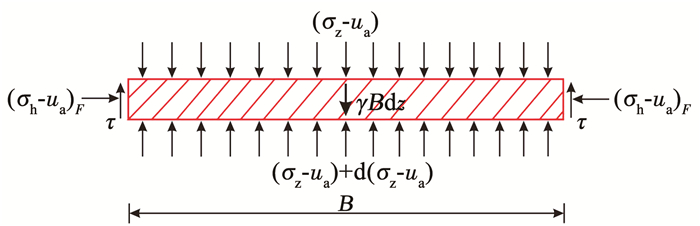
2.2 竖向土压力在图 2深度z处(H-Hc≤z≤H),取厚度为dz、纵向单位长度的薄层单元进行旧坐标系下内土柱受力分析,如图 5所示,其中,γ为非饱和回填土的重度。根据薄层单元的竖向力平衡得
| $ \gamma B \mathrm{d} z-2 \tau \mathrm{d} z-B \mathrm{d}\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)=0 $ | (10) |
|
图 5 内土柱薄层单元受力分析 Fig. 5 Force analysis of a thin layer element from inner soil column |
式中τ为滑移面处的摩擦切应力。
由于在滑移面处回填土处于极限平衡,摩擦切应力τ达到回填土抗剪强度τf。结合式(1)、(2)和(9)得摩擦切应力τ为
| $ \begin{array}{l} \tau=\hat{K} \tan \varphi^{\prime}\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)+\hat{K} c^{\prime}+ \\ \;\;\;\;\;\;\hat{K}\left(u_{\mathrm{a}}-u_{\mathrm{w}}\right)_0\left(1-\frac{z}{D_{\mathrm{w}}}\right) \tan \varphi^{\mathrm{b}} \end{array} $ | (11) |
将式(11)代入式(10),整理得
| $ \begin{array}{c} \frac{\mathrm{d}\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)}{\mathrm{d} z}+\frac{2 \hat{K} \tan \varphi^{\prime}}{B}\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)= \\ \frac{2 \hat{K}\left(u_{\mathrm{a}}-u_{\mathrm{w}}\right)_0 \tan \varphi^{\mathrm{b}}}{B D_{\mathrm{w}}} z- \\ \frac{2 \hat{K} c^{\prime}+2 \hat{K}\left(u_{\mathrm{a}}-u_w\right)_0 \tan \varphi^{\mathrm{b}}}{B}+\gamma \end{array} $ | (12) |
可见,式(12)为一阶非齐次的线性微分方程。当存在等沉面时,结合边界条件z=H-Hc时(σz-ua)=γ(H-Hc),积分得诱导减载涵洞的竖向土压力解析解为
| $ \begin{aligned} \left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)= & C_1\left[\mathrm{e}^{C_2\left(H-H_{\mathrm{c}}-z\right)}-1\right]+\left(H-H_{\mathrm{c}}\right) \times \\ & \left(\gamma-C_3\right) \mathrm{e}^{C_2\left(H-H_{\mathrm{c}}-z\right)}+C_3 z \end{aligned} $ | (13) |
式中
| $ \begin{array}{c} C_1=\frac{\frac{B\left(u_{\mathrm{a}}-u_\mathrm{w}\right)_0 \tan \varphi^{\mathrm{b}}}{D_{\mathrm{w}}}-\left[\gamma B-2 \hat{K} c^{\prime}-2 \hat{K}\left(u_{\mathrm{a}}-u_{\mathrm{w}}\right)_0 \tan \varphi^{\mathrm{b}}\right] \tan \varphi^{\prime}}{2 \hat{K} \tan ^2 \varphi^{\prime}} \\ C_2=\frac{2 \hat{K} \tan \varphi^{\prime}}{B}, C_3=\frac{\left(u_{\mathrm{a}}-u_{\mathrm{w}}\right)_0 \tan \varphi^{\mathrm{b}}}{D_{\mathrm{w}} \tan \varphi^{\prime}} \end{array} $ |
当不存在等沉面时,结合边界条件z=0时(σz-ua)=0,积分得诱导减载涵洞的竖向土压力解析解为
| $ \left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)=C_1\left(\mathrm{e}^{-C_2 z}-1\right)+C_3 z $ | (14) |
当z=H时,忽略减载材料的重量和变形后的剩余厚度,由式(13)和(14)得线性吸力下诱导减载涵洞顶部的竖向土压力(σz-ua)z=H为
存在等沉面时(H>Hc)
| $ \begin{aligned} \left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)_{z=H}= & C_1\left(\mathrm{e}^{-C_2 H_{\mathrm{c}}}-1\right)+\left(H-H_{\mathrm{c}}\right) \times \\ & \left(\gamma-C_3\right) \mathrm{e}^{-C_2 H_{\mathrm{c}}}+C_3 H \end{aligned} $ | (15) |
不存在等沉面时(H≤Hc)
| $ \left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)_{z=H}=C_1\left(\mathrm{e}^{-C_2 H}-1\right)+C_3 H $ | (16) |
对于均匀吸力分布,在式(15)和(16)中存在
| $ \begin{array}{c} C_1=\frac{-\gamma B+2 \hat{K} c^{\prime}+2 \hat{K}\left(u_{\mathrm{a}}-u_{\mathrm{w}}\right)_0 \tan \varphi^{\mathrm{b}}}{2 \hat{K} \tan \varphi^{\prime}} \\ C_2=\frac{2 \hat{K} \tan \varphi^{\prime}}{B}, C_3=0 \end{array} $ |
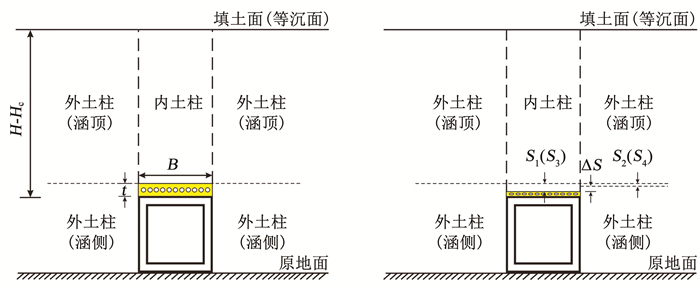
图 6给出了H=Hc时诱导减载涵洞回填土和减载材料的变形情况。其中,S1为内土柱底部的平均沉降量,亦可看作是减载材料的压缩量S3;S2代表涵顶外土柱底部的平均沉降量,亦可看作是涵侧外土柱顶部的平均沉降量S4,并忽略土拱效应对外土柱荷载与涵侧外土柱沉降的影响。
|
图 6 等沉面高度计算 Fig. 6 Height calculation of an equal settlement plane |
内土柱与涵顶外土柱底部的沉降差ΔS=S1-S2可表示为
| $ \Delta S=\frac{1}{E}\left[\frac{\gamma H_{\mathrm{c}}^2}{2}+\frac{C_1}{C_2}\left(\mathrm{e}^{-C_2 H_{\mathrm{c}}}-1\right)+C_1 H_{\mathrm{c}}-\frac{1}{2} C_3 H_{\mathrm{c}}^2\right] $ | (17) |
式中E为回填土的变形模量。
同时,ΔS可表示为减载材料压缩量S3与涵侧外土柱顶部平均沉降量S4之差,即
| $ \Delta S=\frac{t}{E_{\mathrm{p}}}\left[C_1\left(\mathrm{e}^{-C_2 H_{\mathrm{c}}}-1\right)+C_3 H_{\mathrm{c}}\right]-\frac{\gamma H_{\mathrm{c}}(h+t)}{E} $ | (18) |
式中Ep为减载材料的变形模量。
由式(17)与(18)相等建立关于等沉面高度Hc的超越方程,采用Newton-Raphson法求解。
3 应用与验证 3.1 应用步骤本文所建立的非饱和土诱导减载涵洞顶部的竖向土压力解析解即式(15)和(16),可合理解释基质吸力及分布形式、土拱效应、减载材料性能和等沉面高度等因素的综合影响,当忽略基质吸力影响或基质吸力为零时退化为饱和土结果,具有重要理论意义和广泛工程应用前景。
针对具体的诱导减载涵洞工程,在涵洞尺寸、回填土力学与变形参数、减载材料尺寸及变形模量、基质吸力大小和分布等确定后,可按图 7选取相应公式计算涵顶竖向土压力。

|
图 7 解答应用步骤 Fig. 7 Calculation steps of the proposed solution |
Parker等[7]开展诱导减载涵洞竖向土压力的现场实测,涵洞宽度D=3.75 m,高度h=3.75 m(圆形涵洞,内径3.0 m、外径3.75 m)。减载锯末的宽度B=4 m,厚度t=2.75 m,变形模量Ep=185 kPa。回填土参数为[19, 29]:重度γ=21.8 kN/m3,有效黏聚力c′=0 kPa,有效内摩擦角φ′=29.1°,干密度ρd=20.4 kN/m3,含水率w=7.8%,变形模量E=7 MPa。结合干密度ρd和含水率w求得基质吸力(ua-uw)=32.8 kPa[30],因文献[7]未提供地下水位信息,经验假定基质吸力为均匀分布,且设吸力角φb=10°。
根据1.2节知,内土柱宽度取为涵洞宽度D=3.75 m;由2.3节得考虑基质吸力、忽略基质吸力时等沉面高度Hc分别为32.8和34.6 m,均大于最大填土高度17 m,故采用式(16)计算涵顶竖向土压力。图 8为本文涵顶竖向土压力计算值与文献[7]现场实测的对比,其中,(ua-uw)=32.8 kPa代表考虑回填土的非饱和特性,(ua-uw)=0 kPa表示忽略基质吸力按饱和回填土分析。

|
图 8 与现场实测的对比 Fig. 8 Comparison with field measurements |
由图 8可知,考虑回填土非饱和特性相比忽略基质吸力影响时,式(16)与文献[7]现场实测涵顶竖向土压力吻合得更好,平均相对误差绝对值为6.9%,表明本文解析解适用于回填非饱和土的诱导减载涵洞。
4 影响因素分析为定量描述诱导减载效果,定义减载率α为
| $ \alpha=1-\frac{\left(\sigma_{\mathrm{z}}-u_{\mathrm{a}}\right)_{z=H}}{\gamma H} $ | (19) |
由式(19)可知,减载率α越大,诱导减载效果越好。同时,给出等沉面高度Hc的变化以选择涵顶竖向土压力公式。
主要探讨基质吸力及分布形式、吸力角、减载材料厚度和变形模量对减载率α的影响特性。设定某诱导减载涵洞算例,涵洞宽度D=3 m,高度h=2.5 m,填土高度H=12 m,地下水位在原地面以下3 m处;非饱和回填土的重度γ=18.5 kN/m3,有效黏聚力c′=0 kPa,有效内摩擦角φ′=30°,吸力角φb=15°,变形模量E=30 MPa;诱导减载EPS板的宽度B=D=3 m,厚度t=0.5 m,变形模量Ep=1.5 MPa。
4.1 基质吸力基质吸力对诱导减载涵洞竖向土压力的影响包括吸力大小和分布两方面,图 9给出了减载率α随基质吸力的变化关系,其中,UDS代表均布吸力、LDS代表线性吸力,下同。

|
图 9 基质吸力的影响 Fig. 9 Influence of matric suction |
由图 9可知,随着基质吸力的增加,等沉面高度Hc近似线性减小,减载率α先增大后减小。这是因为基质吸力对涵顶竖向土压力具有双重影响:增加基质吸力,外土柱对内土柱向上的摩擦作用就增强(详见式(11)),使得涵顶竖向土压力减小;相反地,等沉面随基质吸力的增加而不断降低(详见2.3节和图 6),代表内/外土柱发生相对沉降的范围减小,继而等沉面以上未受摩擦力影响的土体增高,使得涵顶竖向土压力增大。减载率α的变化体现了双重影响中某一影响相对强弱,峰值意味着双重影响的强弱转变。
此外,当两种吸力分布的基质吸力大小相同时,线性吸力下减载率α低于均布吸力下的,说明均布吸力诱导减载效果优于线性吸力的。若不考虑基质吸力变化而直接按均布吸力计算,将得到偏小的涵顶竖向土压力,从而高估诱导减载效果,需考虑基质吸力对诱导减载涵洞竖向土压力的双重影响并实测吸力分布。
4.2 吸力角由式(2)知吸力角φb代表了基质吸力对非饱和回填土抗剪强度的贡献率,图 10给出了减载率α随吸力角φb的变化关系,其中LDS和UDS下基质吸力分别取40、20 kPa(地表吸力的平均值),下同。

|
图 10 吸力角的影响 Fig. 10 Influence of suction angle |
由图 10可知,随着吸力角φb的增加,减载率α先增大后减小,表明吸力角φb对涵顶竖向土压力亦具有双重影响,具体原因与图 9中基质吸力增加使摩擦作用增强(详见式(11))与等沉面降低(详见2.3节和图 6)相同;均布吸力下减载率α比线性吸力下的稍高且峰值点滞后。
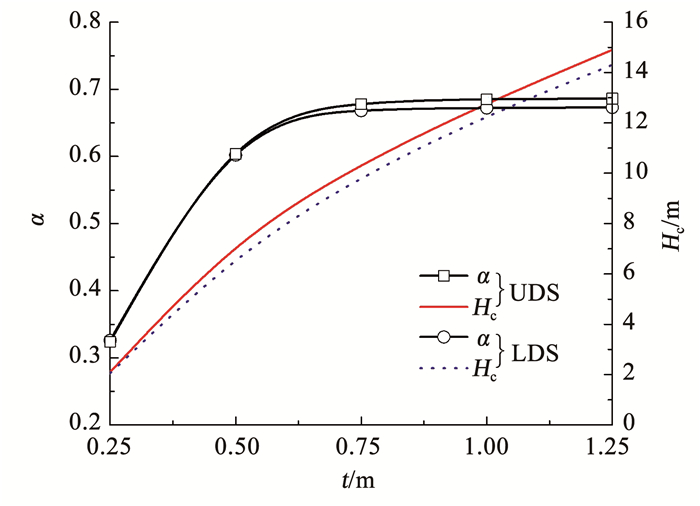
4.3 减载材料厚度减载材料厚度t是影响诱导减载效果的重要因素,图 11给出了减载率α随减载材料厚度t的变化关系。
|
图 11 减载材料厚度的影响 Fig. 11 Influence of compressible material thickness |
由图 11可知,随着减载材料厚度t的增加,等沉面高度Hc非线性增大,减载率α逐渐增大并趋于稳定,意味着减载材料超过一定厚度后诱导减载效果难以再提高,恰当设定减载材料厚度可降低材料费用。
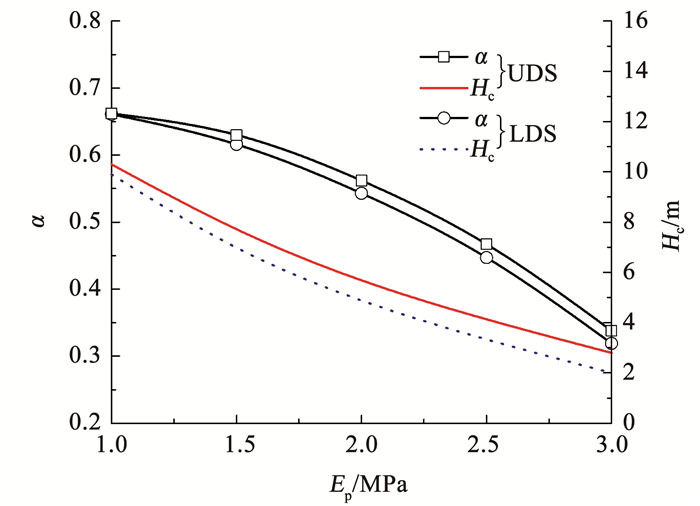
4.4 减载材料变形模量减载材料与回填土的变形模量差异是诱导减载涵洞内/外土柱产生固结沉降差的主要原因,图 12给出了减载率α随减载材料变形模量Ep的变化关系。可以看出,随着减载材料变形模量Ep的提高,减载材料的可压缩性减弱,内/外土柱的固结沉降趋近,进而减载率α非线性减小;当减载材料变形模量Ep从1.0 MPa增加至3.0 MPa时,均布吸力下减载率α减少了49.5%,线性吸力下减载率α减少了51.2%。
|
图 12 减载材料变形模量的影响 Fig. 12 Influence of deformation modulus of compressible materials |
1) 基于非饱和土双应力状态变量强度理论所建立的诱导减载涵顶竖向土压力解析解,合理考虑了基质吸力及分布形式、土拱效应、减载材料性能和等沉面高度的综合影响,与文献现场实测良好吻合验证了其正确性以及对非饱和土诱导减载涵洞的适用性,完善了诱导减载涵洞设计理论,工程应用前景广泛。
2) 由减载率量化诱导减载效果和因素影响特性可知:基质吸力、吸力角对诱导减载涵顶竖向土压力都具有双重影响;当均布吸力取为地表吸力或地表吸力平均值时,均布吸力下减载率均比线性吸力的稍高;减载率随减载材料厚度增加逐渐增大并趋于稳定,表明诱导减载法需设定恰当的减载材料厚度。
| [1] |
蒋承轩, 陈保国, 毛新颖, 等. 柔性地基上高填方减载式涵洞受力特性[J]. 岩土力学, 2019, 40(1): 275. JIANG Chengxuan, CHEN Baoguo, MAO Xinying, et al. Stress characteristics of high fill load-shedding culvert on flexible foundation[J]. Rock and Soil Mechanics, 2019, 40(1): 275. DOI:10.16285/j.rsm.2017.1208 |
| [2] |
杨锡武, 张永兴. 山区公路高填方涵洞加筋桥减载方法及其设计理论研究[J]. 岩石力学与工程学报, 2005, 24(9): 1561. YANG Xiwu, ZHANG Yongxing. Study on the method and theory of load reduction by reinforcement bridge for the culvert beneath high filling[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(9): 1561. DOI:10.3321/j.issn:1000-6915.2005.09.016 |
| [3] |
郑俊杰, 马强, 张军. 加筋减载涵洞的涵顶土压力计算[J]. 岩土工程学报, 2011, 33(7): 1135. ZHENG Junjie, MA Qiang, ZHANG Jun. Calculation of vertical earth pressure on load reduction culverts under embankments by reinforcement[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(7): 1135. DOI:10.1631/jzus.B1000185 |
| [4] |
EL NAGGAR H, TURAN A, VALSANGKAR A. Earth pressure reduction system using geogrid-reinforced platform bridging for buried utilities[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2015, 141(6): 04015024. DOI:10.1061/(ASCE)GT.1943-5606.0001307 |
| [5] |
KANG J, IM H, PARK J S. The effect of load reduction on underground concrete arch structures in embedded trench installations[J]. Tunnelling and Underground Space Technology, 2020, 98: 103240. DOI:10.1016/j.tust.2019.103240 |
| [6] |
顾安全, 吕镇锋, 姜峰林, 等. 高填土盖板涵EPS板减荷试验及设计方法[J]. 岩土工程学报, 2009, 31(10): 1481. GU Anquan, LV Zhenfeng, JIANG Fenglin, et al. Load reduction tests and design methods for culverts with high fill soil using EPS slabs[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(10): 1481. DOI:10.3321/j.issn:1000-4548.2009.10.001 |
| [7] |
PARKER B A, MCAFFEE R P, VALSANGKAR A J. Field performance and analysis of 3-m-diameter induced trench culvert under a 19.4-m soil cover[J]. Transportation Research Record, 2008, 2045(1): 68. DOI:10.3141/2045-08 |
| [8] |
MEGUID M A, YOUSSEF T A. Experimental investigation of the earth pressure distribution on buried pipes backfilled with tire-derived aggregate[J]. Transportation Geotechnics, 2018, 14: 117. DOI:10.1016/j.trgeo.2017.11.007 |
| [9] |
邓谦, 马强, 胡刚, 等. 高填方刚性涵洞EPS板减载模型试验研究[J]. 湖北工业大学学报, 2019, 34(2): 87. DENG Qian, MA Qiang, HU Gang, et al. Load reduction model test of high fill rigid culvert with EPS plate[J]. Journal of Hubei University of Technology, 2019, 34(2): 87. DOI:10.3969/j.issn.1003-4684.2019.02.021 |
| [10] |
WITTHOEFT A F, KIM H. Numerical investigation of earth pressure reduction on buried pipes using EPS geofoam compressible inclusions[J]. Geosynthetics International, 2016, 23(4): 287. DOI:10.1680/jgein.15.00054 |
| [11] |
NI P P, QIN X G, YI Y L. Numerical study of earth pressures on rigid pipes with tire-derived aggregate inclusions[J]. Geosynthetics International, 2018, 25(5): 494. DOI:10.1680/jgein.18.00013 |
| [12] |
张业勤, 陈保国, 孟庆达, 等. 减载条件下高填方涵洞受力机制及基底压力[J]. 岩土力学, 2019, 40(12): 4813. ZHANG Yeqin, CHEN Baoguo, MENG Qingda, et al. Stress mechanism and foundation contact pressure of high-fill culverts under load reduction conditions[J]. Rock and Soil Mechanics, 2019, 40(12): 4813. DOI:10.16285/j.rsm.2018.2291 |
| [13] |
王晓谋, 顾安全. 上埋式管道垂直土压力的减荷措施[J]. 岩土工程学报, 1990, 12(3): 83. WANG Xiaomou, GU Anquan. Measures to reduce the vertical earth pressure of positive buried pipelines[J]. Chinese Journal of Geotechnical Engineering, 1990, 12(3): 83. DOI:10.3321/j.issn:1000-4548.1990.03.009 |
| [14] |
QIN X G, NI P P, ZHOU M. Improved analytical solution of vertical pressure on top of induced trench rigid culverts[J]. Geosynthetics International, 2017, 24(6): 615. DOI:10.1680/jgein.17.00028 |
| [15] |
CHEN B G, MENG Q D, YAN T F, et al. New simplified method for analysis of earth pressure on the imperfect trench installation box culvert[J]. International Journal of Geomechanics, 2020, 20(10): 04020193. DOI:10.1061/(ASCE)GM.1943-5622.0001842 |
| [16] |
FREDLUND D G, RAHARDJO H, FREDLUND M D. Unsaturated soil mechanics in engineering practice[M]. New York: John Wiley and Sons, lnc., 2012
|
| [17] |
LU N, LIKOS W J. Unsaturated soil mechanics[M]. New York: John Wiley and Sons, lnc., 2004
|
| [18] |
陈正汉. 非饱和土与特殊土力学的基本理论研究[J]. 岩土工程学报, 2014, 36(2): 201. CHEN Zhenghan. Research on the basic theory of unsaturated soils and special soils[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(2): 201. DOI:10.11779/CJGE201402001 |
| [19] |
MCAFFEE R P, VALSANGKAR A J. Field performance, centrifuge testing, and numerical modelling of an induced trench installation[J]. Canadian Geotechnical Journal, 2008, 45(1): 85. DOI:10.1139/T07-086 |
| [20] |
FREDLUND D G, MORGENSTEM N R, WIDGER R A. The shear strength of unsaturated soils[J]. Canadian Geotechnical Journal, 1978, 15(3): 313. DOI:10.1139/t78-029 |
| [21] |
蔺港, 孔令刚, 詹良通, 等. 基于太沙基土拱效应考虑基质吸力影响的松动土压力计算模型[J]. 岩土力学, 2015, 36(7): 2095. LIN Gang, KONG Linggang, ZHAN Liangtong, et al. An analytical model for loosening earth pressure considering matric suction based on Terzaghi soil arch effect[J]. Rock and Soil Mechanics, 2015, 36(7): 2095. DOI:10.16285/j.rsm.2015.07.035 |
| [22] |
王成洋, 傅鹤林, 张佳华. 非饱和浅埋隧道稳定性的上限分析[J]. 采矿与安全工程学报, 2019, 36(6): 1161. WANG Chengyang, FU Helin, ZHANG Jiahua. Upper bound analysis of the stability of shallow tunnel in unsaturated soils[J]. Journal of Mining and Safety Engineering, 2019, 36(6): 1161. DOI:10.13545/j.cnki.jmse.2019.06.012 |
| [23] |
ZHANG C G, YAN Q, ZHAO J H, et al. Formulation of ultimate bearing capacity for strip foundations based on the Meyerhof theory and unsaturated soil mechanics[J]. Computers and Geotechnics, 2020, 126: 103734. DOI:10.1016/j.compgeo.2020.103734 |
| [24] |
ALLARD E, EL NAGGAR H. Pressure distribution around rigid culverts considering soil-structure interaction effects[J]. International Journal of Geomechanics, 2016, 16(2): 04015056. DOI:10.1061/(ASCE)GM.1943-5622.0000525 |
| [25] |
张常光, 赵均海, 朱倩. 非饱和土刚性挡墙抗倾覆临界嵌固深度研究[J]. 岩石力学与工程学报, 2014, 33(11): 2360. ZHANG Changguang, ZHAO Junhai, ZHU Qian. Critical embedment depth of rigid retaining walls in foundation pit of unsaturated soils[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(11): 2360. DOI:10.13722/j.cnki.jrme.2014.11.020 |
| [26] |
YAO C, YANG X L. Limit analysis of unsaturated soil slope stability considering intermediate principal stress and strength nonlinearity[J]. Geotechnical and Geological Engineering, 2017, 35(5): 2053. DOI:10.1007/s10706-017-0226-8 |
| [27] |
PAIK K H, SALGADO R. Estimation of active earth pressure against rigid retaining walls considering arching effects[J]. Géotechnique, 2003, 53(7): 643. DOI:10.1680/geot.2003.53.7.643 |
| [28] |
HANDY R L. The arch in soil arching[J]. Journal of Geotechnical Engineering, 1985, 111(3): 302. DOI:10.1061/(ASCE)0733-9410(1985)111:3(302) |
| [29] |
MCAFFEE R P, VALSANGKAR A J. Performance of an induced trench installation[J]. Transportation Research Record, 2005, 1936(1): 230. DOI:10.1177/0361198105193600126 |
| [30] |
张鹏程, 汤连生, 姜力群, 等. 基质吸力与含水量及干密度定量关系研究[J]. 岩石力学与工程学报, 2013, 32(增刊1): 2792. ZHANG Pengcheng, TANG Liansheng, JIANG Liqun, et al. Research of quantitative relations of matric suction with water content and dry density[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S1): 2792. DOI:10.3969/j.issn.1000-6915.2013.z1.028 |
 2023, Vol. 55
2023, Vol. 55