2. 山东高速集团有限公司,济南 250101;
3. 曼彻斯特大学 机械、航空与土木工程学院,曼彻斯特 M13 9PL;
4. 山东大学(齐河)新材料与智能装备研究院, 山东 德州 251100;
5. 山东大学 齐鲁交通学院,济南 250002
2. Shandong Hi-Speed Group Co., Ltd., Jinan 250101, China;
3. School of Mechanical, Aerospace and Civil Engineering, The University of Manchester, Manchester M13 9PL, UK;
4. Research Institute of New Material and Intelligent Equipment, Shandong University (Qihe County), Dezhou 251100, Shandong, China;
5. School of Qilu Transportation, Shandong University, Jinan 250002, China
既有建筑地下增层工程是一项综合性很强的复杂工程,包含既有基础加固、基坑支护结构增设、基础托换、土体开挖、地下室底板浇筑、结构柱和托换桩截除等工序(以群桩基础支承的既有建筑地下增层开挖工程为例,见图 1)。目前,国内外已有既有建筑进行地下增层改造的成功案例[1-5]。桩基础支承的既有建筑地下增层过程中应重点关注土体开挖效应下桩基承载力损失和桩基渐进变形过程,从变形控制角度出发,明确既有建筑地下增层开挖条件下在役桩基竖向承载特性变化过程。鉴于既有建筑地下增层开挖工程的实际情况和复杂性,在役桩基承载特性现场试验很难开展。因此,有必要提出既有建筑地下开挖条件下在役桩基竖向承载特性分析方法。

|
图 1 群桩支承的既有建筑地下增层开挖示意 Fig. 1 Schematic diagram of underground excavation beneath existing building supported by pile groups |
单桩承载特性常用计算方法(如荷载传递法[6-7]、弹性理论法[8-9]和数值分析方法[10-11]等)应用于既有建筑地下开挖工程中,在役桩基承载特性分析时应考虑如下影响因素:1)开挖段桩侧阻力的直接损失;2)开挖卸荷对桩周土应力状态和剪切强度的改变(坑底土体处于超固结状态);3)开挖卸荷引起的桩周土回弹变形。目前已有大量成熟的数值计算软件,结合合理的本构模型和参数取值可用于分析既有建筑地下开挖工程中在役桩基竖向承载特性。然而,既有建筑地下开挖工程中在役桩-土界面的接触模型及其相关参数的确定,仍是数值计算方法中尚需明确的问题。荷载传递法可通过桩-土界面的非线性荷载传递模型较好地模拟桩-土界面的非线性,且计算过程简便,可用于桩基承载特性的快速估算。
荷载传递法用于桩基承载特性分析时能否获得合理的计算结果,关键在于能否选择恰当的荷载传递函数。荷载传递函数可通过试验数据拟合或理论分析获得。目前,国内外学者提出了众多荷载传递模型,如双折线模型[12]、理想弹塑性模型[13]、三折线模型[14]、幂函数模型[15]、软化模型[16-17]和双曲线模型[7, 18]等。张乾青[19]总结了不同桩侧和桩端荷载传递模型,明确了荷载传递模型中参数的意义和取值方法。上述荷载传递模型未考虑开挖引起的土体回弹、应力状态变化对桩基承载特性的影响。为考虑土体开挖对桩基荷载传递特性的影响,龚晓南等[20-22]提出了考虑土体开挖效应的荷载传递函数。
传统荷载传递函数无法直接用于既有建筑地下开挖工程中在役桩荷载传递特性的分析。针对上述问题,本文明确了土体开挖条件下土体应力状态改变、回弹等因素对桩侧和桩端承载特性的影响,建立了考虑土体开挖效应影响的桩侧荷载传递双曲线模型和桩端荷载传递双折线模型,考虑开挖卸荷效应引起的土体超固结状态提出了土体开挖条件下桩侧极限摩阻力计算方法,基于有限差分法和荷载传递法形成了既有建筑地下增层开挖条件下在役桩基竖向承载特性计算方法。
1 荷载传递模型 1.1 桩侧荷载传递双曲线模型竖向受荷单桩某一深度z处桩身位移Ss(z)为桩-土相对位移w(z)和土体位移ws(z)之和,即桩身位移Ss(z)与桩侧单位摩阻力τs(z)关系为[7]
| $ \begin{aligned} S_{\mathrm{s}}(z)= & w(z)+w_{\mathrm{s}}(z)= \\ & \frac{a \tau_{\mathrm{s}}(z)}{1-b \tau_{\mathrm{s}}(z)}+\frac{r_0}{G_0} \ln \left(\frac{r_{\mathrm{m}}}{r_0}\right) \tau_{\mathrm{s}}(z) \end{aligned} $ | (1) |
式中:a和b为双曲线模型参数;G0为桩周土体小应变剪切模量;r0为桩身半径;rm为单桩影响半径,rm=2.5ρ(1-υs)L,L为桩长,υs为桩侧土泊松比,ρ为桩周土体不均匀系数,对于均质土ρ=1,对于成层土
既有建筑地下开挖工程中在役单桩某深度z处的桩身位移Ss(z)除了考虑桩-土相对位移w(z)和桩周土体弹性位移ws(z)外,还应考虑开挖土体回弹位移w′s(z)[23],其中,土体回弹位移w′s(z)可采用式(2)计算,即
| $ w_{\mathrm{s}}^{\prime}(z)=\psi \sum\limits_z^{z_{\mathrm{m}}} \frac{\sigma_{\mathrm{re}}(h)}{E_{\mathrm{ur}}(h)} \Delta h $ | (2) |
式中:h为深度;zm为开挖土体的影响深度,其值为回弹应力为0时对应的土层深度;ψ为修正系数,对于土体开挖范围呈长条形的情况,建议取2.0[24];σre(h)为厚度为Δh的土层回弹应力;Eur(h)为厚度为Δh的土层回弹模量。
某一深度z处土体回弹应力σre(z)(其值应大于0)可表示为[24]
| $ \sigma_{\text {re }}(z)=\alpha_{\mathrm{z}} P_0-\gamma^{\prime} z $ | (3) |
式中:P0为开挖范围内土体自重应力;αz为附加应力系数,可根据Mindlin应力解计算获得;γ′为开挖面至深度z处范围内土体平均有效重度。
回弹模量可根据Duncan-Chang模型[25]计算获得,即
| $ E_{\mathrm{ur}}=K_{\mathrm{ur}} p_{\mathrm{a}}\left(\sigma_3 / p_{\mathrm{a}}\right)^{n_{\mathrm{ur}}} $ | (4) |
式中:pa为大气压力,Kur和nur为回弹模量参数,σ3为土体围压。
由式(1)~(4)可知,土体开挖时竖向受荷桩的桩身位移Ss(z)与桩侧单位摩阻力τs(z)关系为
| $ S_{\mathrm{s}}(z)=\frac{a \tau_{\mathrm{s}}(z)}{1-b \tau_{\mathrm{s}}(z)}+\frac{r_0}{G_0} \ln \left(\frac{r_{\mathrm{m}}}{r_0}\right) \tau_{\mathrm{s}}(z)-f(z) $ | (5) |
其中
| $ f(z)=\psi \sum\limits_z^{z_{\mathrm{m}}} \frac{\Delta \sigma_{{ }_{\mathrm{v}}}^{\prime}-\gamma^{\prime} h}{K_{\mathrm{ur}} p_{\mathrm{a}}\left(K_0 \Delta \sigma^{\prime}{ }_{\mathrm{v}} / p_{\mathrm{a}}\right)^{n_{\mathrm{ur}}}} \Delta h $ | (6) |
式中Δσ′v为开挖土体引起深度z处的竖向附加应力。
1.2 桩侧荷载传递模型参数确定式(1)中参数a为桩-土界面初始剪切刚度ks0的倒数,b的倒数为桩-土相对位移无穷大时对应的单位侧摩阻力,可表示为[7, 18, 26]
| $ \left\{\begin{array}{l} a=1 / k_{\mathrm{s} 0} \\ b=R_{\mathrm{s}} / \tau_{\mathrm{su}} \end{array}\right. $ | (7) |
式中:Rs为桩侧摩阻力破坏比,为0.85~0.95;τsu为桩侧极限单位摩阻力。
桩侧初始承载刚度ks0可根据Randolph和Wroth[27]的弹性理论解求得,即
| $ k_{s 0}=\frac{G_0}{r_0 \ln \left(r_{\mathrm{m}} / r_0\right)} $ | (8) |
对于非剪胀性土,如正常固结黏土,土体开挖前桩侧单位极限摩阻力τsu为
| $ \tau_{\mathrm{su}}=\sigma^{\prime}{ }_{\mathrm{n}} \tan \delta=\left[\left(1-\sin \varphi^{\prime}\right) \sigma^{\prime}{ }_{\mathrm{v}}\right] \tan \delta $ | (9) |
式中:φ′为土体有效内摩擦角;σ′v为土体竖向有效应力;δ为桩-土界面摩擦角,通常取δ=(0.75~1)φ′[28],对于钻孔灌注桩(因施工因素,桩身粗糙度较大),可近似取δ=φ′[29-31]。
非剪胀性土中,土体开挖后考虑土体超固结状态,桩侧单位极限摩阻力τsu为
| $ \tau_{\mathrm{su}}=\left[\left(1-\sin \varphi^{\prime}\right) R_{\mathrm{OC}}^{\sin \varphi} \sigma^{\prime}{ }_{\mathrm{v}}\right] \tan \delta $ | (10) |
式中ROC为增层开挖前、后竖向有效应力之比,即
| $ R_{\mathrm{OC}}=\frac{\bar{\gamma}_1\left(z-h_1\right)+q_0}{\bar{\gamma}_2\left(z-h_2\right)} $ | (11) |
式中:γ1和γ2分别为土体开挖前、后土层平均有效重度,h1和h2为开挖前、后土体深度(从开挖起始面计算),q0为土体开挖前地面荷载。
以图 2中开挖宽度为2a的情况为例,地面下深度h范围内土体开挖导致深度z处竖向有效应力改变量Δσ′v可计算为[21]
| $ \begin{aligned} \Delta \sigma^{\prime}= & \frac{\bar{\gamma}_1}{\pi}\left[h\mathrm{arctan }\frac{a}{z_1}-\frac{a}{2} \ln \left(r_1^2\right)+z \mathrm{arctan } \frac{z_1}{a}+h \mathrm{arctan } \frac{a}{z_2}+\frac{a}{2} \ln \left(r_2^2\right)-z \mathrm{arctan } \frac{z_2}{a}\right]+ \\ & \frac{\bar{\gamma}_1}{2 \pi(1-v)}\left[\frac{a}{2} \ln \left(r_2^2\right)-\frac{a}{2} \ln \left(r_1^2\right)+2 z(1-2 v)\left(\mathrm{arctan } \frac{z_2}{a}-\mathrm{arctan } \frac{z}{a}\right)-\frac{2 a h z}{r_2^2}\right] \end{aligned} $ | (12) |

|
图 2 竖向有效应力改变量计算示意 Fig. 2 Calculation diagram of variation of vertical effective stress |
式中:υ为土体泊松比,z1=z-h,z2=z+h,r12=a2+z12,r22=a2+z22。
地面下深度h处的超载引起z处的土体竖向有效应力增量Δσ′v0为
| $ \begin{aligned} \Delta \sigma_{\mathrm{v}0}^{\prime}= & \frac{q_0}{\pi}\left(\arctan \frac{a}{z_1}+\arctan \frac{a}{z_2}\right)+ \\ & \frac{q_0}{2 \pi(1-v)}\left\{\frac{a z_1}{r_1^2}+\frac{a[h+(3-4 v) z]}{r_2^2}+\frac{4 a h z z_2}{r_2^4}\right\} \end{aligned} $ | (13) |
由式(11)~(13)可知,地表下深度z处土体超固结比ROC为
| $ R_{\mathrm{OC}}=\frac{\bar{\gamma}_1 z+\Delta \sigma_{\mathrm{v}0}^{\prime}-\Delta \sigma_{\mathrm{v}}^{\prime}\left(h_1\right)}{\bar{\gamma}_2 z-\Delta \sigma_{{ }_{\mathrm{v}}}^{\prime}\left(h_2\right)} $ | (14) |
对于剪胀性土,如砂土、砾石土及超固结黏土,土体开挖前桩侧单位极限摩阻力τsu可假定为柱孔扩张问题进行求解[32],即
| $ \tau_{\mathrm{su}}=\left[\left(1-\sin \varphi^{\prime}\right) \sigma_{\mathrm{v}}^{\prime}+\frac{4 G_{\mathrm{s}}}{D} u_{\mathrm{cs}}\right] \tan \delta $ | (15) |
式中:D为桩身直径;Gs为桩周土体剪切模量,Gs=αG0,α为折减系数;ucs为桩-土界面极限剪胀量。
剪胀性土中,土体开挖后考虑土体超固结状态,桩侧单位极限摩阻力τsu为
| $ \tau_{\mathrm{su}}=\left[\left(1-\sin \varphi^{\prime}\right) R_{\mathrm{OC}}^{\mathrm{sin} \varphi} \sigma^{\prime}{ }_{\mathrm{v}}+\frac{4 G_{\mathrm{s}}}{D} u_{\mathrm{cs}}\right] \tan \delta $ | (16) |
G0可根据室内试验和原位试验结果确定,无试验数据时可采用式(17)近似计算获得[33],即
| $ G_0=C_{\mathrm{g}} p_{\mathrm{a}} \frac{\left(e_{\mathrm{g}}-e_0\right)^2}{1+e_0} \sqrt{\frac{p^{\prime}}{p_{\mathrm{a}}}} $ | (17) |
式中:e0为初始孔隙率,Cg和eg为土体无量纲参数,p′为平均主应力。
极限状态下桩土界面剪胀量ucs可计算为[34]
| $ u_{\mathrm{cs}}=\int_0^{\gamma_{\mathrm{cs}}} t_{\mathrm{s}} \tan \psi \mathrm{d} \gamma=t_{\mathrm{s}} \tan \psi_{\mathrm{p}} \frac{\gamma_{\mathrm{cs}}}{2} $ | (18) |
式中:ψ为剪胀角;ψp为峰值剪胀角;γ为剪切应变;γcs为极限状态下剪切应变,可取γcs=60%[34];ts为桩-土界面剪切带厚度,对于桩侧较光滑的预应力管桩或钢管桩,一般认为桩侧不会形成剪切带。对于桩侧较粗糙的钻孔灌注桩,剪切带厚度可取为10~15倍的桩侧土体平均粒径[35]。
根据Bolton[36]以及Rowe[37]的应力-剪胀理论,峰值剪胀角ψp可计算为
| $ \sin \psi_{\mathrm{p}}=\frac{\sin \varphi_{\mathrm{p}}^{\prime}-\sin \varphi_{\mathrm{cv}}^{\prime}}{1-\sin \varphi_{\mathrm{p}}^{\prime} \sin \varphi_{\mathrm{cv}}^{\prime}} $ | (19a) |
| $ \varphi_{\mathrm{p}}^{\prime}-\varphi_{\mathrm{cv}}^{\prime}=m I_{\mathrm{rd}} $ | (19b) |
| $ I_{\mathrm{rd}}=\left\{\begin{array}{l} 5 D_{\mathrm{r}}-1, p^{\prime} \leqslant 150 \;\mathrm{kPa} \\ D_{\mathrm{r}}\left[5-\ln \left(p^{\prime} / 150\right)\right]-1, p^{\prime}>150 \;\mathrm{kPa} \end{array}\right. $ | (19c) |
式中:φ′p为峰值有效内摩擦角,φ′cv为极限状态下的有效内摩擦角,Ird为相对剪胀指数。
需要指出的是,本文中开挖条件下桩侧阻值的确定主要基于条形均布荷载的Mindlin应力解,这种处理假设荷载均匀分布,但实际工程中由于土质各项异性、人为载荷等原因,荷载无法保证是均匀分布,可以通过估算平均应力值将载荷简化为均匀分布荷载。理论上,本文的二维计算模型可适用于轴对称问题或者平面应变问题,即圆形基坑或者长宽比较大的基坑,对于其他形状的基坑开挖,可以采用相应形式的应力解。例如,矩形均布荷载的Mindlin应力解,竖向应力改变量式(12)或(13)需要相应的改变,但方法整体框架保持不变。另一方面,由于Mindlin解是基于弹性假设的,对于实际土体因塑性、各向异性的存在,Mindlin应力解的结果是偏大的。伍程杰等[21]计算结果表明,Mindlin应力解比有限元数值解约大5%,因此,采用Mindlin应力解计算开挖后桩侧阻力时应乘以修正系数0.95。
1.3 桩端荷载传递双折线模型张乾青[38]分析了国内外15个工地30多根不同类型桩(钻孔灌注桩、预制管桩和H型钢桩)的静载试验,结果表明,对于桩端未发生刺入或整体破坏的桩,桩端沉降与桩端阻力间的关系可采用双折线模型进行模拟。既有建筑地下开挖工程中在役桩承受的荷载一般不到其极限承载力的1/2,因此,桩端一般不会发生刺入或整体破坏,可采用双折线模型描述桩端位移Sb与桩端阻力qb间的关系[23]。桩端荷载传递双折线模型的数学表达式可表示为[39-40]
| $ q_{\mathrm{b}}=\left\{\begin{array}{l} k_1 S_{\mathrm{b}}, S_{\mathrm{b}}<S_{\mathrm{bu}} \\ k_1 S_{\mathrm{bu}}+k_2\left(S_{\mathrm{b}}-S_{\mathrm{bu}}\right), S_{\mathrm{b}} \geqslant S_{\mathrm{bu}} \end{array}\right. $ | (20) |
式中:k1和k2为模型参数,分别为桩端阻力-桩端位移关系中第1和第2阶段的斜率;Sbu为双折线模型中第1阶段中极限桩端位移,与施工工艺、桩端土层、沉渣厚度等因素有关,其值可取1~9 mm[38, 41]。
由式(20)可知,桩端沉降Sb可表示为
| $ S_{\mathrm{b}}=\left\{\begin{array}{l} \frac{q_{\mathrm{b}}}{k_1}, q_{\mathrm{b}}<k_1 S_{\mathrm{bu}} \\ \frac{q_{\mathrm{b}}-\left(k_1-k_2\right) S_{\mathrm{bu}}}{k_2}, q_{\mathrm{b}} \geqslant k_1 S_{\mathrm{bu}} \end{array}\right. $ | (21) |
考虑土体回弹作用,土体开挖条件下单桩的桩端沉降Sb与桩端单位阻力qb间关系可表示为
| $ S_{\mathrm{b}}=\left\{\begin{array}{l} \frac{q_{\mathrm{b}}}{k_1}-f(L), q_{\mathrm{b}}<k_1 S_{\mathrm{bu}} \\ \frac{q_{\mathrm{b}}-\left(k_1-k_2\right) S_{\mathrm{bu}}}{k_2}-f(L), q_{\mathrm{b}} \geqslant k_1 S_{\mathrm{bu}} \end{array}\right. $ | (22) |
式中f(L)由式(6)计算确定。
1.4 桩端荷载传递模型参数确定桩端阻力-桩端位移关系中第1阶段斜率k1可根据Randolph和Wroth[27]的弹性理论解计算获得,即
| $ k_1=\frac{4 G_{\mathrm{b}}}{\pi r_0\left(1-v_{\mathrm{b}}\right)} $ | (23) |
式中Gb和υb分别为桩端土剪切模量及泊松比。
桩端阻力-桩端位移关系中第2阶段斜率k2可根据试桩静载试验结果反分析得到[12, 38-41]。当缺乏试桩现场试验数据时,可采用桩端位移为10%D时对应的极限桩端承载力qb0.1进行估算,k2可表示为[42]
| $ k_2=\frac{0.3 q_{\text {bu }}-k_1 S_{\mathrm{bu}}}{0.1 D-S_{\mathrm{bu}}} $ | (24) |
式中qbu为极限桩端阻力。
黏土中单桩的桩端极限承载力qbu为[43]
| $ q_{\mathrm{bu}}=9 S_{\mathrm{u}} $ | (25) |
式中Su为桩端土的不排水强度。
砂土中单桩的桩端极限承载力qbu为[42]
| $ q_{\text {bu }}=N_{\mathrm{q}} \sigma_{{ }_{\mathrm{v}}}^{\prime} $ | (26) |
| $ N_{\mathrm{q}}=\frac{A}{1-\sin \varphi_{\mathrm{cv}}^{\prime}}\left[\frac{G_{\mathrm{b}} / \sigma_{\mathrm{v}}^{\prime}}{B+D\left(G_{\mathrm{b}} / \sigma_{\mathrm{v}}^{\prime}\right)^{-0.8}}\right]^C $ | (27) |
式中参数A,B,C和D可通过式(28)进行计算。
| $ A=\frac{3\left(1+\sin \varphi^{\prime}{ }_{\mathrm{cv}}\right)}{3-\sin \varphi_{\mathrm{cv}}^{\prime}}\left(\frac{1+2 K_0}{3}\right) $ | (28a) |
| $ B=\left(\frac{1+2 K_0}{3}\right) \tan \varphi_{\mathrm{cv}}^{\prime} $ | (28b) |
| $ C=\frac{4 \sin \varphi_{\mathrm{cv}}^{\prime}}{3\left(1+\sin \varphi_{\mathrm{cv}}^{\prime}\right)} $ | (28c) |
| $ D=50\left[\frac{\left(1+2 K_0\right)}{3} \tan \varphi_{\mathrm{cv}}^{\prime}\right]^{1.8} $ | (28d) |
式中K0为土体静止土压力系数。
2 单桩荷载-沉降计算方法竖向荷载作用下单桩桩身位移Ss(z)与桩侧单位侧摩阻力τs(z)间的荷载传递微分方程为
| $ \frac{\mathrm{d}^2 S_{\mathrm{s}}(z)}{\mathrm{d} z^2}=\frac{\pi D \tau_{\mathrm{s}}(z)}{E_{\mathrm{p}} A_{\mathrm{p}}} $ | (29) |
式中:Ep为桩身弹性模量,Ap为桩身横截面积。
对于形式简单的荷载传递函数,可通过求解式(29)获得解析解。对于形式较复杂的荷载传递函数,则无法获得式(29)的解析解,可通过泰勒级数法[44]、龙格-库塔法[45]和有限差分法等数值分析方法将式(29)转换为代数形式进行求解。本文采用有限差分法计算既有建筑土体开挖前、后在役单桩的承载特性。
计算前先将全桩分成若干桩段,对桩身控制方程差分离散后转换成代数方程(式(30))逐段求解桩身轴力-位移关系,即
| $ S_{\mathrm{s}}^{i+1}=\left(\frac{L}{n}\right)^2\left(-\frac{2 \pi r_0}{E_{\mathrm{p}} A_{\mathrm{p}}} \tau^i\right)+2 S_{\mathrm{s}}^i-S_{\mathrm{s}}^{i-1} $ | (30) |
土体开挖前、后竖向受荷单桩承载特性计算步骤如下:
1) 将单桩从桩顶至桩端分成n个桩段,桩顶处桩段编号为1,桩端处桩段编号为n。
2) 假定桩顶荷载Q。
3) 假设桩段1顶面和底面处的位移,Ss1和Ss2(其值假定较小)。
4) 根据式(1)或(5)(土体开挖前、后)计算桩段1顶面和底面处的桩侧单位摩阻力τs1和τs2。
5) 假设桩身轴力线性变化,桩段1底面处的桩身位移修正值可由式(31)计算获得,即
| $ S_{\mathrm{s}}^{2^{\prime}}=S_{\mathrm{s}}^1-S_{\mathrm{c}}^1 $ | (31) |
式中:Sc1为桩段1的桩身压缩量,可根据式(32)计算获得, 即
| $ S_{\mathrm{c}}^1=\frac{\Delta l\left\{Q+\left[Q-\frac{\pi D \Delta l\left(\tau_{\mathrm{s}}^1+\tau_{\mathrm{s}}^2\right)}{2}\right]\right\}}{2 E_{\mathrm{p}} A_{\mathrm{p}}} $ | (32) |
6) 比较式(31)中计算获得的Ss2′与步骤(3)中假定的Ss2值。若|Ss2-Ss2′|≤1×10-6 m,则桩段1底面处的桩身位移可取为Ss2;若|Ss2-Ss2′|>1× 10-6 m,需重新假定步骤3)中的Ss2值,直至|Ss2-Ss2′|≤ 1×10-6 m为止。
7) 采用式(30)计算其他桩段的桩身位移。
8) 由式(33)计算单桩总侧摩阻力Qs,即
| $ Q_{\mathrm{s}}=\sum\limits_1^{n+1} \pi D \Delta l \frac{\left(\tau_{\mathrm{s}}^i+\tau_{\mathrm{s}}^{i+1}\right)}{2} $ | (33) |
9) 根据计算获得的桩段n底面位移Ssn+1和式(21)或(22)(土体开挖前、后)计算桩端阻力Qb (考虑桩端面积)。
10) 根据式(34)计算单桩总承载力Q′,即
| $ Q^{\prime}=Q_{\mathrm{s}}+Q_{\mathrm{b}} $ | (34) |
11) 比较式(34)中计算获得的Q′与步骤2)中假定的Q值。若|Q-Q′|小于一给定的容许误差值,如1 N,则桩段1顶面处位移可取为Ss1;若|Q-Q′|大于该容许误差值,需重新假定步骤3)中的Ss1值,直至|Q-Q′|小于给定的容许误差值为止。
12)假定一系列不同的桩顶荷载值Q,重复步骤3)~11),直至得到桩顶荷载-位移关系曲线。
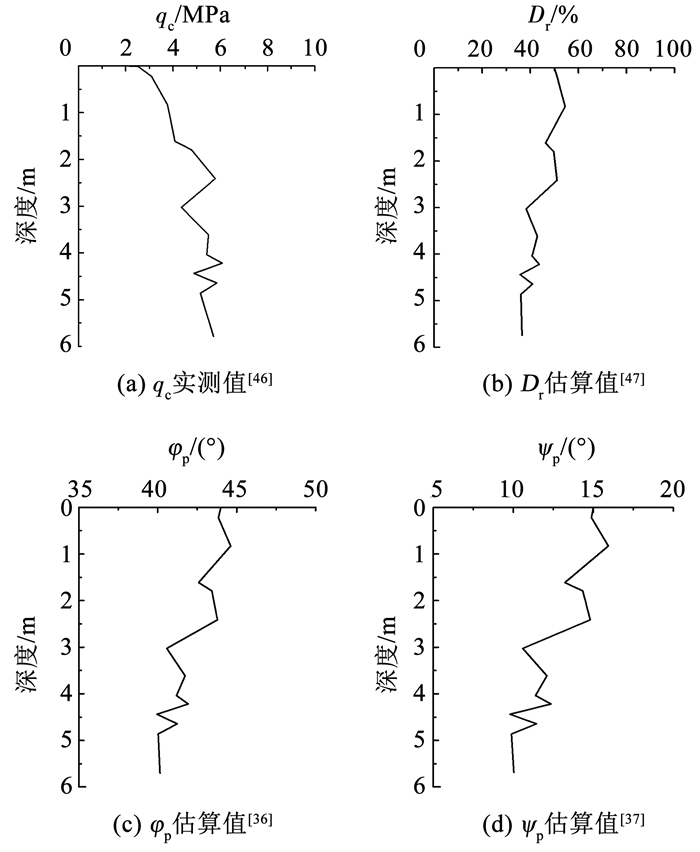
3 算例分析 3.1 算例1此算例来自文献[46]中桩基足尺载荷试验,选用桩长为6 m、桩径为0.6 m、桩身弹性模量约为30 GPa的钻孔灌注桩静载试验结果进行相关分析。现场测试表明,地表下存在约20 m的花岗岩残积土,地下水位位于地表以下约10 m处(即地下水位在桩端以下)。根据现场静力触探试验和Mascarucci[34]、Bolton[36]、Rowe[37]、Viana[46]和Jamiolkowski等[47]研究结果可知,该场地土层临界状态摩擦角约为32°,剪切带厚度ts约为4 mm,剪切模量折减系数α取其平均值0.75,qc实测值、Dr估算值、φp估算值和ψp估算值见图 3。
|
图 3 土层物理力学特性 Fig. 3 Physical and mechanical properties of soil layer |
单桩实测荷载-位移曲线和本文计算方法获得的单桩荷载-位移曲线见图 4。可以看出,本文方法计算得到的预测结果与实测结果较吻合。

|
图 4 桩顶荷载-沉降曲线的计算值和实测值 Fig. 4 Calculated and measured load-settlement curve at pile head |
该算例来自冯若峰等[48]开展的既有建筑地下土体开挖条件下在役桩承载特性模型试验。为模拟实际工程中的开挖过程,模型实验中桩基始终在承担上部荷载的条件下进行桩周土体的开挖。每层土体开挖后待在役桩变形稳定后方可进行下一层土体开挖。该模型试验中模型桩由铝管打磨制成,桩径为0.03 m,桩长为1.0 m,桩身弹性模量为25.9 GPa。试验中所用砂土的平均相对密实度、内摩擦角等参数见文献[48],不同开挖深度时砂土的剪切模量可根据经验公式(17)计算求得。既有建筑地下土体开挖条件下在役单桩实测荷载-归一化沉降(wt/D,即桩顶沉降/桩径)曲线和本文计算方法获得的单桩荷载-归一化沉降曲线见图 5。可以看出,对于地下增层开挖条件下的在役单桩,考虑和不考虑开挖卸荷效应计算得到的极限承载力相近,但考虑开挖效应计算结果要略高于不考虑开挖效应计算结果。对于桩顶刚度,考虑开挖土体回弹计算结果要低于不考虑土体回弹计算结果。考虑开挖卸荷回弹效应的计算结果与试验结果更为吻合。

|
图 5 在役桩顶荷载-归一化沉降曲线的计算值和实测值 Fig. 5 Calculated and measured load-normalized settlement curve at head of in-service pile |
需要指出的是,该算例涉及的是小尺度模型试验,开挖规模较小,土体应力状态变化不显著。对于原位条件下的增层开挖工程,考虑开挖卸荷效应,其计算值的差异可能会更加明显。
为研究坑底土回弹效应对于在役桩承载性能的影响,分析了土体回弹量大小对于荷载传递曲线的影响。分析中采用无量纲化参数减小参数取值对于结果的影响。选取了一系列归一化土体回弹量值wr/wref(wr为土体回弹量,wref为参考土体位移),并计算其对应的荷载传递曲线以及该曲线与不考虑土体回弹荷载传递曲线的偏差。该偏差由正规化方均根差表示,其中,参考土体位移wref由桩侧极限阻力τsu和桩侧初始承载刚度值ks0计算得到:
| $ w_{\text {ref }}=\frac{\tau_{\text {su }}}{k_{\mathrm{s} 0}} $ | (35) |
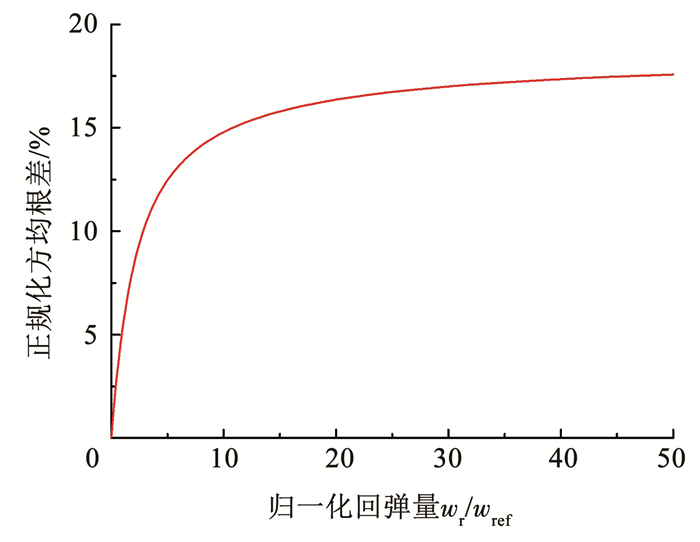
敏感性分析表明,采用无量纲化分析使得参数取值大小对结果不产生影响。计算的正规化方均根差与归一化回弹量的关系见图 6。可以看出,当归一化土体回弹量wr/wref < 1时,荷载传递曲线计算偏差小于5%,此时是否考虑土体回弹对于计算结果影响不大,实际分析中可略去回弹效应;当wr/wref>3时,计算误差已经超过了10%,沉降计算中需考虑土体回弹的影响。
|
图 6 土体回弹量对于荷载传递关系的影响 Fig. 6 Influence of soil rebounding on load transfer relationship of pile |
围绕既有建筑地下土体开挖条件下在役桩竖向承载能力评价等问题展开研究,提出了既有建筑地下土体开挖条件下在役桩基竖向承载特性的计算方法,并通过算例分析验证了本文计算方法的合理性。结论如下:
1) 地下增层在役桩基开挖效应包括开挖段侧阻力的直接损失、开挖卸荷引起的桩周土体应力状态变化及土体回弹引起的桩顶刚度降低。
2) 可采用双曲线模型模拟桩侧单位摩阻力和桩-土相对位移间的关系,可采用双折线模型模拟桩端位移和桩端阻力间的关系。
3) 对于较复杂的荷载传递函数,无法获得竖向荷载作用下单桩荷载传递微分方程的解析解时,可采用有限差分法,结合荷载传递法建立既有建筑地下土体开挖条件下在役桩基竖向承载特性的计算方法。
4) 对地下增层开挖条件下单桩进行分析时,应考虑开挖引起的土体回弹、桩周土超固结状态等因素对桩侧和桩端承载特性的影响。
5) 当归一化土体回弹量小于1时,荷载传递曲线计算偏差小于5%,沉降分析中可不考虑回弹效应。
| [1] |
李志勇. 老旧小区停车难题怎么破?[N]. 经济参考报, 2020-07-03(5)
|
| [2] |
贾强, 张鑫, 刘磊. 既有建筑地下增层技术的发展与展望[J]. 施工技术, 2018, 47(6): 84. JIA Qiang, ZHANG Xin, LIU Lei. Development and expectation of basement-addition technology in existing building[J]. Construction Technology, 2018, 47(6): 84. DOI:10.7672/sgjs2018060084 |
| [3] |
汤永净. 蒙特利尔地下空间扩建中的古建筑保护技术[J]. 地下空间与工程学报, 2010, 6(4): 672. TANG Yongjing. Montreal underground pedestrian network and protection of ancient church[J]. Chinese Journal of Underground Space and Engineering, 2010, 6(4): 672. DOI:10.3969/j.issn.1673-0836.2010.04.003 |
| [4] |
文颖文, 刘松玉, 胡明亮, 等. 地下增层工程中既有结构变形控制技术研究[J]. 岩土工程学报, 2013, 35(10): 1914. WEN Yingwen, LIU Songyu, HU Mingliang, et al. Deformation control techniques for existing buildings during construction process of basement[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(10): 1914. |
| [5] |
SHAN H, YU F, XIA T, et al. Performance of the underpinning piles for basement-supplementing retrofit of a constructed building[J]. Journal of Performance of Constructed Facilities, 2017, 31(4): 4017017. DOI:10.1061/(asce)cf.1943-5509.0001008 |
| [6] |
KRAFT L M, RAY R P, KAGAWA T. Theoretical t-z curves[J]. Journal of the Geotechnical Engineering Division, 1981, 107(11): 1543. DOI:10.1061/AJGEB6.0001207 |
| [7] |
ZHANG Q Q, LIU S W, ZHANG S M, et al. Simplified non-linear approaches for response of a single pile and pile groups considering progressive deformation of pile-soil system[J]. Soils and Foundations, 2016, 56(3): 473. DOI:10.1016/j.sandf.2016.04.013 |
| [8] |
XU K J, POULOS H G. General elastic analysis of piles and pile groups[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2000, 24(15): 1109. DOI:10.1002/1096-9853(20001225)24:15<1109::AID-NAG72>3.0.CO;2-N |
| [9] |
王伟, 杨敏. 竖向荷载下桩基础弹性分析的改进计算方法[J]. 岩土力学, 2006, 27(8): 1403. WANG Wei, YANG Min. An improved elastic analysis method of pile foundation under vertical loading[J]. Rock and Soil Mechanics, 2006, 27(8): 1403. DOI:10.3969/j.issn.1000-7598.2006.08.036 |
| [10] |
SAID I, DE GENNARO V, FRANK R. Axisymmetric finite element analysis of pile loading tests[J]. Computers and Geotechnics, 2009, 36(1/2): 6. DOI:10.1016/j.compgeo.2008.02.011 |
| [11] |
ZHANG Q Q, LIU S W, FENG R F, et al. Finite element prediction on the response of non-uniformly arranged pile groups considering progressive failure of pile-soil system[J]. Frontiers of Structural and Civil Engineering, 2020, 14(4): 961. DOI:10.1007/s11709-020-0632-5 |
| [12] |
ZHANG Q Q, ZHANG Z M, HE J Y. A simplified approach for settlement analysis of single pile and pile groups considering interaction between identical piles in multilayered soils[J]. Computers and Geotechnics, 2010, 37(7/8): 969. DOI:10.1016/j.compgeo.2010.08.003 |
| [13] |
ERNESTO M. Approximate elastic-plastic solution for axially loaded piles[J]. Journal of Geotechnical Engineering, 1994, 120(9): 1616. DOI:10.1061/(asce)0733-9410(1994)120:9(1616) |
| [14] |
ZHAO M H, YANG M H, ZOU J J. Vertical bearing capacity of pile based on load transfer model[J]. Journal of Central South University of Technology (English Edition), 2005, 12(4): 488. DOI:10.4324/9780203880876-11 |
| [15] |
WANG Z J, XIE X Y, WANG J C. A new nonlinear method for vertical settlement prediction of a single pile and pile groups in layered soils[J]. Computers and Geotechnics, 2012, 45(9): 118. DOI:10.1016/j.compgeo.2012.05.011 |
| [16] |
邹健, 张忠苗, 刘俊伟, 等. 一种考虑桩侧土应变软化的荷载传递函数[J]. 岩土工程学报, 2010, 32(7): 1109. ZOU Jian, ZHANG Zhongmiao, LIU Junwei, et al. A load transfer model considering stain softening of soils[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(7): 1109. |
| [17] |
林春金, 张乾青, 梁发云, 等. 考虑桩-土体系渐进破坏的单桩承载特性研究[J]. 岩土力学, 2014, 35(4): 1131. LIN Chunjin, ZHANG Qianqing, LIANG Fayun, et al. Analysis of bearing behavior of a single pile considering progressive failure of pile-soil system[J]. Rock and Soil Mechanics, 2014, 35(4): 1131. |
| [18] |
ZHANG Q Q, LIU S W, FENG R F, et al. Analytical method for prediction of progressive deformation mechanism of existing piles due to excavation beneath a pile-supported building[J]. International Journal of Civil Engineering, 2019, 17(6): 751. DOI:10.1007/s40999-018-0309-9 |
| [19] |
张乾青. 竖向抗压桩承载机理与受力特性分析方法[J]. 山东科技大学学报(自然科学版), 2020, 39(4): 93. ZHANG Qianqing. Bearing mechanism and response analysis method of vertically loaded piles[J]. Journal of Shandong University of Science and Technology (Nature Science), 2020, 39(4): 93. |
| [20] |
龚晓南, 伍程杰, 俞峰, 等. 既有地下室增层开挖引起的桩基侧摩阻力损失分析[J]. 岩土工程学报, 2013, 35(11): 1957. GONG Xiaonan, WU Chengjie, YU Feng, et al. Shaft resistance loss of piles due to excavation beneath existing basements[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(11): 1957. |
| [21] |
伍程杰, 龚晓南, 房凯, 等. 增层开挖对既有建筑物桩基承载刚度影响分析[J]. 岩石力学与工程学报, 2014, 33(8): 1526. WU Chengjie, GONG Xiaonan, FANG Kai, et al. Effect of excavation beneath existing buildings on loading stiffness of piles[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(8): 1526. DOI:10.13722/j.cnki.jrme.2014.08.003 |
| [22] |
曹平, 张敬一, 梁发云. 地下增层开挖时单桩竖向沉降的近似解析方法[J]. 结构工程师, 2019, 35(3): 216. CAO Ping, ZHANG Jingyi, LIANG Fayun. Theoretical analysis about influence of excavation under existing building to vertical settlement of piles[J]. Structural Engineers, 2019, 35(3): 216. DOI:10.3969/j.issn.1005-0159.2019.03.030 |
| [23] |
纠永志, 祝彦知. 开挖条件下非均质地基中单桩竖向承载特性非线性分析[J]. 岩土力学, 2017, 38(6): 1666. JIU Yongzhi, ZHU Yanzhi. Nonlinear analysis for bearing characteristics of vertically loaded single pile in non-homogeneous soil under excavation[J]. Rock and Soil Mechanics, 2017, 38(6): 1666. DOI:10.16285/j.rsm.2017.06.015 |
| [24] |
楼晓明, 李德宁, 刘建航. 深基坑坑底地基的回弹应力与回弹变形[J]. 土木工程学报, 2012, 45(4): 134. LOU Xiaoming, LI Dening, LIU Jianhang. Rebound stress and deformation below the bottom of deep excavations[J]. China Civil Engineering Journal, 2012, 45(4): 134. |
| [25] |
杨建民, 李嘉. 基坑底分层回弹量的实用计算方法[J]. 岩土力学, 2014, 35(5): 1413. YANG Jianmin, LI Jia. A practical method for calculating layerwise rebound at the bottom of foundation pit[J]. Rock and Soil Mechanics, 2014, 35(5): 1413. |
| [26] |
陈明, 李镜培. 开挖卸荷桩土界面荷载传递模型的修正与验证[J]. 哈尔滨工业大学学报, 2014, 46(10): 75. CHEN Ming, LI Jingpei. Improved hyperbolic model of load-transfer for pile-soil interface and its verification considering deep excavation[J]. Journal of Harbin Institute of Technology, 2014, 46(10): 75. DOI:10.11918/j.issn.0367-6234.2014.10.013 |
| [27] |
RANDOLPH M F, WROTH C P. Analysis of deformation of vertically loaded piles[J]. Journal of Geotechnical Engineering, 1978, 104(12): 1465. DOI:10.1061/ajgeb6.0000729 |
| [28] |
KISHIDA H, UESUGI M. Tests of the interface between sand and steel in the simple shear apparatus[J]. Géotechnique, 1987, 37(1): 45. DOI:10.1680/geot.1987.37.1.45 |
| [29] |
LOUKIDIS D, SALGADO R. Analysis of the shaft resistance of non-displacement piles in sand[J]. Géotechnique, 2008, 58(4): 283. DOI:10.1680/geot.2008.58.4.283 |
| [30] |
LEHANE B M. Scale effects on tension capacity for rough piles buried in dense sand[J]. Géotechnique, 2005, 55(10): 709. DOI:10.1680/geot.2005.55.10.709 |
| [31] |
ZHANG Q Q, ZHANG Z M. A simplified nonlinear approach for single pile settlement analysis[J]. Canadian Geotechnical Journal, 2012, 49(11): 1256. DOI:10.1139/cgj-2013-0022 |
| [32] |
FENG R F, ZHANG Q Q, LIU S W. Experimental study of the effect of excavation on existing loaded piles[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2020, 146(9): 04020091. DOI:10.1061/(asce)gt.1943-5606.0002336 |
| [33] |
HARDIN B O, DRNEVICH V P. Shear modulus and damping in soils: design equations and curves[J]. Journal of Soil Mechanics and Foundations Division, 1972, 98(7): 667. DOI:10.1061/jsfeaq.0001760 |
| [34] |
MASCARUCCI Y, MILIZIANO S, MANDOLINI A. 3M analytical method: evaluation of shaft friction of bored piles in sands[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2015, 142(3): 4015086. DOI:10.1061/(asce)gt.1943-5606.0001392 |
| [35] |
WERNICK E. Skin friction of cylindrical anchors in non-cohesive soils[C]//Proceedings Symposium on Soil Reinforcing and Stabilising Techniques in Engineering Practice. Sydney: [s. n. ], 1978: 201
|
| [36] |
BOLTON M D. Strength and dilatancy of sands[J]. Geotechnique, 1986, 36(1): 65. DOI:10.1680/geot.1986.36.1.65 |
| [37] |
ROWE P W. The stress-dilatancy relation for static equilibrium of an assembly of particles in contact[J]. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 1962, 269: 500. |
| [38] |
张乾青. 软土地基桩基受力性状和沉降特性试验与理论研究[D]. 杭州: 浙江大学, 2012 ZHANG Qianqing. Test and theoretical study on bearing capacity behavior and settlement of pile in soft soils[D]. Hangzhou: Zhejiang University, 2012 |
| [39] |
ZHANG Q Q, ZHANG Z M. Simplified calculation approach for settlement of single pile and pile groups[J]. Journal of Computing in Civil Engineering, 2012, 26(6): 750. DOI:10.1061/(asce)cp.1943-5487.0000167 |
| [40] |
ZHANG Q Q, LI L P, CHEN Y J. Analysis of compression pile response using a softening model, a hyperbolic model of skin friction, and a bilinear model of end resistance[J]. Journal of Engineering Mechanics, 2014, 140(1): 102. DOI:10.1061/(asce)em.1943-7889.0000640 |
| [41] |
张乾青, 李术才, 李利平, 等. 考虑侧阻软化和端阻硬化的群桩沉降简化算法[J]. 岩石力学与工程学报, 2013, 32(3): 615. ZHANG Qianqing, LI Shucai, LI Liping, et al. Simplified method for settlement prediction of pile groups considering skin friction softening and end resistance hardening[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(3): 615. |
| [42] |
YASUFUKU N, OCHIAI H, OHNO S. Pile end-bearing capacity of sand related to soil compressibility[J]. Soils and Foundations, 2001, 41(4): 59. DOI:10.3208/sandf.41.4_59 |
| [43] |
SHEIL B B, MCCABE B A. An analytical approach for the prediction of single pile and pile group behavior in clay[J]. Computers and Geotechnics, 2016, 75: 145. DOI:10.1016/j.compgeo.2017.01.008 |
| [44] |
CHENG S, ZHANG Q Q, LI S C, et al. Nonlinear analysis of the response of a single pile subjected to tension load using a hyperbolic model[J]. European Journal of Environmental and Civil Engineering, 2018, 22(2): 181. DOI:10.1080/19648189.2016.1185969 |
| [45] |
PAN D D, ZHANG Q Q, LIU S W, et al. Analysis on response prediction of a single pile and pile groups based on the Runge-Kutta method[J]. KSCE Journal of Civil Engineering, 2018, 22(1): 92. DOI:10.1007/s12205-017-0578-x |
| [46] |
FONSECA A V D, SANTOS J A. International prediction event. Behaviour of CFA, driven and bored piles in residual soil. ISC'2 experimental site[R]. Lisboa: FEUP, 2008
|
| [47] |
JAMIOLKOWSKI M, LO PRESTI D C F, MANASSERO M. Evaluation of relative density and shear strength of sands from CPT and DMT[C]// Symposium on Soil Behavior and Soft Ground Construction. Cambridge: American Society of Civil Engineers, 2003: 201
|
| [48] |
FENG R F, ZHANG Q Q, LIU S W. Experimental study of the effect of excavation on existing loaded piles[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2020, 146(9): 04020091. DOI:10.1061/(asce)gt.1943-5606.0002336 |
 2023, Vol. 55
2023, Vol. 55


