雷电是地球上普遍存在的自然现象,全球平均每年约发生14亿次,频率约为45次/s[1],其中,云地闪电是一种强大雷电流向大地释放能量的过程,每次云地闪电都涉及109~1010 J的能量,尽管其中大部分能量在空气传导中被消耗以产生雷声、热空气、光和无线电波[2-3],仍有约108 J的能量释放进大地中,产生的峰值电流可达数百千安,持续数十微秒,巨大能量和强烈电磁场活动会引发显著的冲击效应、电磁效应、光效应以及热效应,促使土体发生各种物理和化学过程[4-6]。近年来,雷电的相关研究已越来越细致深入,如部分电气工程学者对接地装置的雷电冲击特性开展研究,通过室内试验与数值模拟的方法对含接地极的土体雷电冲击特性进行了大量研究,重点分析了土体电性参数、雷电电流波形及其幅值、接地极结构等因素的影响[7-8],同时,通过X射线透射成像技术拍摄了土中的冲击放电影像[9-10]。航天材料学者们重点研究了用于飞机表层防护的碳纤维增强复合材料(CFRP)的雷击热效应[11-12]和力学损伤[13-16]。
然而,至今国内外以岩土体为对象,针对雷击对其造成的影响研究仍较少。实际上,雷击足以对土体造成破坏,Yokoyama[17]提到雷击会导致一些地方机场停机坪出现塌陷或地坑;Wakasa等[18]通过室内试验模拟雷击对岩石造成的破坏,指出巨大的雷电能量足以使岩石或土体失稳及破坏;Fajingbesi等[19]采用实验与数值模拟探究了雷击大地后土体电导率的变化以及土中放电电流分布;Castro等[20]通过实验分析了闪电与火山岩相互作用过程中的物理和化学变化,并使用电弧焊设备再现了天然闪电熔岩的地球化学和纹理特征;Chen等[21-22]采用理论分析和野外观测指出雷击对岩石中闪电熔岩的形成起着重要作用;Rao等[23-25]利用冲击电流发生器和自行设计的试验装置对不同条件(不同含水量、密实度、含盐量和温度)下的土体进行了模拟雷击试验,同时,采用电热耦合模型分析了雷电作用下岩土体的热效应[26]。另外,在防雷装置设计工作中,雷电冲击作用下,土中接地极等防雷装置的雷电冲击散流效应和防雷效益受其周围土体的影响极大,与土体相关参数息息相关,然而鉴于学科间的差异性和局限性,目前雷电作用下岩土工程和电气工程的交叉融合研究仍十分欠缺。因此,探究雷击对土体的热力等效应、雷电致灾机制等研究可为降低地下雷电灾害损失、指导防雷系统设计等工作提供一定指导,对岩土工程防雷减灾具有重要意义。
本文从雷电冲击波理论与电磁场理论出发,通过理论分析得到雷电过程中对土体引起的雷电冲击压力与脉冲电磁力,并采用有限元方法对土体在雷击冲击作用下的动态变形特性以及应力分布特征进行求解分析,确定土中变形等动态发展特征,在此基础上深入探究土体和雷电流等因素对雷击土体的动态变形响应影响规律。
1 雷击的力学冲击描述 1.1 基本假定1) 假设雷电通道垂直于土体表面,且土体表面为电绝缘平面,无电流流出。
2) 土体为连续均质的各向同性材料,忽略蠕变和松弛效应。
3) 雷击冲击作用时间很短,假定雷击期间土体不发生固结。
1.2 雷电冲击压力雷击放电过程中,由地表发出的回击电流可在几微秒内通过焦耳热的形式使空气急剧升温[27],形成可见的雷电等离子体通道。此过程中,在这极短时间内不足以使空气中雷电离子体通道内的粒子(电子、离子等)密度显著降低,这种温度的快速上升导致等离子体通道内压力大幅增加并产生超压,进而形成以超音速径向膨胀的圆柱形冲击波。假设冲击波内部等离子体的流动是等熵流动的且冲击波内空气为比热恒定的理想气体,则雷电冲击波内的控制方程为等离子体流动的运动方程、连续性方程和热力学流动方程:
| $ \frac{\partial u}{\partial t}+u \frac{\partial u}{\partial r}=-\frac{1}{\rho} \frac{\partial p}{\partial r} $ | (1) |
| $ \frac{\partial \rho}{\partial t}+u \frac{\partial \rho}{\partial r}+\rho\left(\frac{\partial u}{\partial r}+\frac{u}{r}\right)=0 $ | (2) |
| $ \left(\frac{\partial}{\partial t}+u \frac{\partial}{\partial r}\right)\left(\frac{p}{\rho^\kappa}\right)=0 $ | (3) |
式中:u、ρ和p分别为t时刻坐标为r处的速度、密度和压力;κ=cp/cV为空气的质量热容比,对于理想气体,κ=1.4。
在冲击波波阵面上,其以一定的速度移动,是一个强断面,前后的介质状态是不同的,根据Rankine-Hugoniot条件,由前后介质间的质量、动量和能量守恒关系,可以得到速度、密度和压力边界条件:
| $ \frac{u_1}{U}=\frac{2}{\gamma+1}\left(1-\frac{c_0^2}{U^2}\right) $ | (4) |
| $ \frac{\rho_1}{\rho_0}=\frac{\gamma+1}{\gamma-1+2 c_0^2 / U^2} $ | (5) |
| $ \frac{p_1}{p_0}=1+\frac{2 \kappa}{(\kappa+1)} \frac{1-c_0^2 / U^2}{c_0^2 / U^2} $ | (6) |
式中:u1、ρ1和p1分别为波阵面后的速度、密度和压力;ρ0、p0和c0为波阵面前无扰动空气的密度、压力和声速,其中,ρ0=1.293 kg/m3;U=dR/dt为波阵面运动速度。
根据Lin[28]、Karch等[29]的研究,可采用自相似方法对式(1)~(6)进行求解,冲击波前沿半径R(t)可由下式给出:
| $ R(t)=1.004\left(\frac{E_0}{\rho_0}\right)^{1 / 4} t^{1 / 2} $ | (7) |
式中E0为雷电冲击波单位长度扰动的总能量,与雷电流峰值Im有关,E0=0.45×10-2×Im1.25。
雷电冲击波的压力p=(η, t)可由下式描述:
| $ p(\eta, t)=0.180\left(\rho_0 E_0\right)^{1 / 2} f(\eta) t^{-1} $ | (8) |
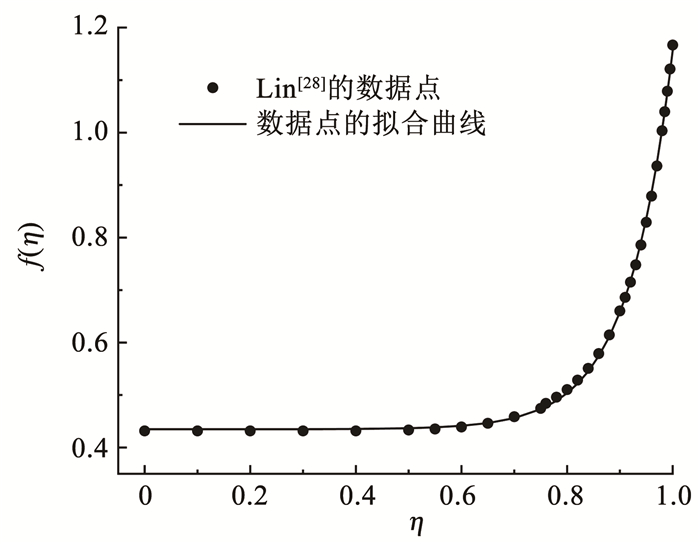
式中:η=r/R(t)为无量纲半径;f(η)为无量纲压力函数,描述了从起始点η=0到冲击波前沿η=1间的柱状压力分布,由于压力的自相似性,对任意时刻t都是有效的。根据Lin[28]的研究,其冲击波内各处的无量纲压力分布如图 1所示,将各f(η)点拟合可得
| $ f(\eta)=5.751 \times 10^{-6} \mathrm{e}^{11.74 \eta}+0.4348 $ | (9) |
|
图 1 f(η)-η拟合曲线 Fig. 1 Fitting curve of f(η)-η |
至此,雷电冲击压力可表示为
| $ \begin{aligned} p(\eta, t)= & 0.180\left(\rho_0 E_0\right)^{1 / 2}(5.751 \times \\ & \left.10^{-6} \mathrm{e}^{11.74 \eta}+0.4348\right) t^{-1} \end{aligned} $ | (10) |
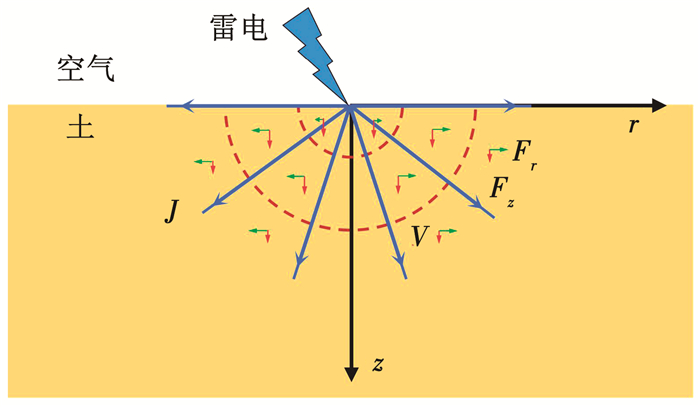
雷击发生时伴有强大的雷电流,其会在周围产生强烈的电磁场,土中将产生电磁力。Lee等[16]采用简化的二维麦克斯韦方程推导了雷电流在CFRP平面板内产生的脉冲电磁力表达式,适用于二维平面结构,但其并不适用于具有三维空间结构的土体,因此有必要进行雷电流在三维土体中的脉冲电磁力分析。如图 2所示,取土中任一纵截面,以雷击点为坐标原点,建立柱坐标系,将雷电流看作位于原点处的点电流源,假设雷电流仅在土中传导,即土体上表面为电绝缘平面。根据电磁场理论[30],土中将产生如图 2虚线的半球形等势面,其各点电势V为
| $ V(r, z)=\frac{I}{2 \pi \sigma \sqrt{r^2+z^2}}, z \geqslant 0 $ | (11) |
|
图 2 雷击电磁力计算示意 Fig. 2 Schematic diagram of lightning strike electromagnetic force calculation |
式中:I为雷电电流,σ为土体电导率。
由J=-σ×□V可得
| $ \left\{\begin{array}{l} J_r(r, z)=\frac{I r}{2 \pi\left(r^2+z^2\right)^{3 / 2}}, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;z \geqslant 0\\ J_z(r, z)=\frac{I z}{2 \pi\left(r^2+z^2\right)^{3 / 2}}, \\ J_\theta(r, z)=0, \end{array}\right. $ | (12) |
由于土体表面为电绝缘平面,无电流穿过,则有
| $ J(r, z)=0, z<0 $ | (13) |
根据麦克斯韦方程,其各点磁场强度H的散度等于电流密度J,即□×H=J,其在柱坐标系内可写为
| $ \begin{aligned} \square \times H(r, \theta, z)= & \left(\frac{1}{r} \frac{\partial H_z}{\partial \theta}-\frac{\partial H_\theta}{\partial z}\right) \boldsymbol{e}_r+\left(\frac{\partial H_r}{\partial z}-\frac{\partial H_z}{\partial r}\right) \boldsymbol{e}_\theta+ \\ & \frac{1}{r}\left[\frac{\partial\left(r H_\theta\right)}{\partial r}-\frac{\partial H_r}{\partial \theta}\right] \boldsymbol{e}_z \end{aligned} $ | (14) |
由于雷电流引起的磁场强度H呈对称分布,其与θ无关,将式(12)、(13)代入式(14),□×H=J可化简为
| $ \left\{\begin{array}{l} -\frac{\partial H_\theta}{\partial z}=\frac{I r}{2 \pi\left(r^2+z^2\right)^{3 / 2}}, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;z \geqslant 0\\ \frac{1}{r} \frac{\partial\left(r H_\theta\right)}{\partial r}=\frac{I z}{2 \pi\left(r^2+z^2\right)^{3 / 2}}, \end{array}\right. $ | (15) |
| $ \left\{\begin{array}{l} -\frac{\partial H_\theta}{\partial z}=0, \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;z<0\\ \frac{1}{r} \frac{\partial\left(r H_\theta\right)}{\partial r}=0, \end{array}\right. $ | (16) |
求解式(15)和(16),可得
| $ H_\theta^{(\mathrm{i})}(r, z)=\frac{I}{2 \pi r}\left(C_1-\frac{z}{\sqrt{r^2+z^2}}\right), z \geqslant 0 $ | (17) |
| $ H_\theta^{(\mathrm{e})}(r, z)=C_2 / r, z <0 $ | (18) |
式中:C1、C2为待定常数,i、e分别表示土体内部与外部空气区域。
代入边界条件
| $ H_\theta^{(\mathrm{i})}(r, z)=0, z \rightarrow+\infty $ | (19) |
| $ H_\theta^{(\mathrm{i})}(r, z)=H_\theta^{(\mathrm{e})}(r, z), z=0 $ | (20) |
可得
| $ C_1=1, C_2=I /(2 \pi) $ | (21) |
则式(17)、(18)可写成
| $ H_\theta^{(\mathrm{i})}(r, z)=\frac{I}{2 \pi r}\left(\frac{\sqrt{r^2+z^2}-z}{\sqrt{r^2+z^2}}\right), z \geqslant 0 $ | (22) |
| $ H_\theta^{(\mathrm{e})}(r, z)=\frac{I}{2 \pi r}, z <0 $ | (23) |
土中电磁力可表示为电流密度J与磁感应强度B的叉乘,则在z≥0土中区域,电磁体积力可计算为
| $ \begin{aligned} F_z \boldsymbol{e}_z= & J_r(r, z) \boldsymbol{e}_r \times B \boldsymbol{e}_\theta=J_r(r, z) \boldsymbol{e}_r \times u_{\mathrm{r}} u_0 H \boldsymbol{e}_\theta= \\ & {\left[J_r(r, z) u_\mathrm{r} u_0 H\right] \boldsymbol{e}_z=\frac{u_\mathrm{r} u_0 I^2}{4 \pi^2} \frac{\sqrt{r^2+z^2}-z}{\left(r^2+z^2\right)^2} \boldsymbol{e}_z } \end{aligned} $ | (24) |
| $ \begin{aligned} F_r \boldsymbol{e}_r= & J_z(r, z) \boldsymbol{e}_z \times B \boldsymbol{e}_\theta=J_z(r, z) \boldsymbol{e}_z \times u_{\mathrm{r}} u_0 H \boldsymbol{e}_\theta= \\ & {\left[J_z(r, z) u_{\mathrm{r}} u_0 H\right] \boldsymbol{e}_r=\frac{u_{\mathrm{r}} u_0 I^2}{4 \pi^2} \frac{z \sqrt{r^2+z^2}-z^2}{r\left(r^2+z^2\right)^2} \boldsymbol{e}_r } \end{aligned} $ | (25) |
式中:u0=4π×10-7 H/m为空气磁导率;ur为相对磁导率,对于土体,ur=1。
为验证电磁力推导的正确性,将本文电磁力结果与文献[16]所得雷电作用在CFRP平面板内产生的脉冲电磁力结果进行对比。由于文献[16]仅得出电磁力的竖向压力表达式,只适用于二维平面分析,而本文土体中电磁力基于三维空间坐标,可进行退化对比,将式(25)沿z方向积分,可得本文脉冲电磁力的竖向分量表达式
| $ F(r)=\int_0^{+\infty} F_z \boldsymbol{e}_z \mathrm{d} z=\frac{u_{\mathrm{r}} u_0 I^2}{8 \pi^2 r^2} $ | (26) |
式(26)结果与文献[16]竖向压力电磁力结果相同,因此,可以验证本文雷电作用下土中脉冲电磁力算法的正确与合理性。
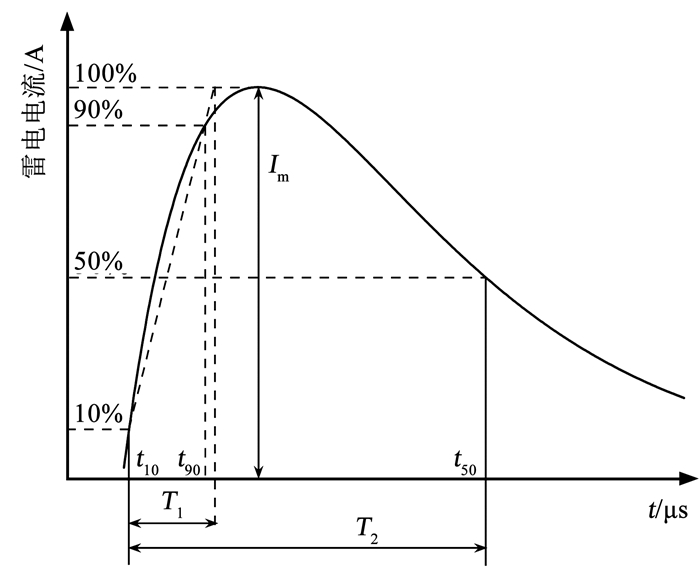
1.4 标准雷电流波形标准雷电流波形的主要参数为雷电流峰值Im、波前时间T1和半峰值时间T2,如图 3所示,雷电流峰值Im表示雷电全过程中的最大电流值,波前时间T1为电流峰值的10%~90%时间间隔的1.25倍,描述雷电流从开始到峰值的时间,半峰值时间T2为电流随时间衰减到峰值50%的时间。双指数波形是国际雷电防护标准IEC62305[31]和建筑物防雷设计规范GB 50057—2010规定的雷电流标准波形,其描述的波形特征和实际测量波形相近,可以很好地反映雷电流的特征值[32],且形式简单,便于计算,本文采用双指数波形模型作为雷电流表达式,即
| $ I(t)=\lambda I_{\mathrm{m}}\left(\mathrm{e}^{-\alpha t}-\mathrm{e}^{-\beta t}\right) $ | (27) |
|
图 3 雷电电流波形 Fig. 3 Waveform of lightning current |
式中:I(t)为雷电流的瞬时值,Im为雷电流峰值,λ为波峰修正系数,α为波前系数,β为波尾系数。
2 有限元模型的建立基于有限元方法的COMSOL Multiphysics软件具有强大的多物理场仿真功能,以灵活开放、易用高效著称,能够很方便地定义出本文由多变量控制的荷载函数。采用COMSOL Multiphysics中的固体力学模块建立雷击作用下土体的动力特性瞬态模型。
2.1 土体本构模型雷击冲击作用下,土体将产生不可恢复的塑性变形,应采用弹塑性本构模型,COMSOL Multiphysics中提供了匹配Mohr-Coulomb准则的Drucker-Prager外接圆(DP1)准则[33],本文采用该模型,其形式为
| $ F=\sqrt{J_2}+\alpha I_1-k $ | (28) |
式中:I1、J2分别为应力张量第一不变量和偏应力第二不变量;α、k为与土体黏聚力c和内摩擦角φ相关的常数,α和k的不同取值在π平面内表示不同的圆,对于DP1准则,α和k表示为
| $ \alpha=\frac{2 \sin \varphi}{\sqrt{3}(3-\sin \varphi)}, k=\frac{2 \sqrt{3} c\mathrm{cos }\varphi}{3-\sin \varphi} $ | (29) |
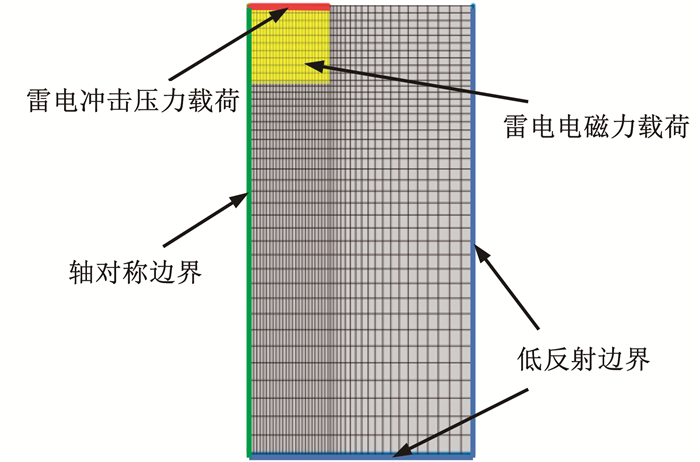
在假定土体为各向同性材料的条件下,雷电冲击作用呈轴对称分布,为简化模型与计算量,可采用二维轴对称模型。如图 4所示,土体几何尺寸为1.0 m×0.5 m,在左侧边界上设置为轴对称边界条件,由于雷击作用是一个瞬态过程,模型计算时还应防止土中压力波和剪切波在边界处发生反射,造成计算结果反复震荡,影响计算精度,将模型下侧以及右侧边界设置为低反射边界以截断计算域,可以很好地减少边界反射造成的影响。采用国际雷电防护标准IEC62305[31]推荐的T1/T2=10/350 μs的标准雷电流波形进行雷电作用模拟,雷电流峰值Im=100 kA,其雷电流与土体参数如表 1所示。
|
图 4 有限元计算模型 Fig. 4 Finite element model |
| 表 1 雷电流和土体参数 Tab. 1 Lightning current and soil parameters |
另外,定义由位置变量r、z以及时间变量t控制的雷电冲击压力与脉冲电磁力函数表达式,并将雷电冲击压力作为边界载荷施加在模型上侧边界,将雷电脉冲电磁力作为体载荷添加在模型左上方矩阵区域内。经对雷电冲击压力和电磁力表达式分析可知,其影响范围主要集中于雷击点附近,冲击力大小随距离增加而迅速减小,本文设置雷电冲击压力边界范围为0.35 m,雷电电磁力作用矩形的尺寸为0.35 m×0.35 m,以模拟雷电对土体的力学冲击作用。采用映射方式划分四边形网格,并对荷载作用区域进行局部加密处理,以提高雷击计算结果的精度,而外部影响较小区域网格相较疏松,以提高模型计算速度。瞬态计算时间步长采用Δt=0.000 1 ms,计算时间共3 ms。
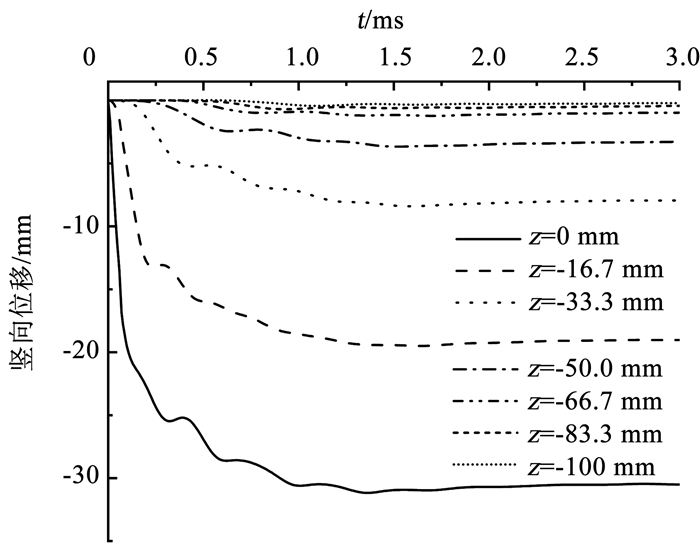
3 雷击动力特性分析图 5和6分别为雷击点以下(即r=0)不同深度处各点的竖向位移时程曲线和Mises应力时程曲线。由图 5可以看出,位移变化较大各点均表现为前期迅速变化,而后变形速度逐渐减缓,最终约在1.5 ms附近达到稳定状态,这主要是因为雷电冲击作用载荷与爆炸作用类似,呈现出急剧变大而后又迅速减小的特点。同时可以看出,竖向变形随深度的增加衰减得很快,在雷击点即z=0 mm的最终稳定位移最大,达到30.51 mm,而雷击点以下各点的位移迅速减小,在z=-66.7 mm处,其稳定位移仅为0.97 mm,说明此处受影响很小,可认为此时雷击有效影响深度为66.7 mm。
|
图 5 不同深度处的位移时程曲线 Fig. 5 Time history of displacement at different depths |
|
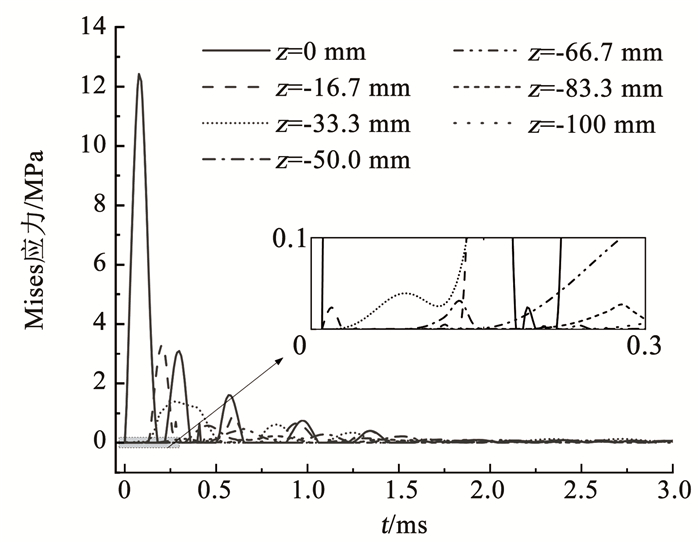
图 6 不同深度处的Mises应力时程曲线 Fig. 6 Time history of Mises stress at different depths |
由图 6可知,雷击作用下各深度处的Mises应力在雷击初期陡增后随时间推移又不断衰减,整体表现出一个主峰值和多个较小峰值,约在1.5 ms附近衰减至0,而后保持不变,这与图 5中竖向位移随时间变化类似,其应力与位移保持同步性。Mises应力曲线主峰值随深度增大也变化明显,在雷击点处其值为12.43 MPa,而在z=-16.7 mm处减小为3.26 MPa。此外,从图 6局部放大图可以看到,不同深度处的Mises应力最初上升时间约为0、0.005、0.02、0.08、0.15、0.20、0.25 ms,随深度增加逐渐延后,反映了应力波在土中的分布特征。
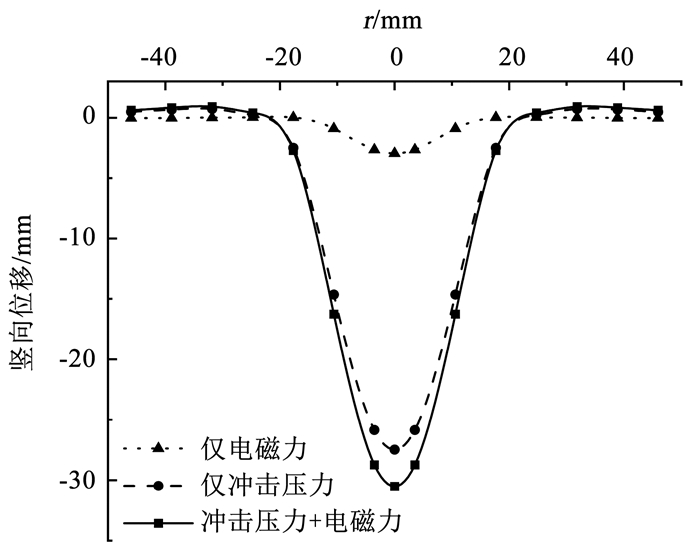
图 7为同时考虑雷电冲击压力和电磁力、仅考虑雷电冲击压力、仅考虑电磁力3种情况下土体表面最终稳定时的竖向位移分布。可以看出,3种情况下各处的竖向位移沿雷击中心点呈对称分布,并在中心点处取得最大值,随着离雷击点距离r增大竖向变形不断减小,并在距离30 mm附近存在土体少量隆起,这是由于在强大的冲击作用下土体内部会产生侧向挤压作用,使得距雷击点周围一定距离处的土体有向上运动趋势,造成隆起变形。在隆起区域外侧的土体表面处,竖向变形逐渐减小为0,此区域的土体位移影响很小。3种情况下表面土体位移随r变化规律相同,但其各点处数值明显不同,对于雷击点处,即竖向位移最大处,其变形值分别为30.51、27.46和2.96 mm,比较这3种情况各自对土体变形的影响可知,电磁力造成的影响仅能达到雷电冲击压力的10.78%,但从图 7中同时考虑这两种效应的曲线可以看出,电磁力对最终土体表面位移仍有较大影响。
|
图 7 土体表面竖向位移 Fig. 7 Vertical displacement of soil surface |
雷电作用下的土体变形是个多因素问题,为探究不同土体力学参数下地表的变形特性及主次影响因素,采用正交分析法[34]进行多因素分析,选取的主要影响因素为弹性模量E、泊松比μ、黏聚力c和内摩擦角φ,每个参数都有4个不同的水平,各因素的水平如表 2所示。
| 表 2 不同水平下的土体因素 Tab. 2 Soil parameters at different levels |
根据正交分析法的设计原则,由于每个因素有4个水平,选用L16(45)的正交表进行研究计算,该表可最多安排5个参数,将所选的4个因素安排在正交表前4列,剩余的第5列不安排因素,作为空白列检验误差水平。各方案设计与地表最大竖向变形计算结果如表 3所示,共有16种方案,相对于全面计算方案的256种,工作量显著减少。
| 表 3 正交分析方案和计算结果 Tab. 3 Orthogonal analysis schemes and calculation results |
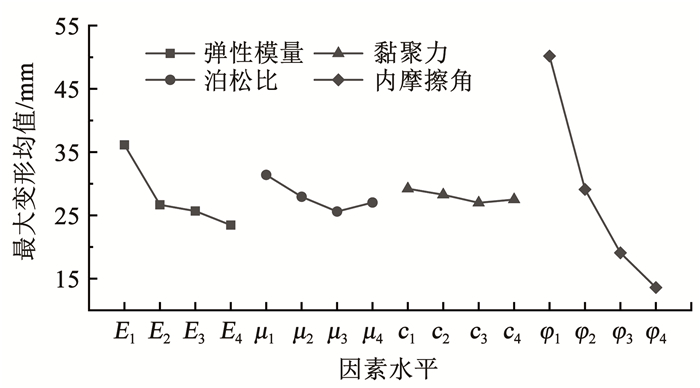
根据表 3中的结果进行极差分析,结果如表 4和图 8所示。通过极差比较,各因素对最大变形的影响从主到次的排序为内摩擦角φ、弹性模量E、泊松比μ、黏聚力c。由图 8可以看出,随着各因素水平的增加,雷击下的地表最大变形均呈不同程度的减小趋势,其中,内摩擦角的影响较为明显,而黏聚力的影响相对较小。
| 表 4 最大变形的极差分析 Tab. 4 Range analysis of maximum deformation |
|
图 8 各影响因素水平与最大变形均值趋势 Fig. 8 Trend of mean value of maximum deformation at each factor level |
对表 3结果进行方差分析,探究各因素显著性水平,结果见5所示。选取显著性水平α分别为0.01、0.05和0.1,由于各因素的自由度为3,误差项的自由度为15-12=3,根据F分布可知F0.01(3, 3)=29.46,F0.05(3, 3)=9.28,F0.1(3, 3)=5.39。若计算的F值大于F0.01时,表示该因素对地表最大变形的影响高度显著,记为“***”;若计算的F值大于F0.05但不大于F0.01时,表示该因素的影响显著,记为“**”;若计算的F值大于F0.1但不大于F0.05时,表示该因素对地表最大变形有一定影响,记为“*”;若计算的F值小于F0.05时,表示该因素的影响不显著。表 5的结果表明:对于雷电冲击作用下的地表最大变形,内摩擦角φ的影响高度显著,这是因为土体变形与本构模型有关,本文采用的DP1准则在主应力空间和π平面上的屈服面半径与内摩擦角密切相关,内摩擦角越小时,主应力空间和π平面上的屈服面半径就越小,弹性范围越窄,此时相同应力状态下土体更易进入塑性状态,土体变形会明显增加,因此,内摩擦角的影响最为显著。
| 表 5 最大变形的方差分析 Tab. 5 Variance analysis of maximum deformation |
由4.1节正交分析法可知,雷电冲击作用下,土体内摩擦角φ对土体变形的影响最为显著,本节重点考察内摩擦角的影响规律,采用内摩擦角φ=10°、20°、30°、40° 4种情况分别进行模拟计算,其他雷电流和土体参数同表 1一致。
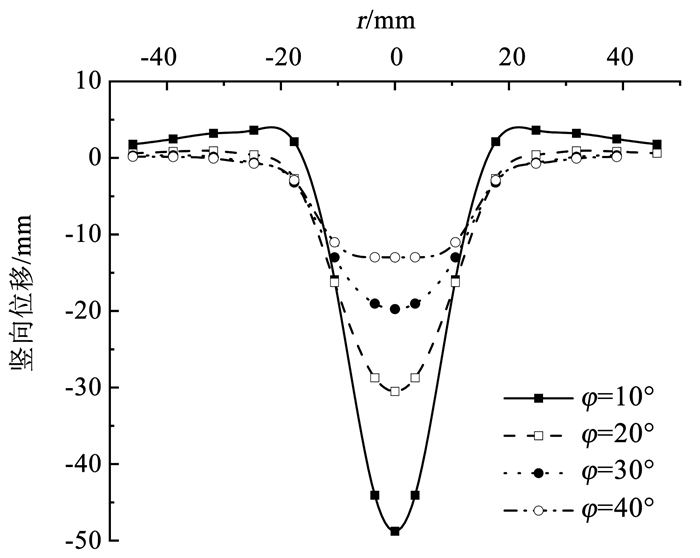
图 9为不同内摩擦角φ条件下的土体表面竖向位移结果。从宏观上看,不同内摩擦角条件下的表面整体变形规律与前述相同,即沿雷击中心点呈对称分布,且在雷击点处变形最大,而后两侧位移逐渐减小,并伴有少量隆起,最终最外侧土体几乎不受影响;从数值上看,内摩擦角的改变对土体变形影响较大,其值越小时,雷击点的竖向位移越大,且土体周围向上隆起程度也明显变大,当φ=10°时,其最大竖向位移为48.78 mm,最大隆起高度为3.99 mm,而当φ=40°时,最大竖向位移仅为12.98 mm,而此时周围土体几乎没有隆起现象;从整体变形曲线来看,内摩擦角较大时,其整体变形曲线仍为深凹状,而随着内摩擦角的减小逐渐呈扁平状,此时雷击点周围一定宽度内的竖向变形大致相同。
|
图 9 不同内摩擦角下的土体表面竖向位移 Fig. 9 Vertical displacement of soil surface under different internal friction angles |
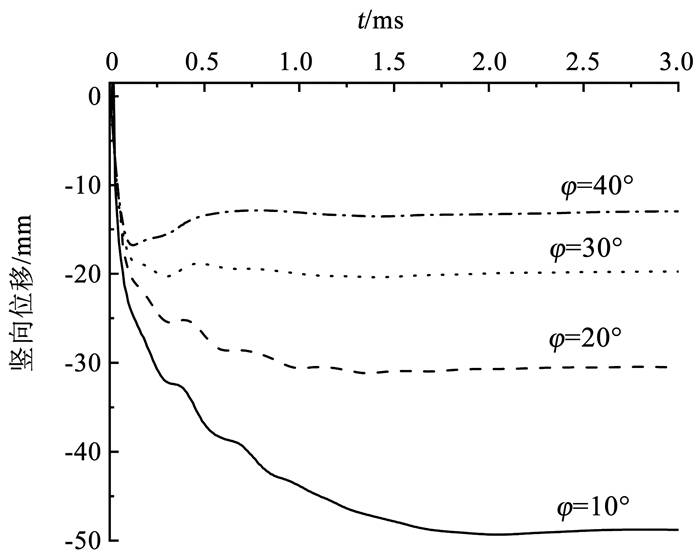
图 10为不同内摩擦角φ下雷击点处即变形最大处的竖向位移时程曲线。可以看出,在不同内摩擦角下,雷电作用初期土体变形基本一致,而后随着时间的推移,整体位移呈现先增大后减小而后逐步趋于稳定的趋势,且内摩擦角越小时其位移达到稳定所需时间越长,这是由于当摩擦角较小时,土体屈服面半径较小,弹性范围较窄,更容易进入塑性状态,在雷电冲击作用数值达到峰值后土体依然处于塑性屈服状态,其变形将继续变大,因此,达到稳定耗时最长。另外,在雷电冲击下土体先出现弹塑性变形,而后随着冲击作用减小直至消失,其弹性变形逐渐恢复,最终稳定时仅剩余塑性变形,这在内摩擦角较大时更加明显。这是因为摩擦角较大时土体屈服面半径较大,弹性范围较广,产生的弹性变形更多,摩擦角较大时回弹现象更明显。如从φ=40°条件下的竖向位移时程曲线可以明显看出,在0.12 ms后出现显著的弹性位移恢复现象,整个雷击作用中,该点最大竖向位移为16.78 mm,最终稳定位移为12.95 mm,恢复了22.82%,而对于其他内摩擦角条件下,其回弹量不足5%,这也是致使图 9中呈扁平状的重要原因。
|
图 10 不同内摩擦角φ下的位移时程曲线 Fig. 10 Time history of displacement under different internal friction angles φ |
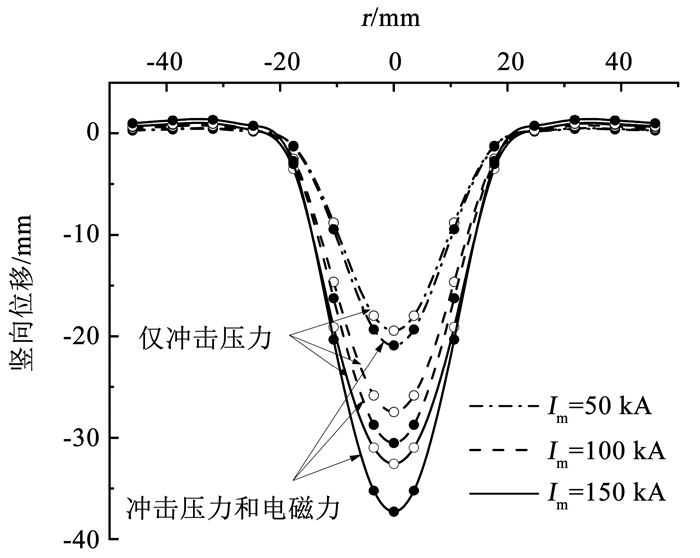
雷电流峰值Im作为衡量雷电能量的重要指标,与雷电冲击压力和电磁力的大小直接相关。为探究雷电流峰值对土体雷击变形的影响,保持表 1其他参数不变,分别选用Im=50、100和150 kA进行模拟计算,并分别考量在此过程中脉冲电磁力的影响,各情况下的表面竖向位移结果如图 11所示。可以看出,其表面变形规律与前所述相同,并呈深凹状。此外,雷电流峰值越大时其变形量越大,并且从仅考虑雷电冲击压力与同时考虑雷电冲击压力和电磁力对比结果中发现,同时考虑这两种冲击作用时土体变形量更大,其雷击点竖向位移分别比仅考虑雷电冲击压力时大7.45%、11.11%和14.53%,说明雷电流峰值越大时电磁力对土体变形影响越大,在大电流作用下应着重考虑其影响。
|
图 11 不同雷电流峰值Im下的土体表面竖向位移 Fig. 11 Vertical displacement of soil surface under different lightning current peaks Im |
应用雷电冲击波理论,并基于麦克斯韦方程推导了雷电在土中产生的电磁力表达式,以此建立雷电冲击压力和电磁力作用下的土体变形特性有限元瞬态模型,主要结论如下:
1) 雷击冲击作用下土体先产生弹塑性变形,随着雷击的结束其弹性变形逐渐恢复,最终仅剩余塑性变形,其整体变形规律表现为雷击初期表面土体急剧变形,而后变形速率逐渐减缓,部分土体回弹后趋于稳定,此外,土中应力分布特征规律与应力波传播规律类似。
2) 通过正交分析可以得到土体各力学参数对雷击效应的影响大小,内摩擦角影响较为显著,弹性模量影响次之,泊松比和黏聚力的影响相对较小。随着内摩擦角和弹性模量的减小,其变形均表现为增大的趋势,并伴有一定隆起,且随着内摩擦角的增大,表面竖向位移曲线由深凹状逐渐过渡为扁平状。
3) 雷电流峰值是衡量雷电荷载大小的重要因素,随着雷电流峰值的不断增大,更大的雷电冲击力将引起更大的土体变形,并且雷电脉冲电磁力对整体变形的影响贡献也逐渐提升,在进行较大雷电流作用对土体的冲击效应研究中应予以重视。
4) 在工程防雷设计中,就特定因素而言,可增大布置在防雷装置周围的土体内摩擦角等力学参数以减小土体变形,减少防雷装置扰动影响,保证防雷装置的雷电冲击散流效应和防雷效益。
5) 本文研究成果对建筑及电力工程地基基础防雷接地系统设计和改造以及保障工程建设区域安全具有一定意义。另外,评估雷击后土体力学性状也为从岩土工程角度研究防雷减灾提供了新思路。
| [1] |
CHRISTIAN H J, BLAKESLEE R J, BOCCIPPIO D J, et al. Global frequency and distribution of lightning as observed from space by the optical transient detector[J]. Journal of Geophysical Research: Atmospheres, 2003, 108: ACL 4-1. DOI:10.1029/2002JD002347 |
| [2] |
RAKOV V A. Lightning makes glass[C]//29th Annual Conference of the Glass Art Society. Tampa: [s. n. ], 1999: 45
|
| [3] |
SAIKIA B J, PARTHASARATHY G, SARMAH N C, et al. Fourier-transform infrared spectroscopic characterization of naturally occurring glassy fulgurites[J]. Bulletin of Materials Science, 2008, 31: 155. DOI:10.1007/s12034-008-0027-z |
| [4] |
RAKOV V A, UMAN M A. Lightning: physics and effects[M]. New York: Cambridge University Press, 2003.
|
| [5] |
MACGORMAN D R, RUST W D. The electrical nature of storms[M]. New York: Oxford University Press, 1998.
|
| [6] |
李景丽, 袁涛, 杨庆, 等. 考虑土壤电离动态过程的接地体有限元模型[J]. 中国电机工程学报, 2011, 31(22): 149. LI Jingli, YUAN Tao, YANG Qing, et al. Finite element model of grounding system considering soil dynamic ionization[J]. Proceedings of the CSEE, 2011, 31(22): 149. DOI:10.1080/17415993.2010.547197 |
| [7] |
LI J L, YUAN T, YANG Q, et al. Numerical and experimental investigation of grounding electrode impulse-current dispersal regularity considering the transient ionization phenomenon[J]. IEEE Transactions on Power Delivery, 2011, 26(4): 2647. DOI:10.1109/TPWRD.2011.2158860 |
| [8] |
司马文霞, 艾琳丰, 袁涛, 等. 土壤介电频变特性试验研究及其对接地极冲击特性的影响[J]. 中国电机工程学报, 2015, 35(16): 4247. SIMA Wenxia, AI Linfeng, YUAN Tao, et al. Experimental study on the frequency characteristic of soil permittivity and the influence on impact characteristics of grounding electrode[J]. Proceeding of the CSEE, 2015, 35(16): 4247. |
| [9] |
SIMA W X, LIU S W, YUAN T, et al. Experimental study of the discharge area of soil breakdown under surge current using X-ray imaging technology[J]. IEEE Transactions on Industry Applications, 2015, 51(6): 5343. DOI:10.1109/TIA.2015.2448615 |
| [10] |
LIU S W, SIMA W X, YUAN T, et al. Study on X-ray imaging of soil discharge and calculation method of the ionization parameters[J]. IEEE Transactions on Power Delivery, 2016, 32(4): 2013. DOI:10.1109/TPWRD.2016.2597238 |
| [11] |
OGASAWARA T, HIRANO Y, YOSHIMURA A. Coupled thermal-electrical analysis for carbon fiber/epoxy composites exposed to simulated lightning current[J]. Composites Part A: Applied Science & Manufacturing, 2010, 41(8): 973. DOI:10.1016/J.COMPOSITESA.2010.04.001 |
| [12] |
DONG Q, WAN G S, GUO Y L, et al. Damage analysis of carbon fiber composites exposed to combined lightning current components D and C[J]. Composites Science and Technology, 2019, 179: 1. DOI:10.1016/j.compscitech.2019.04.030 |
| [13] |
KARCH C, ARTEIRO A, NOBIS F, et al. Modelling and simulation of lightning-induced damage of CFRP structures[C]//International Conference on Lightning and Static Electricity. Nagoya: [s. n. ], 2017
|
| [14] |
KARCH C, ARTEIRO A, CAMANHO P. Modelling mechanical lightning loads in carbon fibre-reinforced polymers[J]. International Journal of Solids and Structures, 2019, 162: 217. DOI:10.1016/j.ijsolstr.2018.12.013 |
| [15] |
LEE J, LACY J T, PITTMAN J C, et al. Numerical estimations of lightning-induced mechanical damage in carbon/epoxy composites using shock wave overpressure and equivalent air blast overpressure[J]. Composite Structures, 2019, 224: 111039. DOI:10.1016/j.compstruct.2019.111039 |
| [16] |
LEE J, LACY J T, PITTMAN J C. Coupled thermal electrical and mechanical lightning damage predictions to carbon/epoxy composites during arc channel shape expansion[J]. Composite Structures, 2021, 255: 112912. DOI:10.1016/j.compstruct.2020.112912 |
| [17] |
YOKOYAMA S. A possible formation of weathering pits triggered by the falling of thunderbolts[J]. Transactions, Japanese Geomorphological Union, 2007, 28: 267. |
| [18] |
WAKASA S A, NISHIMURA S, SHIMIZU H, et al. Does lightning destroy rocks? Results from a laboratory lightning experiment using an impulse high-current generator[J]. Geomorphology, 2012, 161/162. DOI:10.1016/j.geomorph.2012.04.005 |
| [19] |
FAJINGBESI F E, MIDI N S, ELSHEIKH E, et al. Induced current distribution in 3D soil model as lightning impulse discharge strike earth surface[C]//2019 9th International Conference on Power and Energy Systems(ICPES). Perth: IEEE, 2019
|
| [20] |
CASTRO J M, KELLER F, FEISEL Y, et al. Lightning-induced weathering of Cascadian volcanic peaks[J]. Earth and Planetary Science Letters, 2020, 552: 116595. DOI:10.1016/j.epsl.2020.116595 |
| [21] |
CHEN J, ELMI C, GOLDSBY D, et al. Generation of shock lamellae and melting in rocks by lightning-induced shock waves and electrical heating[J]. Geophysical Research Letters, 2017, 44(17): 8757. DOI:10.1002/2017GL073843 |
| [22] |
ELMI C, CHEN J, GOLDSBY D, et al. Mineralogical and compositional features of rock fulgurites: a record of lightning effects on granite[J]. American Mineralogist: Journal of Earth and Planetary Materials, 2017, 102(7): 1470. DOI:10.2138/am-2017-5971 |
| [23] |
RAO P P, CHEN Q S, NIMBALKAR S, et al. Effect of water and salinity on soil behaviour under lightning[J]. Environmental Geotechnics, 2016, 5(1): 56. |
| [24] |
RAO P P, CHEN Q S, NIMBALKAR S, et al. Laboratory study on impulse current characteristics of clay[J]. Environmental Geotechnics, 2017, 4(3): 199. DOI:10.1680/jenge.15.00051 |
| [25] |
饶平平, 刘洋, 刘彬. 改善雷电压冲击土体中电压降分布模拟试验[J]. 上海理工大学学报, 2016, 38(3): 276. RAO Pingping, LIU Yang, LIU Bin. Simulation test for improving the distribution of voltage drop in soil under the action of lightning impulse[J]. University of Shanghai for Science and Technology, 2016, 38(3): 276. |
| [26] |
RAO P P, XIANG Y B, OUYANG P H, et al. Finite element analysis of electro-thermal coupling of sandstone under lightning currents[J]. Geotechnical and Geological Engineering, 2022, 1. DOI:10.1007/s10706-022-02048-2 |
| [27] |
ORVILLE R E. A high-speed time-resolved spectroscopic study of the lightning return stroke[J]. Journal of Atmospheric Sciences, 1968, 25: 852. DOI:10.1175/1520-0469(1968)025<0852:AHSTRS>2.0.CO;2 |
| [28] |
LIN S C. Cylindrical shock waves produced by instantaneous energy release[J]. Journal of Applied Physics, 1954, 25(1): 54. DOI:10.1063/1.1721520 |
| [29] |
KARCH C, SCHREINER M, HONKE R, et al. Shock waves from a lightning discharge[C]//2018 34th International Conference on Lightning Protection(ICLP). Rzeszow: IEEE, 2018: 1
|
| [30] |
赵凯华, 陈熙谋. 电磁学[M]. 北京: 高等教育出版社, 2011. ZHAO Kaihua, CHEN Ximou. Electromagnetism[M]. Beijing: Higher Education Press, 2011. |
| [31] |
Protection against lightning Part 1. General principles: IEC 62305-1: 2010[S]. Geneva: International Electrotechnical Commission(IEC), 2010
|
| [32] |
张岩, 刘福贵, 汪友华, 等. 改进的双指数函数雷电流波形及其辐射电磁场的计算[J]. 电工技术学报, 2013, 28(增刊2): 133. ZHANG Yan, LIU Fugui, WANG Youhua, et al. A modify double exponential base-current and its application in evaluating the lightning EM fields[J]. Transactions of China Electrotechnical Society, 2013, 28(S2): 133. |
| [33] |
邓楚键, 何国杰, 郑颖人. 基于M-C准则的D-P系列准则在岩土工程中的应用研究[J]. 岩土工程学报, 2006, 28(6): 735. DENG Chujian, HE Guojie, ZHENG Yingren. Studies on Drucker-Prager yield criterions based on M-C yield criterion and application in geotechnical engineering[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(6): 735. |
| [34] |
任露泉. 试验设计及其优化[M]. 北京: 科学出版社, 2009. REN Luquan. Experimental design and optimization[M]. Beijing: Science Press, 2009. |
 2023, Vol. 55
2023, Vol. 55


