2. 浙江大学 滨海和城市岩土工程研究中心,杭州 310058
2. Research Center of Coastal and Urban Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China
土体的渗透系数及体积变化均会不同程度地受到温度的影响,同时,渗透系数及体积变化规律也会影响土体的固结过程,因此,温度的改变对土体固结理论的影响不容忽视。Passwell[1]通过试验发现了土体体积会受到温度的影响,较早地提出了土体热固结的概念。Booke等[2-3]推导了点热源和球热源影响下的土体内温度场和超静孔压分布解答。随后软土地基热排水固结处理技术的提出[4-6],进一步促进了考虑温度效应的土体固结理论的发展,如考虑变荷载作用[7-8]、天然地基成层性[9]、土体流变特性[10]等对土体一维热固结的影响作用。但以上研究均假定土体在固结过程中土性(压缩和渗透)参数保持不变,事实上这样的假定并不能反映土体真实的力学特性。
考虑到土体的非线性特性,Davi等[11]基于e-lg σ′关系,假定固结过程中渗透系数与体积压缩系数同步变化且自重应力沿深度保持不变,获得了土体一维非线性固结解析解。Xie等[12-13]在Davis和Raymond的假定基础上推导了单级加载下单层及双层地基一维非线性固结解析解;随后求解了循环荷载的单层地基一维非线性固结问题[14]。Chen等[15]利用DQM法求解了成层地基非线性固结问题。但目前综合考虑温度影响和土体非线性的固结研究较为少见。Liu等[16]基于Davis和Raymond的假定,推导出了考虑二次固结和温度耦合效应下的一维非线性热固结方程,得到了温度对土体固结的影响关系。郭志光等[17]考虑热-水-力耦合过程,建立了饱和土热固结的非线性模型并获得数值解。白冰等[18-19]基于多孔颗粒材料的粒子重排原则,建立了热-水-力学本构模型,并利用改良的温控三轴装置,研究了热循环作用下土体的变形作用。以上固结问题的研究均沿用了Terzaghi一维固结理论中的边界条件,即假设土体边界为完全透水和完全不透水。在该边界条件下,土体边界处的孔压会瞬时完成消散,并不能反映土体边界孔压的时间效应。
实际上,土体边界属于土体的一部分,其孔压的消散规律也应该服从一般的固结规律——孔压随时间逐渐消散。由此看来,自然排水边界的透水性应该介于完全透水和完全不透水之间。Gray[20]较早地认识到此客观事实,并基于此提出了一种半透水边界。但半透水边界的形式较为复杂,很难得到相应的固结解析解。白冰等[21]引入了一种与时间有关的“半渗透性”边界条件,求解了饱和孔热弹性球体的不可逆固结问题,推导出了球体与球腔在承受可变机械和热载荷时的分析解。为了考虑边界孔压的时间效应,梅国雄等[22-23]提出一种能够反映排水面处超静孔隙水压力随时间逐渐消散的连续排水边界,并基于连续排水边界推导出了瞬时荷载下一维固结解析解。Wu等[24]基于连续排水边界,分别研究了双层地基及成层地基一维固结特性。随后,不同学者进一步考虑土体非线性[25-27]、变荷载[28]、非饱和[29]等特性,对连续排水边界下土体一维固结特性进行了研究。宗梦繁等[30-31]基于Davis和Raymond的假定,获得了连续排水边界下单层及双层地基一维非线性固结解析解。然而,目前关于连续排水边界下的土体一维非线性固结理论研究鲜见考虑温度效应的影响。
在实际工程中,有时土体会受到温度的影响,如供热管道设计、地热资源开采、高放射性废弃物处理等,因此,考虑土体的温度效应至关重要。本文在考虑土体非线性变形和渗透特性的基础上,同时考虑边界孔压的时间效应,建立了连续排水边界条件下一维非线性土体热固结模型。采用分离变量法和Laplace变换得到相应的固结解析解。基于所得解析解,通过参数敏感性分析,深入探究连续排水边界条件下一维非线性土体热固结性状。
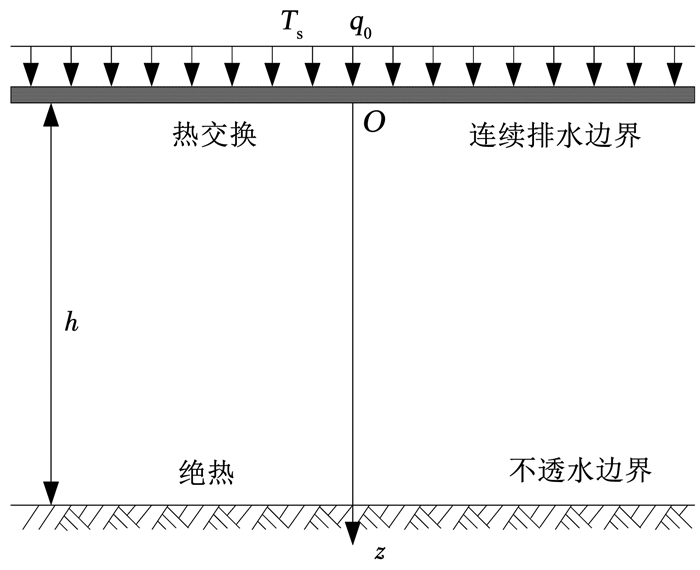
1 基本问题 1.1 固结模型的建立如图 1所示,h为土体厚度,q0为瞬时施加的大面积无限均匀分布的外荷载,Ts为无限均匀施加于土层顶面的温度增量。土层顶面为连续排水边界并且可进行热交换,土层底面为不透水边界并且绝热。土层的初始有效应力均匀分布。
|
图 1 地基固结模型 Fig. 1 Foundation consolidation model |
根据线性热应力理论,由应力变化引起和由温度变化引起的土体变形可以线性叠加[30]。因此, 孔隙比的变化包括由有效应力引起和由温度引起两部分组成,其中,由有效应力引起的部分为
| $ e_1-\Delta e_{\mathrm{c}}=e_1-C_{\mathrm{p}} \lg \frac{\sigma^{\prime}}{\sigma_0^{\prime}} $ | (1) |
式中: σ′和σ′0分别为有效应力和初始有效应力,Cp为不考虑温度影响的压缩指数,ec为有效应力引起的孔隙比表达式,e1为初始孔隙比,Δec为有效应力引起的孔隙比变化。
由温度引起的孔隙比变化表达式为
| $ e_T=e_1-\Delta e_T=e_1+a \theta\left(1+e_1\right) $ | (2) |
式中: θ为温度增量,a为土的线性膨胀系数,eT为温度引起的孔隙比表达式,ΔeT为温度引起的孔隙比变化。
总的孔隙比变化为
| $ \Delta e=\Delta e_{\mathrm{c}}+\Delta e_T=C_{\mathrm{p}} \lg \frac{\sigma^{\prime}}{\sigma_0^{\prime}}-a \theta\left(1+e_1\right) $ | (3) |
采用Liu等[16]提出的固结过程中孔隙比的变化与有效应力为对数关系假定,孔隙比表达式为
| $ e=e_1-\Delta e=e_1-C_{\mathrm{c}T} \lg \frac{\sigma^{\prime}}{\sigma_0^{\prime}} $ | (4) |
式中:CcT为考虑温度影响后的压缩指数,包括荷载作用和温度作用下e-lg σ′曲线的斜率。
同时认为固结过程中孔隙比的变化与渗透系数为对数关系[16],孔隙比与渗透系数表达式为
| $ e-e_1=C_{\mathrm{k} T} \lg \frac{k_{\mathrm{v}}}{k_{\mathrm{v} 0}} $ | (5) |
式中:kv和kv0分别为渗透系数和初始渗透系数,CkT为考虑温度影响后的渗透指数。
由式(4)和(5)知
| $ k_{\mathrm{v}}=k_{\mathrm{v} 0}\left(\frac{\sigma_0^{\prime}}{\sigma^{\prime}}\right)^{\frac{C_{\mathrm{c} T}}{C_{\mathrm{k} T}}} $ | (6) |
假定土体中渗流服从达西定律
| $ v=k_{\mathrm{v}} i=-\frac{k_{\mathrm{v}}}{\gamma_{\mathrm{w}}} \frac{\partial u}{\partial z} $ | (7) |
式中:v为渗透流速,i为水力坡降,u为超静孔隙水压力,z为土体深度方向,γw为水的重度。
土体体积变化为
| $ \begin{aligned} \frac{\partial V}{\partial t}= & -\frac{1}{1+e_1}\left(\frac{\partial e_{\mathrm{c}}}{\partial t}+\frac{\partial e_T}{\partial t}\right) \mathrm{d} x \mathrm{d} y \mathrm{d} z= \\ & \frac{1}{\left(1+e_1\right) \ln 10}\left[\frac{C_{\mathrm{p}}}{\sigma^{\prime}} \frac{\partial \sigma^{\prime}}{\partial t}-a\left(1+e_1\right) \ln 10 \frac{\partial \theta}{\partial t}\right] \mathrm{d} x \mathrm{d} y \mathrm{d} z \end{aligned} $ | (8) |
式中: V为土体体积,t为时间,x和y分别表示水平x方向和y方向。
由于饱和土在固结过程中土体体积变化与水流流量变化相等,有
| $ \frac{\partial V}{\partial t} \mathrm{d} t=\frac{\partial v}{\partial z} \mathrm{d} z \mathrm{d} y \mathrm{d} x \mathrm{d} t $ | (9) |
由式(8)和(9)可得
| $ \frac{1}{\left(1+e_1\right) \ln 10}\left[\frac{C_{\mathrm{p}}}{\sigma^{\prime}} \frac{\partial \sigma^{\prime}}{\partial t}-a\left(1+e_1\right) \ln 10 \frac{\partial \theta}{\partial t}\right]=\frac{\partial v}{\partial z} $ | (10) |
根据有效应力原理
| $ \sigma^{\prime}=\sigma_{\mathrm{f}}-u $ | (11) |
式中σf为土体所受总应力。
将式(11)和(7)代入式(10),可得
| $ \begin{gathered} \frac{1}{\left(1+e_1\right) \ln 10}\left[-\frac{C_{\mathrm{p}}}{\sigma^{\prime}} \frac{\partial u}{\partial t}-a\left(1+e_1\right) \ln 10 \frac{\partial \theta}{\partial t}\right]= \\ -\frac{\partial}{\partial z}\left[\left(\frac{\sigma^{\prime}}{\sigma^{\prime}}\right)^{\frac{C_\mathrm{c} T}{C_{\mathrm{k} T}} } \frac{k_{\mathrm{v0}}}{\gamma_{\mathrm{w}}} \frac{\partial u}{\partial z}\right] \mathrm{d} z \end{gathered} $ | (12) |
| $ C \frac{\partial \theta}{\partial t}=K \frac{\partial^2 \theta}{\partial z^2} $ | (13) |
式中:C为土体的体积热容,K为土的导热系数。
| $ C=(1-n) \rho_{\mathrm{s}} c_{\mathrm{s}}+n \rho_{\mathrm{w}} c_{\mathrm{w}} $ | (14) |
| $ K=(1-n) \lambda_{\mathrm{s}}+n \lambda_{\mathrm{w}} $ | (15) |
式中:n为土体的孔隙率,ρs和ρw分别为土颗粒密度和水的密度,cs和cw分别为土颗比热容和水的比热容,λs和λw分别为土颗粒热传导系数和水的热传导系数。
由于一维非线性固结方程较为复杂,很难求得解析解,Davis[11]在求解一维非线性固结方程时,假定压缩指数与渗透指数比等于1。此外,根据Li等[30]的研究发现,一般土的压缩指数和渗透指数较为接近,故假定CcT/CkT=1,则式(12)为
| $ -\frac{1}{\sigma^{\prime}} \frac{\partial u}{\partial t}-\frac{a\left(1+e_1\right) \ln 10}{C_{\mathrm{p}}} \frac{\partial \theta}{\partial t}=-c_{\mathrm{v}}\left[\frac{1}{\sigma^{\prime 2}}\left(\frac{\partial u}{\partial z}\right)^2+\frac{1}{\sigma^{\prime}} \frac{\partial^2 u}{\partial z^2}\right] $ | (16) |
式中cv为固结系数,表达式为
| $ c_{\mathrm{v}}=\frac{k_{\mathrm{v} 0}}{\gamma_{\mathrm{w}} m_{\mathrm{v} 0}} $ | (17) |
mv0为初始体积压缩系数,表达式为
| $ m_{\mathrm{v} 0}=\frac{C_{\mathrm{p}}}{\sigma_0^{\prime}\left(1+e_1\right) \ln 10} $ | (18) |
方程求解条件为
| $ \left\{\begin{array}{l} z=0: u=q_0 \mathrm{e}^{-\alpha \frac{c_{\mathrm{v}} t}{h^2}}, \theta=T_{\mathrm{s}} \\ z=h: \frac{\partial u}{\partial z}=0, \frac{\partial \theta}{\partial z}=0 \\ t=0: u=q_0, \theta=0 \end{array}\right. $ | (19) |
式中α为连续排水边界的界面参数。
1.2 模型求解定义无量纲参数
| $ T_{\mathrm{v}}=\frac{c_{\mathrm{v}} t}{h^2}, Z=\frac{z}{h}, N_\sigma=\frac{\sigma_{\mathrm{f}}^{\prime}}{\sigma_0^{\prime}} $ |
同时令
| $ \kappa=\frac{K}{C} $ | (20) |
将以上无量纲参数代入式(16),可得
| $ -\frac{1}{\sigma^{\prime}} \frac{\partial u}{\partial T_{\mathrm{v}}}-a \frac{N_\sigma-1}{q_0 m_{\mathrm{v} 0}} \frac{\partial \theta}{\partial T_{\mathrm{v}}}=-\left[\frac{1}{\sigma^{\prime 2}}\left(\frac{\partial u}{\partial Z}\right)^2+\frac{1}{\sigma^{\prime}} \frac{\partial^2 u}{\partial Z^2}\right] $ | (21) |
设
| $ \theta_1=\theta-T_{\mathrm{s}} $ | (22) |
则式(13)和求解条件(19)可化为
| $ \left\{\begin{array}{l} \frac{\partial \theta_1}{\partial T_{\mathrm{v}}}=\frac{\kappa}{c_{\mathrm{v}}} \frac{\partial^2 \theta_1}{\partial Z^2} \\ Z=0: \theta_1=0 \\ Z=1: \frac{\partial \theta_1}{\partial z}=0 \\ T_{\mathrm{v}}=0, \theta_1=-T_{\mathrm{s}} \end{array}\right. $ | (23) |
根据特征函数法可得
| $ \theta_1=-2 T_{\mathrm{s}} \sum\limits_{n=1}^{\infty} \frac{1}{M} \mathrm{e}^{-\frac{\kappa}{c_{\mathrm{v}}} M^2 T_\mathrm{v}} \sin (M Z) $ | (24) |
其中
| $ M=\frac{(2 n-1) \pi}{2} $ | (25) |
将式(24)代入式(22),可得温度增量表达式为
| $ \theta=T_{\mathrm{s}}-2 T_{\mathrm{s}} \sum\limits_{n=1}^{\infty} \frac{1}{M} \mathrm{e}^{-\frac{\kappa}{c_{\mathrm{v}}} M^2 T_{\mathrm{v}}} \sin (M Z) $ | (26) |
令
| $ \omega=\ln \frac{\sigma^{\prime}}{\sigma_{\mathrm{f}}^{\prime}} $ | (27) |
将式(27)代入式(21),可得
| $ \frac{\partial \omega}{\partial T_{\mathrm{v}}}-a \frac{N_\sigma-1}{q_0 m_{\mathrm{v} 0}} \frac{\partial \theta}{\partial T_{\mathrm{v}}}=\frac{\partial^2 \omega}{\partial Z^2} $ | (28) |
结合有效应力原理(式(11)),将式(27)代入式(19)并齐次化可得
| $ \left\{\begin{array}{l} Z=0: \omega=\omega_\alpha\left(T_{\mathrm{v}}\right) \\ Z=1: \frac{\partial \omega}{\partial z}=0 \\ T_{\mathrm{v}}=0: \omega=-\ln N_\sigma \end{array}\right. $ | (29) |
其中
| $ \omega_\alpha\left(T_{\mathrm{v}}\right)=\ln \frac{\sigma_{\mathrm{f}}^{\prime}-q_0 \mathrm{e}^{-\alpha T_{\mathrm{v}}}}{\sigma_{\mathrm{f}}^{\prime}}=\ln \left[1-\frac{\left(N_\sigma-1\right) \mathrm{e}^{-\alpha T_{\mathrm{v}}}}{N_\sigma}\right] $ | (30) |
为了进一步将边界条件齐次化,令
| $ \omega=v+\omega_\alpha\left(T_{\mathrm{v}}\right) $ | (31) |
将式(31)代入式(28),固结方程式(28)和求解条件(29)可齐次化为
| $ \left\{\begin{array}{l} \frac{\partial v}{\partial T_{\mathrm{v}}}=\frac{\partial^2 v}{\partial Z^2}+f\left(Z, T_{\mathrm{v}}\right) \\ Z=0: v=0 \\ Z=1: \frac{\partial v}{\partial Z}=0 \\ T_{\mathrm{v}}=0: v=0 \end{array}\right. $ | (32) |
其中
| $ \begin{gathered} f\left(Z, T_{\mathrm{v}}\right)=a \frac{N_\sigma-1}{q_0 m_{\mathrm{v} 0}} \frac{\partial \theta}{\partial T_{\mathrm{v}}}-\frac{\mathrm{d} \omega_\alpha}{\mathrm{d} T_{\mathrm{v}}}= \\ 2 T_{\mathrm{s}} a \frac{N_\sigma-1}{q_0 m_{\mathrm{v} 0}} \sum\limits_{n=1}^{\infty} \frac{\kappa}{c_{\mathrm{v}}} M \mathrm{e}^{-\frac{\kappa}{c_{\mathrm{v}}} \mathrm{M}^2 T_{\mathrm{v}}} \sin (M Z)- \\ \frac{\alpha\left(N_\sigma-1\right) \mathrm{e}^{-\alpha T_{\mathrm{v}}}}{N_\sigma-\left(N_\sigma-1\right) \mathrm{e}^{-\alpha T_{\mathrm{v}}}} \end{gathered} $ | (33) |
由特征函数法,设方程(32)解的形式为
| $ v\left(Z, T_{\mathrm{v}}\right)=\sum\limits_{n=1}^{\infty} v_n\left(T_{\mathrm{v}}\right) \sin (M Z) $ | (34) |
| $ f\left(Z, T_{\mathrm{v}}\right)=\sum\limits_{n=1}^{\infty} f_n\left(T_{\mathrm{v}}\right) \sin (M Z) $ | (35) |
其中
| $ \begin{gathered} f_n\left(T_{\mathrm{v}}\right)=2 \int_0^1 f\left(Z, T_{\mathrm{v}}\right) \sin (M Z) \mathrm{d} Z= \\ \frac{2 T_{\mathrm{s}} \kappa a}{c_{\mathrm{v}}} \frac{N_\sigma-1}{q_0 m_{\mathrm{v} 0}} M \mathrm{e}^{-\frac{\kappa}{c_{\mathrm{v}}} M^2 T_{\mathrm{v}}}- \\ \frac{2 \alpha\left(N_\sigma-1\right) \mathrm{e}^{-\alpha T_{\mathrm{v}}}}{M\left[N_\sigma-\left(N_\sigma-1\right) \mathrm{e}^{-\alpha T_{\mathrm{v}}}\right]} \end{gathered} $ | (36) |
将式(34)和(35)代入式(32)可得
| $ \begin{gathered} \sum\limits_{n=1}^{\infty} v_n^{\prime}\left(T_{\mathrm{v}}\right) \sin (M Z)=-M^2 \sum\limits_{n=1}^{\infty} v_n\left(T_{\mathrm{v}}\right) \sin (M Z)+ \\ \sum\limits_{n=1}^{\infty} f_n\left(T_{\mathrm{v}}\right) \sin (M Z) \end{gathered} $ | (37) |
考虑式(37)的恒等性,可得
| $ v^{\prime}{ }_n\left(T_v\right)+M^2 v_n\left(T_{\mathrm{v}}\right)-f_n\left(T_{\mathrm{v}}\right)=0 $ | (38) |
将式(38)进行Laplace变换可得
| $ s V_n(s)+M^2 V_n(s)=F_n(s) $ | (39) |
其中Vn(s)和Fn(s)分别为vn(Tv)和fn(Tv)的Laplace变换式。
由式(39)可得
| $ V_n(s)=\frac{F_n(s)}{s+M^2} $ | (40) |
对式(40)进行Laplace逆变换可得
| $ \begin{gathered} v_n\left(T_{\mathrm{v}}\right)=\int_0^{T_{\mathrm{v}}} f_n(\tau) \mathrm{e}^{-M^2\left(T_{\mathrm{v}}-\tau\right)} \mathrm{d} \tau= \\ \frac{2 T_{\mathrm{s}} \kappa a}{c_{\mathrm{v}} M\left(1-\frac{\kappa}{c_{\mathrm{v}}}\right)} \frac{N_\sigma-1}{q_0 m_{\mathrm{v} 0}}\left(\mathrm{e}^{-\frac{\kappa}{c_{\mathrm{v}}} M^2 T_{\mathrm{v}}}-\mathrm{e}^{-M^2 T_{\mathrm{v}}}\right)- \\ \frac{2 \alpha}{M} \sum\limits_{k=1}^{\infty}\left(1-\frac{1}{N_\sigma}\right)^k \frac{\mathrm{e}^{-k \alpha T_{\mathrm{v}}}-\mathrm{e}^{-M^2 T_{\mathrm{v}}}}{M^2-k \alpha} \end{gathered} $ | (41) |
令
| $ A_1=\frac{2 T_{\mathrm{s}} \kappa a}{c_{\mathrm{v}} M\left(1-\frac{\kappa}{c_{\mathrm{v}}}\right)} \frac{N_\sigma-1}{q_0 m_{\mathrm{v} 0}} $ | (42) |
| $ A_2=\frac{2 \alpha}{M\left(M^2-\kappa \alpha\right)}\left(1-\frac{1}{N_\sigma}\right)^\kappa $ | (43) |
则式(41)可进一步转化为
| $ v_n\left(T_v\right)=A_1\left(\mathrm{e}^{-\frac{\kappa}{c_{\mathrm{v}}} M^2 T_\mathrm{v}}-\mathrm{e}^{-M^2 T_\mathrm{v}}\right)-\sum\limits_{k=1}^{\infty} A_2\left(\mathrm{e}^{-\kappa \alpha T_\mathrm{v}}-\mathrm{e}^{-M^2 T_\mathrm{v}}\right) $ | (44) |
将式(44)和(30)代入式(31)可得
| $ \begin{aligned} \omega= & \sum\limits_{n=1}^{\infty} A_1\left(\mathrm{e}^{-\frac{\kappa}{c_\mathrm{v}} M^2 T_\mathrm{v}}-\mathrm{e}^{-M^2 T_\mathrm{v}}\right) \sin (M Z)- \\ & \sum\limits_{n=1}^{\infty} \sum\limits_{k=1}^{\infty} A_2\left(\mathrm{e}^{-\kappa \alpha T_\mathrm{v}}-\mathrm{e}^{-M^2 T_\mathrm{v}}\right) \sin (M Z)+ \\ & \ln \left[1-\frac{\left(N_\sigma-1\right) \mathrm{e}^{-\alpha T_\mathrm{v}}}{N_\sigma}\right] \end{aligned} $ | (45) |
按沉降定义的平均固结度为
| $ \begin{gathered} U_{\mathrm{s}}=\frac{\int_0^h \varepsilon \mathrm{d} z}{\int_0^h \varepsilon_{\mathrm{f}} \mathrm{d} z}=1+\frac{\int_0^1 \omega \mathrm{d} Z}{\ln N_\sigma}= \\ 1+\sum\limits_{n=1}^{\infty} \frac{A_1}{M \ln N_\sigma}\left(\mathrm{e}^{-\frac{\kappa}{c_{\mathrm{v}}} \mathrm{M}^2 T_{\mathrm{v}}}-\mathrm{e}^{-M^2 T_{\mathrm{v}}}\right)- \\ \sum\limits_{n=1}^{\infty} \sum\limits_{k=1}^{\infty} \frac{A_2}{M \ln N_\sigma}\left(\mathrm{e}^{-\kappa \alpha T_\mathrm{v}}-\mathrm{e}^{-M^2 T_\mathrm{v}}\right)+ \\ \frac{1}{\ln N_\sigma} \ln \left[1-\frac{\left(N_\sigma-1\right) \mathrm{e}^{-\alpha T_\mathrm{v}}}{N_\sigma}\right] \end{gathered} $ | (46) |
式中:ε为土的竖向应变,且有
按孔压定义的平均固结度为
| $ U_{\mathrm{p}}=\frac{\int_0^h\left(\sigma^{\prime}-\sigma_0^{\prime}\right) \mathrm{d} z}{\int_0^h q_0 \mathrm{d} z}=1-\int_0^1 \bar{u} \mathrm{d} Z $ | (47) |
式中u=u/q0为无量纲化的超孔压。
1.4 土体沉降解答土体沉降表达式为
| $ S=\int_0^h \frac{\Delta e}{1+e_1} \mathrm{~d} z=\int_0^1\left[\frac{C_{\mathrm{p}} H}{1+e_1}\left(\lg N_\sigma+\frac{\omega}{\ln 10}\right)-a \theta H\right] \mathrm{d} Z $ | (48) |
通过与现有解答对比分析验证本文解答的合理性,并分析热应力与边界条件对固结特性的影响。基本参数:土体初始孔隙比e1为1.3,土体热扩散系数κ为10-4 m2/s,不考虑温度的土体压缩指数Cp为0.4,初始有效应力σ′0为25 kPa,无量纲参数Nσ为4,温度增量Ts为60 ℃,界面参数α为8,κ/cv=2。
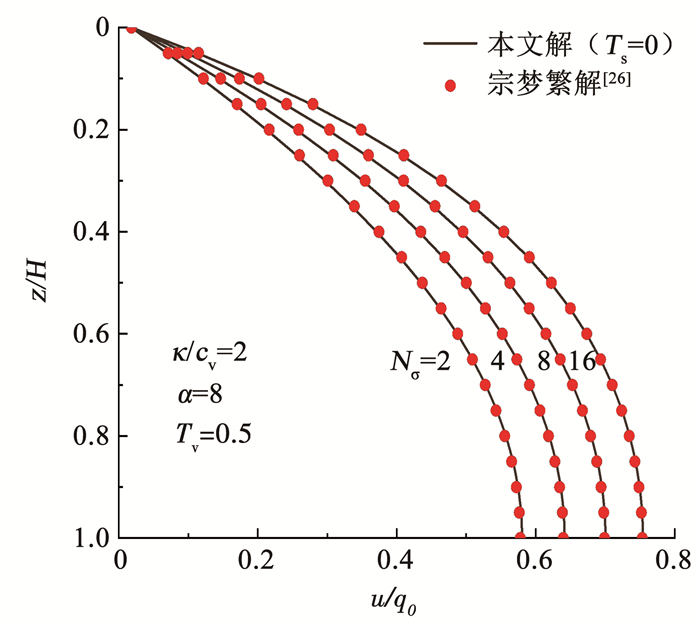
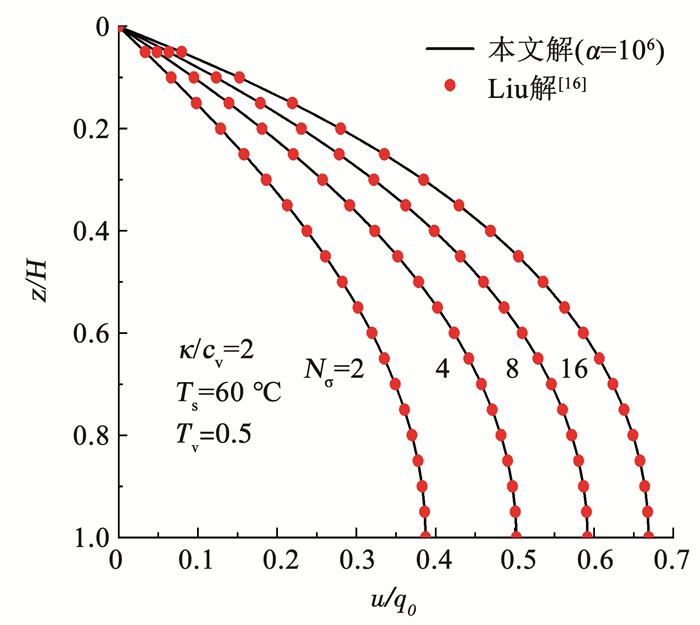
2.1 解答的退化验证宗梦繁等[26]在不考虑热应力作用的条件下,得到了连续排水边界条件下非线性土体的一维固结解析解。图 2为Ts=0(即不考虑热应力作用)条件下,本文解与宗梦繁解[26]的超静孔隙水压力对比曲线。可以看出,退化后的本文解与宗梦繁解[26]完全一致,验证了在不考虑热应力作用条件下本文解的正确性。图 3为Liu解[16]与本文解(考虑热应力作用)得到的超静孔隙水压力曲线。其中,本文解基于连续排水边界条件,而Liu解基于Terzaghi单面排水边界条件。由连续排水边界的定义可知,当界面参数取值趋于无穷时,连续排水边界会退化为Terzaghi排水边界。由图 3可以看出,当界面参数α=106时,基于本文解与Liu解得到的超静孔隙水压力完全重合,进一步验证了本文解的合理性,同时说明本文解可以完全退化为Terzaghi排水边界下的解,是一种更具普适性的解。此外,由图 2和3对比可知,无论是否考虑热应力作用,超静孔隙水压力均会随Nσ的减小而减小。由Nσ=σ′f/σ′0可知,当初始有效应力固定时,Nσ的变化由施加荷载决定,即施加荷载越小,Nσ越小。由图 2和3还可以看出,施加的外荷载越小,超静孔隙水压力越小。
|
图 2 不考虑热应力时不同Nσ下的超静孔隙水压力曲线 Fig. 2 Excess pore water pressure curves for different Nσ without thermal stress |
|
图 3 考虑热应力时不同Nσ下的超静孔隙水压力曲线 Fig. 3 Excess pore water pressure curves for different Nσ with thermal stress |
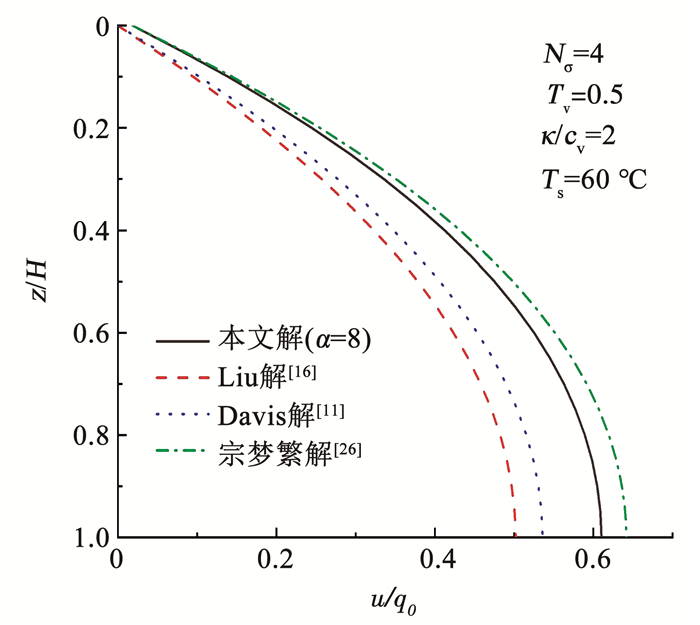
图 4对比了不同解答下得到的超静孔隙水压力,其中,Liu解[16]为基于Terzaghi边界考虑热应力作用得到的一维非线性固结解析解,宗梦繁解[26]为基于连续排水边界得到的一维非线性固结解析解,Davis解[11]为基于Terzaghi边界得到的一维非线性固结解析解。对比本文解与宗梦繁解[26]以及Liu解[16]与Davis解[11]可以发现,当边界条件相同时,考虑热应力作用得到的超静孔隙水压力更小,说明热应力作用可以促进土体超静孔隙水压力的消散。对比分析本文解与Liu解[16]以及宗梦繁解[26]与Davis解[11]可以发现,连续排水边界下的超静孔隙水压力大于Terzaghi边界下的超静孔隙水压力,这是由于连续排水边界是一种阻碍型的排水边界,当边界孔隙水排出受阻时,会导致超静孔隙水压力消散速率变慢。
|
图 4 不同解答下超静孔隙水压力曲线 Fig. 4 Excess pore water pressure curves under different solutions |
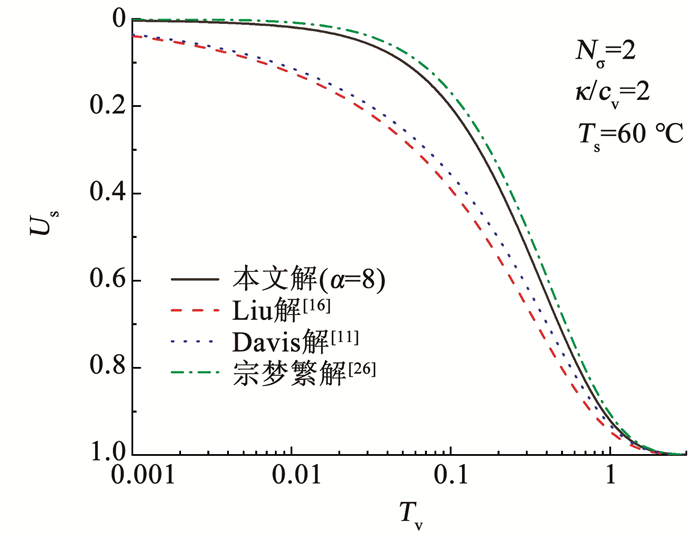
图 5对比了不同解答下按沉降定义的平均固结度。可以看出,当边界条件相同时,考虑热应力作用得到的土体固结速率更快,说明热应力可以促进土体的固结。此外,当热应力条件相同时,连续排水边界下的固结速率小于Terzaghi边界下的固结速率,这是由于Terzaghi边界假定为完全透水边界,土体可以快速排出孔隙水,土体的固结速率更快。
|
图 5 不同解答下Us曲线 Fig. 5 Curves of Us under different solutions |
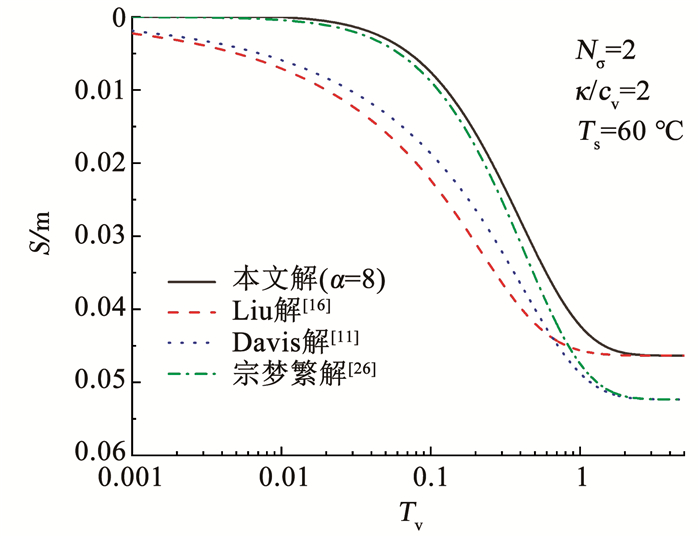
图 6对比了不同解答得到的沉降曲线。当边界条件相同时,考虑热应力作用得到的最终沉降量更小,这是由于随着温度的升高,土体会发生膨胀,导致土体的最终沉降量会小于不考虑热应力时的最终沉降量。在温度荷载及其他参数不变的条件下,只改变边界排水性能,土体的最终沉降量相同,说明边界条件对土体最终沉降量没有影响。此外,连续排水边界下的沉降速率小于Terzaghi边界下的沉降速率,这是由于连续排水边界会阻碍孔隙水的排出,从而导致土体沉降速率降低。
|
图 6 不同解答下的土体沉降曲线 Fig. 6 Soil settlement curves under different solutions |
基于本文解答,对模型进行参数的敏感性分析,从而探究连续排水边界条件下的非线性饱和土体一维热固结特性。基本参数取值与上节相同。
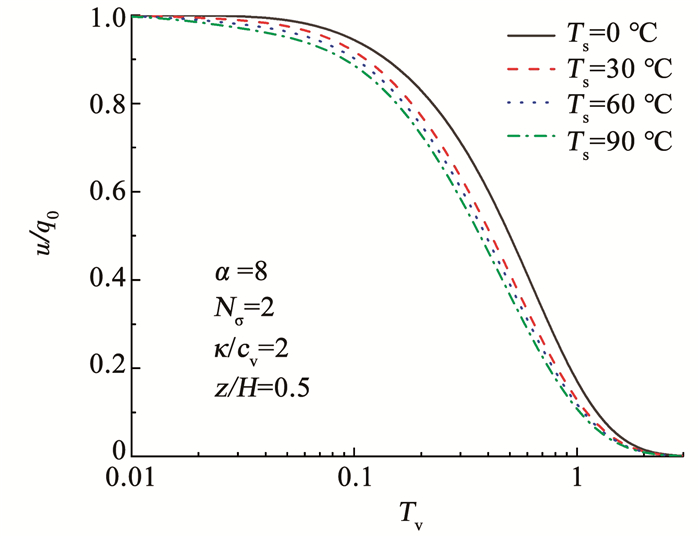
图 7分析了土体深度为土体总深度一半时温度增量Ts对超静孔隙水压力的影响。可以看出,温度增量Ts越大,土体孔压越小,超静孔隙水压力消散速率越快。说明提高温度可以促进孔隙水压力的消散。
|
图 7 Ts对超静孔隙水压力曲线的影响 Fig. 7 Influence of Ts on curves of excess pore water pressure |
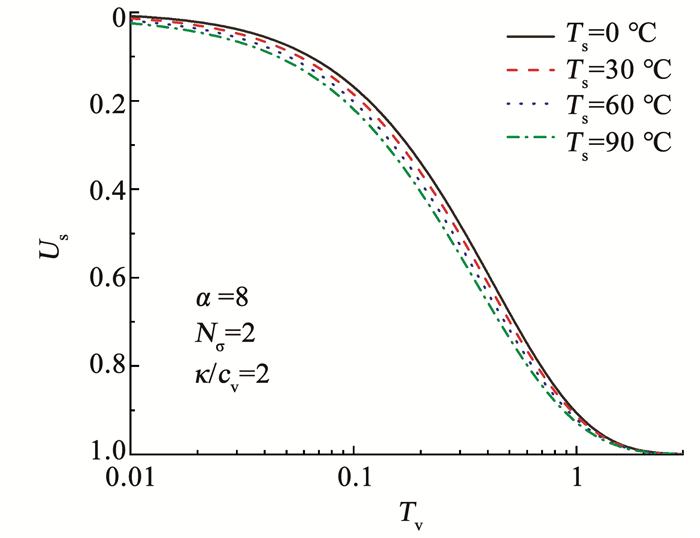
图 8反映了温度增量Ts对按沉降定义的平均固结度的影响。可以看出,当温度增量Ts增大时,土体的固结速率会加快,说明提高温度可以促进土体的固结沉降。
|
图 8 Ts对Us曲线的影响 Fig. 8 Influence of Ts on Us |
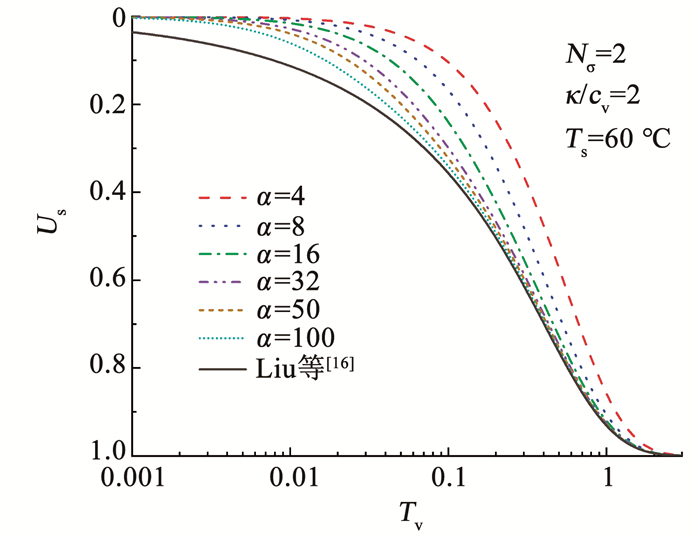
在连续排水边界中,界面参数α反映了土体边界的排水能力,α越大,边界排水能力越强[19-20]。图 9分析了界面参数α对按沉降定义的平均固结度Us的影响。可以看出,界面参数越大,土体的排水能力越强,越接近Terzaghi排水边界条件。当界面参数α=100时,图像与Liu[16]十分接近,因此,α的取值应为0~100。连续排水边界条件可以通过调整界面参数的取值模拟不同排水性能的边界条件,这是传统Terzaghi边界条件不能够达到的效果。
|
图 9 α对Us曲线的影响 Fig. 9 Influence of α on Us |
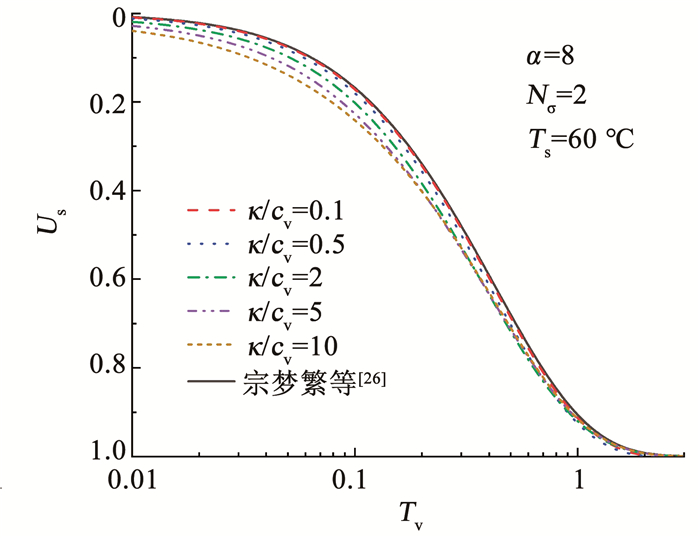
图 10分析了κ/cv对按沉降定义的平均固结度的影响。κ/cv为热扩散系数与固结系数的比值,其值越大代表热扩散系数所起的作用越大。可以看出,在固结前期,随着κ/cv的增大,热扩散作用增强,固结速率明显增大,平均固结度曲线逐渐偏离宗梦繁解[26]得到的平均固结度曲线,但后期所有曲线达到完全固结所用的时间近似相同,说明改变κ/cv主要会在固结前期加快固结速率,但对平均固结速率没有太大影响。
|
图 10 κ/cv对Us曲线的影响 Fig. 10 Influence of κ/cv on Us |
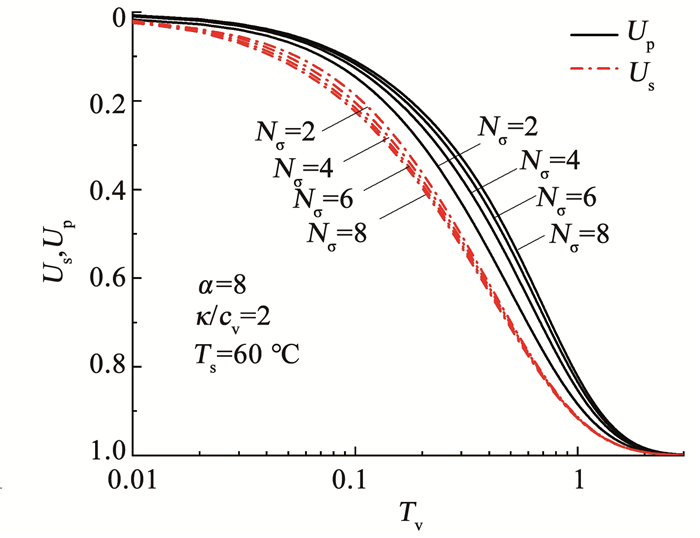
图 11分析了非线性参数Nσ对按沉降定义的平均固结度和按孔压定义的平均固结度的影响。可以看出,随着Nσ的增大,土体所受的施加荷载增大,按沉降定义的固结度会随着施加荷载的增大而速率增大,但按孔压定义的固结度会随着施加荷载的增大而速率降低,这是由于施加荷载的大小会同时影响土体的渗透系数和体积压缩系数[32],这两个系数对土体的影响作用相反但随Nσ的变化相同。因此,在不同的定义下,由于两个系数所起作用的大小不同,呈现的变化规律不同。
|
图 11 Nσ对固结度曲线的影响 Fig. 11 Influence of Nσ on curves of consolidation degree |
1) 本文所得解严格满足初始条件,并且退化结果合理适定,具有明确的物理意义。还可通过调节温度增量Ts和界面参数α来近似模拟热应力作用和土体的透水性,使解答更具有普适性。
2) 热应力作用可以促进孔隙水压力的消散,提高土体固结速率,减小土体的最终沉降量。
3) 对参数进行敏感性分析可知,当温度增量Ts增大或界面参数α增大时,土体的排水能力增强;反之,土体排水能力减弱。
4) 当温度增量Ts增大或热扩散系数与固结系数的比κ/cv增大时,土体的固结速率增大,但Ts增大提高的是整个固结过程的固结速率,而κ/cv的增大主要是提高土体的前期固结速率,对总固结速率影响不大。当非线性参数Nσ增大时,两种不同定义下的固结速率变化趋势相反,按沉降定义的固结速率提高,按孔压定义的固结速率降低;当Nσ减小时,按沉降定义的固结速率降低,按孔压定义的固结速率提高。
| [1] |
PAASWELL R. Temperature effects on clay consolidation[J]. Journal of Soil Mechanics and Foundation Engineering Division, 1967, 93(3): 9. DOI:10.1061/JSFEAQ.0000982 |
| [2] |
BOOKER J R, SAVVIDOU C. Consolidation around a point heat source[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1985, 9(2): 173. DOI:10.1002/nag.1610090206 |
| [3] |
BOOKER J R, SAVVIDOU C. Consolidation around a spherical heat source[J]. International Journal of Solids and Structures, 1984, 20(11/12): 1079. DOI:10.1016/0020-7683(84)90091-X |
| [4] |
ABUEL-NAGA H M, BERGADO D T, CHAIPRAKAIKEOW S. Innovative thermal technique for enhancing the performance of prefabricated vertical drain during the preloading process[J]. Geotextiles & Geomembranes, 2006, 24(6): 359. DOI:10.1016/j.geotexmem.2006.04.003 |
| [5] |
POTHIRAKSANON C, BERGADO D T, ABUEL-NAGA H M. Full scale embankment consolidation test using prefabricated vertical thermal drains[J]. Soils and Foundations, 2010, 50(5): 599. DOI:10.3208/sandf.50.599 |
| [6] |
ARTIDTEANG S, BERGADO D T, SAOWAPAKPIBOON J, et al. Enhancement of efficiency of prefabricated vertical drains using surcharge, vacuum and heat preloading[J]. Geosynthetics International, 2011, 18(1): 35. DOI:10.1680/gein.2011.18.1.35 |
| [7] |
孙德安, 薛垚, 汪磊. 变荷载作用下考虑半透水边界热传导性的一维饱和土热固结特性研究[J]. 岩土力学, 2020, 41(5): 1465. SUN Dean, XUE Yao, WANG Lei. Analysis of one-dimensional thermal consolidation of saturated soil considering heat conduction of semi-permeable drainage boundary under varying loading[J]. Rock and Soil Mechanics, 2020, 41(5): 1465. DOI:10.16285/j.rsm.2019.0649 |
| [8] |
吴瑞潜, 谢康和, 程永锋. 变荷载下饱和土一维热固结解析理论[J]. 浙江大学学报(工学版), 2009, 43(8): 1532. WU Ruiqian, XIE Kanghe, CHENG Yongfeng. Analytical theory for one-dimensional thermal consolidation of saturated soil under time-dependent loading[J]. Journal of Zhejiang University (Engineering Science), 2009, 43(8): 1532. DOI:10.3785/j.issn.1008-973X.2009.08.033 |
| [9] |
BAI B. Thermal consolidation of layered porous half-space to variable thermal loading[J]. Applied Mathematics and Mechanics (English Edition), 2006, 27(11): 153. DOI:10.3321/j.issn:1000-0887.2006.11.011 |
| [10] |
WANG L J, WANG L H. Semianalytical analysis of creep and thermal consolidation behaviors in layered saturated clays[J]. International Journal of Geomechanics, 2020, 20(4): 06020001. DOI:10.1061/(ASCE)GM.1943-5622.0001615 |
| [11] |
DAVIS E H, RAYMOND G P. A non-linear theory of consolidation[J]. Géotechnique, 1965, 15(2): 161. DOI:10.1680/geot.1965.15.2.161 |
| [12] |
XIE K H, LI B H, LI Q L. A nonlinear theory of consolidation under time-dependent loading[C]//Proceedings of the Second International Conference on Soft Soil Engineering. Nanjing: Hohai University Press, 1996: 193
|
| [13] |
XIE K H, XIE X Y, JIANG W. A study on one-dimensional nonlinear consolidation of double-layered soil[J]. Computers and Geotechnics, 2002, 29(2): 151. DOI:10.1016/S0266-352X(01)00017-9 |
| [14] |
谢康和, 周瑾, 董亚钦. 循环荷载作用下地基一维非线性固结解析解[J]. 岩石力学与工程学报, 2006, 25(1): 21. XIE Kanghe, ZHOU Jin, DONG Yaqin. Analytical solution for one-dimensional nonlinear consolidation of soil under cyclic loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(1): 21. DOI:10.3321/j.issn:1000-6915.2006.01.004 |
| [15] |
CHEN R P, ZHOU W H, WANG H Z, et al. One-dimensional nonlinear consolidation of multi-layered soil by differential quadrature method[J]. Computers and Geotechnics, 2005, 32(5): 358. DOI:10.1016/j.compgeo.2005.05.003 |
| [16] |
LIU Q, DENG Y B, WANG T Y. One-dimensional nonlinear consolidation theory for soft ground considering secondary consolidation and the thermal effect[J]. Computers and Geotechnics, 2018, 104: 22. DOI:10.1016/j.compgeo.2018.08.007 |
| [17] |
郭志光, 白冰. 描述饱和土热固结过程的一个非线性模型及数值分析[J]. 岩土工程学报, 2018, 40(11): 2061. GUO Zhiguang, BAI Bing. Nonlinear model and numerical simulation of thermal consolidation process of saturated soils[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(11): 2061. DOI:10.11779/CJGE201811012 |
| [18] |
BAI Bing, YANG Guangchang, LI Tao, et al. A thermodynamic constitutive model with temperature effect based on particle rearrangement for geomaterials[J]. Mechanics of Materials, 2019, 139: 103180. DOI:10.1016/j.mechmat.2019.103180 |
| [19] |
BAI Bing, SHI Xiaoying. Experimental study on the consolidation of saturated silty clay subjected to cyclic thermal loading[J]. Geomechanics and Engineering, 2017, 12(4): 707. DOI:10.12989/gae.2017.12.4.707 |
| [20] |
GRAY H. Simultaneous consolidation of contiguous layers of unlike compressible soils[J]. Transactions of the American Society of Civil Engineering, 1945, 110: 1327. |
| [21] |
BAI Bing, LI Tao. Irreversible consolidation problem of a saturated porothermoelastic spherical body with a spherical cavity[J]. Applied Mathematical Modelling, 2013, 37(4). DOI:10.1016/j.apm.2012.05.003 |
| [22] |
MEI G X, THOMAS M H L, XIA J, et al. One-dimensional consolidation with asymmetrical exponential drainage boundary[J]. Geomechanics and Engineering, 2014, 6(1): 47. DOI:10.12989/gae.2014.6.1.047 |
| [23] |
MEI G X, CHEN Q M. Solution of Terzaghi one-dimensional consolidation equation with general boundary conditions[J]. Journal of Central South University, 2013, 22(8): 2239. DOI:10.1007/s11771-013-1730-5 |
| [24] |
WU W B, ZONG M F, EL NAGGAR M H. Analytical solution for one-dimensional consolidation of double-layered soil with exponentially time-growing drainage boundary[J]. International Journal of Distributed Sensor Networks, 2018, 14(10): 1. DOI:10.1177/1550147718806716 |
| [25] |
LIU J C, LEI G H. One-dimensional consolidation of layered soils with exponentially time-growing drainage boundaries[J]. Computers and Geotechnics, 2013, 54(10): 202. DOI:10.1016/j.compgeo.2013.07.009 |
| [26] |
宗梦繁, 吴文兵, 梅国雄, 等. 连续排水边界条件下土体一维非线性固结解析解[J]. 岩石力学与工程学报, 2018, 37(12): 2838. ZONG Mengfan, WU Wenbing, MEI Guoxiong, et al. An analytical solution for one-dimensional nonlinear consolidation of soils with continuous drainage boundary[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(12): 2838. DOI:10.13722/j.cnki.jrme.2018.0602 |
| [27] |
ZONG M F, WU W B, EL NAGGAR M H, et al. Analytical solution for one-dimensional nonlinear consolidation of double-layered soil with improved continuous drainage boundary[J]. European Journal of Environmental and Civil Engineering, 2020. DOI:10.1080/19648189.2020.1813207 |
| [28] |
SUN M, ZONG M F, MA S J, et al. Analytical solution for one-dimensional consolidation of soil with exponentially time-growing drainage boundary under a Ramp Load[J]. Mathematical Problems in Engineering, 2018, 1. DOI:10.1155/2018/9385615 |
| [29] |
WANG L, SUN D A, QIN A F. Semi-analytical solution to one-dimensional consolidation for unsaturated soils with exponentially time-growing drainage boundary conditions[J]. International Journal of Geomechanics, ASCE, 2018, 18(2): 04017144. DOI:10.1061/(ASCE)GM.1943-5622.0001056 |
| [30] |
李维特, 黄保海, 毕仲波. 热应力理论分析及应用[M]. 北京: 中国电力出版社, 2004. LI Weite, HUANG Baohai, BI Zhongbo. The theoretical analysis and application of thermal stress[M]. Beijing: China Power Press, 2004. |
| [31] |
LI C X, WANG C J, LU M M, et al. One-dimensional large-strain consolidation of soft clay with non-Darcian flow and nonlinear compression and permeability of soil[J]. Journal of Central South University, 2017, 24(4): 967. DOI:10.1007/s11771-017-3499-4 |
| [32] |
DAVIS E H, RAYMOND G P. A non-linear theory of consolidation[J]. Géotechnique, 1965, 15(2): 161. |
 2023, Vol. 55
2023, Vol. 55


