2. 土木工程防灾国家重点实验室(同济大学),上海 200092
2. State Key Lab of Disaster Reduction in Civil Engineering (Tongji University), Shanghai 200092, China
随着现代桥梁跨径的日益增大,风荷载逐渐成为大跨度桥梁的主要控制荷载,风对桥梁的作用逐渐成为影响桥梁设计的一个重要因素[1]。桥梁断面的气动力特性受气动外形和来流特性等因素影响,如虎门大桥因布置水马改变了气动外形,被认为是诱导涡激共振现象的原因之一。文献[2]发现特定的箱梁断面在湍流来流下的涡振幅值远大于均匀来流下的幅值。文献[3]通过对结构响应计算发现大跨度桥梁在均匀流和湍流场下的扭转发散形式不同,且湍流明显降低了扭转发散的临界风速。文献[4]指出来流湍流导致了颤振导数和临界风速的不确定性,并提出使用颤振导数的概率分布计算临界风速的方法。文献[5]研究了湍流对翼型升力展向相关性的影响,指出湍流的三维效应使得片条假定并不成立,需要进行一定的修正。文献[6]使用频域计算方法分析了各国规范采用的水平和竖向风速谱对抖振相应的影响。以上研究大多从抗风设计需要角度出发,着眼于来流湍流对结构静风稳定性和动力响应的影响。
众多学者研究了湍流来流对圆柱、矩形柱等非流线型断面气动力特性的影响。文献[7]研究发现小尺度的来流湍流通过扰动圆柱的剪切层改变了表面平均和脉动风压分布。文献[8]发现高湍流度(Iu=18%)的小尺度(Lux/D=0.5)来流使得雷诺数超临界区的圆柱的升力系数增大。文献[9]进行二维薄平板测压试验,研究表明表面平均风压受湍流强度影响较大,但积分尺度对其几乎没有影响。文献[10-11]在湍流度为7%和11%、积分尺度Lux/D= 0.5~24的风场中对宽高比B/D=17~102的矩形断面进行测压试验,发现小积分尺度湍流使得分离涡提前附着,脱落涡的尺寸随湍流强度增加而减小。文献[12-13]指出平板的平均风压系数受湍流强度影响较大,受较小的湍流积分尺度(Lux/D=0.4~3.6)影响较小。上述研究多集中于简单断面外形,其结论难以直接应用于实际桥梁断面。桥梁断面外形复杂、折点较多,其断面绕流常呈现复杂的分离和再附着流动状态,气动力易受大气湍流的影响,因此有必要通过测试桥梁断面表面风压系数分布,考察绕桥梁断面的复杂分离再附着流动形态随来流湍流强度变化的特点,研究湍流对桥梁断面气动力特性的影响并探讨其影响机理。
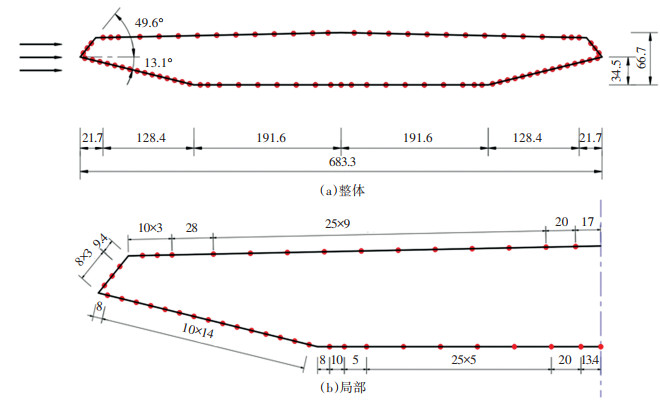
1 风洞试验概况节段模型测压试验在同济大学土木工程防灾国家重点实验室TJ-2边界层风洞中进行。流线型闭口扁平钢箱梁原型的宽约41 m,中心线处高4 m,试验用节段模型缩尺比为1∶60,宽B=68.3 cm,高D=6.7 cm,宽高比B/D=10.2,风嘴处上下斜腹板倾角分别为49.6°和13.1°。模型为薄壁箱型结构,由纵梁和加劲梁构成,采用亚克力材料制作。模型测压段长50 cm,两侧各有长为50 cm的延伸段,模型两端设置端板,用以减少端部三维绕流效应的影响。模型表面共设置了83个内径为1.1 mm的测压孔,如图 1所示,在模型上下表面沿宽度方向呈对称布置。测压孔通过塑料管与PSI电子压力扫描阀相连,采用ESP-64HD扫描阀收集压力信号,采样频率300 Hz,连续采样时长60 s。为了尽可能地减小测压管对压力信号畸变的影响,所有测压管长度均为1 000 mm,并使用Bergh-Tijdeman方程来对风压测试结果进行修正[14-15]。
|
图 1 节段模型尺寸及测压点布置(mm) Fig. 1 Geometric dimensions of a segment model and layout of pressure taps (mm) |
采用格栅装置获得测压试验所需的湍流风场,格栅可调整相关参数(格栅板宽c,相邻板间距a),格栅也可以在风洞内前后移动以改变与模型之间的距离d,如图 2(a)所示。在测试空流场湍流特性时,在拟放置模型位置处安装Cobra-100风速仪测量来流风速时程,采样频率为300 Hz,采样时长60 s。在测试模型表面压力分布时,在不受模型影响的模型前方利用皮托管测量来流平均风速并提供参考风压。试验模型布置如图 2(b)所示。

|
图 2 节段模型风洞试验概况 Fig. 2 Segment model and testing conditions |
湍流强度定义为脉动风速标准差与平均风速的比值,即
| $ I_i=\frac{\sigma_i}{U} $ | (1) |
式中:i取u、v、w分别为顺风向、水平侧向和竖向的脉动风速,U为平均风速。
探头布置距离较近时,相互之间会对流场产生较明显的干扰,本研究中采用基于单点脉动风速测量的方法计算3个脉动风速的湍流积分尺度。基于泰勒的“涡流冻结传输”假说,即假设湍流中的旋涡不衰减地以平均风速向下游传输,湍流积分尺度空间积分可以转化为时间尺度的积分:
| $ L_i^x=\frac{1}{\sigma_i^2} \int_0^{\infty} R_{a_1 a_2}(x) \mathrm{d} x=\frac{U}{\sigma_i^2} \int_0^{\infty} R_a(\tau) \mathrm{d} \tau $ | (2) |
式中:Ra1a2(τ)为空间两点处脉动风速i的互协方差函数,Ra(τ)为脉动风速i的自协方差函数,τ为时间延迟的偶函数。
格栅湍流特性与板条宽度、间距以及格栅与模型的距离有关。以往研究表明板条宽度越大、间距越小,试验段距格栅越近,湍流强度越大,而湍流积分尺度随着格栅与模型距离的增加而增大[16]。作为前期工作,本研究也测试了格栅湍流场(a=0.38 m, c=0.15 m)的湍流强度和湍流尺度在距离格栅4.25 m处前后1.25 m之内的变化,如图 3(a)所示,其在流动方向上表现出一定程度的衰减,但在桥梁节段模型宽度范围内变化相对较小。图 3(b)所示为湍流强度和湍流尺度在距离格栅4.5 m处的展向(横风向)变化,湍流强度在展向较为均匀,湍流尺度的波动相对桥梁节段模型宽度较小。通过测试不同格栅,最终获得平均风速约保持在8 m/s、积分尺度约保持在0.160 m(Lux/D=2.4)、湍流度分别约为5%、10%和15%的3种湍流风场,试验雷诺数约为3.5×105。保持平均风速不变可以减小桥梁断面气动力特性对雷诺数的依存性,保持积分尺度不变可以便于明确湍流强度对桥梁断面气动力特性的影响。湍流风场的具体参数见表 1。

|
图 3 湍流强度和积分尺度的空间分布 Fig. 3 Spatial distribution of turbulence intensity and integral scale |
| 表 1 湍流风场特性 Tab. 1 Turbulence flow characteristics |
模型表面风压系数定义如下:
| $ C_p=\frac{2\left(p-p_0\right)}{\rho U^2} $ | (3) |
式中:p为作用于模型表面的风压,p0为不受模型影响的前方来流静压,U为来流风速。
以0°,6°和-6°攻角为例说明均匀来流下桥梁断面表面风压系数平均值(

|
图 4 均匀流下不同攻角表面风压分布 Fig. 4 Pressure coefficient distribution at different attack angles under smooth flow |
3个攻角下的压力分布不同表明它们的断面绕流情况有所差异。0°攻角时,上表面前缘L点由于角度较小未发生流动分离现象,直至a点附近有明显的压力下降,在此处发生流动分离,但随即在约0.12距离处压力已经基本恢复,表明分离边界层已经再附着,且一直到后缘T点没有强烈的负压区存在;下表面前缘L点处角度较大,立即发生了分离,在折点d和e两处再次发生较明显的分离。在后缘T点上下表面的压力系数趋于一致,这是因为不同于在前缘L点处的上下表面两分离层之间缺少相互干涉,在后缘T点附近流场由上下表面流动的共同作用决定。
与上述流动特性相对应,脉动压力系数在上表面出现一个峰值,在下表面出现3个峰值,分别与折点处的流动分离有关。当攻角为6°时,前缘L在上下表面均未立即发生分离,上表面在折点a点发生分离,直到0.5距离处仍有明显的负压区,下表面在折点d和e两处发生分离,且下游折点e处的分离更强烈。由脉动风压分布可知,上下表面都在0.4距离附近发生了再附着,该特点将在后面3.3节进一步讨论。当攻角为-6°时,上表面基本上为迎风面,在折点a处压力下降,但未发生稳定的流动分离;下表面在前缘L发生大尺寸的分离,因此折点d处未显示再分离,折点e处的流动分离也不明显。同时脉动风压分布显示流动在上表面0.5距离附近发生了再附着。
以上结果表明桥梁断面绕流和气动力特性随攻角依存性非常强。考虑到山区强风和台风过程中风速具有较大的风攻角[18-19],本文在研究湍流对桥梁节段模型气动力特性影响时,考虑了较大的风攻角范围(-12°~12°)。
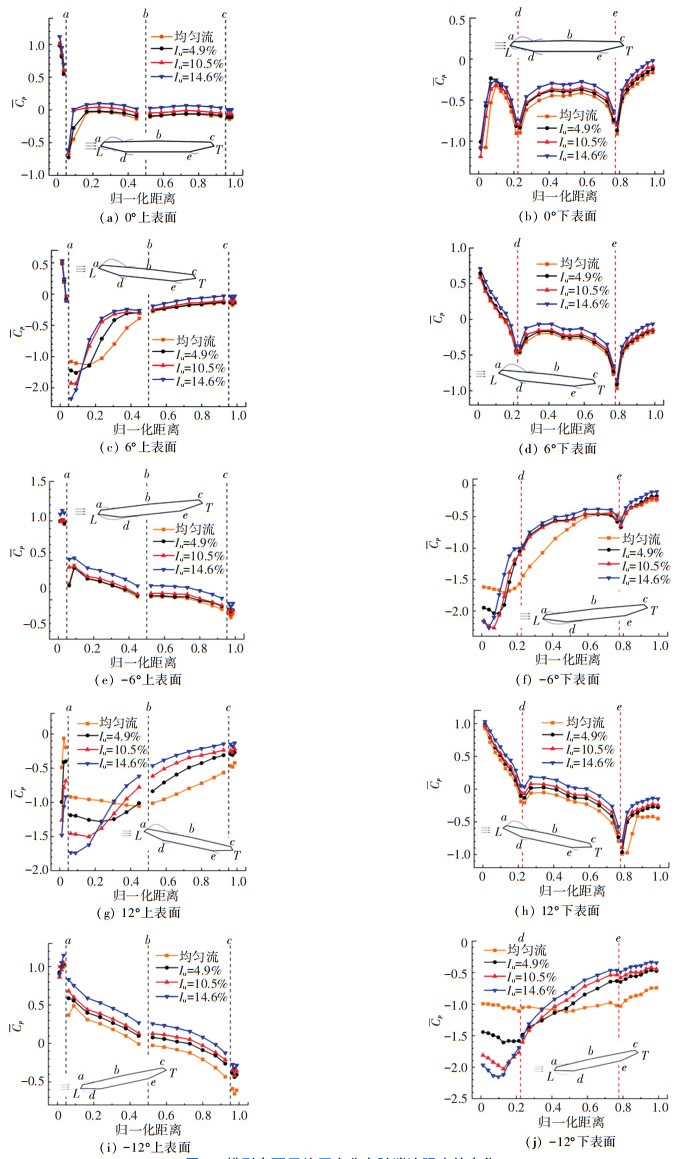
3.2 湍流强度对平均风压系数的影响图 5给出不同攻角(0°, 6°,-6°, 12°,-12°)和湍流强度(4.9%,10.5%,14.6%)下,节段模型上、下表面的平均压力系数分布。在0°攻角下,来流湍流强度对上、下表面的平均压力分布形状影响较小,但平均压力系数在上表面分离点a之后随着湍流强度的增大而增大,与均匀来流相比,压力恢复较快,表明分离边界层较早地在上表面再附着。随后的上表面压力系数以及下表面自分离点L之后的平均压力系数均随着湍流强度的增大而增大(趋向零值),表明湍流强度削弱了分离边界层强度。该结果与钝体和自由边界层的湍流效应相类似。文献[10]指出来流湍流与钝体两侧分离边界层的相互作用使得分离边界层的曲率增大、分离泡长度减小。文献[20]发现来流湍流会使得山坡坡顶附近放出的分离边界层较早地湍流化,从而减小再附着长度。
|
图 5 模型表面平均压力分布随湍流强度的变化 Fig. 5 Variation of mean pressure coefficient distribution with turbulence intensity |
正攻角(6°)下,上表面前缘压力分布受湍流强度影响较大,上表面后缘和下表面压力分布受湍流强度影响相对较小。和均匀来流下的情况一致,3种湍流强度下的上表面的分离都发生在折点a处,并且a点的负压幅值随着湍流强度的增大逐渐增大,伴随a点处分离产生的强负压区长度随着湍流强度的增大逐渐减小。上表面中后缘和下表面的压力分布随湍流强度的增大表现出增大的趋势。负攻角(-6°)下,上表面受湍流强度影响较小,下表面影响与正攻角的下表面情况类似。
更大攻角(12°, -12°)时上下表面压力系数分布随湍流强度的整体变化趋势与攻角(6°, -6°)的情况比较接近。较为不同的是,攻角12°时在上表面前缘L点处已经发生了局部分离,并且湍流强度越大,负压幅值越大。
3.3 湍流强度对脉动风压系数和再附着点位置的影响上节已经表明湍流强度影响的复杂性主要体现在湍流对正攻角时的节段模型上表面和负攻角时的下表面的分离边界层和再附着的影响,发生于模型前缘;而在模型后缘,湍流强度的作用基本一致,即压力系数随着湍流强度的增大而增大。因此,本节主要讨论正攻角时的节段模型上表面和负攻角时的下表面的分离边界层和再附着特性。
图 6给出节段模型上表面在0°,6°,12°攻角和下表面在0°,-6°,-12°下的脉动风压系数分布随湍流强度的变化。上下表面脉动压力系数都随着湍流强度的增加而增加,并且在断面前缘的增加明显。必须强调的是,上表面ab间的脉动风压系数的极值点随着湍流强度的增加向折点a点移动,下表面的极值点也向前缘L点移动。

|
图 6 模型表面脉动风压系数分布随湍流强度的变化 Fig. 6 Variation of fluctuating pressure coefficient distribution with turbulence intensity |
为进一步定量描述湍流对桥梁节段模型分离再附着流动状态的影响,本文引入如下再附着点位置定义[17]:再附着点为靠近分离点的下游最大脉动压力处,其表达式为
| $ X_r=\left.X\right|_{\max C_\sigma} 0.95 $ | (4) |
式中:Xr为再附着长度,
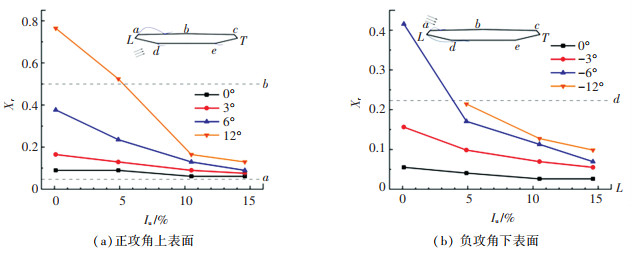
图 7给出了上下表面再附着长度随湍流强度的变化。随着湍流强度的增加,再附着长度减小,再附着点位置向分离点移动,即伴随分离的涡尺度减小。湍流度较小时湍流对再附着长度的作用较为明显。这些特征随着风攻角的增加越发显著,这是因为随着风攻角的增大,桥梁节段模型从准流线型向非流线型改变,分离和再附着特性变得更加明显。以上湍流对桥梁节段模型绕流分离和再附着状态影响的分析是基于模型表面压力测试结果,拟通过数值模拟进行更深一步的验证和分析。
|
图 7 节段模型表面附着长度随湍流强度的变化 Fig. 7 Variation of reattachment length with turbulence intensity |
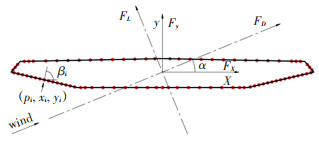
忽略表面摩擦力的影响,通过对离散的压力进行积分来获得桥梁结构的气动三分力系数,阻力、升力和升力矩系数可由下式得出:
| $ C_D=\frac{2 F_D}{\rho U^2 D} \approx \frac{2 \sum \bar{p}_i L_i \cos \left(\beta_i-\alpha\right)}{\rho U^2 D} $ | (5) |
| $ C_L=\frac{2 F_L}{\rho U^2 B} \approx \frac{2 \sum \bar{p}_i L_i \sin \left(\beta_i-\alpha\right)}{\rho U^2 B} $ | (6) |
| $ C_M=\frac{2 M}{\rho U^2 B^2} \approx \frac{2 \sum \bar{p}_i L_i\left(y_i \sin \beta_i-x_i \sin \beta_i\right)}{\rho U^2 B} $ | (7) |
式中:
|
图 8 压力积分示意图 Fig. 8 Schematic diagram of pressure integral |
图 9给出不同湍流度下的节段模型三分力系数,其随风攻角变化的整体趋势与风洞测力结果基本一致[21]。在小攻角下,不同湍流度下的三分力系数差异较小。在大攻角下,有无湍流对阻力系数影响较大,但并无明显规律;对于升力和升力矩,随着湍流度的增加,静力失速现象发生在更高的攻角下。

|
图 9 气动三分力系数随湍流强度的变化 Fig. 9 Variation of force coefficients with turbulence intensity |
为进一步分析湍流强度对三分力系数的影响,将断面分为前缘区(LR)、中部区(CR)和后缘区(TR)3个区域,分别计算各个区域上的压力积分。图 10给出了均匀流中典型攻角下各区域对气动力的贡献,对于阻力系数CD,小攻角下,CR区由于表面与风轴几乎平行,因而贡献较小,阻力主要由LR和TR区贡献,随着攻角增加,CR区的贡献占比增加;对于升力系数CL,由于TR区流动分离并不明显,上下表面风压差较小,因此贡献较小;对于升力矩系数CM,前缘LR区贡献比例较大。

|
图 10 各区域对三分力的贡献 Fig. 10 Force coefficients distribution at different regions |
图 11给出了0°攻角下各区域上下表面气动力改变值随湍流强度的变化。对于阻力系数CD,LR区上、下表面改变值为正,TR区上、下表面改变值为负;对于升力系数CL,LR、CR、TR区上表面改变值为正,下表面改变值为负;对于升力矩系数CM,LR区上表面和TR区下表面改变值为正,LR区下表面和TR区上表面改变值为负。随着湍流强度的增加,改变值增加,现象更加明显。

|
图 11 各区域气动力改变比例随湍流强度的变化(0°攻角) Fig. 11 Variation of force coefficients distribution at different regions with turbulence intensity (0° attack angle) |
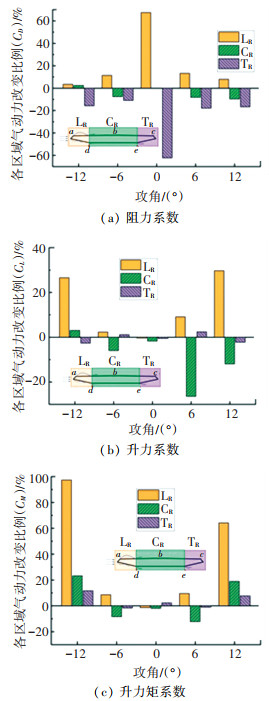
湍流强度为14.6%风场下各攻角气动力变化如图 12所示,0°攻角下LR和TR区阻力系数改变比例较大,但方向相反,因此总体阻力变化并不明显。LR和CR区在大攻角时升力和升力矩系数改变比例较大,是气动力改变的主要贡献区域。
|
图 12 各区域气动力改变值随攻角的变化(Iu= 14.6%) Fig. 12 Variation of force coefficients distribution at different regions with attack angle (Iu=14.6%) |
在保持湍流积分尺度约为(Lux/D=2.4,D为模型高度)的基础上,模拟了具有不同湍流度的3种湍流风场。通过桥梁节段模型测压试验,研究了湍流强度对桥梁断面气动特性影响及其机理,主要结论如下:
1) 湍流强度对桥梁节段模型气动力特性的影响较为复杂。湍流显著影响零攻角、正攻角时的模型上表面和负攻角时的模型下表面的分离、再附着特性,大幅改变模型前缘的平均风压系数分布。
2) 随着湍流强度的增加,上表面分离点(前缘下游首个折点)和下表面分离点(前缘点)处的负压幅度增大,压力恢复点伴随分离涡向上游分离点移动。在模型后缘,平均压力系数随着湍流强度的增加而增大。
3) 湍流对边界层扰动现象较为明显,零攻角、正攻角时的上表面和负攻角时的下表面脉动风压系数在整个断面宽度范围内都随着湍流强度的增加而增大,脉动压力系数极值点(再附着点)向上游分离点移动。
4) 对于桥梁断面的整体气动性能,小攻角下湍流强度对三分力系数影响较小,大攻角下随着湍流强度的增加,失速现象出现在更高的攻角下。前缘LR区和后缘TR区平均压力分布的改变是阻力系数变化的主要区域,前缘LR区和中部CR区变化对升力和升力矩系数改变贡献较大,上述改变在大攻角下更为明显。
| [1] |
项海帆. 结构风工程研究的现状和展望[J]. 振动工程学报, 1997, 10(3): 258. XIANG Haifan. State of the art and prospect in studies on structural wind engineering[J]. Journal of Vibration Engineering, 1997, 10(3): 258. DOI:10.16385/j.cnki.issn.1004-4523.1997.03.004 |
| [2] |
MATSUMOTO M, SHIRAISHI N, SHIRATO H, et al. Mechanism of, and turbulence effect on vortex-induced oscillations for bridge box girders[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993, 49(1): 467. DOI:10.1016/0167-6105(93)90041-L |
| [3] |
张志田, 陈政清, 葛耀君, 等. 紊流中大跨桥梁的扭转发散特性[J]. 工程力学, 2010, 27(2): 108. ZHANG Zhitian, CHEN Zhengqing, GE Yaojun, et al. Torsional divergence characteristics of long span bridge in turbulence[J]. Engineering Mechanics, 2010, 27(2): 108. |
| [4] |
MANNINI C, BARTOLI G. Aerodynamic uncertainty propagation in bridge flutter analysis[J]. Structural Safety, 2015, 52: 29. DOI:10.1016/j.strusafe.2014.07.005 |
| [5] |
LI S, LI M, LIAO H. The lift on an aerofoil in grid-generated turbulence[J]. Journal of Fluid Mechanics, 2015, 771: 16. DOI:10.1017/jfm.2015.162 |
| [6] |
李利孝, 肖仪清, 胡钢, 等. 积分尺度和风速谱对桥梁抖振响应影响分析[J]. 哈尔滨工业大学学报, 2012, 44(12): 23. LI Lixiao, XIAO Yiqing, HU Gang, et al. Influences of integral scale and wind spectrum on buffeting response of long-span bridge[J]. Journal of Harbin Institute of Technology, 2012, 44(12): 23. |
| [7] |
BASU R I. Aerodynamic forces on structures of circular cross-section. Part 2. The influence of turbulence and three-dimensional effects[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1986, 24(1): 33. DOI:10.1016/0167-6105(86)90071-1 |
| [8] |
BLACKBURN H, MELBOURNE W H. The effect of free-stream turbulence on sectional lift forces on a circular cylinder[J]. Journal of Fluid Mechanics, 1996, 306: 267. DOI:10.1017/S0022112096001309 |
| [9] |
HILLIER R, CHERRY N J. The effects of stream turbulence on separation bubbles[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1981, 8(1): 49. DOI:10.1016/0167-6105(81)90007-6 |
| [10] |
NAKAMURA Y, OZONO S. The effects of turbulence on a separated and reattaching flow[J]. Journal of Fluid Mechanics, 1987, 178: 477. DOI:10.1017/S0022112087001320 |
| [11] |
NAKAMURA Y, OHYA Y, OZONO S. The effects of turbulence on bluff-body mean flow[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1988, 28: 251. DOI:10.1016/0167-6105(88)90121-3 |
| [12] |
LI Q S, MELBOURNE W H. An experimental investigation of the effects of free-stream turbulence on streamwise surface pressures in separated and reattaching flows[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1995, 54. DOI:10.1016/0167-6105(94)00050-N |
| [13] |
LI Q S, MELBOURNE W H. The effect of large-scale turbulence on pressure fluctuations in separated and reattaching flows[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999, 83(1): 159. DOI:10.1016/S0167-6105(99)00069-0 |
| [14] |
BERGH H, TIJDEMAN H. Theoretical and experimental results for the dynamic response of pressure measuring systems[R]. Amsterdam: Nationaal Lucht-en Ruimtevaartlaboratorium, 1965
|
| [15] |
HOLMES J, LEWIS R E. Optimization of dynamic-pressure-measurement systems. I. single point measurements[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1987, 25: 249. DOI:10.1016/0167-6105(87)90021-3 |
| [16] |
HIDEHARU M. Realization of a large-scale turbulence field in a small wind tunnel[J]. Fluid Dynamics Research, 1991, 8(1): 53. DOI:10.1016/0169-5983(91)90030-M |
| [17] |
SHU Z R, LI Q S. An experimental investigation of surface pressures in separated and reattaching flows: effects of freestream turbulence and leading edge geometry[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2017, 165: 58. DOI:10.1016/j.jweia.2017.03.004 |
| [18] |
CHU X, CUI W, ZHAO L, et al. Probabilistic flutter analysis of a long-span bridge in typhoon-prone regions considering climate change and structural deterioration[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2021, 215: 104701. DOI:10.1016/j.jweia.2021.104701 |
| [19] |
LIAO H, JING H, MA C, et al. Field measurement study on turbulence field by wind tower and Windcube Lidar in mountain valley[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2020, 197: 104090. DOI:10.1016/j.jweia.2019.104090 |
| [20] |
CAO S, TAMURA T. Experimental study on roughness effects on turbulent boundary layer flow over a two-dimensional steep hill[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2006, 94(1): 1. DOI:10.1016/j.jweia.2005.10.001 |
| [21] |
同济大学. 《苏通长江公路大桥初步设计阶段主梁抗风性能研究(三)》风洞试验报告[R]. 上海: 同济大学, 2002 Tongji University. Study on wind resistance of main girder of Sutong Yangtze River Highway Bridge in preliminary design stage (Third)[R]. Shanghai: Tongji University, 2002 |
 2023, Vol. 55
2023, Vol. 55


