2. 岩土及地下工程教育部重点实验室(同济大学),上海 200092;
3. 中国电建集团华东勘测设计研究院有限公司,杭州 311122;
4. 河海大学 岩土工程科学研究所,南京 210098
2. Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education(Tongji University), Shanghai 200092, China;
3. Huadong Engineering Corporation Limited, Hangzhou 311122, China;
4. Geotechnical Research Institute, Hohai University, Nanjing 210098, China
中国幅员辽阔,地质条件极其复杂,50%以上国土面积为7度以上高烈度区。拟建和已建的高速铁路(以下简称高铁)及其周边地区常为地震多发区,如京沪高铁沿线穿越了4条较大的地震构造带,20世纪以来发生7次危及高铁正常运营的危险性地震[1]。实际上,地震导致的铁路安全问题多有报道,如2004年日本新泻地震和2010年中国台湾高雄地震造成了严重的出轨事故[2-3]。因此,地震灾害是高铁建设与运营必须面对与解决的问题。
1989年美国加州Loma Prieta 6.9级地震中远场(断层距77.4 km,软土场地,剪切波速为155 m/s)地震动加速度时程[4]与中国秦沈高铁距轨道中心3.5 m路基表面处振动加速度[5]对比结果表明两者振动强度相当(加速度峰值约为0.1g),且高铁荷载引起的地基振动也存在一定的低频成分,可能与地震荷载产生震动放大效应。因此,地震发生时高铁地基承受地震和行车荷载的共同作用,仅考虑地震荷载作用而忽略高铁荷载的影响并不合理。
目前,地震-高铁荷载共同作用下车-轨系统动力响应研究成果较为丰富(不考虑地基土影响),如Matsuura[6]、Yang等[7]、Tanabe等[8]分析了地震作用下列车与轨道的动力相互作用,并讨论了地震中导致列车脱轨的影响因素。然而,两动载共同作用下车-轨系统动力响应研究中均未考虑地基土的影响。实际上,高速列车通过不同场地条件的地基时引起的地面振动及其衰减规律有差异[9]。震害调查及地震理论研究均表明:土体对地震响应及震害分布影响显著,如Darragh等[10]对1989年Loma Prieta地震中软土场地和砂页岩场地的地震记录进行对比分析,结果表明强震作用下软土场地的地面运动与岩石场地相比在0.5~2.0 Hz之间被放大了近3倍。因此,研究地震-高铁荷载共同作用需要考虑地基土的影响。
2.5维有限元法是分析地震或高铁移动荷载引起地面振动的常用方法。Hwang和Lysmer[11]将2.5维有限元应用于地震工程,杨永斌等[12]首次提出了2.5维有限元法研究列车荷载引起的地面振动。近年来,该方法分析高铁荷载引起的层状弹性地基、饱和地基和横观各向同性地基的地面振动已取得丰富的研究成果,代表性学者有高广运等[13-14]、边学成等[15]、Colaço等[16]和巴振宁等[17]。迄今为止,2.5维有限元法分析地基震动仅限于列车载荷或地震单一荷载作用,未见两动载共同作用的相关报道。
地震荷载引起的路基震动研究中,武思宇等[18]基于振动台试验研究了地震荷载作用下刚性桩复合地基的震动规律。Morteza等[19]基于有砟轨道路基有限元模型分析了路基抗震性能;杨长卫等[20]开展了地震荷载作用下有砟轨道路基动力响应规律振动台试验研究。目前,地震荷载引起的路基震动研究仅考虑地震荷载而忽略高铁荷载的影响。
文献分析表明,目前地震-高铁荷载共同作用下车-轨系统动力响应研究忽略地基土的影响。地震或高速列车单一动载荷载作用下地基震动研究较多,同时考虑两动载共同作用下地基震动研究鲜有报道。为此,本文建立了地震-高铁共同作用下非线性分层地基震动2.5维有限元计算模型,计算分析了地震-高铁荷载共同作用下分层地基的震动响应规律,研究车速和地基软硬对两动载共同作用下地面震动的影响,旨在为地震期间高速列车走行的安全性评价提供依据。
1 地震-高铁荷载共同作用下非线性地基2.5维有限元模型图 1为地震和高铁荷载共同作用下轨道和地基的有限元网格模型示意图,轨道中心为坐标原点。本文假定列车运行方向上所受地震波仅为时间的函数,并且仅考虑远源地震波垂直入射的情况。

|
图 1 轨道和地基的有限元模型示意图 Fig. 1 Schematic diagram of finite element model for the track and ground |
采用上标“-”表示频率内的量,“~”表示波数域内的量,定义关于时间t和列车运行方向x的双重Fourier正逆变换为
| $ \tilde{\bar{u}}\left(\varepsilon_x, y, z, \omega\right)=\int_{-\infty}^{+\infty} u(x, y, z, t) \mathrm{e}^{-\mathrm{i} \omega t} \mathrm{e}^{\mathrm{i} \varepsilon_x x} \mathrm{~d} x \mathrm{~d} t $ | (1) |
| $ u(x, y, z, t)=\frac{1}{4 \pi^2} \int_{-\infty}^{+\infty} {\tilde{\bar{u}}}\left(\varepsilon_x, y, z, \omega\right) \mathrm{e}^{\mathrm{i} \omega t} \mathrm{e}^{-\mathrm{i} \varepsilon_x x} \mathrm{~d} \varepsilon_x \mathrm{~d} \omega $ | (2) |
式中:ω和εx分别表示为圆频率和x方向的波数,i为虚数单位,u为振动位移。
假设列车运行方向轨道和地基是连续均匀,将轨道模型模拟成铺设在地基上的欧拉梁,轨道宽7 m,弯曲刚度EI为13.254 MN·m2, 单位质量为540 kg/m,轨道上作用荷载为f(x, y, z, t),则轨道动力方程矩阵形式为
| $ {\widetilde{\bar{\boldsymbol{K}}}_{I T}}{\widetilde{\bar{\boldsymbol{U}}}_{I T}}=\widetilde{\bar{\boldsymbol{F}}}_{I T}+\widetilde{\bar{\boldsymbol{F}}}_T $ | (3) |
式中:
杨永斌等[12]推导了弹性地基2.5维有限元方程:
| $ \left(\widetilde{\bar{\boldsymbol{K}}}-\omega^2 \widetilde{\bar{\boldsymbol{M}}}\right) \widetilde{\bar{\boldsymbol{U}}}=\widetilde{\bar{\boldsymbol{F}}} $ | (4) |
其中:M、K和F分别为质量矩阵、刚度矩阵和外力矢量,具体表达式详见文献[12]。
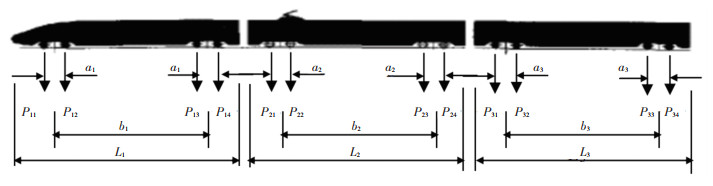
1.3 列车荷载表达式采用复兴号动车组CRH380的列车荷载模型,动车组计算模型如图 2所示。已有研究表明取4节车厢即满足模拟列车多轮负载效应[13, 21],故本文取6节车厢计算满足列车荷载模拟的精度要求。每节车厢共4组轮对,列车荷载的持续时间与地震周期一致,以保证时域内列车荷载与地震荷载共同作用。
| $ \begin{aligned} & \tilde{\bar{f}}\left(\varepsilon_x, y, z, \omega\right)=\frac{2 \pi}{c} \delta\left(\varepsilon_x-\frac{\omega-\omega_0}{c}\right) \sum\limits_{n=1}^{N-1}\left[p_{n 1}(1+\right. \\ &\;\;\;\; \left.\mathrm{e}^{-\mathrm{i} a \varepsilon_x}\right)+p_{n 2}\left(\mathrm{e}^{-\mathrm{i}\left(a_n+b_n\right) \varepsilon_x}+\right. \\ & \;\;\;\;\left.\left.\mathrm{e}^{-\mathrm{i}\left(2 a_n+b_n\right) \varepsilon_x}\right)\right] \mathrm{e}^{-\mathrm{i} \sum\limits_{k=0}^{N-1} L_k \varepsilon_x} \end{aligned} $ | (5) |
|
图 2 列车荷载模型 Fig. 2 Train load model |
式中:pn1, pn2分别为车厢前后轮对的轴重;Li为车厢长度;an, bn分别为前后轴之间的距离;δ为Dirac函数;c为车速;ω0为列车自振圆频率;n为车厢数。列车模型参数取值详见文献[13]。
1.4 地震荷载表达式刘晶波等[22]采用数值模型底部粘弹性人工边界上施加等效荷载的方法进行地震波输入,地震荷载输入公式为
| $ F_B(t)=F\left(x_B, y_B, t\right)+C \dot{u}\left(x_B, y_B, t\right)+K u\left(x_B, y_B, t\right) $ | (6) |
式中:u(xB, yB, t)为人工边界上地震荷载引起的位移;FB(t)为施加在人工边界上的总荷载;F(xB, yB, t)表示入射波引起的位移产生的人工边界上的应力,下标B表示模型底部人工边界上的节点;xB, yB和zB分别表示B点的坐标。详细推导过程见文献[22]。
假设时间相同时地震荷载F(t)仅沿轨道方向不变,则施加在人工边界点上的地震荷载可表示为
| $ F_B(x, t)=\delta\left(x-x_0\right) F_B(t) A_j $ | (7) |
式中:x0为观测点处的坐标,Aj为节点影响面积。
设观测点的坐标x0为0,对式(7)进行双重傅里叶变换,可得
| $ \begin{aligned} \tilde{\bar{F}}_B\left(\varepsilon_x, \omega\right)= & {\left[\tilde{F}_u\left(x_B, y_B, \omega\right)+\mathrm{i} \omega C \tilde{u}\left(x_B, y_B, \omega\right)+\right.} \\ & \left.K \tilde{u}\left(x_B, y_B, \omega\right)\right] A_j \end{aligned} $ | (8) |
写成矩阵形式为
| $ \tilde{\bar{\boldsymbol{F}}}_B=\left[\tilde{\boldsymbol{F}}_u+i \omega \boldsymbol{C \boldsymbol {\tilde{U}}}_B+\boldsymbol{K} \tilde{\boldsymbol{U}}_B\right] \boldsymbol{A}_j $ | (9) |
式中:
通过双重傅里叶变换将列车荷载和地震荷载表达式转化到频域-波数域,基于频率与波数相关关系,可将两动载的荷载表达式均转化为频率相关的函数,最终得到地震和高铁荷载共同作用下地基震动的矩阵方程式(10)。求解式(10)即可得到两动载共同作用下地基震动的频域响应结果,再通过双重傅里叶逆变换即可得到时域的解答。
| $ \left.{(\tilde{\bar{\boldsymbol{K}}}}-\omega^2 \widetilde{\bar{\boldsymbol{M}}}\right) \widetilde{\bar{U}}=\widetilde{\bar{\boldsymbol{F}}}+\widetilde{\bar{\boldsymbol{F}}}_{\mathrm{B}} $ | (10) |
Hwang和Lysmer[11]指出频域内求解土体震动响应时应采用等效线性化方法考虑土体的非线性特性。因此本文采用SHAKE91软件[23]计算得到地震荷载下自由场地的等效剪切模量和阻尼比作为模型计算参数,以反映土体非线性特性的影响。
1.6 粘弹性人工边界频域内2.5维有限元粘弹性边界方程为
| $ \tilde{\boldsymbol{F}}_j=\boldsymbol{K}_j \tilde{\boldsymbol{U}}_j+\mathrm{i} w \boldsymbol{C}_j \tilde{\boldsymbol{U}}_j $ | (11) |
基于刘晶波等[24]给出了物理元件模拟三维人工法向边界和切向边界参数,即可得到2.5维有限元粘弹性人工边界为
| $ \begin{array}{l} {\mathit{\boldsymbol{\widetilde F}}_j} = \\ \left[ {\begin{array}{*{20}{c}} {\left( {\frac{{2G}}{R} + {\rm{i}}\omega \rho {c_s}} \right){A_j}}&0&0\\ 0&{\left( {\frac{{2G}}{R} + {\rm{i}}\omega \rho {c_s}} \right){A_j}}&0\\ 0&0&{\left( {\frac{{4G}}{R} + {\rm{i}}\omega \rho {c_p}} \right){A_j}} \end{array}} \right] \end{array} $ |
式中:j =x, y, z;cs和cp分别为剪切波速和压缩波速。G为土体剪切模量,ρ为土体密度,R为荷载作用点到粘弹性边界点的距离。编写程序时,只需将矩阵Fj组装到边界节点对应的总体刚度矩阵上,即可完成粘弹性边界的施加。
2 数值模型的验证高速列车和地震荷载共同作用下地基震动2.5维有限元模型分别采用两个算例进行验证。算例1中地震荷载取零,对比移动点荷载作用下弹性地基振动与解析解结果,可验证模型计算列车引起的地面振动计算结果的准确性。算例2取列车载荷为零,研究了竖向入射波作用下分层地基地面响应,验证频域中采用等效载荷法输入地震波的可靠性。
2.1 地表移动常荷载解析解验证(算例1)计算模型如图 1所示,选取深度×宽度=30.0 m× 60.0 m的均匀土层近似代表半空间地基,网格尺寸为0.5 m×0.5 m,竖向移动点荷载运行速度为70.0 m/s,土体参数见文献[25]。计算模型固定坐标(0, -30, -30)处的节点,防止地基模型产生刚性位移,模型两侧与底部均施加粘弹性人工边界。
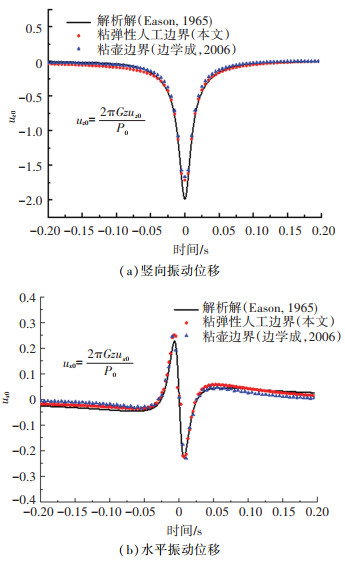
图 3为移动点荷载正下方1 m深处(0 m,0 m,-1 m)的水平向位移和竖向位移响应的计算结果与Eason(1965年)[25]得到的均匀弹性半空间地基解析解结果及边学成等(2006年)[15]采用粘壶边界计算得到的结果对比,图中计算结果均乘以2πρcs2/p进行归一化处理。由图 3可知,本文计算结果与Eason[25]及边学成等(2006年)[15]得到的结果吻合较好,证明了本文2.5维有限元求解列车荷载作用下地面振动的可靠性和正确性。需要说明是,适用于求解高铁荷载下均质地基地面振动的2.5维有限元法,对层状地基也具有较好的适用性[13-14]。
|
图 3 移动点荷载作用下地基中(0 m, 0 m, -1 m)处震动位移 Fig. 3 Ground vibration displacement at the point (0 m, 0 m, -1 m) under a moving point load |
考虑半无限地基覆盖30.0 m厚土层,分3层,层厚分别为2 m、2 m和26 m,在距地表 30 m深处入射如图 4所示的位移时程[22]。计算模型如图 1示,采用30.0 m×60.0 m的分层地基来近似代表半空间地基,土层层厚由上到下分别设置为2 m、2 m和26 m,观测点位于轨道中心点处。地表作用的列车荷载速度为0 m/s,根据文献[26-27]中场地实测结果选取地基土层计算参数(分层地基工况1),见表 1。计算时间间隔Δt取0.002 5 s。各层土体的动剪切模量和阻尼比随剪应变的变化规律见文献[26-27]。采用SHAKE91计算得到了图 4入射波作用下地基土的剪切模量比(剪切模量G/ 小应变剪切模量Gmax)和阻尼比,见表 2。
| 表 2 土体动剪切模量和阻尼比等效线性化结果(工况1) Tab. 2 Equivalent linearization results of soil dynamic shear modulus and damping ratio (case Ⅰ) |
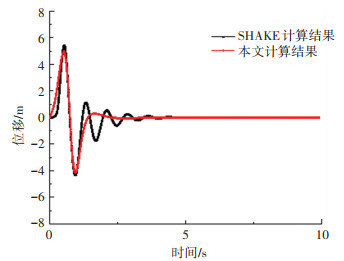
图 5对比了SHAKE91软件[23]计算结果与本文数值方法计算得到的分层地基自由表面观测点处竖向振动位移时程结果。由图 5可知,本文计算得到的地面震动位移响应与SHAKE91软件计算结果总体吻合较好,表明2.5维有限元程序中采用频域内等效荷载法在粘弹性边界上进行地震动输入是合理可行的,且具有良好的计算精度。需要指出的是,SHAKE 91软件中模型底部边界为固定边界[23],波的反射效应明显,地基受迫振动后位移响应会产生一定的震荡;本文计算模型底部边界为粘弹性人工边界,吸波效果更好,可更好地模拟半无限地基。
|
图 5 分层地基自由场观测点处位移时程对比 Fig. 5 Comparison of displacement time history of free field at observation point for layered ground |
由于缺少地震-高铁共同作用下地基震动的实测数据,因此未能进行两种荷载共同作用下地基震动响应验证。实际上,本文编制的程序中已将列车荷载和地震荷载均转化为频率相关的函数,计算地基震动响应即求解频域内矩阵方程,两动载共同作用时矩阵方程多一项已知变量,不影响矩阵方程的求解。算例1和算例2仅退化为频域地震荷载相关的已知变量取零和频域内列车荷载相关的已知变量取零的特例。因此,本文基于2.5维有限元原理和等效荷载法提出的地震-高铁荷载共同作用下非线性地基2.5维有限元计算模型可有效地分析地震-高铁荷载引起的三维地基震动问题。
3 地震和高铁荷载共同作用下非线性分层地基震动规律选取1989年Loma Prieta地震作为地震输入荷载,地震波加速度时程如图 6所示。为分析地基软硬对地震-高铁荷载下地面震动的影响,根据文献[26-27]中场地实测场地土层设置了另一组场地计算参数(分层地基工况2)见表 3。计算模型示意图和地基土层厚度设置与前文一致。采用SHAKE91计算得到了Loma Prieta地震下两种工况地基土层等效动剪切模量和阻尼比,见表 4。

|
图 6 Loma Prieta地震波 Fig. 6 Loma Prieta seismic wave |
| 表 4 土体动剪切模量和阻尼比等效线性化结果 Tab. 4 Equivalent linearization results of soil dynamic shear modulus and damping ratio |
图 7为轨道中心处(0 m, 0 m, 0 m)不同车速时地震和高铁荷载共同作用与地震荷载单独作用下两工况地基地面震动位移时程曲线对比。由图 7可知,同一地震事件中场地条件相同的条件下,地震和高铁荷载共同作用引起的地面震动位移随车速的增大而增大。车速60 m/s时,两动载共同作用与地震荷载单独作用时两种工况地面震动位移曲线均差异较小。车速75 m/s时,两动载共同作用下较硬地基(工况2,等效剪切波速410.5 m/s)地面震动位移与地震荷载单独作用时的结果差异仍较小,但较软地基(工况1,等效剪切波249.7 m/s)中两动载共同作用引起的地面震动位移大于地震荷载单独作用的结果。车速等于和大于94.5 m/s时,两种地基工况中地震与高铁荷载共同作用引起的地面震动位移均大于地震荷载单独作用的结果,较软地基中差异尤为明显,且相同地基车速越大差异越大。对于确定的地基工况,地震和高铁荷载共同作用存在一个临界车速,车速低于临界值时,仅研究考虑地震荷载单独作用即可,车速大于临界值时则需考虑两荷载共同作用,临界车速随地基刚度的增加而增大。

|
图 7 地震-高铁共同作用与地震单独作用下轨道中心处地基震动位移时程对比 Fig. 7 Comparison of ground displacement time history at track center under combined seismic and high-speed train loads and seismic load alone |
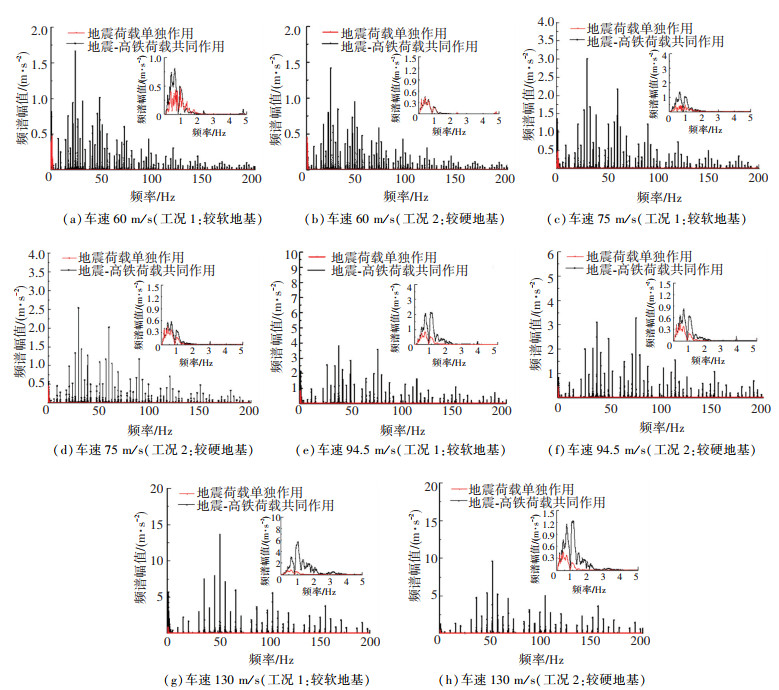
从图 7还可以看出,车速相同时地震与高铁荷载作用下较软地基的震动大于硬土地基,产生该现象的原因可能有如下两点:一是相同列车荷载在较软地基上产生的振动大于较硬地基;二是地震作用下软土地基的地面震动放大效应比硬土更明显[10],故地震期间列车在较硬地基上运行的安全性高于软土地基。图 8为地震和高铁荷载共同作用与地震荷载单独作用下轨道中心处(0 m, 0 m, 0 m)地基震动加速度频谱对比结果。由图 8可知,与地震单独作用相比,地震-高铁荷载共同作用时中高频震动成分显著增加,表明两荷载共同作用时中高频震动由列车荷载产生。地震和高铁荷载共同引起地基的低频震动,对于较硬地基,车速60 m/s时地震和高铁荷载共同作用下低频震动成分与地震荷载单独作用差异小,低频震动放大效应不明显;随车速的增大,两动载的低频震动放大效应逐步增加。对于较软地基,车速较低时已经产生低频震动放大效应,车速增大则低频震动放大效应更为显著。列车荷载作用下地面以中高频震动为主,但仍会产生一定的低频震动成分,与地震荷载作用时会产生低频放大现象;车速较高、地基土较软时列车荷载引起的低频震动成分更加丰富,故与地震荷载共同作用时低频放大现象更明显。
|
图 8 地震-高铁共同作用与地震单独作用下轨道中心处地基地面震动频谱对比 Fig. 8 Comparison of ground motion frequency spectrum at track center under combined seismic and high-speed train loads and seismic load alone |
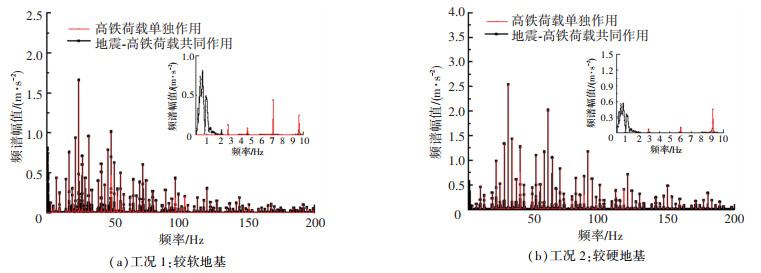
以车速75 m/s为例,对比了地震和高铁荷载共同作用与高铁荷载单独作用下轨道中心处(0 m, 0 m, 0 m)地基震动加速度频谱结果,如图 9所示。由图 9可知,地震和高铁荷载共同作用与高铁荷载单独作用时中高频差异很小,进一步证明了两动载共同作用时中高频震动由列车荷载产生。与高铁荷载单独作用相比,两动载共同作用时低频震动显著增大,表明地震和高铁荷载共同作用时的地震动存在低频放大效应,与前文结论一致。
|
图 9 地震-高铁共同作用与高铁单独作用下轨道中心处地基地面震动频谱对比 Fig. 9 Comparison of ground motion frequency spectrum at track center under combined seismic and high-speed train loads and high-speed train load alone |
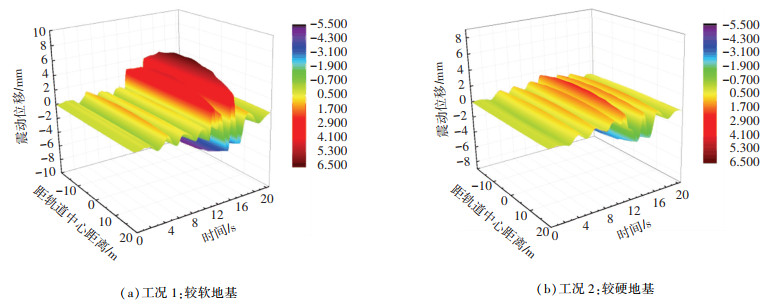
图 10为车速75 m/s时Loma Prieta地震-高铁荷载作用下垂直轨道方向软硬两类地基震动位移云图。由图 10可知,车速相同的条件下,近轨道中心处震动位移大于距轨道较远处,表明近轨道中心处,地面震动受地震和高铁荷载共同作用影响较大;距轨道中心较远处,地面震动主要受地震荷载影响,高铁荷载的影响较小。从图 10中还可以看出,较硬地基的轨道中心处地面震动位移幅值与轨道中心较远处差异相对较小,较软地基则两者差异较大,表明两种荷载共同作用下地基较硬时列车荷载影响较小,地基较软时列车荷载影响增大,地震与高铁荷载耦合放大效应更明显。
|
图 10 车速75 m/s地震-高铁荷载下两类地基震动位移云图 Fig. 10 Vibration displacement cloud diagram of two types of ground under combined seismic and high-speed train loads at a train speed of 75 m/s |
本文建立了地震和高铁荷载共同作用下地基震动2.5维有限元计算模型,研究了两动载共同作用下地面震动响应规律,分析了车速和地基软硬条件对地面震动位移影响,得到以下结论:
1) 相同场地条件下,地面震动位移随车速的增大而增大。相同车速的条件下,地震和高铁荷载引起的较软地基震动位移大于较硬地基。
2) 地震和高铁荷载共同作用下存在一个临界车速,车速低于临界值时仅考虑地震荷载单独作用即可,车速高于临界值时则需考虑两荷载共同作用,临界车速随地基刚度的增加而增大。
3) 地震和高铁荷载共同作用时地基震动会产生低频放大效应,车速越高、地基越软时地基低频震动放大效应越明显;两动载共同作用引起的地基中高频震动由列车荷载控制,受地震影响较小。
4) 近轨道中心处,地面震动受地震和高铁荷载共同作用影响较大;距轨道中心较远处,地震荷载对地面震动影响较大,高铁荷载的影响较小。
| [1] |
陈令坤, 蒋丽忠, 余志武, 等. 高速铁路简支梁桥地震反应特性研究[J]. 振动与冲击, 2011, 30(12): 216. CHEN Lingkun, JIANG Lizhong, YU Zhiwu, et al. Seismic response characteristics of a high-speed railway simply-supported girder bridge[J]. Journal of Vibration and Shock, 2011, 30(12): 216. DOI:10.3969/j.issn.1000-3835.2011.12.042 |
| [2] |
IKEDA T. The construction of earthquake damage data archives for earthquake disaster mitigation[C]//The 14th World Conference on Earthquake Engineering. Beijing: [s. n. ], 2008: 731
|
| [3] |
陈伟文, 倪四道, 汪贞杰, 等. 2010年高雄地震震源参数的近远震波形联合反演[J]. 地球物理学报, 2012, 55(7): 2319. CHEN Weiwen, NI Sidao, WANG Zhenjie, et al. Joint inversion with both local and teleseismic waveforms for source parameters of the 2010 Kaohsiung earthquake[J]. Chinese Journal of Geophysics, 2012, 55(7): 2319. DOI:10.6038/j.issn.0001-5733.2012.07.017 |
| [4] |
LIAMFINN W D, VENTURA C E, WU G. Analysis of ground motions at Treasure Island site during the 1989 Loma Prieta earthquake[J]. Soil Dynamics and Earthquake Engineering, 1993, 12(7): 383. DOI:10.1016/0267-7261(93)90001-8 |
| [5] |
陈功奇. 基于现场测试的列车引起地基振动分析[J]. 岩石力学与工程学报, 2015, 34(3): 601. CHEN Gongqi. Ground vibration analysis induced by high-speed train based on in-situ data[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(3): 601. |
| [6] |
MATSURA A. Simulation for analyzing direct derailment limit of running vehicle on oscillatingtracks[J]. Journal of Earthquake Engineering, 1998, 15(591): 19. |
| [7] |
YANG Y B, WU Y S. Dynamic stability of trains moving over bridges shaken by earthquakes[J]. Journal of Sound and Vibration, 2002, 258(1): 65. DOI:10.1006/jsvi.2002.5089 |
| [8] |
TANABE M, MATSUMOTO N, WAKUI H, et al. A simple and efficient numerical method for dynamic interaction analysis of a high-speed train and railway structure during an earthquake[J]. Journal of Computational and Nonlinear Dynamics, 2008, 3(4): 1896. |
| [9] |
高广运, 谢伟, 陈娟, 等. 高铁运行引起的高架桥群桩基础地面振动衰减分析[J]. 岩土力学, 2019, 40(8): 3197. GAO Guangyun, XIE Wei, CHEN Juan, et al. Ground vibration attenuation of viaduct and pile-group foundation induced by moving high-speed train[J]. Rock and Soil Mechanics, 2019, 40(8): 3197. DOI:10.16285/j.rsm.2018.0952 |
| [10] |
DARRAGH R B, SHAKAL A F. The site response of two rock and soil station pairs to strong and weak ground motion[J]. Bulletin of the Seismological Society of America, 1991, 81(5): 1885. DOI:10.1785/BSSA0810051885 |
| [11] |
HWANG R N, LYSMER J. Response of buried structures to traveling waves[J]. Journal of the Geotechnical Engineering Division, 1981, 107(2): 183. DOI:10.1061/AJGEB6.0001096 |
| [12] |
YANG Y B, HUNG H H. A 2.5D finite/infinite element approach for modelling visco-elastic bodies subjected to moving loads[J]. International Journal for Numerical Methods in Engineering, 2001, 51(11): 1317. DOI:10.1002/nme.208 |
| [13] |
GAO G Y, CHEN Q S, HE J F, et al. Investigation of ground vibration due to trains moving on saturated multi-layered ground by 2.5D finite element method[J]. Soil Dynamics and Earthquake Engineering, 2012, 40: 87. DOI:10.1016/j.soildyn.2011.12.003 |
| [14] |
GAO G Y, XU C X, CHEN J, et al. Investigation of ground vibrations induced by trains moving on saturated transversely isotropic ground[J]. Soil Dynamics and Earthquake Engineering, 2018, 104: 40. DOI:10.1016/j.soildyn.2017.09.030 |
| [15] |
边学成, 陈云敏. 基于2.5维有限元方法分析列车荷载产生的地基波动[J]. 岩石力学与工程学报, 2006, 25(11): 2335. BIAN Xuecheng, CHEN Yunmin. Ground vibration generated by train moving loadings using 2.5D finite element method[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(11): 2335. |
| [16] |
COLAÇO A, COSTA P A, CONNOLLY D P. The influence of train properties on railway ground vibrations[J]. Structure and Infrastructure Engineering, 2015, 12(5): 1. |
| [17] |
BAZ N, LEE V W, LIANG J W, et al. Dynamic 2.5D Green's functions for moving distributed loads acting on an inclined line in a multi-layered TI half-space[J]. Soil Dynamics and Earthquake Engineering, 2017, 99: 172. |
| [18] |
武思宇, 宋二祥, 刘华北, 等. 刚性桩复合地基的振动台试验研究[J]. 岩土工程学报, 2005, 27(11): 1334. WU Siyu, SONG Erxiang, LIU Huabei, et al. Shaking table test of composite foundation with rigid pile[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(11): 1334. |
| [19] |
MORTEZA E, HAMIDREZA H N. Investigating seismic behavior of ballasted railway track in earthquake excitation using finite-element model in three-dimensionalspace[J]. Journal of Transportation Engineering, 2013, 139(7): 697. |
| [20] |
杨长卫, 童心豪, 王栋, 等. 地震作用下有砟轨道路基动力响应规律振动台试验[J]. 岩土力学, 2020, 41(7): 2216. YANG Changwei, TONG Xinhao, WANG Dong, et al. Shaking table test of dynamic response law of subgrade with ballast track under earthquake[J]. Rock and Soil Mechanics, 2020, 41(7): 2216. |
| [21] |
YANG Y B, HUNG H H, CHANG D W. Train-induced wave propagation in layered soils using finite/infinite element simulation[J]. Soil Dynamic and Earthquake Engineering, 2003, 23(4): 263. |
| [22] |
LIU J B, LU Y D. A direct method for analysis of dynamic soil-structure interaction based on interface idea[J]. Developments in Geotechnical Engineering, 1998, 83: 261. |
| [23] |
IDRISS I M, SUN J I. SHAKE91: a computer program for conducting equivalent linear seismic response analyses of horizontally layered soil deposits[R]. Davis: University of California, Davis, 1992
|
| [24] |
LIU J B, DU Y X, DU X L, et al. 3D viscous-spring artificial boundary in time domain[J]. Earthquake Engineering and Engineering Vibration, 2006, 5(1): 93. |
| [25] |
EASON G. The stresses produced in a semi-infinite solid by a moving surface force[J]. International Journal of Engineering Science, 1965, 2(6): 581. |
| [26] |
朱姣, 陈国兴, 许汉刚. 地震基岩面的选取对深厚场地地表地震动参数的影响[J]. 岩土工程学报, 2015, 37(11): 2079. ZHU Jiao, CHEN Guoxing, XU Hangang. Effect of seismic bedrock interface depth on surface motion parameters of deep site[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(11): 2079. |
| [27] |
杜修力, 许紫刚, 许成顺, 等. 基于等效线性化的土-地下结构整体动力时程分析方法研究[J]. 岩土工程学报, 2018, 40(12): 2155. DU Xiuli, XU Zigang, XU Chengshun., et al. Time-history analysis method for soil-underground structure system based on equivalent linear method[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(12): 2155. |
 2023, Vol. 55
2023, Vol. 55



