故障诊断指故障检测和故障隔离的过程。其中,故障检测的目的是检查是否发生故障和确定故障发生时间,故障隔离的目的是寻找故障发生位置[1]。先进的故障诊断技术有利于提高多能域工程系统的安全性、可靠性以及运行效率。其中,基于解析冗余关系的故障诊断(analytical redundancy relations-based fault diagnosis,ARRBFD)方法,因其具有适用范围广、解释性强、可实现在线监测等优势[2],正被广泛运用到各个工程领域。但是在实际非线性系统故障诊断的应用中,单纯使用ARRBFD方法往往只能实现故障检测,而无法完成故障隔离。根据ARRBFD故障诊断结果可以推断出潜在故障参数集(potential fault parameters set,PFPS)。此时,如果可以得到PFPS内各参数估计值,再将其与标称值进行对比,即可实现故障隔离。考虑到经ARRFD得到的PFPS中各参数,不仅其种类和真实值未知,且其是否随时间变化也未知[3]。本文假设各参数为时变参数,将故障隔离问题转换为系统状态与时变参数联合估计问题。
对于联合估计问题,目前主要有两种方法:一是基于扩展状态空间的方法[4],将待估计参数作为状态的扩展项,利用滤波器同时对系统状态和参数进行估计。该方法结构简单,易于实现,但扩展后的状态空间维度较高,容易导致维数灾难问题[5]。且估计值易受量测噪音等系统不确定性的影响而发散,导致精度降低甚至估计失效[6]。二是基于双重滤波器的方法[7],使用两个滤波器分别对系统状态和参数进行估计。该方法暂时分离了状态和代估参数变量,在文献[8]中,使用了EF算法复杂度计算方法[9],证明了使用相同的粒子数量时,基于双重滤波器的方法在计算速度和估计精度上均优于基于扩展状态空间的方法。
上述两种联合估计方法的有效性及估计精度都依赖所选取的滤波器。对于线性系统或者简单的非线性系统,卡尔曼滤波器、扩展卡尔曼滤波器和无迹卡尔曼滤波器等都具有出色的表现[10],但在复杂的非线性系统中往往表现不佳甚至无法使用。随着滤波技术的发展,粒子滤波方法在非线性系统中具有优越性。文献[11]早在1997年就开始利用粒子滤波器解决联合估计问题。但粒子滤波器普遍存在粒子退化和样本匮乏现象[12],导致粒子集无法正确表示真实后验概率分布,需要采取一定措施遏制粒子退化并增加粒子多样性。常用的一种方法是将各种智能优化思想如遗传算法、粒子群算法和生物地理学优化算法等引入到粒子滤波算法的采样过程中[13-15],改进采样粒子质量。
此外,在参数滤波过程中,由于代估参数的先验概率密度分布未知,需要人工定义其参数时间更新方法。在时变参数假设下,随机扰动法[15]是一种常用的参数时间更新方法,为了提高粒子有效性,需要大量增加采样粒子数量或扩大随机项,进而导致所需计算资源陡升;另一方面抗干扰能力较差,易受噪声等系统不确定性因素的影响。为了解决上述问题,文献[8]在随机扰动法的基础上引入预测误差思想,对参数采样过程进行改进。与单纯使用随机扰动法相比,该方法得到的参数估计精度更高且收敛速度更快,证明了该方法的有效性,但仅适合对预定义的固定参数集进行估计。由于PFPS是由ARRBFD结果推断得出,并不是固定的,无法事先定义,所以文献[8]方法难以扩展应用到潜在故障参数集。文献[15]提出了一种基于最大似然估计的参数时间更新方法,该方法结构简单且易于扩展,但仅适用于时不变参数的离线估计中。
本文提出一种基于双重改进粒子滤波器的联合估计方法,在基于解析冗余关系的故障诊断应用中完成故障隔离。其中,为了提升联合估计模型的性能,本文从两个方面对其所采用的粒子滤波算法进行改进:1)将文献[8]和文献[15]方法相结合,在传统的基于随机扰动法的参数时间更新方法上,引入最大似然估计法,提出一种改进随机扰动法实现参数时间更新;2)在标准粒子滤波算法的基础上,引入粒子群和模拟退火优化思想,提出一种采样粒子质量改进方法。
1 潜在故障参数集的获取在ARRBFD中,当系统在无故障状态下运行时,各个解析冗余关系(analytical redundancy relations,ARR),应均为零值或近似零值;当系统在有故障状态下运行时,若表现为某系统参数偏离正常值,则含该参数的ARR会偏离零值。根据这个特性,可以设计故障特征矩阵[2],其可以根据系统实际运行过程中ARR的响应来推导出PFPS。
如表 1所示,3个参数都具备可检测性,标记为Db=1。若ARR1和ARR2同时偏离零值,则PFPS内只有一个潜在故障参数为参数3,具备可隔离性,标记为Ib=0。但若只有ARR1偏离零值,则PFPS内含有两个潜在故障参数为参数1和参数2,不具备可隔离性,标记为Ib=0。
| 表 1 故障特征矩阵示例 Tab. 1 Example of fault characteristic matrix |
对于非线性随机系统而言,其状态变量xt和量测值yt随时间演变过程可以描述为一个离散随机时间模型:
| $ x_t=f\left(x_{t-1}, \theta_t\right)+\mu_t $ | (1) |
| $ y_t=g\left(x_t, \theta_t\right)+v_t $ | (2) |
其中:t∈N为系统的离散随机序列;xt∈Rnx和yt∈Rny为时刻t系统状态变量和量测值;θt∈Rnθ为时刻t系统参数;
联合估计问题需要根据系统由时刻1到t的所有量测值y1:t估计联合后验概率密度函数
| $ E\left(\hat{\theta}_{p, t}\right)=E\left(\hat{\theta}_t\right)=\int \hat{\theta}_t p\left(\hat{\theta}_t \mid x_{t-1}, y_{1: t}\right) \mathrm{d} \hat{\theta}_t $ | (3) |
| $ E\left(\hat{x}_t\right)=\int \hat{x}_t p\left(\hat{x}_t \mid \hat{\theta}_t, y_{1: t}\right) \mathrm{d} \hat{x}_t $ | (4) |
式中:
基于贝叶斯估计,可以得到以下递归形式的时刻t系统状态与故障参数值的后验边缘概率密度:
| $ \begin{gathered} p\left(\theta_t \mid y_{1: t}, x_{t-1}\right)=p\left(\theta_{t-1} \mid y_{1: t-1}, x_{t-2}\right) \times \\ \frac{p\left(y_t \mid x_{t-1}, \theta_t\right) p\left(\theta_t \mid \theta_{t-1}, x_{t-1}\right)}{\int p\left(y_t \mid x_{t-1}, \theta_t\right) p\left(\theta_t \mid y_{1: t-1}, x_{t-1}\right) \mathrm{d} \theta_t} \end{gathered} $ | (5) |
| $ \begin{array}{r} p\left(x_t \mid y_{1: t}, \theta_t\right)=p\left(x_{t-1} \mid y_{1: t-1}, \theta_{t-1}\right) \times \\ \frac{p\left(y_t \mid x_t, \theta_t\right) p\left(x_t \mid x_{t-1}, \theta_t\right)}{\int p\left(y_t \mid x_t, \theta_t\right) p\left(x_t \mid y_{1: t-1}, \theta_t\right) \mathrm{d} x_t} \end{array} $ | (6) |
本文使用粒子滤波算法对式(5)、(6)进行近似计算,其通过在每一次迭代中产生一组具有权重的粒子对非线性系统进行递归估计,式(5)、(6)经粒子滤波算法近似计算后可得式(7)、(8),代入式(3)、(4)即可计算t时刻系统状态值与潜在故障参数值的数学期望。
| $ \hat{p}\left(\theta_{\mathrm{p}, t} \mid y_{1: t}, x_{t-1}\right) \mathrm{d} \theta_{\mathrm{p}, t}=\sum\limits_{j=1}^N \omega_{\theta_t(j)} \delta\left(\theta_t-\theta_t^{(j)}\right) \mathrm{d} \theta_t $ | (7) |
| $ \hat{p}\left(x_t \mid y_{1: t}, \theta_t\right) \mathrm{d} x_t=\sum\limits_{i=1}^N \omega_{x_t(i)} \delta\left(x_t-x_t^{(i)}\right) \mathrm{d} x_t $ | (8) |
式中:
标准的粒子滤波器由时间更新和量测更新构成一个迭代周期,使用粒子滤波器对状态和参数进行滤波估计的过程中,两者仅在时间更新处有所区别。以状态估计为例,其算法归纳如下:
1) 初始化,由先验概率p(x1)产生粒子群
2) 时间更新(采样),
3) 量测更新,包括权值更新、重采样以及估计值输出。权值更新
yt为量测值;ypred为量测预测值,由
| $ \tilde{\theta}_{p, t}=\hat{\theta}_{p, t}+\sqrt{Q} \cdot n $ | (9) |
式中:Q为参数随机扰动方差;n~U(0, 1)。
2.3 基于双重粒子滤波器的联合估计方案假设在某一时刻ARRBFD检测到系统故障,令此时系统状态值和参数值为粒子滤波算法的初始值
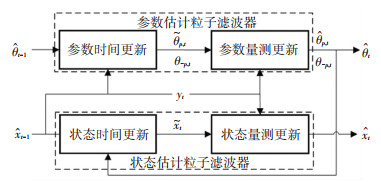
|
图 1 基于双重粒子滤波器的联合估计方案 Fig. 1 Joint estimation method based on dual particle filter |
随机扰动法是一种常用的参数时间更新方法,在每次迭代中,通过定义一个随机项
为了解决随机扰动法采样得到的粒子有效性低的问题,本文在其基础上引入最大似然估计法对θp, t进行初步时间更新;同时考虑到参数具有时变特性,对文献[16]传统的基于粒子滤波的最大似然估计法进行改进,得到一种改进随机扰动法(modified random perturbation method,MRD)作为参数时间更新方法。该方法仅利用两个相邻的量测值
算法归纳如下,其中λ、c、α和β的参数调整方法可从文献[18]中得到。
1) 初始化,已知时刻t-1带权值的粒子为
2) 在时刻t分别对每个
与RD相比,MRD方法在每次迭代中,利用量测值获得的梯度
在粒子滤波器的实际运用中,由于使用次优的重要性函数进行采样,并没有考虑当前量测值,在迭代的的过程中往往会出现粒子退化现象。为了解决上述问题,常用的一种方法是在采样过程中引入优化算法,改进采样粒子质量。粒子群优化(Particle swarm optimization,PSO)是由Kennedy和Eberhart等[14]于1995年提出的一类模拟群体智能行为的优化算法。由于与粒子滤波算法有很多相似性,PSO能较易地应用到粒子滤波算法中,提升标准滤波算法的性能。本文将PSO引入粒子滤波算法中,利用最新的量测值计算适应度值,将所有粒子向最优粒子移动,使采样粒子集在权重值更新前趋向于高似然区域,从而解决粒子退化问题。定义适应度函数为
| $ F=\exp \left[-\frac{1}{2 Q_t}\left(y_t-y_{\text {pred }}\right)^2\right] $ | (10) |
式中:Qt为量测噪音;yt为时刻t量测值;ypred为时刻t预测量测值。
利用下式对采样粒子的速度和位置进行更新:
| $ \begin{aligned} v_t^{(i)}= & \gamma v_1+c_1|\operatorname{Rand} n|\left(p_{\text {best }}-x_t^{(i)}\right)+ \\ & c_2|\operatorname{Rand} n|\left(p_{\text {gbest }}-x_t^{(i)}\right) \end{aligned} $ | (11) |
| $ \tilde{x}_t^{(i)}=x_t^{(i)}+v_t^{(i)} $ | (12) |
式中:
考虑到采用重采样技术,会导致粒子多样性缺失。而且PSO算法中,粒子群在追逐最优粒子的过程时,也会表现出较强的趋同性。上述两种因素共同作用会放大样本匮乏问题,不利于粒子滤波器逼近系统的真实后验概率分布。为了解决这个问题,本文使用模拟退火优化算法(simulated annealing optimization,SAO)对粒子位置更新条件进行改进,增加粒子多样性。其基本思路如下,当优化后粒子的适应值大于当前全局最优适应值时,则接受该粒子;当优化后粒子的适应值小于当前全局最优适应值时,则根据式(13)计算的模拟退火概率Psa决定是否接受该粒子。
| $ P_{\mathrm{sa}}=\mathrm{e}^{-\alpha\left(P_{p_{\text {gbest }}}-\tilde{\omega}_t^{(i)}\right)^2} $ | (13) |
式中:α为退火系数,由式(13)计算而得;
| $ \alpha=-\ln \beta /\left(P_{p_{\text {best }}}-\bar{\omega}_t\right)^2 $ | (14) |
式中:β为平均权值接受率;
| $ \tilde{\omega}_t^{(i)}=\exp \left[-0.5\left(y_t-y_{\text {pred }}^{(i)}\right)^2 Q_t\right] $ | (15) |
结合PSO和SA,得到一种采样粒子质量改进方法,其算法归纳如下:
1) 初始化,令当前粒子个体最优粒子pbest(i)=x(i)t和权值P(i)pbest=ω(i)t、全局最优粒子pgbest为Ppbest的最大值对应的粒子和权值Ppgbest为Ppbest的最大值、β=0.5,计算权值均值ωt和退化系数α。
2) 对每个粒子i进行迭代计算。更新速率
3) 返回更新后粒子的位置与权值{
至此,在2.3节联合估计方案的基础上,使用2.4节和2.5节方法对其所采用的粒子滤波算法进行改进,得到本文提出的基于双重改进粒子滤波器的联合估计方案,如图 2所示。

|
图 2 基于双重改进粒子滤波器的联合估计方案示意图 Fig. 2 Joint estimation method based on dual improved particle filter |
本文以某定排量变转速型电动静液作动器(electro hydrostatic actuator,EHA)为对象,假设系统存在参数突变型故障或参数渐变型故障,前者代表一类参数在系统工作过程中可能会发生突变的故障,如阀口堵塞而导致阀口过流系数降低等;后者代表一类参数随时间逐渐变化的故障,如缸体磨损而导致运动阻尼系数逐渐增大等,在MATLAB/SIMULINK仿真环境中,首先,参考文献[17]方法,搭建EHA动态仿真模型,部分模型参数注释及标称值见表 2,以获取正常状态下的动态响应,分别为电枢绕组电流i、液压泵转速ω和液压泵进出口压差p。然后,为了得到基于仿真模型的故障动态响应,本文设计了以下两类故障的故障注入方法。
| 表 2 模型参数注释和标称值 Tab. 2 Annotation and nominal value of model parameters |
对于参数突变型故障,在SIMULINK环境中,通过使用一个阶跃信号实现故障注入。本文考虑EHA的电机电枢绕组电阻发生参数突变型故障,定义延迟阶跃函数:
| $ R_{\mathrm{a}}(t)= \begin{cases}0.36 \Omega, & 0 \leqslant t \leqslant 1.5 \mathrm{~s} \\ 0.5 \Omega, & t>1.5 \mathrm{~s}\end{cases} $ | (16) |
添加Ra突变型故障注入模块后的EHA电机部分仿真模型[18]如图 3所示。
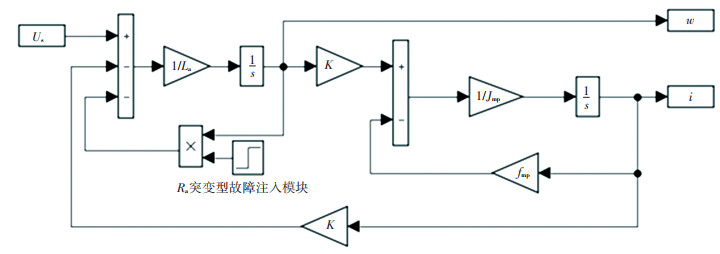
|
图 3 基于SIMULINK环境的EHA电机仿真模型 Fig. 3 EHA motor simulation model in the environment of SIMULINK |
对于参数渐变型故障,在SIMULINK环境中,通过使用MATLAB-FUNCTION来实现故障注入。本文考虑EHA的液压缸总阻尼系数发生参数渐变型故障,定义其退化函数为式(17)。添加Fj渐变型故障注入模块后的EHA负载仿真模型[19]如图 4所示。
| $ F_{\mathrm{j}}(t)=\left\{\begin{array}{l} 100, \quad 0 \leqslant t \leqslant 1.5 \mathrm{~s} \\ 100 \mathrm{e}^{0.16(t-1.5)}, \quad t>1.5 \mathrm{~s} \end{array}\right. $ | (17) |
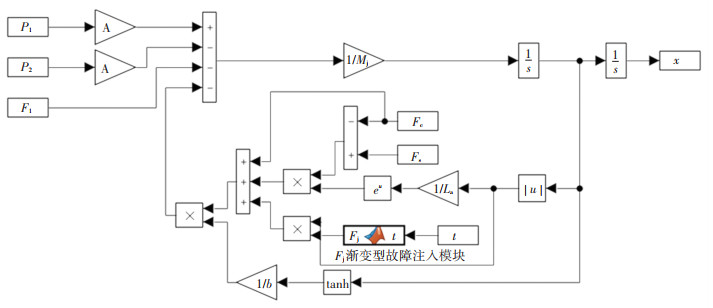
|
图 4 基于SIMULINK环境的EHA负载部分仿真模型 Fig. 4 Load part of EHA simulation model in the environment of SIMULINK |
最后,根据文献[2]的ARRBFD方法,可推导EHA参数型故障诊断解析冗余关系表达式为式(18)~(20),并据此得到故障特征矩阵见表 3。
| $ \mathrm{ARR}_1: U_{\mathrm{s}}-L_{\mathrm{a}} \frac{\mathrm{d} i}{\mathrm{~d} t}-R_{\mathrm{a}} i-K \omega=0 $ | (18) |
| $ \mathrm{ARR}_2: K i-J_{\mathrm{mp}} \frac{\mathrm{d} \omega}{\mathrm{d} t}-f_{\mathrm{mp}} \omega-\frac{p}{D p}=0 $ | (19) |
| $ \begin{gathered} \mathrm{ARR}_3: F_{\mathrm{j}}^{-1} p A^2-D_{\mathrm{p}}^{-1} F_{\mathrm{j}}^{-1} M_{\mathrm{j}} \frac{\mathrm{d} \omega}{\mathrm{d} t}+F_{\mathrm{j}}^{-1} M_{\mathrm{j}} C_{\mathrm{h}} \frac{\mathrm{d}^2 p}{\mathrm{~d} t^2}+ \\ R_{\mathrm{l}}^{-1} F_{\mathrm{j}}^{-1} M_{\mathrm{j}} \frac{\mathrm{d} p}{\mathrm{~d} t}-F_{\mathrm{j}}^{-1} A F_1+R_{\mathrm{l}}^{-1} p+ \\ C_{\mathrm{h}} \frac{\mathrm{d} p}{\mathrm{~d} t}-D_{\mathrm{p}}^{-1} \omega=0 \end{gathered} $ | (20) |
| 表 3 EHA故障特征矩阵 Tab. 3 Fault characteristic matrix of EHA |
仿真实验的硬件环境为英特尔I5-9400处理器,8 GB内存),软件环境为MATLAB 2012b。仿真模型在两类故障下,设置采样频率为1 000 Hz、求解器为ode45,分别运行5 s。利用MATLAB工具箱的AWGN函数对i、ω、p和v数据引入高斯白噪声,设置SNR=60 dB,并使用ARRBFD进行故障诊断。对于Ra突变型故障,在诊断过程中,只有ARR1超过了诊断阈值。所以只展示ARR1诊断结果,如图 5所示,可以观察到在1.5 s后,ARR1偏离零值并超出诊断阈值。此时,根据表 3可以推断出PFPS为

|
图 5 参数Ra突变型故障ARR1诊断结果 Fig. 5 ARR1 results for parameter mutation fault Ra |
而对于Fj渐变型故障,只展示ARR3诊断结果如图 6所示,可以观察到在1.5 s后,ARR3开始逐渐偏离零值,直到约在2.45 s时超出诊断阈值。此时,根据表 3可以推断出PFPS为
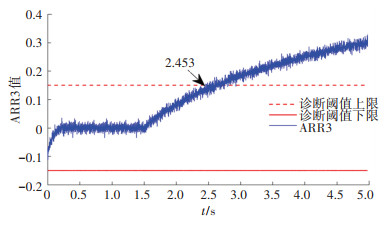
|
图 6 参数Fj渐变型故障ARR3诊断结果 Fig. 6 ARR3 results for parameter gradient fault Fj |
为了验证本文提出的基于双重粒子滤波器的联合估计模型对解决故障隔离问题的有效性和优越性。分别采用文献[15]的基于扩展状态空间的粒子滤波器联合估计模型(extend particle filter,EPF)和本文提出的DPF,对PFPS进行故障隔离仿真对比分析。同时,为了验证本文所提出两种改进方法的优越性,本文在基于双重粒子滤波器的联合估计模型中,采用4种基于不同优化思想的采样粒子质量改进方法的粒子滤波器和两种参数时间更新方法进行仿真对比分析。其中所采用的4种粒子滤波器分别为标准PF(记为PF)、文献[13]中的遗传算法优化PF(记为GA-PF)、文献[14]中的生物地理学优化PF(记为BBO-PF)和本文PSOSA-PF。两种参数更新方法分别为文献[15]中的随机扰动法,记为RD和本文提出的MRD。
本文采用状态平均有效粒子数
| $ \operatorname{RMSE}_x=\left[\frac{1}{N_T} \sum\limits_{t=1}^{N_T}\left(x_t-\hat{x}_t\right)^2\right]^{0.5} $ | (21) |
| $ \overline{N_{\mathrm{eff} x}}=\frac{1}{N_T} \sum\limits_{t=1}^{N_T}\left[1 / \sum\limits_{i=1}^N\left(\omega_t^{(i)}\right)^2\right] $ | (22) |
式中:NT为样本数量;N为粒子数量。
得到PFPS为
| $ \left\{\begin{array}{l} x_1(t)=x_1(t-1)+x_2(t-1) \cdot T+Q_\mu \\ x_2(t)=\left(x_9(t)-x_7(t) \cdot x_1(t-1)-\right. \\ \left.\;\;\;\;\;\;\;K \cdot x_3(t-1)\right) / x_8(t)+Q_\mu \\ x_3(t)=x_3(t-1)+x_4(t-1) \cdot T+Q_\mu \\ x_4(t)=\left(K \cdot x_1(t-1)-f_{\mathrm{mp}} \cdot x_3(t-1)-\right. \\ \left.\;\;\;\quad x_5(t-1) / D_{\mathrm{p}}\right) / J_{\mathrm{mp}}+Q_\mu \\ x_5(t)=x_5(t-1)+x_6(t-1) \cdot T+Q_\mu \\ x_6(t)=\left(F_{\mathrm{j}}^{-1} \cdot x_5(t-1) \cdot A^2-D_{\mathrm{p}}^{-1} \cdot F_{\mathrm{j}}^{-1} \cdot M_{\mathrm{j}} \cdot\right. \\ \;\;\;\quad x_4(t-1)+R_1^{-1} \cdot F_{\mathrm{j}}^{-1} \cdot M_{\mathrm{j}} \cdot x_6(t-1)- \\ \;\;\;\;\;\;\;F_{\mathrm{j}}^{-1} \cdot A \cdot F_1+R_1^{-1} \cdot x_5(t-1)+ \\ \left.\;\;\;\;\;\;\;C_{\mathrm{h}} \cdot x_6(t-1)-D_{\mathrm{p}}^{-1} \cdot x_3(t-1)\right) \cdot T /\left(F_{\mathrm{j}}^{-1} \cdot\right. \\ \left.\;\;\;\;\;\;\;M_{\mathrm{j}} \cdot C_{\mathrm{h}}\right)+Q_\mu \end{array}\right. $ | (23) |
首先,分别调用DPF和EPF对状态变量集和PFPS进行联合估计。此时,联合估计模型内均采用本文提出PSOSA-PF和MRD,且粒子数均为100。
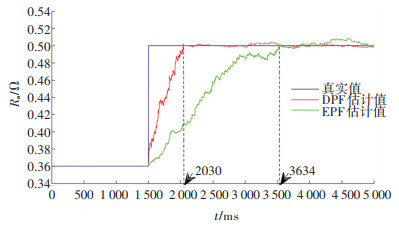
图 7是在系统过程噪音方差Qμ=1、量测噪音方差Qv=10,使用DPF和EPF得到的参数Ra估计效果图。如图 5所示,滤波器在1.5 s处开始工作,参数估计结果显示Ra估计值偏离标称值,可以判断故障发生在Ra,实现参数型故障隔离。其次,DPF方法得到的参数收敛值与预设值基本一致,但EPF方法得到的参数收敛值与预设值存在一定偏差;另一方面,使用DPF方法得到的Ra估计值在tc=2.03 s开始收敛,而EPF方法在tc=3.63 s时才开始收敛。联合估计仿真结果汇总见表 4,结果表明,对于参数突变型故障,DPF参数估计抗干扰能力更强、收敛速度更快且每次迭代运行时间更短。
|
图 7 参数Ra估计效果图 Fig. 7 Parameter estimation results for Ra |
| 表 4 参数突变型故障下DPF与EPF联合估计仿真结果 Tab. 4 Joint estimation simulation results by DPF and EPF algorithms under parameter mutation fault |
然后,在DPF中,分别调用4种粒子滤波器和两种参数时间更新方法进行联合估计。设置Qμ=1、Qv=10、λ=0.005、c=1和σ=1×10-3,且各算法中粒子数N均为100。仿真结果汇总见表 5,其中每种方法共运行1 000次,统计指标结果的平均值。表 5中,对于参数突变型故障,一方面,在使用同一种参数时间更新方法时,PSOSA-PF相较于其他粒子滤波,其
| 表 5 参数突变型故障下4种滤波器及两种参数时间更新方法的联合估计仿真结果 Tab. 5 Joint estimation simulation results by four filters and two parameter time update methods under parameter mutation fault |
得到PFPS为
|
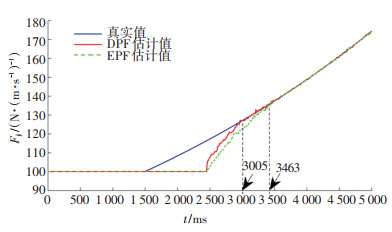
图 8 参数Fj估计效果图 Fig. 8 Parameter estimation results for Fj |
显然,DPF和EPF在第二阶段都能实现对参数的准确跟踪,但在第一阶段,DPF能更快地接近当前参数真实值,意味着DPF会得到更小的RMSEθ。
联合估计仿真结果汇总见表 6,可以看出采用DPF参数估计精度和计算速度较EPF更优。
| 表 6 参数渐变型故障下DPF与EPF联合估计仿真结果 Tab. 6 Joint estimation simulation results by DPF and EPF algorithms under parameter gradient fault |
此外,设置Qμ=1、Qv=10、λ=0.05、c=1和σ=0.1,各算法中粒子数N均为100。表 7为联合估计仿真对比结果。如表 7所示,在使用同一种参数时间更新方法时,与节3.3结果一样,本文提出的PSOSA-PF相对于其他改进粒子滤波器性能更具优势。值得注意的是,在N=100时,虽然使用MRD能较使用RD得到更多的
| 表 7 参数渐变型故障下4种滤波器及两种参数时间更新方法的联合估计仿真结果 Tab. 7 Joint estimation simulation results by four filters and two parameter time update methods under parameter gradient fault |
| 表 8 PSOSA-PF(RD)中采用不同粒子数量的联合估计仿真结果 Tab. 8 Joint estimation simulation results by PSOSA-PF (RD) algorithm with different numbers of particles |
本文针对基于解析冗余关系的故障诊断应用中难以实现故障隔离的问题,提出了一种基于双重改进粒子滤波器的状态和参数联合估计方法来实现参数型故障隔离,并在MATLAB/SIMULINK环境下,对EHA进行参数突变型和参数渐变型故障隔离仿真实验。主要结论如下:
1) 在本文假设的两类参数型故障下,DPF在鲁棒性、计算速度和估计精度上均优于EPF,更适合用以解决本文提出的故障隔离问题。
2) 本文提出的改进方法(PSOSA-PF(MRD)能显著提升DPF性能,进而提升参数估计精度与计算效率。其较使用传统方法(PF(RD)),对于参数突变型故障,参数收敛所需迭代数减少了81.5%、参数收敛所需总运行时间降低了64%和参数估计相对误差降低了1.6%;而对于参数渐变型故障,参数均方根误差降低了40.3%。
综上,本文提出的基于双重改进粒子滤波器的联合估计方法基本满足参数型故障隔离对估计精度和计算的要求,可作为基于解析冗余关系故障诊断中的故障隔离方法。
| [1] |
周东华, 胡艳艳. 动态系统的故障诊断技术[J]. 自动化学报, 2009, 35(6): 748. ZHOU Donghua, HU Yanyan. Fault diagnosis techniques for dynamic systems[J]. Acta Automatica Sinica, 2009, 35(6): 748. DOI:10.3724/SP.J.1004.2009.00748 |
| [2] |
DJEZIRI M A, BOUAMAMA B O, MERZOUKI R. Modelling and robust FDI of steam generator using uncertain bond graph model[J]. Journal of Process Control, 2009, 19(1): 149. DOI:10.1016/j.jprocont.2007.12.009 |
| [3] |
YU Ming, WANG Danwei, LUO Ming. Prognosis of hybrid systems with multiple incipient faults: augmented global analytical redundancy relations approach[J]. IEEE Transactions on Systems, Man, and Cybernetics—Part A: Systems and Humans, 2011, 41(3): 540. DOI:10.1109/TSMCA.2010.2076396 |
| [4] |
HUANG Jie, AN Honglei, LANG Lin, et al. A data-driven multi-scale online joint estimation of states and parameters for electro-hydraulic actuator in legged robot[J]. IEEE Access, 2020, 8: 36885. DOI:10.1109/ACCESS.2020.2974984 |
| [5] |
BIAN Xiaomeng, LI X R, CHEN Huimin, et al. Joint estimation of state and parameter with synchrophasors—Part I: state tracking[J]. IEEE Transactions on Power Systems, 2011, 26(3): 1196. DOI:10.1109/TPWRS.2010.2098422 |
| [6] |
BIAN Xiaomeng, LI X R, CHEN Huimin, et al. Joint estimation of state and parameter with synchrophasors—Part Ⅱ: parameter tracking[J]. IEEE Transactions on Power Systems, 2011, 26(3): 1209. DOI:10.1109/TPWRS.2010.2098423 |
| [7] |
CHOI K R, PARK C G. Design of fault isolator of satellite reaction wheel system using dual filter and multi-hypothesis extended Kalman filter[J]. Journal of the Korean Society for Aeronautical and Space Sciences, 2009, 37(12): 1225. DOI:10.5139/JKSAS.2009.37.12.1225 |
| [8] |
DAROOGHEH N, MESKIN N, KHORASANI K. A dual particle filter-based fault diagnosis scheme for nonlinear systems[J]. IEEE Transactions on Control Systems Technology, 2018, 26(4): 1317. DOI:10.1109/TCST.2017.2705056 |
| [9] |
KARLSSON R, SCHON T, GUSTAFSSON F. Complexity analysis of the marginalized particle filter[J]. IEEE Transactions on Signal Processing, 2005, 53(11): 4408. DOI:10.1109/TSP.2005.857061 |
| [10] |
VAFAMAND N, SAFARINEJADIAN B. State and parameter estimation of CSTR using joint-UKF[C]// International Conference on Control, Instrumentation, and Automation. Tehran: IEEE, 2013: 165. DOI: 10.1109/ICCIAutom.2013.6912828
|
| [11] |
BERZUINI C, BEST N G, GILKS W R, et al. Dynamic conditional independence models and Markov chain Monte Carlo methods[J]. Journal of the American Statistical Association, 1997, 92(440): 1403. DOI:10.2307/2965410 |
| [12] |
孟庆旭. 粒子滤波算法研究及其在非线性估计中的应用[D]. 武汉: 华中科技大学, 2019 MENG Qingxu. Research on particle filtering algorithm and its application in nonlinear estimation[D]. Wuhan: Huazhong University of Science & Technology, 2019 |
| [13] |
QIU Zhenbing, QIAN Huaming. Adaptive genetic particle filter and its application to attitude estimation system[J]. Digital Signal Processing, 2018, 81: 163. DOI:10.1016/j.dsp.2018.06.015 |
| [14] |
方正, 佟国峰, 徐心和. 粒子群优化粒子滤波方法[J]. 控制与决策, 2007, 22(3): 273. FANG Zheng, TONG Guofeng, XU Xinhe. Particle swarm optimized particle filter[J]. Control and Decision, 2007, 22(3): 273. DOI:10.3321/j.issn:1001-0920.2007.03.007 |
| [15] |
YU Ming, LAN Dun, JIANG Canghua, et al. Hybrid condition monitoring of nonlinear mechatronic system using biogeography based optimization particle filter and optimized extreme learning machine[J]. ISA Transactions, 2021, 120: 342. DOI:10.1016/j.isatra.2021.03.018 |
| [16] |
YANG Xiaojun, SHI Kunlin, HUANG Tao, et al. Combine parameter and state estimation in particle filtering[C]// IEEE International Conference on Control and Automation. Guangzhou: IEEE, 2007: 1036. DOI: 10.1109/ICCA.2007.4376514
|
| [17] |
SONG Jixin, YU Liming, HAN Xudong, et al. Modeling and simulation of redundancy management of electro-hydrostatic actuator[C]// JIA Y, ZHANG W, FU Y. Proceedings of 2020 Chinese Intelligent Systems Conference. Singapore: Springer, 2021: 542. DOI: 10.1007/978-981-15-8458-9_58
|
| [18] |
康荣杰, 焦宗夏, MAREJ C, 等. 电动静液作动器非线性框图建模与鲁棒控制方法[J]. 航空学报, 2009, 30(3): 518. KANG Rongjie, JIAO Zongxia, MARE J C, et al. Nonlinear block diagram model and robust control of electro-hydrostatic actuator[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(3): 518. DOI:10.3321/j.issn:1000-6893.2009.03.020 |
| [19] |
SPALL J C. Implementation of the simultaneous perturbation algorithm for stochastic optimization[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(3): 817. DOI:10.1109/7.705889 |
 2023, Vol. 55
2023, Vol. 55


