地铁的迅猛发展支撑起了城市的快速扩张,为城市人口的出行通勤提供了高效、快捷的选择。但与此同时,地铁运行引起了沿线环境的振动,特别是对周边建筑物的振动激励,已成为公众反映强烈的环境污染源和社会公害,对地铁沿线居民的工作、生活乃至身体健康都产生了负面影响。开展相关减隔振措施以及振动预测方法研究对于城市建设发展有着重大意义。
地铁所致振动主要是由地铁运行时车轮与轨道之间的相互作用力而产生的[1],经由复杂的传播途径传递至地面和邻近建筑物,诱发建筑结构的振动。为降低地铁所致邻近建筑物的振动响应,最大程度地消除地铁所致振动的危害,国内外学者近年来开展了大量研究工作。在振源减振方面,文献[2]在实验的基础上,基于有限元法和“车-轨”相互作用动力学理论,建立了“车辆-轨道-隧道-土壤”耦合系统的动力学模型;文献[3]针对轨道扣件、道床,开展了减振效果方面的探究;文献[4]针对某新建桩筏基础建筑物,分析了不同行驶工况下地铁列车运行对建筑结构及内部精密仪器的振动影响,对地铁列车钢轨扣件最佳刚度及阻尼的选取给出了建议。在传播途径方面,文献[5]通过数值模拟计算分析了隔振屏障设计参数对建筑室内楼板隔振效果的影响规律;文献[6]基于实验研究结果建立的隔振墙体可以有效降低4 Hz以上频域的振动;文献[7]建立了“轨道-碴堤-桩筏基础建筑物”三维有限元模型,研究了高速列车运行所致动力响应情况,发现改善地基情况可以缓解相应振动。在受振体方面,文献[8]通过建立1/8缩尺模型开展了地铁所致振动激励下砂袋垫层基础隔振试验,分析和预测了应用砂袋垫层提高楼盖竖向振动舒适度的有效性;文献[9]通过计算得出,采用厚肉橡胶支座既能达到普通橡胶支座隔震相同的效果,又能起到降低地铁所致振动的作用;文献[10]以苏州某高科技电子厂房为例,通过现场实测和有限元分析,认为桩筏基础对地面振动控制具有积极作用。
工程实践表明,对于采用筏板基础的建筑物,加厚其筏板基础的底板(筏板)具有良好的减振作用,后文将加厚筏板基础建筑物底板简称为加厚建筑物底板。加厚建筑物底板作为一种方便易行的手段具有很强的工程适用性,本文通过建立“隧道-土体-建筑物”三维有限元模型,在不同道床条件下对加厚建筑物底板的减振效果进行研究,分析建筑物距离地铁隧道水平距离对减振效果的影响,提出能快速预测加厚建筑物底板减振效果的计算方法,为实际工程提供参考。
1 有限元模型的建立与验证 1.1 有限元模型的建立地铁列车运行过程中,引起的环境振动具有振动量微小、频率范围宽的特点[11],土壤中产生的应变较小,可按弹性介质考虑[12],有限元分析时假定:1)每一层土为均质、各向同性体;2)动力作用下各层土之间、土体与结构之间不发生脱离和相对滑动,采取共节点来协调变形;3)列车运行时产生的振动激励传递至道床。
1.1.1 材料参数选取根据北京市海淀区某场地资料建立有限元模型,将动力学性质相似的土层进行合并,简化为5层。土层动力参数见表 1。
| 表 1 土层动力参数 Tab. 1 Dynamic parameters of soil layer |
取该区域中邻近地铁隧道的某平板式筏形基础形式的办公楼为研究模型,根据其设计资料在有限元中建立5层框架结构,柱截面尺寸为500 mm×500 mm,梁截面尺寸为300 mm×700 mm,楼板厚度为150 mm。根据筏板基础的特点,在建模时忽略柱底与筏形基础底板连接处局部构造措施的影响,将建筑物平板式筏形基础的底板设定为建筑物底板,故建筑物底板厚度取自筏板基础底板的实际厚度。建筑物底板原始厚度为500 mm,框架结构材料均为C30混凝土。
1.1.2 单元选取及网格划分地层模型、隧道、建筑物底板均采用solid185单元模拟,框架建筑物中的梁、柱采用beam188单元模拟,楼板采用shell181单元模拟。隧道中心距离建筑物最小水平距离为10 m,建筑物底板中心距离隧道水平距离为30 m。
共划分网格单元100 578个,节点108 816个。为满足计算稳定性及地铁列车高频振动的要求,3个方向的单元网格长度应小于土层最小剪切波长的1/20[13],故网格尺寸取为1~3 m。
1.1.3 边界条件处理及阻尼特性底面(Z=0 m)采用固定约束,为了避免地铁所致振动波在有限元模型边界处产生反射叠加问题,两侧(X=0 m及X=200 m,Y=0 m及Y=162 m)采用对称约束并设置粘弹性人工边界[14]。
由于土体形变极小,材料阻尼不便于反映阻尼作用,故在“隧道-土体-建筑物”全系统模型中输入整体瑞利阻尼[15]。选取阻尼比为0.03,由于地铁振动的能量覆盖频域较宽[16],故ωi和ωj分别取为10 Hz与80 Hz,再计算得出瑞利阻尼系数α=5.585,β=1.768×10-4。
1.2 有限元模型及列车荷载验证为真实反映地铁列车运行所致的振动,利用北京交通大学自编分析软件DRVB[17],输入实际地铁列车轨道参数[18],根据车轨耦合的动力学程序计算得到普通道床、弹性长枕道床、钢弹簧浮置板道床对应的地铁列车荷载,进一步优化后得到连续时刻下6节编组的标准B1型地铁列车在不同道床条件下沿运行方向的移动时程荷载数值,典型荷载时程如图 1所示,所涉及的实测数据详细描述见表 2[18]。

|
图 1 列车荷载时程 Fig. 1 Train load time history |
| 表 2 振动测试详细情况说明(垂向) Tab. 2 Detailed description of vibration test (vertical direction) |
最终建立“隧道-土体-建筑物”三维有限元模型如图 2所示,振源荷载频率为256 Hz,即数值模拟所覆盖的频率为1~256 Hz,荷载所模拟的地铁列车运行时速为80 km/h。

|
图 2 三维有限元模型 Fig. 2 3D finite element model |
在有限元中采用瞬态动力分析,使用直接积分法中稳定性更好的隐式计算方法,在隧道内的轨道板上设置23个连续的加载点,输入前述移动时程荷载。一共2 000个荷载步,时间步长为0.003 906 25 s,己小于场地周期的1/100[19],可以保证满足计算稳定性和高频振动所需的精度要求。总计算时程为7.812 5 s,采用阶跃加载的方式。
根据《城市区域环境振动标准》(GB 10070—88)[20]和《环境影响评价技术导则——城市轨道交通》(HJ 453—2018)[21]的规定,采用Z向振动加速度级作为评价指标,后文简称为振级,单位为dB,记为VL,计算公式为
| $ V L=20 \lg \frac{a^{\prime}}{a_0} $ | (1) |
式中:a′为频率计权加速度,m/s2;a0为基准加速度,a0=10-6 m/s2。
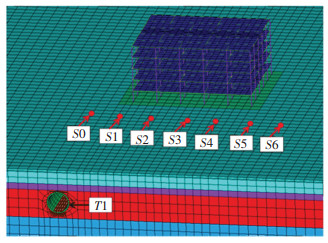
利用“1/3倍频程法”[22]进行计算,按ISO 2631-1[22]规定的全身振动不同频率计权因子进行修正,计算得到提取点的振级。提取隧道右壁内中心点T1,隧道正上方地面处点S0,地面上距隧道水平距离10 m至60 m处的点S1、S2、S3、S4、S5、S6的加速度时程数据(提取点如图 3所示),限于篇幅,仅展开分析普通道床条件下的计算情况。将数值计算所得隧道壁振级与《地铁噪声与振动控制规范》(DB11/T 838—2019)[23]中附录所列振源强度参考值以及根据北京市地铁某类似线路地段实测得到的隧道壁振级进行对比,结果见表 3。
|
图 3 提取点的选取 Fig. 3 Selection of extraction points |
| 表 3 隧道壁提取点振级对比 Tab. 3 Comparison of vibration levels at extraction points of tunnel wall |
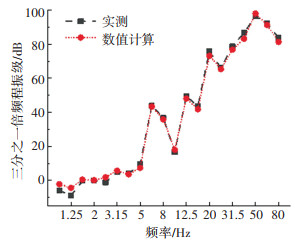
将数值计算得到的隧道壁三分之一倍频程振级与实测数据进行对比,如图 4所示。数值计算所得隧道壁振级为85.4 dB,与实测结果及规范给出的参考值接近。且三分之一倍频程振级的数值计算结果与实测结果也基本吻合。
|
图 4 T1点三分之一倍频程振级 Fig. 4 One-third octave of T1 vibration level |
将地表各提取点的振级与《环境影响评价技术导则城市轨道交通》(HJ453—2018)[21]中经验预测结果(经验预测公式中设定振动源强为85 dB,土层相关参数选取与有限元模型中参数保持一致)以及某类似地铁线路段的地表实测数据进行对比,结果见表 4。
| 表 4 距离隧道不同水平距离的地表提取点振级 Tab. 4 Vibration levels of surface points at different horizontal distances from the tunnel |
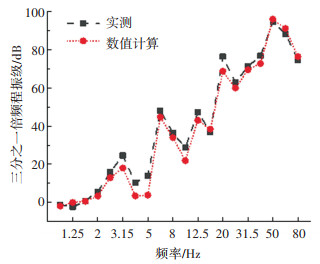
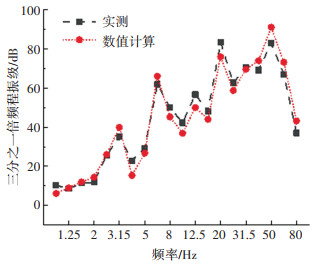
提取点S0和S3的三分之一倍频程振级,数值计算结果与实测结果的对比如图 5和图 6所示。数值计算得到的地表振动传递规律与规范中的经验公式预测结果、实测结果都基本一致。当采用弹性长枕道床、钢弹簧浮置板道床条件下的激励输入时,计算结果也与实测和经验预测的结果基本吻合。
|
图 5 S0点三分之一倍频程振级 Fig. 5 One-third octave of S0 vibration level |
|
图 6 S3点三分之一倍频程振级 Fig. 6 One-third octave of S3 vibration level |
综上所述,本文所采用的列车荷载、激励的输入方式以及建立的有限元模型均符合实际情况。
2 建筑物底板减振性能研究选取建筑物底板中心点以及各楼层中心点作为拾取振动加速度时程数据的提取点,分别为Z1(建筑物底板中心点)、Z2、Z3、Z4、Z5、Z6,如图 7所示。

|
图 7 建筑物内提取点的选取 Fig. 7 Selection of extraction points in the building |
分别研究建筑物底板从0.5 m依次增厚0.25 m至2 m以及特殊情况4 m时底板及各层楼板中心点的振动响应。基于前述方法计算在普通道床、弹性长枕道床、钢弹簧浮置板道床条件下建筑物的振动响应。
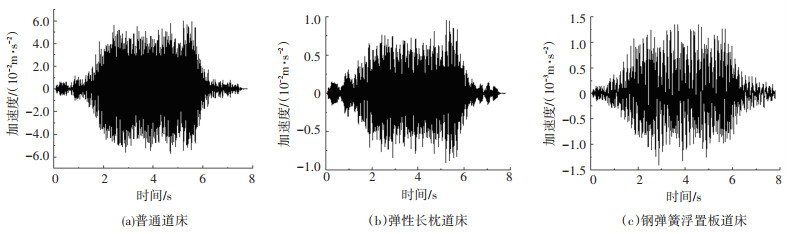
得到不同道床条件下底板厚度为0.5 m时底板中心点Z1的加速度时程曲线如图 8所示,不同道床条件下各提取点的振级、底板中心点Z1的三分之一倍频程振级分别如图 9、10所示,图例表示底板厚度。
|
图 8 不同道床条件下底板中心点加速度时程曲线 Fig. 8 Acceleration time history curves of base floor central point under different track bed conditions |

|
图 9 不同道床条件下各提取点的振级 Fig. 9 Vibration level of each point under different track bed conditions |

|
图 10 不同各道床条件下底板中心点三分之一倍频程振级 Fig. 10 One-third octave of vibration level of base floor central point under different track bed conditions |
可以看出,在不同道床条件下,建筑物底板越厚,建筑物底板及楼板上各提取点的振级越小,即地铁运行所致建筑物的振动响应越小,其中建筑物底板中心点处的振级变化最为明显,加厚建筑物底板后底板中心点的振级相对于原始厚度0.5 m时的减小量见表 5(负号代表振级减小)。
| 表 5 不同道床条件下底板中心点处减振量 Tab. 5 Vibration reduction effect at base floor central point under different track bed conditions |
建筑物底板从0.5 m开始依次增厚0.25 m至2 m时,不同道床条件下底板中心处的振级相对于0.5 m厚度时的振级平均降低0.65、1.13、1.88、3.66、5.46、7.88 dB,加厚至4 m时振级平均降低9.52 dB。从三分之一倍频程曲线可以看出,加厚建筑物底板可以明显使得大部分频段的振动响应都减弱。这是因为加厚的建筑物底板能够有效地耗散掉地铁所致振动中的部分能量,从而减少其传递至上部结构的振动,使整个建筑物的振动响应减小。
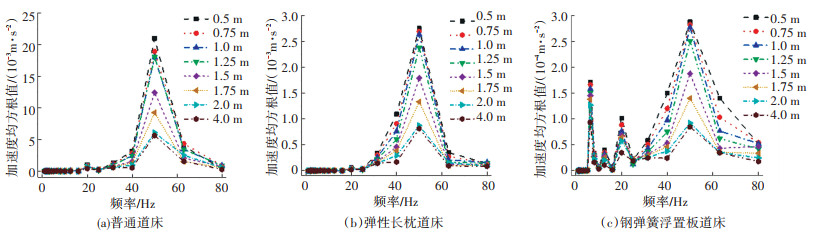
根据《建筑工程容许标准》(GB 50868—2013)[24]中建筑物内人体舒适性评价要求,计算加厚建筑物底板时Z2点处振动加速度均方根值,得到不同道床条件下的计算结果,如图 11所示。可以看出,加厚建筑物底板能减小各频段加速度均方根值,在40~60 Hz之间效果最为显著,说明加厚建筑物底板能有效提高建筑物内的人体舒适度。
|
图 11 不同各道床条件下底板中心点处振动加速度均方根值 Fig. 11 Root mean square vibration acceleration of base floor central point under different track bed conditions |
由分析结果可知,当采用减振道床时,加厚建筑物底板的减振效果会有所减弱,且减振道床的减振性能越好,加厚建筑物底板的减振效果越弱。这是因为减振道床已经在底板发挥减振作用之前有效隔离和耗散掉大部分振动能量。
综上所述,加厚建筑物底板是一种能有效降低地铁运行所致临近建筑物振动响应的方法,且底板越厚减振效果越明显。
3 加厚底板减振效果预测方法除道床条件外,建筑物中心距离地铁隧道中心的水平距离(下文简称为水平距离)也会影响加厚建筑物底板的减振效果。
3.1 水平距离对加厚底板减振效果影响分析分别建立水平距离为0 m(建筑物位于地铁隧道正上方)、10 m、20 m、30 m(即上一节所研究的模型)、40 m、50 m、60 m时的有限元模型,如图 12所示。

|
图 12 不同水平距离时的有限元模型 Fig. 12 Finite element model under different horizontal distance conditions |
当采用普通道床对应的激励荷载进行计算时,不同水平距离条件下,建筑物底板中心点振级随底板厚度的变化如图 13所示。当水平距离分别为0、10、20、30、40、50、60 m时,底板每加厚0.25 m,底板中心点振级平均可降低1.82、1.68、1.62、1.48、1.23、0.99、0.68 dB。

|
图 13 不同水平距离时底板中心点振级曲线 Fig. 13 Vibration level curves of base floor central point under different horizontal distance conditions |
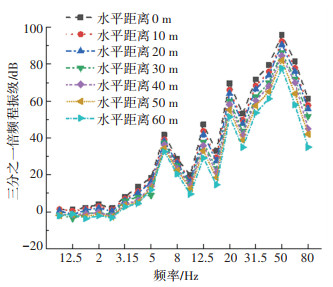
当底板厚度为0.5 m时,不同水平距离条件下底板中心点的三分之一倍频程振级曲线如图 14所示。可以看出,随着水平距离的增大,地铁运行所致建筑物的振动响应越小,加厚建筑物底板的减振效果会随之减弱, 但依然有良好的减振作用。显然,随着水平距离的增大,大部分频段的振动响应会有不同程度的减弱,但高频部分相对来说衰减的更快。根据上述分析可知,水平距离的增大会减弱加厚建筑物底板的减振效果。
|
图 14 不同水平距离时底板中心点三分之一倍频程振级 Fig. 14 One-third octave of vibration level of base floor central point under different horizontal distance conditions |
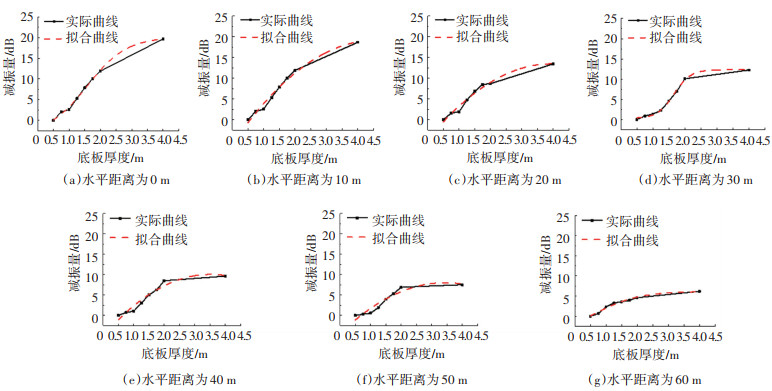
基于前述计算结果,提出加厚建筑物底板减振效果预测方法,计算过程分为以下3步:1)在不同水平距离情况下,在MATLAB中通过Boltzmann函数(式(2),x为底板厚度值,F(x)为减振量,其中A1、A2、A3、A4为回归参数)对加厚建筑物底板时底板中心处的减振量进行回归分析,其中普通道床条件下的拟合情况如图 15所示;2)再将分析得到的回归参数与水平距离值L进行二次多项式拟合(式(3),B1、B2、B3为拟合分析所得参数),得到其计算关系式;3)最后在考虑道床条件的影响下,整理得到加厚底板减振效果的预测公式(式(4),x2、x1分别为加厚底板前后的底板厚度值,Kr为道床条件修正系数)。
| $ F(x)=\frac{A_1-A_2}{1+\mathrm{e}^{\left(x-A_3\right) / A_4}}+A_2 $ | (2) |
| $ G(L)=B_1+B_2 \cdot L+B_3 \cdot L^2 $ | (3) |
| $ C=\left[F\left(x_1\right)-F\left(x_2\right)\right] \times K_{\mathrm{r}} $ | (4) |
|
图 15 不同水平距离时减振量拟合情况 Fig. 15 Fitting of vibration reduction under different horizontal distance conditions |
根据前述步骤,在考虑道床条件与水平距离的影响下,提出加厚建筑物底板时底板中心处减振量的预测方法,预测公式见式(5)。该方法适用于距离城市轨道交通地铁建设项目中心线两侧60 m之内单体建筑物的振动评估。
| $ C=K_{\mathrm{r}} \times\left(\frac{A_1}{1+\mathrm{e}^{\left(X_1-A_2\right) / A_3}}-\frac{A_1}{1+\mathrm{e}^{\left(X_2-A_2\right) / A_3}}\right) $ | (5) |
式中:C为加厚建筑物底板后底板中心点减振量,dB;对于道床条件修正系数Kr,当采用普通道床时取值为1,当采用弹性长枕道床时建议取值为0.8,当采取钢弹簧浮置板道床时建议取值为0.4,当采用其他减振道床或扣件时可依据其减振性能参考上述减振道床的建议值来合理选取;X1为拟加厚之后的建筑物底板厚度值, m;X2为建筑物底板初始厚度值, m;A1、A2、A3为计算所需参数,见式(6)~(8);L为建筑物底板中心点距地铁隧道中心线的水平距离, m。
| $ A_1=-23.677+0.564 L-4.02 \times 10^{-3} L^2 $ | (6) |
| $ A_2=1.579+0.021 L-6.11 \times 10^{-4} L^2 $ | (7) |
| $ A_3=0.630-0.026 L+4.56 \times 10^{-4} L^2 $ | (8) |
北京市某新建公共设施总建筑面积为9.7万平方米,由北侧的A结构和南侧的B结构两部分组成,如图 16所示,整个建筑为复杂的组合空间结构体系。该建筑所在场地有多条轨道交通穿过,其中地铁M1线可能对该建筑产生较严重的振动影响。

|
图 16 建筑物与地铁线路位置关系 Fig. 16 Location between the building and metro line |
M1地铁线路区间设计埋深约30 m,设计速度为80 km/h,采用弹性长枕道床。A结构距离地铁M1最近的部分已位于地铁线路正上方,故对距离地铁隧道更近的A结构进行振动评估,根据前述方法建立有限元模型,如图 17所示。

|
图 17 A结构有限元模型 Fig. 17 Finite element model of model A |
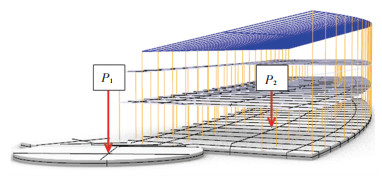
选取A结构下沉广场位置处中心点P1和地下一层底板中心点P2为研究对象,如图 18所示。P1、P2分别距离隧道水平距离约为10、50 m。A结构的底板初始设计厚度为1 m,为降低地铁运行所致振动响应,决定采取加厚底板的减振措施,虽然底板越厚减振效果越好,但是工程造价也会越高、施工也更复杂,项目决策者在充分考虑工程实际条件之后最终决定将底板加厚至2 m。
|
图 18 A结构模型提取点的空间位置分布 Fig. 18 Spatial distribution of extraction points in model A |
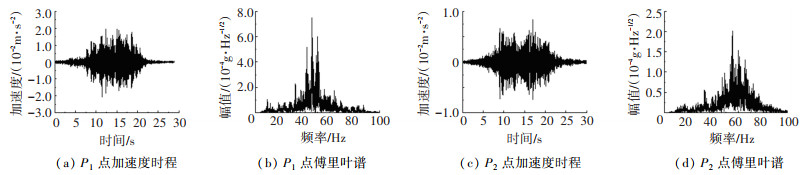
在早晚高峰时段实测P1、P2位置处的振动响应,其典型加速度时程及傅里叶谱如图 19所示,对应振级分别为58.71、49.15 dB。
|
图 19 P1、P2实测加速度时程及傅里叶谱 Fig. 19 Measured results of acceleration time history curves and Fourier spectra at P1 and P2 |
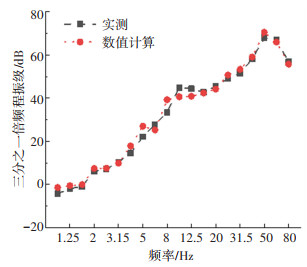
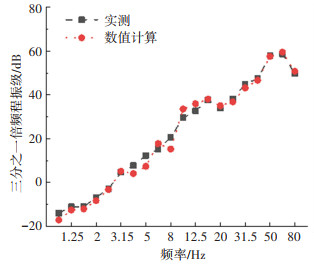
分别在有限元模型中计算底板厚度为1 m和2 m时P1、P2的振动响应,当底板厚度为2 m时,其三分之一倍频程振级与实测结果对比如图 20、21所示,说明数值计算结果合理。
|
图 20 P1点三分之一倍频程振级 Fig. 20 One-third octave of vibration level of P1 |
|
图 21 P2点三分之一倍频程振级 Fig. 21 One-third octave of vibration level of P2 |
同时利用提出的式(5)计算加厚底板至2 m时的减振量,预测公式计算结果与数值模拟结果对比情况见表 6。
| 表 6 减振量计算结果对比 Tab. 6 Comparison of calculation results of vibration reduction effect |
两结果相差不足0.5 dB,证明了本文所提出的预测公式的准确性,也再次说明加厚建筑物底板可以有效降低地铁所致邻近结构的振动响应。本文所提出的加厚建筑物底板减振效果预测公式能为地铁减振工程作出快速判断。
4 结论1) 加厚筏板基础建筑物的底板能有效消耗地铁所致振动能量,使得建筑物大部分频段的振动响应均有所减弱,从而能够降低地铁所致邻近建筑物的振动响应,提高建筑物内人体舒适度。建筑物底板越厚,其减振效果越显著。当建筑物中心距离地铁隧道中心水平距离为30 m时,在普通道床条件下建筑物底板每增厚0.25 m可使建筑物底板中心位置处振动量级平均降低1.48 dB。
2) 当地铁线路采用减振道床时,加厚建筑物底板依然具有一定减振效果,但其减振作用会减弱。相对于普通道床,当地铁线路采用弹性长枕道床、钢弹簧浮置板道床时,加厚建筑物底板的减振效果大约会降低20%、60%。地铁线路自身的道床条件越好,加厚底板的减振效果越弱。
3) 加厚建筑物底板的减振效果会随着建筑物中心距离地铁隧道中心水平距离的增加而减弱,但是在所研究的60 m范围内加厚建筑物底板仍有一定的减振效果。在普通道床条件下,当水平距离为60 m时,底板每增厚0.25 m,底板中心位置处振动量级可降低0.68 dB。
4) 在考虑道床条件和水平距离的影响后,提出了加厚建筑物底板减振效果的预测方法。结合某实际工程进行验证,说明本预测方法能针对地铁所致振动对加厚建筑物底板的减振效果作出快速、合理的初步判断。加厚建筑物底板具有良好的减振性能,但在实际工程运用中可能会一定程度增大施工难度、产生工程残渣,如何更加科学合理地采用此方法降低地铁振动,值得进一步研究。
| [1] |
夏禾, 吴萱, 于大明. 城市轨道交通系统引起的环境振动问题[J]. 北方交通大学学报, 1999, 23(4): 7. XIA He, WU Xuan, YU Daming. Environmental vibration induced by urban rail transit system[J]. Journal of Northern Jiaotong University, 1999, 23(4): 7. |
| [2] |
CAI X P, WANG Q H, LI D C, et al. Theoretical study of long elastic sleeper track to reduce vibrations induced by subway trains[J]. Proceedings of the Institution of Mechanical Engineers, 2020, 234(5): 538. DOI:10.1177/0954409719848598 |
| [3] |
MA R, GENG C. Analysis of vibration reduction effect of the floating slab track with different base forms in a small radius curve of metro lines[J]. IOP Conference Series: Earth and Environmental Science, 2019, 218: 012109. DOI:10.1088/1755-1315/218/1/012109 |
| [4] |
熊学详. 某地铁运营状态对周边医技楼建筑结构微振动影响分析[D]. 广州: 华南理工大学, 2018 XIONG Xuexiang. Analysis of the influence of a subway operation status on the micro-vibration of the surrounding medical technical building structure[D]. Guangzhou: South China University of Technology, 2018 |
| [5] |
邬玉斌, 宋瑞祥, 何蕾, 等. 地面列车荷载作用下地屏障对建筑楼板的隔振效果分析[J]. 振动工程学报, 2020, 33(2): 322. WU Yubin, SONG Ruixiang, HE Lei, et al. Isolation effect of barriers on building floor under the vibration induced by trains of ground line[J]. Journal of Vibration Engineering, 2020, 33(2): 322. DOI:10.16385/j.cnki.issn.1004-4523.2020.02.012 |
| [6] |
DIJCKMANS A, EKBLAD A, SMEKAL A, et al. Efficacy of a sheet pile wall as a wave barrier for railway induced ground vibration[J]. Soil Dynamics and Earthquake Engineering, 2016, 84(1): 55. DOI:10.1016/j.soildyn.2016.02.001 |
| [7] |
FU Q, LIU H L, DING X M, et al. Numerical investigation of piled raft foundation in mitigating embankment vibrations induced by high-speed trains[J]. Journal of Central South University, 2015, 22(11): 4434. DOI:10.1007/s11771-015-2991-y |
| [8] |
盛涛, 李水明, 刘干斌, 等. 地铁邻近建筑的砂袋垫层基础隔振试验研究[J]. 振动与冲击, 2017, 36(24): 44. SHENG Tao, LI Shuiming, LIU Ganbin, et al. Tests for subway nearby building′s base vibration isolation with sandbag layers[J]. Journal of Vibration and Shock, 2017, 36(24): 44. DOI:10.13465/j.cnki.jvs.2017.24.007 |
| [9] |
周颖, 陈鹏, 陆道渊, 等. 地铁上盖多塔楼隔震与减振设计研究[J]. 土木工程学报, 2016, 49(增刊1): 84. ZHOU Ying, CHEN Peng, LU Daoyuan, et al. Design and seismic response analysis for multiple buildings with large podium using inter-story isolation technology[J]. China Civil Engineering Journal, 2016, 49(Sup.1): 84. DOI:10.15951/j.tmgcxb.2016.s1.015 |
| [10] |
GAO G Y, CHEN J, YANG J, et al. Field measurement and FE prediction of vibration reduction due to pile-raft foundation for high-tech workshop[J]. Soil Dynamics and Earthquake Engineering, 2017, 101(1): 264. DOI:10.1016/j.soildyn.2017.08.009 |
| [11] |
SADEGHI J, ESMAEILI M H. Effectiveness of track stiffness reduction in attenuation of metro induced vibrations received by historical buildings[J]. Latin American Journal of Solids and Structures, 2018, 15(11): 142. DOI:10.1590/1679-78255252 |
| [12] |
GUO T, CAO Z L, ZHANG Z Q, et al. Numerical simulation of floor vibrations of a metro depot under moving subway trains[J]. Journal of Vibration and Control, 2018, 24(18): 4353. DOI:10.1177/1077546317724322 |
| [13] |
王丁丁, 肖周芳, 陈建军, 等. 三维有限元网格尺寸场光滑化的优化模型和算法[J]. 计算机辅助设计与图形学学报, 2016, 28(12): 2097. WANG Dingding, XIAO Zhoufang, CHEN Jianjun, et al. An optimization model and algorithm for the smoothing of sizing functions of three-dimensional finite element meshes[J]. Journal of Computer-Aided Design & Computer Graphics, 2016, 28(12): 2097. |
| [14] |
刘晶波, 王振宇, 杜修力, 等. 波动问题中的三维时域粘弹性人工边界[J]. 工程力学, 2005, 22(6): 46. LIU Jingbo, WANG Zhenyu, DU Xiuli, et al. Three-dimensional visco-elastic artificial boundaries in time domain for wave motion problems[J]. Engineering Mechanics, 2005, 22(6): 46. |
| [15] |
刘延柱, 陈立群, 陈文良. 振动力学[M]. 3版.北京: 高等教育出版社, 2019. LIU Yanzhu, CHEN Liqun, CHEN Wenliang. Vibration mechanics[M]. 3rd ed. Beijing: Higher Education Press, 2019. |
| [16] |
高广运, 张继严, 谢伟, 等. 高铁弹塑性地基振动与变形的2.5维有限元算法[J]. 哈尔滨工业大学学报, 2021, 53(11): 37. GAO Guangyun, ZHANG Jiyan, XIE Wei, et al. Improved 2.5D finite element method for vibration and deformation of elastoplastic subgrade under high-speed train load[J]. Journal of Harbin Institute of Technology, 2021, 53(11): 37. DOI:10.11918/201912079 |
| [17] |
夏禾. 交通环境振动工程[M]. 北京: 科学出版社, 2010. XIA He. Trafficinduced environmental vibrations and controls[M]. Beijing: Science Press, 2010. |
| [18] |
马蒙. 基于敏感度的地铁列车振动环境影响预测及动态评价体系研究[D]. 北京: 北京交通大学, 2012 MA Meng. Study on the prediction of metro train-induced vibrations based on sensitivity of environmental influence and design stage-accompanied evaluation system[D]. Beijing: Beijing Jiaotong University, 2012 |
| [19] |
蒋新新, 李建波, 林皋, 等. 利用ANSYS瞬态分析直接进行结构静——动力分析的一种方法[J]. 计算机应用, 2014, 34(增刊1): 338. JIANG Xinxin, LI Jianbo, LIN Gao, et al. Direct method for static-dynamic analysis of structure based on transient analysis in ANSYS[J]. Journal of Computer Applications, 2014, 34(Sup.1): 338. |
| [20] |
中华人民共和国环境保护局. 城市区域环境振动标准: GB 10070—88[S]. 北京: 中国标准出版社, 1988 National Environmental Protection Agencyof the People′s Republic of China. Standard of environmental vibration in urban area: GB 10070—88[S]. Beijing: Standards Press of China, 1988 |
| [21] |
中华人民共和国生态环境部. 环境影响评价技术导则城市轨道交通: HJ 453—2018[S]. 北京: 中国环境科学出版社, 2018 Ministry of Ecology and Environment of the People′s Republic of China. Technical guidelines for environmental impact assessment—Urban rail transit: HJ 453—2018[S]. Beijing: China Environmental Science Press, 2018 |
| [22] |
International Organization for Standardization. Mechanical vibration and shock-Evaluation of human exposure to whole-body vibration—Part 1: General requirements: ISO 2631-1[S]. Geneva: [s. n. ], 1997
|
| [23] |
地铁噪声与振动控制规范: DB 11/T 838—2019[S]. 北京: 中国环境科学出版社, 2019 Code for application technique of metro noise and vibration control: DB 11/T 838—2019[S]. Beijing: China Environmental Science Press, 2019 |
| [24] |
中华人民共和国住房和城乡建设部. 建筑工程容许振动标准: GB 50868—2013[S]. 北京: 中国计划出版社, 2013 Ministry of Housing and Urban-Rural Development of the People′s Republic of China. Standard for allowable vibration of building engineering: GB 50868—2013[S]. Beijing: China Planning Press, 2013 |
 2023, Vol. 55
2023, Vol. 55


