2. 综合交通运输大数据应用技术交通运输行业重点实验室(北京交通大学),北京 100044
2. Key Laboratory of Transport Industry of Big Data Application Technologies for Comprehensive Transport (Beijing Jiaotong University), Beijing 100044, China
轨道交通快速建设的同时,出现了轨道交通供给与需求不匹配、乘客服务水平低以及轨道交通企业运营成本高等问题。因此,通过多交路运营[1]、换乘组织[2]、可变编组和多编组运营[3]等网络化运营组织技术来优化列车运输组织、改善交通供给与需求的匹配度、提高乘客服务水平、降低企业运营成本成为了国内外学者的研究热点。其中,直通运营的运输组织方法已在国内外城市投入使用,如东京的东武东上线—副都心线、巴黎的RER—B线、北京的4号线—大兴线等,实际的运行效果证明直通运营模式可以有效地缓解通勤时段的乘客出行不便、节省乘客换乘时间,提升轨道交通吸引力。
国外关于直通运营组织的研究开展较早,文献[4]基于英国桑德兰地铁与轻轨的案例发现直通运营可以增加轨道交通系统的吸引力,并且分析了直通运营在供电、信号、车辆等方面存在的技术难点。文献[5]针对主线和支线之间的直通运营进行了研究,寻找各自最优的发车频率以减少换乘次数以及运用车底数。
国内学者主要研究直通运营的组织形式和开行方案,文献[6]提出了一种城市轨道交通列车直通运营开行方案编制技术,采用固定的列车编组和停站方案,优化列车交路和开行频率。文献[7]分析了地铁与市郊铁路的直通运营特点,研究“一”字型线路直通运营下列车开行方案,分析了开行快慢车模式下的停站方案。文献[8]构建了直通运营条件下的列车运力配置模型,发现直通客流强度越大,直通运营的效益越明显。
从表 1的研究结果中来看,既有的国内外学者对直通运营条件下的轨道交通列车开行方案进行了大量的研究,但考虑的因素尚不全面,大多只考虑了交路设计方案和发车频率等因素,对于列车多编组以及列车满载率均衡性对直通运营条件下的列车开行方案的影响,缺乏相关研究。
| 表 1 近年来直通运营开行方案研究 Tab. 1 Studies on train planning for through operation in recent years |
实际上,列车满载率均衡是影响乘客服务水平的一个重要因素[12],文献[13]研究了客流变化情况下以各列车满载率均衡性为目标的时刻表优化模型。文献[14]分析了开通大小交路对乘客候车时间以及列车满载率的影响。文献[15]考虑了列车满载率的均衡性,将过高或过低的列车满载率作为惩罚加入到列车开行方案优化的目标函数中。
通过考虑列车多编组方式来均衡列车满载率和降低企业运营成本的方法是被国内外学者进行过研究并被认为可行的。列车多编组的运营组织技术最初是借鉴于常规公交的多车型开行方案[16],同样是为了解决客流时空分布的不均衡性,减少运能与客流需求的不匹配。文献[17]考虑多车型协同作业,对快速公交发车频率进行了优化。从常规公交逐渐演化,列车的多编组运营组织技术逐渐成熟,文献[3]以城际铁路为研究对象,考虑多编组列车方式,建立了一个能准确计算乘客候车时间和列车拥挤成本的列车开行方案优化模型,证明高峰时段开行大编组列车、平峰时段开行小编组列车具有更高的效率。文献[18]探究了不同列车编组和不同编组列车的发车间隔对满载率均衡性的影响,发现多编组列车非均衡发车可以提高列车满载率的时空均衡性。文献[19]考虑多交路多编组建立了城市轨道交通列车交路计划优化模型,发现采用多编组的交路计划可以有效地降低乘客候车时间以及列车平均满载率。
因此,本文根据直通运营的技术特点,以直通运营区间范围、不同列车发车频率、不同列车编组为决策变量,构建了考虑满载率均衡性的城市轨道交通直通运营开行方案优化模型,并设计混合编码的遗传算法进行求解。最后,利用实际案例分别在高峰和平峰时期验证了模型和算法的合理性和高效性,并对目标函数权重取值进行了灵敏度分析。
1 问题描述为便于问题描述及模型建立,本文研究对象为两条相接的地铁线路的直通运营,如图 1所示。地铁A线路为车站1至车站N,地铁B线路为车站N至车站N+M,两条线路一端在车站N衔接。直通列车由地铁A车站N0出发,经由车站N直通运营至地铁B车站N1。以不同类型列车运行的交路折返点为边界,将线路划分为四个区段,ZⅠ区段由地铁A列车单独服务,ZⅡ区段由地铁A列车和直通列车共同服务,ZⅢ区段由地铁B列车和直通列车共同服务,ZⅣ区段由地铁B列车单独服务。
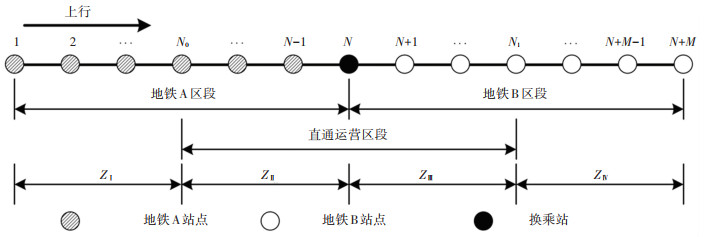
|
图 1 直通运营区段示意图 Fig. 1 Schematic diagram of through operation section |
直通运营条件下的轨道交通开行方案的编制受多种因素影响,根据建模及算法求解形式要求,结合既有研究[1, 9]作出以下假设:
1) 所有列车均采用站站停模式,不存在跨站及越行情况;2)研究时段内乘客到达强度均匀,不存在留乘情况且平均候车时间为发车间隔的一半;3)客流在各列车中的分配比例,由不同类型列车的发车频率、编组数量等供给特征决定,不考虑乘客的主观选择;4)不考虑列车折返对线路通过能力带来的影响。
2.2 参数及变量定义本文模型所用参数、中间变量如下:n为第n个车站,车站n与车站n+1之间为区间n,共N+M-1个区间;N′为具有折返条件的站点集合;i={1, 2, 3}为第i种类型的交路,i=1为地铁A运行交路,i=2为地铁B运行交路,i=3为直通运营交路;ln为区间n的长度,m;Li为第i种交路的线路长度,m;vi为i交路的列车平均旅行速度,m·s-1; fmin为最小发车频率,列/h;fmax为最大发车频率,列/h;qo, d为从o站到d站的乘客数,人;θ为折返作业的时间,min;μ为一次换乘所需的时间,min;Λ为可行的列车编组集合;C为一节车辆编组的定员,人;ZⅠ、ZⅡ、ZⅢ、ZⅣ分别为如图 1所示的区段;pn, iup、pn, idown分别为上行方向和下行方向的第n个区间内,交路为i的列车分担的断面客流;ηn, iup、ηn, idown分别为上行方向和下行方向的第n个区间内,交路为i的列车满载率;ηaveup、ηavedown分别为上行方向和下行方向的平均满载率;ηmax为列车最大满载率;T为乘客总出行时间,h;T1为乘客总候车时间,h;T2为乘客总换乘时间,h;S为车辆总走行公里,km;W为总车辆运用数,辆;U为满载率不均衡系数。
本文模型所用决策变量:N0、N1为直通运营交路的两个折返站;fi为交路i的发车频率,列/h;mi为交路i的列车编组数。为便于理解,本文对部分变量进行了说明和数学定义:
1) 断面客流pn, iup。根据直通运营条件下的交路及区段的设置,按上行方向的乘客OD需求可将客流分为10种类型,如图 2所示,一个箭头代表一个客流类型。与独立运营时乘客只可选择一种列车不同,直通运营时乘客可选择的列车是多样的,如由ZⅠ区段前往ZⅢ区段的乘客乘坐地铁A列车后可在N0站换乘直通列车,也可以在N站换乘地铁B列车。基于换乘次数最少的原则,本文假设了由ZⅠ区段前往ZⅣ区段的乘客只选择地铁A列车换乘地铁B列车的方式,不考虑换乘直通运营列车;由ZⅡ区段前往ZⅢ区段的乘客只选择直通运营列车,其他乘客按照不同列车的发车频率来选择列车。基于此,得到了上行方向不同区段内乘坐不同交路列车的断面客流计算方法,如式(1)所示。
| Pupn,j{n∑o=1N+M∑d=n+1qo,d,i=1,n∈ZⅠN0−1∑o=1N∑d=n+1qo,d+N0−1∑o=1N+M∑d=N1+1qo,d+f2f2+f3N0−1∑o=1N1∑d=N+1qo,d+f1f1+f3(n∑o=N0N∑d=n+1qo,d+n∑o=N0N+M∑d=N1+1qo,d),i=1,n∈ZⅡn∑o=N0N1∑d=N+1qo,d+f3f2+f3N0−1∑o=1N1∑d=N+1qo,d+f3f1+f3(n∑o=N0N∑d=n+1qo,d+n∑o=N0N+M∑d=N1+1qo,d),i=3,n∈ZⅡN0−1∑o=1N+M∑d=N1+1qo,d+n∑o=NN+M∑d=N1+1qo,d+f1f1+f3N−1∑o=N0N+M∑d=N1+1qo,d+f2f2+f3(N0−1∑o=1N1∑d=n+1qo,d+n∑o=NN1∑d=n+1qo,d),i=2,n∈ZⅡN−1∑o=N0N1∑d=n+1qo,d+f3f1+f3N−1∑o=N0N+M∑d=N1+1qo,d+f3f2+f3(N0−1∑o=1N1∑d=n+1qo,d+n∑o=NN1∑d=n+1qo,d),i=3,n∈ZⅢn∑o=1N+M∑d=n+1qo,d,i=2,n∈ZⅣ | (1) |
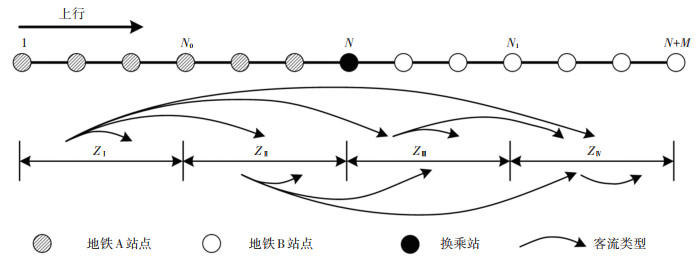
|
图 2 上行方向直通运营条件下客流分类 Fig. 2 Passenger flow classification of up direction for through operation |
由于地铁线路上下行具有对称性,参照pn, iup的计算方法可以求得pn, idown,限于篇幅,这里不再赘述。
2) 交路长度Li。直通运营条件下共开行有3种不同的交路,分别的交路长度计算方法为
| L1=N−1∑n=1ln | (2) |
| L2=N+M−1∑n=Nln | (3) |
| L3=N1−1∑n=N0ln | (4) |
3) 满载率ηn, iup。根据上行方向的断面客流,可计算上行方向不同区段内的不同交路列车的满载率,计算方法为
| ηupn,i=pupn,ifi⋅mi⋅C | (5) |
同理,参照ηn, iup的计算方法可以求得下行方向不同区段内的不同交路列车的满载率ηn, idown。
4) 加权平均满载率ηaveup。地铁线路具有明显的潮汐现象,上下行方向的列车满载率往往相差悬殊,使用同一个平均满载率不能很好的表现出此特性,因此本文分别计算了上下行的平均满载率。同时,考虑到区间的不同长度会影响乘客对满载率的感知,本文采用了区间长度加权的方法来计算平均满载率。根据上行方向不同区段内的不同交路列车的满载率以及不同区间的长度,可求得上行方向区间长度加权后的全线平均满载率,计算方法为
| ηupave=N−1∑n=1(ηupn,1⋅ln)+N+M−1∑n=N(ηupn,2⋅ln)+N1−1∑n=N0(ηupn,3⋅ln)3∑i=1Li | (6) |
同理,参照ηaveup的计算方法可以求得下行方向的加权平均满载率ηavedown。
2.3 目标函数列车开行方案的编制需要同时考虑乘客服务水平与企业运营成本,在直通运营条件下,乘客服务水平由乘客总出行时间以及满载率不均衡系数来代表,企业运营成本由车辆走行公里及车辆运用数代表,具体如下所示:
1) 最小化乘客出行成本。由于开通直通运营几乎不改变乘客的在车时间,所以本文的乘客总出行时间只包括有乘客总候车时间与总换乘时间,乘客总候车时间计算方法为
| T1=12f1(N0−1∑o=1N+M∑d=o+1qo,d+N0∑o=2o−1∑d=1qo,d+N+M∑o=N0+1N0−1∑d=1qo,d)+12f2(N1−1∑o=1N+M∑d=N1+1qo,d+N+M−1∑o=N1N+M∑d=o+1qo,d+N+M∑o=N1+1o−1∑d=1qo,d)+12f3(N−1∑o=N0N1∑d=N+1qo,d+N1∑o=N+1N−1∑d=N0qo,d)+12(f1+f3)(N−1∑o=N0N∑d=o+1d=N0+N−1∑o=N0N+M∑d=N1+1qo,d+N+M∑o=N1+1N−1∑d=N0qo,d+N∑o=N0+1o−1∑d=N0qo,d)+12(f2+f3)(N0−1∑o=1N1∑d=N+1qo,d+N1−1∑o=NN1∑d=o+1qo,d+N1∑o=N+1o−1∑d=Nqo,d+N1∑o=N+1N0−1∑d=1qo,d) | (7) |
乘客总换乘时间计算方法为
| T2=μ[f2f2+f3(N0−1∑o=1N1∑d=N+1qo,d+N1∑o=N+1N0−1∑d=1qo,d)+N0−1∑o=1N+M∑d=N1+1qo,d+f1f1+f3(N−1∑o=N0N+M∑d=N1+1qo,d+N+M∑o=N1+1N−1∑d=N0qo,d)+N+M∑o=N1+1N0−1∑d=1qo,d] | (8) |
最小化乘客总出行时间计算方法为
| min | (9) |
2) 最小化满载率不均衡系数。城市轨道交通客流在高峰时段的到站或出行强度是不均衡的,可能导致不同区段或不同类型列车的服务水平相差较大。因此,本文考虑将满载率不均衡系数最低作为目标函数之一,以提高最优开行方案下的乘客服务水平。满载率不均衡系数U可由所有列车在各区间的加权满载率的方差之和表示,考虑区间长度作为权重取值。最小化满载率不均衡系数计算方法为
| \begin{aligned} & \min U=\left(\sum\limits_{n=1}^{N-1}\left(\left(\left(\eta_{n, 1}^{\mathrm{up}}-\eta_{\mathrm{ave}}^{\mathrm{up}}\right)^2+\left(\eta_{n, 1}^{\mathrm{down}}-\eta_{\mathrm{ave}}^{\mathrm{down}}\right)^2\right) \cdot l_n\right)+\right. \\ & \sum\limits_{n=N}^{N+M-1}\left(\left(\left(\eta_{n, 2}^{\mathrm{up}}-\eta_{\mathrm{ave}}^{{up}}\right)^2+\left(\eta_{n, 2}^{\mathrm{down}}-\eta_{\mathrm{ave}}^{\mathrm{down}}\right)^2\right) \cdot l_n\right)+ \\ & \left.\sum\limits_{n=N_0}^{N_1-1}\left(\left(\left(\eta_{n, 3}^{\mathrm{up}}-\eta_{\mathrm{ave}}^{\mathrm{up}}\right)^2+\left(\eta_{n, 3}^{\mathrm{down}}-\eta_{\mathrm{ave}}^{\mathrm{down}}\right)^2\right) \cdot l_n\right)\right) / \sum\limits_{i=1}^3 L_i \end{aligned} | (10) |
3) 最小化企业运营成本。企业运营成本包含范围较广,针对本文研究的直通运营条件下的列车开行方案优化问题,选用了车辆总走行公里及车辆运用数代表企业运营成本。最小化车辆总走行公里计算方法为
| \min S=2 \sum\limits_{i=1}^3 L_i \cdot f_i \cdot m_i | (11) |
最小化车辆运用数计算方法为
| \min W=\sum\limits_{i=1}^3\left(\left[\frac{2\left(\frac{L_i}{v_i}+\theta\right) f_i}{60}\right]^{+} \cdot m_i\right) | (12) |
本文所建模型为多目标非线性整数规划模型,通常的求解思路是采用加权系数法将多目标转为单目标进行优化[9, 12]。由于乘客出行时间、满载率不均衡系数和企业运营成本的单位不同,本文首先对式(9)~(12)中的多个目标函数进行了无量纲化,再通过式(13)为各目标引入权重系数,将模型转化为单目标模型。经过处理后的目标函数为
| \min X=\omega_1 X_1+\omega_2 X_2+\omega_3 X_3+\omega_4 X_4 | (13) |
式中:X1=T/T′,X2=U/U′,X3=S/S′,X4=W/W′,其中,T′、U′、S′、W′分别代表独立运营条件下的乘客出行时间、满载率不均衡系数、车辆总走行公里、车辆运用数;X1、X2、X3、X4分别代表直通运营条件下的各目标值与独立运营条件下T′、U′、S′、W′的比值,以此来体现直通运营的优化效果;ω1、ω2、ω3、ω4分别代表相应的目标权重,且满足ω1+ω2+ω3+ω4=1,后文4.3节中会对权重取值进行详细分析。
2.4 约束条件式(14)表示地铁A和地铁B独立运营区段的发车频率需要满足列车最小发车频率的约束,由最低乘客服务水平限制,一般不小于6列/h;式(15)表示直通运营区段的发车频率需要满足列车最大发车频率的约束,由线路条件限制,一般不大于30列/h;式(16)保证发车频率为正整数;式(17)保证直通运营区段的折返站分别处于地铁A区段和地铁B区段内;式(18)保证直通运营区段的折返站必须具有折返条件;式(19)为列车最大满载率约束,一般不大于120%;式(20)为列车编组约束,需满足可行的列车编组集合。
| f_1, f_2 \geqslant f_{\min } | (14) |
| \left\{\begin{array}{l} f_1+f_3 \leqslant f_{\max } \\ f_2+f_3 \leqslant f_{\max } \end{array}\right. | (15) |
| f_1, f_2, f_3 \in N^* | (16) |
| 1 \leqslant N_0<N<N_1 \leqslant N+M | (17) |
| N_0, N_1 \in N^{\prime} | (18) |
| \eta_n^i \leqslant \eta_{\max } | (19) |
| m_i \in {\mathit{\Lambda}} | (20) |
上文所建的直通运营条件下的轨道交通开行方案优化模型为非线性整数规划模型,很难在多项式时间内进行求解。针对此类开行方案问题,前人多采用启发式算法进行求解[1, 3],故本文继承并设计了遗传算法求解模型,算法步骤如下:
步骤1 编码。本文模型决策变量为不同类型列车的发车频率f1、f2、f3,不同类型列车的列车编组m1、m2、m3,直通运营折返站N0、N1。发车频率和折返站可采用二进制方法进行编码,由于约束条件的限制,染色体长度为5时即可满足要求。但是列车编组数的可行解较少且离散,利用二进制编码会导致交叉变异后产生可行解的概率极低,因此可采用实数方法进行编码。图 3为一组可行解的混合编码对应形式示意。
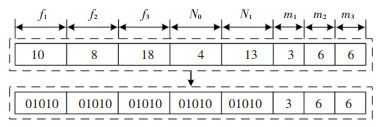
|
图 3 混合编码 Fig. 3 Hybrid coding |
步骤2 生成初始种群。随机生成符合约束的可行解并利用步骤1中方法进行混合编码,重复该过程ps次,生成初始种群。
步骤3 计算适应度。将目标函数式(13)中得到目标值作为个体的适应度fitness(k)=
步骤4 生成子代。选择操作是计算每个个体被选中的概率,按照“轮盘赌”方式抽样进入下一代;交叉操作是随机选择种群中的两个个体,以交叉概率pc交换随机交叉点的染色体,检测可行性后进入下一代;变异操作是随机选择种群中的一个个体,随机选择染色体的变异位置,如果选中前25位则按变异概率pm将0-1值互换,如果选中后3位则按变异概率pm将值变为Λ中的其他可行值,检测可行性后进入下一代。
步骤5 终止。重复步骤3~4,直到迭代次数达到预设最大值G,输出当前种群中最优个体编码及目标值,进行染色体解码得到最优的列车开行方案。
4 案例分析为证明本文构建的模型与算法的正确性和高效性,以北京地铁房山线和9号线为案例进行了验证,两线线路图如图 4所示,站间距如表 2所示。两条地铁线具有折返条件的车站分别为苏庄、良乡大学城、篱笆房、稻田、郭公庄、丰台东大街、六里桥、北京西站、白堆子、国家图书馆。本文以苏庄开往国家图书馆方向作为上行方向,反之为下行方向。
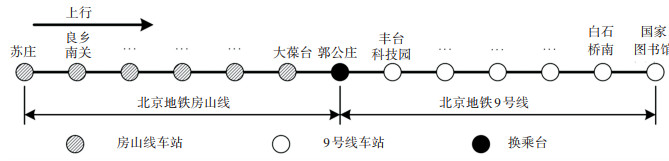
|
图 4 地铁房山线—9号线线路示意图 Fig. 4 Schematic diagram of Beijing Metro Fangshan Line and Line 9 |
| 表 2 地铁房山线—9号线站间距 Tab. 2 Station spacing of Beijing Metro Fangshan Line and Line 9 |
本文以2017年10月份某工作日的北京地铁AFC刷卡数据为基础,经过数据处理得到了地铁房山线以及9号线的早高峰小时的客流OD数据,绘制如图 5所示的客流OD热力图。可以发现,地铁9号线的客流明显高于房山线,并且在六里桥和北京西站等换乘站具有更大的乘降量。

|
图 5 地铁房山线—9号线客流OD Fig. 5 Passenger flow OD of Beijing Metro Fangshan Line and Line 9 |
结合北京地铁房山线和9号线的实际情况和相关文献研究,本文设置最小发车频率fmin=6列/h[18],最大发车频率fmax=30列/h[18],可行的列车编组集合Λ= 3, 6 [18],一节车辆编组的定员为C=240人[8],列车平均旅行速度为vi=10 m/s[12],折返时间θ=5 min,换乘时间μ=2 min,最大满载率ηmax=120%[12],目标函数权重为ω1=0.3、ω2=0.2、ω3=0.3、ω4=0.2。根据多次试验,最优遗传算法的参数设置为:G=500、ps=50、pc=0.3、pm=0.2。
4.2 求解结果利用MATLAB进行算法编程,进行了模型求解,遗传算法求解过程如图 6所示,发现算法具有良好的优化效果和求解效率,在372代时获得最优值并实现稳定。
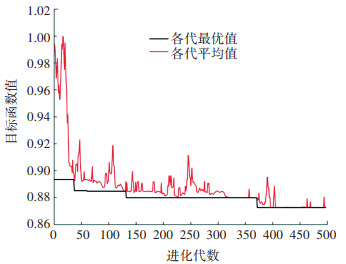
|
图 6 遗传算法求解过程 Fig. 6 Solving process of genetic algorithm |
为体现算法的优化效果,将直通运营优化结果与独立运营的列车开行方案下结果进行了对比,如表 3所示,可得在不改变列车编组的条件下,总目标值降低了12.85%,乘客候车时间略有增加(12.30%),但是乘客换乘时间得到了大幅度减少(-61.61%),乘客总出行时间下降了8.04%,满载率不均衡系数下降了51.67%,车辆总走行公里下降了0.37%,车辆运用数不变。证明了在适当的客流需求条件下,开通直通运营列车可以在有效地减少乘客出行时间、提高满载率均衡性的同时降低轨道交通运营企业的运营成本。
| 表 3 早高峰优化结果 Tab. 3 Optimization results for peak hour |
为了证明相较于独立运营而言,直通运营的开行方案在减少乘客出行时间的同时可以提高满载率的均衡性,本文对比两种运营模式下的区间满载率,如图 7(a)、7(b)所示。由于城市轨道交通的潮汐现象,上下行的满载率差别较大,因此分开进行比较。从图 7(a)中可以明显的看出,上行方向直通运营和独立运营的平均区间满载率差别不大,分别为74.13%和75.54%;但是,直通运营的区间满载率更为均衡,最高和最低的极值分别为111.75%和22.92%,而独立运营下的极值分别为117.07%和12.06%,尤其是在直通运营区段(篱笆房—北京西站)内,直通运营的区间满载率明显低于独立运营,说明直通运营可以有效地缓解直通运营区段内的拥挤程度。从图 7(b)中也可以明显的看出,下行方向直通运营的区间满载率同样更为均衡。
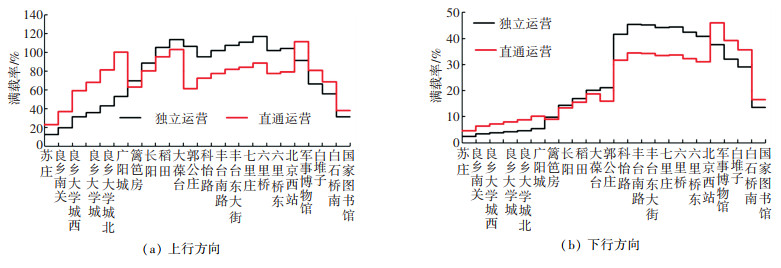
|
图 7 早高峰区间满载率对比分析 Fig. 7 Comparative analysis of load factors for peak hour |
但是,由于早高峰时期的客流量较大,最优的开行方案中3种交路均未选用小编组列车。因此,本文对平峰时期同样进行了研究,利用与早高峰同一天的工作日平峰小时数据,相关参数设置与早高峰相同。得到优化结果见表 4。
| 表 4 平峰优化结果 Tab. 4 Optimization results for off-peak hour |
从表 4中可以发现,开通直通运营列车在平峰小时同样具有良好的优化效果。与独立运营相比,直通运营的候车时间、换乘时间、满载率不均衡系数、车辆走行公里和车辆运用数均得到了大幅下降。由于房山线和9号线的客流相差较大,所以在最优结果中,房山线本线和直通运营交路采用小编组运行,9号线本线继续采用大编组运行,减少了平峰时期运能的浪费,提高了全线满载率的均衡性。
图 8表示了在平峰时段区间满载率的对比分析,与早高峰时具有相同的特征,上下行方向的直通运营和独立运营的平均区间满载率差别不大,但是直通运营的区间满载率均衡性高于独立运营。直通运营的区间满载率最小值在上行和下行方向分别为13.29%和3.19%,而独立运营的区间满载率最小值分别为5.69%和1.37%。
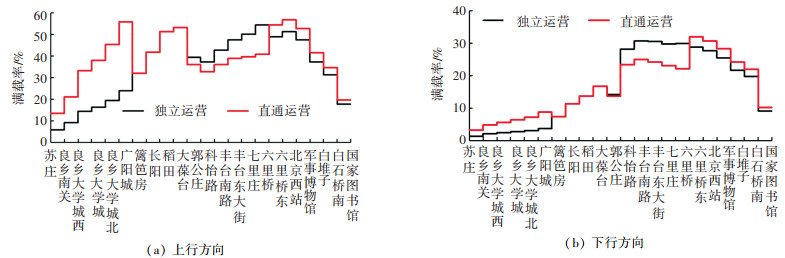
|
图 8 平峰区间满载率对比分析 Fig. 8 Comparative analysis of load factors for off-peak hour |
本文所提出的直通运营条件下城市轨道交通列车开行方案优化模型为多目标模型,前文采用了加权系数法将多目标模型转为单目标模型进行求解,导致各目标权重的取值会直接影响到求解的结果,因此本节对于不同权重取值下的优化结果进行对比分析。为体现乘客和运营企业的博弈思想,将4个目标归纳为两个部分,乘客出行时间和满载率不均衡系数属于乘客服务水平部分,车辆总走行公里和车辆运用数属于运营企业成本部分。权重取值依照乘客服务水平权重逐步降低、运营企业成本权重逐步升高来递进实现,结果如表 5所示,优化结果的总目标值呈现上升趋势,为不失一般性,本文选择中间值(ω1=0.3、ω2=0.2、ω3=0.3、ω4=0.2)为前文案例分析的权重取值。
| 表 5 不同权重优化结果对比 Tab. 5 Comparison of optimization results of different target weights |
根据表 5还可以发现,随着乘客服务水平权重的下降、运营企业成本权重的上升,乘客出行时间以及满载不均衡系数都呈现上升趋势,而车辆总走行公里和车辆运用数均呈现下降趋势。同时可以发现直通列车的发车频率下降,而本线列车的发车频率上升,并且直通运营的区段逐渐变小,这是因为直通运营的发车频率越高、运营区段范围越大在减少乘客的候车时间和换乘时间的同时会带来企业运营成本的上升,因此,当运营企业成本权重的上升时,开通直通运营列车的效果逐渐变差。
5 结论1) 本文以城市轨道交通的直通运营为研究对象,根据可乘坐的列车不同划分了直通运营条件下的乘客的OD类型;基于此客流分配原则,提出了满载率不均衡系数的计算方法;考虑了列车多编组以及满载率不均衡性的影响,建立了直通运营条件下的轨道交通列车开行方案优化模型。
2) 根据本文所建非线性整数规划模型的特点,设计了混合编码的遗传算法进行求解,并以北京地铁房山线与9号线为例进行了模型与算法的验证。结果表明:在高峰时段,与独立运营模式相比,直通运营模式下的乘客总出行时间下降了8.04%,满载率不均衡系数下降了51.67%,车辆总走行公里下降了0.37%,车辆运用数不变,证明了直通运营可以显著减少乘客出行时间、企业运营成本,提高乘客服务水平。
3) 在平峰时段,与独立运营模式相比,直通运营模式的优化效果达到了14.52%。在最优结果中,房山线本线和直通运营交路采用小编组运行,9号线本线继续采用大编组运行,此方法减少了平峰时期运能的浪费,提高了全线的满载率均衡性29.18%。
| [1] |
YANG A A, WANG B, HUANG J L, et al. Service replanning in urban rail transit networks: cross-line express trains for reducing the number of passenger transfers and travel time[J]. Transportation Research Part C: Emerging Technologies, 2020, 115: 102629. DOI:10.1016/j.trc.2020.102629 |
| [2] |
宁丽巧, 赵鹏, 谢秉磊, 等. 柔性间隔发车下城轨网络换乘协同优化[J]. 哈尔滨工业大学学报, 2019, 51(9): 68. NING Liqiao, ZHAO Peng, XIE Binglei, et al. Transfer synchronization of urban rail transit network with flexible departure headways[J]. Journal of Harbin Institute of Technology, 2019, 51(9): 68. DOI:10.11918/j.issn.0367-6234.201804099 |
| [3] |
NIU H M, ZHANG M H. An optimization to schedule train operations with phase-regular framework for intercity rail lines[J]. Discrete Dynamics in Nature and Society, 2012, 2012(1): 1. DOI:10.1155/2012/549374 |
| [4] |
GRIFFIN T. Shared track—a new dawn?[J]. Proceedings of the Institution of Mechanical Engineers Part F: Journal of Rail & Rapid Transit, 2002, 216(1): 15. DOI:10.1243/0954409021531647 |
| [5] |
RIEJOS F A O, BARRENA E, ORTIZ J D C, et al. Analyzing the theoretical capacity of railway networks with a radial-backbone topology[J]. Transportation Research Part A: Policy and Practice, 2016, 84: 83. DOI:10.1016/j.tra.2015.03.018 |
| [6] |
于剑, 张星臣, 徐彬, 等. 城市轨道交通过轨开行方案编制技术[J]. 城市轨道交通研究, 2015, 18(11): 18. YU Jian, ZHANG Xingchen, XU Bin, et al. On the compiling technique of urban rail transit over-track operation line plan[J]. Urban Mass Transit, 2015, 18(11): 18. DOI:10.16037/j.1007-869x.2015.11.004 |
| [7] |
李明高, 刘剑锋, 刘新华, 等. 地铁与市郊铁路过轨运营下列车开行方案研究[J]. 交通运输系统工程与信息, 2017, 17(6): 178. LI Minggao, LIU Jianfeng, LIU Xinhua, et al. Train planning for through operation between subway and suburban railway[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(6): 178. DOI:10.16097/j.cnki.1009-6744.2017.06.026 |
| [8] |
杨安安, 汪波, 陈艳艳, 等. 基于能力影响的城市轨道交通跨线列车开行方案研究[J]. 交通运输系统工程与信息, 2017, 17(6): 221. YANG Anan, WANG Bo, CHEN Yanyan, et al. Plan of cross-line train in urban rail transit based on the capacity influence[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(6): 221. DOI:10.16097/j.cnki.1009-6744.2017.06.032 |
| [9] |
ZHAO X M, SUN Q X, ZHU Y T, et al. Multi-routing planning design of Y-type urban rail transit[J]. Advances in Mechanical Engineering, 2016, 8(8): 1. DOI:10.1177/1687814016667385 |
| [10] |
LIU Y, HAN B M. Study on train routing plan of Y-line of urban rail transit considering passenger travel purpose[J]. IOP Conference Series Materials Science and Engineering, 2020, 787: 012021. DOI:10.1088/1757-899X/787/1/012021 |
| [11] |
梁青槐, 柴树山, 邓京维. 区域轨道交通跨线运行行车密度优化模型[J]. 北京交通大学学报, 2020, 44(1): 20. LIANG Qinghuai, CHAI Shushan, DENG Jingwei. Optimization model of train operation density for cross-line in regional rail transit[J]. Journal of Beijing Jiaotong University, 2020, 44(1): 20. DOI:10.11860/j.issn.1673-0291.20190047 |
| [12] |
许得杰, 曾俊伟, 麻存瑞, 等. 考虑满载率均衡性的大小交路列车开行方案优化研究[J]. 交通运输系统工程与信息, 2017, 17(6): 185. XU Dejie, ZENG Junwei, MA Cunrui, et al. Optimization for train plan of full-length and short-turn routing considering the equilibrium of load factor[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(6): 185. DOI:10.16097/j.cnki.1009-6744.2017.06.027 |
| [13] |
CEDER A, PHILIBERT L. Transit timetables resulting in even maximum load on individual vehicles[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(6): 2605. DOI:10.1109/TITS.2014.2318834 |
| [14] |
CANCA D, BARRENA E, LAPORTE G, et al. A short-turning policy for the management of demand disruptions in rapid transit systems[J]. Annals of Operations Research, 2016, 246(1/2): 145. DOI:10.1007/s10479-014-1663-x |
| [15] |
LI S J, XU R H, HAN K. Demand-oriented train services optimization for a congested urban rail line: integrating short turning and heterogeneous headways[J]. Transportmetrica A: Transport Science, 2019, 15(2): 1. DOI:10.1080/23249935.2019.1608475 |
| [16] |
HASSOLD S, CEDER A. Public transport vehicle scheduling featuring multiple vehicle types[J]. Transportation Research Part B: Methodological, 2014, 67: 129. DOI:10.1016/j.trb.2014.04.009 |
| [17] |
代存杰, 李引珍, 马昌喜, 等. 时间依赖需求下多车型快速公交发车频率优化[J]. 交通运输工程学报, 2017, 17(1): 129. DAI Cunjie, LI Yinzhen, MA Changxi, et al. Optimization of departure frequency for bus rapid transit with multi-type vehicles under time-dependent demand[J]. Journal of Traffic and Transportation Engineering, 2017, 17(1): 129. DOI:10.3969/j.issn.1671-1637.2017.01.015 |
| [18] |
戎亚萍. 基于多编组的列车满载率均衡化方法研究[J]. 交通运输系统工程与信息, 2019, 19(4): 187. RONG Yaping. Optimization of multi-group train operations for transit urban rail with even load[J]. Journal of Transportation Systems Engineering and Information Technology, 2019, 19(4): 187. DOI:10.16097/j.cnki.1009-6744.2019.04.027 |
| [19] |
李正洋, 赵军, 彭其渊. 考虑多交路多编组的城市轨道线路列车交路计划优化[J]. 铁道学报, 2020, 42(6): 1. LI Zhengyang, ZHAO Jun, PENG Qiyuan. Optimizing the train service route plan in an urban rail transit line with multiple service routes and multiple train sizes[J]. Journal of the China Railway Society, 2020, 42(6): 1. DOI:10.3969/j.issn.1001-8360.2020.06.001 |
 2023, Vol. 55
2023, Vol. 55



