2. 四川建筑职业技术学院, 成都 610031
2. Sichuan College of Architectural Technology, Chengdu 610031, China
中国是地震频繁国,近10年来发生5级以上地震共363次[1],地震主要集中在地震带分布密集的西部地区。而在中国已建成的“四纵四横”高速铁路网中有“三纵两横”处于地震区,在建和新规划的“四纵四横”在空间和时间上都无法完全避开潜在的地震区域,而正在开工建设的渝昆高铁就将穿过数条活动地震断裂带,其中38 km位于近断层9度地震区,100多公里位于8度地震区。为跨越西部艰险山区复杂地形,保证高速铁路线路的持续高平顺性,铁路桥梁结构被大量采用,同时随着列车运营速度的不断提高,高速铁路的“公交化”运营趋势已经显现,最小追踪间隔有时已经缩短至4 min。而历次强震震害[2]表明:桥梁上部结构的落梁失效是地震中较为常见也是极为严重的震害之一。一旦发生落梁震害会很容易引起高速列车落桥,严重威胁人民群众的生命安全,同时整条线路中断,短时间内修复困难,严重制约震后抢险救灾工作,因此近断层地震严重威胁着西南山区高速铁路桥梁及桥上行车安全。
为了保证近断层地震区桥梁结构的运营安全,防止桥梁发生落梁震害,防落梁装置被广泛采用,目前国内外学者对桥梁防落梁装置开展了大量的研究,公路桥梁防落梁措施普遍采用混凝土挡块[3]、高强度钢拉杆[4]、高强度钢索[5]等。而铁路桥梁广泛采用各类型钢挡块,其中最为常见的是工字钢防落梁[6],但这种防落梁缺乏缓冲能力,刚性限位,地震下传递到桥墩的碰撞力大,可修复性差,设计方法不明确[7]。针对上述钢防落梁的不足,文献[8]研发了X形弹塑性挡块装置,并对某公路连续梁桥弹塑性挡块的布置进行了参数分析。文献[9]研发了一种铁路桥梁用减震榫装置,并提出了装置的设计方法,研究了减震榫对铁路简支梁桥的减震性能。文献[10]提出了一种榫形防落梁装置,并推导了装置关键力学参数计算公式,研究了装置在铁路桥梁中的适应性。文献[11]提出了一种桥梁用缓冲型防落钢圈限位装置,利用钢圈使防落梁具备了缓冲能力。文献[12]针对大跨度漂浮体系铁路桥梁,研发了一种金属弹塑性限位耗能装置,该装置能够有效限制列车牵引制动力引起的梁端位移,同时地震作用下装置可发挥耗能作用。上述学者研究的减震防落梁装置可以分为两类,一类缓冲限位能力强,但减震耗能相对较弱,而另一类是减震耗能能力强,但限位防落梁能力有限。而对于同时兼顾限位和耗能能力的铁路桥梁防落梁装置研究较少。
因此,为研究适用于铁路桥梁的防落梁,使其同时兼顾减震耗能与防落梁功能,本文研发了一种耗能防落梁装置,建立了该装置力学参数计算方法,提出了装置设计方法,研发了对应的设计软件,并开展了装置的拟静力力学性能试验,研究了装置的滞回耗能能力,通过仿真模拟和试验测试结果验证本文所提计算与设计方法的正确性。以渝昆高铁强震区典型大跨度连续梁桥为工程背景,通过全桥模型的时程分析,确定了桥梁耗能防落梁装置的合理力学参数,进而设计出装置的具体构造参数,使大桥抗震性能满足设计要求。研究成果为近断层地震区铁路桥梁的抗震设计提供依据。
1 耗能防落梁装置设计研究 1.1 耗能防落梁设计思路目前中国高速铁路桥梁防落梁装置普遍采用型钢挡块,如图 1所示,即在梁体与桥墩之间设置型钢挡块,预留一定的间隙,当梁体与墩身的相对变形超出该间隙时,型钢挡块发挥作用,限制主梁进一步的位移。已有研究[13]表明:这种防落梁刚性碰撞问题突出,功能单一,无耗能能力,可修复性差,且地震下限位碰撞问题极为复杂,计算方法不明确,现有的《铁路工程抗震设计规范》(GB 20111—2006)[14]仅给出了铁路简支梁桥防落梁装置一种简化的检算方法。

|
图 1 铁路桥梁常用钢防落梁装置 Fig. 1 Common anti-drop-beam device for railway bridges |
为了解决目前防落梁装置存在的不足,本文拟研发一种新型耗能防落梁装置,实现如下功能:1)减震耗能+刚性限位功能组合,装置抗震性能可设计;2)装置耗能元件耗散梁体动能,增加撞击缓冲时间,降低碰撞力;3)震后维护性好、更换方便,价格经济实惠。
为了实现上述功能,提高铁路桥梁传统钢防落梁的耗能能力,同时兼顾防落梁功能,本文提出了一种铁路桥梁用新型耗能防落梁装置(见图 2)。即在传统工字钢防落梁的基础上进行改进,在钢防落梁中间位置添加了核心波纹钢金属阻尼器(见图 3)来弥补防落梁装置缺乏减震耗能的功能,研发了一种波形钢板耗能防落梁装置,核心波纹钢一端与防落梁挡块固定,另一端与前端挡板固定,而耗能防落梁装置底板与桥墩连接,前端挡板与主梁连接。

|
图 2 耗能防落梁装置设计方案示意图 Fig. 2 Design scheme of energy dissipation anti-drop-beam device |

|
图 3 波纹钢板耗能元件示意图 Fig. 3 Schematic diagram of corrugated steel energy dissipation element |
新型耗能防落梁装置的特点:在桥梁正常运营状态下,不参与工作;在地震作用下,波纹钢板将随着墩、梁出现相对变形而发生压缩或拉伸,而在压缩过程中,波纹钢板波峰、波谷将向外侧凸出,凸出到一定位置时波纹钢将与两侧限位板接触,侧板会约束波纹钢板外凸,并在接触面发生摩擦耗能,波纹钢板的拉压弹塑性变形耗散了地震能量,同时波纹钢板也起到缓冲作用,保护桥梁结构不发生破坏;当波纹钢板压缩到设计位移时,前端挡板与型钢挡块接触,耗能型防落梁将起到限位的功能,限制墩梁继续发生更大的位移,起到防落梁的作用,有效地防止发生落梁震害。
1.2 波纹钢耗能元件力学性能参数计算方法本文设计的金属耗能构件为等截面圆弧形波纹钢板,其利用波纹钢金属阻尼器拉伸、压缩耗散地震能量,在拉压变形过程中波纹钢截面受弯矩、剪力和轴力共同作用。下面将运用力学理论建立波纹钢耗能元件的力学性能参数计算公式。
本文提出的耗能防落梁装置,其核心波纹钢耗能元件一端固定,另一端为活动端,活动端在水平力作用下延波纹方向发生拉伸或压缩变形。但由于波纹钢板受压变形时其波峰、波谷向外凸出,会与两侧钢板接触摩擦,相互作用机理复杂,故本文在研究波纹钢耗能元件力学性能参数计算方法时,不考虑两侧钢板对波纹钢板约束和摩擦作用的影响,仅研究波纹钢板自身在水平外力作用下拉伸或压缩时的力学参数计算方法。
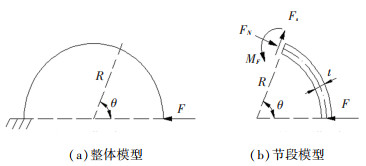
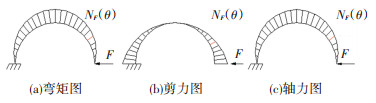
1.2.1 单个波纹钢耗能元件力学性能参数计算方法首先选取单个半圆波纹钢作为研究对象,力学计算模型可以如图 4所示,波纹钢板横断面为矩形截面,板厚为t,板宽度b,半圆波纹钢板半径为R。耗能元件在最右端施加水平荷载F作用下,其内力分布如图 5所示。
|
图 4 耗能元件力学性能计算模型 Fig. 4 Calculation model of mechanical properties of energy dissipation element |
|
图 5 耗能元件内力分布 Fig. 5 Internal force distribution of energy dissipation element |
当耗能元件为弹性时,由虚功原理[15]可得到F力作用时半圆波纹钢板的水平变形位移为
| $ \begin{aligned} w_1= & \sum \int \frac{M_F(\theta) M_o(\theta)}{E \times I(\theta)} \mathrm{d} s+\sum \int \frac{k F_s(\theta) F_{s o}(\theta)}{G \times A(\theta)} \mathrm{d} s+ \\ & \sum \int \frac{F_N(\theta) F_{N o}(\theta)}{E \times A(\theta)} \mathrm{d} s \end{aligned} $ | (1) |
式中:MF(θ)、Fs(θ)、FN(θ)分别为水平力F作用下,转动θ位置处截面承受的弯矩、剪力和轴力,即MF(θ)=R·sin θ·F、Fs(θ)=F·cos θ、FN(θ)=F·sin θ;Mo(θ)、Fso(θ)、FNo(θ)分别为单位水平力作用下,转动θ位置处截面承受的弯矩、剪力和轴力;E为弹性模量;G为剪切模量;I、A分别为波纹钢横截面惯性矩和面积;k为切应力延截面分布不均匀而引起的修正系数[15],其值与截面形状有关,矩形截面时k=1.2,圆截面时k=10/9;ds为转动θ角度处截面微段长度,ds=R·dθ;将上述参数代入式(1),求解积分函数可得
| $ \begin{aligned} w_1= & \int_0^\pi \frac{R^3 \cdot \sin ^2 \theta \cdot F}{E I} \mathrm{~d} \theta+\int_0^\pi \frac{k \cdot F \cdot \cos ^2 \theta \cdot R}{G A} \mathrm{~d} \theta+ \\ & \int_0^\pi \frac{F \cdot \sin ^2 \theta \cdot R}{E A} \mathrm{~d} \theta= \\ & \frac{F R^3}{E I} \int_0^\pi \sin ^2 \theta \mathrm{d} \theta+\frac{F R}{E A} \int_0^\pi \sin ^2 \theta \mathrm{d} \theta+ \\ & \frac{k F R}{G A} \int_0^\pi \cos ^2 \theta \mathrm{d} \theta= \\ & \frac{\pi F R^3}{2 E I}+\frac{\pi F R}{2 E A}+\frac{\pi k F R}{2 G A}= \\ & \frac{\pi F R^3}{2 E I}\left(1+\frac{I}{R^2 A}+\frac{k E I}{R^2 G A}\right) \end{aligned} $ | (2) |
式(2)中,第1项为弯矩的影响,第2项、第3项分别为轴力和剪力的影响。其中A=bt,I=bt3/12,G=0.4E代入式(2)得
| $ w_1=\frac{\pi F R^3}{2 E I}\left(1+\frac{t^2}{12 R^2}+\frac{t^2}{4 R^2}\right) $ | (3) |
可以看出,波纹截面厚度与波纹钢的半径之比t/R越大,则轴力和剪力影响所占的比重愈大,考虑波纹钢板加工工艺,R/t取值一般需大于6,而对于圆弧波纹钢板元件,轴力和剪力对耗能元件水平位移贡献较小,故在后文研究波纹钢板非线性变形和受力时,本文忽略了轴力和剪力影响。
故波纹钢板弹性刚度:
| $ k_{\mathrm{e}}=\frac{F}{w_1}=\frac{2 E I}{\pi R^3\left(1+\frac{I}{R^2 A}+\frac{k E I}{R^2 G A}\right)} $ | (4) |
假设波纹钢材料屈服应力为σs,波纹钢板极限弹性力为Fe。由图 5(a)弯矩图可知,最大弯矩发生在θ=90 °对应截面,当钢板处于弹性状态时,各截面外侧应力相等,其应力计算可采用:
| $ \sigma_{\max }(\theta)=\frac{F R \sin \theta \times t}{2 I} $ | (5) |
取θ=90°处截面为研究对象,将σs、R、θ、t代入式(5),反算Fe,即
| $ \sigma_{\mathrm{s}}=\frac{\frac{1}{2} F_{\mathrm{e}} R t}{\frac{1}{12} b t^3}=\frac{6 F_{\mathrm{e}} R}{b t^2} \Rightarrow F_{\mathrm{e}}=\frac{\sigma_{\mathrm{s}} b t^2}{6 R} $ | (6) |
则波纹钢板的弹性极限位移为
| $ w_{\mathrm{e}}=\frac{F_{\mathrm{e}}}{k_{\mathrm{e}}}=\frac{\sigma_s \pi R^2}{E t}\left(1+\frac{t^2}{12 R^2}+\frac{t^2}{4 R^2}\right) $ | (7) |
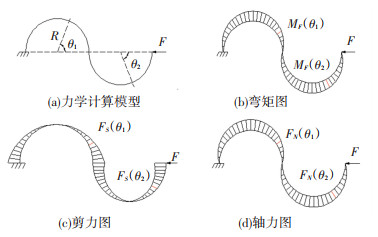
下面研究多个半圆波纹钢耗能元件的力学参数计算方法,以两个半圆波纹钢为例进行分析,波纹钢一端固定,一端活动,活动端作用水平荷载F,其计算力学模型及内力分布如图 6所示。
|
图 6 耗能元件力学计算模型及内力图 Fig. 6 Mechanical calculation model and internal force distribution of energy dissipation element |
参考单个半圆波纹钢的求解方法,即基于结构力学的虚位移原理可以得到两个半圆波纹钢耗能元件在荷载F作用点的水平位移w2为
| $ \begin{aligned} w_2= & \int_0^\pi \frac{R^3 \cdot \sin ^2 \theta_1 \cdot F}{E I} \mathrm{~d} \theta_1+ \\ & \int_0^{-\pi} \frac{R^3 \cdot \sin ^2 \theta_2 \cdot F}{E I} \mathrm{~d} \theta_2+ \\ & \int_0^\pi \frac{k \cdot F \cdot \cos ^2 \theta_1 \cdot R}{G A} \mathrm{~d} \theta_1+ \\ & \int_0^{-\pi} \frac{k \cdot F \cdot \cos ^2 \theta_2 \cdot R}{G A} \mathrm{~d} \theta_2+ \\ & \int_0^\pi \frac{F \cdot \sin ^2 \theta_1 \cdot R}{E A} \mathrm{~d} \theta_1+ \\ & \int_0^{-\pi} \frac{F \cdot \sin ^2 \theta_2 \cdot R}{E A} \mathrm{~d} \theta_2= \\ & \frac{\pi F R^3}{E I}+\frac{\pi F R}{E A}+\frac{\pi k F R}{G A}= \\ & \frac{\pi F R^3}{E I}\left(1+\frac{I}{R^2 A}+\frac{k E I}{R^2 G A}\right) \end{aligned} $ | (8) |
式中θ1、θ2分别代表两个半圆波纹钢与水平线的夹角,其他符号同前,计算结果表明w2=2w1,利用相同的方法可以推导出N1个半圆波纹钢耗能元件一端固定,另一端在水平荷载F作用下,作用点位移值wN1=N1×w1,即N1个半圆波纹钢元件变形值是单个波纹钢变形值的N1倍,变形值是串联叠加的关系,此时耗能元件弹性刚度kNe=F/wN1=F/(w1×N1)=ke/N1,而N1个半圆波纹钢耗能元件的弹性极限水平力FNe=Fe,与半圆波纹钢数量无关,此时对应的弹性极限位移wNe=FNe/kNe=we×N1。
综上所述,耗能元件中半圆波纹钢的数量多少直接影响耗能元件的变形和刚度值,但不影响耗能元件的水平承载力。相同水平荷载作用下,半圆波纹钢数量越多,位移变形越大、刚度越小,但波纹钢元件承载力不变。
因此在计算多个半圆波纹钢弹性变形、弹性刚度时,只需要计算单个半圆波纹钢的结果,然后通过半圆波纹钢数量的换算,便可得到多个半圆波纹钢耗能元件的力学参数值。
1.3 波纹钢耗能元件力-位移骨架曲线计算运用材料力学、弹塑性力学计算方法,建立金属波纹钢耗能片力学计算公式,但在推导金属波纹钢耗能片的力学计算公式前,假设如下:1)受力变形后满足平截面假设;2)忽略了轴力和剪力影响,只考虑弯矩对波纹钢的作用;3)半圆波纹钢板材料力学性能各方同性。
目前金属波纹钢材料采用高延性钢材为主,经过了特殊处理增大了钢材的断面收缩率、伸长率和冲击吸收功。让波纹钢在地震工况下的变形和受力范围主要集中在钢材应力平台段,故采用理想弹塑性模型作为波纹钢的本构关系。
当F > Fe时,耗能片截面进入弹塑性,应力分布见图 7。图中波纹钢板厚为t,塑性段高为B1,弹性段高为B2,由弹塑性理论可知,半圆波纹钢的水平变形w可按下式[16]计算:
| $ EI\frac{{{{\rm{d}}^2}w}}{{{\rm{d}}\mathit{s}}} = \left\{ \begin{array}{l} - M\left( s \right)\;\;\left( {{\rm{弹性段}}} \right)\\ - \frac{{{M_u}}}{B} \cdot \frac{{I\left( s \right)}}{{2{S_o}}} \cdot {\mathop{\rm sgn}}\;M\;\;\left( {{\rm{弹塑性段}}} \right) \end{array} \right. $ |

|
图 7 截面应力分布图[12] Fig. 7 Diagram of section stress distribution |
式中:ds为转动θ角度处截面微段长度,ds=R·dθ;M(s)为s位置处弯矩;I(s)为s位置处截面惯性矩;E是构件的弹性模量;Mu为耗能片能承受的极限弯矩,So为半截面对中性轴的静矩。
金属波纹钢弹塑性变形可按如下方法求解:首先确定半圆波纹钢板的弯矩图,判断半圆波纹钢各截面的应力分布情况,判断各个截面弹塑性和弹性段截面B1和B2值,再结合边界条件及半圆波纹钢变形的连续性,采用数值分析法[17]进行求解,可求出水平荷载F作用下半圆波纹钢弹塑性变形。
上述方法涉及高次微分方程求解,计算过程复杂,要想得到波纹钢的力-位移骨架曲线,需大量计算,不便于工程应用,因此本文提出一种简化方法:
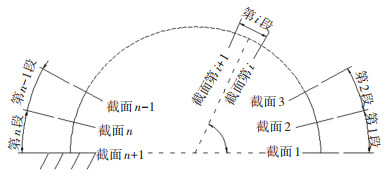
1) 同样先以单个半圆波纹钢为研究对象,波纹钢半径为R,将波纹钢延圆弧方向上划分n个小节段(如图 8所示),单个节段长度为s,每个小节段的夹角为Δθ,第i小段中心截面转角为θi=(i-1)×Δθ(i=1,…,n+1),单个节段纯弯变形图详见文献[12]中的图 5。
|
图 8 装置力学性能计算模式 Fig. 8 Mechanical property calculation mode of device |
2) 假设第i个微段截面尺寸、曲率相同,第i个微段厚度是ti,在荷载F作用下,第i个微段承受的弯矩为Mi,对应的微段截面边缘应变εi,由平截面假定可得第i个微段截面曲率ϕi,即
| $ \frac{s(1+\varepsilon)}{s(1-\varepsilon)}=\frac{R+0.5 t_i}{R-0.5 t_i} \Rightarrow 4 \varepsilon=2 t_i / R \Rightarrow \varphi_i=2 \varepsilon_i / t_i $ | (9) |
3) 采用文献[18]中的离散型积分求解w=
| $ w=\sum \int \bar{M} \varphi(\theta) R \mathrm{~d} \theta=\Delta \theta \times R^2 \sum\limits_{i=1}^n \sin \theta_i \varphi\left(\theta_i\right) $ | (10) |
由式(10)可知,求解w的关键就是求解各截面曲率ϕi,要想求解曲率则必须求解应变εi,截面的弹性应变为
| $ \varepsilon=M t /(2 E I) $ | (11) |
截面塑性应变为
| $ \varepsilon=t \varepsilon_{\mathrm{s}} /\left(t-2 B_1\right) $ | (12) |
式中εs为屈服应变,其他符号同前。
采用上述方法可以求解得到多个半圆波纹钢串联的耗能元件对应的塑性变形位移值,即:多个半圆波纹钢水平位移值=单个波纹钢位移值×半圆波纹钢数量,这里不再详细给出推导过程。
利用上述简化算法,便可计算出半圆波纹钢耗能片的弹塑性位移。
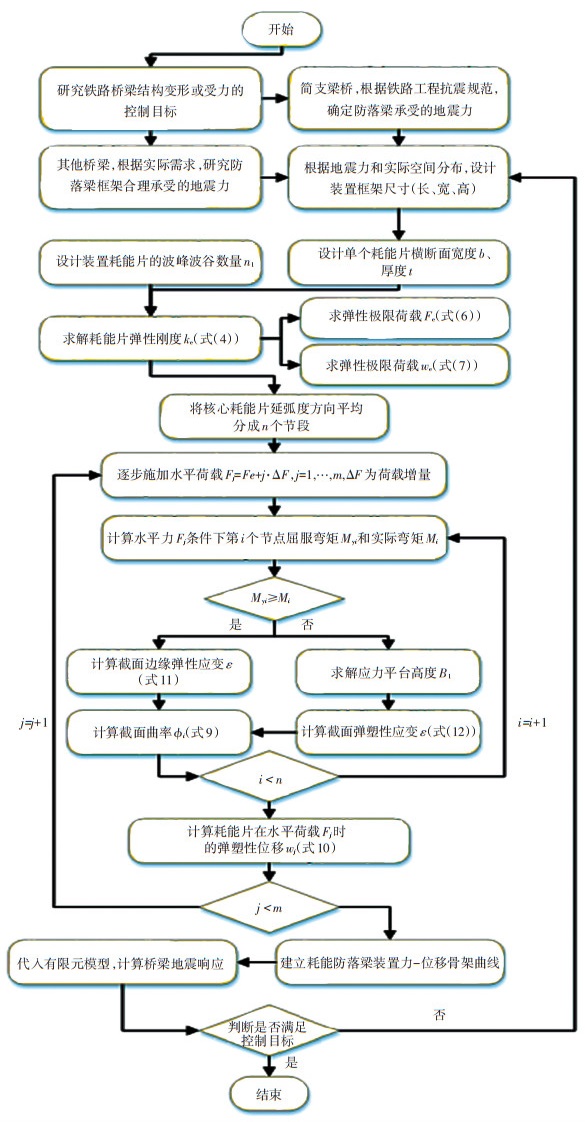
1.4 建立波纹钢耗能防落梁装置设计方法结合上述1.1~1.3节建立的计算理论,论文提出了一种耗能防落梁装置设计方法,具体步骤如图 9所示。运用提出的方法,可针对不同类型桥梁结构运营阶段、地震工况下桥梁位移和内力实际需求,设计出合理可行的耗能防落梁装置,并通过本设计方法计算出装置的力学性能参数和本构骨架曲线。
|
图 9 耗能防落梁装置简化设计方法流程 Fig. 9 Simplified design method flow of energy dissipation anti-drop-beam device |
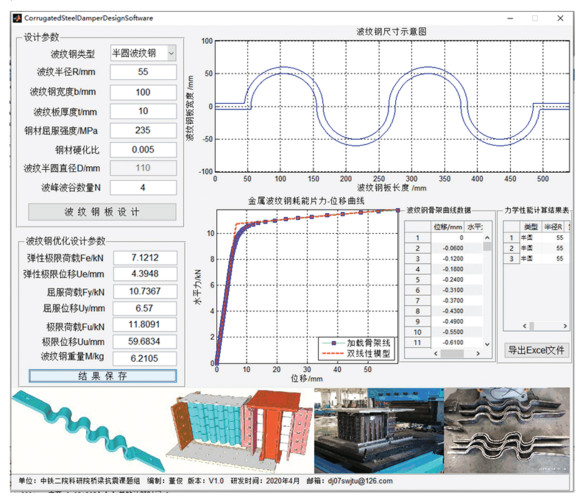
基于本文分析方法,结合文献[19-20]规定,研发了铁路桥梁波纹钢耗能防落梁分析软件,软件界面如图 10所示。在“设计参数”栏中输入相关参数,可得耗能片力学参数及其力-位移骨架曲线。
|
图 10 软件操作界面 Fig. 10 Software operation interface |
为了研究半圆波纹钢耗能元件的耗能能力及低周疲劳性能,本文开展了耗能防落梁装置的拟静力试验研究。
2.1 试验设计 2.1.1 金属耗能片试件设计本实验在洛阳特种装备有限公司实验室的2 000 t多功能试验机上进行,设备如图 11所示。

|
图 11 2 000 t多功能试验机 Fig. 11 2 000 t multi-function testing machine |
耗能元件试件样品制作数量见表 1,将耗能元件分成两组,一组试验试验考察耗能元件的滞回性能,分别按10、50、10、150 mm 4种位移幅值逐级加载,每级按3次往复进行加载。另一组试验考察耗能元件在极限位移工况下的低周疲劳性,按100 mm位移幅值进行30次往复加载。
| 表 1 试验件参数 Tab. 1 Test piece parameters |
耗能片构造参数见表 2,耗能元件按照两片叠放进行设计,布置形式如图 12所示,利用编制的金属波纹钢分析软件计算出试验元件的力-位移骨架曲线及关键力学参数如图 13所示。试验元件的弹性极限力Fe=6.02 kN,弹性极限位移Ue=6.1 mm,屈服荷载Fy=9.43 kN,屈服位移Uy=10.81 mm,极限位移Uu≥200 mm。
| 表 2 耗能片构造参数 Tab. 2 Structure parameters of energy dissipator |

|
图 12 耗能片构造形式图 Fig. 12 Structure form of energy dissipator |

|
图 13 单个试验元件力-位移骨架曲线 Fig. 13 Force-displacement skeleton curve of single test element |
试验装置包括梁底挡块、防落梁框架以及半圆波纹钢耗能片,耗能防落梁梁底挡块部件固定在试验机上板,防落梁框架部分固定在试验机下板,耗能波纹板将梁底部件与约束框架连为一体。水平作动器带动试验机下板进行往复运动,同时采集运动过程的位移及力信号,从而实现对耗能构件性能的测试,试验装置如图 14所示。

|
图 14 装置加载与安装示意图 Fig. 14 Device loading and installation diagram |
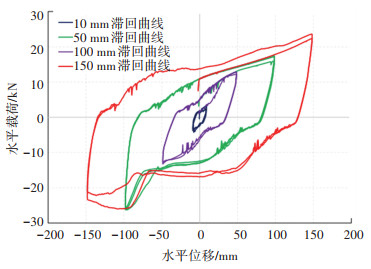
给出4个不同位移幅值(10、50、100、150 mm)载荷随时间的变化曲线,正值载荷时半圆波纹耗能片为拉拔状态,负值载荷时半圆波纹耗能片为压缩状态。10、50 mm拉压峰值载荷基本相等,100、150 mm出现明显的拉压载荷不对称现象。
由图 15分析可知:1)半圆波纹钢耗能片在初始加载阶段,位移和荷载之间基本上呈直线变化,滞回环所包围的面积极小,属于弹性阶段;随着加载位移幅值的加大,半圆波纹钢耗能片进入了塑性屈服阶段,滞回环趋于饱满,耗能能力增强;加载位移幅值继续增大,荷载还在上升,但上升速率减慢,滞回环形状更加饱满,耗能能力进一步增强。2)当加载位移幅值达到100、150 mm时,即耗能片进入受压阶段后期,半圆波纹钢波峰波谷向两侧往外凸,当向外变形一定程度后,受到两侧钢板约束,此时波纹钢片载荷出现突增,耗能片进入约束状态,耗能效果进一步增强。
|
图 15 标准加载工况单个耗能片力学性能滞回曲线 Fig. 15 Hysteretic curve of mechanical properties of a single energy dissipator under standard loading condition |
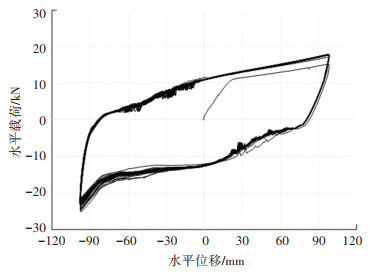
图 16给出了加载位移幅值为100 mm时,循环周期为30次的位移载荷曲线。从图可以看出,30次循环滞回曲线重合度极高,证明该耗能结构力学本构极其稳定。多次往复荷载试验后耗能构件对其进行外观检查(见图 17),除发现有磨损现象外,未发现明显裂纹萌生现象,低周疲劳性能良好。
|
图 16 位移幅值100 mm的低周往复滞回曲线 Fig. 16 Low cycle reciprocating hysteretic curve under displacement amplitude of 100 mm |

|
图 17 循环试验30次后金属波纹钢耗能片试验变形状态 Fig. 17 Deformation and failure of metal corrugated steel energy dissipator after 30 times of cyclic test |
这里需要单独分析一下耗能片在拉伸、压缩的变形状态,由于耗能片压缩过程中受到两侧钢板约束,耗能片波峰波谷与两侧钢板接触摩擦,波纹钢波峰波谷有凹陷或压扁的状态,复杂的摩擦接触作用使各波峰波谷变形不均匀,压缩时,受力最前端的半圆波纹钢变形较大(图 17(b))。而拉伸时,两侧钢板与波纹钢无接触摩擦,此时各半圆波纹钢变形相对均匀(图 17(a))。循环往复数30次后,由于两侧钢板对波纹钢约束摩擦作用及拉压荷载作用,使整个耗能片发生的不均匀的塑性变形,其变形状态见图 17(c)。但从30次低周疲劳滞回曲线可知:滞回环趋于饱满,30圈滞回曲线吻合较高,说明耗能元件并未受到自身不均匀的塑性变形而影响滞回性能。
2.2.3 理论、数值模拟及试验结果对比分析为了验证本文理论推导的正确性,本文采用数值仿真、试验测试与理论分析结果进行对比验证。
运用Ansys建立试验构件有限元模型,波纹钢板采用shell43板单元模拟,采用BISO考虑钢板材料的非线性,模型构造参数见表 2,金属波纹钢耗能片有限元模型及滞回曲线如图 18所示。

|
图 18 金属波纹钢有限元模型及滞回曲线 Fig. 18 Finite element model and hysteretic curve of metal corrugated steel |
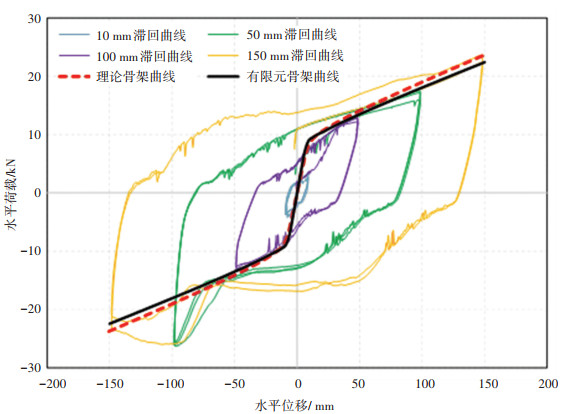
为了进一步比较理论、数值模拟和试验测试3种结果的差异性,将3种结果绘制于图 19中,同时表 3给出了波纹钢耗能装置在理论分析、数值模拟及试验测试中得到的关键力学参数。
|
图 19 试验、理论、数值模拟本构骨架曲线对比分析 Fig. 19 Comparison and analysis of constitutive skeleton curves of experimental, theoretical, and numerical simulation |
| 表 3 金属波纹钢耗能片试件力学参数对比 Tab. 3 Comparison of mechanical parameters of metal corrugated steel energy dissipator specimens |
由图 19和表 3可知,在耗能片处于拉伸变形时,3种方法得到的的骨架曲线基本重合,关键力学参数偏差较小,这表明本文建立的金属波纹板耗能片数值模型和力学性能理论计算方法是正确的。可以通过本文算法开展新型耗能防落梁装置的设计研发。在耗能片处于压缩变形中,当半圆波纹钢与两侧钢板发生接触摩擦,耗能片承载力会上升,此时与理论值有偏差,主要是理论分析过程中,未考虑两侧钢板对波纹钢的约束和摩擦作用,但不影响理论分析方法的工程应用。
3 工程实例 3.1 工程概况及有限元模拟以渝昆高铁8度0.3g强震区大跨度连续梁为工程背景,主桥桥跨为70 m+128 m+70 m,桥上线路为双线,主梁为预应力钢筋混凝土箱梁,C50混凝土,圆端形桥墩,C35混凝土,ZK活载,21#固定墩支座采用KZQZ-LX-60000GD/HX-0.3g,20#主墩支座采用KZQZ-LX-60000ZX/DX-e150/10-0.3g,19#和22#边墩支座采用KZQZ-LX-8000ZX/DX-e150/10-0.3g,金属波纹钢耗能防落梁装置各桥墩沿纵桥向设置两个,用于纵桥向耗能限位,两个中墩采用CSXFB-800型,两个边墩采用CSXFB-400型,此外每个桥墩还设置两个横向钢防落梁挡块(矩形空心截面)用于横向限位,耗能防落梁设计参数见表 4,支座和防落梁挡块参数见表 5和表 6,全桥布置如图 20所示,钢防落梁挡块和耗能防落梁装置布置如图 21所示。
| 表 4 金属波纹钢耗能防落梁设计参数 Tab. 4 Design parameters of energy dissipation anti-drop-beam device |
| 表 5 双曲面球型减隔震支座参数 Tab. 5 Parameters of hyperboloid spherical seismic isolation bearing |
| 表 6 钢防落梁挡块 Tab. 6 Steel anti-drop-beam retaining block |

|
图 20 70 m+128 m+70 m连续梁全桥布置示意图(cm) Fig. 20 Schematic diagram of full-bridge layout of 70 m+128 m+70 m continuous beam (cm) |

|
图 21 耗能防落梁装置布置图(mm) Fig. 21 Layout of energy dissipation anti-drop-beam device (mm) |
利用Engineer′s studio软件建立全桥模型,梁单元模拟主梁、纤维单元模拟桥墩,根据《铁路工程抗震设计规范》(GB 20111—2006)[14]考虑二期恒载和列车活载的质量;混凝土本构采用Kent-Scott-Park模型[21],钢筋本构采用双折线模型;支座用双线性理想弹塑性弹簧单元模拟[2],波纹钢耗能片采用金属双折线滞回本构模型[9],耗能片初始间隙采用Engineer′s studio软件自带的Gap/Hook间隙本构进行模拟,耗能防落梁框架和横向钢防落梁挡块本构模型也采用Engineer′s studio软件自带的具有初始间隙的双折线模型模拟,整个耗能防落梁装置的模拟方法为:将Gap/Hook间隙本构与耗能片本构组成串联体系,而后将串联体系与防落梁框架本构进行并联,桩基础采用6个弹簧单元进行等效模拟[22],全桥模型如图 22所示。

|
图 22 全桥模型示意图 Fig. 22 Finite element model of the bridge |
为研究金属波纹钢耗能防落梁对桥梁抗震性能的影响,本文分析了3种减隔震体系方案包括:1)方案1,普通支座体系(传统硬抗模型);2)方案2,双曲面球型减隔震支座+型钢挡块;3)方案3,双曲面球型减隔震支座+耗能防落梁。
根据地震安评报告提供的多遇、设计、罕遇地震各3条进行时程分析,考虑纵向地震动输入,下文将重点研究设计、罕遇地震作用下金属波纹钢耗能装置对大桥抗震性能的影响,分析结果根据规范[14]取3条地震波的最大值进行分析。
图 23给出了罕遇地震动下采用方案2和方案3工况下边墩支座位移时程曲线。分析可知,相较于仅采用双曲面减隔震支座+型钢挡块的方案,耗能防落梁装置可显著降低连续梁桥的支座变形,以罕遇地震下,边墩支座变形由204 mm减低到148 mm,位移减震率为27.45%,表 7给出了各条设计、罕遇地震作用下各桥墩支座变形计算结果的最大值,分析表明:相比方案2,方案3在罕遇地震作用下支座位移减震率达到25%~30%,金属耗能防落梁装置耗散了地震能量,可有效限制墩梁相对位移变形,减震效果良好,可用于高烈度地震区大跨连续梁桥抗震及减震设计。

|
图 23 边墩支座位移时程曲线对比图(罕遇地震1) Fig. 23 Comparison of time history curves of side pier bearing displacement (rare earthquake 1) |
| 表 7 设计、罕遇地震作用下支座变形及减震率(mm) Tab. 7 Bearing deformation and damping rate under design and rare earthquakes (mm) |
表 8和表 9给出了设计、罕遇地震作用下3种方案对应的大桥各墩墩底最大弯矩、剪力计算结果,分析可知,方案3相比传统硬抗支座体系方案,使21#固墩在设计、罕遇地震下弯矩、剪力减震率达65%~82%,使19#和22#边墩弯矩、剪力减震率达10%~26%;而方案3相比方案2,在设计、罕遇地震作用下各桥墩墩底弯矩减震率达17%~30%,各桥墩墩底剪力减震率达13%~32%,这表明限位减震装置较好地耗散了地震能量,对桥墩的减震效果明显,对大跨度铁路桥梁适应性良好。
| 表 8 各种方案下桥墩墩底最大弯矩及减震率 Tab. 8 Maximum bending moment and damping rate of each pier bottom under different schemes |
| 表 9 各种方案下桥墩墩底最大剪力及减震率 Tab. 9 Maximum shear force and damping rate of each pier bottom under different schemes |
1) 提出了一种高烈度地震区铁路桥梁用新型耗能防落梁装置,建立了新型耗能防落梁中波纹钢耗能片力学参数计算方法,提出了耗能防落梁的设计方法,编制了新型耗能防落梁装置的设计分析软件。
2) 开展了金属波纹钢耗能防落梁装置拟静力试验研究,试验结果表明:装置滞回环饱满,耗能能力增强,低周疲劳性能良好。通过对比分析理论、数值模拟和试验测试得到的装置本构骨架曲线表明:本文提出的装置力-位移骨架曲线计算方法正确,便于工程应用。
3) 设计了渝昆高铁8度地震区典型大跨连续梁桥的耗能防落梁装置,运用有限元法对大桥的抗震性能进行了分析,分析表明:装置对梁端具有良好的限位效果,保证了高铁桥梁运营安全,在罕遇地震下可使梁端位移减震率达到25%~32%,墩底内力减震率可达60%。
| [1] |
中国地震局. 中国历史地震列表[M/OL]. 2021: 1-25[2021-06-26]. https://www.cea.gov.cn/eportal/ui?struts.portlet.mode=view&struts.portlet.action=/portlet/earthquakeHistory!toListView.action&pageId=366506&startDate=2011-01-01%2000:00:00&endDate=2021-06-26%2023:59:59&startMagnitude=5&endMagnitude=10&areaname=%25E4%25B8%25AD%25E5%259B%25BD&searchType=2&isshow=yes
|
| [2] |
董俊. 铁路高墩大跨刚构-连续组合体系桥梁近场地震易损性分析研究[D]. 成都: 西南交通大学, 2016 DONG Jun. Fragility analysis of railway long span rigid frame-continuous combination system bridge with high pier subjected to near-fault ground motion[D]. Chengdu: Southwest Jiaotong University, 2016 |
| [3] |
徐略勤. 钢筋混凝土横向挡块抗震性能试验研究[D]. 上海: 同济大学, 2012 XU Lueqin. Experimental research on seismic behavior of reinforced concrete transverse retainers[D]. Shanghai: Tongji University, 2012 |
| [4] |
易莉帮, 李建中. 连续梁桥纵向阻挡型限位装置防落梁效果分析[J]. 世界地震工程, 2016, 32(2): 238. YI Libang, LI Jianzhong. Analysis of unseating prevention effect of longitudinal blocking restrainers in continuous girder bridges[J]. World Earthquake Engineering, 2016, 32(2): 238. |
| [5] |
AASHTO. AASHTO guide specifications for LRFD seismic bridge design[S]. Washington: American Association of State Highway and Transportation Officials, 2007
|
| [6] |
曾永平, 董俊, 陈克坚, 等. 九度地震区高铁简支梁减隔震体系适应性分析[J]. 铁道工程学报, 2020, 37(2): 46. ZENG Yongping, DONG Jun, CHEN Kejian, et al. Adaptability analysis of the seismic isolation system for high-speed railway simply supported beam bridge in nine-degree seismic regions[J]. Journal of Railway Engineering Society, 2020, 37(2): 46. |
| [7] |
SETYOWULAN D. Dynamic analysis of ultimate state for bridges with multiple restrainers[J]. Rekayasa Sipil, 2016, 10(2): 160. |
| [8] |
黄小国. 连续梁桥防落梁装置试验和理论研究[D]. 上海: 同济大学, 2009 HUANG Xiaoguo. Experimental and theoretical research on anti-falling beam device of continuous beam bridge[D]. Shanghai: Tongji University, 2009 |
| [9] |
孟兮. 减震榫的减震性能及其在铁路桥梁中的应用[D]. 北京: 北京交通大学, 2015 MENG Xi. Damping performance of shock absorber and its application research on railway bridge [D]. Beijing: Beijing Jiaotong University, 2015 |
| [10] |
曾永平, 陈克坚, 樊启武, 等. 近断层地震作用下铁路桥梁减震卡榫原理及试验研究[C]//"川藏铁路建设的挑战与对策"2016学术交流会论文集. 北京: 人民交通出版社, 2016 ZENG Yongping, CHEN Kejian, FAN Qiwu, et al. Study on the performance of railway bridge structure with shock absorber system under near-fault ground motions[C]// Sichuan-Tibet Railway Construction Challenges and Countermeasures Symposium. Beijing: China Communications Press, 2016 |
| [11] |
王占飞, 孙巨搏, 程浩波, 等. 缓冲型防落梁钢圈限位装置力学性能研究[J]. 桥梁建设, 2018, 48(6): 18. WANG Zhanfei, SUN Jubo, CHENG Haobo, et al. Study on mechanical properties of a steel ring anti-fall restrainer with buffer capacity[J]. Bridge Constructuion, 2018, 48(6): 18. |
| [12] |
董俊, 曾永平, 陈克坚, 等. 大跨铁路桥梁金属限位减震装置设计与力学性能[J]. 哈尔滨工业大学学报, 2020, 52(3): 136. DONG Jun, ZENG Yongping, CHEN Kejian, et al. Design of metal limit damping device and analysis of mechanical properties for long span railway bridge[J]. Journal of Harbin Institute of Technology, 2020, 52(3): 136. |
| [13] |
王占飞, 孙巨搏, 程浩波, 等. 缓冲型防落梁钢圈限位装置力学性能研究[J]. 桥梁建设, 2018, 48(6): 18. WANG Zhanfei, SUN Jubo, CHENG Haobo, et al. Study on mechanical properties of a steel ring anti-fall restrainer with buffer capacity[J]. Bridge Construction, 2018, 48(6): 18. |
| [14] |
中华人民共和国铁道部. 铁路工程抗震设计规范: GB 50111—2006[S]. 北京: 中国计划出版社, 2006 Ministry of Railways of the People′s Republic of China. Code for seismic design of railway engineering: GB 50111—2006[S]. Beijing: China Planning Press, 2006 |
| [15] |
李廉锟. 结构力学[M]. 6版. 北京: 高等教育出版社, 2017. LI Liankun. Structural mechanics[M]. 6th ed. Beijing: Higher Education Press, 2017. |
| [16] |
潘晋, 吴成亮, 全强, 等. E型钢阻尼器数值仿真及试验研究[J]. 振动与冲击, 2009, 28(7): 192. PAN Jin, WU Chengliang, TONG Qiang, et al. Simulation and experimental study on an E-shape steel damper[J]. Journal of Vibration and Shock, 2009, 28(7): 192. |
| [17] |
罗亮生, 包雪松, 王国英. 数值分析[M]. 北京: 科学出版社, 2002. LUO Liangsheng, BAO Xuesong, WANG Guoying. Numerical analysis[M]. Beijing: Science Press, 2002. |
| [18] |
同济大学数学系. 高等数学[M]. 7版. 北京: 高等教育出版社, 2014. Department of Mathematics of Tongji University. Higher mathematics[M]. 7th ed. Beijing: Higher Education Press, 2014. |
| [19] |
中铁大桥勘测设计院有限公司. 铁路桥梁钢结构设计规范: TB 10091—2017[S]. 北京: 中国铁道出版社, 2017 China Railway Bridge Survey and Design Institute Group Corporation. Code for design on steel structure of railway bridge: TB 10091—2017[S]. Beijing: China Railway Press, 2017 |
| [20] |
中华人民共和国建设部. 钢结构设计规范: GB 50017—2003[S]. 北京: 中国计划出版社, 2003 Ministry of Construction of the People′s Republic of China. Code for design of steel structures: GB 50017—2003[S]. Beijing: China Planning Press, 2003 |
| [21] |
KENT D C, PARK R. Flexural members with confined concrete[J]. Journal of the Structural Division, 1971, 97(7): 1969. |
| [22] |
董俊, 单德山, 张二华, 等. 非规则桥梁近、远场地震易损性对比分析[J]. 哈尔滨工业大学学报, 2016, 48(3): 159. DONG Jun, SHAN Deshan, ZHANG Erhua, et al. Near and far-field seismic fragility comparative analysis of irregular bridge[J]. Journal of Harbin Institute of Technology, 2016, 48(3): 159. |
 2023, Vol. 55
2023, Vol. 55


