由于复杂地形和工程造价等因素受限,弯坡组合路段在中国较为常见[1]。然而,由于公路线形的变化,驾驶人视觉和心理易产生较大估计误差,进而导致操纵失误,使该类型路段成为公路交通事故频发且集中的路段[2]。因此,研究弯坡路段的线形设计优劣对行车安全尤为重要[3]。现行的国内外公路设计标准或指南[4-5]所用的公路线性设计方法是确定性的,仅给出了单个公路几何的极限值和一般值,但该方法忽略了设计输入的固有可变性(例如,车辆的行驶速度、驾驶人感知-反应时间、制动减速度等)[6-7],缺乏对不确定因素的定量测量,因此,设计公路的安全裕度是未知的。可靠性分析可通过数学关系将不确定性因素与公路的安全性能建立关系,是量化设计公路不确定性输入和安全裕度的有效方法。
目前,可靠性分析在公路设计和事故预测的应用中取得了一定成果。文献[8]提出将可靠性分析用于评估公路和铁路交叉口的视距的设计。文献[9]通过视距不足失效概率提出了适用于挖方路段的平曲线和平缓纵坡、凸形纵坡、凹形纵坡组合的公路安全评估方法。文献[6]建立了考虑视距不足失效概率的事故预测模型。文献[10]评估了一系列具有不同水平视距限制的水平曲线及中央分隔带宽度组合的视距不足失效概率。文献[11]基于视距不足失效模式假设不同的概率失效水平,校核设计指南中的中央分隔带边缘与相邻车道中心线之间的横向距离。个别研究者将可靠性分析引入除视距不足之外的其他失效模式,例如,文献[3, 12]将可靠性分析引入货车的制动失效,并通过建立多模式失效系统对弯坡路段的设计进行了改进。文献[13]基于车辆的侧滑和侧翻两种失效模式分别建立了轿车和卡车的多模式失效系统。文献[14-15]证明了多模式失效概率(包括侧滑、侧翻、视距不足)在平曲线设计中的应用。现有文献虽已在基于可靠性分析的公路设计方面取得了一定成果,但仍不全面。总结如下:1)过去的学者将可靠性分析引入公路安全设计的研究多针对视距不足一种失效模式,个别学者针对车辆的侧翻和侧滑两种失效失效模式进行了研究,基于可靠性分析的多模式失效的研究较少,仍需深入研究;2)上述成果多数将失效概率直接应用于公路设计,鲜少文献将失效概率与公路交通事故关联对失效概率能否应用于公路安全设计进行验证,个别文献将视距不足失效概率与公路交通事故建立关系,未见到多模式失效概率与公路交通事故关系的研究。
将多模式失效概率与车辆事故建立联系,建立事故预测模型是必要的。过去的研究者常用负二项模型进行事故预测[16],但该模型不能刻画未被搜集但会影响事故发生的因素,这些因素构成未观察到的异质性因素(例如,驾驶人的生理特征、车辆制造年份、未观察到的时变天气条件、驾驶人对车道和路肩宽度变化的反应等)[17]。目前,学者们用于解释未观察到的异质性模型主要有潜在类(有序)混合模型[18-19]、马尔可夫转换模型[20]、随机效应/随机参数Tobit模型[21-22]、随机效应/随机参数负二项模型[17, 23-24]等。潜在类(有序)混合模型更适于事故损伤严重性的研究[17],马尔可夫转换和随机效应/随机参数Tobit两类模型是零膨胀类模型,适用于零值较多的样本研究,随机效应/随机参数负二项模型通常用于计数模型,能很好地捕获影响因素中未观察到的异质性的影响。部分学者[24-25]已对随机效应/随机参数负二项模型分别进行研究。然而,从拟合优度、参数估计、准确性等方面对随机效应负二项模型和随机参数负二项模型进行比较分析,仍值得进一步研究。
针对过去研究存在的不足,本文基于弯坡路段可能导致轿车交通事故的失效模式建立多模式失效系统,并通过建立事故预测模型将多模式失效系统的失效概率与轿车单车事故数关联,建立的事故预测模型包括负二项模型、随机效应/随机参数负二项模型。基于最优的事故预测模型分析多模式失效概率与轿车单车事故的关系。
1 多模式失效系统的建立及其概率求解可靠性分析是通过数学关系将不确定性因素与结构的性能之间建立关系,并通过概率统计方法(失效概率)对结构完成预定功能的能力进行定量分析和评估。结构可靠与不可靠之间的状态称为临界状态,通过极限状态功能函数Z来表示结构的临界状态,即
| $ Z=f(S, D)=S-D=f\left(u_1, u_2, \cdots, u_c\right) $ | (1) |
式中:Z=0表示失效面,当Z < 0时,结构发生失效;S表示供给函数;D表示需求函数;uc表示供给或需求函数中的随机变量。
在公路安全设计中,极限状态功能函数表示公路所能提供的设计参数与车辆安全通过该路段所需求的公路设计参数的差值。若车辆安全通过的需求超过公路的实际供应(即Z < 0),则认为车辆有事故风险[10]。
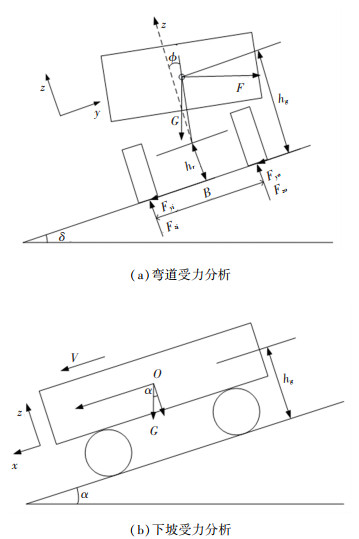
1.1 侧滑极限状态功能函数为更清晰表示车辆在弯坡路段行驶时的受力,本文将对车辆在弯道和坡道上的行驶分别进行受力分析,如图 1所示。假设车辆稳态行驶,忽略纵向力和空气阻力,车辆在弯道行驶时的离心力为
| $ F=\frac{G V^2}{g R} $ | (2) |
|
图 1 车辆的受力分析 Fig. 1 Force analysis of vehicles |
式中:V为车辆的行驶速度,R为平曲线半径,G为车辆的重力,g为重力加速度。
车辆在y轴方向的横向力分量为
| $ F_y^{\prime}=-F \cos \delta-G \cos \alpha \sin \delta $ | (3) |
式中:α为纵坡角,δ为横坡角。
车辆在z轴方向的垂向力分量为
| $ F_z^{\prime}=-F \sin \delta-G \cos \alpha \cos \delta $ | (4) |
车辆在y轴方向受力平衡公式为
| $ F_{y i}+F_{y o}=F_y^{\prime}=F \cos \delta-G \cos \alpha \sin \delta $ | (5) |
式中:Fyi为内侧车轮受到的横向力;Fyo为外侧车轮受到的横向力,内侧为靠近弯道中心的一侧。
车辆在z轴方向上的受力平衡公式为
| $ F_{z i}+F_{z o}=-F_z^{\prime}=F \sin \delta+G \cos \alpha \cos \delta $ | (6) |
式中Fzi和Fzo分别为内侧车轮和外侧车轮受到的垂向力。
轿车在弯坡路段行驶的横向摩擦系数为
| $ f_r=\frac{F_{y i}+F_{y o}}{F_{z i}+F_{z o}}=\frac{\frac{V^2}{R} \cos \delta-g \cos \alpha \sin \delta}{\frac{V^2}{R} \sin \delta+g \cos \alpha \cos \delta} $ | (7) |
由于公路的纵坡角和横坡角通常较小,因此sin δ≈e,sin α≈i,cos α≈1,cos δ≈1。e和i分别为超高和纵坡坡度,则fr简化为
| $ f_r=\frac{V^2-g R e}{V^2 e+g R} $ | (8) |
侧滑引起的轿车事故通常发生在湿滑路面,因此,选择湿滑路面的附着系数0.4作为路面提供的附着系数fp。则车辆即将发生侧滑的极限状态功能函数Z1为
| $ Z_1=f_p-f_r $ | (9) |
车辆在弯坡路段上行驶时,在离心力的作用下,弯道内侧和外侧车轮的垂向力逐渐发生转移,外侧车轮受到的垂向力逐渐增加,内侧车轮的垂向力逐渐减小。当内侧车轮的垂向力减至0时,车辆即将侧翻,此时车辆状态即为临界侧翻状态,以车辆的外侧车轮与路面接触点为力矩平衡点的力矩平衡公式为
| $ F_{z i} B+F_y^{\prime} h_g-\left|F_z^{\prime}\right|\left[\frac{B}{2}-\left(h_g-h_r\right) \varphi\right]=0 $ | (10) |
式中:hg为车辆的重心高度;B为轮距;φ为车辆侧倾角,φ=rφ·[V2/(gR)];rφ为侧倾率;hr为侧倾中心高度。
当内侧车轮即将抬起时,则有Fzi=0,将式(2)~ (4)代入式(10),并求解车辆即将翻车时所需的平曲线半径为
| $ R_D=R=f\left(V, \alpha, \delta, h_g, h_r, B, r_{\varphi}\right) $ | (11) |
假设RS为所研究的弯坡路段的设计半径,则轿车即将侧翻的极限状态功能函数Z2为
| $ Z_2=R_S-R_D $ | (12) |
停车视距是弯坡路段安全设计的重要指标,若路段的停车视距不足会增加该路段发生交通事故的可能性[26]。弯坡路段的停车视距指的是车辆行驶的过程中,从看到需要紧急制动的信号开始,到车辆完全停止结束车辆行驶过的最短距离[13]。车辆在弯坡路段行驶时,弯道内侧的路边障碍物(例如山体、高大的建筑物、树木等),以及纵断面的凸形变坡处会遮挡驾驶人视线,极易导致车辆发生事故。根据文献[5]弯坡路段驾驶人的可用视距LASD和所需视距LSSD分别为
| $ L_{\mathrm{ASD}}=2 R \times \cos ^{-1}\left(1-\frac{d}{R}\right) $ | (13) |
| $ L_{\mathrm{SSD}}=0.278 \mathrm{~V} \times t+\frac{0.039 V^2}{a+9.81 i} $ | (14) |
式中:a为制动减速度,m/s2;t为驾驶人的感知和制动反应时间,s;d为横净距,表示弯道内侧车道中心线至路边障碍物的距离,m。
则视距不足失效的极限状态功能函数公式Z3表示为
| $ \begin{aligned} {Z_3} =& {L_{{\rm{ASD}}}} - {L_{{\rm{SSD}}}} = 2R \times {\cos ^{ - 1}}\left( {1 - \frac{d}{R}} \right) - \\ & 0.278V \times t + \frac{{0.039{V^2}}}{{a + 9.81i}} \end{aligned} $ | (15) |
本文将功能函数中能反映行车过程中驾驶人不确定性输入(驾驶人的性别、年龄、驾驶熟练程度,以及不同驾驶人对公路线形、路面条件的反应等)的3个变量:车辆的运行车速、制动减速度、驾驶人的感知和制动反应时间视为随机变量,用于量化驾驶人的不确定输入。基于文献[26]不同轿车车型的设计参数(重心和侧倾中心高度、侧倾率、轮距)相差不大,且不受主观因素影响,因此,本文将其视为固定变量,固定变量hr/hg取值为0.5,rϕ取值为0.1,B/(2hg)为1。
驾驶人的感知和制动反应时间包括驾驶人的制动反应和执行制动两个时间,即驾驶人接到制动信号到车辆停止所用的时间。该时间受驾驶人的异质性、公路线形的复杂性等因素的影响。然而,公路设计规范将驾驶人的感知和制动反应时间视为定值[4-5]。依据学者们对该变量的研究,对数正态分布更适合描述该变量[14, 27],该变量的均值为1.5 s,标准差为0.4 s。
车辆的运行车速指的是车辆在特定路段长度的实际行驶车速,该车速受公路因素(公路线形、路面特征、路侧景观等)、驾驶人的特性(性别、年龄及心理预期等)、车辆状况等多重因素的影响。基于文献[28]对弯坡路段行驶的轿车车速的研究,弯坡路段的轿车车速符合正态分布,运行车速平均值V85[29]和标准差SD[3]分别为
| $ V_{85}=\left\{\begin{array}{l} 100.87-(2720.78 / R), -9 \% \leqslant i<0 \\ 106.30-(3595.29 / R), 0 \leqslant i<4 \% \\ 96.64-(2744.49 / R), 4 \% \leqslant i<9 \% \end{array}\right. $ | (16) |
| $ S_{\mathrm{D}}=0.14 \cdot V_{85} $ |
式中:V85为85分位的速度,km/h;R为平曲线半径,m;i为纵坡坡度。
制动减速度是指车辆在行驶过程中迅速降低车辆的行驶车速直到车辆停止的能力。制动减速度受路面条件、驾驶人的反应时间、车辆的性能等因素的影响。正态分布适合用于描述制动减速度[14],正态分布的均值为4.2 m/s2,标准差为0.6 m/s2。
1.5 多模式失效系统及概率求解根据式(1),第k个失效模式的极限状态功能函数Zk记为
| $ Z_k=f_k\left(u_1, u_2, \cdots u_c\right), k=1, 2, 3 $ | (17) |
式中k为极限状态功能函数的个数。
则第k种失效模式的失效概率为
| $ p_{f k}=\operatorname{Pr}\left(Z_k \leqslant 0\right) $ | (18) |
由于本文建立的极限状态功能函数的非线性程度较高,功能函数的导数不易求解,因此,单个失效模式失效概率的求解采用蒙特卡洛方法[30]。蒙特卡洛方法首先需要对极限状态功能函数Z=fk(U)中的随机变量进行随机抽样,通过抽样值计算功能函数值Z,若Z < 0,表示在模拟中事件失效一次。若模拟了N次,Z < 0出现了Nf次,那么,失效概率的估计值表示为
| $ \hat{p}_{f k}=\frac{N_f}{N} $ | (19) |
假设第k种失效模式发生的事件Ok表示为
| $ O_k=f_k(U) \leqslant 0, k=1, 2, 3 $ | (20) |
弯坡路段车辆发生的交通事故可能由一种失效模式引起,也可能由多种失效模式共同作用,因此交通事故的发生是系统失效。车辆在弯坡路段行驶时,以失效模式为研究对象,任意一种失效模式出现,公路交通事故均可能发生,因此,可将失效系统视为串联系统[14]。则多模式失效系统的失效事件O表示为
| $ O=O_1 \cup O_2 \cup O_3 $ | (21) |
失效系统的失效概率为
| $ \begin{gathered} p_f=\operatorname{Pr}\left(\bigcup\limits_{k=1}^3 Z_k \leqslant 0\right)=\operatorname{Pr}(O)=\sum\limits_{k=1}^3 \operatorname{Pr}\left(O_k\right)- \\ \sum\limits_{1 \leqslant l \leqslant m \leqslant 3} \operatorname{Pr}\left(O_l O_m\right)+\operatorname{Pr}\left(O_1 O_2 O_3\right) \end{gathered} $ | (22) |
由于失效系统的多模式失效概率的精确解不易求,需要寻求多模式失效概率的近似值。本文采用宽界限法求解失效系统的近似解[31]。
假定失效模式之间正相关,即失效事件Ol和Om的相关系数ρlm>0。意味着Pr(Ol|Om)≥Pr(Ol),第k个失效模式失效概率为prf=Pr(Ok)。宽界限法[30]得出系统的失效概率为
| $ \mathop {\max }\limits_{1 \le k \le 3} {p_{fk}} \le {p_f} \le 1 - \prod\limits_{k = 1}^3 {\left( {1 - {p_{fk}}} \right)} $ | (23) |
本文将两个临界平均值作为多模式系统的失效概率,即pf为
| $ {p_f} = \frac{{\mathop {\max }\limits_{1 \le k \le 3} {p_{fk}} + \left( {1 - \prod\limits_{k = 1}^3 {\left( {1 - {p_{fk}}} \right)} } \right)}}{2} $ | (24) |
为将多模式失效概率与车辆的事故建立联系,本文将多模式失效概率作为解释变量,同其他公路因素一并分别建立负二项模型、随机效应负二项模型、随机参数负二项模型,并将3个模型进行对比优选出最优模型,挖掘多模式失效概率与弯坡路段轿车单车事故的关系。
2.1 模型构建不同路段上事故的发生是随机的小概率事件且事故数的方差显著大于均值,根据事故的特点,负二项模型可用来描述不同路段上事故的分布,负二项模型的数学期望λi表示为
| $ \lambda_i=\exp \left(\beta X_i+\varepsilon_i\right) $ | (25) |
式中:ε为误差项,Xi为路段i的解释变量向量,β为预估参数向量。
路段i的概率函数为
| $ f\left( {{y_i}} \right) = \frac{{\mathit{\Gamma }\left( {{y_i} + \theta } \right)}}{{{y_i}\mathit{\Gamma }(\theta )}}{\left( {\frac{\theta }{{{\lambda _i} + \theta }}} \right)^\theta }{\left( {\frac{{{\lambda _i}}}{{{\lambda _i} + \theta }}} \right)^{{y_i}}} $ | (26) |
式中:Г(·)为gamma函数,θ为过离散系数。
为解释未观察到的异质性因素,Greene[33]开发了将随机参数纳入计数模型的估算程序,解释变量的参数在不同观测值之间变化,以解释可能存在的未观测到的异质性因素,随机参数负二项模型的参数为
| $ \beta_i=\beta+\omega_i $ | (27) |
式中ωi为随机分布误差项。
随机参数负二项模型的参数及相应的对数似然函数为
| $ \lambda_i \mid \omega_i=\exp \left(\beta_i X_i+\varepsilon_i\right) $ | (28) |
| $ LL = \sum\limits_{\forall i} {\ln } \int\limits_{{\omega _i}} {g\left( {{\omega _i}} \right)} P\left( {{y_i}\mid {\omega _i}} \right){\rm{d}}{\omega _i} $ | (29) |
式中g(·)为ωi的概率密度函数。
如果参数估计的标准偏差不为零,且显著,则该参数为随机参数,否则为固定参数。
由于需要对负二项式函数在随机参数分布上进行数值积分,因此,随机参数负二项模型的最大似然估计计算复杂。本文中参数的估计采用NLOGIT中的估计程序进行估计,随机参数的估计通过Halton序列随机抽样的方式估计[33]。若仅有截距项是随机的,则该模型被简化为随机效应负二项模型。
2.2 模型检验本文中事故预测模型的拟合优度的评估采用赤池信息准则(AIC)和麦克费登ρ2[24]两个拟合优度指标,AIC越小,ρ2越大越好。两个指标的表达式为
| $ A_{\mathrm{IC}}=-2 L L(\beta)+2 q $ | (30) |
| $ \rho^2=1-\frac{L L(\beta)}{L L(0)} $ | (31) |
式中:q为估计参数个数(包括截距项);LL(β)为模型的对数似然值;LL(0)为模型仅含有截距项时的对数似然值。
事故预测模型拟合的准确性采用平均绝对偏差(MD)和均方根误差(RE)两个指标。MD和RE越小越好,指标的表达式为
| $ M_{\mathrm{D}}=\frac{1}{n} \sum\limits_{i=1}^n\left|y_i-y_i^{\prime}\right| $ | (32) |
| $ R_{\mathrm{E}}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(y_i-y_i^{\prime}\right)^2} $ | (33) |
式中:yi为实际轿车单车事故数,yi′为第i个路段预测的轿车单车事故数,n为弯坡路段的个数。
2.3 弹性分析本文估计了各解释变量的弹性,用于估计各解释变量对因变量的影响程度[32]。弹性反映的是某一解释变量变化一定百分比(其他解释变量取均值),因变量变化的百分比,弹性分析公式为
| $ E_{x_{i j}}^{\lambda_i}=\frac{\partial \lambda_i}{\partial x_{i j}} \cdot \frac{x_{i j}}{\lambda_i} $ | (34) |
式中xij为第i个弯坡路段第j个解释变量的值。
连续解释变量的弹性为
| $ {E_j} = {\beta _j}{\bar x_j} $ | (35) |
式中:βj为第j个解释变量的预估参数,xj表示解释变量xj的平均值。
离散变量的弹性通过近似弹性进行估计[32],近似弹性的公式为
| $ E_j=\frac{\exp \left(\beta_j\right)-1}{\exp \left(\beta_j\right)} $ | (36) |
本文中的事故数据和公路数据来自美国公路安全信息系统。提取华盛顿州2006—2015年公路弯坡路段发生的交通事故数据及事故公路设计参数作为基础数据,根据半径一致性从基础数据中筛选出1 590段弯坡路段,随机选取1 431个路段(占总数据的9/10)用于事故预测模型的建立,其余159个路段(占总数据的1/10)用于模型检验。所研究时间间隔内,筛选路段共发生64 143起交通事故,其中单车事故21 221起,占总事故数的1/3,轿车单车事故12 224起,占单车事故的57.6%。因此,本文将占单车事故一半以上的轿车单车事故作为研究对象,提取发生事故的驾驶人、车辆、公路及环境数据。删除受酒精、药物、毒品、生病等显著人为因素所致的事故,筛选路段共发生轿车单车事故共10 241起。表 1为提取的弯坡坡路段的轿车单车事故数、交通情况、弯坡路段的设计参数、路面情况以及所建失效系统的多模式失效概率的连续变量的统计特征,表 2为离散变量的统计特征。
| 表 1 连续变量的统计特征 Tab. 1 Statistical characteristics of continuous variables |
| 表 2 离散变量的统计特征 Tab. 2 Statistical characteristics of discrete variables |
本文中随机效应/随机参数负二项模型中的随机项分别对正态分布和均匀分布两种分布类型进行了测试。两种分布中,正态分布的拟合优于均匀分布,该结果与之前的研究结果一致[23]。因此,模型的随机变量均为正态分布。
表 3为3个模型的连续变量估计结果,表 4为3个模型的离散变量估计结果。估计结果表明负二项模型中10个解释变量是显著的,随机效应负二项模型中11个解释变量是显著的。随机参数负二项模型中12个解释变量是显著的,除了截距项为随机项外,随机参数负二项模型仅鉴别出路段长度、年平均日交通量、车道数3个解释变量为随机变量,该结果可能的原因是部分随机变量已在多模式失效系统中被考虑。另外,随机参数负二项模型截距的估计系数的绝对值2.478小于随机效应负二项模型的估计系数的绝对值2.581,该结果可能的解释是部分随机效应由3个随机解释变量反映。表 5为3个模型的拟合优度和准确性对比。3个模型的拟合优度指标AIC表明随机参数负二项模型的AIC最小,ρ2最大,其次是随机效应负二项模型,负二项模型的AIC最大,ρ2最小,即两个指标均表明随机参数负二项模型优于随机效应负二项模型,随机效应负二项模型优于负二项模型。两个拟合准确性指标(MD和RE)表明,随机参数负二项模型的拟合准确性最高,其次是随机效应负二项模型,负二项模型的拟合准确性最低。综上,模型的拟合优度和准确性均显示随机参数负二项模型的拟合最好[23]。
| 表 3 轿车单车事故预测模型连续变量的估计结果和弹性 Tab. 3 Estimation results and elasticity of continuous variables of single-car crash prediction models |
| 表 4 轿车单车事故预测模型离散变量的估计结果和弹性 Tab. 4 Estimation results and elasticity of discrete variables of single-car crash prediction models |
| 表 5 模型拟合优度和准确性对比 Tab. 5 Comparison of goodness-of-fit and accuracy of models |
为使对比更清晰,如图 2所示本文仅画出前100个路段(按照路段序号选择)3个模型预测事故数与实际事故数对比。从图中可看出3个预测模型中负二项模型的预测值曲线(蓝色虚线)与实际事故数曲线(红色实线)重合度最低,随机效应负二项模型(绿色虚线)和随机参数负二项模型(黑色实线)预测值曲线与实际事故数曲线重合度较高。尤其事故高风险路段(事故数较大),随机效应/随机参数负二项模型明显优于负二项模型,该结果与之前的学者的研究结论一致[34]。另外,图 2表明随机参数负二项模型的预测值比随机效应负二项模型的预测值更接近实际事故值。因此,下文仅对随机参数负二项模型进行弹性分析,如表 3和表 4最后一列所示。

|
图 2 弯坡路段预测的轿车单车事故数与实际事故数的对比 Fig. 2 Comparison between the predicted number of single-car crashes and the actual number of crashes on combination sections of vertical and horizontal curves |
由于部分路段长度比较小,取对数后小于0(无意义),因此,本文将路段长度乘以10作为暴露变量。弹性分析显示,两个暴露变量对轿车单车事故数影响显著,年平均日交通量的弹性最大2.815,即对轿车单车事故数的影响最大,其次是路段长度0.535。除两个暴露变量外,多模式失效概率对轿车单车事故数影响最大,弹性为0.204,大于任一公路设计参数的弹性。
除上述3个解释变量(路段长度、年平均日交通、多模式失效概率)的弹性大于0.1外,仅有法定限速、车道数、车道宽度、路面类型4个解释变量对轿车单车事故影响显著且弹性大于0.1,其他解释变量的弹性均小于0.1。该结果可能的解释为系统的失效功能函数(多模式失效概率)中包含多个公路设计参数(例如弯道半径、纵坡、超高等),因此削弱了公路设计参数对轿车单车事故的影响。
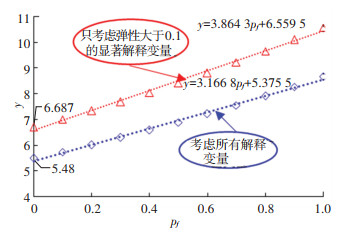
为进一步找出多模式失效概率与轿车单车事故之间的关系,假定最优模型(随机参数模型)中的连续解释变量为所研究路段相应解释变量的平均值,等级变量按照弹性选择不易发生事故的等级,例如路面类型的弹性为正值,则相较于其他路面,沥青路面更不易发生事故,因此选择沥青路面。此取值下轿车单车事故数y随多模式失效概率pf的变化如图 3中蓝色虚线所示。若只考虑弹性大于0.1的解释变量(解释变量取值同上)时,弯坡路段轿车单车事故数y随多模式失效概率pf变化如图 3中红色虚线所示。
|
图 3 轿车单车事故随多模式失效概率的变化 Fig. 3 Variation of single-car crashes with multi-mode failure probability |
虽然在随机效应负二项模型中多模式失效概率与轿车单车事故数为指数关系,但两条拟合曲线均接近直线,即随着多模式失效概率增加,轿车单车事故数近似线性增加,该结果与仅考虑一种失效模式的研究中失效概率与事故数呈指数不同[6]。考虑所有解释变量的拟合直线的斜率为3.166 8,只考虑弹性大于0.1的解释变量的拟合直线的斜率为3.864 3,两条拟合直线斜率相差较小,再次说明多模式失效概率影响了公路的平纵横设计参数对轿车单车事故数的影响(减弱)。另外,图 3表明多模式失效概率为0时,两个拟合直线的截距均不为0,轿车单车事故数分别为6.687和5.480,该值表明即使多模式失效概率为0,所研究路段也会发生事故。截距反映路段长度、年平均日交通量、公路限速及驾驶人-车辆-公路-环境(公路环境、气候环境)等因素之间的耦合对轿车单车事故的影响。
3.3 模型验证将用于模型验证的159个路段的解释变量输入随机参数负二项模型,获得的预测事故数和实际事故数决定系数R2仅为0.374。图 4预测事故数和实际事故数对比图,该图表明随机参数负二项模型对于高风险路段(事故数>20)的预测精度较低,风险相对低的路段(事故数≤20)的准确性较高。仅有风险相对低的路段,预测事故数和实际事故数决定系数R2为0.631。决定系数也表明风险相对较低路段准确性较高。另外,决定系数偏低的原因是由于本文仅研究公路相关因素对轿车单车事故数的影响,未考虑环境、驾驶人、车辆及耦合因素,因此,此验证用于说明公路因素对轿车单车事故的影响程度更有意义,若要将该模型用于事故预测还需考虑更多因素。

|
图 4 模型验证 Fig. 4 Model validation |
本文基于弯坡路段轿车可能的3种失效模式建立多模式失效系统,以华盛顿州10年公路弯坡路段的轿车单车事故数据为研究对象,建立考虑多模式失效概率的事故预测模型,将多模式失效概率与轿车单车事故建立联系,并挖掘两者的关系。
1) 本文所建的3个事故预测模型中,拟合优度和拟合准确性最好的为随机参数负二项模型,随机效应负二项模型次之,最后是负二项模型。
2) 随机参数负二项模型的弹性分析可看出,年平均日交通量对轿车单车的事故影响最大,其次是路段的长度,除该两个暴露变量,多模式失效概率对轿车单车事故影响最大。
3) 轿车单车事故数与多模式失效概率近似线性相关,但拟合曲线的截距不为0。
4) 当事故预测模型将多模式失效概率作为解释变量时,削弱了公路设计参数对轿车单车事故数的影响。
本文通过建立事故预测模型挖掘多模式失效概率与轿车单车事故数之间的关系,取得了显著成果,为可靠性分析应用于公路设计及事故预测提供了依据。由于基础数据的局限性,车辆事故与多模式失效概率之间的关系若用于国内公路还需进一步优化。
| [1] |
于海鹏. 山区高速公路弯坡路段车辆运行速度预测模型[J]. 交通科技, 2021(1): 94. YU Haipeng. Vehicle operating speed prediction model on curve and steep section of mountain expressway[J]. Transportation Science & Technology, 2021(1): 94. DOI:10.3963/j.issn.1671-7570.2021.01.021 |
| [2] |
张岩. 高速公路弯坡组合路段载重车最小安全行车间距研究[D]. 西安: 长安大学, 2019 ZHANG Yan. Study on the minimum trucks security following distances on curved slope combination freeway[D]. Xi'an: Chang'an University, 2019 |
| [3] |
陈富坚, 邓伟建, 徐培培, 等. 弯坡组合路段可靠性设计方法研究[J]. 公路工程, 2017, 42(3): 99. CHEN Fujian, DENG Weijian, XU Peipei, et al. Reliability design method for combination of vertical and horizontal curves[J]. Highway Engineering, 2017, 42(3): 99. |
| [4] |
公路工程技术标准: JTG B01—2014[S]. 北京: 人民交通出版社, 2015 Technical standard of highway engineering: JTG B01—2014[S]. Beijing: China Communications Press, 2015 |
| [5] |
Apolicy on geometric design of highways and streets[R]. Washington: American Association of State Highway and Transportation Officials, 2004
|
| [6] |
IBRABIM S E, SAYED T. Developing safety performance functions incorporating reliability based risk measures[J]. Accident Analysis and Prevention, 2011, 43(6): 2153. DOI:10.1016/j.aap.2011.06.006 |
| [7] |
IBRAHIM S E, SAYED T, ISMAIL K. Methodology for safety optimization of highway cross-sections for horizontal curves with restricted sight distance[J]. Accident Analysis and Prevention, 2012, 49: 476. DOI:10.1016/j.aap.2012.03.016 |
| [8] |
FAGHRI A, DEMETSKY M J. Reliability and risk assessment in the prediction of hazards at rail-highway grade crossing[J]. Transportation Research Record, 1988, 1160: 45. |
| [9] |
SARHAN M, HASSAN Y. Three-dimensional, probabilistic highway design: sight distance application[J]. Transportation Research Record Journal of the Transportation Research Board, 2008, 2060: 10. DOI:10.3141/2060-02 |
| [10] |
RICHL L, SAYED T. Evaluating the safety risk of narrow medians using reliability analysis[J]. Journal of Transportation Engineering, 2006, 132(5): 366. DOI:10.1061/(ASCE)0733-947X(2006)132:5(366) |
| [11] |
HUSSEIN M, SAYED T, ISMAIL K, et al. Calibrating road design guides using risk-based reliability analysis[J]. Journal of Transportation Engineering, 2014, 140(9): 1. DOI:10.1061/(ASCE)TE.1943-5436.0000694 |
| [12] |
陈富坚, 郭忠印, 陈富强, 等. 公路平曲线半径的可靠性设计[J]. 哈尔滨工业大学学报, 2012, 44(4): 100. CHEN Fujian, GUO Zhongyin, CHEN Fuqiang, et al. Reliability design method for horizontal curve radius of highway alignment[J]. Journal of Harbin Institute of Technology, 2012, 44(4): 100. |
| [13] |
YOU K, SUN L, GU W. Reliability-based risk analysis of roadway horizontal curves[J]. Journal of Transportation Engineering, 2012, 138(8): 1071. DOI:10.1061/(ASCE)TE.1943-5436.0000402 |
| [14] |
ESSA M, SAYED T, HUSSEIN M. Multimode reliability-based design of horizontal curves[J]. Accident Analysis and Prevention, 2016, 93: 124. DOI:10.1016/j.aap.2016.04.023 |
| [15] |
ALSALEH R, SAYED T, ISMAIL K, et al. Systemreliability as a surrogate measure of safety for horizontal curves: methodology and case studies[J]. Transportmetrica A: Transport Science, 2020, 16(3): 1. DOI:10.1080/23249935.2020.1720859 |
| [16] |
RUSLI R, HAQUE M M, AFGHARI A P, et al. Applying a random parameters Negative Binomial Lindley model to examine multi-vehicle crashes along rural mountainous highways in Malaysia[J]. Accident Analysis and Prevention, 2018, 119: 81. DOI:10.1016/j.aap.2018.07.006 |
| [17] |
MOOMEN M, REZAPOUR M, RAJA M, et al. Predicting downgrade crash frequency with the random-parameters negative binomial model: insights into the impacts of geometric variables on downgrade crashes in Wyoming[J]. IATSS Research, 2020, 44(2): 95. DOI:10.1016/j.iatssr.2019.09.002 |
| [18] |
YASMIN S, ELURU N, BHAT C R, et al. A latent segmentation based generalized ordered logit model to examine factors influencing driver injury severity[J]. Analytic Methods in Accident Research, 2014, 1: 23. DOI:10.1016/j.amar.2013.10.002 |
| [19] |
ELURU N, BAGHERI M, MIRANDA-MORENO L F, et al. A latent class modeling approach for identifying vehicle driver injury severity factors at highway-railway crossings[J]. Accident Analysis and Prevention, 2012, 47: 119. DOI:10.1016/j.aap.2012.01.027 |
| [20] |
MALYSHKINA N V, MANNERING F L. Zero-state Markov switching count-data models: an empirical assessment[J]. Accident Analysis and Prevention, 2010, 42(1): 122. DOI:10.1016/j.aap.2009.07.012 |
| [21] |
GUO Y, LI Z, LIU P, et al. Modeling correlation and heterogeneity in crash rates by collision types using full Bayesian random parameters multivariate Tobit model[J]. Accident Analysis and Prevention, 2019, 128: 164. DOI:10.1016/j.aap.2019.04.013 |
| [22] |
HOU Q, HUO X, LENGA J. A correlated random parameters tobit model to analyze the safety effects and temporal instability of factors affecting crash rates[J]. Accident Analysis and Prevention, 2020, 134: 4. DOI:10.1016/j.aap.2019.105326 |
| [23] |
HOU Q, TARKO A P, MENG X. Investigating factors of crash frequency with random effects and random parameters models: new insights from Chinese freeway study[J]. Accident Analysis and Prevention, 2018, 120: 5. DOI:10.1016/j.aap.2018.07.010 |
| [24] |
MA Z, ZHANG H, CHIEN S I, et al. Predicting expressway crash frequency using a random effect negative binomial model: a case study in China[J]. Accident Analysis and Prevention, 2017, 98: 220. DOI:10.1016/j.aap.2016.10.012 |
| [25] |
YAN Y, ZHANG Y, YANG X, et al. Crash prediction based on random effect negative binomial model considering data heterogeneity[J]. Physica A: Statistical Mechanics and its Applications, 2020, 547: 1. DOI:10.1016/j.physa.2019.123858 |
| [26] |
游克思. 基于车辆动力学和可靠性理论的道路安全分析及优化设计研究[D]. 南京: 东南大学, 2012 YOU Kesi. Vehicle dynamic and reliability based highway safety analysis and design optimization[D]. Nanjing: Southeast University, 2012 |
| [27] |
LERNER N. Age anddriver perception-reaction time for sight distance design requirements[C]// Institute of Transportation Engineers 65th Annual Meeting. Washington: Transportation Research Board, 1995: 626
|
| [28] |
MALAGHAN V, PAWAR D S, DIA H. Modeling operating speed using continuous speed profiles on two-lane rural highways in India[J]. Journal of Transportation Engineering Part A: Systems, 2020, 146(11): 9. DOI:10.1061/JTEPBS.0000447 |
| [29] |
FITZPATRICK K, ELEFTERIADOU L, HARWOOD D W, et al. Speed prediction for two-lane rural highways[R]. Washington: Transportation Research Board, 2000: 217
|
| [30] |
张明. 结构可靠度分析—方法与程序[M]. 北京: 科学出版社, 2009: 131. ZHANG Ming. Structural reliability analysis—Methods and procedures[M]. Beijing: Science Press, 2009: 131. |
| [31] |
张晶. 结构体系失效概率计算方法研究[D]. 大连: 大连理工大学, 2010 ZHANG Jing. Study on the computation methods of structural system failure probability[D]. Dalian: Dalian University of Technology, 2010 |
| [32] |
WASHINGTON S P, KARLAFTIS M G, MANNERING F. Statistical andeconometric methods for transportation data analysis[M]. New York: CRC Press, 2010.
|
| [33] |
GREENE W H. LIMDEP Version 11: econometric modeling guide[M]. Weaverton: Econometric Software Inc., 2016.
|
| [34] |
ZHANG C, HE J, KING M, et al. A crash risk identification method for freeway segments with horizontal curvature based on real-time vehicle kinetic response[J]. Accident Analysis and Prevention, 2021, 150: 8. DOI:10.1016/j.aap.2020.105911 |
 2023, Vol. 55
2023, Vol. 55


