2. 浙江交工集团股份有限公司,杭州 310051
2. Zhejiang Communications Construction Group Co., Ltd., Hangzhou 310051, China
自密实混凝土作为一种准脆性多孔建筑材料,其特点是能够在没有外部机械振捣的情况下达到密实效果[1]。与普通混凝土相比,自密实混凝土具有节能、经济、环保三大优点,已广泛应用于桥面、桥墩、近海结构、铁路轨枕、机场及公路路面等许多混凝土结构中。然而,这些混凝土结构在服役过程中更容易受弯曲疲劳荷载而非静荷载作用[2-3],这会导致其力学性能下降甚至疲劳失效或断裂。疲劳作用是在混凝土使用寿命内由循环荷载引起的一种渐进的、局部的及不可逆的损伤过程[4],对混凝土结构的安全运行起到了决定性作用,因此受到国内外学者的广泛关注。文献[5]认为混凝土结构在承受重复荷载作用时会发生低于静载强度的脆性破坏。文献[6]通过弯曲疲劳试验,得出混凝土的弯曲疲劳寿命符合Weibull分布。文献[7]通过研究弯曲疲劳试验得到的S-N曲线发现,自密实混凝土的疲劳性能优于普通混凝土。
此外,在中国北方寒冷地区,这些混凝土结构不但会受到疲劳荷载,还往往经受冻融损伤作用。冰的离析及由于孔隙水结冰体积膨胀9%左右而产生的孔隙水压力被认为是混凝土冻融破坏的基本原因[8],并且文献[9]和文献[10]研究得出自密实混凝土的抗冻融能力强于普通混凝土。冻融作用下混凝土的损伤过程可以描述为复杂的裂纹扩展过程[11-12],包括不可恢复的拉应变和不断萌生的微裂纹[13],从而导致混凝土的物理劣化。这种劣化造成的累积损伤会造成混凝土表面结垢、开裂及水泥基质脱落等现象[14],这在一定程度上影响了混凝土结构在承受外部疲劳荷载时的疲劳寿命。因此,研究冻融循环和疲劳荷载联合作用对混凝土结构疲劳寿命的影响意义重大。然而,由于两者的联合试验数据离散型大、机理分析较复杂,导致国内外鲜有对经受冻融损伤混凝土在疲劳荷载作用下的疲劳寿命分布规律、疲劳寿命预测模型及疲劳寿命可靠性概率的相关研究报道。
针对上述问题,本文对经受不同冻融循环后的自密实混凝土试块进行了不同应力水平下的四点弯曲试验,并利用Weibull分布概率模型对混凝土试块的弯曲疲劳寿命分布规律进行分析,建立经受不同冻融循环后的混凝土试块在不同可靠性概率下的疲劳寿命预测模型,为实际混凝土结构的设计和维修评估提供理论支撑。
1 试验 1.1 试样制备浇筑自密实混凝土试块所使用的原料包括:1)马鞍山海螺水泥厂生产的P·O 42.5级普通硅酸盐水泥,碱含量不大于0.60%,密度为3 150 kg/m3;2)粗骨料为破碎石灰石,粒径采用5~19 mm连续级配,细骨料为河砂,其各项物理性能指标见表 1;3)硅灰和Ⅰ级粉煤灰;4)南京瑞迪材料有限公司生产的聚羧酸高效减水剂,含固量为30%,减水率为35%。自密实混凝土中水泥、水、粉煤灰、硅灰、粗骨料、细骨料、减水剂的配合比为385∶200∶139∶26∶800∶1 018∶7.5。其中试验采用的水灰比为0.519,自密实混凝土的塌落扩展度为705 mm,J环扩展度为690 mm。随后,利用塑料试模浇筑成型尺寸为400 mm×100 mm×100 mm的自密实混凝土试块。所有混凝土试块在浇筑24 h后脱模,然后在20 ℃±2 ℃、RH>90%的标准养护室中养护28 d后进行相关试验。
| 表 1 骨料的物理性能参数 Tab. 1 Physical property parameters of aggregates |
根据GB/T 50082—2009《普通混凝土长期性能和耐久性能试验方法标准》[15],浇筑成型的自密实混凝土试块被分为5组,分别进行冻融循环次数F为0、50、100、150、200和250次的快速冻融试验,中心温度控制在-20~7 ℃之间,一次冻融循环历时4 h。经过一定的冻融循环后,将混凝土试块从快速冻融箱中取出,拭去表面的水分,然后依次测量其质量和动态弹性模量,并利用式(1)和式(2)分别计算相对质量损失和归一化动态弹性模量:
| $ \Delta m_F=\frac{m_0-m_F}{m_0} \times 100 \% $ | (1) |
式中:m0为混凝土试块冻融前的质量,g;mF为混凝土试块经受F次冻融循环后的质量,g。
| $ \Delta E_F=\frac{E_F}{E_0} $ | (2) |
式中:E0为混凝土试块冻融前的动态弹性模量,GPa;EF为混凝土试块经受F次冻融循环后的动态弹性模量,GPa。
1.3 四点弯曲静态及疲劳试验为了确定疲劳试验的最小和最大应力,每组选取3个混凝土试块在MTS试验机上进行四点弯曲静态试验,以获得经受不同冻融循环后混凝土试块的静态弯曲强度(fr)。试验通过荷载控制,加载跨度和加载速率分别为300 mm和100 N/s,如图 1所示。其中,经受不同冻融循环后混凝土试块的平均静态弯曲强度见表 2。

|
图 1 四点弯曲试验装置 Fig. 1 Four-point flexural test setup |
| 表 2 经受不同冻融循环后混凝土试块的四点弯曲强度 Tab. 2 Four-point flexural strength of concrete beams subjected to different FT cycles |
随后,将经受不同冻融循环后的混凝土试块进行四点弯曲疲劳试验,疲劳测试在不同的应力水平S(S=fmax/fr,fmax为最大疲劳应力,fr为静态弯曲强度)下进行,其中应力水平分别设置为0.75、0.80和0.85三种。值得注意的是,在相同应力水平下,经受冻融次数较多的自密实混凝土试块对应的最大疲劳荷载比经受冻融次数较少的要低。为了在可接受的时间范围内完成各个自密实混凝土试块的疲劳试验,试验都采用等幅加载,其中加载频率和应力比Q(Q=fmin/fmax,fmin和fmax分别为最小和最大疲劳应力)分别设置为2 Hz和0.1。试验中把自密实混凝土试块从开始加载到完全破坏的循环次数记为疲劳寿命N。其中受冻自密实混凝土试块在疲劳荷载作用下的典型应力-应变曲线如图 2所示。由于疲劳试验是一个耗时的加载过程,所以本文把200万次疲劳寿命作为试验上限,即当自密实混凝土试块完全破坏或者N达到设定的试验上限,无论哪个条件先满足,疲劳试验即终止。
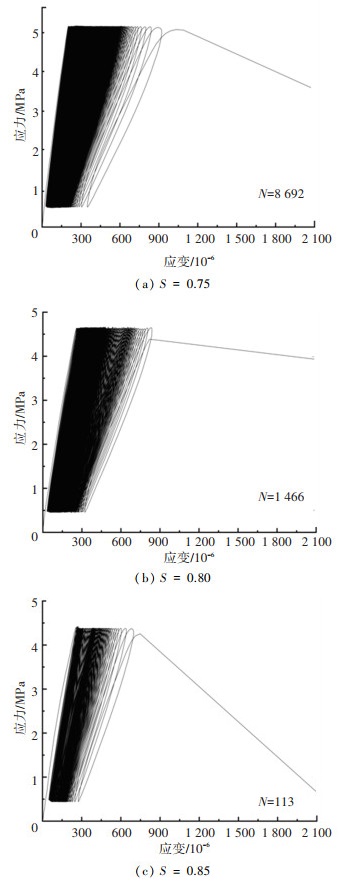
|
图 2 经受150次冻融循环后自密实混凝土典型的应力-应变曲线 Fig. 2 Typical stress-strain curves of self-compacting concrete subjected to 150 FT cycles |
为了定量表征冻融循环对自密实混凝土的损伤程度,利用式(1)和式(2)确定了经受不同冻融损伤后混凝土试块的相对质量损失和归一化动态弹性模量,如图 3所示。
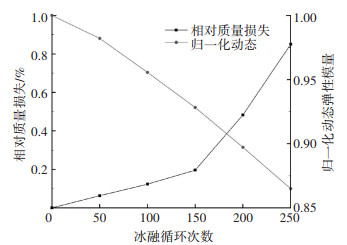
|
图 3 相对质量损失和归一化动态弹性模量随冻融循环次数的变化趋势 Fig. 3 Variation of relative mass loss and normalized dynamic elastic modulus with FT cycles |
由图 3可知,相对质量损失随冻融循环次数的增加,呈现出两阶段特征[16-17]:在前150次冻融循环中,混凝土的质量损失较缓慢,低于初始质量的0.2%;而在150次冻融循环之后,质量损失明显加快,表面结垢严重。这主要是由于混凝土内部的孔隙水在结冰和融化过程中,会对多孔骨架产生明显的疲劳损伤[18]。并且这种内部损伤会随着冻融循环次数的增加而累积,当达到一定的冻融循环后,混凝土表面发生大量的层状脱落,致使质量损失急剧增加[19]。与此同时,动态弹性模量也随着冻融循环次数的增加而下降,而其与混凝土的完整性有关。当混凝土内部微裂纹数量增加时,声波通过这些微裂缝会发生反射、折射、衍射、散射等作用,致使测量的动弹性模量减少。所以动态弹性模量随冻融循环次数的增加而下降,间接证明了混凝土内部微裂纹的萌生。此外,当冻融循环次数达到250次时,自密实混凝土的归一化动态弹性模量仅下降了0.14;对于普通混凝土[20],仅100次冻融循环后,归一化动态弹性模量就已经下降了0.38,这表明本文浇筑的自密实混凝土比普通混凝土具有更强的抗冻性。
3 弯曲疲劳寿命分布拟合经受不同冻融循环后自密实混凝土试块的弯曲疲劳寿命见表 3。由表 3可知,在相同应力水平下混凝土试块的疲劳寿命随冻融循环次数的增加而减小,这是由于冻融损伤破坏了混凝土的内部结构,使混凝土试块抵抗弯曲疲劳荷载的能力下降。而当冻融损伤一定时,混凝土试块的疲劳寿命随应力水平的增加而迅速减小。由以上分析可知,混凝土试块的抗疲劳性能受冻融损伤和应力水平的共同影响。
| 表 3 受冻自密实混凝土的弯曲疲劳寿命试验结果 Tab. 3 Test results of flexural fatigue life of self-compacting concrete subjected to FT damage |
作为一种非均质材料,即使最大化地控制试验条件,混凝土的疲劳寿命在试验中也会表现出较大的离散性,与此同时,冻融损伤加剧了这种离散性。因此,在评估经受冻融循环后混凝土试块的抗疲劳能力时需引入一种概率分布方法来变相表征自密实混凝土的疲劳寿命分布。而Weibull分布是一种基于令人信服的定量分析方法,已被证实可用于准确分析混凝土的疲劳破坏[21]。素混凝土和橡胶自密实混凝土的疲劳寿命分布已经被之前的文献论证近似符合两参数Weibull分布[22-24],所以本文利用两参数Weibull分布建立冻融作用下自密实混凝土疲劳寿命的离散分布模型。
Weibull分布的累积分布函数FR(n)可表示为下述形式[22-23, 25]:
| $ F_R(n)=1-\exp \left[-\left(\frac{n-n_0}{u-u_0}\right)^\alpha\right] $ | (3) |
式中:n为随机变量N的具体值;α和u分别为Weibull分布的形状参数和标度参数;n0为位置参数或最小疲劳寿命参数;u0为标度参数的最小值。
令1-FR(n)得到的函数定义为生存函数LR(n),其表达式为
| $ L_R(n)=\exp \left[-\left(\frac{n-n_0}{u-u_0}\right)^\alpha\right] $ | (4) |
假设某一应力水平下混凝土试块的最小疲劳寿命n0=0,则上式可简化为
| $ L_R(n)=\exp \left[-\left(\frac{n}{u}\right)^\alpha\right] $ | (5) |
矩分析法是基于样本的矩量(例如,样本期望和样本方差)来估计受冻自密实混凝土的Weibull分布两参数。其中Weibull分布的矩量表达式[23, 26-28]可以写为
| $ E(n)=u T\left(\frac{1}{\alpha}+1\right) $ | (6) |
| $ E\left(n^2\right)=u^2 T\left(\frac{2}{\alpha}+1\right) $ | (7) |
式中:E(·)为样本的期望;T(·)为伽马函数。其中上式中的E(n)为某一应力水平下试块疲劳寿命的平均值,即μ= E(n),而某一应力水平下试块疲劳寿命的方差σ2= E(n2)-E2(n)= E(n2)-μ2。
把式(6)和式(7)联立计算可得
| $ \frac{\sigma}{\mu}=\frac{T\left(\frac{2}{\alpha}+1\right)}{T\left(\frac{1}{\alpha}+1\right)}-1 $ | (8) |
式中:σ/μ定义为自密实混凝土疲劳寿命的变异系数,记为CoV,其中σ为样本的标准偏差。之前的研究利用以上公式给出了求解Weibull分布两参数(形状参数α和标度参数u)的简捷表达式[26-27]:
| $ \alpha=(\mathrm{CoV})^{-1.08} $ | (9) |
| $ u=\frac{\mu}{T\left(\frac{1}{\alpha}+1\right)} $ | (10) |
本文通过式(9)和式(10)分别得到经受不同冻融损伤后的自密实混凝土在不同应力水平下疲劳寿命的Weibull分布两参数(形状参数α和标度参数u)见表 4。而形状参数α的相对大小是衡量混凝土疲劳寿命分布离散性的标尺,也就是说,形状参数相对较大表明对应的疲劳寿命分布离散性相对较小,反之亦然。由表 4可知,对于自密实混凝土而言,其疲劳寿命的离散性随F的增加而增大,随S的增大而减小。
| 表 4 经受不同冻融循环后自密实混凝土在不同应力水平下的弯曲疲劳寿命Weibull分布参数估计值 Tab. 4 Estimation of Weibull distribution parameters for flexural fatigue life of self-compacting concrete subjected to different FT cycles at different stress levels |
为了进一步证实经受冻融循环后自密实混凝土疲劳寿命的概率分布可以用两参数Weibull分布表征,本文利用Kolmogorov-Smirnov(K-S)检验方法对经受冻融循环后的自密实混凝土在不同应力水平下的疲劳数据概率分布进行了拟合优度检验[29-30]。其中,拟合优度检验可通过式(11)实现。
| $ {D_1} = \mathop {\max }\limits_{0 \le i \le k} \left| {{F^*}\left( {{x_i}} \right) - P\left( {{x_i}} \right)} \right| $ | (11) |
式中:F*(xi)=i/k为累积直方图,i为试验序列号,k为某一应力水平下总的试验次数,P(xi)为假设累积分布函数,通过式(12)求得。
| $ P\left(x_i\right)=1-\exp \left(-\frac{x_i{ }^\alpha}{u^\alpha}\right) $ | (12) |
表 5给出了未经受冻融损伤的自密实混凝土在应力水平S=0.75下拟合优度检验的计算过程。从计算结果可知,|F*(xi)-P(xi)|的最大差值为0.386 427,记为D1=0.386 427。在该条件下的试验总次数k = 3,则通过查询K-S临界值表[29]可得在5%显著性水平下的判断值DC= 0.707 60。因为D1<DC,所以未受冻自密实混凝土在S=0.75下的拟合度是可以接受的。采用上述检验方法,对经受不同冻融循环后的自密实混凝土在不同应力水平下进行了拟合优度检验见表 6。检验结果表明,在5%显著性水平下拟合度都是可以接受的,这说明采用矩估计法确定的弯曲疲劳寿命Weibull分布双参数,能够满足经受冻融循环后的自密实混凝土在不同应力水平下疲劳寿命分布函数计算的需要。
| 表 5 未受冻自密实混凝土在S =0.75下疲劳寿命的K-S检验 Tab. 5 K-S test for fatigue life of self-compacting concrete without FT cycles at S=0.75 |
| 表 6 经受不同冻融循环后自密实混凝土在不同应力水平下的拟合优度检验参数D1 Tab. 6 Goodness-of-fit test parameter (D1) of self-compacting concrete subjected to different FT cycles at different stress levels |
早期的研究者在研究自密实混凝土的S-N曲线时很少考虑可靠性概率Pf对混凝土疲劳寿命的影响,而在混凝土结构的设计阶段,需要选用不同Pf对应的N,因此需要确定具有不同Pf对应的N与强度之间的关系,即Pf-S-N曲线。由于上文已经证明经受冻融循环后自密实混凝土的疲劳寿命遵循两参数Weibull分布,所以本节利用该规律计算不同可靠性概率下的疲劳寿命。其中,生存函数为
| $ L_R=1-P_f $ | (13) |
根据式(5)和式(13)可得具有不同可靠性概率下疲劳寿命的表达式为
| $ N_{P_f}=u\left(\ln \frac{1}{P_f}\right)^{\frac{1}{\alpha}} $ | (14) |
式中NPf为在可靠性概率Pf下混凝土的疲劳寿命。
由式(10)可知,具有不同可靠性概率的疲劳寿命与其数学期望有关,则式(14)可改写为
| $ N_{P_f}=\frac{\mu}{T\left(\frac{1}{\alpha}+1\right)}\left(\ln \frac{1}{P_f}\right)^{\frac{1}{\alpha}} $ | (15) |
因此,利用上文所得受冻自密实混凝土的疲劳寿命Weibull分布两参数(形状参数α和标度参数u),可计算不同可靠性概率Pf(Pf=0.10、0.30、0.50、0.70、0.90和0.95)对应的弯曲疲劳寿命。自密实混凝土的疲劳寿命随冻融循环次数的增加及应力水平和可靠性概率的增大而减少,这一现象与材料的物理特性相吻合。此外,在相同应力水平下,弯曲疲劳寿命的Pf随F的增加而降低,这表明受冻越严重的自密实混凝土,Pf越低。并且由曲线的下降趋势可知,N的离散性随F的增加而增大,随S的增大而减小,这一规律与上文Weibull分布两参数的变化趋势一致。
为了定量表征冻融循环次数、应力水平及疲劳寿命对可靠性概率的影响,利用指数函数拟合了它们之间的相关关系,如图 4所示。其中,拟合公式为
| $ P_f=\frac{a}{1+\exp [-k(N-b)]} $ | (16) |

|
图 4 经受不同冻融循环的自密实混凝土在不同应力水平下疲劳寿命次数与可靠性概率的关系 Fig. 4 Relationship between fatigue life and reliability probability of self-compacting concrete subjected to different FT cycles at different stress levels |
式中:a、b和k为与冻融循环次数和应力水平相关的系数常量,如表 7所示。
| 表 7 经受不同冻融循环后自密实混凝土在不同应力水平下的系数常量 Tab. 7 Coefficient constants of self-compacting concrete subjected to different FT cycles at different stress levels |
由拟合分析可知,所有工况的拟合度都大于0.95,标准差基本都控制在小于0.10,说明拟合公式(16)可以较准确地表征冻融循环次数、应力水平及疲劳寿命对可靠性概率的影响,且精度较高,这对于实际混凝土结构受冻融循环和疲劳荷载联合作用时疲劳寿命的预测具有指导意义。
为了更加直观地表征冻融循环F、可靠性概率Pf 、应力水平S和疲劳寿命N四者之间的关系,对一定可靠性概率的疲劳寿命计算值进行回归分析,可得经受不同冻融循环后的混凝土在不同可靠性概率下的疲劳寿命方程,以此获得自密实混凝土的Pf-S-N曲线簇,如图 5所示。由图 5可知,在一定的冻融循环和应力水平下,随可靠性概率的增大,自密实混凝土的疲劳寿命成倍减小;同样地,在一定的疲劳寿命下,随可靠性概率的增大,自密实混凝土所能承受的耐久性强度(应力水平S)也逐渐减小。以10 000次疲劳寿命为例,对于未经受冻融损伤的自密实混凝土,Pf=0.10和0.95对应的耐久性强度分别为静态弯曲强度的78%和74%,如图 5(a)所示;而对于经受250次冻融循环后的自密实混凝土,Pf=0.10和0.95对应的耐久性强度分别为静态弯曲强度的76%和71%,分别下降了2.56%和4.05%,如图 5(f)所示。这表明冻融损伤显著降低了自密实混凝土抵抗疲劳变形的能力。因此,在实际工程中,选择合适的结构可靠性概率,对准确预测其抗疲劳性能具有重要作用[31-32]。通过确定冻融循环、可靠性概率和应力水平,即可利用上述确定的疲劳寿命方程确定经受不同冻融循环后自密实混凝土的疲劳寿命。

|
图 5 经受不同冻融循环后自密实混凝土的Pf-S-N关系图 Fig. 5 Pf-S-N curves of self-compacting concrete subjected to different FT cycles |
此外,根据式(15)和疲劳寿命期望E(n)的关系,等式可变形为
| $ N_{P_f}=\frac{\mu\left(\ln \frac{1}{P_f}\right)^{\frac{1}{\alpha}}}{T\left(\frac{1}{\alpha}+1\right)} $ | (17) |
令
| $ \gamma_{P_f}=\frac{T\left(\frac{1}{\alpha}+1\right)}{\left(\ln \frac{1}{P_f}\right)^{\frac{1}{\alpha}}} $ | (18) |
则上式可表示为
| $ N_{P_f}=\frac{\mu}{\gamma_{P_f}} $ | (19) |
式中γPf定义为具有可靠性概率Pf的混凝土疲劳寿命安全系数。
对经受不同冻融循环后的自密实混凝土设计疲劳寿命,利用式(19)可得不同可靠性概率下混凝土的疲劳寿命安全系数,如表 8~10所示。由表可知,对于相同的可靠性概率水平,自密实混凝土的疲劳寿命所需的安全系数随冻融循环次数的增加而不断增大,这表明对经受冻融损伤较严重的自密实混凝土,其弯曲疲劳寿命必须采用较大的安全系数才能保证结构的安全运行。因此,在进行弯曲疲劳寿命设计时,对可能遭受较严重冻融损伤的自密实混凝土构件,应适当增加其疲劳寿命的安全系数,才能满足结构安全要求。本文确定的自密实混凝土的弯曲疲劳寿命安全系数可为中国北方受冻地区的实际混凝土工程提供技术参考。
| 表 8 经受不同冻融循环的自密实混凝土在S =0.75下具有不同可靠性概率的疲劳寿命安全系数 Tab. 8 Safety factors of fatigue life with different reliability probabilities for self-compacting concrete subjected to different FT cycles at S=0.75 |
| 表 9 经受不同冻融循环的自密实混凝土在S =0.80下具有不同可靠性概率的疲劳寿命安全系数 Tab. 9 Safety factors of fatigue life with different reliability probabilities for self-compacting concrete subjected to different FT cycles at S=0.80 |
| 表 10 经受不同冻融循环的自密实混凝土在S =0.85下具有不同可靠性概率的疲劳寿命安全系数 Tab. 10 Safety factors of fatigue life with different reliability probabilities for self-compacting concrete subjected to different FT cycles at S=0.85 |
1) 冻融损伤破坏了混凝土的内部结构,产生了大量的微裂缝,表面出现层状剥落现象,致使自密实混凝土试块的质量、动态弹性模量、四点弯曲强度及疲劳寿命都随冻融循环次数的增加而急剧减少。
2) 通过K-S拟合优度检验证明,经受不同冻融循环后的自密实混凝土在不同应力水平下疲劳寿命的概率分布可用两参数Weibull分布表征,并利用矩估计法获得了不同工况下混凝土试块的弯曲疲劳寿命Weibull分布参数。结果表明,自密实混凝土疲劳寿命的离散性随冻融次数的增加而增大,随应力水平的增大而减小。
3) 通过对疲劳寿命计算值进行回归分析,得到了经受不同冻融循环的自密实混凝土在不同可靠性概率下的疲劳寿命方程。通过确定冻融循环F、可靠性概率Pf和应力水平S,即可利用疲劳寿命方程确定经受不同冻融循环后自密实混凝土的疲劳寿命N。
4) 对于相同的可靠性概率水平,自密实混凝土的疲劳寿命所需的安全系数随冻融循环次数的增加而不断增大,这表明对经受冻融损伤较严重的自密实混凝土,其弯曲疲劳寿命必须采用较大的安全系数才能保证结构的安全运行。本文确定的自密实混凝土的弯曲疲劳寿命安全系数可为寒冷地区的实际混凝土结构提供技术支撑。
| [1] |
YEHIA S, DOUBA A E, ABDULLAHI O, et al. Mechanical and durability evaluation of fiber-reinforced self-compacting concrete[J]. Construction and Building Materials, 2016, 121: 120. DOI:10.1016/j.conbuildmat.2016.05.127 |
| [2] |
季文玉, 王珏, 李旺旺. 预应力RPC-NC叠合梁弯曲疲劳性能试验分析[J]. 哈尔滨工业大学学报, 2019, 51(6): 64. JI Wenyu, WANG Jue, LI Wangwang. Experimental analysis on bending fatigue performance of prestressed RPC-NC composite beam[J]. Journal of Harbin Institute of Technology, 2019, 51(6): 64. |
| [3] |
DING Z, FENG D C, REN X, et al. Physically based constitutive modeling of concrete fatigue and practical numerical method for cyclic loading simulation[J]. Engineering Failure Analysis, 2019, 101: 230. DOI:10.1016/j.engfailanal.2019.03.020 |
| [4] |
FATHIMA K M P, KISHEN J M C. A thermodynamic framework for the evolution of damage in concrete under fatigue[J]. Archive of Applied Mechanics, 2015, 85(7): 921. DOI:10.1007/s00419-015-1001-z |
| [5] |
游帆, 念梦飞, 郑建岚, 等. 再生骨料混凝土弯曲疲劳性能研究[J]. 建筑结构学报, 2022, 43(4): 134. YOU Fan, NIAN Mengfei, ZHENG Jianlan, et al. Study on flexural fatigue performance of recycled aggregate concrete[J]. Journal of Building Structures, 2022, 43(4): 134. |
| [6] |
李北星, 尹立愿, 樊立龙. 机制砂混凝土抗弯曲疲劳性能研究[J]. 建筑材料学报, 2017, 20(5): 801. LI Beixing, YIN Liyuan, FAN Lilong. Analysis on flexural fatigue performance of manufactured sand concrete[J]. Journal of Building Materials, 2017, 20(5): 801. |
| [7] |
GOEL S, SINGH S P. Fatigue performance of plain and steel fibre reinforced self compacting concrete using S-N relationship[J]. Engineering Structures, 2014, 74: 65. DOI:10.1016/j.engstruct.2014.05.010 |
| [8] |
曹万林, 赵羽习, 叶涛萍. 再生混凝土结构长期工作性能研究进展[J]. 哈尔滨工业大学学报, 2019, 51(6): 1. CAO Wanlin, ZHAO Yuxi, YE Taoping. A review of recent advances in the long-term working characteristic of recycled concrete structure[J]. Journal of Harbin Institute of Technology, 2019, 51(6): 1. |
| [9] |
龙广成, 刘赫, 马昆林, 等. 考虑冻融作用的混凝土单轴压缩损伤本构模型[J]. 中南大学学报(自然科学版), 2018, 49(8): 1884. LONG Guangcheng, LIU He, MA Kunlin, et al. Uniaxial compression damage constitutive model of concrete subjected to freezing and thawing[J]. Journal of Central South University (Science and Technology), 2018, 49(8): 1884. |
| [10] |
贺成林, 韩风霞, 刘清, 等. 冻融作用下自密实混凝土梁抗弯力学性能研究[J]. 中国科技论文, 2020, 15(10): 1157. HE Chenglin, HAN Fengxia, LIU Qing, et al. Study on the flexural mechanical properties of self-compacting concrete beams under the action of freeze-thaw[J]. China Sciencepaper, 2020, 15(10): 1157. |
| [11] |
ZOU D, WANG Z, SHEN M, et al. Improvement in freeze-thaw durability of recycled aggregate permeable concrete with silane modification[J]. Construction and Building Materials, 2021, 268: 121097. DOI:10.1016/j.conbuildmat.2020.121097 |
| [12] |
金浏, 张仁波, 杜修力, 等. 温度对混凝土结构力学性能影响的研究进展[J]. 土木工程学报, 2021, 54(3): 1. JIN Liu, ZHANG Renbo, DU Xiuli, et al. Research progress on the influence of temperature on the mechanical performance of concrete structures[J]. China Civil Engineering Journal, 2021, 54(3): 1. |
| [13] |
ŠELIH J. Performance of concrete exposed to freezing and thawing in different saline environments[J]. Journal of Civil Engineering and Management, 2010, 16(2): 306. |
| [14] |
ERIKSSON D, WAHLBOM D, MALM R, et al. Hygro-thermo-mechanical modeling of partially saturated air-entrained concrete containing dissolved salt and exposed to freeze-thaw cycles[J]. Cement and Concrete Research, 2021, 141: 106314. |
| [15] |
中华人民共和国住房和城乡建设部. 普通混凝土长期性能和耐久性能试验方法标准: GB/T 50082—2009[S]. 北京: 中国建筑工业出版社, 2009 Ministry of Housing and Urban-Rural Development of thePeople's Republic of China. Standard for test methods of long-term performance and durability of ordinary concrete: GB/T 50082—2009[S]. Beijing: China Building Industry Press, 2009 |
| [16] |
GARCIA-GIMENEZ R, FRIAS M, ARRIBAS I, et al. Freeze-thaw effect on the durability of binary cements containing activated coal-mining waste[J]. Construction and Building Materials, 2018, 190: 140. |
| [17] |
WANG Y, LIU Z, FU K, et al. Experimental studies on the chloride ion permeability of concrete considering the effect of freeze-thaw damage[J]. Construction and Building Materials, 2020, 236: 117556. |
| [18] |
GONG F, SICAT E, ZHANG D, et al. Stress analysis for concrete materials under multiple freeze-thaw cycles[J]. Journal of Advanced Concrete Technology, 2015, 13(3): 124. |
| [19] |
GONG F, SICAT E, UEDA T, et al. Meso-scale mechanical model for mortar deformation under freeze thaw cycles[J]. Journal of Advanced Concrete Technology, 2013, 11(2): 49. |
| [20] |
覃丽坤. 高温及冻融循环后混凝土多轴强度和变形试验研究[D]. 大连: 大连理工大学, 2003 QIN Likun. Study on the strength and deformation of concrete under multiaxial stress after high-temperature or freeze-thaw cycling[D]. Dalian: Dalian University of Technology, 2003 |
| [21] |
严佳川, 邹超英. 冻融循环作用下混凝土材料寿命评估方法[J]. 哈尔滨工业大学学报, 2011, 43(6): 11. YAN Jiachuan, ZOU Chaoying. Evaluation method for the service life of concrete under the freeze-thaw action[J]. Journal of Harbin Institute of Technology, 2011, 43(6): 11. |
| [22] |
OH B H. Fatigue analysis of plain concrete in flexure[J]. Journal of Structural Engineering, 1986, 112(2): 273. |
| [23] |
OH B H. Fatigue life distributions of concrete for various stress levels[J]. Materials Journal, 1991, 88(2): 122. |
| [24] |
GANESAN N, RAJ J B, SHASHIKALA A P. Flexural fatigue behavior of self compacting rubberized concrete[J]. Construction and Building Materials, 2013, 44: 7. |
| [25] |
SHI X P, FWA T F, TAN S A. Flexural fatigue strength of plain concrete[J]. Materials Journal, 1993, 90(5): 435. |
| [26] |
MOHAMMADI Y, KAUSHIK S K. Flexural fatigue-life distributions of plain and fibrous concrete at various stress levels[J]. Journal of Materials in Civil Engineering, 2005, 17(6): 650. |
| [27] |
Committee on Fatigue and Fracture Reliability of the Committee on Structural Safety and Reliability of the Structural Division, American Society of Civil Engineers. Fatigue reliability: introduction[J]. Journal of the Structural Division, 1982, 108(1): 3. DOI:10.1061/JSDEAG.0005869 |
| [28] |
SINGH S P, KAUSHIK S K. Flexural fatigue life distributions and failure probability of steel fibrous concrete[J]. Materials Journal, 2000, 97(6): 658. |
| [29] |
KENNEDY J B, NEVILLE A M. Basic statistical methods for engineers and scientists[M]. New York: IEP, 1976.
|
| [30] |
南京大学金陵学院大学数学教研室. 概率论与数理统计简明教程[M]. 南京: 东南大学出版社, 2014. Department of Mathematics of Nanjing University Jinling College. A concise course in probability theory and mathematical statistics[M]. Nanjing: Southeast University Press, 2014. |
| [31] |
欧祖敏, 孙璐. 冻融损伤混凝土的弯曲疲劳寿命可靠性分析[J]. 浙江大学学报(工学版), 2017, 51(6): 1074. OU Zumin, SUN Lu. Flexural fatigue-life reliability of frost-damaged concrete[J]. Journal of Zhejiang University (Engineering Science), 2017, 51(6): 1074. |
| [32] |
洪锦祥, 缪昌文, 黄卫, 等. 冻融损伤对混凝土疲劳性能的影响[J]. 土木工程学报, 2012, 45(6): 83. HONG Jinxiang, MIAO Changwen, HUANG Wei, et al. Influence of freeze-thaw damage on the fatigue life of concrete[J]. China Civil Engineering Journal, 2012, 45(6): 83. |
 2023, Vol. 55
2023, Vol. 55


