高精度协同导航定位是复杂环境下跟踪多智能体系统(Multi-agent system, MAS)状态、完成任务分配、实现协同控制的重要保障,它在军民领域均有广阔的应用前景。然而,现实中MAS动力学和量测行为往往具有高动态特性,如何高效融合处理时空域复杂耦合的量测信息、获得智能体状态最优估计、实现系统自主导航是当前协同导航理论和技术发展面临的关键难题[1-3]。
最近几年,国、内外学者针对不同领域MAS协同导航定位问题开展了广泛研究,取得了许多创新性成果。徐博等[1]从协同导航编队构型、系统建模和信息融合算法等角度综述了多自主水下航行器领域相关研究进展;许晓伟等[2]分析讨论了多无人机系统协同导航技术的发展现状和趋势;张辰等[3]总结了多机器人系统协同导航定位、路径规划和任务分配等方面的研究进展。目前,分布式协同导航算法是重要研究课题,并且现有算法大多是由传统滤波算法改进得到,其中分布式卡尔曼滤波算法应用最广[4-8]。
针对MAS协同导航建模与多源信息融合等问题,Win等[9-14]构建了时空一体化信息网络研究框架,发展了网络导航理论。首先,他们将智能体在不同测量时刻的运动状态作为不同的网络节点,用锚点表示状态已知的参考点,并通过节点、锚点之间的连线来表示MAS在时空域复杂的动力学和量测信息交互关系,将系统抽象为时空信息网络模型;其次,基于费歇耳信息理论赋予网络各节点和边相应的信息量,构造费歇耳信息矩阵(Fisher information matrix, FIM)来表征网络中所有信息的量化关系,获取系统的全局特征;并通过计算克拉美-罗下界(Cramér-Rao lower bound, CRLB)即费歇耳信息矩阵的逆来获得时空协同导航的最优性能界限;最后,引入等价费歇耳信息矩阵(Equivalent Fisher information matrix, EFIM)来表示智能体在信息融合处理后获得的信息量,将多源信息融合处理问题转化为信息沿网络传播规律推理问题。
上述研究框架能够充分考虑动力学和量测信息复杂的耦合关系,并能获得理论上的最优导航性能,这正是多智能体协同导航最优滤波算法所需要的。但由于网络节点会随着时间和空间的变化不断增多,对应的全局FIM阶数也会不断增大,尤其是对于复杂耦合的大规模网络结构,FIM分布式求逆获得EFIM显式表达式将十分困难。Mazuelas等[13]以无向网络导航模型为研究对象,采用分块矩阵求逆法推导了无环网络结构(节点串联或并联)中各节点的EFIM,并总结了信息沿网络传播的衰减特性,而在研究耦合型网络结构时,仅讨论了网络中存在一个闭环的情形,并指出了任意耦合型网络EFIM形式的复杂性,因此限制了对网络协同导航机理的深入理解和分析。张立川等[15]采用上述方法对AUV集群网络协同导航定位精度进行了分析,同样强调了3个及3个以上节点相互耦合时EFIM的复杂性,因此其研究范围局限在少量节点主从式编队结构上。
为解决上述难题,本文提出了一种矩阵分块对角化求逆方法,结合费歇耳信息矩阵对称特点及其元素与网络拓扑间的对应关系,将其分解为两个分块对角矩阵的线性组合,它们分别包含了所有节点和边的费歇耳信息量;应用矩阵求逆引理,推导了克拉美-罗下界和网络节点等价费歇耳信息矩阵的显式表达式;引入迭代过程,将整个求逆过程完全分解为若干个低阶矩阵间的运算,减小了单步运算量。值得注意的是,本文算法在求解费歇耳信息逆矩阵时, 要求各节点的费歇耳信息矩阵均可逆,因此存在一定的局限性。
1 问题描述本文参考文献[13]的符号体系简要描述了无向网络导航定位模型以及基于费歇耳信息分析法构造费歇耳信息矩阵的过程。
1.1 无向网络导航定位模型考虑由S个节点构成的无向网络,其所有节点均彼此相连,并用xiRn(i∈S, S={1, 2, …, S})表示第i个节点的状态向量,它通常包含节点的位置、速度或者姿态等信息,那么网络所有节点状态的集合X∈RnS可以表示为
| $ \boldsymbol{X}=\left\{\boldsymbol{x}_i\right\}_{i=1}^S=\left[\boldsymbol{x}_1^{\mathrm{T}}, \cdots, \boldsymbol{x}_i^{\mathrm{T}}, \cdots, \boldsymbol{x}_S^{\mathrm{T}}\right]^{\mathrm{T}} $ | (1) |
同时用Y表示系统所有测量的集合:
| $ \boldsymbol{Y}=\left[\boldsymbol{Y}_{\text {out }}^{\mathrm{T}}, \boldsymbol{Y}_{\text {in }}^{\mathrm{T}}\right]^{\mathrm{T}} $ | (2) |
| $ \left\{\begin{array}{l} \boldsymbol{Y}_{\text {out }}=\left\{\boldsymbol{y}_i\right\}_{i=1}^S=\left[\boldsymbol{y}_1^{\mathrm{T}}, \boldsymbol{\cdots}, \boldsymbol{y}_i^{\mathrm{T}}, \boldsymbol{\cdots}, \boldsymbol{y}_S^{\mathrm{T}}\right]^{\mathrm{T}} \\ \boldsymbol{Y}_{\text {in }}=\left\{\boldsymbol{y}_{i, j}\right\}_{i, j=1, i<j}^{S, S}=\left[\boldsymbol{y}_{1, 2}^{\mathrm{T}}, \boldsymbol{y}_{1, 3}^{\mathrm{T}}, \cdots, \boldsymbol{y}_{i, j}^{\mathrm{T}}, \cdots, \boldsymbol{y}_{S-1, S}^{\mathrm{T}}\right]^{\mathrm{T}} \end{array}\right. $ | (3) |
式中:Yout为系统所有外部测量,它由S个任意维列向量yi组成;yi为i节点与外部状态已知的锚点之间的测量,其中包括节点从自身传感器获得的测量信息以及先验信息等,并假设yi测量误差仅与i节点的状态xi有关,其条件概率密度函数用f(yi; xi)表示;Yin为系统所有内部测量,即节点间测量的集合,它由Q=(S-1)S/2个任意维列向量yi, j(i < j) 构成,Q为网络节点的最大连接数;yi, j为i、j节点之间的测量,例如节点间距离、相对速度、相对方位角、信号到达时间等,并假设yi, j测量误差仅与i, j节点相对状态(xi-xj) 有关,其条件概率密度函数用f(yi, j; xi, xj)表示;同时还假设概率密度函数f(yi; xi) 和f(yi, j; xi, xj)满足如下正则条件:
| $ \boldsymbol{E}\left\{\frac{\partial \ln f\left(\boldsymbol{y}_i ; \boldsymbol{x}_i\right)}{\partial \boldsymbol{x}_i}\right\}=\mathit{\pmb{0}} $ | (4) |
| $ \boldsymbol{E}\left\{\frac{\partial \ln f\left(\boldsymbol{y}_{i, j} ; \boldsymbol{x}_i, \boldsymbol{x}_j\right)}{\partial \boldsymbol{x}_i}\right\}=-\boldsymbol{E}\left\{\frac{\partial \ln f\left(\boldsymbol{y}_{i, j} ; \boldsymbol{x}_i, \boldsymbol{x}_j\right)}{\partial \boldsymbol{x}_j}\right\}=\mathit{\pmb{0}} $ | (5) |
式中:E{ }表示取数学期望。那么最优导航定位算法的目的是需要根据网络中所有测量信息Y获得各节点状态xi的最优估计值和估计精度。
1.2 费歇耳信息分析由概率论可知,在上述正则条件(4)~(5)的假设下,系统状态的任意无偏估计
| $ \operatorname{Cov}(\hat{\boldsymbol{X}})=\boldsymbol{E}_{\boldsymbol{Y} ; \boldsymbol{X}}\left\{(\hat{\boldsymbol{X}}-\boldsymbol{X})(\hat{\boldsymbol{X}}-\boldsymbol{X})^{\mathrm{T}}\right\} \geqslant[\boldsymbol{J}(\boldsymbol{Y} ; \boldsymbol{X})]^{-1} $ | (6) |
其中J(Y; X)∈ RnS×nS为费歇耳信息矩阵(FIM),即
| $ \boldsymbol{J}(\boldsymbol{Y} ; \boldsymbol{X})=-\boldsymbol{E}\left\{\frac{\partial^2 \ln f(\boldsymbol{Y} ; \boldsymbol{X})}{\partial \boldsymbol{X} \partial \boldsymbol{X}^{\mathrm{T}}}\right\} $ |
式中f(Y; X)为测量Y关于状态X的条件概率密度函数。
克拉美-罗下界(CRLB)即费歇耳信息矩阵的逆表示无偏估计
| $ \operatorname{Cov}\left(\hat{\boldsymbol{x}}_i\right)_{\mathrm{opt}}=\left[\boldsymbol{J}^{-1}(\boldsymbol{Y} ; \boldsymbol{X})\right]_{\boldsymbol{x}_i} $ | (7) |
引入等价费歇耳信息矩阵(EFIM)[13]:
| $ \boldsymbol{J}_{\mathrm{e}}\left(\boldsymbol{Y} ; \boldsymbol{x}_i\right)=\left[\operatorname{Cov}\left(\hat{\boldsymbol{x}}_i\right)_{\mathrm{opt}}\right]^{-1}=\left[\boldsymbol{J}^{-1}(\boldsymbol{Y} ; \boldsymbol{X})\right]_{\boldsymbol{x}_i}^{-1} $ | (8) |
它表示网络测量信息Y经过最优融合处理后节点i获得的有效信息量,它与i节点的后验协方差矩阵互为逆矩阵,因此同样能表征i节点状态估计精度。
由式(6)可知,最优估计的表达式以及对应的估计精度取决于具体的概率密度函数f(Y; X),而推导分布式最优估计算法的关键难点在于获得任意阶费歇耳信息矩阵J(Y; X)的分布式求逆公式,因此接下来分析矩阵J(Y; X)的结构。i节点与锚点之间的测量yi给出了关于节点状态xi的费歇耳信息[11]:
| $ \boldsymbol{J}\left(\boldsymbol{y}_i ; \boldsymbol{x}_i\right)=-\boldsymbol{E}\left\{\frac{\partial^2 \ln f\left(\boldsymbol{y}_i ; \boldsymbol{x}_i\right)}{\partial \boldsymbol{x}_i \partial \boldsymbol{x}_i^T}\right\}=\boldsymbol{K}_{i, i} $ | (9) |
式中Ki, i≥ 0为n阶实对称半正定方阵,它表示i节点自身的有效信息量,若i节点无外部测量yi,则Ki, i= 0。同样,i、j节点间的测量yi, j给出了关于节点状态xi、xj的费歇耳信息[13]:
| $ \boldsymbol{J}\left(\boldsymbol{y}_{i, j} ; \boldsymbol{x}_i, \boldsymbol{x}_j\right)=\left[\begin{array}{rr} \boldsymbol{K}_{i, j} & -\boldsymbol{K}_{i, j} \\ -\boldsymbol{K}_{i, j} & \boldsymbol{K}_{i, j} \end{array}\right]=\left[\begin{array}{rr} 1 & -1 \\ -1 & 1 \end{array}\right] \otimes \boldsymbol{K}_{i, j} $ | (10) |
| $ \boldsymbol{K}_{i, j}=\boldsymbol{E}\left\{\frac{\partial^2 \ln f\left(\boldsymbol{y}_{i, j} ; \boldsymbol{x}_i, \boldsymbol{x}_j\right)}{\partial \boldsymbol{x}_i \partial \boldsymbol{x}_j^{\mathrm{T}}}\right\} $ | (11) |
式中:⊗为克罗内克积,Ki, j≥ 0为n阶实对称半正定方阵,且Ki, j=Kj, i。那么结合式(9)~(11)可得,网络中所有测量Y提供的关于所有节点状态X的费歇耳信息构成矩阵J (Y; X)[13]:
| $ \boldsymbol{J}(\boldsymbol{Y} ; \boldsymbol{X})=\sum\limits_{(i, j) \in S^2, i \leqslant j} \boldsymbol{G}_{i, j}^S \otimes \boldsymbol{K}_{i, j} $ | (12) |
其中
| $ \boldsymbol{G}_{i, j}^S= \begin{cases}\boldsymbol{e}_i^S\left(\boldsymbol{e}_i^S\right)^{\mathrm{T}}, & i=j \\ \boldsymbol{e}_{i, j}^S\left(\boldsymbol{e}_{i, j}^S\right)^{\mathrm{T}}, & i \neq j\end{cases} $ |
式中eiS为S维列向量,它除第i个元素为1外,其余元素均为0,ei, jS=(eiS-ejS)。当i≠j时,Gi, jS⊗Ki, j称为i、j节点间的信息链[13]:
| $ \boldsymbol{G}_{i, j}^S \otimes \boldsymbol{K}_{i, j}=\left[\begin{array}{ccccc} \bf{0} & \cdots & \cdots & \cdots & \bf{0} \\ \vdots & \boldsymbol{K}_{i, j} & \vdots & -\boldsymbol{K}_{i, j} & \vdots \\ \vdots & \cdots & \cdots & \cdots & \vdots \\ \vdots & -\boldsymbol{K}_{i, j} & \vdots & \boldsymbol{K}_{i, j} & \vdots \\ \bf{0} & \cdots & \cdots & \cdots & \bf{0} \end{array}\right], i \neq j $ | (13) |
式中省略号部分均为0。无向/有向信息网络的主要区别即体现在信息链的对称性上,对于无向信息网络,其所有信息链均满足如下对称性条件:
| $ \boldsymbol{G}_{i, j}^S \otimes \boldsymbol{K}_{i, j}=\boldsymbol{G}_{j, i}^S \otimes \boldsymbol{K}_{j, i}, \forall(i, j) \in \boldsymbol{S}^2, i \neq j $ | (14) |
而在有向信息网络中,则至少存在一条信息链不满足上述条件。矩阵(13)还可以简写为:
| $ \boldsymbol{G}_{i, j}^S \otimes \boldsymbol{K}_{i, j}=\left(\boldsymbol{e}_{i, j}^S \otimes \boldsymbol{I}_n\right) \cdot \boldsymbol{K}_{i, j} \cdot\left(\boldsymbol{e}_{i, j}^S \otimes \boldsymbol{I}_n\right)^{\mathrm{T}} $ | (15) |
式中:In为n阶单位矩阵,Ki, j为信息链的容量,若i, j节点间无测量,则Ki, j= 0。在无向信息网络中Ki, j称为ij边的有效信息量,Ki, j= 0表示节点不相连;反之,Ki, j≠ 0表示i、j节点是相连的。上述J(Y; X)具体展开,可表示为如下分块对称矩阵的形式[14]:
| $ \boldsymbol{J}(\boldsymbol{Y} ; \boldsymbol{X})=\left[\begin{array}{cccc} \boldsymbol{K}_{1, 1}+\boldsymbol{K}_{1, 2}+\cdots+\boldsymbol{K}_{1, S} & -\boldsymbol{K}_{1, 2} & \cdots & -\boldsymbol{K}_{1, S} \\ -\boldsymbol{K}_{2, 1} & \boldsymbol{K}_{2, 1}+\boldsymbol{K}_{2, 2}+\cdots+\boldsymbol{K}_{2, S} & \cdots & -\boldsymbol{K}_{2, S} \\ \vdots & \vdots & \ddots & \vdots \\ -\boldsymbol{K}_{S, 1} & -\boldsymbol{K}_{S, 2} & \cdots & \boldsymbol{K}_{S, 1}+\boldsymbol{K}_{S, 2}+\cdots+\boldsymbol{K}_{S, S} \end{array}\right] $ | (16) |
或者简写为
| $ \boldsymbol{J}(\boldsymbol{Y} ; \boldsymbol{X})=\left\{\boldsymbol{J}_{i, j}\right\}_{i, j=1}^{S, S}, \boldsymbol{J}_{i, j}=\left\{\begin{array}{l} \sum\limits_{k=1}^S \boldsymbol{K}_{i, k}, i=j \\ -\boldsymbol{K}_{i, j}, i \neq j ; \end{array}\right. $ | (17) |
式中J≥ 0为nS阶实对称半正定方阵,如果所有Ki, i正定,则J正定,但值得注意的是,所有Ki, i正定并非J正定的必要条件[13]。在时空一体化信息网络模型中,网络节点数S会随时间和空间的变化不断增大,因此费歇耳信息矩阵J的阶数也会不断增大。
2 高阶费歇耳信息矩阵求逆高阶矩阵求逆通常用到LU分解法、矩阵分块迭代求逆法等,属于集中式算法。然而对于MAS,在算法实现中,直接对高阶费歇耳信息矩阵进行数值求逆往往存在局限性。
1) 由于矩阵阶数较大,直接求逆困难,运算过程对处理器性能要求较高。
2) 每个节点需要等待整个求逆运算完成后才能获得自身的相关信息,效率较低。
因此,在工程应用中对分布式求逆算法有迫切需求,其核心是简化运算过程、减小单步计算量,降低算法对处理器性能的要求。
针对分布式求逆问题,本文结合费歇耳信息矩阵的实际物理含义及其对称特点,提出了矩阵分块对角化求逆法,获得了费歇耳信息矩阵求逆公式,便于后续分布式估计算法推导。下面详细介绍矩阵分块迭代求逆法和分块对角化求逆法的求解过程,并分析算法特点。假设涉及的Ki, i和K i, j矩阵全部可逆,对于部分Ki, i或Ki, j矩阵不可逆的情形,将在文中进行分析说明。
2.1 矩阵分块迭代求逆法当矩阵J的阶数较高时,将其划分为2×2阶分块矩阵仍不能有效避免高阶矩阵求逆问题,因此需要运用如下形式的迭代算法,将J矩阵逐级分解为低阶分块子矩阵求解。引入符号表示:
| $ \widetilde{\boldsymbol{J}}_s=\left\{\boldsymbol{J}_{i, j}\right\}_{i, j=1}^{s, s}, \widetilde{\boldsymbol{J}}_{s-1}=\left\{\boldsymbol{J}_{i, j}\right\}_{i, j=1}^{s-1, s-1}, \boldsymbol{\beta}_s=\left\{\boldsymbol{J}_{s, j}\right\}_{j=1}^{s-1} $ | (18) |
式中
| $ \widetilde{\boldsymbol{J}}_s=\left[\begin{array}{cc} \widetilde{\boldsymbol{J}}_{s-1} & \boldsymbol{\beta}_s^{\mathrm{T}} \\ \boldsymbol{\beta}_s & \boldsymbol{J}_{s, s} \end{array}\right] $ | (19) |
式中:
| $ \widetilde{\boldsymbol{J}}_s^{-1}=\left[\begin{array}{rr} \widetilde{\boldsymbol{J}}_{s-1}^{-1}+\widetilde{\boldsymbol{J}}_{s-1}^{-1} \boldsymbol{\beta}_s^{\mathrm{T}} \boldsymbol{\alpha} \boldsymbol{\beta}_s \widetilde{\boldsymbol{J}}_{s-1}^{-1} & -\widetilde{\boldsymbol{J}}_{s-1}^{-1} \boldsymbol{\beta}_s^{\mathrm{T}} \boldsymbol{\alpha}_s \\ -\boldsymbol{\alpha} \boldsymbol{\beta}_s \widetilde{\boldsymbol{J}}_{s-1}^{-1} & \boldsymbol{\alpha}_s \end{array}\right] $ | (20) |
式中:
| $ \widetilde{\boldsymbol{J}}_1^{-1}=\boldsymbol{J}_{1, 1}^{-1}=\left(\sum\limits_{j=1}^S \boldsymbol{K}_{1, j}\right)^{-1} $ | (21) |
当s=S时,
由式(16)可知,费歇耳信息矩阵J具有对称性,结合式(12)~(15)可以将它写为如下形式:
| $ \boldsymbol{J}=\boldsymbol{J}_0+\sum\limits_{(i, j) \in S^2, i<j} \boldsymbol{G}_{i, j}^S \otimes \boldsymbol{K}_{i, j} $ | (22) |
其中
| $ \begin{aligned} \boldsymbol{J}_0= & \sum\limits_{i=1}^S\left(\boldsymbol{e}_i^S\left(\boldsymbol{e}_i^S\right)^{\mathrm{T}}\right) \otimes \boldsymbol{K}_{i, i}= \\ & \operatorname{blkdiag}\left(\boldsymbol{K}_{1, 1}, \cdots, \boldsymbol{K}_{i, i}, \cdots, \boldsymbol{K}_{S, S}\right) \end{aligned} $ |
式中J0为分块对角矩阵,用blkdiag(·)表示,即矩阵的主对角线由S个方阵Ki, i构成,其余元素均为0。J0包含了所有节点自身的有效信息,而等式(22)右侧第2项则包含了所有节点间的信息链。
接下来讨论一般情形,即所有Ki, i和Ki, j矩阵均可逆。结合式(15)信息链矩阵的简写形式,对等式(22)右侧第2项进行分块对角化,可得
| $ \begin{aligned} & \sum\limits_{(i, j) \in S^2, i<j} \boldsymbol{G}_{i, j}^S \otimes \boldsymbol{K}_{i, j}=\widetilde{\boldsymbol{L}}^{\mathrm{T}} \cdot \widetilde{\boldsymbol{K}} \cdot \widetilde{\boldsymbol{L}} \\ & \widetilde{\boldsymbol{L}}=\boldsymbol{L} \otimes \boldsymbol{I}_n \\ & \widetilde{\boldsymbol{K}}=\operatorname{blkdiag}\left(\boldsymbol{K}_{1, 2}, \cdots, \boldsymbol{K}_{1, S}, \boldsymbol{K}_{2, 3}, \cdots, \boldsymbol{K}_{i, j}, \cdots, \boldsymbol{K}_{S-1, S}\right) \\ & \boldsymbol{L}=\left[\boldsymbol{e}_{1, 2}^S, \cdots, \boldsymbol{e}_{1, S}^S, \boldsymbol{e}_{2, 3}^S, \cdots, \boldsymbol{e}_{i, j}^S, \cdots, \boldsymbol{e}_{S-1, S}^S\right]^{\mathrm{T}}, i<j \end{aligned} $ | (23) |
式中:
| $ \mathit{\boldsymbol{L}} = {\left[ \begin{array}{l} {\mathit{\pmb{1}}_{S - 1}}\;\; - {\mathit{\boldsymbol{I}}_{S - 1}}\\ {\mathit{\pmb{0}}_{S - 2}}\;\;{\mathit{\pmb{1}}_{S - 2}}\;\; - {\mathit{\boldsymbol{I}}_{S - 2}}\\ {\mathit{\pmb{0}}_{S - 3}}\;\;{\mathit{\pmb{0}}_{S - 3}}\;\;\;{\mathit{\pmb{1}}_{S - 3}}\;\; - {\mathit{\boldsymbol{I}}_{S - 3}}\\ ...\\ 0\;\;\;0\;\;0\;\;\;...\;\;\;\;0\;\;\;1\;\; - 1 \end{array} \right]_{Q \times S}} $ |
式中:1S、0S分别为元素全为1或0的S维列向量,IS为S阶单位矩阵。进一步用Lk(k=1, …, S) 表示L的第k列元素,L=[L1, …, Lk, …, LS],Lk有如下性质:
| $ \boldsymbol{L}_k^{\mathrm{T}} \boldsymbol{L}_j=\left\{\begin{array}{c} S-1, k=j \\ -1, k \neq j \end{array}\right. $ | (25) |
令
| $ \widetilde{\boldsymbol{L}}=\left[\widetilde{\boldsymbol{L}}_1, \cdots, \widetilde{\boldsymbol{L}}_k, \cdots, \widetilde{\boldsymbol{L}}_S\right] $ | (26) |
综上所述,费歇耳信息矩阵J最终表示为
| $ \boldsymbol{J}=\boldsymbol{J}_0+\widetilde{\boldsymbol{L}}^{\mathrm{T}} \widetilde{\boldsymbol{K}} \widetilde{\boldsymbol{L}} $ | (27) |
对式(27)应用矩阵求逆引理,可得
| $ \boldsymbol{J}^{-1}=\left(\boldsymbol{J}_0+\widetilde{\boldsymbol{L}}^{\mathrm{T}} \widetilde{\boldsymbol{K}} \widetilde{\boldsymbol{L}}\right)^{-1}=\boldsymbol{J}_0^{-1}-\boldsymbol{J}_0^{-1} \widetilde{\boldsymbol{L}}^{\mathrm{T}} \boldsymbol{R}^{-1} \widetilde{\boldsymbol{L}} \boldsymbol{J}_0^{-1} $ | (28) |
| $ \boldsymbol{R}=\widetilde{\boldsymbol{K}}^{-1}+\widetilde{\boldsymbol{L}} \boldsymbol{J}_0^{-1} \widetilde{\boldsymbol{L}}^{\mathrm{T}} $ | (29) |
式中J0-1、
| $ \boldsymbol{R}=\widetilde{\boldsymbol{K}}^{-1}+\sum\limits_{k=1}^S \widetilde{\boldsymbol{L}}_k \boldsymbol{K}_{k, k}^{-1} \widetilde{\boldsymbol{L}}_k^{\mathrm{T}} $ | (30) |
对矩阵Rs求逆,本文运用递推公式,令
| $ \begin{gathered} \boldsymbol{R}_s \triangleq \widetilde{\boldsymbol{K}}^{-1}+\sum\limits_{k=1}^s \widetilde{\boldsymbol{L}}_k \boldsymbol{K}_{k, k}^{-1} \widetilde{\boldsymbol{L}}_k^{\mathrm{T}}, s=0, 1, \cdots, S \\ \boldsymbol{R}_s=\boldsymbol{R}_{s-1}+\widetilde{\boldsymbol{L}}_s \boldsymbol{K}_{s, s}^{-1} \widetilde{\boldsymbol{L}}_s^{\mathrm{T}} \end{gathered} $ | (31) |
对Rs应用矩阵求逆引理,可得
| $ \boldsymbol{R}_s^{-1}=\boldsymbol{R}_{s-1}^{-1}-\boldsymbol{R}_{s-1}^{-1} \widetilde{\boldsymbol{L}}_s\left(\boldsymbol{K}_{s, s}+\tilde{\boldsymbol{L}}_s^{\mathrm{T}} \boldsymbol{R}_{s-1}^{-1} \tilde{\boldsymbol{L}}_s\right)^{-1} \tilde{\boldsymbol{L}}_s^{\mathrm{T}} \boldsymbol{R}_{s-1}^{-1} $ | (32) |
当s=0时,即
| $ \boldsymbol{R}_0=\widetilde{\boldsymbol{K}}^{-1}, \boldsymbol{R}_0^{-1}=\widetilde{\boldsymbol{K}} $ | (33) |
当s=S时,R=RS,R-1=RS-1迭代终止。运用递推公式(31)~(33)求R-1时,仅需要对S个n阶方阵
| $ \boldsymbol{P}_{i, j}^s=\widetilde{\boldsymbol{L}}_i^{\mathrm{T}} \boldsymbol{R}_s^{-1} \widetilde{\boldsymbol{L}}_j, (s, i, j) \in S^3 $ | (34) |
式中:
对等式(32)~(33)两端分别左乘
| $ \boldsymbol{P}_{i, j}^s=\boldsymbol{P}_{i, j}^{s-1}-\boldsymbol{P}_{i, s}^{s-1}\left(\boldsymbol{K}_{s, s}+\boldsymbol{P}_{s, s}^{s-1}\right)^{-1} \boldsymbol{P}_{s, j}^{s-1} $ | (35) |
当s=0时,
| $ \boldsymbol{P}_{i, j}^0=\left\{\begin{array}{l} \sum\limits_{k=1, k \neq i}^S \boldsymbol{K}_{i, k}, i=j \\ -\boldsymbol{K}_{i, j}, \quad i \neq j \end{array}\right. $ | (36) |
当s=S时,
| $ \boldsymbol{P}_{i, j}=\widetilde{\boldsymbol{L}}_i^{\mathrm{T}} \boldsymbol{R}^{-1} \widetilde{\boldsymbol{L}}_j $ | (37) |
将J0-1和L代入式(28),并结合式(37)可求得费歇耳信息矩阵的逆J-1,它可以表示为S×S个n阶子方块构成的矩阵:
| $ \boldsymbol{J}^{-1}=\left[\begin{array}{cccc} \boldsymbol{K}_{1, 1}^{-1}-\boldsymbol{K}_{1, 1}^{-1} \boldsymbol{P}_{1, 1} \boldsymbol{K}_{1, 1}^{-1} & -\boldsymbol{K}_{1, 1}^{-1} \boldsymbol{P}_{1, 2} \boldsymbol{K}_{2, 2}^{-1} & \cdots & -\boldsymbol{K}_{1, 1}^{-1} \boldsymbol{P}_{1, S} \boldsymbol{K}_{S, S}^{-1} \\ -\boldsymbol{K}_{2, 2}^{-1} \boldsymbol{P}_{2, 1} \boldsymbol{K}_{1, 1}^{-1} & \boldsymbol{K}_{2, 2}^{-1}-\boldsymbol{K}_{2, 2}^{-1} \boldsymbol{P}_{2, 2} \boldsymbol{K}_{2, 2}^{-1} & \cdots & -\boldsymbol{K}_{2, 2}^{-1} \boldsymbol{P}_{2, S} \boldsymbol{K}_{S, S}^{-1} \\ \vdots & \vdots & \ddots & \vdots \\ -\boldsymbol{K}_{S, S}^{-1} \boldsymbol{P}_{S, 1} \boldsymbol{K}_{1, 1}^{-1} & -\boldsymbol{K}_{S, S}^{-1} \boldsymbol{P}_{S, 2} \boldsymbol{K}_{2, 2}^{-1} & \cdots & \boldsymbol{K}_{S, S}^{-1}-\boldsymbol{K}_{S, S}^{-1} \boldsymbol{P}_{S, S} \boldsymbol{K}_{S, S}^{-1} \end{array}\right] $ | (38) |
式(38)可简写为:
| $ \boldsymbol{J}^{-1}=\left\{\left(\boldsymbol{J}^{-1}\right)_{i, j}\right\}_{i, j=1}^{S, S} $ | (39) |
| $ \left(\boldsymbol{J}^{-1}\right)_{i, j}= \begin{cases}\boldsymbol{K}_{i, i}^{-1}-\boldsymbol{K}_{i, i}^{-1} \boldsymbol{P}_{i, i} \boldsymbol{K}_{i, i}^{-1}, & i=j \\ -\boldsymbol{K}_{i, i}^{-1} \boldsymbol{P}_{i, j} \boldsymbol{K}_{j, j}^{-1}, & i \neq j\end{cases} $ | (40) |
结合式(8),可得第i个节点的等价费歇耳信息矩阵:
| $ \begin{aligned} \boldsymbol{J}_e\left(\boldsymbol{Y} ; \boldsymbol{x}_i\right)= & {\left[\left(\boldsymbol{J}^{-1}\right)_{i, i}\right]^{-1}=} \\ & \left(\boldsymbol{K}_{i, i}^{-1}-\boldsymbol{K}_{i, i}^{-1} \widetilde{\boldsymbol{L}}_i^{\mathrm{T}} \boldsymbol{R}^{-1} \widetilde{\boldsymbol{L}}_i \boldsymbol{K}_{i, i}^{-1}\right)^{-1}= \\ & \boldsymbol{K}_{i, i}+\widetilde{\boldsymbol{L}}_i^{\mathrm{T}}\left(\boldsymbol{R}-\widetilde{\boldsymbol{L}}_i \boldsymbol{K}_{i, i}^{-1} \widetilde{\boldsymbol{L}}_i^{\mathrm{T}}\right)^{-1} \widetilde{\boldsymbol{L}}_i \end{aligned} $ | (41) |
由式(30)可得,式(41)中
| $ \boldsymbol{R}-\widetilde{\boldsymbol{L}}_i \boldsymbol{K}_{i, i}^{-1} \widetilde{\boldsymbol{L}}_i^{\mathrm{T}}=\widetilde{\boldsymbol{K}}^{-1}+\sum\limits_{k=1, k \neq i}^S \widetilde{\boldsymbol{L}}_k \boldsymbol{K}_{k, k}^{-1} \widetilde{\boldsymbol{L}}_k^{\mathrm{T}} $ | (42) |
由于k≠i,它与Ki, i无关,其求逆过程同r,运用递推公式(31)~(33)时少迭代一次即可。式(41)中Je(Y; xi)表示i节点后验费歇耳信息量,而等号右侧第1项Ki, i则为先验费歇耳信息量,第2项为信息增量,它与网络拓扑结构密切相关,能表征网络导航节点定位精度的提升程度。不同网络拓扑(如无环型、耦合型等)中节点和边费歇耳信息量的变化规律将在后续进行研究。
综上所述,式(40)即为网络导航任意阶费歇耳信息矩阵分布式求逆公式,它将整个求逆过程完全分解为若干个低阶矩阵间的运算,因此简化了算法过程,符合智能体低性能计算需求。值得注意的是,该算法在求解J-1时需要对所有Ki, i矩阵求逆,因此仅适用于Ki, i均为非奇异矩阵的情形,具有一定的局限性,而在求解等价费歇耳信息矩阵Je(Y; xi)时则不要求Ki, i可逆。对于Ki, j为奇异矩阵的情形算法同样适用。
3 数值试验与分析下面通过数值试验对费歇耳信息矩阵分布式求逆过程进行验证,并将计算结果与矩阵分块迭代求逆法进行比较分析。软件平台为MATLAB R2018b,计算机配置为Core i5-8250u CPU,8 G RAM。
作为算例,智能体状态向量维数取n=6,网络节点总数S在0~1 000以内间隔50取值,共20组,那么费歇耳信息矩阵的阶数为nS∈[300, 6 000]。利用随机函数构造相应数量的实对称矩阵作为Ki, i和Ki, j,其元素数值大小在±10 000范围内,并根据式(18)获得矩阵J。
在试验中,首先验证了矩阵J的对角化过程,即式(27)的准确性:对于随机构成的20组不同阶矩阵J,式(16)和式(27)均得到相同的结果;其次,对比分析了本文两种矩阵求逆算法的运算效率和精度,这里以MATLAB标准求逆函数inv( )获得的结果作为“精确”解,以矩阵元素最大偏差量的绝对值作为算法计算精度。试验结果如图 1、2所示,其中方法1、2分别表示矩阵分块迭代求逆法和矩阵分块对角化求逆法。
|
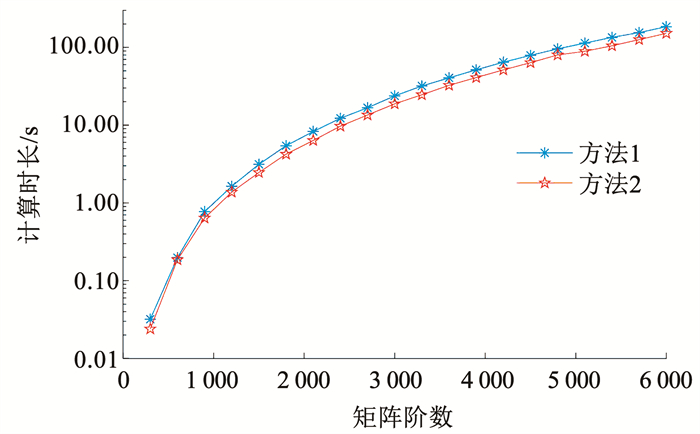
图 1 两种方法计算时长对比曲线 Fig. 1 Comparison of calculation time of two methods |

|
图 2 两种方法计算精度对比曲线 Fig. 2 Comparison of calculation accuracy of two methods |
图 1给出了两种方法计算时长对比曲线。由图 1可知,随着FIM矩阵阶数的增加,两种方法计算时长均会急剧增大:当矩阵为600阶时,即100个节点的情形,两者时长约为0.20 s,而当节点数或矩阵阶数增大10倍后,计算时长分别为184.60,151.50 s。另外,针对同一阶矩阵,方法2运算效率更高,它的计算时长比方法1平均缩短约18.00%。值得说明的是,inv()是MATLAB经过优化后的内部函数,采用LU分解法,以C语言等编译,对6 000阶FIM矩阵求逆用时约5.00 s,而本文的试验是基于MATLAB语言,方法1、2的程序运算效率和计算精度虽远不及inv()函数,但不影响两者之间进行对比分析。
图 2给出了两种方法计算精度对比曲线。当FIM矩阵增大时,方法1的计算精度保持在10-20量级,而方法2的计算精度则会由10-18量级逐渐降低至10-16,两种方法计算精度相差2~4个数量级,尽管如此,方法2的误差相对于矩阵元素数值大小±10 000是非常微小的,可以忽略不计。
综上所述,通过数值试验与分析验证了本文两种高阶FIM矩阵求逆方法的准确性和有效性,结果表明,两者均具有较高的计算效率和精度,但分布式求逆方法运算量更小,计算速度更快。
4 结论1) 针对多智能体系统任意耦合型无向网络导航中,高阶费歇耳信息矩阵分布式求逆问题,提出了矩阵分块对角化求逆法,并与矩阵分块迭代求逆法进行了对比分析。数值结果表明,两者均具有较高的计算效率和精度。
2) 本文提出的求逆方法在算法结构上具有分散性特点,它将整个求逆过程完全拆分为低阶矩阵间的运算,因此能有效减小单步运算量,降低计算过程对处理器性能的要求。
3) 所获得的费歇耳信息逆矩阵和等价费歇耳信息矩阵的显式表达式,适用于在理论上针对网络各节点或边进行信息融合过程分析。
| [1] |
徐博, 白金磊, 郝燕玲, 等. 多AUV协同导航问题的研究现状与进展[J]. 自动化学报, 2015, 41(3): 445. XU Bo, BAI Jinlei, HAO Yanling, et al. The research status and progress of cooperative navigation for multiple AUVs[J]. Acta Automatica Sinica, 2015, 41(3): 445. DOI:10.16383/j.aas.2015.c140047 |
| [2] |
许晓伟, 赖际舟, 吕品, 等. 多无人机协同导航技术研究现状及进展[J]. 导航定位与授时, 2017, 4(4): 1. XU Xiaowei, LAI Jizhou, LV Pin, et al. A literature review on the research status and progress of cooperative navigation technology for multiple UAVs[J]. Navigation Positioning & Timing, 2017, 4(4): 1. DOI:10.19306/j.cnki.2095-8110.2017.04.001 |
| [3] |
张辰, 周乐来, 李贻斌. 多机器人协同导航技术综述[J]. 无人系统技术, 2020, 3(2): 1. ZHANG Chen, ZHOU Lelai, LI Yibin. Overview of multi-robot collaborative navigation technology[J]. Unmanned Systems Technology, 2020, 3(2): 1. |
| [4] |
KHAN U A, MOURA J M F. Distributing the Kalman filter for large-scale systems[J]. IEEE Transactions on Signal Processing, 2008, 56(10): 4919. DOI:10.1109/TSP.2008.927480 |
| [5] |
戴孟元. 卫星星座分布式协同定轨方法研究[D]. 长沙: 国防科学技术大学, 2016 DAI Mengyuan. Decentralized cooperative orbit determination for satellite constellations[D]. Changsha: National University of Defense Technology, 2016 |
| [6] |
张国良, 汤文俊, 孙一杰, 等. 多无人平台协同导航与控制方法[M]. 北京: 国防工业出版社, 2020. ZHANG Guoliang, TANG Wenjun, SUN Yijie, et al. Cooperative navigation and control method for multiple unmanned platforms[M]. Beijing: National Defense Industry PresS, 2020. |
| [7] |
ZHANG Ya, SUN Lucheng, HU Guoqiang. Distributed consensus-based multi-target filtering and its application in formation-containment control[J]. IEEE Transactions on Control of Network SystemS, 2020, 7(1): 503. DOI:10.1109/tcns.2019.2926281 |
| [8] |
WANG Shizhuang, ZHAN Xingqun, ZHAI Yawei, et al. Performance estimation for Kalman filter based multi-agent cooperative navigation by employing graph theory[J]. Aerospace Science and Technology, 2021, 112: 106628. DOI:10.1016/j.ast.2021.106628 |
| [9] |
WIN M Z, CONTI A, MAZUELAS S, et al. Network localization and navigation via cooperation[J]. IEEE Communications Magazine, 2011, 49(5): 56. DOI:10.1109/MCOM.2011.5762798 |
| [10] |
MAZUELAS S, SHEN Yuan, WIN M Z. Information coupling in cooperative localization[J]. IEEE Communications LetterS, 2011, 15(7): 737. DOI:10.1109/LCOMM.2011.060111.110402 |
| [11] |
SHEN Yuan, MAZUELAS S, WIN M Z. Network navigation: Theory and interpretation[J]. IEEE Journal on Selected Areas in CommunicationS, 2012, 30(9): 1823. DOI:10.1109/JSAC.2012.121028 |
| [12] |
MAZUELAS S, SHEN Yuan, WIN M Z. Spatio-temporal information coupling in cooperative network navigation[C]//Proceeding of IEEE Global Telecommunications Conference. Anaheim, CA: IEEE, 2012. DOI: 10.1109/GLOCOM.2012.6503476
|
| [13] |
MAZUELAS S, SHEN Yuan, WIN M Z. Spatiotemporal information coupling in network navigation[J]. IEEE Transactions on Information Theory, 2018, 64(12): 7759. DOI:10.1109/TIT.2018.2859330 |
| [14] |
WIN M Z, DAI Wenhan, SHEN Yuan, et al. Network operation strategies for efficient localization and navigation[J]. Proceedings of the IEEE, 2018, 106(7): 1224. DOI:10.1109/JPROC.2018.2835314 |
| [15] |
张立川, 王永召, 屈俊琪. 基于等价Fisher信息矩阵的AUV集群网络导航精度分析[J]. 水下无人系统学报, 2019, 27(3): 254. ZHANG Lichuan, WANG Yongzhao, QU Junqi. Network navigation accuracy analysis of AUV swarm based on equivalent Fisher information matrix[J]. Journal of Unmanned Undersea SystemS, 2019, 27(3): 254. DOI:10.11993/j.issn.2096-3920.2019.03.003 |
 2023, Vol. 55
2023, Vol. 55


