软体机械臂^[1]是一种由柔性材料制成，可沿躯干连续变形的新概念仿生机械臂，具有天生的灵活性与固有的柔顺性^[2]。与刚性机械臂^[3]相比，软体机械臂在应用过程中不仅需要控制末端位置，还需要对连续形状进行变形控制。

作为高非线性与强不确定性的系统，软体机械臂在应用时存在接触形变、节段间驱动耦合等难题，开环控制的精度难以令人满意。针对上述问题，形状伺服控制是一种有效的控制方案，它将形状信息整合到机械臂的控制回路中，通过闭环控制得到软体机械臂理想的空间构型^[4]。因此，实时的形状信息不仅是形状伺服控制器设计、轨迹规划等一系列后续研究的基础性工作，也是控制过程可视化的重要窗口，开发一种精确的形状传感系统是十分必要的^[5]。众多传感方案已应用于软体机械臂的三维形状感知。Godage等^[6]利用编码器测量关节变量，并通过运动学模拟连续体机械臂的空间姿态。但该方案过度依赖常曲率假设，原理样机无法始终维持常曲率形态，特别是与环境交互时，该方法不再适用。光纤传感器^[7]和电磁传感器^[8]等针对连续变化介质的传感方法，对应用成本和环境噪声的要求较高且对机械臂的运动存在一定约束。

相比之下，基于机器视觉的检测方法^[9]能够在不影响机械臂可操作性的情况下，仅通过图像数据开展三维形状重建，是一种低成本、高精度的非接触式测量。Hannan等^[10]最早使用单目相机提取象鼻机械臂的截面中心点，从而确定形状。但该方法仅考虑了机械臂的平面运动。在立体视觉中，安装基准标记点是形状检测最常用的方法^[11-12]。然而，标记点只能安装在机械臂的某一截面，当它运动到相机无法捕捉的角度时，将直接导致算法失效。因此，无标记法更具有研究价值。Croom等^[13]将SOM算法应用于软体机械臂的形状感知，通过对图像点云聚类进行机械臂的中心线辨识。结果表明，基于学习的SOM算法在静态数据聚类和拓扑映射方面表现稳健，特别适用于解决软体机械臂这种形态多变且不规则的中心线辨识问题，但该文未涉及对动态目标的实时性研究。不仅如此，目前现有的大部分形状感知系统，仅对单段机械臂或简易模型进行简单的平面弯曲实验^[14-15]，对构型复杂的多段机械臂的实时三维形状重建的研究仍鲜有所闻。

本文提出了一种基于SOM算法的软体机械臂三维形状实时感知方法并验证了有效性，与现有研究比较，本文将SOM算法应用于软体机械臂三维形状的动态实时感知; 针对三段式软体机械臂及其复杂空间构型，所提算法仍具有较高的精度与实时性能(与其他文献相比); 所提算法具有较强的通用性，可拓展应用到其他类型的软体机械臂。

1 物理实验平台概述

作为连续型机械臂，变形控制是软体机械臂独有的控制方式，为实现高精度的变形控制，需要形状反馈变量进行实时监测。因此，必须考虑在控制系统的反馈环节上设计一个实时形状感知系统，如图 1所示，以形成一个完整的强鲁棒闭环控制系统。

为实现上述系统(本文不涉及控制器设计)，物理实验平台的搭建如图 2(a)所示。空压机与阀岛提供高压气源，DA转换器将控制信号转换为模拟电压信号，以此控制比例阀的输出气压，最终以气压驱动的方式完成软体机械臂的空间形状控制。采用ZED双目深度相机作为敏感器，深度感知范围可达0.3~15.0 m。ZED相机被固定在高度可调的三脚支架上，与工作站(Intel Xeon Bronze六核处理器，32 GB内存)的USB3.0端口建立串行通信，并在Pycharm3.3环境下完成形状感知算法的程序设计。此外，为了更好地进行图像辨识，实验背景设置为白色。

本文以冷劲松教授团队^[16]研制的三段式气动软体机械臂为研究对象开展实验验证，如图 2(b)所示。该机械臂分为：1)由4根收缩弯曲型气动肌肉(Pneumatic muscle actuator, PMA)组成，加压时收缩变粗；2)由2根伸长弯曲型PMA组成，加压时伸长变细并产生弯曲运动；3)由1根伸长扭转型PMA，加压时可出现弯曲扭转。每段之间通过3D打印底座紧密连接，机械臂总长度68.5 cm，最大直径5 cm。

2 实时形状感知算法设计

本文提出的形状感知算法不依赖任何数学模型，仅通过图像处理技术获得机械臂的轮廓图像数据，并基于学习的方式聚类形成中心线结构，最终利用双目视差完成三维形状重构。算法流程示意图如图 3所示。

实时性是形状感知算法至关重要的性能之一。因此，在以下各步算法设计中，采取了很多工程技术方法来减少数据计算量，缩短程序执行时间。

2.1 图像预处理

形状感知算法的第1步是分别对左、右图像帧进行图像预处理，将软体机械臂的左、右轮廓数据从背景中提取出来。相机分辨率设置为1 280×720。具体流程如下。

2.1.1 相机标定与图像校正

本文由ZED-API直接获取出场标定的相机内、外参数，并通过自校准实时获得两个无畸变的左、右图像帧。

2.1.2 滤波去噪与二值化^[17]

首先利用高斯滤波器抑制图像噪声。然后选取合适的HSV阈值(H∈[0, 128], S∈[0, 49], V∈[0, 33])进行二值化。最后，应用形态学滤波器进行开运算，去除孤立像素点，使机械臂轮廓更平滑。

2.1.3 轮廓提取与降采样^[13]

将机械臂全部图像数据作为SOM输入样本的方法^[18]，对于实时检测而言，数据量过大。本文基于Canny边缘检测算法进行轮廓提取。为防止视野中其他黑色元素干扰，设计最大轮廓提取算法，提高了预处理的鲁棒性，上述算法均由OpenCV库提供。为进一步提高帧率，通过等间隔按序取点对轮廓数据进行降采样，最终将2 000+的二维数据点压缩至200+(每帧间的数据量稍有波动，可稳定维持在[211, 220]之间)。图像预处理结果如图 4所示(以左图像为例)。

2.2 SOM神经网络算法设计

由于软体机械臂是一种均匀对称的管状物体，中心线可以很好的描述其三维空间形状。本文采用SOM神经网络算法，对图像预处理得到的轮廓数据进行中心线辨识。

2.2.1 基本原理

SOM神经网络由输入层和输出层组成，如图 5所示。输入层共有m个神经元，对应输入样本P_i(i∈[1, m])的维度；输出层神经元的数量n由输出聚类中心的个数决定，与权值向量W_j(j∈[1, n])一一对应。

基于上述结构模型，机械臂二维轮廓数据作为输入样本进行SOM训练。设机械臂轮廓数据为P={p_k=[p_{k, 1}, p_{k, 2}], k∈[1, r]}∈ R^2r(r为数据点个数)，故输入样本维度m=2。SOM输出的权值向量W_{L, j}=[x_{L, j}, y_{L, j}] 为软体机械臂中心线骨干点的二维坐标(以左图像为例)。SOM算法的训练过程归纳为以下几步：

1) 网络参数初始化。初始化权值向量W_j(0)，设定优胜领域半径N∈ N^*，学习率α与迭代次数λ。

2) 计算优胜神经元。随机选取输入样本p_k，运用竞争学习的机理，计算每一个权值向量W_j与该输入样本p_k的相似度，即

$ \left\|\boldsymbol{p}_k-\boldsymbol{W}_j\right\|=\sqrt{\left(\boldsymbol{p}_k-\boldsymbol{W}_j\right)^{\mathrm{T}}\left(\boldsymbol{p}_k-\boldsymbol{W}_j\right)} $

(1)

欧式距离最小的权值向量W_j^*所对应的输出神经元定义为优胜神经元，记为j^*。公式如下:

$ j^*=\arg \max\limits_{j \in[1, n]}\left(\left\|\boldsymbol{p}_k-\boldsymbol{W}_j\right\|\right) $

(2)

3) 设计领域函数。以优胜神经元j^*为中心，N为邻域半径，确定优胜领域N_j^*(t)。优胜领域内，输出神经元更新自身权值的规律满足邻域函数η(R)：与获胜神经元的拓扑距离R越远，更新权值的幅度越小。

4) 更新权值向量。基于梯度下降法的思想，更新优胜领域内所有权值向量，更新率参考如下：

$ \boldsymbol{W}_j(t+1)=\boldsymbol{W}_j(t)+\eta(R) \alpha(t)\left[\boldsymbol{p}_k-\boldsymbol{W}_j(t)\right], j \in N_{j^*}(t) $

(3)

式中α(t)为学习率函数，常用1/(1+t/λ)表示。

5) 终止条件判断。检测当前训练次数是否达到预设值λ。如果未达到，训练次数+1，返回步骤2)继续训练，直至达到预设值λ，输出权值向量W_j。

2.2.2 参数优化设计

尽管SOM算法相对稳健，但可调参数众多，现有研究通常是以盲目试凑的方法进行调参^[13]，无法将算法性能发挥极致，进而阻碍了SOM算法在动态视觉领域的应用。本文定义两种误差来评价训练精度，针对软体机械臂初始状态，进行SOM训练，开展多组误差仿真对比，以一种更为科学的方法完成SOM算法的参数优化。

首先定义拓扑误差。拓扑误差描述了存在拓扑错误的输入样本占总输入样本的比例。当优胜神经元j^*与次优胜神经元j^**不相邻时，存在一个拓扑误差。具体定义式为:

$ \varepsilon_{\mathrm{t}}=\frac{1}{r} \sum\limits_{k=1}^r \tau\left(\boldsymbol{p}_k\right), \tau\left(\boldsymbol{p}_k\right)=\left\{\begin{array}{l} 1, \left|c\left(j^*\right)-c\left(j^{* *}\right)\right| \neq 1 \\ 0, \left|c\left(j^*\right)-c\left(j^{* *}\right)\right|=1 \end{array}\right. $

(4)

式中c为神经元序号。当拓扑误差存在时，输出权向量的拓扑关系混乱，会导致三维重建错误。因此，必须消除拓扑误差。

量化误差是计算每一个输入样本p_k与对应最近的输出权向量W_j^*的平均欧氏距离，是衡量SOM训练精度的重要评价指标，虽然不可消除，但会在训练过程中逐渐收敛，具体公式如下：

$ \varepsilon_{\mathrm{q}}=\frac{1}{r} \sum\limits_{k=1}^r\left\|\boldsymbol{p}_k-\boldsymbol{W}_{j^*}\right\| $

(5)

接下来开展SOM算法的误差分析，对输出权向量个数n、优胜邻域半径N∈ N^*、学习率初始值α以及训练次数λ进行参数设计。

本文通过拓扑误差选择输出权向量的个数，这是因为SOM其他参数不会影响数据的拓扑映射。为避免因训练不足而产生拓扑误差，设定充足的训练次数，进行仿真实验，如图 6(a)所示。仿真结果表明，当n≤45时，ε_t=0。选取n=20, 30, 40，进一步研究训练次数对拓扑误差收敛的影响，由图 6(b)可得，n=20, 30时，误差收敛速度基本一致，而n=40时则需要更多的迭代次数，考虑实时性与精度间的平衡，设n=25。

优胜领域N与学习率α是决定量化误差的两个重要因素，而训练次数λ只影响量化误差的收敛速度。设立N=2, 3, 4, 5，探索学习率与量化误差的规律，依然设置充足的训练次数，仿真实验如图 6(c)所示。在任何学习率的条件下，优胜领域半径越小，量化误差越小。这是因为大优胜领域会使权值向量向同一个聚类点调整，从而偏离样本真实分布。由此设N=2。此外，学习率过大或过小都不利于数据的训练。过大的学习率会造成无法精确学习，量化误差较大。而学习率过小也会导致陷入局部学习的现象。因此，选择α=0.2最为合适。接下来缩短学习率的仿真范围(0≤α≤0.4)，通过设计λ=10, 20, 30, 40，寻找训练次数对量化误差收敛的作用。由仿真结果图 6(d)可得，尽管量化误差的收敛值趋于一致，但训练次数的增加，会延长算法解算的时间，这与实时性的设计思路相悖，因此λ=20是一个较好的折衷选择。

2.2.3 训练结果

依据上述分析结果，SOM参数的选取见表 1。以软体机械臂初始状态为例，开展SOM算法的实验验证。首先，对权值向量W_j(0)进行线性初始化，如图 7(a)所示(以左图像为例)，考虑软体机械臂竖直下垂的初始状态，选择线性初始化可以快速跟踪软体机械臂真实形状，且之后每一帧的初始权向量为前一帧SOM算法的训练结果，从而进一步减少SOM训练时间。最终，左、右图像的SOM算法训练结果如图 7(b)所示。

值得一提的是，经过图像校正后，物理空间中同一点在左、右图像的投影不存在y轴方向的偏移。而由于左、右图像的SOM训练是单独进行的，对应同名点仍然存在y轴偏差。下面定义这一误差为非对齐误差，即

$ \varepsilon_{\mathrm{w}}=\frac{1}{n} \sum\limits_{j=1}^n\left|y_{\mathrm{L}, j}-y_{\mathrm{R}, j}\right| $

(6)

经上述公式计算，初始时刻软体机械臂的非对齐误差为1.54 mm。为完全补偿这一误差，以左图像为基准，对右图像的输出权向量进行3次样条插值，并在生成的插值数据中寻找与左图像输出权向量纵坐标相同的数据点，作为误差补偿后右图像的输出权向量。补偿前、后的数值仿真图如图 7(c)所示, 误差补偿后SOM聚类结果如图 7(d)所示。

2.2.4 对比其他算法

为了阐明SOM算法的优越性，针对软体机械臂复杂形状中心线提取问题，采用了其他3种中心线识别算法进行比较研究。

K均值算法是机器学习中最经典的聚类算法。它以拓扑距离为评价标准，将输入样本分配到不同的聚类中心。聚类中心再根据包含的所有输入样本实时更新位置。重复上述过程，直到迭代结束。伪代码在算法1中给出。

算法1     K-Means algorithm for centerline recognition

1. Select the center number n and iterations number l=M. 2. Initialize W(0) randomly, and input 2D contour p. 3. Define the set $C=\left\{C_1, \cdots, C_n\right\}=\varnothing$ 4.    for l=1; l < M+1; l+ + do 5.        for each pk do 6.             $\text { Calculate } j^{\prime}=\arg \min _{j \in[1, n]}\left(\left\|\boldsymbol{p}_k-\boldsymbol{W}_j\right\|\right)$                        Assign Cj′=Cj′∪pk. 7.    end for 8.    for j=1; j < n+1; j+ + do 9.        Update $\boldsymbol{W}_j=\sum\limits_{\boldsymbol{p}_k \in C_{j^{\prime}}} \boldsymbol{p}_k /\left|C_{j^{\prime}}\right| \text { using all } \boldsymbol{p}_k \text { belonging to } C_{j^{\prime}}$. 10.        end for 11. end for 12. Output W

高斯混合模型作为一种K均值优化算法，可以计算出输入样本属于每个聚类中心的概率。它假设每个聚类中心的输入样本服从高斯分布，且输入样本集由每个聚类中心的高斯分布叠加而成。算法2中也给出了详细的伪代码。

算法 2     GMM for centerline recognition

1. Select the component number n and define mixing coefficient β, expectation μ, covariance Γ and iterations number l=0 2. Initialize θ0=(μ, Γ, β) randomly, and input contour data p. 3. while $\left(l=0 \mid\left\|\boldsymbol{\theta}_l-\boldsymbol{\theta}_{l-1}\right\|>0.01\right)$ do 4.         $l=l+1$ 5.         for k = 1; k < r; k + + do 6.                 for j = 1; j < n; j + + do 7.                         Compute the possibility that input sample pk comes from component j:                         $\gamma_{k j}=\beta_j \boldsymbol{\varPhi}\left(\boldsymbol{p}_k \mid \mu_j, \varGamma_j\right) / \sum\limits_{j=1}^n \beta_j \boldsymbol{\varPhi}\left(\boldsymbol{p}_k \mid \mu_j, \varGamma_j\right)$ 8.                         end for 9.                 end for 10.         for j = 1; j < n; j + + do 11.                     Estimate the model parameters θj based on Maximum Likelihood Estimation:                     $\boldsymbol{\mu}_j=\sum\limits_{k=1}^r\left(\gamma_{k j} \boldsymbol{p}_k\right) / \sum\limits_k^r \gamma_{k j}, j=1, \cdots, n$ 12.                     $\boldsymbol{\varGamma}_j=\sum\limits_{k=1}^r \gamma_{k j}\left(\boldsymbol{p}_k-\mu_j\right)\left(\boldsymbol{p}_k-\mu_j\right)^{\mathrm{T}} / \sum\limits_k^r \gamma_{k j}, j=1, \cdots, n$ 13.                     $\boldsymbol{\beta}_j=\sum\limits_k^r \gamma_{k j} / r, j=1, \cdots, n$ 14.         end for 15.         θl=(μ, Γ, β) 16. end while 17. Output W=μ

针对软体机械臂的初始形状，3种无监督学习算法的聚类结果如图 8所示。结果表明，K均值算法不适合本文的研究工作，因为它只对圆形分布的数据产生较好的结果，这可以从该算法平均值迭代的本质来解释。而高斯混合模型尽管对数据分布没有要求，但它很容易陷入局部优化，没有智能学习的过程。

此外，利用机器视觉算法进行中心线提取也是一种有效方法。细化^[19]是一种提取目标骨干的常用方法。它可以将二值图像的连通分量细化为像素宽度，用于特征提取和拓扑表示。算法流程如图 9(a)所示。然后在已得到的骨干上以等间隔取点的方法来获取期望数量的中心点。然而，当软体机械臂不是沿某一轴单调变形时，通过该方法获得的中心点具有错误的拓扑关系，如图 9(b)所示。这表明细化需要额外的排序算法。

综上所述，通过与其他3种算法的比较，总结了SOM在解决本文工作中的优势。1)SOM是一种人工神经网络，能够智能地学习输入样本的拓扑关系，具有较好的泛化能力。2)输出具有保序性，无需额外增加排序算法即可获得正确的拓扑结构，便于实时性设计。

2.3 三维形状重构

三维重构是指利用软体机械臂在左、右图像的二维中心线骨干点恢复三维结构的过程，包括数值法与解析法。利用最小二乘法寻找线性超定方程组最优解的数值方法^[20]无法得到精确解且计算量较大。鉴于ZED双目相机严格平行的结构，本文采用三角测距的解析方法，通过计算左、右图像中同名点的视差来获取其深度信息。三角测距模型如图 10所示。

设三维空间中某一输出权向量M在左、右像平面的投影点分别为m_L与m_R，其横坐标记为x_{L, j}、x_{R, j}，根据空间三角形相似的几何原理，求解深度信息Z为

$ Z_j=\frac{f T_x}{d_j} $

(7)

式中，$d_j=x_{\mathrm{L}, j}-x_{\mathrm{R}, j}$为视差，即点M在左、右图像中x轴的位置偏差。T_x为基线长度，焦距f满足f_L=f_R=f。在这里，默认左相机坐标系$O_{\mathrm{L}}-X_{\mathrm{L}} Y_{\mathrm{L}} Z_{\mathrm{L}}$为世界坐标系$O_{\mathrm{W}}-X_{\mathrm{W}} Y_{\mathrm{W}} Z_{\mathrm{W}}$。根据上述深度模型，同理计算可得x、y轴的维度信息：

$ X_j=\frac{x_{\mathrm{L}, j} Z_j}{f} $

(8)

$ Y_j=\frac{y_{\mathrm{L}, j} Z_j}{f} $

(9)

由于SOM算法的保序性，左、右图像的输出权向量无需任何排序算法，一一对应即可自动匹配为同名点，基于三角测距模型依次迭代，生成三维点云向量$\boldsymbol{Q}_j=\left[X_j, Y_j, Z_j\right] \in \bf{R}^3$，至此完成软体机械臂的三维形状重建，整个形状感知算法的伪代码如算法3所示。

算法 3    Shape Recognition Algorithm

1. Initialize W(0), N, α and λ 2. loop 3.     Get current left/right camera frame 4.     Extract the 2D contour point cloud of the 2D contour point cloud of soft manipulator         $\boldsymbol{P}=\left\{\boldsymbol{p}_k=\left[p_{1, k}, p_{2, k}\right], k=1, \cdots, r\right\}$ 5.     for $\lambda(0)=1 ; \lambda(t)<\lambda ; \lambda(t)++$ do 6.         for each pk do 7.             for j = 1; j < n + 1; j + + do 8.                 $\left\|\boldsymbol{p}_k-\boldsymbol{W}_j\right\|=\sqrt{\left(\boldsymbol{p}_k-\boldsymbol{W}_j\right)^{\mathrm{T}}\left(\boldsymbol{p}_k-\boldsymbol{W}_j\right)}$ 9.             end for 10.            Find j*=arg max(‖pk－Wj‖)as the winner neuron, and define Nj*(t) 11.            for all j∈Nj*(t) do 12.                 $\boldsymbol{W}_j(t+1)=\boldsymbol{W}_j(t)+\eta(R) \alpha(t)\left[\boldsymbol{p}_k-\boldsymbol{W}_j(t)\right]$ 13.            end for 14.        end for 15. end for 16. Obtain Wj of left and right image respectively 17. for j=1; j < n+1; j+ + do 18.        $\boldsymbol{Q}_j=\left[X_j=\frac{x_{\mathrm{L}, j} Z_j}{f}, Y_j=\frac{y_{\mathrm{L}, j} Z_j}{f}, Z_j=\frac{f T_x}{d_j}\right]$ 19. end for 20. end loop

3 结果与对比验证

在本文中，为评估所提形状感知算法的性能，分别开展了三维形状感知实验与对比验证实验，对该算法的精度与实时性进行了评价。

3.1 实验结果

本文设计了实时形状感知实验，对形状感知算法的可行性与鲁棒性进行验证。首先，通过比例阀电压驱动程序连续增加每段软体机械臂的气压，其中$P_1(t), P_2(t), P_3(t) \in[0, 160]$kPa，使机械臂逐渐作动至最大弯曲形态。同时运行形状感知算法程序，实时跟踪软体机械臂的三维空间形状。为便于分析，选取运动过程中较为典型的4种姿态，如图 11(a)所示。对应的三维感知仿真结果如图 11(b)所示。每种姿态的25个实验数据Q_j由式(7)~(9)产生，并使用6次多项式拟合形成平滑的三维空间曲线，以连续体的形式更好地描述。

需要说明的是，第1段机械臂是向后弯曲的，与第2段机械臂的弯曲方向正交。除此之外，第3段机械臂的弯曲也出现扭转，而非平面运动，但从上述拍摄角度来看，这些作动特性并不明显。由此可见，该算法可以实时感知软体机械臂多种复杂的三维空间形状，验证了这一算法的可行性与鲁棒性，并在以下文中进一步验证其准确性。

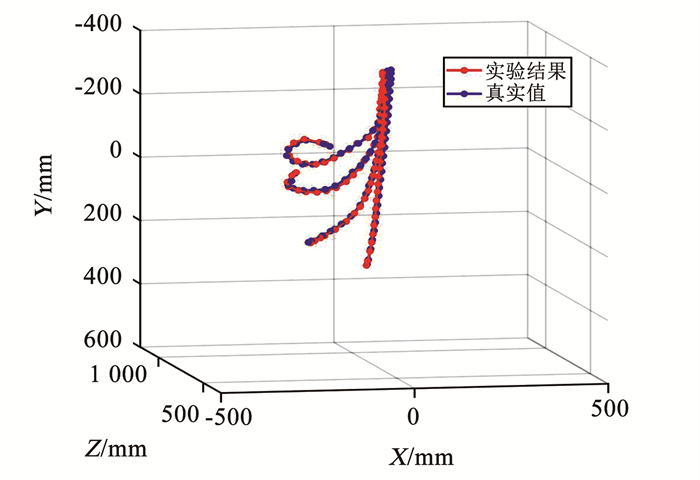
3.2 对比验证

准确性是评价形状感知系统至关重要的性能之一, 本文通过设计对比验证实验对该算法的精度进行量化评价。本文采用ZED双目相机内置深度检测功能，可由目标像素点的二维左图像坐标直接获得三维坐标，即$\left[X^{\prime}, Y^{\prime}, Z^{\prime}\right]=g\left(\left[x_{\mathrm{L}}, y_{\mathrm{L}}\right]\right)$。忽略微小误差不计，将相机深度检测值默认为真实值。具体验证思路如下：在同一程序框架下，针对每一帧图像的SOM聚类结果，直接使用相机深度检测生成真实值$\boldsymbol{Q}_j^{\prime}=\left[X_j^{\prime}, Y_j^{\prime}, Z_j^{\prime}\right]$，与应用所提算法计算得到的实验结果Q_j进行比较，仿真对比验证如图 12所示。

由图 12可以看出，实验结果可以较好的逼近真实值，下面进行详细的误差分析量化这一精度。分别计算每种姿态下，实验结果与真实值在每个轴上的误差ξ，数值仿真如图 13(a)~13(c)所示。通过横向对比可知，在全部姿态中，z轴的误差最大，原因在于深度值Z是基于视差模型计算得到。通过纵向对比可得，构型越复杂的姿态，每个维度的误差越大。

基于上述误差数据，计算4种姿态在每个维度的均方根误差$\mathrm{Re}=\left(\sum\limits_{j=1}^n \xi_j^2 / n\right)^{1 / 2}$，见表 2，鉴于整个机械臂的尺寸，仍在可接受的范围内。误差的产生由以下原因造成：1)ZED相机的深度检测自身具有一定误差(< 1%)；2)三角测距模型默认左、右两个相机的内参完全相同，但实际制作工艺很难达到；3)由于对左、右图像分别进行SOM聚类，中心线对应骨干点可能不是来源于物理空间中的同一点。

在实时性方面，使用getTickCount函数测量可得，整个形状感知算法以10帧/s的速度稳定运行。其中，图像预处理基本不消耗时间；SOM算法的程序执行时间为0.061 s，主要原因在于需要对左、右图像分别运行1次。三维可视化程序运行时间为0.037 s，这是因为matplotlib-3D模块的实时绘图速度较慢，今后会考虑使用其他三维可视化模块代替。影响实时性的因素还包括处理器速度，相机分辨率等外部因素。但实际上，该算法目前的帧率已经足够为控制器提供实时的形状信息了。

最后，将本文所提算法与其他文献中针对软体机械臂的视觉形状感知算法进行了比较。表 3反映了本文算法在各方面性能上均有所提升。

4 结论

1) 使用最大轮廓提取与降采样技术，将样本数据压缩至200+，保证了实时轮廓提取的稳定性与快速性。

2) 实验表明，SOM算法比其他3种聚类算法具有更强的稳定性和保序性。针对SOM算法可调参数多的问题，通过设计误差仿真实验，完成了参数优化与误差补偿，实现了SOM算法在动态形状检测的在线应用。

3) 开展了软体机械臂三维形状的实时感知实验和对比验证实验。结果表明，最大误差为10.41 mm，运行速度可稳定在10帧/s。值得一提的是，与其他文献中的视觉形状检测算法相比，本文算法以构型复杂的三段式软体机械臂为研究对象，在精度与实时性能方面仍具有较好的表现。补充文件中提供了三维形状实时感知的视频，以进一步演示本文算法效果。