2. 陕西省飞行控制与仿真技术重点实验室(西北工业大学),西安 710072;
3. 西安爱生技术集团公司,西安 710065
2. Key Laboratory of Flight Control and Simulation Technology (Northwestern Polytechnical University), Shaanxi Province, Xi'an 710072, China;
3. Xi'an ASN Technology Group Co., Ltd., Xi'an 710065, China
无人机(Unmanned aerial vehicle, UAV)目标对峙(standoff)跟踪广泛应用于侦察、监视、护航等场景。无人机对峙跟踪指无人机从初始位置出发,飞向静止或移动的地面目标环绕其飞行,并保持一定的相对距离(对峙半径)。针对这一问题已有许多研究成果,这些成果大约可以分为两类:基于几何学的方法[1-2]和基于矢量场[3-5]的方法。在文献[1]中,作者采用常曲率段逼近路径,并利用地图信息提高了逼近精度。文献[2]根据建立的无人机跟踪地面目标的极坐标形式,通过控制无人机的航向不断趋近于地面目标牵连跟踪圆切线方向,实现了无人机编队跟踪制导。但是几何方法的不足也很明显,计算较为复杂,并且需要针对不同的情况建立不同的几何关系。与复杂的几何方法相比,矢量场(Vector feild, VF)方法更加简洁,成为人们关注的焦点。矢量场在空间中产生方向吸引子,引导无人机从任意点到目标点。在众多的矢量场中,Lyapunov矢量场(Lyapunov vector field, LVF)受到了最广泛的关注。LVF首先被引入到无人机路径跟踪控制[3]。文献[4]结合了切向矢量场(Tangent vector field, TVF)和LVF的优点,推导了基于无人机作战约束理论的最短路径算法。文献[5]则考虑了曲率约束问题,提出了一种带有循环修正项的曲率约束(Curvature constrained, CC)LVF。而上述的LVF方法要么没有同时考虑收敛速度和曲率约束,要么过于保守,无法发挥无人机的全部能力,如文献[5],同时也没有给出参数选择的指导方法。
由于单架无人机机载设备数量的限制,多架无人机用于standoff目标跟踪受到了人们的关注[2, 6-10]。然而,这些文献主要关注点在于跟踪时的相位保持等问题,而很少有人考虑无人机同时到达目标点。不同位置出发的无人机同时到达目标点具有很强的实际意义,比如打击地面目标时,不同机场出发的无人机只有同时到达目标点才能造成致命一击,不会延误战机。文献[9]为了控制无人机到达目标点的时间,需要对速度和路径进行连续积分,计算复杂度高。文献[11-12]也考虑了带有时间协同的四维轨迹跟踪问题,但是使用的方法仍然是需要计算剩余路径,通过调整速度来控制剩余时间。在寻找更简洁的方法时,tau(τ)理论给了本文很多启发。τ理论是一种仿生学理论,由Lee[13]于1976年首先提出,然后发展为一般的τ理论,试图涵盖所有的感知系统和所有的运动[14]。随后,由于τ变量直接包含时间信息的优势,文献[15-19]将τ理论衍生出的常数τ导引策略和τ耦合策略应用于无人机的四维制导,实现了定时飞行、制动、对接着陆和拦截。
在已有工作的基础上,本文研究了多架无人机同时到达的standoff跟踪问题。首先提出了一种新的比例Lyapunov矢量场(Ratio lyapunov vector field, RLVF)来引导无人机跟踪目标并保持距离。然后与现有的LVF相比,在矢量场中加入一个可设置的参数c,以便同时考虑收敛速度和最大航向角速率。此外,还详细分析了参数c的影响,并给出了给定最大航向角速率的情况下,对c进行如何选择能够最大程度发挥无人机的性能。最后采用τ耦合策略设计协同速度控制器,实现不同初始位置的无人机同步到达目标点。同时这一方法也避免了文献[9, 11-12]中的复杂积分和需要计算不规则路径的缺点。仿真和实验结果表明,所设计的控制器均能实现期望目标。
1 数学模型和问题描述 1.1 无人机模型假定无人机配有自动驾驶仪,能够进行高度保持,具有跟踪速度和航向指令的能力。因此在二维平面下,第i个无人机模型可简化为如下运动学模型:
| $ \left\{\begin{array}{l} \dot{x}_i=V_i \cos \psi_i \\ \dot{y}_i=V_i \sin \psi_i \\ \dot{V}_i=\frac{1}{a_V}\left(V_{i c}-V_i\right) \\ \dot{\psi}_i=\frac{1}{a_\psi}\left(\psi_{i c}-\psi_i\right) \end{array}\right. $ | (1) |
式中:[xi, yi]、Vi、ψi分别为无人机的位置、速度和航向角;Vic、ψic分别为无人机速度指令和航向角指令;aV、aψ分别为自动驾驶仪简化模型的时间常数。对于固定翼无人机,由于其本身性能限制,需要满足相应的限制条件:
定义1 运动间距(或间距)χ是物体当前运动状态和目标运动状态之间的差,在本文中运动间距指无人机当前位置和目标位置的直线距离。
定义2
运动间距的τ变量包含有从当前运动状态到目标运动状态的接触时间(Time to contact, TTC)信息,其定义为运动间距χ和运动间距变化率
| $ \tau_\chi=\frac{\chi(t)}{\dot{\chi}(t)} $ | (2) |
定义3 τ耦合策略。对于两个运动间距X和Y,为了同时闭合这两个运动间距,在闭合过程中,需要保持τX和τY的比值为常数k,即
| $ \tau_X=k \tau_Y $ | (3) |
同时到达的多无人机standoff跟踪示意图如图 1所示。当无人机1获取到地面目标位置后立即向目标位置飞行并保持指定距离进行持续跟踪;同时向无人机2和无人机3发送协同指令。针对处于不同位置的无人机,本文设计速度和航向控制律,实现:1)每个无人机都能够快速跟踪地面目标并保持给定距离,同时满足速度和航向角速率限制;2)所有无人机能够同时到达给定的standoff距离。为了更清楚的描述问题,本文假设无人机处于不同高度且高度无障碍物,因此碰撞问题可以避免。
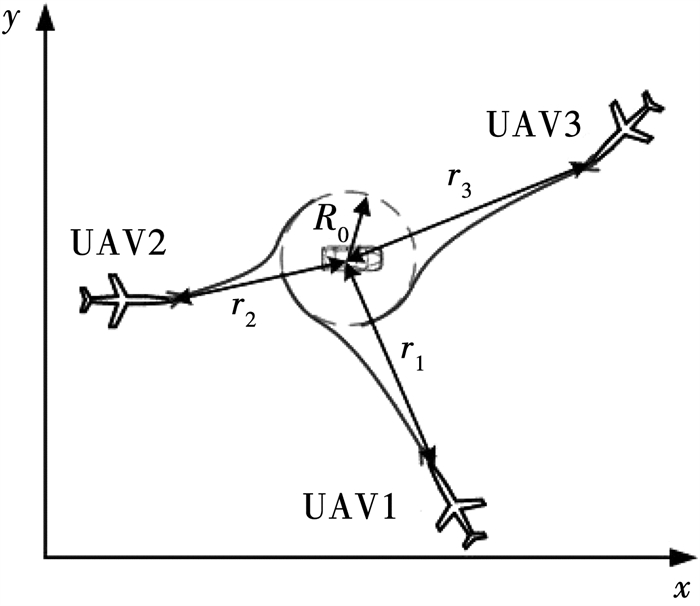
|
图 1 Standoff跟踪示意 Fig. 1 Diagram of standoff tracking |
鉴于已有LVF的缺点,本文提出一种新的比例Lyapunov矢量场(RLVF)。相比于其他LVF,RLVF更易于对矢量场的特点进行分析,这在后面的分析可以看出。设第i架无人机当前位置为[xi, yi],巡航速度为Vi;地面目标位置为[xt, yt],移动速度为[vtx, vty](vtx=vty=0时目标是静止的)。为了保证无人机能够追上目标,要求
| $ \left\{\begin{array}{l} v_{i x}=\frac{V_{i g}\left(-x_{i r}\left(r_i / R_0\right)-c y_{i r} r_i / R_0\right)}{r_i \sqrt{\left(r_i / R_0-1\right)^2+c^2 r_i^2 / R_0^1}} \\ v_{i y}=\frac{V_{i g}\left(-y_{i r}\left(r_i / R_0\right)+c x_{i r} r_i / R_0\right)}{r_i \sqrt{\left(r_i / R_0-1\right)^2+c^2 r_i^2 / R_0^1}} \\ V_{i c}=\sqrt{v_{i x}^2+v_{i y}^2} \\ \psi_{i c}=\arctan \left(\frac{v_{i y}}{v_{i x}}\right) \end{array}\right. $ | (4) |
式中c≠0为设计参数。当c>0时,跟踪方向为逆时针;c < 0时跟踪方向为顺时针。
需要说明的是,如果无人机初始航向角与ψic的差较大时,无人机需要先按照最大航向角速率进行掉头,然后再按照导航控制律(4)飞行。
定理1 对于无人机(1),导航控制律(4)能够导引无人机跟踪上目标,即无人机到目标的距离ri能渐进收敛到给定对峙距离R0。
证明 选取Lyapunov函数为L=(ri/R0-1)2,对L求导可得
| $ \begin{aligned} \frac{\mathrm{d} L}{\mathrm{~d} t}= & \frac{\partial L}{\partial r_i} \frac{\partial r_i}{\partial x_{i r}} \dot{x}_{i r}+\frac{\partial L}{\partial r_i} \frac{\partial r_i}{\partial y_{i r}} \dot{y}_{i r}= \\ & -\frac{V_{i g}\left(r_i / R_0-1\right)^2}{\sqrt{\left(r_i / R_i-1\right)^2+c^2 r_i^2 / R_0^2}} \leqslant 0 \end{aligned} $ | (5) |
这意味着ri/R0-1能够渐进收敛到0,即ri能够渐进收敛到R0。图 2展示了RLVF(c=0.15, R0=20 m)。
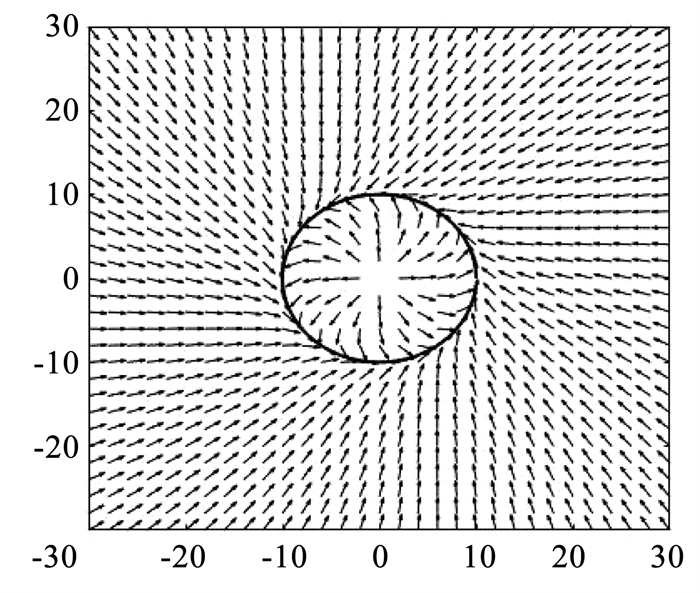
|
图 2 比例Lyapunov矢量场 Fig. 2 Ratio Lyapunov vector field |
对ri求导,可以得到:
| $ \begin{aligned} \dot{r}_i= & \frac{\partial r_i}{\partial x_{i r}} \dot{x}_{i r}+\frac{\partial r_i}{\partial y_{i r}} \dot{y}_{i r}= \\ & -\frac{V_{i g}\left(r_i / R_0-1\right)}{\sqrt{\left(r_i / R_0-1\right)^2+c^2 r_i^2 / R_0^2}} \end{aligned} $ | (6) |
显然,|c|越小,收敛速度越快,并且当|c|→0时,
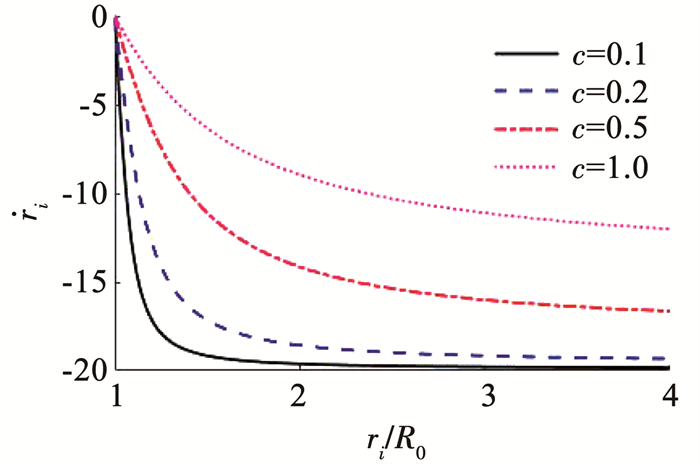
|
图 3 不同参数c对应的收敛速度曲线 Fig. 3 Convergence speed curves with different c |
为了简化分析,仅考虑目标静止时情况,即vtx=vty=0(目标运动时只需将速度修正为飞行实际速度即可)。对
| $ \begin{aligned} \omega_i= & \dot{\psi}_i=\left(\arctan \left(\frac{v_{i y}}{v_{i x}}\right)\right)^{\prime}=\frac{v_{i x} \dot{v}_{i y}-\dot{v}_{i x} v_{i y}}{v_{i x}^2+v_{i y}^2}= \\ & \frac{V_i c\left(\left(r_i / R_0-1\right)\left(r_i / R_0-2\right)+c^2 r_i^2 / R_0^2\right)}{R_0\left(\left(r_i / R_0-1\right)^2+c^2 r_i^2 / R_0^2\right)^{3 / 2}} \end{aligned} $ | (7) |
可以看出,当ri/R0→∞(无人机离目标较远时)时,航向角速率|ωi|→0(直线追及目标);当ri/R0→1(跟踪)时,|ωi|→ωf=Vi/R0(盘旋角速度)。这与实际是相符的。为了进一步求出在追及过程中航向角速率ωi的最大值,定义κ=ri/R0,对ωi求偏导并令其等于0,可得
| $ \begin{gathered} \frac{\partial \omega_i}{\partial \kappa}=0 \\ \Downarrow \\ \kappa^3\left(c^2+1\right)^2-5 \kappa^2\left(c^2+1\right)+\kappa\left(4 c^2+7\right)-3=0 \end{gathered} $ | (8) |
方程(8)的解析解较为复杂,本文通过数值解方法获取结果。图 4展示了方程(8)的数值解集合(极值点坐标合集)。
|
图 4 方程(8)的解集 Fig. 4 Solution of Eq.(8) |
由式(7)进一步可得
| $ \frac{\omega_i}{\omega_f}=\frac{c\left((\kappa-1)(\kappa-2)+c^2 \kappa^2\right)}{\left((\kappa-1)^2+c^2 \kappa^2\right)^{3 / 2}} $ | (9) |
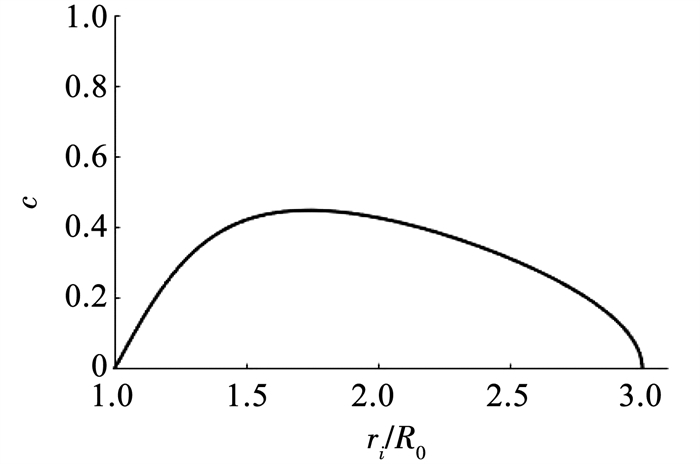
将方程(8)的数值解带入式(9),可得到相应的ωi/ωf的最大值(即ωi的最大值)。图 5展示了|ωi/ωf|的曲线(c < 0时曲线与c>0呈沿x轴轴对称)。当给定最大航向角速率,给定巡航速度(最大速度)和对峙半径后,计算出ωi/ωf,然后根据图 5即可选择出合适的参数c,既能保证在全过程中不超过给定限制,又能最大程度发挥出无人机性能。
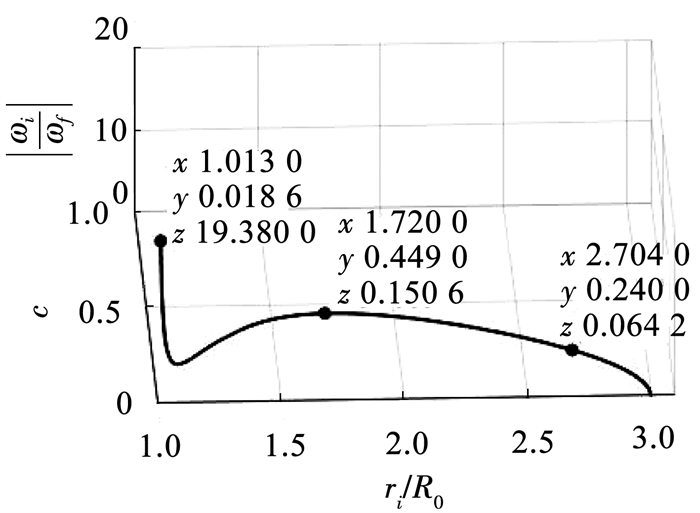
|
图 5 不同参数c对应的|ωi/ωf|最大值 Fig. 5 Maximum values of |ωi/ωf| with different c |
对于多机协同对地监视和打击任务,往往要求多机同时到达目标点。现有的方式都是通过规划剩余路程和速度来实现,需要对路径和速度进行积分,这使得计算过程十分复杂。而运动的τ变量所包含的信息正是“接触时间”,避免了非规则路径复杂计算的问题。本文基于τ耦合策略,提出一种新的协同速度控制算法,利用Leader-Follower方法,通过直接耦合两个无人机的τ变量而非本征制导运动(与文献[16, 18]相比),实现多机的同时到达跟踪目标。
假设无人机1为Leader,无人机i(i>1)为follower,分别选择运动间距为r1和ri,则定义各自的τ变量为:
| $ \tau_1=-\frac{r_1}{V_1} $ | (10) |
| $ \tau_i=-\frac{r_i}{V_i} $ | (11) |
设计无人机i的协同τ速度控制器为
| $ V_{i g}=V_g-\left(k_P\left(\tau_1-\tau_i\right)\right) $ | (12) |
式中kP>0为控制参数。
定理2 通过设计控制参数kP,则式(12)能够保证τ1-τi=0,即τ1=τi。由τ耦合策略可知,当满足τi=τ1时,间距ri与r1可同时闭合,即无人机i与无人机1同时到达目标点。
证明 由τi(i=1, 2, …)定义可知,τi包含的信息为无人机以直线飞行到达目标点所剩余的时间。实际中,临近目标点的最后一段往往是直线飞行,因此只要τi=τ1(i=2, …),即剩余时间一样,可同时到达。
定义e=τi-τ1,假设无人机直线飞行且目标点静止,对e求导可得
| $ \dot{e}=\frac{\dot{r}_1}{V_1}-\frac{\dot{r}_i V_i-r_i \dot{V}_i}{V_i^2} $ | (13) |
根据假设,由ri的定义可得
| $ \begin{array}{*{20}{l}} \dot{r}_i= & \frac{1}{r_i}\left[\left(x_i-x_t\right) V_i \cos \psi_i+\left(y_i-y_t\right) V_i \sin \psi_i\right]= \\ & V_i \cos ^2 \psi_i+V_i \sin ^2 \psi_i=V_i \end{array} $ | (14) |
所以有
| $ \begin{aligned} \dot{e}= & \frac{V_1}{V_1}-\frac{V_i^2-r_i\left(\frac{1}{a_V}\left(V_g-k_P e-V_i\right)\right)}{V_i^2}= \\ & -\frac{k_P r_i}{a_V V_i^2} e+\frac{r_i}{a_V V_i^2}\left(V_g-V_i\right) \end{aligned} $ | (15) |
可以看出,对于状态e来说,是典型的一阶惯性环节,且系统是稳定的,因此,e→0,即τi→τ1。
飞行过程中,无人机1直线飞行,无人机i因避障等原因没有按直线飞行,即ri没有减小或减小较慢,那么|τ1| < |τi|,也就是无人机1的剩余时间少,而无人机i的剩余时间多,如果依然按照当前速度飞行,就不能同时达到。此时控制律(12)就会起作用,增加无人机i的速度。值得注意的是,间距ri和r1的定义是无人机到目标点的直线距离,而非剩余飞行距离(当有避障、转弯等行为时,航迹可能为弧线等不规则形状)。该控制器的优点在于,控制器只需要计算ri和r1而不用计算剩余实际飞行距离,这是很容易的;不论实际飞行轨迹的形状如何,只要无人机有着在给定的速度限制下存在同时到达的可能性,那么该控制器就能通过调整飞行速度来保证同时到达。这在后面的仿真中会得到验证。
4 跟踪仿真与分析 4.1 数字仿真验证目标静止和运动情况下数字仿真所得结论是一致的,为了避免内容重复冗长,数字仿真主要描述目标静止情况下的仿真结果。设置有3架无人机,其中无人机1为Leader,无人机2、3为Followers。设置初始条件为:[x1, y1]=[0 m, 0 m],[x2, y2]=[0 m, 1 700 m],[x3, y3]=[1 600 m, 1 000 m],V1=V2=V3=20 m/s;ψ1=ψ2=ψ3=0°。地面目标初始位置[xt, yt]=[800 m, 700 m],standoff半径R0=200 m。根据无人机性能,设置Vmin=12 m/s,Vmax=30 m/s,ωmax=15(°)/s,Vg=20 m/s。仿真在Matlab环境下完成,仿真步长为0.02 s。设置vtx=vty=0,即目标是静止的。此时ωf=5.73(°)/s。因此根据图 5,选择参数c≥0.1,即可全过程中|ωi/ωf| < 2.6。此处选择c=0.1。选择参数k=1,kP=2。仿真结果如图 6~10所示。

|
图 6 无人机轨迹 Fig. 6 Trajectory of UAVs |
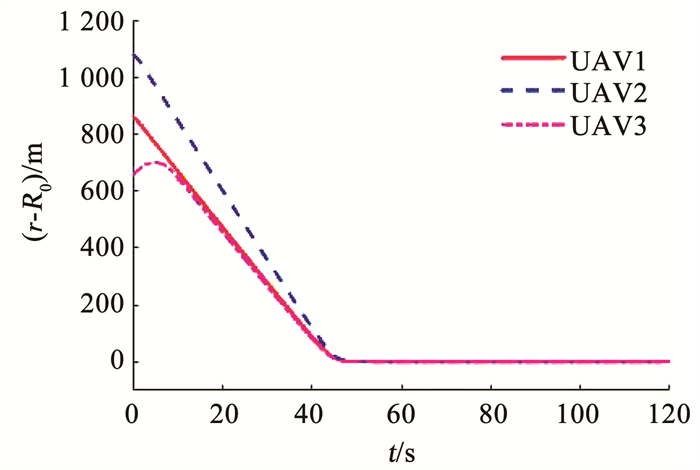
|
图 7 无人机的(ri-R0)距离 Fig. 7 (ri-R0) distance of UAVs |
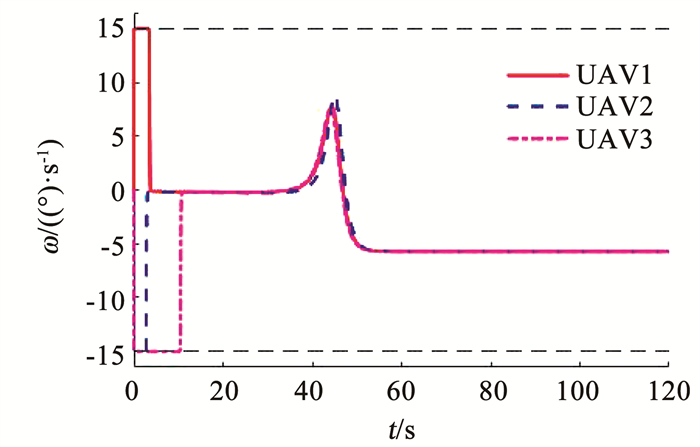
|
图 8 无人机航向角速率ωi曲线 Fig. 8 Heading angular rate ωi of UAVs |
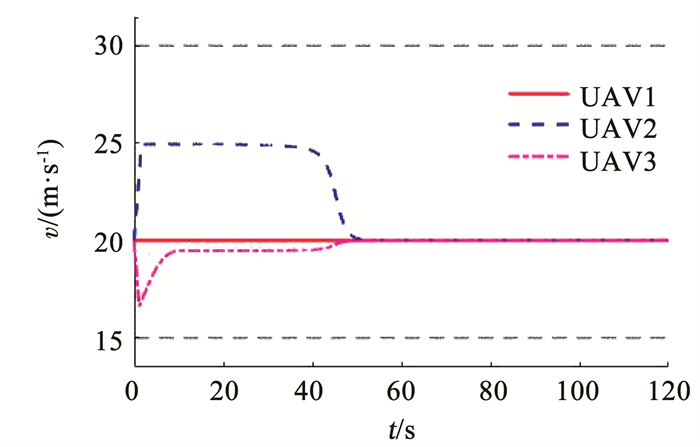
|
图 9 无人机速度曲线 Fig. 9 Velocity curves of UAVs |
|
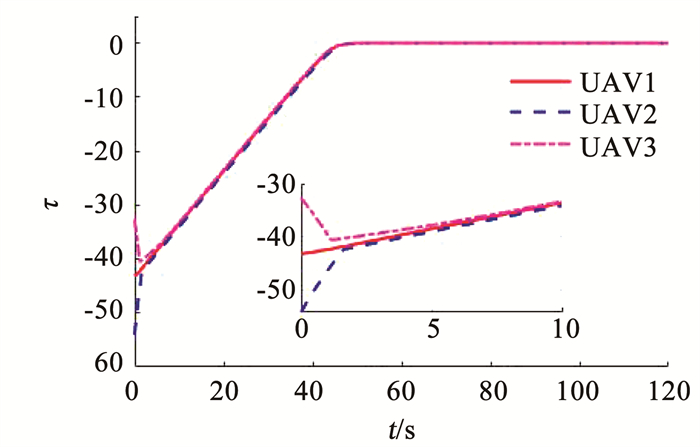
图 10 无人机τi曲线 Fig. 10 τi curves of UAVs |
图 6为3架无人机追及目标的轨迹,图 7展示了追及过程中距离(ri-R0)的收敛过程。在图中可以看出,在45 s的时候,3架无人机同时追及到对峙距离;需要注意,由于无人机的初始航向角并不是对着目标,因此开始阶段有一个以最大航向角速率转弯的过程,这在图 8中可以看到;而这段过程的路径长度不容易计算,一般的制导律(如文献[11-12]中)处理起来较为复杂,但是本文提出的控制律(12)依然保证了3架无人机的同时到达。图 8为无人机的航向角速率曲线,可以看出,全过程中航向角速率未超过给定的限制。相比于无人机1,由于无人机2距离目标较远,无人机3距离目标较近,因此为了保证同时到达,无人机2需要加速,无人机3需要减速,图 9展示了这一过程;最终使得τ1=τ2=τ3,如图 10所示。
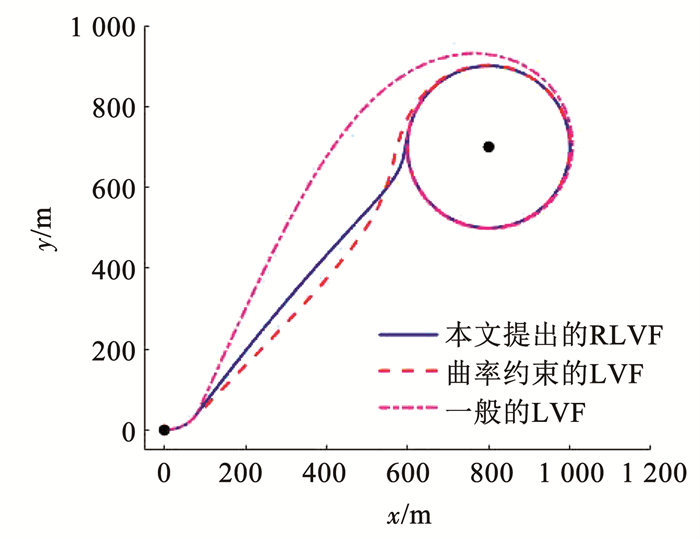
图 11~13展示了同样条件下不同的Lyapunov向量场下无人机追击目标过程的对比。可以看出,在本文提出的RLVF作用下,无人机追及目标需要45 s,而文献[5]中曲率约束的LVF作用下需要58 s,一般的LVF[3, 7]作用下则需要95 s,即本文提出的方法能够更快的追及到目标。图 13展示了不同LVF下航向角速率对比,可以看到,本文提出的RLVF方法有着更长的直线追及目标的过程(0~35 s),然后以较大的航向角速率进行转弯(35~44 s)以更快的收敛到跟踪圆上,最大程度的挖掘了无人机的性能;同时,由于参数的选择是通过定量分析完成的,因此能够保证航向角速率不超过给定的最大值。
|
图 11 不同LVF下无人机1的轨迹 Fig. 11 Trajectory of UAV1 with different LVF |

|
图 12 不同LVF下无人机1的(ri-R0)距离 Fig. 12 (ri-R0) distance of UAV1 with different LVF |

|
图 13 不同LVF下无人机1的航向角速率ω1 Fig. 13 Heading angular rate ω1 of UAV1 with different LVF |
为了进一步验证本文提出的控制律的有效性,且具有较强的工程实现性,针对目标运动情况,开展了硬件在环的仿真验证,实验设备如图 14所示,其中,下位机使用研华科技的工控机,装载XPC实时系统,下载有实验室自行设计开发的倒V尾小型无人机非线性模型;上位机的配置为i5-9500处理器,8 G内存,使用Matlab2016b软件;飞控计算机使用STM32F429处理器,下载了自驾仪程序以及本文设计的导航程序。飞控计算机与下位机通过串口服务器交换数据,下位机中的飞机模型将获取到的飞机姿态、速度、位置等信息通过串口服务器发给飞控计算机,飞控计算机解算控制律后将舵偏值和推力通过串口服务器返回给下位机飞机模型。因为目前实验室开发的飞控计算机还未装载电台模块,因此无人机间的信息交互也是通过串口服务器完成的。

|
图 14 硬件在环实验设备 Fig. 14 Hardware-in-loop experimental equipment |
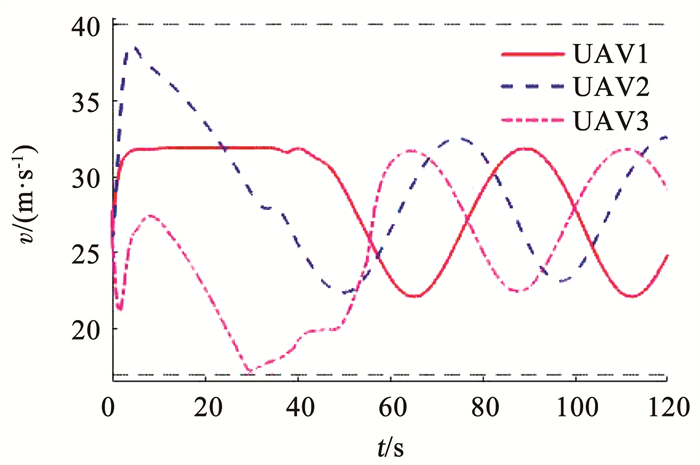
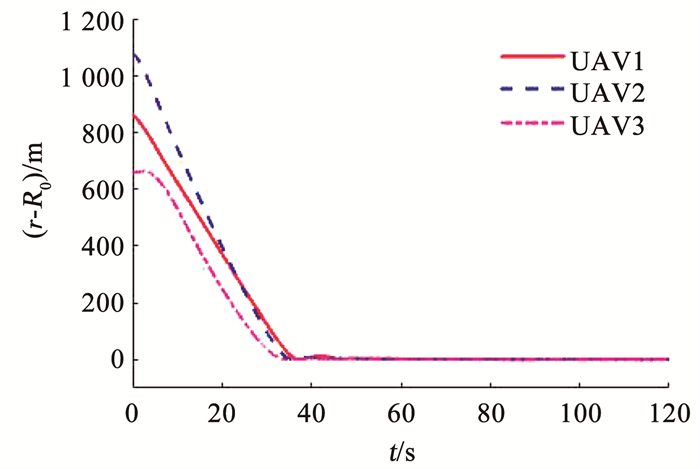
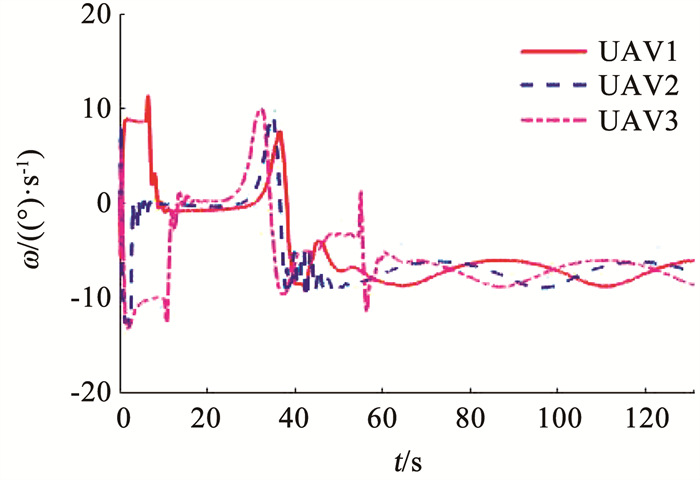
设置初始条件为[x1, y1]=[0 m, 0 m],[x2, y2]= [0 m, 1 700 m],[x3, y3]=[1 600 m, 1 000 m],地面目标的移动速度为[vtx, vty]=[3 m/s, 4 m/s],跟随半径为R0=200 m。无人机的速度限制为Vmin=17 m/s,Vmax=40 m/s,最大航向角速率为12(°)/s,因此设置c=0.17。仿真结果如图 15~18所示。图 15展示了无人机跟踪动态目标的轨迹,图 16为无人机为了同时跟踪到目标的速度响应,因为此时目标是移动的,因此速度调整也是一个动态的过程。从图 17中可以看到,在τ耦合算法控制下,3架无人机同时追踪到目标。图 18展示了在追及过程中无人机的航向角速率,可以看出,整个过程中航向角速率都在给定限制内。

|
图 15 无人机追踪动态目标轨迹 Fig. 15 Trajectory of UAVs tracking moving target |
|
图 16 无人机速度曲线 Fig. 16 Velocity curves of UAVs |
|
图 17 无人机的(ri-R0)距离 Fig. 17 (ri-R0) distance of UAVs |
|
图 18 无人机航向角速率ωi Fig. 18 Heading angular rate ωi of UAVs |
1) 理论分析了新的比例Lyapunov矢量场,分析结果表明,可调参数值越小,收敛速度越快,但航向角速率越大。
2) 通过数值求解非线性二元方程,给出了最大航向角速率与可调参数的关系图,以帮助选择合适的参数来平衡收敛速度和最大航向角速率。
3) 利用τ耦合理论所设计的多架无人机协同速度控制器直接耦合了无人机之间的τ信息,实现了多架无人机的同步到达。
4) 数字实验(目标静止)和硬件在环实验(目标运动)均表明了该方法能够导引无人机同时到达目标点,且最大程度的发挥了无人机性能,比其他方法更快的跟踪到地面目标,并且能够应用于工程实际。
| [1] |
OH H, KIM S, TSOURDOS A. Road-map-assisted standoff tracking of moving ground vehicle using nonlinear model predictive control[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(2): 975. DOI:10.1109/TAES.2014.130688 |
| [2] |
张民, 夏卫政, 黄坤, 等. 基于Leader-Follower编队的无人机协同跟踪地面目标制导律设计[J]. 航空学报, 2018, 39(2): 321497. ZHANG Min, XIA Weizhen, HUANG Kun, et al. Guidance law for cooperative tracking of a ground target based on leader-follower formation of UAVs[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(2): 321497. DOI:10.7527/S1000-6893.2017.21497 |
| [3] |
LAWRENCE D A, FREW E W, PISANO W J. Lyapunov vector fields for autonomous unmanned aircraft flight control[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(5): 1220. DOI:10.2514/1.34896 |
| [4] |
CHEN Hongda, CHANG Kuochu, AGATE C S. UAV path planning with tangent-plus-Lyapunov vector field guidance and obstacle avoidance[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 840. DOI:10.1109/TAES.2013.6494384 |
| [5] |
POTHEN A A, RATNOO A. Curvature-constrained Lyapunov vector field for standoff target tracking[J]. Journal of Guidance, Control, and Dynamics, 2017, 40(10): 2729. DOI:10.2514/1.G002281 |
| [6] |
SHIN Dongmin, SONG Yeongho, OH J, et al. Nonlinear disturbance observer-based standoff target tracking for small fixed-wing UAVs[J]. International Journal of Aeronautical and Space Sciences, 2021, 22(1): 108. DOI:10.1007/s42405-020-00275-6 |
| [7] |
CHE Fei, NIU Yifeng, LI Jie, et al. Cooperative standoff tracking of moving targets using modified Lyapunov vector field guidance[J]. Applied Sciences, 2020, 10(11): 3709. DOI:10.3390/app10113709 |
| [8] |
HE Shaoming, WANG Jiang, LIN Defu. Unknown ground moving target tracking using multiple unmanned aerial vehicles[J]. Journal of Aerospace Engineering, 2019, 233(3): 1021. DOI:10.1177/0954410017744812 |
| [9] |
LIM Seunghan, KIM Yeongju, LEE Dongjin, et al. Standoff target tracking using a vector field for multiple unmanned aircrafts[J]. Journal of Intelligent & Robotic Systems, 2013, 69(1): 347. DOI:10.1007/s10846-012-9765-7 |
| [10] |
HYONDONG O, SEUNGKEUN K. Persistent standoff tracking guidance using constrained particle filter for multiple UAVs[J]. Aerospace Science and Technology, 2019, 84: 257. DOI:10.1016/j.ast.2018.10.016 |
| [11] |
崔乃刚, 韦常柱, 郭继峰. 导弹协同作战四维制导控制研究[J]. 飞行力学, 2010, 28(2): 63. CUI Naigang, WEI Changzhu, GUO Jifeng. Research on four-dimensional guidance and control for missile cooperative engagement[J]. Flight Dynamics, 2010, 28(2): 63. DOI:10.13645/j.cnki.f.d.2010.02.23 |
| [12] |
陆冠华, 夏洁, 周锐. 基于路径自主规划的无人机四维战术轨迹跟踪[J]. 导弹与航天运载技术, 2018(4): 56. LU Guanhua, XIA Jie, ZHOU Rui. 4D tactical trajectory tracking of UAV based on autonomous planning[J]. Missiles and Space Vehicles, 2018(4): 56. DOI:10.7654/j.issn.1004-7182.20180412 |
| [13] |
LEE D D. A theory of visual control of braking based on information about time to collision[J]. Perception, 1976, 5(4): 437. DOI:10.1068/p050437 |
| [14] |
LEE D D. General Tau Theory: Evolution to date[J]. Perception, 2009, 38(6): 837. DOI:10.1068/pmklee |
| [15] |
FARID K. Four-dimensional guidance and control of movement using time-to-contact: Application to automated docking and landing of unmanned rotorcraft systems[J]. International Journal of Robotics Research, 2014, 33(2): 237. DOI:10.1177/0278364913509496 |
| [16] |
YANG Zuqiang, FANG Zhou, LI Ping. Decentralized 4D trajectory generation for UAVs based on improved intrinsic tau guidance strategy[J]. International Journal of Advanced Robotic Systems, 2016, 13(3): 88. DOI:10.5772/63431 |
| [17] |
FARID K, BILAL A. Bio-inspired tau pilot for automated aerial 4D docking and landing of unmanned aircraft systems[C]//IEEE International Conference on Intelligent Robots and Systems. Algarve: [s. n. ], 2012: 480
|
| [18] |
YANG Zuqiang, FANG Zhou, LI Ping. Bio-inspired collision-free 4D trajectory generation for UAVs using tau strategy[J]. Journal of Bionic Engineering, 2016, 13(1): 84. DOI:10.1016/S1672-6529(14)60162-1 |
| [19] |
ZHANG Zhen, ZHANG Shutao, XIE Pu, et al. Bioinspired 4D trajectory generation for a UAS rapid point-to-point movement[J]. Journal of Bionic Engineering, 2014, 11(1): 72. DOI:10.1016/S1672-6529(14)60021-4 |
 2023, Vol. 55
2023, Vol. 55


