旋翼类飞行器在高下降速度和接近垂直下降角度下降时,会陷入称为涡环状态(VRS)的高度不稳定和湍流的飞行状态,升力、扭矩、俯仰和滚转力矩均发生不规则变化,使飞行器振动,极易导致飞行器坠毁[1]。倾转旋翼机有左、右两副旋翼,在下降过程中两副旋翼均可能遭遇涡环问题,不仅存在类似直升机旋翼拉力降低导致坠毁的问题,而且也存在因涡环状态导致旋翼两边拉力不对称、滚转力矩失衡而倾覆的问题,更需要重视其飞行安全。美国的倾转旋翼机V-22的几次坠机事故与涡环状态的影响相关,因为倾转旋翼机在下降过程中,对称的旋翼的涡环产生非对称破碎,倾转旋翼机滚转力矩失衡而侧翻。基于此,研究倾转旋翼机的涡环状态特性,了解其涡环状态时流场的演变规律,制定准确的倾转旋翼机的涡环边界,对倾转旋翼机的设计和安全飞行具有重要意义。
Stack[2]在水洞中模拟了旋翼涡环状态的流场, Green等[3]通过PIV试验研究了涡环状态的流场变化,该类文献通过试验研究揭示了涡环状态的演变规律。Johnson[4]使用风洞和飞行试验数据,给出了基于动量理论的旋翼的涡环模型。Wolkovitch[5]提出利用动量理论结合试验数据预测涡环边界的方法,制定了Wolkovitch判据。Peter等[6]引入了动态入流理论,重新计算了涡环状态的边界,并制定Peter判据。辛宏等[7]对直升机垂直下降涡环状态进行了实验研究,并制定了高/辛判据涡环边界模型。Brown等[8]使用涡量传输模型对在涡环状态附近和涡环状态内运行的旋翼的涡流尾流进行了高分辨率计算模拟,模拟了涡环的运动规律。Prasad等[9]提出了环形涡流理论模型,可用于实时仿真。黄明其等[10]通过试验,研究了直升机旋翼的涡环特性,并给出了参数对涡环特性的影响。Betzina[11]采用试验方法研究了倾转旋翼机进入涡环状态时的气动特性,主要集中在旋翼力和扭矩的变化。Takii等[12]采用CFD方法研究了倾转旋翼机的涡环状态时涡量的变化细节,表现了倾转旋翼机涡环状态流场的复杂性。但该类研究仍存在不足:一方面,机翼干扰对旋翼涡环状态的影响较大,相关研究较少采用数值模拟方法,难以模拟倾转旋翼机涡环状态的演变细节和非定常流场;另一方面,相关涡环边界模型均以直升机为主,而关于倾转旋翼机的涡环边界模型在国内外文献中较少。
针对上述问题,采用基于非结构滑移网格技术生成围绕旋翼和机翼的高质量网格,建立一套考虑机翼对旋翼涡环状态干扰的数值模拟方法,分析垂直下降状态下倾转旋翼机的涡环状态的演化过程以及旋翼受力和扭矩的变化规律,建立垂直和斜下降状态下倾转旋翼机的涡环边界模型,并制定改出策略。
1 计算方法 1.1 几何模型研究的倾转旋翼机构型如图 1(a),倾转旋翼机下降时旋翼的涡环状态干扰主要来源于机翼与旋翼之间干扰,机身对旋翼涡环状态影响较小,为了研究方便,忽略机身;为了提高计算效率,采用对称的方式,对模型进行简化,如图 1(b),主要参数见表 1。

|
图 1 研究对象 Fig. 1 Research model |
| 表 1 倾转旋翼机简化计算模型主要参数 Tab. 1 Parameters of the simplified calculation model of the Tiltrotor |
根据倾转旋翼机存在“旋翼运动,机翼静止”的特点,采用非结构滑移网格技术处理旋翼网格运动的问题,将计算域划分为包含旋翼的动域和包含机翼的静域。倾转旋翼机的旋翼、机翼附面层网格采用棱柱体网格生成,其他部分网格采用非结构网格。
为了确认网格无关性,考虑了黏性效应的影响,分别分析了旋翼第1层边界层网格的高度和网格密度对计算结果的影响。
参考旋翼的弦长,研究的倾转旋翼机的旋翼处的雷诺数处于105~106范围,雷诺数较低,边界层具有较为复杂的流动结构。需要适当的边界层网格来更好地模拟边界层内的黏性相互作用以及在进入涡环状态期间发生的复杂流动结构。在网格独立性验证中,边界层网格采用逐步加密的方式,第1层边界层网格的网格高度(d1)分别设置为0.000 10,0.000 05,0.000 03,0.000 01 m,增长率设置为1.1,总层数为15。表 2展示了不同网格高度对计算结果的影响,d1=0.000 03 m的网格高度可以满足计算要求。
| 表 2 旋翼第1层网格高度对旋翼拉力的影响 Tab. 2 Lift coefficient of the rotor with different heights of the first boundary layer |
在研究网格密度对计算结果的影响中,分别对动域、静域、整体加密的方式生成网格。网格节点总数分别为1 000万、1 300万、2 000万和800万。网格密度对计算结果的影响见表 3。考虑到计算的准确性和经济性,选用1 300万个网格节点计算模型的气动性能。
| 表 3 网格密度对计算结果的影响 Tab. 3 Influence of grid density on calculation results |
网格无关性验证表明,1 300万个节点、第1层边界层网格高度为0.000 03 m的计算网格可以满足计算精度要求。倾转旋翼机的网格如图 2所示。

|
图 2 网格示意图 Fig. 2 Grid diagram |
计算的旋翼转速为2 400 r/min,Ma>0.3,飞行器处于低雷诺数环境,考虑黏性影响,考虑压缩性影响。控制方程为雷诺平均Navier-Stokes(N-S)方程,守恒形式为
| $ \frac{\partial}{\partial t} \int_{\Omega} \boldsymbol{W} \mathrm{d} \Omega+\int_{\partial \Omega}\left(\boldsymbol{F}_c-\boldsymbol{F}_v\right) \mathrm{d} s=\int_{\Omega} \boldsymbol{Q} \mathrm{d} \Omega $ | (1) |
式中:Q为源项,Ω为控制体单元体积,dΩ为控制体表面单元面积,ds为微元面积。
守恒变量W表达式为
| $ \boldsymbol{W}=\left[\begin{array}{lllll} {\rho} & {\rho u} & {\rho} v & \rho w & \rho E \end{array}\right]^{\mathrm{T}} $ | (2) |
式中:ρ为密度,E为单位质量的总能量,u、v、w为绝对速度在坐标系的分量。
对流通量Fc的表达式为
| $ \boldsymbol{F}_c=\left[\begin{array}{c} \rho V \\ \rho u V+n_x p \\ \rho v V+n_y p \\ \rho w V+n_z p \\ \rho H V \end{array}\right] $ | (3) |
式中:p为流体静压,单位质量总焓
黏性通量Fv表达式为
| $ \boldsymbol{F}_v=\left[\begin{array}{c} 0 \\ n_x \tau_{x x}+n_y \tau_{x y}+n_z \tau_{x z} \\ n_x \tau_{y x}+n_y \tau_{y y}+n_z \tau_{y z} \\ n_x \tau_{z x}+n_y \tau_{z y}+n_z \tau_{z z} \\ n_x \varTheta_x+n_y \varTheta_y+n_z \varTheta_z \end{array}\right] $ | (4) |
式中:τij为黏性张量分量,μ为分子黏性,k为热传导系数,Θ为黏性和热传导相关项。
1.4 湍流模型倾转旋翼机的旋翼具有相对较低的雷诺数,为了准确模拟旋翼的桨尖涡和尾流,选用k-ω SST(shear stress transport)湍流模型[13],k-ω模型能准确模拟湍流边界层底层流动,k-ε模型稳定性较好,对存在复杂流动和可压缩流动适应性较好。k-ω SST湍流模型能准确模拟倾转旋翼机的边界层流动和涡环状态时的非定常流场。湍流模型对旋翼气动流场特性的影响主要表现在对边界层流场的模拟,直接关系到拉力和扭矩的计算精度,使用k-ω SST湍流模型计算的边界层流速分布如图 3所示,沿旋翼壁面法线方向速度从0 m/s增长到80 m/s(此处旋翼相对速度),变化趋势符合边界层理论,可验证采用SST湍流模型的合理性。

|
图 3 旋翼边界层流速分布 Fig. 3 Boundary layer velocity distribution |
求解Navier-Stokes方程的数值方法在空间和时间上单独离散。本文采用有限体积法进行空间离散,空间对流项离散采用近似Riemann求解器的Roe格式。为了提高求解非定常流场的效率,采用双时间隐式LU-SGS迭代法进行时间离散[14]。
1.6 方法验证建立的数值模拟方法的准确性通过文献[15]进行验证。Kolaei等[15]进行了旋翼垂直下降时的风洞试验,具体试验细节详见文献[15]。试验几何模型采用T-motor 18.0×6.1的旋翼,直径为0.457 2m,采用DAVISSM翼型,弦长和扭转角分布如图 4所示。

|
图 4 T-motor 18.0×6.1旋翼弦长和扭转角分布 Fig. 4 Rotor chord and twist angle distribution of T-motor 18.0×6.1 |
根据网络划分中的网格设置方法生成网格,网格总数约600万,网格图如图 5所示。旋翼转速设置为3 000 r/min。

|
图 5 验证模型的网格 Fig. 5 Grid of verification model |
旋翼的拉力系数CT和功率系数CP分别由CFD计算值换算,换算公式为:
| $ C_T=\frac{2 T}{\rho \boldsymbol{A}(\omega R)^2} $ | (5) |
| $ C_P=\frac{2 Q}{\rho \boldsymbol{A} R(\omega R)^2} $ | (6) |
式中:T为CFD计算旋翼拉力,N;Q为CFD计算旋翼扭矩,N·m;ρ为空气密度;A为旋翼桨盘面积,m2。
CFD的计算结果与文献中的实验值对比如图 6所示。从图 6中可以看出,旋翼在下降速度较小和下降速度较大时,拉力和功率的误差均较小,但在下降速度为6 m/s时,误差较大,此时可判断旋翼处于涡环状态,总体来说,拉力系数误差最大值在5%以内,功率系数误差最大值在20%以内。一方面,误差来源于旋翼在涡环状态时的流动结构复杂,仿真难度大。另一方面,误差来源于试验几何模型和CFD计算时网格无法准确捕捉流场。总体来说,本文建立的CFD方法适用于倾转旋翼机涡环状态的计算。

|
图 6 计算方法验证 Fig. 6 Method validation |
倾转旋翼机悬停时,旋翼转速为2 400 r/min,总距为14°,单个旋翼拉力TH为199 N。根据动量定理,旋翼悬停时的诱导速度vh为
| $ v_h=\sqrt{T_H / 2 \rho A} $ | (7) |
算出诱导速度vh大小为8.577 m/s。
图 7为倾转旋翼机以不同下降速度vH(垂直下降速度)垂直下降时的流线图,其中红色线为旋翼和机翼。由图 7(a)、7(b)可看出,倾转旋翼机下降率(vH/vh)较小,旋翼诱导速度远大于旋翼下降速度,仍然能卷起较大的环状涡,但环状涡离桨盘平面下方和桨尖均较远,环状涡体积较大,涡的强度不大,对倾转旋翼机的气动性能影响有限,旋翼力与扭矩的波动不大。此时,旋翼的桨尖涡的自诱导速度大于桨盘平面下降速度,大部分桨尖涡仍然能向下运动直到耗散。旋翼形成的涡环离桨盘平面较远,诱导速度占主导优势,但仍存在下方旋翼尾迹绕流到旋翼上方,造成旋翼上方的入流场逐渐不连续,形成颠簸等非定常现象,主要表现是旋翼气动力和力矩出现脉动,机体出现轻微的振动,随着下降速度的增大,非定常特性会更加明显。在vh=3 m/s时(vH/vh=0.350)时,可看到涡环上部靠近桨盘平面,说明倾转旋翼机此时开始进入涡环状态早期,此时旋翼周围的气流紊乱不太严重,对旋翼升力和扭矩影响不大。

|
图 7 倾转旋翼机流场流线图 Fig. 7 Flow diagram of the Tiltrotor flow field |
由图 7(d)可看出,vh=7 m/s(vH/vh=0.816)时,旋翼进入涡环状态中期。此时,涡环的涡核半径不断增大,但环状涡体积逐渐减小,涡环的强度增大。随着倾转旋翼机下降率的增大,自由流和诱导速度共同作用,使得旋翼桨尖涡和尾迹聚集在旋翼下方,向旋翼周围输运,形成靠近桨盘平面外围的环状涡流结构,桨盘上方形成回流区[16]。当倾转旋翼机下降率继续增加时,旋翼卷吸周围的桨尖涡的涡量而增加其环量,涡环体积继续缩小并逐步靠近桨盘平面,涡环强度继续增大,进入成熟的涡环状态。如图 8所示,旋翼周围不断形成大尺度涡结构和涡环结构的内在不稳定性,涡结构被不断切割和破碎;同时机翼位于旋翼下方,旋翼产生的桨尖涡和尾迹会冲击机翼,旋翼由于部分阻塞效应也增加了旋翼的部分性能,综合影响导致旋翼和机翼周围流场的极不稳定,使得旋翼拉力和扭矩剧烈波动,如图 9所示。图 10为下降速度为7 m/s时桨盘垂直截面Z轴方向速度云图,由于机翼对气流的阻塞效应,使得每个旋翼所处的涡环不完整,机翼上方集聚的桨尖涡仍能向周围耗散,这降低了涡环的破坏作用。倾转旋翼机左、右两边均有旋翼,2个旋翼均有明显的拉力损失,同时2个旋翼拉力不规律脉动也足以导致倾转旋翼机坠毁。此时,采取提高总距角的方式,会使得涡环状态更加恶化,周围气流环境更加紊乱,不规律脉动现象进一步明显。

|
图 8 涡量图(vH=7 m/s) Fig. 8 Vorticity diagram(vH=7m/s) |
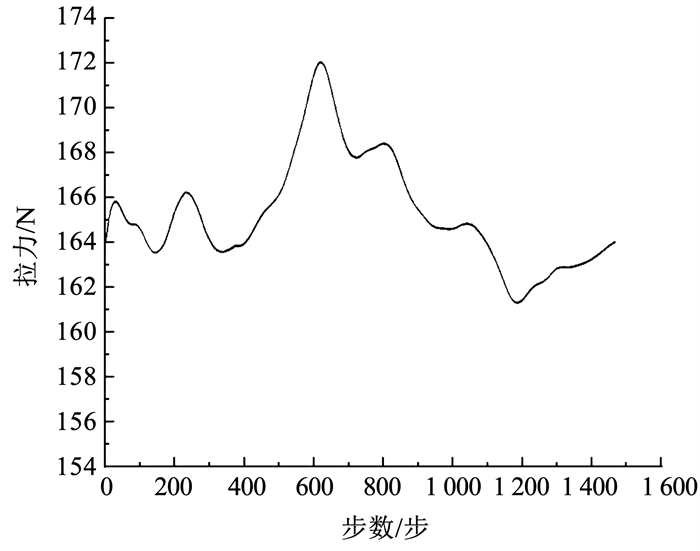
|
图 9 旋翼拉力非定常计算结果(vH=7 m/s) Fig. 9 Rotor lift calculation results(vH=7 m/s) |

|
图 10 截面流线图和速度云图(vH=7 m/s) Fig. 10 Flow diagram and speed cloud of cross section(vH=7 m/s) |
随着下降率的增加,旋翼进入涡环状态后期,可见图 7(e)、7(f)、7(g),此时,自由来流对旋翼尾流的挤压作用逐渐增加,环流主要集中在桨盘平面上方,环流的体积也逐渐增大,涡环的强度逐渐减弱。但环流仍包裹着桨盘平面,旋翼仍然存在拉力损失,倾转旋翼机仍处于危险状态。图 7(g)可以看出vh=13 m/s时即将离开涡环状态,聚集的桨尖涡穿过桨盘平面,输送至桨盘平面的上方,此时,旋翼向上的自由流速度大于旋翼诱导速度,旋翼进入紊流状态,仍存在桨尖涡与旋翼的碰撞、桨尖涡之间的自干扰,气流仍存在部分高水平的扰动,但扰动远小于涡环状态。自由来流占主导地位,倾转旋翼机的环状涡已移到旋翼上方,但旋翼下方的入流场仍不连续。
由图 7(h)可看出当vh=15 m/s时,此时自由来流远大于诱导速度,气流从下方穿过桨盘平面,旋翼入流场扰动较少,变得基本连续稳定,倾转旋翼机进入了较为稳定的风车状态。向上的自由流可带动倾转旋翼机的旋翼旋转,此时可关闭发动机,通过调整旋翼总距角,实现自转着陆。
从图 11(a)中可以看出,倾转旋翼机下降时的总体趋势为:随着倾转旋翼机下降率(vH/vh)的增大,旋翼拉力平均值“先减小后增加”,分别对应的涡环状态和风车状态。倾转旋翼机在下降速率为0.900左右时,进入成熟的涡环状态,拉力损失最大,达到18%,此时的拉力脉动幅度也达到最大,如图 9所示,因为被环流所占据的桨盘外缘部分无法有效地产生升力,使拉力平均值减小,而整个旋翼被一个不稳定的大气团所包围,周围流场极不均匀稳定,其大气团的胀大和破裂造成拉力和扭矩脉动,会引起飞行器的颠簸或坠毁,跟前文的非定常现象相对应,此时对应的流线图为图 7(d)。之后,随着下降速度的增大,涡环输送到桨盘平面上面,旋翼拉力呈现缓慢递增状态,但仍伴随着脉动。图 11(b)为各个旋翼需用功率与下降速度之间的关系,可以看出扭矩呈现“先减小、后增大、再减小”的趋势。“先减小、后增大”趋势与旋翼拉力的变化趋势一致。之后进入风车状态,自由来流自下而上穿过旋翼,给旋翼提供能量,需用扭矩减小。在下降速率为0.933时,功率最小,也就是“功率沉陷”,此时对应的是成熟的涡环状态。将图 7与图 11对比分析,可看到当拉力损失大于4%时,旋翼处于涡环状态,此时下降速率约为0.583≤vH/vh≤1.516;当拉力损失大于10%时,旋翼处于成熟的涡环状态,主要在涡环状态的中后期,下降速率约为0.816≤vH/vh≤1.283。

|
图 11 旋翼拉力与扭矩的变化规律 Fig. 11 Variation law of the lift and torque of the rotor |
为了建立更通用的涡环边界模型,根据倾转旋翼机的涡环的破坏程度,将涡环边界定义为中风险区域和高风险区域。中风险区域主要为涡环状态的早期,倾转旋翼机的主要风险为左、右两边旋翼拉力脉动,使得滚转力矩不对称,从而倾覆;高风险区域主要为涡环状态的中后期,倾转旋翼机的主要风险不仅为左、右两边旋翼拉力脉动,使得滚转力矩不对称而倾覆,而且飞行器旋翼拉力损失过大导致坠毁。根据本文倾转旋翼机垂直下降时的涡环状态流场演变规律,现定义涡环状态中风险区旋翼拉力的变化范围为
| $ 4 \% \leqslant \frac{\Delta T}{T_{\text {hover }}}<10 \% $ | (8) |
定义涡环状态高风险区旋翼拉力变化范围为
| $ \frac{\Delta T}{T_{\text {hover }}} \geqslant 10 \% $ | (9) |
上文建立了垂直下降时倾转旋翼机的涡环边界,但没考虑斜下降时的涡环边界,本文采用动量定理和CFD方法建立倾转旋翼机全飞行状态下的涡环边界。虽然动量定理在涡环状态和紊流状态不完全适用,但通过动量定理仍可能找到涡环状态的边界。现定义‖Vtv‖为桨尖涡的逸出速度,定义εcr为桨尖涡的临界速度。通过以下标准定义了临界区域:
| $ \left\|\boldsymbol{V}_{t v}\right\| \leqslant \varepsilon_{c r} $ | (10) |
根据Wolkovitch入流模型,速度关系如图 12所示,Vs为桨盘平面内气流的速度,桨尖涡的逸出速度Vtv为
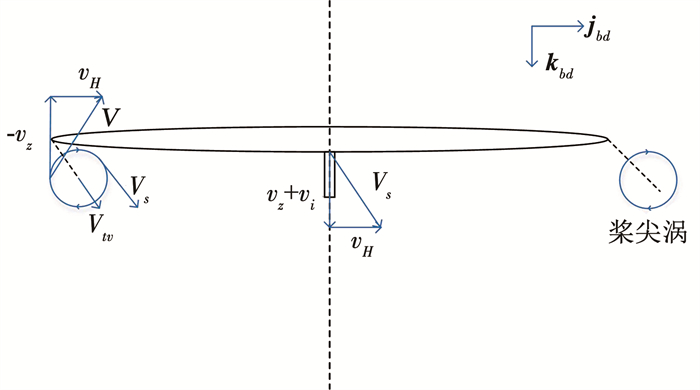
|
图 12 斜下降时的叶尖涡速度关系 Fig. 12 Tip vortex velocities in oblique descent |
| $ \boldsymbol{V}_{t v}=v_H \boldsymbol{j}_{\mathrm{bd}}+\left(v_i / 2+v_z\right) \boldsymbol{k}_{b d} $ | (11) |
式中:vH、vz分别为桨盘平面的水平速度和垂向速度,vi为桨盘平面的诱导速度,jbd、kbd分别为与桨盘平面平行和垂直的单位向量。假设倾转旋翼机下降时周期变距为零。
由式(10)、(11)可得
| $ \left\|\boldsymbol{V}_{t v}\right\|=\sqrt{V_{t v H}^2+V_{t v Z}^2} \leqslant \varepsilon_{\text {cr }} $ | (12) |
式中,
设Ⅰ和Ⅱ为两个以相同速度离开旋翼,但分别在平行和垂直方向运动的桨尖涡。经过一段时间t,他们将移动距离d。而从图 13可以看出,桨尖涡I仍然与叶盘接触,会与旋翼形成干扰,而桨尖涡Ⅱ则不再与桨盘平面接触,但桨尖涡会与机翼接触。为提高该模型的准确性,考虑非对称效应,在水平方向速度上加入修正系数k1,考虑机翼的干扰,在垂直方向诱导速度上加入修正系数k2,即
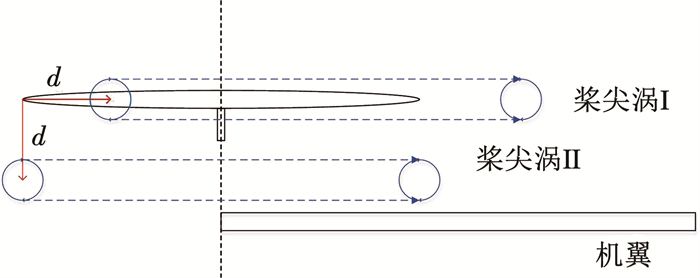
|
图 13 桨尖涡在不同方向上的运动 Fig. 13 Motion of the tip vortex in different directions |
| $ \sqrt{\left(v_H / k_1\right)^2+\left(k_2 v_i / 2+v_Z\right)^2} \leqslant {\boldsymbol{\epsilon}}_{c r} $ | (13) |
式中k1≥1、k2≥1,可通过将这个模型与CFD计算数据进行拟合得到。
为了满足式(13),需要具备以下约束条件:
| $ \left\{\begin{array}{l} V_{t v_H} \leqslant {\boldsymbol{\epsilon}}_H \\ V_{t v_z} \leqslant {\boldsymbol{\epsilon}}_z \end{array}, {\boldsymbol{\epsilon}}_z \leqslant {\boldsymbol{\epsilon}}_H\right. $ | (14) |
式中:
运用动量理论来表达诱导速度与自由来流速度之间的关系:
| $ v_i \sqrt{v_H^2+\left(v_i+v_Z\right)^2}=v_H^2 $ | (15) |
旋翼悬停时的诱导速度vh由式(7)给出。
定义ϵ为
| $ {\boldsymbol{\epsilon}}=\sqrt{\left(v_H / k_1\right)^2+\left(k_2 v_i / 2+v_Z\right)^2} $ | (16) |
对倾转旋翼机斜下降时的气动载荷进行了CFD计算,根据旋翼拉力变化值与悬停时拉力比值ΔT/Th的大小,设定4%为中风险区分界线,10%为高风险区分界线,散点图如图 14所示。根据数值进行拟合,计算得k1=4.00,k2=1.25,εcr=1.4是涡环状态高风险线(红线),εcr=2.0是涡环状态中风险线(绿线),并根据涡环边界数学模型建立涡环边界曲线,如图 14所示,对比可知,涡环边界数学模型能准确展现倾转旋翼机下降时的涡环边界。
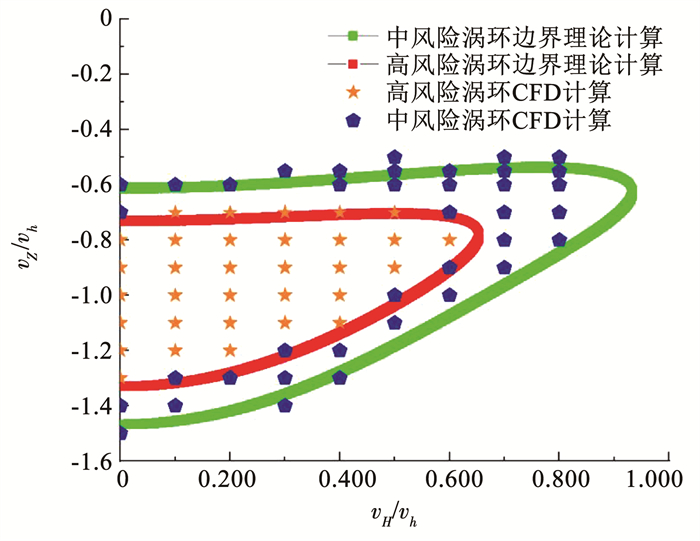
|
图 14 涡环风险边界曲线 Fig. 14 Vortex ring state domains |
当倾转旋翼机处于涡环中风险区,即
1) 采用基于非结构滑移网格技术生成围绕旋翼和机翼的高质量网格,发展了一套适用于倾转旋翼机,考虑机翼对旋翼涡环状态干扰的数值模拟方法,并将计算结果与文献结果进行了对比,能有效模拟倾转旋翼机下降状态的流场及气动载荷的演变。
2) 倾转旋翼机随着垂直下降速度vh的增大,依次会进入涡环状态、湍流状态和风车状态,涡环状态拉力损失较大,易导致坠毁,在下降速率vH/vh为0.900时,旋翼拉力损失最大,为18%。倾转旋翼机的机翼降低了单个旋翼涡环状态的影响,但倾转旋翼机旋翼分布的对称性,提高了飞行器滚转力矩失衡的风险,涡环状态对应的下降速率为0.583≤vH/vh≤ 1.516,风险一方面来源于倾转旋翼机左、右两部分旋翼拉力不对称导致倾覆,一方面来源于倾转旋翼机旋翼拉力损失过大导致坠毁。
3) 根据涡环破坏程度,建立了倾转旋翼机垂直下降和斜下降工况时的涡环边界通用数学模型。当倾转旋翼机处于涡环中风险区,即
| [1] |
TALAEIZADEH A, ANTUNES D, PISHKENARI H N, et al. Optimal-time quadcopter descent trajectories avoiding the vortex ring and autorotation states[J]. Mechatronics, 2020, 68: 102362. DOI:10.1016/j.mechatronics.2020.102362 |
| [2] |
STACK J. Experimental investigation of rotor vortex wakes in descent[C]//Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit. Reno, Nevada: AIAA, 2004: 297. DOI: 10.2514/6.2004-297
|
| [3] |
GREEN R B, GILLIES E A, BROWN R E. The flow field around a rotor in axial descent[J]. Journal of Fluid Mechanics, 2005, 534(1): 237. DOI:10.1017/S0022112005004155 |
| [4] |
JOHNSON W. Model for vortex ring state influence on rotorcraft flight dynamics[C]//Presented at the AHS 4th Decennial Specialist's Conference. San Francisco, California: American Helicopter Society International, Inc., 2004
|
| [5] |
WOLKOVITCH J. Analytical prediction of vortex-ring state boundaries for helicopter in steep descent[J]. Journal of the American Helicopter Society, 1972, 17(3): 13. DOI:10.4050/JAHS.17.13 |
| [6] |
PETER D A, CHEN S Y. Momentum theory dynamic inflow, and the vortex-ring state[J]. Journal of the American Helicopter Society, 1982, 28(3): 18. |
| [7] |
辛宏, 高正. 直升机涡环区域边界包线的确定[J]. 气动实验与测量控制, 1996, 10(1): 14. XIN Hong, GAO Zheng. A prediction of the helicopter vortex-ring state boundary[J]. Journal of Experiments in Fluid Mechanics, 1996, 10(1): 14. |
| [8] |
BROWN R E, LINE A J. Efficient high-resolution wake modeling using the vorticity transport equation[J]. AIAA Journal, 2005, 43(7): 1434. DOI:10.2514/1.13679 |
| [9] |
PRASAD J V R, CHEN Chang. Prediction of vortex ring state using ring vortex model for single-rotor and multi-rotor configurations[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit. Keystone, Colorado: AIAA, 2006: 1. DOI: 10.2514/6.2006-6632
|
| [10] |
黄明其, 兰波, 何龙. 旋翼模型垂直下降状态气动特性风洞试验[J]. 哈尔滨工业大学学报, 2019, 51(4): 131. HUANG Mingqi, LAN Bo, HE Long. Wind tunnel test of aerodynamic characteristics of rotor model in vertical descent state[J]. Journal of Harbin Institute of Technology, 2019, 51(4): 131. DOI:10.11918/j.issn.0367-6234.201801071 |
| [11] |
BETZINA, M D. Tiltrotor descent aerodynamics: A small-scale experimental investigation of vortex ring state[C]//American Helicopter Society 57th Annual Forum. Washington, DC: American Helicopter Society International, Inc., 2001
|
| [12] |
TAKⅡ A, YAMAKAWA M, ASAO S, et al. Descending flight simulation of tiltrotor aircraft at different descent rates[C]//Proceedings of the 20th International Conference on Computational Science. Cham: Springer, 2020: 178. DOI: 10.1007/978-3-030-50436-6_13
|
| [13] |
CATALANO P, AMATO M. An evaluation of RANS turbulence modelling for aerodynamic applications[J]. Aerospace Science and Technology, 2003, 7(7): 493. DOI:10.1016/S1270-9638(03)00061-0 |
| [14] |
LUO Hong, BAUM J D, LÖHNER R. An accurate, fast, matrix-free implicit method for computing unsteady flows on unstructured grids[J]. Computers & Fluids, 2001, 30(2): 137. DOI:10.1016/S0045-7930(00)00011-6 |
| [15] |
KOLAEI A, BARCELOS D, BRAMESFELD G. Experimental analysis of a small-scale rotor at various inflow angles[J]. International Journal of Aerospace Engineering, 2018, 2018: 1. DOI:10.1155/2018/2560370 |
| [16] |
王军杰, 陈仁良, 王志瑾, 等. 多旋翼飞行器涡环状态数值模拟[J]. 航空动力学报, 2020, 35(5): 1018. WANG Junjie, CHEN Renliang, WANG Zhijin, et al. Numerical simulation of multi-rotor aircraft in vortex ring state[J]. Journal of Aerospace Power, 2020, 35(5): 1018. DOI:10.13224/j.cnki.jasp.2020.05.014 |
 2023, Vol. 55
2023, Vol. 55


