2. 重庆交通大学 绿色航空技术研究院,重庆 401120
2. Green Aerotechnics Research Institute of Chongqing Jiaotong University, Chongqing 401120, China
催化惰化技术由于其流程简单、效率高,被认为是新一代飞机油箱防火抑爆技术[1-3]。催化惰化技术的基本原理是将燃油箱上部的混合气体导入催化反应器,进行可控催化燃烧,整个过程不断消耗O2和燃油蒸汽,生成CO2和水蒸气,并再次送入燃油箱上部,从而降低氧含量达到惰化目的,理论上该系统可将油箱氧浓度拉低至0%[4-7]。
催化反应器作为催化惰化系统核心部件,对系统安全有至关重要的影响。实际上航空煤油的自燃点普遍约在200 ℃,为了消除对燃油箱的潜在安全隐患,系统设计时必须保证催化反应器出口气体温度在燃油自燃温度以下[8]。谢辉辉等[9]的研究显示,采用RP-3燃油时,在没有额外冷却的情况下催化反应器会发生飞温,出口气体温度最高温度可达500 ℃; Phyre公司[10]的实验研究显示,催化反应器温度可以较好的控制在250 ℃左右,但在流量较大的情况下,催化反应器存在飞温的风险; Zhao等[11]在RP-3燃油环境下的研究表明,催化反应器适宜工作温度范围在166~241 ℃之间,而低于120 ℃时催化反应器不再有效工作。大量相关研究[12-13]都表明,催化反应器易于出现飞温现象,且过低的催化反应温度也是对于整个惰化过程不利的。
催化反应器出现飞温,本质原因在于参与氧化反应的可燃蒸汽过量。常温条件下,国内常用的RP-3号燃油饱和蒸汽压约为6 kPa,舰载机常用的RP-5号燃油饱和蒸汽压约为13.6 kPa,而国外JET A和JP-8号燃油饱和蒸汽压约为0.8 kPa和0.6 kPa。各类型号燃油蒸汽压差异较大[14-17],这种燃油理化特性的差异必然带来了反应条件的变化,如果从油箱所抽吸的混合油气中燃油蒸汽所占比例较高,氧气可能会被完全消耗,产生较高热量,最终使得催化反应器产生飞温现象。
Phyre公司的催化惰化系统设计流程中,引入了一种外界补气功能[10],即通过在催化反应器入口处补充外界空气,达到降低燃油蒸汽浓度的目的,实现可控的催化燃烧,实验研究显示系统启动后大约7 min左右,就将油箱气相空间氧浓度惰化至12%以下,催化反应器并未飞温,且油箱温度始终低于43 ℃; Feng等[18]设计了一种适合国产RP-3号燃油使用的低温可控耗氧催化惰化系统,该系统采用了风机进行补气,研究结果表明外界补气可以有效降低催化反应器最大发热功率; 彭孝天等[19]在飞行包线下,分析了外界补气对惰化性能的影响,结果表明系统可以有效降低氧体积分数,且更为可控。
外界补气实质上就是通过牺牲氧浓度下降速率换取催化反应可控性的技术手段,外界补气功能具有两面性:一方面进入催化反应器的燃油蒸汽浓度降低,催化反应更为可控; 另一方面,由于增加了催化反应器进口氧含量,油箱氧浓度下降速率会降低,且理论上如果补气量较大,催化惰化不再能将油箱氧浓度拉低至0%。如果外界补气较多,随着惰化的进行,最终会出现催化反应器出口氧浓度与油箱气相空间氧浓度一致的情况,此后油箱气相空间氧浓度无法继续降低,而是维持在某个稳定氧浓度(Stable oxygen concentration,SOC),一定量的补气必然会对应一个SOC。燃油蒸汽压、外界补气量、催化反应效率等输入参数直接影响SOC的大小,而SOC的大小又间接影响到催化反应放热功率、水蒸气生成量和氧浓度下降速率等参数,可以认为控制了SOC的变化,就控制了整个惰化过程,而遗憾的是目前并没有相关研究从SOC控制的角度展开分析。
有鉴于此,本文在参考前述系统的基础上,针对催化惰化系统提出SOC控制理论方法,以实现外界补气和油箱抽吸气配比的精确控制,并对燃油蒸汽压、气量配比和催化反应效率等参数对惰化效果的影响进行分析。
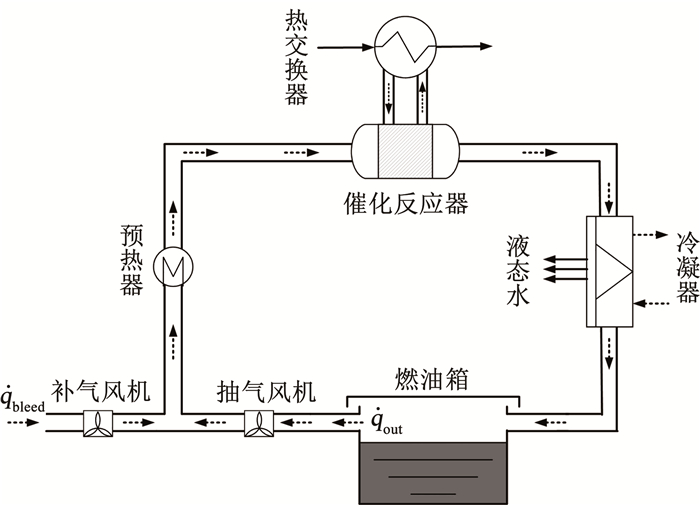
1 稳定氧浓度特性模型 1.1 系统流程及基本假设催化惰化系统流程如图 1所示。工作时,通过风机将燃油箱上部气体与外界补气混合,燃油箱上部抽取气体包含燃油蒸汽、O2、N2、CO2、少量水蒸气和微量氮化物等杂质,外界补气为环境大气,混合后气体进入电预热器达到反应所需温度后,进入催化反应器氧化,反应后的气体流过冷侧通道,去除气体中的水分及降低惰化气的温度,最后将产品气充入油箱。
|
图 1 GOBIGGS系统主要部件示意 Fig. 1 Diagram of main components of GOBIGGS system |
模型包含以下几个假设:
1) 燃油是多种烃类物质混合而成,此外还有少量的杂质,如硫化物、氮化物等。考虑主要因素,本文统一将燃油其分子式可表示为CaHb通式,且忽略氧、硫、氮等微量元素;
2) 气相混合过程瞬间完成,且不考虑油箱与外界及气体与燃油之间的传热影响,认为油箱温度基本恒定;
3) 冷凝器能力足够将混合惰气温度降低至40 ℃,且认为水蒸气能被完全脱除;
4) 燃油蒸汽分压按饱和蒸汽压考虑,且饱和蒸汽压按照里德蒸汽压计算,忽略低气液比时真实蒸汽压与里德蒸汽压的差异;
5) 不同海拔高度下,认为两个风机的体积流量恒定。
1.2 稳定氧浓度特性建模及验证催化惰化系统的催化反应过程,应该满足以下关系:
| $ \mathrm{C}_{\mathrm{a}} \mathrm{H}_{\mathrm{b}}+\left(\mathrm{a}+\frac{\mathrm{b}}{4}\right) \mathrm{O}_2=\mathrm{aCO}_2+\frac{\mathrm{b}}{2} \mathrm{H}_2 \mathrm{O} $ | (1) |
式中, a、b分别为燃油分子中碳原子和氢原子的系数。
考虑催化反应受到流速、接触面积等工作参数的影响,即使氧气过量也并非所有的燃油蒸汽均可参与反应,因此定义催化反应效率ηcat为
| $ \eta_{\text {cat }}=\left(1-\frac{q_{\text {cat }, \mathrm{o}, \mathrm{vapor}}}{q_{\text {cat }, \mathrm{i}, \mathrm{vapor}}}\right) \times 100 \% $ | (2) |
式中,qcat, o, vapor、qcat, i, vapor分别为催化反应器出口和进口燃油蒸汽的摩尔流量,mol/s。
补气风机与抽气风机的气体经过混合后进入催化反应器,存在如下关系:
| $ \left\{\begin{array}{l} q_{\text {bleed }}=\frac{q_{\text {cat }, \mathrm{i}} Q_{\mathrm{R}}}{Q_{\mathrm{R}}+1} \\ q_{\text {out }}=\frac{q_{\text {cat }, \mathrm{i}}}{Q_{\mathrm{R}}+1} \end{array}\right. $ | (3) |
式中:qcat, i为进入催化反应器的总气体流量; qbleed为补气风机摩尔流量; qout为抽气风机摩尔流量,mol/s; QR为补气风机与抽气风机的流量比,即qbleed/qout。
根据式(1)可以看出,只要燃油蒸汽和氧气两者缺一时,整个催化反应过程立刻停止,因而计算模型,需要根据燃油蒸汽或氧气是否富余进行过程判断:
1) 当燃油蒸汽不足,氧气富余时,根据式(1)需满足如下关系:
| $ \left(\mathrm{a}+\frac{\mathrm{b}}{4}\right) \eta_{\text {cat }} x_{\mathrm{U}, \mathrm{vapor}} q_{\text {out }}<0.21 q_{\text {bleed }}+x_{\mathrm{U}, \mathrm{O}} q_{\text {out }} $ | (4) |
式中,xU, vapor、xU, O分别为油箱中燃油蒸汽和氧气的体积分数。
计算模型采用富氧过程条件,催化反应以燃油蒸汽消耗的物质量为基础条件,因此所消耗的O2和燃油蒸汽的摩尔量为:
| $ n_{\text {cat }, \mathrm{i}, \mathrm{O}}^*=\left(\mathrm{a}+\frac{b}{4}\right) \eta_{\text {cat }} x_{\mathrm{U}, \text { vapor }} q_{\text {out }} $ | (5) |
| $ n_{\text {cat }, \mathrm{i}, \text { vapor }}^*=\eta_{\mathrm{cat}} x_{\mathrm{U}, \mathrm{vapor}} q_{\text {out }} $ | (6) |
催化反应器出口生成的CO2和H2O的摩尔量为:
| $ n_{\text {cat , o, C }}^*=\mathrm{a} \eta_{\text {cat }} x_{\mathrm{U}, \mathrm{vapor}} q_{\text {out }} $ | (7) |
| $ n_{\text {cat }, \mathrm{o}, \mathrm{H}}^*=\frac{\mathrm{b}}{2} \eta_{\text {cat }} x_{\mathrm{U}, \mathrm{vapor}} q_{\text {out }} $ | (8) |
2) 当燃油蒸汽富余,氧气不足时,即催化反应满足以下关系:
| $ \left(\mathrm{a}+\frac{\mathrm{b}}{4}\right) \eta_{\text {cat }} x_{\mathrm{U}, \text { vapor }} q_{\text {out }}>0.21 q_{\text {bleed }}+x_{\mathrm{U}, \mathrm{O}} q_{\text {out }} $ | (9) |
计算采用贫氧过程条件,催化反应以氧气消耗的物质量为基础条件,因此所消耗的氧气和燃油蒸汽的摩尔量为:
| $ n_{\text {cat }, \mathrm{i}, \mathrm{O}}^*=0.21 q_{\text {bleed }}+x_{\mathrm{U}, \mathrm{O}} q_{\text {out }} $ | (10) |
| $ n_{\text {cat }, \mathrm{i}, \text { vapor }}^*=\frac{0.84 q_{\text {bleed }}+4 x_{\mathrm{U}, \mathrm{O}} q_{\text {out }}}{4 \mathrm{a}+\mathrm{b}} $ | (11) |
催化反应器出口所生成的CO2和H2O的摩尔量为:
| $ n_{\text {cat }, \mathrm{o}, \mathrm{C}}^*=\frac{0.84 \mathrm{a} q_{\text {bleed }}+4 \mathrm{a} x_{\mathrm{U}, \mathrm{O}} q_{\text {out }}}{4 \mathrm{a}+\mathrm{b}} $ | (12) |
| $ n_{\text {cat }, \mathrm{o}, \mathrm{H}}^*=\frac{0.42 \mathrm{b} q_{\text {bleed }}+2 \mathrm{b} x_{\mathrm{U}, \mathrm{O}} q_{\text {out }}}{4 \mathrm{a}+\mathrm{b}} $ | (13) |
综合富氧和贫氧反应过程,流出催化反应器的O2、N2、CO2、H2O和燃油蒸汽分别为:
| $ n_{\text {cat }, \mathrm{o}, \mathrm{O}}=0.21 q_{\text {bleed }}+x_{\mathrm{U}, \mathrm{O}} q_{\text {out }}-n_{\text {cat }, \mathrm{i}, \mathrm{O}}^* $ | (14) |
| $ n_{\text {cat }, \mathrm{o}, \mathrm{N}}=0.79 q_{\text {bleed }}+x_{\mathrm{U}, \mathrm{N}} q_{\text {out }} $ | (15) |
| $ n_{\text {cat }, \mathrm{o}, \mathrm{C}}=x_{\mathrm{U}, \mathrm{C}} q_{\text {bleed }}+n_{\text {cat }, \mathrm{o}, \mathrm{C}}^* $ | (16) |
| $ n_{\text {cat }, \mathrm{o}, \mathrm{H}}=n_{\text {cat }, \mathrm{o}, \mathrm{H}}^* $ | (17) |
| $ n_{\text {cat }, \mathrm{o}, \text { vapor }}=q_2 x_{\mathrm{U}, \mathrm{vapor}}-n_{\text {cat }, \mathrm{i}, \text { vapor }}^* $ | (18) |
式中xU, N、xU, C为油箱中N2和CO2的体积分数。
催化反应器氧化反应的放热功率为
| $ P_{\text {cat }}=H_{\mathrm{u}} n_{\text {cat }, \mathrm{i}, \text { vapor }}^* $ | (19) |
式中Hu为燃油燃烧热值,MJ/mol。本文假设在冷凝器中可以去除所有水蒸气,则进入油箱的混合惰气中O2浓度为
| $ x_{\mathrm{U}, \mathrm{i}, \mathrm{O}}=\frac{n_{\text {cat }, \mathrm{o}, \mathrm{O}}}{n_{\text {cat }, \mathrm{o}, \mathrm{O}}+n_{\mathrm{cat}, \mathrm{o}, \mathrm{N}}+n_{\text {cat }, \mathrm{o}, \mathrm{C}}+n_{\text {cat }, \mathrm{o}, \text { vapor }}} $ | (20) |
在贫氧条件下,根据式(14)计算ncat, o, O一直为0,表明油箱氧浓度一直会降低到0%。而在富氧条件下,根据式(14)可以看出,除了式中第2项逐渐降低外,其余两项均为定值,随着惰化的进行,xU, O会逐渐降低,会出现xU, O与xU, i, O相等的情况,此时表明油箱氧浓度不能降低,出现一个稳定氧浓度SOC。根据上述思想对式(20)进行求解,可获得SOC与QR的关系:
| $ \begin{gathered} Q_{\mathrm{R}}=\frac{\mathrm{SOC}\left(1-\eta_{\text {cat }} x_{\mathrm{U}, \text { vapor }}-\eta_{\text {cat }} x_{\mathrm{U}, \text { vapor }} \mathrm{b} / 4\right)}{x_{\text {air }, \mathrm{O}}-\mathrm{SOC}}+ \\ \frac{\eta_{\text {cat }} x_{\mathrm{U}, \text { vapor }}(\mathrm{a}+\mathrm{b} / 4)-\mathrm{SOC}}{x_{\text {air }, \mathrm{O}}-\mathrm{SOC}} \end{gathered} $ | (21) |
式中xair, O为空气中的氧气体积分数。
式(21)的意义就在于表明了SOC与QR的内在联系,提供了一种通过控制外界补气流量QR,间接实现对SOC精确控制的方法。
基于基本假设中的燃油蒸汽分压力简化为燃油饱和蒸汽压,其只与温度相关,因此该分压始终保持不变,但是O2、N2和CO2的分压随时间会发生变化。因此,以燃油箱气相空间为控制体,对除燃油蒸汽以外的各气体组分建立质量平衡方程,即:
| $ Q_{\mathrm{U}, \mathrm{i}, \mathrm{O}}+Q_{\mathrm{amb}, \mathrm{O}}+\frac{\mathrm{d} m_{\mathrm{F}, \mathrm{O}}}{\mathrm{d} t}-Q_{\mathrm{U}, \mathrm{o}, \mathrm{O}}=\frac{V_{\mathrm{U}}}{R_\mathrm{O} T_{\mathrm{U}}} \frac{\mathrm{d} p_{\mathrm{U}, \mathrm{O}}}{\mathrm{d} t} $ | (22) |
| $ Q_{\mathrm{U}, \mathrm{i}, \mathrm{N}}+Q_{\mathrm{amb}, \mathrm{N}}+\frac{\mathrm{d} m_{\mathrm{F}, \mathrm{N}}}{\mathrm{d} t}-Q_{\mathrm{U}, \mathrm{o}, \mathrm{~N}}=\frac{V_{\mathrm{U}}}{R_{\mathrm{N}} T_{\mathrm{U}}} \frac{\mathrm{d} p_{\mathrm{U}, \mathrm{N}}}{\mathrm{d} t} $ | (23) |
| $ Q_{\mathrm{U}, \mathrm{i}, \mathrm{C}}+Q_{\mathrm{amb}, \mathrm{C}}+\frac{\mathrm{d} m_{\mathrm{F}, \mathrm{C}}}{\mathrm{d} t}-Q_{\mathrm{U}, \mathrm{o}, \mathrm{C}}=\frac{V_{\mathrm{U}}}{R_{\mathrm{C}} T_{\mathrm{U}}} \frac{\mathrm{d} p_{\mathrm{U}, \mathrm{C}}}{\mathrm{d} t} $ | (24) |
式中:QU, i, O、QU, i, N和QU, i, C为进入油箱的O2、N2和CO2的质量流量,kg/s; Qamb, O、Qamb, N和Qamb, C分别为燃油箱与外界环境所交换的气体中O2、N2和CO2的质量流量,kg/s; QU, o, O、QU, o, N和QU, o, C为抽吸气的O2、N2和CO2的质量流量,kg/s; mF, O、mF, N和mF, C为O2、N2和CO2在燃油中的质量,kg。
油箱中气体分压力之和与外界环境压力pt相同,满足:
| $ p_{\mathrm{t}}=p_{\mathrm{U}, \mathrm{O}}+p_{\mathrm{U}, \mathrm{N}}+p_{\mathrm{U}, \mathrm{C}}+p_{\mathrm{v}} $ | (25) |
| $ \mathrm{d} p_{\mathrm{t}}=\mathrm{d} p_{\mathrm{U}, \mathrm{O}}+\mathrm{d} p_{\mathrm{U}, \mathrm{N}}+\mathrm{d} p_{\mathrm{U}, \mathrm{C}} $ | (26) |
式中:pU, O、pU, N、pU, C和pv为油箱中的O2、N2、CO2和燃油蒸汽的分压,Pa。
飞机在爬升或下降过程中,油箱所处的外界压力随着高度发生变化,由于压力变化,气体会从油箱中排出或从外界进入油箱。催化惰化过程中水蒸气被冷凝排出,其催化反应过程本身是一个气体物质量减少的过程,但由于增加了补气,相当于为油箱提供了一定增压。因此,气体流动状态是从油箱排出还是流入油箱,必须从物质总量变化来判断:
1) 当流入油箱的气体足够为油箱增压时,即存在如下关系:
| $ n_{\text {cat }, \mathrm{o}, \mathrm{O}}+n_{\text {cat }, \mathrm{o}, \mathrm{~N}}+n_{\text {cat }, \mathrm{o}, \mathrm{C}}+n_{\text {cat }, \mathrm{o}, \text { vapor }}-q_{\text {out }}>\frac{\mathrm{d} p_{\mathrm{t}} V_{\mathrm{U}}}{R T_{\mathrm{U}}} $ | (27) |
则油箱中的气体向外界排放,排出气体满足:
| $ \frac{p_{\mathrm{U}, \mathrm{O}}}{p_{\mathrm{U}, \mathrm{N}}}=\frac{Q_{\mathrm{amb}, \mathrm{O}} M_{\mathrm{N}}}{Q_{\mathrm{amb}, \mathrm{N}} M_{\mathrm{O}}} $ | (28) |
| $ \frac{p_{\mathrm{U}, \mathrm{N}}}{p_{\mathrm{U}, \mathrm{C}}}=\frac{Q_{\mathrm{amb}, \mathrm{N}} M_{\mathrm{C}}}{Q_{\mathrm{amb}, \mathrm{C}} M_{\mathrm{N}}} $ | (29) |
式中:MO、MN和MC分别为O2、N2和CO2的摩尔质量,kg/mol。
2) 当流入油箱的气体不足以为油箱增压时,即存在如下关系:
| $ n_{\text {cat }, \mathrm{o}, \mathrm{O}}+n_{\text {cat }, \mathrm{o}, \mathrm{N}}+n_{\text {cat }, \mathrm{o}, \mathrm{C}}+n_{\text {cat }, \mathrm{o}, \text { vapor }}-q_{\text {out }}<\frac{\mathrm{d} p_{\mathrm{t}} V_{\mathrm{U}}}{R T_{\mathrm{U}}} $ | (30) |
则外界气体充入油箱,充入气体满足:
| $ \frac{Q_{\mathrm{amb}, \mathrm{O}}}{Q_{\mathrm{amb}, \mathrm{N}}}=\frac{p_{\mathrm{air}, \mathrm{O}} M_{\mathrm{O}}}{p_{\mathrm{air}, \mathrm{N}} M_{\mathrm{N}}} $ | (31) |
| $ Q_{\mathrm{amb}, \mathrm{C}}=0 $ | (32) |
式中:pair, O、pair, N分别为空气中的O2和N2的分压,Pa。
根据上述方法,采用MATLAB进行编程,可对催化惰化补气控制过程进行仿真建模,其流程图如图 2所示。

|
图 2 SOC控制模型流程图 Fig. 2 Schematic process of SOC control model |
2007年5月GOBIGGS系统在FAA大西洋城市技术中心进行了技术验证[20],测试选用了短程FL-350飞行包线。该飞行包线下,总飞行时间约为105 min,所惰化的油箱为标准的中央翼油箱,油箱总容积为0.481 m3,装载有0.038 m3的JP-8燃油,风机流量为56 L/min; 由于国外GOBIGGS系统没有外界补气,因此流量比QR取为0; 考虑到JP-8燃油蒸汽压较低,氧气量较为富余,因此选取催化反应效率ηcat为100%。将以上条件代入本文建立的数学模型中,将计算结果与实验结果进行比较,以验证模型的正确性。
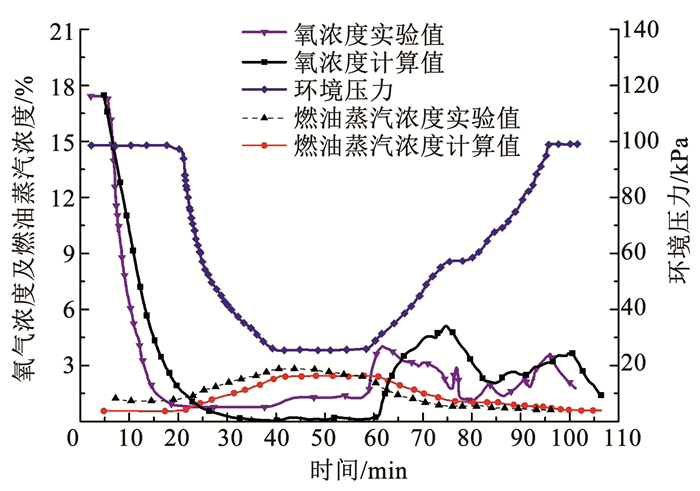
图 3给出了计算结果与实验结果的对比,通过数据相关性验证,氧浓度的计算与实验结果相关系数为0.977 2、燃油蒸汽浓度的计算与实验结果相关系数为0.900 7,表明了本文所建立的催化惰化模型具有较高的准确性。
|
图 3 计算与实验的结果对比 Fig. 3 Comparison between calculation and experiment results |
本文选取的几种燃油理化参数见表 1[21],将表 1中参数代入式(1)计算可知,不同燃油类型会产生不同的氧气消耗量和热量。
| 表 1 4种燃料的物理和化学参数 Tab. 1 Physicochemical parameters of four fuels |
以使用RP-5燃油的标准中央翼油箱为对象,在40 ℃下,油箱体积0.481 m3,载油率(即燃油体积占油箱总体积的百分比)为50%,风机流量为80 L/min,催化反应器效率20%为计算条件,带入本文数学模型中进行计算。
图 4给出了不同流量比下O2浓度随时间的变化曲线,从图中可以看出惰化开始后,气相空间的O2浓度随时间逐渐降低,最后趋于稳定,且不同的流量比对应的SOC也不相同。

|
图 4 不同流量比下氧浓度随时间变化曲线 Fig. 4 Curves of oxygen concentration versus time under different flow ratios |
通过式(29)可以看出,SOC与流量比、燃油化学分子式、催化反应效率和燃油蒸汽压浓度有关,在其余影响因素不变的情况下,改变流量比就能控制油箱气相空间的SOC。
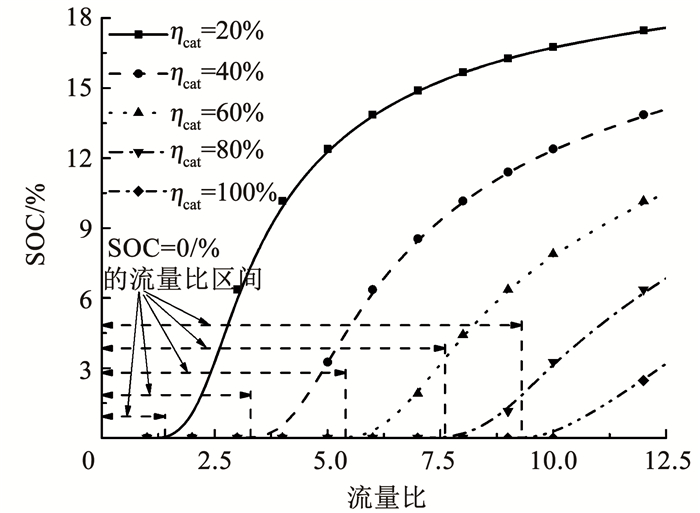
图 5给出了不同催化反应效率下,流量比与SOC的关系。从图 5中可以看出,当流量比较小时SOC稳定在0 %,由此可见适当补气并不会导致SOC上升; 随着流量比的增大SOC开始由0 %逐渐升高,且随着催化反应效率的增加,SOC= 0%的流量比区间增大。
|
图 5 不同反应效率下SOC与流量比关系曲线 Fig. 5 Relationship curves between SOC and flow ratio under different reaction efficiencies |
在催化过程中燃油蒸汽被氧化会产生大量的热和水蒸气,惰化系统实际工作过程中,必须在任一时刻保证催化反应器不产生飞温、惰性气体温度不超限。为此,分析催化反应器功率和产水峰速率对SOC的影响。
图 6给出了不同催化反应效率下,产水速率、发热功率与SOC的关系。研究结果表明:催化反应器的产热峰值功率和产水峰值速率随着SOC的增大而逐渐降低; 在相同SOC下,随着催化反应效率的增加,催化反应器的产热峰值功率和产水峰值速率增大。

|
图 6 不同反应效率下发热功率、产水速率与SOC关系曲线 Fig. 6 Relationship curves between heat generation rate and water production rate with SOC under different reaction efficiencies |
从图 5、6分析可知,各个催化反应效率下存在着不同的SOC=0%的流量比区间,在这个区间内随着流量比的增大SOC并不会变化,但是流量比的变化会直接影响催化反应器的发热产水性能,因此对这部分区间的流量比进行分析。
图 7给出了不同催化反应效率下,产水速率、发热功率与流量比的关系。研究结果表明:SOC=0%时,随着流量比的增大,发热功率和产水速率均会出现极大值,且该极大值随着催化反应效率的增加而增大。出现这种现象的主要原因是:一开始催化反应器内的燃油蒸汽过量,随着流量比的增大进入催化反应器的O2逐步增多,使得催化反应器的发热功率和产水速率升高; 当进入催化反应器的O2与燃油蒸汽刚好完全反应时,发热功率和产水速率达到极大值; 随着流量比的继续增加,参与反应的燃油蒸汽减少,发热功率和产水速率迅速下降。随着催化反应器效率的提高,原本不发生反应的燃油蒸汽也参与到反应过程中,这导致催化反应器的发热功率和产水速率极大值在更大的流量比下出现,这也就是图 7中ηcat越大极值点出现越晚的原因。

|
图 7 不同反应效率下发热功率、产水速率与流量比关系曲线 Fig. 7 Relationship curves between heat generation rate and water production rate with flow ratio under different reaction efficiencies |
不同类型的燃油,其燃油蒸汽压具有较大的差异,对于燃油蒸汽压较大的燃油来说,抽吸气中燃油蒸汽所占比例较高,氧气可能会被完全消耗,因此惰化效果具有很大差异。将表 1中的4种燃油,代入本文建立的催化惰化系统数学模型进行求解,计算中选择油箱容积为0.481 m3的标准中央翼油箱,载油率为50%,催化反应器效率ηcat为20%,风机流量为80 L/min。
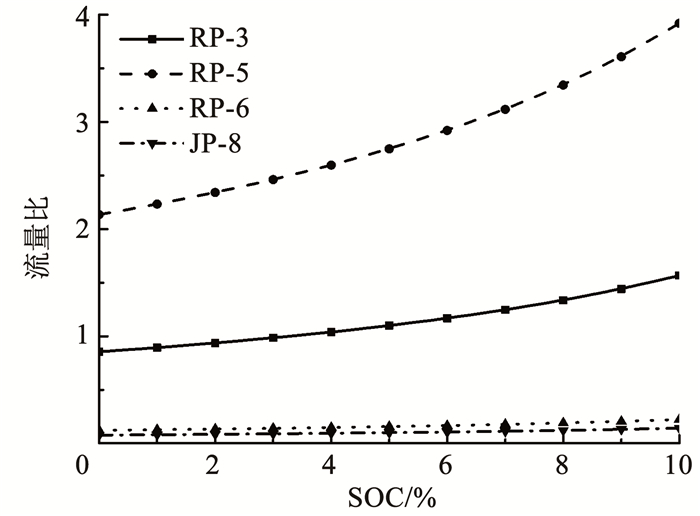
图 8给出了不同燃油类型下,SOC随流量比的变化曲线。从图中可以看出在同一SOC下,4种燃油对应的流量比存在RP-5>RP-3>RP-6>JP-8的关系。其主要原因在于,RP-5、RP-3、RP-6和JP-8的燃油蒸汽压分别为13.84、6.00、0.75和0.60 kPa,当燃油蒸汽压越高时,所消耗的氧越多,所以在相同的SOC时需要的外界补气就越多,流量比就越大。
|
图 8 不同燃油类型下流量比与SOC关系曲线 Fig. 8 Relationship curves between flow ratio and SOC under different fuel types |
大气压会随着海拔高度的变化而改变,这必将对耗氧性惰化系统的SOC带来影响,本文以RP-5燃油为例,计算中选择油箱容积为0.481 m3的标准中央翼油箱,载油率为50%,风机流量为80 L/min,催化反应器效率为20%,在不考虑温度变化的情况下研究海拔高度以及爬升率对SOC的影响。不同海拔高度下的大气压是根据下式确定:
| $ P=P_0 \mathrm{e}^{-\frac{M g Z}{R T}} $ | (33) |
式中:P0为海平面大气压,Pa; g为重力加速度,m/s2; T为海平面温度,K; R为气体状态常数,J/(mol/K); M为空气摩尔质量,kg/mol; Z为海拔高度,m。
图 9给出了不同流量比下,SOC随海拔高度的变化曲线。从图中可以看出随着海拔高度的升高SOC降低,使得原本不能将SOC拉低至0%的流量比也可以将SOC降低至0%,出现这样现象的原因是随着海拔的升高,大气压逐渐降低,使得燃油蒸汽分压增大,弥补了大流量下氧过量的情况。

|
图 9 不同流量比下海拔高度与SOC关系曲线 Fig. 9 Relationship curves between altitude and SOC under different flow ratios |
在爬升过程中,由于大气压时刻发生变化,此时的SOC不再是趋向于一个确定值,而是随着高度的变化时刻变化着,为了方便研究,取每步计算结果的氧浓度为爬升阶段的SOC,在上述计算条件中取QR=3进行计算,对不同爬升率下SOC的变化进行研究。
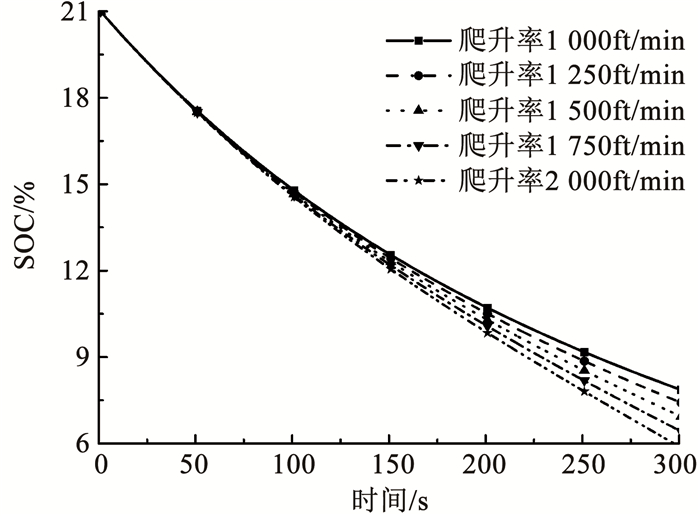
图 10给出了不同爬升率下SOC随时间的变化曲线。从图中可以看出SOC的下降速度随爬升率的增大而加速,在相同时间内爬升率越大终了时的SOC就越低。出现这样的原因主要是爬升率越大在相同的时间内飞机到达的海拔高度越高,而SOC会随着海拔高度的升高而下降,所以呈现出爬升率越大SOC下降速度越快的现象。
|
图 10 不同爬升速率下SOC随时间变化曲线 Fig. 10 Curves of SOC versus time under different climbing rates |
1) 存在着稳定氧浓度为0%的流量比区间,在该区间内稳定氧浓度不随流量比的变化而变化,且该区间随着催化反应器效率的提高而增大,催化反应效率ηcat =100%的该区间是ηcat=20%的5倍。
2) 提高SOC可以有效降低催化反应器的发热功率和产水速率,SOC从1%提高到9%,发热功率和产水速率下降了36.1%。
3) SOC与流量比的对应关系受到燃油类型的影响,蒸汽压越高的燃油需要更大的外界补气才能维持相同的SOC。
4) 随着海拔高度的增加无需增大流量比SOC也会下降; 在爬升过程中爬升率会对SOC下降速率产生影响,越大的爬升率SOC下降速率越快。
| [1] |
GUPTA A. Method and system for making a fuel-tank inert without an inert gas[J]. SAE International Journal of Aerospace, 2009, 2(1): 75. DOI:10.4271/2009-01-3134 |
| [2] |
SADATAKHAVI S M R, TABEJAMAAT S, ZADE M E A, et al. Experimental and numerical study of combustion characteristics in a liquid fuel CAN micro-combustor[J]. Aerospace Science and Technology, 2020, 105: 106023. DOI:10.1016/j.ast.2020.106023 |
| [3] |
HARDMAN S, CHANDAN A, STEINBERGER-WILCKENS R. Fuel cell added value for early market applications[J]. Journal of Power Sources, 2015, 287: 297. DOI:10.1016/j.jpowsour.2015.04.056 |
| [4] |
JOHNSON R W, ZAKI R, YATES S F. Advancedcarbon dioxide fuel tank inerting system: US20060560290[P]. 2011-03-15
|
| [5] |
WALKER S, JUNG W, ROBERTSON S, et al. Demonstration of anovel catalyst based Green On Board Inert Gas Generation System (GOBIGGS)for fuel tank inerting[C]//Presented at the AHS 69th Annual Forum. Phoenix, Arizona: American Helicopter Society International, Inc., 2013: 550
|
| [6] |
JR MORRIS R W, MILLER J, LIMAYE S. Fuel Deoxygenation and Aircraft Thermal Management[C]//Proceedings of the 4th International Energy Conversion Engineering Conference and Exhibit (IECEC). San Diego, California: AIAA, 2006: 1. DOI: 10.2514/6.2006-4027
|
| [7] |
SHAO Lei, LIU Weihua, LI Chaoyue, et al. Experimental comparison between aircraft fuel tank inerting processes using NEA and MIG[J]. Chinese Journal of Aeronautics, 2018, 31(7): 151. DOI:10.1016/j.cja.2018.04.016 |
| [8] |
FAN Xuejun, YU Gong, LI Jianguo, et al. Combustion and ignition of thermally cracked kerosene in supersonic model combustors[J]. Journal of Propulsion and Power, 2007, 23(2): 317. DOI:10.2514/1.26402 |
| [9] |
谢辉辉, 冯诗愚, 彭孝天, 等. 耗氧型惰化系统反应器性能理论[J]. 北京航空航天大学学报, 2019, 45(11): 2312. XIE Huihui, FENG Shiyu, PENG Xiaotian, et al. Theoretical of reactor performance in oxygen consumption based inerting system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(11): 2312. DOI:10.13700/j.bh.1001-5965.2019.0117 |
| [10] |
PENG Xiaotian, WANG Hongming, HUANG Long, et al. Experimental study on RP-3 aviation fuel tank using oxygen-consuming inerting technology[J]. Journal of Aerospace Engineering, 2022, 35(1): 06021008. DOI:10.1061/(asce)as.1943-5525.0001377 |
| [11] |
ZHAO Wenqi, DAI Yitong, CHENG Xinxin, et al. All-silicon zeolite supported Pt nanoparticles for Green On-Board Inert Gas Generation System[J]. Combustion Science and Technology, 2021, 193(12): 2009. DOI:10.1080/00102202.2020.1723565 |
| [12] |
YUAN Wenhao, LI Yuyang, DAGAUT P, et al. Investigation on the pyrolysis and oxidation of toluene over a wide range conditions. I. Flow reactor pyrolysis and jet stirred reactor oxidation[J]. Combustion and Flame, 2015, 162(1): 3. DOI:10.1016/j.combustflame.2014.07.009 |
| [13] |
WANG Bo, LI Lifeng, SCHÄFER F, et al. Thermal reduction of iron-manganese oxide particles in a high-temperature packed-bed solar thermochemical reactor[J]. Chemical Engineering Journal, 2021, 412: 128255. DOI:10.1016/j.cej.2020.128255 |
| [14] |
ZHANG Ke, HUANG Xudong, XIE Zhifeng, et al. Design and optimization of a novel electrically controlled high pressure fuel injection system for heavy fuel aircraft piston engine[J]. Chinese Journal of Aeronautics, 2018, 31(9): 1920. DOI:10.1016/j.cja.2018.06.013 |
| [15] |
CAI Yan, BU Xueqin, LIN Guiping, et al. Experimental study of an aircraft fuel tank inerting system[J]. Chinese Journal of Aeronautics, 2015, 28(2): 394. DOI:10.1016/j.cja.2015.02.002 |
| [16] |
KLETTLINGER J, SURGENOR A, YEN C. Thermal stability testing of a fischer-tropsch fuel and various blends with jet A[C]//Proceedings of the 49th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Orlando, Florida: AIAA, 2011: 9233. DOI: 10.2514/6.2011-693
|
| [17] |
WANG Xiaoyu, JIA Tinghao, PAN Lun, et al. Review on the relationship between liquid aerospace fuel composition and their physicochemical properties[J]. Transactions of Tianjin University, 2021, 27(2): 87. DOI:10.1007/s12209-020-00273-5 |
| [18] |
FENG Shiyu, PENG Xiaotian, CHEN Chen, et al. Effect of air supplementation on the performance of an onboard catalytic inerting system[J]. Aerospace Science and Technology, 2020, 97: 105605. DOI:10.1016/j.ast.2019.105605 |
| [19] |
彭孝天, 冯诗愚, 任童, 等. 飞行包线下燃油箱耗氧型催化惰化系统性能研究[J]. 北京航空航天大学学报, 2021, 47(8): 1565. PENG Xiaotian, FENG Shiyu, REN Tong, et al. Performance of oxygen-consuming catalytic inerting system of fuel tank under flight envelope[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(8): 1565. DOI:10.13700/j.bh.1001-5965.2020.0283 |
| [20] |
LIVNE E. Aircraft active flutter suppression: state of the art and technology maturation needs[J]. Journal of Aircraft, 2018, 55(1): 410. DOI:10.2514/1.C034442 |
| [21] |
VOZKA P, KILAZ G. A review of aviation turbine fuel chemical composition-property relations[J]. Fuel, 2020, 268: 117391-1. DOI:10.1016/j.fuel.2020.117391 |
 2023, Vol. 55
2023, Vol. 55


