2. 智能机器人湖北省重点实验室 (武汉工程大学),武汉 430205;
3. 雷达信号处理国家重点实验室(西安电子科技大学),西安 710071
2. Hubei Key Laboratory of Intelligent Robot (Wuhan Institute of Technology), Wuhan 430205, China;
3. National Laboratory of Radar Signal Processing (Xidian University), Xi'an 710071, China
自适应波束形成在声呐、雷达、生物科学、语音信号处理以及医学工程等领域已经得到了广泛应用,是阵列信号处理领域中的研究热点之一[1-4]。自适应波束形成算法对导向矢量失配的误差非常敏感,即使很小的导向矢量误差,如方向误差、阵列扰动和运动目标等因素,都会使算法性能急剧下降。另外,当训练数据中含有期望信号时,期望信号可能被当作干扰信号,产生自消现象[5]。传统的波束形成算法在干扰处形成的零陷非常窄,如出现阵列扰动时,必然会导致干扰偏离零陷位置,甚至会导致算法完全失效[6-7]。因此有必要研究增强算法的稳健性来克服上述问题。
增强算法的稳健性大致可以分为两类:一类是基于协方差矩阵的算法:对角加载(Diagnoal loading, DL)算法[8]、特征空间算法[9]、以及协方差矩阵重构算法[10](Interference plus noise, IPN)。DL算法就是在协方差矩阵的对角线上加入一个加载因子,从而抑制权向量中的噪声,但是最优加载因子的选取很难确定。特征空间算法是通过求解协方差矩阵的特征值,并对其进行划分,大特征值对应的导向矢量张成的是期望信号加干扰信号的子空间,小特征值对应导的向矢量张成的则是噪声子空间。再将存在误差的期望信号向期望信号加干扰信号的子空间进行投影,进而消除误差。杨志伟等[11]对特征子空间进行重构,利用空间张量积性质重构全维信号子空间,并且采用子空间投影算法计算加权矢量,进一步提高了波束的稳健性。协方差矩阵重构算法[12]是将干扰加噪声的协方差矩阵重构,预设零陷的范围,重新进行积分重构,展宽零陷从而提高稳健性。另一类是对导向矢量进行优化[13-15],通常采用CVX工具包[16],连续二次约束二次规划(Successive quadratically constrained quadratic programming, QCQP)技术和半正定松弛技术(Semidefinite relaxation, SDR)[17-19]求解。但是这些技术在实际应用中计算量复杂、耗费时间长、计算复杂度高。
基于此,为有效提高传统波束形成器在干扰位置发生扰动和导向矢量失配下的算法性能,提出一种基于协方差矩阵重构和交替方向乘子法(Alternating direction method of multipliers, ADMM)的零陷展宽鲁棒波束形成算法。首先在波束形成器最大输出功率条件下,设计求解最优导向矢量的优化模型。其次,为了展宽零陷并增强系统抗运动干扰能力,利用阵列输出功率及定义的干扰零陷范围重构协方差矩阵; 接着,为了求解关于导向矢量的二次不等式约束问题,本文利用ADMM对模型进行迭代求解,并在每次迭代中获得导向矢量的具体解。最后,仿真实验结果证明了所提方法的有效性。
1 信号模型及问题描述 1.1 阵列信号模型不失一般性,本文考虑接收端是由N个阵元构成的均匀线性阵列(ULA),其阵元间距为d,于是窄带波束形成器在k时刻的输出为
| $ y(k)=\boldsymbol{w}^{\mathrm{H}} \boldsymbol{x}(k) $ | (1) |
式中:w为N×1的加权矢量,(·)H为共轭转置,x(k)为阵列接收数据向量,其表示为
| $ \begin{aligned} \boldsymbol{x}(k)= & \boldsymbol{A} \boldsymbol{S}(k)+\boldsymbol{n}(k)= \\ & s_0(k) \boldsymbol{a}\left(\theta_0\right)+\sum\limits_{i=1}^P s_i(k) \boldsymbol{a}\left(\theta_i\right)+\boldsymbol{n}(k) \end{aligned} $ | (2) |
式中:
| $ \boldsymbol{a}(\theta)=\left[1, \mathrm{e}^{\mathrm{j} 2 \pi \mathrm{d} \sin \theta / \lambda}, \cdots, \mathrm{e}^{\mathrm{j} 2 \pi \mathrm{d}(N-1) \sin \theta / \lambda}\right]^{\mathrm{T}} $ | (3) |
假设期望信号、干扰信号和噪声信号皆不相关。则阵列数据协方差矩阵可表示为
| $ \begin{aligned} \boldsymbol{R}= & E\left\{\boldsymbol{x}(k) \boldsymbol{x}(k)^{\mathrm{H}}\right\}= \\ & \sigma_0^2 \boldsymbol{a}\left(\theta_0\right) \boldsymbol{a}^{\mathrm{H}}\left(\theta_0\right)+\sum\limits_{i=1}^P \sigma_i^2 \boldsymbol{a}\left(\theta_i\right) \boldsymbol{a}^{\mathrm{H}}\left(\theta_i\right)+ \\ & \sigma_n^2 \boldsymbol{I}=\boldsymbol{R}_s+\boldsymbol{R}_i+\sigma_n^2 \boldsymbol{I}=\boldsymbol{R}_s+\boldsymbol{R}_{i+n} \end{aligned} $ | (4) |
式中:E{·}为统计期望值,σ02、σi2、σn2分别为期望信号功率、干扰信号功率和噪声功率,I为N维单位矩阵,Rs、Ri、Ri+n分别为期望信号的协方差矩阵、干扰信号的协方差矩阵和干扰加噪声的协方差矩阵。
于是,根据最小方差无失真响应(MVDR)波束形成器,即
| $ \begin{array}{ll} \min\limits _\boldsymbol{w} & \boldsymbol{w}^{\mathrm{H}} \boldsymbol{R}_{i+n} \boldsymbol{w} \\ \text { s.t. } & \left|\boldsymbol{w}^{\mathrm{H}} a^*\right|=1 \end{array} $ | (5) |
式中a*为最优导向矢量值。可得最优权值为
| $ \boldsymbol{w}_{\mathrm{opt}}=\frac{\boldsymbol{R}_{i+n}^{-1} \boldsymbol{a}^*}{\boldsymbol{a}^{* \mathrm{H}} \boldsymbol{R}_{i+n}^{-1} \boldsymbol{a}^*} $ | (6) |
但在实际应用中,协方差矩阵R通常由式(5)估计:
| $ \hat{\boldsymbol{R}}=\frac{1}{K} \sum\limits_{i=1}^K \boldsymbol{x}(i) \boldsymbol{x}^{\mathrm{H}}(i) $ | (7) |
式中K为快拍数。
根据文献[20],样本求逆波束形成器(SMI)为
| $ \boldsymbol{w}_{\mathrm{SMI}}=\frac{\hat{\boldsymbol{R}}^{-1} \boldsymbol{a}^*}{\boldsymbol{a}^{* \mathrm{H}} \hat{\boldsymbol{R}}^{-1} \boldsymbol{a}^*} $ | (8) |
每当协方差矩阵中存在期望信号时, SMI波束形成器本质上是最小功率无失真响应(MPDR) 波束形成器, 而不是MVDR波束形成器[10]。当
本文研究在限制期望信号方向不收敛于干扰信号方向的条件下,通过重构协方差矩阵以加宽干扰的零陷宽度并提高波束的鲁棒性。同时利用ADMM迭代求解出最优的导向矢量,避免导向矢量失配带来的误差,再次提高波束的鲁棒性。最后利用式(8),设计最优滤波器,达到输出SINR最大化,以抑制干扰信号和噪声。
结合式(1),阵列的输出功率为
| $ \begin{aligned} P(\boldsymbol{w})= & E\left[|y(k)|^2\right]=E\left[\left|\boldsymbol{w}_{\mathrm{opt}}^{\mathrm{H}} \boldsymbol{x}(k)\right|^2\right]= \\ & \boldsymbol{w}^{\mathrm{H}} E\left[\boldsymbol{x}(k) \boldsymbol{x}^{\mathrm{H}}(k)\right] \boldsymbol{w}= \\ & \boldsymbol{w}^{\mathrm{H}} \boldsymbol{R} \boldsymbol{w} \approx \boldsymbol{w}^{\mathrm{H}} \hat{\boldsymbol{R}} \boldsymbol{w} \end{aligned} $ | (9) |
将式(8)代入式(9),可以得到:
| $ P(\boldsymbol{w}) \approx \boldsymbol{w}^{\mathrm{H}} \hat{\boldsymbol{R}} \boldsymbol{w}=\frac{1}{\boldsymbol{a}^{\mathrm{H}} \hat{\boldsymbol{R}}^{-1} \boldsymbol{a}} $ | (10) |
式中导向矢量a为所需的先验知识,通常是不够准确的,必须尽可能少的利用不准确的先验知识在一定的约束下获得准确的导向矢量。
与文献[19]不同,为了强制要求期望方向的导向矢量不收敛于任何干扰信号及其线性组合相关的导向矢量,结合文献[15]的约束条件,本文考虑期望信号导向矢量不收敛于干扰信号及其线性组合的条件下,最大化阵列输出功率,其数学模型如下:
| $ \begin{array}{cc} \min\limits _\boldsymbol{a} & \boldsymbol{a}^{\mathrm{H}} \hat{\boldsymbol{R}}^{-1} \boldsymbol{a} \\ \text { s.t. } & \boldsymbol{a}^{\mathrm{H}} \widetilde{C} \boldsymbol{a} \leqslant \Delta_0 \\ & \|\boldsymbol{a}\|^2=N \end{array} $ | (11) |
其中:
| $ \begin{aligned} \widetilde{C} & =\int_{\varTheta} \boldsymbol{d}(\theta) \boldsymbol{d}^{\mathrm{H}}(\theta) \mathrm{d} \theta \\ \Delta_0 & =\max _{\theta \in \widetilde{\varTheta}} \boldsymbol{d}^{\mathrm{H}}(\theta) \widetilde{C} \boldsymbol{d}(\theta) \end{aligned} $ |
式中: 定义
式(11)中的第1个约束条件限制了Θ范围内的任何角度的导向矢量a,使其均不收敛于干扰信号及其线性组合相关的导向矢量的方向,且不收敛于定义的区间的补集中任何角度及其线性组合相关的导向矢量。换句话说,Δ0相当于一个边界线,如图 1所示。第2个约束条件保证更新后的导向矢量与实际导向矢量具有相同的范数。
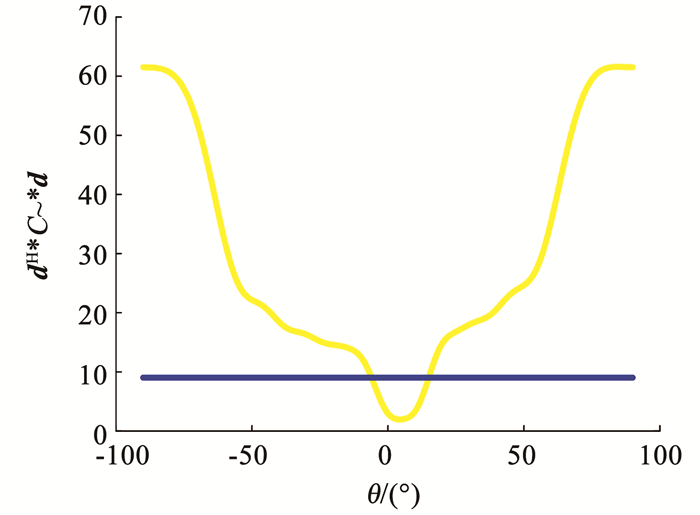
|
图 1 式(12)和式(13)仿真图 Fig. 1 Simulation diagram of Eq.(12) and Eq.(13) |
本文首先提出干扰加噪声协方差矩阵的重构。接着,考虑通过ADMM迭代求解的方法得到最优导向矢量a*。最后,根据式(8)求得最优的加权矢量。
2.1 协方差矩阵重构由文献[15]可知,干扰加噪声的协方差矩阵为
| $ \hat{\boldsymbol{R}}_{i+n}=\int_{\tilde{\varTheta}} P_{\text {Capon }} \boldsymbol{a}(\theta) \boldsymbol{a}^{\mathrm{H}}(\theta) \mathrm{d} \theta $ | (12) |
式中,
令干扰区域范围
| $ \hat{\boldsymbol{R}}_i=\sum\limits_{i=1}^P \int_{\theta_i-\frac{\Delta \delta_i}{2}}^{\theta_i+\frac{\Delta \delta_i}{2}} \frac{\boldsymbol{a}(\theta)^{\mathrm{H}} \boldsymbol{a}(\theta)}{\boldsymbol{a}(\theta)^{\mathrm{H}} \hat{\boldsymbol{R}}^{-1} \boldsymbol{a}(\theta)} $ | (13) |
于是,重构的干扰加噪声协方差矩阵如下:
| $ \hat{\boldsymbol{R}}_{i+n}=\hat{\boldsymbol{R}}_i+\widetilde{\sigma}_n^2 \boldsymbol{I} $ | (14) |
式中
观察式(11)可知,该优化问题包含了凸目标函数和非齐次二次不等式约束,是一个二次不等式约束的二次规划问题(Quadratical constraint quadratic programming, QCQP)。针对该问题,文献[15]利用半正定规划(Semidefinite programming, SDP)技术,将其转化成松弛问题,从一般秩松弛解中找到唯一秩解; 然而,SDP方法在每次转化为松弛问题时,必须判定其局部最优解是否满足全局最优解。
对此,本文利用ADMM通过迭代求解式(11),并在每一次迭代过程中求得闭合解。ADMM有两个重要且独特的特征。首先,它将一个凸优化约束问题分解成多个较小的子问题,这些子问题的解被协调以找到全局最优解。这种形式的分解协调过程允许并行或分布式处理[21-22]。其次,它在参数更新过程中提供了优越的收敛性[23]。
首先,针对式(11)中的不等式约束,引入辅助变量z,将其转化为等式约束,即
| $ \begin{array}{cl} \min\limits _{\boldsymbol{a}} & \boldsymbol{a}^{\mathrm{H}} \hat{\boldsymbol{R}}^{-1} \boldsymbol{a} \\ \text { s. t. } & \boldsymbol{a}^{\mathrm{H}} \widetilde{C} \boldsymbol{a}+z=\Delta_0 \\ & \boldsymbol{a}^{\mathrm{H}} \boldsymbol{a}=N \end{array} $ | (15) |
为了获得式(15)的有效解,引入辅助变量h,且令h = a,则式(15)转化为
| $ \begin{array}{ll} \min\limits _{\boldsymbol{a}} & \boldsymbol{a}^{\mathrm{H}} \hat{\boldsymbol{R}}^{-1} \boldsymbol{a} \\ \text { s. t. } & \boldsymbol{h}^{\mathrm{H}} \widetilde{C} \boldsymbol{a}+z-\Delta_0=0, z \geqslant 0 \\ & \boldsymbol{h}^{\mathrm{H}} \boldsymbol{a}-N=0 \\ & \boldsymbol{h}-\boldsymbol{a}=0 \end{array} $ | (16) |
本文利用ADMM的缩放形式解决式(16),并根据ADMM框架,引入辅助变量s,u,v,则式(16)的增广拉格朗日函数为
| $ \begin{aligned} \mathrm{L}(\boldsymbol{a}, \boldsymbol{h}, z, s, u, \boldsymbol{v})= & \boldsymbol{a}^{\mathrm{H}} \hat{\boldsymbol{R}}^{-1} \boldsymbol{a}+ \\ & \frac{\rho_1}{2}\left\|\boldsymbol{h}^{\mathrm{H}} \widetilde{C} \boldsymbol{a}+z-\Delta_0+s\right\|^2+ \\ & \frac{\rho_2}{2}\left\|\boldsymbol{h}^{\mathrm{H}} \boldsymbol{a}-N+u\right\|^2+\frac{\rho_3}{2}\|\boldsymbol{h}-\boldsymbol{a}+v\|^2 \end{aligned} $ | (17) |
式中ρ1, ρ2, ρ3>0为惩罚系数。
一般来说,在ADMM中,原始变量的更新是通过最小化增广拉格朗日乘子获得的,而拉格朗日乘子的更新是通过对偶上升方法获得。基于式(17),利用ADMM可通过如下循环方式得到封闭解。在第(m+1)次迭代过程中,{a, h, z, s, u, v}的更新分别如下:
| $ \boldsymbol{h}^{m+1}=\arg \min\limits _{\boldsymbol{h}} \mathrm{L}\left(\boldsymbol{a}^m, \boldsymbol{h}, z^m, s^m, u^m, \boldsymbol{v}^m\right) $ | (18) |
| $ \boldsymbol{a}^{m+1}=\arg \min\limits _{\boldsymbol{a}} \mathrm{L}\left(\boldsymbol{a}, \boldsymbol{h}^{m+1}, z^m, s^m, u^m, \boldsymbol{v}^m\right) $ | (19) |
| $ z^{m+1}=\arg \min\limits _z \mathrm{~L}\left(\boldsymbol{a}^{m+1}, \boldsymbol{h}^{m+1}, z, s^m, u^m, \boldsymbol{v}^m\right) $ | (20) |
| $ s^{m+1}=s^m+\left(\boldsymbol{h}^{m+1}\right)^{\mathrm{H}} \widetilde{C} \boldsymbol{a}^{m+1}+z^{m+1}-\Delta_0 $ | (21) |
| $ u^{m+1}=u^m+\left(\boldsymbol{h}^{m+1}\right)^{\mathrm{H}} \boldsymbol{a}^{m+1}-N $ | (22) |
| $ \boldsymbol{v}^{m+1}=\boldsymbol{v}^m+\boldsymbol{h}^{m+1}-\boldsymbol{a}^{m+1} $ | (23) |
下面将具体考虑式(18)~(20)的求解。
1) 更新h。
对于给定
| $ \begin{array}{c} \min\limits _\boldsymbol{h} \frac{\rho_1}{2}\left\|\boldsymbol{h}^{\mathrm{H}} \widetilde{C} \boldsymbol{a}^m+z^m-\Delta_0+s^m\right\|^2+ \\ \frac{\rho_2}{2}\left\|\boldsymbol{h}^{\mathrm{H}} \boldsymbol{a}^m-N+u^m\right\|^2+\frac{\rho_3}{2}\left\|h-\boldsymbol{a}^m+\boldsymbol{v}^m\right\|^2 \\ \end{array} $ | (24) |
令
| $ \begin{gathered} \min\limits _{\boldsymbol{h}} \frac{\rho_1}{2}\left\|\boldsymbol{h}^{\mathrm{H}} \widetilde{C} \boldsymbol{a}^m+\tilde{s}^m\right\|^2+ \\ \frac{\rho_2}{2}\left\|\boldsymbol{h}^{\mathrm{H}} \boldsymbol{a}^m-N+u^m\right\|^2+\frac{\rho_3}{2}\left\|h-\boldsymbol{a}^m+\boldsymbol{v}^m\right\|^2 \end{gathered} $ | (25) |
为了获得式(25)的最小值,本文对式(25)求解关于h的一阶导,并使得导数为0,则对式(25)中3项分别求导为:
| $ \begin{aligned} \nabla_{\boldsymbol{h}}\left\|\boldsymbol{h}^{\mathrm{H}} \widetilde{C} \boldsymbol{a}^m+\tilde{s}^m\right\|^2= & \nabla_{\boldsymbol{h}}\left(\boldsymbol{h}^{\mathrm{H}} \widetilde{C} \boldsymbol{a}^m+\tilde{s}^m\right)\left(\boldsymbol{h}^{\mathrm{H}} \widetilde{C} \boldsymbol{a}^m+\tilde{s}^m\right)^{\mathrm{H}}= \\ & 2 \widetilde{C} \boldsymbol{a}^m\left(\boldsymbol{a}^m\right)^{\mathrm{H}} \widetilde{C}^{\mathrm{H}} \boldsymbol{h}+2 \widetilde{C} \boldsymbol{a}^n\left(\tilde{s}^m\right)^{\mathrm{H}} \end{aligned} $ | (26) |
| $ \begin{aligned} & \nabla_{\boldsymbol{h}}\left\|\boldsymbol{h}^{\mathrm{H}} \boldsymbol{a}^m-N+u^m\right\|^2= \\ & \nabla_{\boldsymbol{h}}\left(\boldsymbol{h}^{\mathrm{H}} \boldsymbol{a}^m-N+u^m\right)\left(\boldsymbol{h}^{\mathrm{H}} \boldsymbol{a}^m-N+u^m\right)^{\mathrm{H}}= \\ & 2 \boldsymbol{a}^m\left(\boldsymbol{a}^m\right)^{\mathrm{H}} \boldsymbol{h}-2 \boldsymbol{a}^m\left(N-u^m\right)^{\mathrm{H}} \end{aligned} $ | (27) |
| $ \begin{array}{c} \nabla_{\boldsymbol{h}}\left\|\boldsymbol{h}-\boldsymbol{a}^m+\boldsymbol{v}^m\right\|^2=\nabla_{\boldsymbol{h}}\left(\boldsymbol{h}-\boldsymbol{a}^m+\boldsymbol{v}^m\right)\left(\boldsymbol{h}-\boldsymbol{a}^m+\boldsymbol{v}^m\right)^{\mathrm{H}}= \\ 2 \boldsymbol{h}-2\left(\boldsymbol{a}^m-\boldsymbol{v}^m\right) \end{array} $ | (28) |
令
| $ \boldsymbol{h}^{m+1}=\boldsymbol{\varXi}^{-1} \boldsymbol{\gamma} $ | (29) |
其中Ξ、γ的定义分别如下:
| $ \begin{aligned} & \boldsymbol{\varXi}=\rho_1 \widetilde{C} \boldsymbol{a}^m\left(\boldsymbol{a}^m\right)^{\mathrm{H}} \widetilde{C}^{\mathrm{H}}+\rho_2 \boldsymbol{a}^m\left(\boldsymbol{a}^m\right)^{\mathrm{H}}+\rho_3 \boldsymbol{I} \\ & \boldsymbol{\gamma}=\rho_3\left(\boldsymbol{a}^m-\boldsymbol{v}^m\right)+\rho_2 \boldsymbol{a}\left(N-u^m\right)^{\mathrm{H}}-\rho_1 \widetilde{C} \boldsymbol{a}\left(\tilde{s}^m\right)^{\mathrm{H}} \end{aligned} $ |
2) 更新a。
对于给定
| $ \begin{gathered} \min\limits _{\boldsymbol{a}} \boldsymbol{a}^{\mathrm{H}} \hat{\boldsymbol{R}}^{-1} \boldsymbol{a}+\frac{\rho_1}{2}\left\|\left(\boldsymbol{h}^{m+1}\right){ }^{\mathrm{H}} \widetilde{\boldsymbol{C}} \boldsymbol{a}+\tilde{s}^m\right\|^2+ \\ \frac{\rho_2}{2}\left\|\left(\boldsymbol{h}^{m+1}\right){ }^{\mathrm{H}} \boldsymbol{a}-N+u^m\right\|^2+\frac{\rho_3}{2}\left\|\boldsymbol{h}^{m+1}-\boldsymbol{a}+\boldsymbol{v}^m\right\|^2 \end{gathered} $ | (30) |
同理,对式(30)中3项分别求导,并且令
| $ \begin{aligned} & \left(\hat{\boldsymbol{R}}^{-1}+\left(\hat{\boldsymbol{R}}^{-1}\right)^{\mathrm{H}}\right) \boldsymbol{a}+\rho_1\left(\widetilde{C}^{\mathrm{H}} \boldsymbol{h}^{m+1}\left(\boldsymbol{h}^{m+1}\right)^{\mathrm{H}} \widetilde{C} \boldsymbol{a}+\right. \\ & \left.\widetilde{C}^{\mathrm{H}} \boldsymbol{h}^{m+1} \tilde{s}^n\right)+\rho_2\left(\boldsymbol{h}^{m+1}\left(\boldsymbol{h}^{m+1}\right)^{\mathrm{H}} \boldsymbol{a}-\boldsymbol{h}^{m+1}\left(N-u^m\right)\right)+ \\ & \rho_3\left(\boldsymbol{a}-\left(\boldsymbol{h}^{m+1}+\boldsymbol{v}^m\right)\right)=0 \end{aligned} $ | (31) |
解得
| $ \boldsymbol{a}^{m+1}=\boldsymbol{\varOmega}^{-1} \xi $ | (32) |
其中Ω、ξ的定义如下:
| $ \begin{aligned} \boldsymbol{\varOmega}= & \hat{\boldsymbol{R}}^{-1}+\left(\hat{\boldsymbol{R}}^{-1}\right)^{\mathrm{H}}+\rho_1 \widetilde{C}^{\mathrm{H}} \boldsymbol{h}^{m+1}\left(\boldsymbol{h}^{m+1}\right)^{\mathrm{H}} \widetilde{C}+ \\ & \rho_2 \boldsymbol{h}^{m+1}\left(\boldsymbol{h}^{m+1}\right)^{\mathrm{H}}+\rho_3 \boldsymbol{I} \\ \xi= & \rho_2 \boldsymbol{h}^{m+1}\left(N-u^m\right)+\rho_3\left(\boldsymbol{h}^{m+1}+\boldsymbol{v}^n\right)- \\ & \rho_1 \widetilde{C}^{\mathrm{H}} \boldsymbol{h}^{m+1} \tilde{s}^m \end{aligned} $ |
3) 更新z。
对于给定
| $ \begin{aligned} & \min\limits _z \frac{\rho_1}{2}\left\|\boldsymbol{h}^{\mathrm{H}} \widetilde{C} \boldsymbol{a}^m+z^{m+1}-\Delta_0+s^m\right\|^2 \\ & \text { s. t. } z^{m+1} \geqslant 0 \end{aligned} $ | (33) |
对式(33)求导并令其为0,解得zm+1=Δ0-sm-
| $ z^{m+1}=\max \left\{0, \Delta_0-s^m-\boldsymbol{h}^{m+1} \widetilde{C} \boldsymbol{a}^{m+1}\right\} $ | (34) |
综上所述,本文提出的基于协方差矩阵重构和ADMM的零陷展宽鲁棒波束形成的步骤见表 1。
| 表 1 ADMM的零陷展宽鲁棒波束形成的步骤 Tab. 1 Steps of null widening robust beamforming based on ADMM |
本文利用ADMM更新
为了验证本文所提方法的有效性,通过仿真实验验证存在干扰、杂波和导向矢量失配情况下,DL算法、协方差矩阵求逆(SMI)算法、文献[10]的算法和文献[16]的算法与本文方法的性能分析对比。实验中阵元数为N=10,输入SNR=10 dB,两个干扰的预设零陷宽度分别为
图 2给出了在不同的INR情况下不同算法的波束图比较。首先,从图 2(a)中可以看出所有算法均可以在干扰处形成零陷,但是DL算法和文献[16]的算法没有展宽零陷的效果,并且文献[16]的算法没有准确的指向干扰方向70°,无法准确的抑制干扰。而SMI算法、文献[10]的算法和本文提出的算法均可以在零陷处进行展宽。从图 2可以看出,在不同的INR值下,SMI算法的零陷加深和展宽效果都随着INR的值增大逐渐加深,但是指向的干扰角度发生了偏移; 文献[10]的算法随着INR值越大,零陷的加深效果越好; 本文所提算法在不同的INR值下,零陷加深效果随着INR的增大略有增大,受INR的影响小,且本文所提算法的零陷加深效果均优于SMI算法和文献[10]的算法,并且可以精确到所控制的零陷范围。综上可知,本文算法抗干扰扰动性能优于所有对比算法。

|
图 2 不同INR情况下不同算法的归一化波束图比较 Fig. 2 Normalized beam pattern comparison of different algorithms under different INR conditions |
在该实验中,当前实际期望方向角度为θ0=10.0°,假设估计的期望方向角度为

|
图 3 不同失配角度情况下不同算法的归一化波束图比较 Fig. 3 Normalized beam pattern comparison of different algorithms under different mismatch angles |
在该实验中,实验条件同实验2。图 4对比分析了不同输入SNR对输出SINR的影响。可以看出SMI和DL算法无法解决导向矢量失配的问题,所以性能远偏离了理论最优值,文献[16]的算法、文献[10]的算法和本文提出的算法可以进行导向矢量的校正,因此在估计角度为8.0°和5.0°时,输出的SNIR性能都比较好,但是由于文献[16]的算法单从噪声空间进行投影,因此在高信噪比时,输出的SINR变化较小。在输入SNR大于30 dB时,性能急剧恶化,而文献[10]的算法可以准确的抑制干扰信号,校正失配导向矢量的能力也比文献[16]的算法强,故而输出的SINR大于文献[16]的算法,本文算法在输入高SNR的情况下,依旧可以准确抑制和加宽干扰零陷,并且主瓣波束依然能够准确指向真实方向,故而输出SINR的值较高。本文提出的算法在低输入SNR的情况下性能较为一般,但是在失配角较大时,对比其他算法性能较为不错。综上可知,本文提出的算法在角度失配和干扰扰动情况下,可保持其稳定性,性能优于其他算法。

|
图 4 输出SINR随输入SNR的变化 Fig. 4 Variation of output SINR with input SNR |
当前实际期望方向角度为θ0=10.0°,估计的期望方向角度为θ0=5.0°,两个干扰零陷的宽度分别为8.0°和5.0°,输入SNR=30 dB。图 5给出了输出SINR随快拍数变化情况。由图 5可知,本文所提算法明显优于其余对比算法,在低快拍数的情况下,也能输出高SINR,且是最接近理论最优值的。相较于本文提出的算法,文献[10]的算法在低快拍数时也收敛了,但是与最优理论值的差别较大。文献[16]的算法和SMI算法均在快拍数大于30时趋近收敛,文献[16]的算法输出SINR高于SMI算法。DL算法受快拍影响较大。

|
图 5 输出SINR随快拍数变化情况 Fig. 5 Variation of output SINR with the number of snapshots |
当前实际期望方向角度为θ0=10.0°,输快拍数N=100,两个干扰零陷的宽度分别为8.0°和5.0°,输入SNR=30 dB,失配角度从-8.0°~8.0°进行变化,每种快拍数进行100次的独立实验。由图 6可知,当失配角度较大时,本算法依旧可以输出接近最优值的SINR。文献[10]的算法虽然也输出高SINR,当失配角度大于3.0°时,文献[10]的算法输出SINR开始下降,在失配角度大于5.0°时,文献[10]的算法明显下降。文献[16]的算法在未发生角度失配时输出较高的SINR,但是总体在角度失配大于3.0°时输出SINR就开始明显下降。SMI算法和DL算法完全没有校正导向矢量失配的性能。本文所提算法均可校正导向矢量,并且输出接近最优值的信噪比。
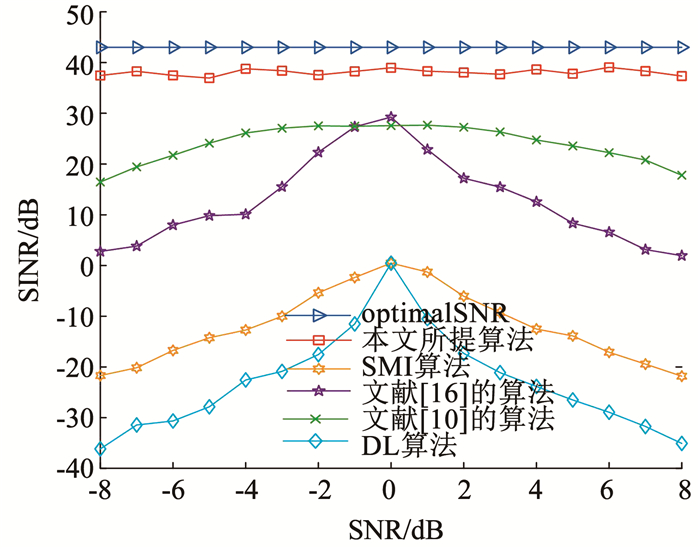
|
图 6 不同失配角度下输出SINR变化情况 Fig. 6 Variation of output SINR under different mismatch angles |
在该实验中,当前实际期望方向角度为θ0=10.0°,假设估计的期望方向角度为
| 表 2 算法运行时间比较 Tab. 2 Algorithm running time comparison |
1) 本文提出的算法与SMI算法和文献[10]的算法相比,在展宽零陷的同时将期望信号分量滤出,有效提高了算法抗系统误差的鲁棒性,并且零陷展宽范围精确,展宽效果优势明显。
2) 与DL算法、SMI算法相比,限制期望方向导向矢量不收敛于干扰方向的导向矢量及其线性组合的导向矢量,避免了“自消”现象的产生。
3) 与文献[10]的算法和文献[16]的算法相比,提高了算法的抗阵列模型失配和抗运动干扰的能力。
4) 由于本文在求解导向矢量时协方差矩阵包含了期望信号信息,对于低信噪比情况下输出的SINR值较低。针对这一问题,有待进行更加深入的研究。
| [1] |
CAPON J. High resolution frequency-wavenumber spectrum analysis[J]. Proceedings of the IEEE, 1969, 57(8): 1408. DOI:10.1109/PROC.1969.7278 |
| [2] |
BRENNAN L, MALLET J D, REED I S. Adaptive arrays in airborne MTI radar[J]. IEEE Transactions on Antennas and Propagation, 1976, 24(5): 607. DOI:10.1109/TAP.1976.1141412 |
| [3] |
刘可, 钱华明, 马俊达. 一种基于导向矢量约束的恒模盲波束形成算法[J]. 哈尔滨工业大学学报, 2016, 48(9): 151. LIU Ke, QIAN Huaming, MA Junda. A constant modulus blind beamforming algorithm based on steering vector constraint[J]. Journal of Harbin Institute of Technology, 2016, 48(9): 151. DOI:10.11918/j.issn.0367-6234.2016.09.026 |
| [4] |
AGRAWAL S, RANA V, JAGANNATHAM A K. Queuing analysis for multiple-antenna cognitive radio wireless networks with beamforming[J]. IEEE Signal Processing Letters, 2017, 24(3): 334. DOI:10.1109/LSP.2017.2659541 |
| [5] |
GERSHMAN A B. Robust adaptive beamforming: An overview of recent trends and advances in the field[C]//Proceedings of the 4th International Conference on Antenna Theory and Techniques. Sevastopol, Ukraine: IEEE, 2003(1): 30. DOI: 10.1109/ICATT.2003.1239145
|
| [6] |
FELDMAN D D, GRIFFITHS L J. A projection approach for robust adaptive beamforming[J]. IEEE Transactions on Signal Processing, 1994, 42(4): 867. DOI:10.1109/78.285650 |
| [7] |
WIDROW B, DUVALL K M, GOOCH R P, et al. Signal cancellation phenomena in adaptive antennas: causes and cures[J]. IEEE Transactions on Antennas and Propagation, 1982, 30(3): 469. DOI:10.1109/TAP.1982.1142804 |
| [8] |
COX H, ZESKIND R M, OWEN M M. Robust adaptive beamforming[J]. IEEE Transactions on Acoustics Speech and Signal Processing, 1987, 35(10): 1365. DOI:10.1109/TASSP.1987.1165054 |
| [9] |
刘晓军, 刘聪锋, 廖桂生. 子空间投影稳健波束形成算法及其性能分析[J]. 系统工程与电子技术, 2010, 32(4): 669. LIU Xiaojun, LIU Congfeng, LIAO Guisheng. Robust adaptive beamforming algorithm based on subspace projection method and its performance analysis[J]. Systems Engineering and Electronics, 2010, 32(4): 669. |
| [10] |
GU Yujie, LESHEM A. Robust adaptive beamforming based on interference covariance matrix reconstruction and steering vector estimation[J]. IEEE Transactions on Signal Processing, 2012, 60(7): 3881. DOI:10.1109/TSP.2012.2194289 |
| [11] |
杨志伟, 贺顺, 廖桂生. 子空间重构的一类自适应波束形成算法[J]. 电子与信息学报, 2012, 34(5): 1115. YANG Zhiwei, HE Shun, LIAO Guisheng. Adaptive beam-forming algorithm with subspace reconstructing[J]. Journal of Electronics & Information Technology, 2012, 34(5): 1115. DOI:10.3724/SP.J.1146.2011.00883 |
| [12] |
沈肖雅, 葛俊祥, 王奇. 一种稳健自适应波束形成算法[J]. 中国电子科学研究院学报, 2019, 14(4): 373. SHEN Xiaoya, GE Junxiang, WANG Qi. A robust adaptive beamforming algorithm[J]. Journal of CAEIT, 2019, 14(4): 373. DOI:10.3969/j.issn.1673-5692.2019.04.008 |
| [13] |
HASSANIENH A, VOROBYOV S A, WONG K M. Robust adaptive beamforming using sequential quadratic programming: An iterative solution to the mismatch problem[J]. IEEE Signal Processing Letters, 2008, 15(15): 733. DOI:10.1109/LSP.2008.2001115 |
| [14] |
LANDAU L, DE LAMARE R C, HAARDT M. Robust adaptive beamforming algorithms using low-complexity mismatch estimation[C]//Proceedings of the IEEE Statistical Signal Processing Workshop(SSP). Nice, France: IEEE, 2011: 445. DOI: 10.1109/SSP.2011.5967727
|
| [15] |
HUANG Yongwei, ZHOU Mingkang, VOROBYOV S A. New designs on MVDR robust adaptive beamforming based on optimal steering vector estimation[J]. IEEE Transactions on Signal Processing, 2019, 67(14): 3624. DOI:10.1109/TSP.2019.2918997 |
| [16] |
JIA Weimin, JIN Wei, ZHOU Shuhua, et al. Robust adaptive beamforming based on a new steering vector estimation algorithm[J]. Signal Processing, 2013, 93(9): 2539. |
| [17] |
CUI Guolong, LI Hongbin, RANGASWAMY M. MIMO radar waveform design with constant modulus and similarity constraints[J]. IEEE Transactions on Signal Processing, 2014, 62(2): 343. DOI:10.1109/TSP.2013.2288086 |
| [18] |
DE MAIO A, HUANG Yongwei, PIEZZO M, et al. Design of optimized radar codes with a peak to average power ratio constraint[J]. IEEE Transactions on Signal Processing, 2011, 59(6): 2683. DOI:10.1109/TSP.2011.2128313 |
| [19] |
KHABBAZIBASMENJ A, VOROBYOV S A, HASSANIENH A. Robust adaptive beamforming based on steering vector estimation with as little as possible prior information[J]. IEEE Transactions on Signal Processing, 2012, 60(6): 2974. DOI:10.1109/TSP.2012.2189389 |
| [20] |
REED I S, MALLETT J D, BRENNAN L E. Rapid convergence rate in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1974, 10(6): 853. DOI:10.1109/TAES.1974.307893 |
| [21] |
BOYD S, PARIKH N, CHUA E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends in Machine Learning, 2010, 3(1): 1. DOI:10.1561/2200000016 |
| [22] |
ALDAYEL O, MONGA V, RANGASWAMY M. Successive QCQP refinement for MIMO radar waveform design under practical constraints[J]. IEEE Transactions on Signal Processing, 2016, 64(14): 3760. DOI:10.1109/TSP.2016.2552501 |
| [23] |
巩朋成, 王兆彬, 谭海明, 等. 杂波背景下基于交替方向乘子法的低截获频控阵MIMO雷达收发联合优化方法[J]. 电子与信息学报, 2021, 43(5): 1267. GONG Pengcheng, WANG Zhaobin, TAN Haiming, et al. Joint design of the transmit and receive beamforming via alternating direction method of multipliers for LPI of frequency diverse array MIMO radar in the presence of clutter[J]. Journal of Electronics and Information Technology, 2021, 43(5): 1267. DOI:10.11999/JEIT200445 |
 2023, Vol. 55
2023, Vol. 55


