直流漂移是指电路在工作过程中随着时间变化,静态工作点偏离正常点导致的时域信号中存在的不稳定趋势。一般表现为单向漂移或周期漂移。造成这种现象的原因: 一是电路中电压波动及电子器件老化、温度升高; 二是元件及电路本身的噪声和电源工频噪声及其他周围环境噪声[1-2]。且采集到的信号中带有的直流漂移往往表现为不稳定和随机性且无法测量的,使用普通滤波器很难将其消除。直流漂移与有用信号相混淆会对信号的分析和应用产生一系列影响。比如信号标准差增大、能量谱密度的低频数值增大等[3-4],从而使得电路的性能下降,时域和频域分析出现严重偏差[5]。因此从原始数据中去除直流漂移获得真实准确的信号具有非常重要的意义。
以往有关消除原始信号中直流漂移的方法较有限,主要集中在腐蚀领域电化学噪声技术的研究和应用。一类是实时模拟高通滤波,但是当滤波器截止频率非常低时,理想的大容量电容器难以实现且稳定时间较长。另一种是对时域信号的数字高通滤波,但有一定局限性。Tan等[6]提出移动平均值法消除电化学噪声原始信号的直流漂移,然而此方法被认为在滤波窗口选择、参数p的选择等方面缺乏深入考虑。Mansfeld等[7]提出了线性拟合消除法,线性拟合方法适用范围局限,对信号的线性特性要求较高。之后Bertocci等[8]提出了多项式拟合消除法,该方法算法简便,尽管多项式幂次选择物理意义不明确,但仍然能够有效应用于直流漂移消除问题。由于大部分信号均具有非线性、非平稳性,传统的统计特性分析方法作为一种研究数据内在规律的方法处理的效果并不理想。Huang等[9]提出小波变换方法,该方法也是根据小波变换下低频信号能够反映直流漂移趋势的思想。小波变换是时频分析的一个重要方法,它在一定程度上克服了短时傅里叶变换的时间和频率分辨率不能兼顾的弱点。但是小波变换也受到测不准原理的限制[10],以及存在如何选取小波基的问题[3, 11-12]。
Huang等[9]提出的经验模态分解(Empirical mode decomposition, EMD)是一种具有自适应性,能够将信号按照不同特征尺度逐层分解为具有物理意义的一组数据序列的数据处理方法。EMD算法已经广泛应用于数字、图像、光学信号处理、故障诊断等许多领域,各自取得了很好的效果也提供了新的思路。由于EMD具有通过分解得到最低频的IMF分量就能够有效提取信号的趋势或均值的天然优势,可以认为EMD方法是解决信号直流漂移问题最好的方法之一[13-15]。EMD算法是一种高效的信号分析方法,然而EMD算法本身不具有滤波或消除某类信号的能力,它只是提供了一种分析思路,利用其计算结果有潜力完成去噪、滤波等目标。但是单独使用EMD算法只能达到对原始信号分解的效果,因此针对具体的问题,需要在EMD算法的思想下结合更具体的分析方法。同时EMD理论与应用仍然需要不断地进行完善。
基于此本文提出了一种基于分段经验模态分解的漂移消除方法,本文根据本征模态函数(Intrinsic mode function, IMF)分量中的特征点设置信号分段点,针对分段信号分别进行直流漂移的消除,改善了信号电平变化而拟合信号滞后的问题;提出了基于自相关函数筛选噪声主导和有用信号主导的IMF分量的方法,利用峰度指标能够更加准确区分分界IMF阶数。结合分解所得的IMF分量进行能量权值分析[16]对信号进行重构,从而达到降低信号噪声并一定程度保留有用信号,提高信号精确度的目的。针对如何证明漂移被正确消除,而有用信号没有严重受损的问题,通过仿真模拟漂移信号验证了有效性并与其他方法做了对比,并通过实验进行了说明。
1 EMD算法概述EMD的基本思想是将信号分解成一系列频率从高到低的IMF分量,即本征模态函数。EMD方法所定义的基函数等价于具有自适应分解特性[2],不需要事先预定或强制给定,而是依靠信号的本质特征,根据分解过程中信号的特征而自适应改变。经验模态分解具体计算过程不再赘述,在很多文献中均有详细介绍[17]。然而EMD计算过程中有广泛存在的问题需要解决,需要注意的是,每一频段包含频率成分是不同的,同一个IMF分量在不同时刻的瞬时频率也是不同的,在所有时刻内,高阶的IMF分量的频率不一定总是比低阶的IMF分量的频率高。这也印证了EMD的局部时间分布是根据信号本身特点变化的。
EMD方法目前所涉及到的问题,一是端点效应处理,在分解IMF的过程中,要通过计算信号的局部极大值和极小值,通过样条插值算法求取上、下包络线。由于信号的左、右端点只能是极大值或极小值一种情况,那么上包络线或下包络线中的一个必然无法确认它的一端终点。因此在数据两端不可避免会出现发散现象,使得所得结果严重失真。本文采用对信号两端进行延拓的方法解决端点问题。二是在实际分解过程中,上、下包络线的均值很难为零,过度的分解也会导致IMF分量成为纯粹的频率调制信号。所以要确定分解的停止准则[18]。文献[19]定义了IMF判据准则,该判据要多次计算局部均值,导致迭代次数较多,但精度较高。本文采用该停止准则。另外在对非线性和非平稳性的信号做EMD时,也会出现其他情况:一个本征模态函数中含有不同时间尺度的分量,或者不同的本征模态函数中包含了相同的时间尺度的成分,产生了这样模态混叠的现象,本征模态函数就失去了其物理意义。许多学者针对此问题也做了大量研究,主要有多分辨率EMD思想,斜向极值点改进的方法和聚合经验模态分解的方法[3]。但是涉及到了牺牲算法自适应性或使算法更加复杂,不利于算法移植等问题。
2 基于分段EMD的信号处理 2.1 分段点提取原始信号中包含着漂移和噪声成分,消除信号漂移及噪声之前需要进行预处理。将原信号F(t)看作是由有用信号和直流漂移信号两部分组成,直流漂移表现为低频的光滑曲线,因此采用低频的IMF分量拟合直流漂移信号,但是对于幅值、频率在短时间急剧变化的高频信号,会造成较大误差。对此本文提出利用特征IMF分量进行分段直流漂移消除的方法,如图 1所示。具体步骤如下:

|
图 1 基于IMF的分段点提取示意 Fig. 1 Schematic diagram of segmentation points extraction based on IMF |
1) 原始信号F(t)进行第1次EMD分解,得到A个IMF分量和一个残量。可表示为
| $ F(t)=\sum\limits_{i=1}^A \mathrm{imf}_i^{(1)}(t)+r^{(1)}(t) $ | (1) |
式中: imf1(1)(t), imf2(1)(t), ⋯, imfA(1)(t)的频段按照从高到低排列,残量r(1)(t)为原信号的大致趋势或均值。
2) 从步骤1)的A个IMF分量中选择出现尖峰幅值最大者,设为第I项即特征IMF分量。可计算比较每个IMF分量最大值与上包络线平均值的差值,最大差值d对应的即为特征IMF分量。
| $ d=\max \left[\operatorname{imf}_I^{(1)}(t)\right]-\frac{1}{N} \sum \operatorname{Envelop}\left(\operatorname{imf}_I^{(1)}(t)\right) $ | (2) |
式中: N为数据长度,Envelop(imfI(1)(t), p)为包络线函数,max[]为最大值函数,均通过MATLAB的内置函数实现。
求取其极大值波峰或极小值波谷,即代表着信号幅值瞬时发生变化的位置。瞬时幅值较大的极值点对应原始信号产生阶跃的位置,由于极值点常常以簇的形式出现,会造成分段点交叠,降低分段效率。提出通过已经构造的特征IMF包络线,对原数据进行降采样,并与阈值作比较从而筛选出分段点位置。阈值的大小决定区间分段数量。式(3)为本文的阈值选取规则。
| $ \begin{gathered} \delta=\left(\frac{1}{N} \sum \text { Envelop }\left(\operatorname{imf}_I^{(1)}(t)\right)+\right. \\ \left.\max \left[\operatorname{imf}_I^{(1)}(t)\right]\right) / 2 \end{gathered} $ | (3) |
3) 在步骤2) 中包络线中的极值点对应的时间为
P段信号中某一段Fs(t)再次进行EMD分解,将分解得到的分量以k作为分界点分开,表达式为
| $ \begin{array}{c} F_s(t)=\sum\limits_{i=1}^k \operatorname{imf}_i^{(2)}(t)+\sum\limits_{i=k+1}^B \mathrm{imf}_i^{(2)}(t)+ \\ r^{(2)}(t)(1 \leqslant s \leqslant P) \\ \end{array} $ | (4) |
式中: B为IMF分量个数, imfi(2)(t)为Fs(t)再次进行EMD分界得到的IMF分量, r(2)(t)对应信号的低频成分, P段信号都按式(4)进行分解。
在B个IMF分量中存在一个imfk(2)(t),在其之前的分量中噪声为主导成分,在其之后的分量中有用信号占主导成分。关于找到分界IMF分量即分界k值的方法,Boudraa等[20]提出了基于连续均方误差准则的EMD去噪方法,文献[17]指出,该方法处理信噪比较大的信号性能不是十分稳定,且对于实际采集信号,噪声和信号经常会在同频段中出现,在舍弃噪声的同时,也会丢失有用信号。
自相关函数是信号与延迟后信号之间在时域特性的相似性度量[21]。它表示时域信号在不同时刻t与t+τ的相似程度。自相关函数的公式为
| $ R_i(\tau)=\sum\limits_{t=\tau+1}^T \operatorname{imf}_i^{(2)}(t) \operatorname{imf}_i^{(2)}(t+\tau)(1 \leqslant i \leqslant B) $ | (5) |
式中: τ为对时间t的时间延迟,T为采样点数。
原始信号经过EMD分解之后,虽然IMF分量中包含的已不是原来意义上的噪声,但随机特性依然存在。由于白噪声具有弱相关性和随机性,在零点处自相关函数最大,其他点处随着时间变化迅速衰减。由于有用信号本身的关联性,在零点处自相关函数有最大值,其他点的值随时间变化有一定衰减,但是过程比较缓慢[17],因此噪声和信号的自相关函数有着明显区别。按照IMF分量的自相关系数曲线的收敛性进行比较,k值比较容易选择出来。提出利用峰度衡量自相关函数值分布的陡峭程度,根据峰度定理[22],其自相关函数的峰度 < 3时,IMF分量中的噪声占比越小,自相关函数衰减程度越不明显,当自相关函数的峰度>3时,IMF分量中的噪声为主导。因此可以将自相关函数峰度超过3的作为噪声占主导IMF分量,< 3的作为力信号占主导的IMF分量。峰度的计算公式为
| $ \operatorname{Kurt}\left[R_i\right]=\frac{E\left[\left(R_i-\mu\right)^4\right]}{\left(E\left[\left(R_i-\mu\right)^2\right]\right)^2} $ | (6) |
式中: Kurt为峰度,Ri为自相关函数,μ为均值。
基于上述特点,本文提出了基于自相关函数峰度的分界k值的筛选方法,即计算每个IMF分量的自相关函数并通过比较相互之间的峰度值便可得到分界k值。
2.3 漂移信号重构直流漂移信号一般为非周期低频信号,EMD去直流漂移的本质就是信号的高通多尺度滤波[3],即去除包含直流漂移的低频率的IMF分量再进行信号重构的过程。关键在于IMF分量的选取。
在确定分界k值以后,如果有用信号中存在与直流漂移频段相同的低频成分,那么经过EMD分解后,残量中会同时包含漂移和低频成分。信号经过分段处理后,可以一定程度上避免残量中的有用信号存在幅值变化。因此残量中有用信号低频分量应该为常量,所以残量中发生的波动都属于直流漂移分量,可以将其全部去除而不影响有用信号。
对低频的IMF分量进行FFT分析,根据IMF分量的频带范围选择IMF重构得到直流漂移。当残量r(2)(t)频带较小不足以满足漂移信号频率范围,对每一阶IMF分量做FFT。如图 2所示,不同颜色波形分别表示各阶IMF分量的频谱,相邻的IMF分量的频谱通常会有交叠,按照漂移信号频率范围选择之前阶次IMF分量再与残量r(2)(t)进行重构从而适当提高漂移重构信号频率,提高重构精度。因为信号已经经过分段处理,残量r(2)(t)的频段已经很低,通常在0.5 Hz以内,直接用残量r(2)(t)表示漂移分量即可,但是为了筛选IMF分量更加准确可以将此次选择的IMF分量阶次作为先验信息,用作此后重构直流漂移信号选择的IMF分量阶次。

|
图 2 直流漂移成分的选取 Fig. 2 Selection of DC drift components |
对原始信号良好的分段处理为基于EMD对低频直流漂移的重构并消除起到了不错的铺垫作用。并且通过IMF分量的重构能够简便且快速的复现出漂移趋势。另外,消除的直流漂移信号自身具有一定的幅值,它代表原始信号的平均幅值大小,因此在消除漂移分量之后要将该幅值加回到重构信号中。
2.4 能量分析法滤波在筛选出有用信号占主导和噪声占主导的分界k值之后,对k阶之前的分量即噪声和有用信号交叠部分的信号做能量分析。
由于k阶之前的分量中也包含着有用信号,直接舍弃会导致信号失真。根据各个分量占总能量的比重确定权值保留高频中能量较大的分量[16],能够较大比例地保留高频分量中的有用信号,又不至于让噪声成分干扰到低频信号[23]。计算IMF分量能量的公式为
| $ E n_i=\sum\limits_{t=1}^n\left|\operatorname{imf}_i^{(2)}(t)\right|^2 $ | (7) |
式中n为分段信号的数据序列长度。
信号每一阶IMF分量占总能量比值的公式为
| $ E_i=\frac{E n_i}{\sum\limits_{i=1}^k E n_i} \times 100 \% $ | (8) |
式中Eni为第i阶IMF分量的能量。
式(7)、(8)均将k阶之前所有IMF分量加入到计算中,然而一般在实际应用中对于imf1(2)(t)或前几阶分量由于其主要成分为高频噪声,通常直接将其去除,具体要取决于实验本身的要求及系统特性。每一段信号分别求取k阶之前的分量在总能量中的占比,最后每个分量乘自身的权值进行重构。表达式如下:
| $ F^{\prime}(t)=\sum\limits_{s=1}^P F_s^{\prime}(t)=\sum\limits_{s=1}^P\left(\sum\limits_{i=1}^k \operatorname{imf}_i^{(2)}(t) \cdot E_i\right) $ | (9) |
本文采用基于分段EMD的去除直流漂移的方法,根据特征IMF分量将信号分区间进行处理,结合自相关函数确定有用信号占主导成分的低频IMF分量,并通过能量分析对中频IMF分量加权进行重构,从而实现了对原始信号的漂移消除和降噪。图 3为改进EMD信号处理的具体流程。

|
图 3 基于分段EMD的直流漂移消除流程 Fig. 3 Process of DC drift elimination based on segmented EMD |
下面分别采用5种不同方法对数字信号Fs(t)直流漂移消除效果进行定量分析,Fs(t)是采样频率为1 kHz, 时长为10 s的仿真信号。引入信噪比(Signal-noise ratio, SNR)和均方根误差(Root mean squared error, RMSE)作为评价指标。Fs(t)表达式如下:
| $ \begin{array}{l} F_s(t)= 0.1 \cos \left(2 \pi w_1 t\right)+0.1 \cos \left(2 \pi w_2 t\right)+w(t)+ \\ \;\;\;\;\;\;\;\;\;\;\;x(t)+d(t)\\ x(t)=\left\{\begin{array}{l} 0.4, 3.33 <t <6.66 \\ 0, \;\;\;\;\text { others } \end{array}, t \subset[0, 10]\right. \end{array} $ | (10) |
式中: w1、w2分别为两叠加信号的频率, w(t)为白噪声序列, x(t)为矩形波信号,d(t)为实验装置中采集得到的直流漂移信号。
3.1 分段点提取实验在下面处理中,仿真信号选择w1=6 rad/s,w2=10 rad/s并添加0.5 dB的白噪声,如图 4所示。

|
图 4 仿真信号 Fig. 4 Simulation signal |
在对仿真信号Fs(t)进行第1次EMD分解得到的IMF分量中,第8阶的本征模态函数具有能够明显显示信号幅值发生突变的特点,如图 5所示。根据信号频率和长度,包络线的数据移动间隔取为0.2 s。根据该分量极大值点的位置信息可得到仿真信号幅值发生变化的位置,即可将仿真信号在该位置进行分段。从该IMF分量中可获取3个分段点,与左、右端点共组成4个区间,因此可将Fs(t)分为4段。阈值的选择、IMF分量选取、包络线的数据移动间隔等均可影响分段个数,分段个数的变化能够影响对漂移信号拟合的精确度,上文已对这些参数的确定进行了阐述,能够对信号幅值真实变动的位置准确分段。

|
图 5 仿真信号EMD分解得到的特征分量 Fig. 5 Component with characteristic obtained from EMD decomposition of simulation signal |
选取分段信号的低频IMF分量进行重构,图 6为其中一段信号经过EMD分解得到的IMF分量与其对应的频谱,图 7为该段信号的经过EMD分解得到的IMF分量的自相关函数。图中可发现,除残量r(2)(t)外,只有imf9(2)(t)的频带在漂移信号频率范围内。因此可以选取最后一阶IMF分量与残量进行重构。

|
图 6 仿真信号IMF分量及对应频谱 Fig. 6 IMF components and corresponding spectrum of simulation signal |

|
图 7 仿真信号IMF分量对应自相关函数 Fig. 7 Autocorrelation function corresponding to IMF component of simulation signal |
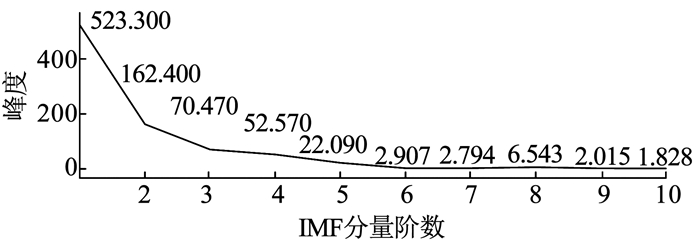
对k之前阶次的IMF分量进行能量分析。以上文的一段信号为例,如图 8所示,已知经EMD分解得到的IMF分量阶数B=9,在对其IMF分量进行相关函数峰度值求解找到分界k值。当峰度值< 3时,自相关函数衰减速率偏慢,因此可知在之后阶数的IMF分量噪声占比较小,因此可以将分界k值定为7。则保留第7阶到第10阶分量。
|
图 8 仿真信号各阶IMF分量自相关函数的峰度 Fig. 8 Kurtosis of the autocorrelation function of each IMF component of the simulation signal |
对之前每一阶IMF分量进行FFT分析,一般对于高频噪声进行直接舍弃,这里将200 Hz以上高频分量当作噪声进行舍弃,则前两阶分量直接舍弃,对3~6阶IMF分量进行能量分析, 每一阶分量乘对应权值进行重构,如图 9所示。

|
图 9 仿真信号的IMF分量能量占比 Fig. 9 Energy proportion of IMF components of simulation signal |
去除直流漂移后再对信号进行降噪处理。基于EMD的能量分析方法,得到每段信号的IMF分量的能量占比,对每段分量分别加权重构,得到降噪的信号。
3.3 仿真数据对比基于多项式拟合方法选择的阶次为5[1];基于小波分析重构去除直流漂移的方法选择db6小波基[24];采用基本的高通滤波器选择合适的截止频率保留信号的低频成分也能够分离出直流漂移趋势;另外采用EMD方法构造低频直流漂移分量。最后再利用本文方法对该信号进行处理。在多种方法的对比中,本文方法仅进行到直流漂移信号消除部分为止。
如表 1所示,对仿真信号处理方法的评估选择了两种频率w1=0.1 rad/s,w2=0.5 rad/s和w1= 6 rad/s,w2=10 rad/s。可以看出基于分段EMD的方法对漂移信号的拟合程度明显优于其他方法,有着更优的信噪比和均方根误差。
| 表 1 5种方法消除直流漂移效果比较 Tab. 1 Comparison of the effects of five methods for DC drift elimination |
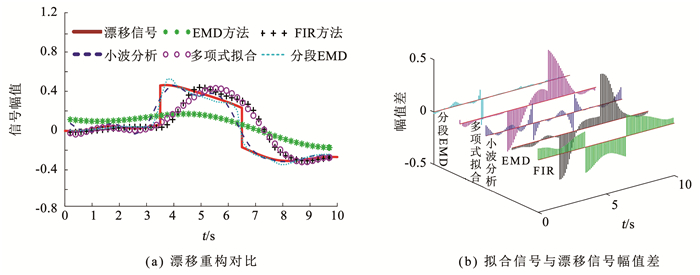
图 10所示为采用各个方法从仿真信号中提取直流漂移信号的效果对比,仿真信号选择w1=6 rad/s,w2=10 rad/s并添加0.5 dB的白噪声。
|
图 10 5种方法拟合直流漂移信号效果对比 Fig. 10 Comparison of the effects of five methods to fit DC drift signal |
由上述数据可见,本文的分段经验模态分解消除低频直流漂移方法,基于经验模态分解得到特征分量首先进行信号分段, 有效排除了阶跃对EMD分解得到的残量的影响,然后利用噪声与有用信号的自相关性不同和不同IMF分量的能量占比,能够较好地滤除高频和同频噪声,且在信号频率较低,与直流漂移信号频率接近的情况下,依然能够较好地拟合出直流漂移趋势。
4 结果与分析 4.1 实验装置本文采用天津大学等单位研发的“MicroHand”微创外科手术机器人的机械手部分采集原始信号,该具有力感知能力的四维度机械手结构如图 11所示。通过右端的快换接口能够完成机械手与主机械臂的拆卸。应变片安装于机械手前端,与电路板上的电桥产生模拟信号并随后转换为数字电压信号输出。该实验数据的采样时长为10 s, 采样频率为1 kHz,应用该算法处理时长为1 s。

|
图 11 应变信号采集系统 Fig. 11 Strain signal acquisition system |
对应变信号进行采集,该信号为空载状态下加载20 g砝码之后卸载20 g砝码的过程,总时长为10 s,采样频率为1 000 Hz,根据实际采集的应变力信号数据的特点和采样频率,选取第3阶的本征模态函数作为特征IMF分量,根据该分量极大值点的位置信息可得到应变信号电压幅值发生变化的位置,即可将应变信号在该位置进行分段。
分段信号分别选取低频IMF分量对直流漂移进行重构,将漂移信号频率范围定为0~1 Hz, 对各段信号的IMF分量的频谱进行分析,选取最后一阶IMF分量与残量进行直流漂移信号的重构。
去除直流漂移后再对信号进行降噪处理。按本实验数据的要求,有用信号的频谱需要限制在50 Hz以内。根据自相关函数的峰度将分界k值定为7,则保留imf7(2)(t)以后的分量,对其他每一阶IMF分量进行FFT分析,得到最高频率为50 Hz频谱对应IMF分量阶数为3,则前两阶分量直接舍弃。
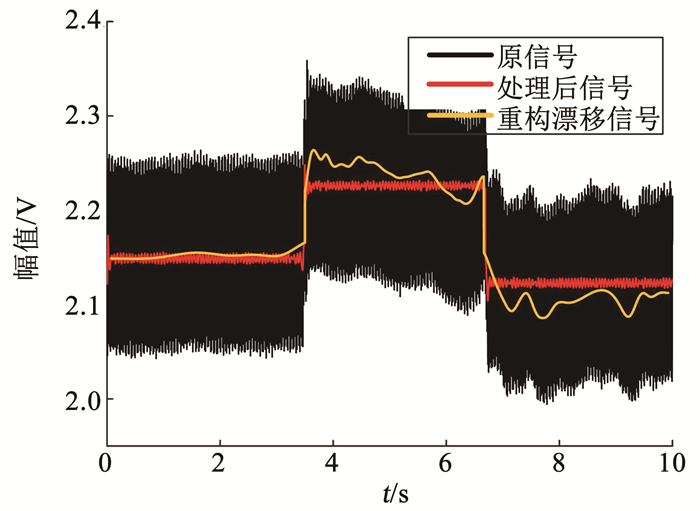
对imf7(2)(t)之前的分量进行能量分析。即对3~6阶IMF分量进行能量分析,得到每段信号的IMF分量的能量占比,对每段分量分别加权重构得到降噪的信号,再与分界k值之后的去除直流漂移信号成分的低频重构信号相加即可得到处理之后的信号。原始信号与经过处理之后的信号对比如图 12所示。
|
图 12 20 g砝码载荷下原信号与处理之后的信号对比 Fig. 12 Comparison of original signal and processed signal under 20 g weight load |
另外,采用上文4种解决直流漂移相关问题的方法处理该应变信号,由于以上4种对比方法只针对直流漂移分量进行消除,并没有对信号进行高频降噪,本文提出的分段EMD采用的降噪方法并不适合与其他对比方法相结合,因此在对比实验中,小波分析消除漂移可以结合小波低频重构方法对应变信号进行高频噪声的消除;而其他对比方法选择使用FIR滤波器保留50 Hz以内的有用信号,与本文分段EMD方法保留有用信号频谱一致。对应变信号处理效果如图 13所示。

|
图 13 对比方法对应变信号的应用 Fig. 13 Application of contrast methods in strain signal |
从图 13中信号形态可以发现,处理之后的信号与实际信号之间均存在较大的偏差,尤其会在信号发生跳变时产生更大的误差,本文方法与之相比,重构漂移信号的幅值误差以及时域上的延迟均有较好的提升并具有良好的降噪性能。
5 结论1) 该方法通过本征模态函数分量的特征对信号进行分区间处理,用低频部分IMF分量进行重构拟合出直流漂移信号趋势从而消除漂移,能够有效去阶跃分量对于重构漂移分量的干扰。
2) 基于自相关函数峰度对若干分量的噪声占比进行区分,按能量占比进行加权重构。得到的数据符合理想结果,通过对模拟信号的仿真表明本文方法处理结果有着较高的信噪比和更小的均方根误差,且对漂移信号拟合程度较高。
3) 相对于EMD方法,有着更好的分界点判别依据和较好的去噪效果,在尽可能保留信号中的有用成分的基础上去除噪声。为信号后续的分析与应用提供了良好基础。
| [1] |
孙会娇, 代煜, 张建勋, 等. 直流电源激励下的电路高分辨力应变信号处理[J]. 仪器仪表学报, 2019, 40(8): 184. SUN Huijiao, DAI Yu, ZHANG Jianxun, et al. High resolution strain signal processing for the circuit under DC source excitation[J]. Chinese Journal of Scientific Instrument, 2019, 40(8): 184. DOI:10.19650/j.cnki.cjsi.J1905271 |
| [2] |
崔昊, 郭锐, 李兴强, 等. 面向位置敏感器件的反馈堆叠信号滤波[J]. 光学精密工程, 2020, 28(7): 1568. CUI Hao, GUO Rui, LI Xingqiang, et al. Complex signal filter method for position sensitive devices application using a feedback stacking model based on extreme learning machine[J]. Optics and Precision Engineering, 2020, 28(7): 1568. DOI:10.37188/OPE.20202807.1568 |
| [3] |
COTTIS R A. Interpretation of electrochemical noise data[J]. Corrosion, 2001, 57(3): 265. DOI:10.5006/1.3290350 |
| [4] |
罗玉昆, 罗诗途, 罗飞路, 等. 激光超声信号去噪的经验模态分解实现及改进[J]. 光学精密工程, 2013, 21(2): 47. LUO Yukun, LUO Shitu, LUO FeiIu, et al. Realization and improvement of laser ultrasonic signal denoising based on empirical mode decomposition[J]. 0ptics and Precision Engineering, 2013, 21(2): 47. DOI:10.3788/OPE.20132102.0479 |
| [5] |
张涛, 杨延格, 邵亚薇, 等. 电化学噪声分析方法的研究进展[J]. 中国腐蚀与防护学报, 2014, 34(1): 1. ZHANG Tao, YANG Yange, SHAO Yawei, et al. Advances of the analysis methodology for electrochemical noise[J]. Journal of Chinese Society for Corrosion and Protection, 2014, 34(1): 1. DOI:10.11902/1005.4537.2013.275 |
| [6] |
TAN Y J, BAILEY S, KINSELLA B. The monitoring of the formation and destruction of corrosion inhibitor films using electrochemical noise analysis(ENA)[J]. Corrosion Science, 1996, 38(10): 1681. DOI:10.1016/S0010-938X(96)00061-3 |
| [7] |
MANSFELD F, SUN Z, HSU C H, et al. Concerning trend removal in electrochemical noise measurements[J]. Corrosion Science, 2001, 43(2): 341. DOI:10.1016/S0010-938X(00)00064-0 |
| [8] |
BERTOCCI U, HUET F, ROUSSEAU P, et al. Drift removal procedures in the analysis of electrochemical noise[J]. Corrosion, 2002, 58(4): 337. DOI:10.5006/1.3287684 |
| [9] |
HUANG J Y, QIU Y B, GUO X P. Comparison of polynomial fitting and wavelet transform to remove drift in electrochemical noise analysis[J]. Corrosion Engineering, Science and Technology, 2010, 45(4): 288. DOI:10.1179/147842208X338956 |
| [10] |
代煜, 张建勋. 基于小波变换和维纳滤波的半导体器件1/f噪声滤波[J]. 物理学报, 2011, 60(11): 110516-1. DAI Yu, ZHANG Jianxun. Reduction of 1/f noise in semiconductor devices based on wavelet transform and Wiener filter[J]. Acta Physica Sinica, 2011, 60(11): 110516-1. DOI:10.7498/aps.60.110516 |
| [11] |
陈真诚, 吴贤亮, 赵飞骏. EEMD结合小波阈值的光电容积脉搏波信号降噪[J]. 光学精密工程, 2019, 27(6): 1327. CHEN Zhencheng, WU Xianliang, ZHAO Feijun. Denoising and implementation of photoplethysmography signal based on EEMD and wavelet threshold[J]. Optics and Precision Engineering, 2019, 27(6): 1327. DOI:10.3788/OPE.20192706.1327 |
| [12] |
孙田川, 刘洁瑜. 一种新的MEMS陀螺仪信号去噪方法[J]. 哈尔滨工业大学学报, 2017, 49(10): 60. SUN Tianchuan, LIU Jieyu. A novel noise reduction method for MEMS gyroscope[J]. Journal of Harbin Institute of Technology, 2017, 49(10): 60. DOI:10.11918/j.issn.0367-6234.201606079 |
| [13] |
张军, 潘泽鑫, 郑玉新, 等. 振动信号趋势项提取方法研究[J]. 电子学报, 2017, 45(1): 22. ZHANG Jun, PAN Zexin, ZHENG Yuxin, et al. Research on vibration signal trend extraction[J]. Acta Electronica Sinica, 2017, 45(1): 22. DOI:10.3969/j.issn.0372-2112.2017.01.004 |
| [14] |
李晨, 梁书锋, 刘传鹏, 等. 基于改进的集合经验模态分解的爆破振动信号趋势项消除方法[J]. 北京理工大学学报, 2021, 41(6): 636. LI Chen, LIANG Shufeng, LIU Chuanpeng, et al. Trend removing method of blasting vibration signals based on MEEMD[J]. Transactions of Beijing Institute of Technology, 2021, 41(6): 636. DOI:10.15918/j.tbit1001-0645.2020.052 |
| [15] |
赵昱宇, 赵辉, 霍鑫, 等. 陀螺飞轮信号的EMD/LPF混合去噪方法[J]. 哈尔滨工业大学学报, 2020, 52(4): 1. ZHAO Yuyu, ZHAO Hui, HUO Xin, et al. A hybrid EMD/LPF-based denoising method for gyrowheel[J]. Journal of Harbin Institute of Technology, 2020, 52(4): 1. DOI:10.11918/201812144 |
| [16] |
王金海, 岳晨飞, 韦然, 等. 基于EMD的动态脉搏数据处理研究[J]. 仪器仪表学报, 2016, 37(增刊1): 34. WANG Jinhai, YUE Chenfei, WEI Ran, et al. Research in dynamic pulse data processing based on EMD[J]. Chinese Journal of Scientific Instrument, 2016, 37(Sup.1): 34. DOI:10.19650/j.cnki.cjsi.2016.s1.006 |
| [17] |
王婷. EMD算法研究及其在信号去噪中的应用[D]. 哈尔滨: 哈尔滨工程大学, 2010 WANG Ting. Research on EMD algorithm and its application in signal denoising[D]. Harbin: Harbin Engineering University, 2010. DOI: 10.7666/d.y1809491 |
| [18] |
胥保春, 袁慎芳. IMF筛选停止条件的分析及新的停止条件[J]. 振动测试与诊断, 2011, 31(3): 348. XU Baochu, YUAN Shenfang. IMF stopping criterion of EMD and new stopping criterion[J]. Journal of Vibration Measurement & Diagnosis, 2011, 31(3): 348. DOI:10.3969/j.issn.1004-6801.2011.03.017 |
| [19] |
RILLING G, FLANDRIN P, GONÇALVES P. On empirical mode decomposition and its algorithms[C]//Proceedings of IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing NSIP-03. Grado, Italy: [s. n.], 2003
|
| [20] |
BOUDRAA A O, CEXUS J C. EMD-Based signal filtering[J]. IEEE Transactions on Instrumentation and Measurement, 2007, 56(6): 2196. DOI:10.1109/TIM.2007.907967 |
| [21] |
席旭刚, 武昊, 罗志增. 基于EMD自相关的表面肌电信号消噪方法[J]. 仪器仪表学报, 2014, 35(11): 2494. XI Xugang, WU Hao, LUO Zhizeng. De-noising method of the sEMG based on EMD autocorrelation[J]. Chinese Journal of Scientific Instrument, 2014, 35(11): 2494. DOI:10.19650/j.cnki.cjsi.2014.11.011 |
| [22] |
PEARSON K. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1900, 50(302): 157. DOI:10.1080/14786440009463897 |
| [23] |
王文波, 张晓东, 汪祥莉. 基于独立成分分析和经验模态分解的混沌信号降噪[J]. 物理学报, 2013, 62(5): 27. WANG Wenbo, ZHANG Xiaodong, WANG Xiangli. Chaotic signal denoising method based on independent component analysis and empirical mode decomposition[J]. Acta Physica Sinica, 2013, 62(5): 27. DOI:10.7498/aps.62.050201 |
| [24] |
LIU Jiangchao, GAO Wenxue. Vibration signal analysis of water seal blasting based on wavelet threshold denoising and HHT transformation[J]. Advances in Civil Engineering, 2020, 2020: 4381480. DOI:10.1155/2020/4381480 |
 2023, Vol. 55
2023, Vol. 55


