多智能体系统(multi-agent systems)是由多个可以自主感知与决策的个体组成的群体系统，其编队、集结、跟踪等行为的实现在太空探测^[1]、智能电网^[2-3]、传感器网络^[4]等领域的实际工程中具有巨大的应用价值。因此，多智能体系统的协同控制问题研究受到了大量专家学者的关注。在文献[5]中，作者通过引入一个一阶离散模型研究了一类粒子系统朝向问题，提出了多智能体的一致性分析方法。文献[6]中，多智能体系统的一致性协议概念被提出，作者深入讨论了不同网络通讯拓扑结构下的一致性问题。文献[7]总结了分布式多智能体系统的一致性协议，并指出多智能体系统达成一致性的条件是：智能体之间信息通讯拓扑包含有向生成树，并且在强连通的有向拓扑结构下，系统的平均一致收敛性可以得到保证。为了适应现实中更复杂的实际工程，越来越多的专家学者关注到异构多智能体的研究^[8-12]，主要应用于异构车队的速度与间距控制^[13]、舞台机器人协同^[14]、无人机编队控制^[15]等。

在诸多多智能体系统实际运行过程中，智能体之间的信息交互往往需要通过通信网络实现，网络的开放性使得这样一类网络化动态系统可能会遭遇到网络攻击，例如：欺骗攻击^[16]和Dos攻击^[17]。Dos攻击是网络攻击中的一个常见的信道攻击行为，通过大量占用通信通道中的资源，使得智能体之间无法进行正常的信息交互^[18]，危害多智能体系统的运行安全。在网络多智能体系统研究领域，学者们针对DoS攻击的防御进行了大量的研究，例如文献[19]设计了一个基于事件采样的分布式安全控制器，在未知攻击策略的DoS攻击不定期发生的情况下，保证了多智能体系统的一致性。文献[20]提出了一种新的切换系统方法研究异构线性多智能体系统在DoS攻击下的鲁棒H_∞一致性问题，并给出了DoS攻击强度与多智能体系统一致性能之间的定量关系。然而上述这些研究建立在系统信息完全正确地传达至控制器并与控制器同步运行的前提上。由于网络攻击会导致的不正常的丢包^[21]，此外传输时滞等物理限制的因素也会存在于这样一类网络化系统中，因此，系统的信息不一定完全、及时、正确地传达到控制器，将导致系统与控制器的异步现象。针对该问题，文献[22]引入一条马尔可夫链描述了一类复杂网络耦合的随机变化过程，解决了随机复杂网络的状态估计问题。文献[23]用两条相互独立的齐次马尔可夫链，模拟系统与控制器的异步现象，在此基础上得到了异构多智能体系统一致性条件。相比于文献[22]，文献[23]提出的双马尔可夫链结构更能体现系统异步现象的复杂性。但是在系统的异步过程中，控制器的状态与系统的状态之间是有一定联系的，而两条不相关的齐次马尔可夫链并不能体现其中的联系。隐马尔可夫模型作为由一条可直接观测马尔科夫链与一条隐藏的马尔科夫链组成相互关联的双重随机结构模型，更适合描述这类异步现象，因此得到了众多研究这类问题的学者们的青睐^[24-27]。

耗散性概念最先由Willems^[28]提出，在控制领域发挥着重要作用^[29-32]。耗散性是一种考虑输入输出能量与系统存储能量关系的系统性质。相比于控制领域的其他控制方法，如：鲁棒稳定^[33]、H_∞控制^[34-35]、滑模控制^[36-37]、耗散性控制具有出色的降噪能力，而成为近年来的一个热门研究课题。例如，文献[38]基于隐马尔可夫模型描述了系统的异步现象，在状态反馈控制器设计过程中引入耗散性考虑，保证了闭环系统的稳定性。但是在多智能体系统的安全协同问题研究中，耗散性问题还研究甚少，尤其是一类存在隐蔽DoS攻击行为影响下的异构多智能体系统。

本文针对有向通讯拓扑结构下异构多智能体系统的异步问题，重点研究存在耗散性能的异步输出反馈控制器设计问题。首先，采用隐马尔科夫模型对由于隐蔽攻击行为引起的系统模态与控制器模态之间的异步现象进行描述。其次，因为系统状态可能无法完全精确测量得到，设计了一个输出反馈控制器。基于输出调节方程和解耦控制技术得到了两个低阶的闭环控制系统模型，给出了闭环误差系统的随机稳定性与严格耗散性条件。最后通过求解一组线性矩阵不等式得到了输出反馈控制器参数，并通过实例仿真验证了算法的有效性。

1 预备知识与问题描述 1.1 图论基础与引理

有向图$\boldsymbol{G}$由集合$(\boldsymbol{V}, \boldsymbol{E})$构成, 其中$\boldsymbol{V}=\left\{v_1\right.$, $\left.v_2, \cdots, v_n\right\}$表示$n$个节点的集合, $\boldsymbol{E} \subseteq \boldsymbol{V} \times \boldsymbol{V}$表示一对有序节点对构成的边集合。定义邻接矩阵为$\boldsymbol{A}=$ $\left[a_{i j}\right]$, 当$\left(v_i, v_j\right) \in \boldsymbol{E}$时, $a_{i j}=a_{j i}>0$表示节点$i$可以从节点$j$获取信息, 否则$a_{i j}=0$。节点$i$的邻居节点集合定义为${\bf{N}}_\mathit{i}=\left\{\mathit{j }\mid \mathit{a}_\mathit{i j}>0\right\}$。人度矩阵定义为$\boldsymbol{D}=$ $\operatorname{diag}\left\{d_i\right\}, d_i=\sum\limits_{j \in {\bf{N}}_i} a_{i j}$表示节点$i$的人度权重。拉普拉斯矩阵定义为$\boldsymbol{L}=\boldsymbol{D}-\boldsymbol{A}$。定义牛引矩阵$\boldsymbol{S}=\operatorname{diag}\left\{g_1\right.$, $\left.g_2, \cdots, g_n\right\}$, 表示领导者与跟随者之间的信息交互关系, 若第$i$个跟随者可以从领导者获取信息, 那么$g_i>0$, 否则$g_i=0$。

引理1^[39]   (舒尔补)对于给定的块矩阵Δ= $ \left(\begin{array}{ll} \boldsymbol{A} & \boldsymbol{B} \\ \boldsymbol{D} & \boldsymbol{C} \end{array}\right), \boldsymbol{D}=\boldsymbol{B}^{\mathrm{T}}$以下3个矩阵不等式等价：

1) Δ < 0;

2) 若A可逆，A <0，C－DA^－1B < 0;

3) 若C可逆，C < 0，A－BC^－1D < 0。

引理2 ^[23]   对于任意矩阵P ≥0，存在正定矩阵Q使得不等式－Q^TP^－1Q ≤－Q－Q^T+ P成立。

引理3 ^[40]   对于适维矩阵S、W、U、V，S+he(WV) < 0成立的充分条件为

$ \left(\begin{array}{cc} \boldsymbol{S} & * \\ \boldsymbol{W}^{\mathrm{T}}+\boldsymbol{U} \boldsymbol{V} & -\boldsymbol{U}-\boldsymbol{U}^{\mathrm{T}} \end{array}\right)<0 $

(1)

引理4 ^[41]    如果对于$q=\{1, 2, 3, 4\}$, 有$\boldsymbol{\varTheta}_0+$ $\operatorname{Re}\left(\bar{\lambda}_q\right) \boldsymbol{\varTheta}_1+\operatorname{Im}\left(\bar{\lambda}_q\right) \boldsymbol{\varTheta}_2 <0$, 那么对于所有$q=\{1$, $2, \cdots, n\}$, 都有: $\boldsymbol{\varTheta}_0+\operatorname{Re}\left(\lambda_q\right) \boldsymbol{\varTheta}_1+\operatorname{Im}\left(\lambda_q\right) \boldsymbol{\varTheta}_2 <0$成立, 其中$\boldsymbol{\varTheta}_0 、\boldsymbol{\varTheta}_1 、\boldsymbol{\varTheta}_2$是与特征值无关的实对称矩阵。

1.2 系统建模

假设1   异构多智能体系统的通讯拓扑有一条有向生成树。

假设2^[42]   DoS攻击持续时间有上界，且攻击行为满足马尔可夫随机过程。

在本文中，首先考虑领航者-跟随者形式的异构多智能体系统。

领航者模型为

$ \left\{\begin{array}{l} \dot{\boldsymbol{x}}_0(t)=\boldsymbol{M} \boldsymbol{x}_0(\boldsymbol{t}) \\ \boldsymbol{y}_0(t)=\boldsymbol{R} \boldsymbol{x}_0(t) \end{array}\right. $

(2)

式中: $\dot{\boldsymbol{x}}_0(t) \in {\bf{R}}^m 、\dot{\boldsymbol{y}}_0(t) \in {\bf{R}}^n$分别为领导者的状态变量与输出变量, $\boldsymbol{M} \in {\bf{R}}^{m \times m}$与$\boldsymbol{R} \in {\bf{R}}^{n \times m}$为两个适维常数矩阵。

跟随者模型为

$ \left\{\begin{array}{l} \dot{\boldsymbol{x}}_i(t)=\boldsymbol{A}_i \boldsymbol{x}_i(t)+\boldsymbol{B}_i \boldsymbol{u}_i(t)+\boldsymbol{D}_i \boldsymbol{w}_i(t) \\ \boldsymbol{y}_i(t)=\boldsymbol{C}_i \boldsymbol{x}_i(t), i=1, 2, \cdots, n \end{array}\right. $

(3)

式中: $\boldsymbol{x}_i(t) \in {\bf{R}}^{m_i} 、\boldsymbol{u}_i(t) \in {\bf{R}}^{p_i} 、\boldsymbol{w}_i(t) \in {\bf{R}}^{n_i}$和$\boldsymbol{y}_i(t) \in$ ${\bf{R}}^n$分别为第$i$个跟随者的状态变量、控制输人变量、外部干扰变量与输出变量, $\boldsymbol{A}_i \in {\bf{R}}^{m_i \times m_i} 、\boldsymbol{B}_i \in$ ${\bf{R}}^{m_i \times p_i} 、\boldsymbol{C}_i \in {\bf{R}}^{n \times n_i} 、\boldsymbol{D}_i \in {\bf{R}}^{m_i \times n_i}$分别为4个适维常数矩阵。并且在异构系统中, 不同的$i$意味着不同的跟随者, 而它们对应的系统矩阵不同。

由于实际系统通常采用离散的数字化系统，因此在本文中，采用采样周期T，对连续的模拟系统进行采样，得到对应的离散化系统。在复杂网络攻击环境下，异构多智能体系统的通信拓扑可能会被切断，导致在正常采样周期内不能对系统进行成功地采样。本文中的智能体采用零阶保持机制更新状态，在下一次采样之前会保持当前采样的信号，因此在不同持续时间的复杂网络攻击下，系统的采样周期可能会变为2T、3T、⋯，假设在复杂网络攻击下的采样周期集合$\boldsymbol{R}=\left\{\delta_1 T, \delta_2 T, \delta_3 T, \cdots, \delta_n T\right\}$, 其中$\delta_j$, $j=1, 2, \cdots, n$为正整数。$k$为采样时间点。

设定在不同采样周期下的系统模态集合$\rho(k) \in \boldsymbol{J} \triangleq$ $\{1, 2, \cdots, N\}$。由一条齐次马尔可夫链描述系统模态随时间的跳变过程, 且系统模态跳变过程服从模态转移概率矩阵。设定模态转移概率矩阵为$\boldsymbol{\varPi}=$ $\left\{\pi_{m l}\right\}$, 系统模态转移概率定义为$\pi_{m l}=\operatorname{Pr}\{\rho(k+1)=$ $l \mid \rho(k)=m\}$, 并且$m, l \in \boldsymbol{J}, \sum\limits_{l=1}^N \pi_{m l}=1$。

由于攻击行为的复杂性，系统模态信息不能正确、及时地传达到控制器，在这种情况下无法采用传统的马尔可夫模型^[43]对其精确刻画。因此本文引入隐马尔可夫模型描述系统与控制器之间的这种异步现象。假设存在多种控制器模态$\sigma(k) \in \boldsymbol{N} \triangleq\{1$, $2, \cdots, M\}$, 并且在系统的不同模态下, 可以观测到的控制器模态概率分布服从观测概率矩阵为$\boldsymbol{\varLambda}=$ $\left\{\theta_{m p}\right\}$, 定义$\theta_{m p}=\operatorname{Pr}\{\sigma(k)=p \mid \rho(k)=m\}$, 且$m \in \boldsymbol{J}$, $p \in \boldsymbol{N}, \sum\limits_{p=1}^M \theta_{m p}=1 。$

定义1 ^[44]   定义系统能量供给函数为$\boldsymbol{J}(\boldsymbol{w}, \boldsymbol{e}$, $\boldsymbol{T}) \triangleq\langle\boldsymbol{e}, \boldsymbol{D} \boldsymbol{e}\rangle_T+2\langle\boldsymbol{e}, \boldsymbol{E} \boldsymbol{w}\rangle_T+\langle\boldsymbol{w}, \boldsymbol{F} \boldsymbol{w}\rangle_T$, 式中: $\boldsymbol{D}$ $\boldsymbol{E} 、\boldsymbol{F}$为适维实矩阵, $\boldsymbol{D}$与$\boldsymbol{F}$为对称矩阵。不失一般性的, 假设矩阵$\boldsymbol{D} \leqslant 0$, 且$\boldsymbol{D}=-\overline{\boldsymbol{D}}^{\mathrm{T}} \overline{\boldsymbol{D}}$。在零初始条件下, 对于给定的标量$\alpha>0$, 若有

$ \boldsymbol{E}\{\boldsymbol{J}(\boldsymbol{w}, \boldsymbol{e}, T)\}>\alpha\langle\boldsymbol{w}, \boldsymbol{w}\rangle_T $

(4)

则称系统为严格(D, E, F)-α耗散的。

基于上述分析，异构多智能体系统中领航者离散系统模型可以描述为

$ \left\{\begin{array}{l} \boldsymbol{x}_0(k+1)=\boldsymbol{M}_{\rho(k)} \boldsymbol{x}_0(k) \\ \boldsymbol{y}_0(k)=\boldsymbol{R} \boldsymbol{x}_0(k) \end{array}\right. $

(5)

跟随者离散系统模型为

$ \left\{\begin{array}{l} \boldsymbol{x}_i(k+1)=\boldsymbol{A}_{i \rho(k)} \boldsymbol{x}_i(k)+\boldsymbol{B}_{i \rho(k)} \boldsymbol{u}_i(k)+\boldsymbol{D}_{i \rho(k)} \boldsymbol{w}_i(k) \\ \boldsymbol{y}_i(k)=\boldsymbol{C}_i x_i(k), i=1, 2, \cdots, n \end{array}\right. $

(6)

式中: $\boldsymbol{A}_{i \rho(k)}=\left(\boldsymbol{A}_{i 0}\right)^{\delta_{\rho(k)}}, $ $ \boldsymbol{B}_{i \rho(k)}=\sum\limits_{i=1}^{\delta_{\rho(k)}}\left(\boldsymbol{A}_{i 0}\right)^{t-1} \boldsymbol{B}_{i 0}, $ $\boldsymbol{D}_{i \rho(k)}=\sum\limits_{i=1}^{\delta_{\rho(k)}}\left(\boldsymbol{A}_{i 0}\right)^{t-1} \boldsymbol{D}_{i 0}, $ $ \boldsymbol{M}_{\rho(k)}=\boldsymbol{M}_0 \delta_{\rho(k)}, $ $ \text { 且 } \boldsymbol{A}_{i 0}= $ $\mathrm{e}^{A_i T_0}, \boldsymbol{M}_{i 0}=\mathrm{e}^{M T_0}, $ $ \boldsymbol{B}_{i 0}=\boldsymbol{B}_i \int_0^{T_0} \mathrm{e}^{A_i \tau} \mathrm{d} \tau, $ $ \boldsymbol{D}_{i 0}=\boldsymbol{D}_i \int_0^{T_0} \mathrm{e}^{A_i \tau} \mathrm{d} \boldsymbol{\tau}。$

为实现多智能体系统的协同控制，构建如下所示的输出调节方程：

$ \left\{\begin{array}{l} \boldsymbol{A}_{i \rho(k)} \boldsymbol{\varPhi}_i+\boldsymbol{B}_{i \rho(k)} \boldsymbol{\varPsi}_{i \rho(k)}=\boldsymbol{\varPhi}_i \boldsymbol{M}_{\rho(k)} \\ \boldsymbol{C}_i \boldsymbol{\varPhi}_i=\boldsymbol{R}, i=1, 2, \cdots, n \end{array}\right. $

(7)

式中$\boldsymbol{\varPhi}_i \in {\bf{R}}^{m_i \times m}, \boldsymbol{\varPsi}_{i p(k)} \in {\bf{R}}^{p_i \times m} $。

针对异构多智能体系统，本文设计如下局部状态补偿器和系统控制律：

$ \begin{aligned} \boldsymbol{\xi}_i(k+1)= & \boldsymbol{M}_{\rho(k)} \boldsymbol{\xi}_i(k)+\boldsymbol{F}_{\sigma(k)}\left\{\sum _ { j \in {\bf { N }} _ { i } } a _ { i j } \left[\boldsymbol{\xi}_j(k)-\right.\right. \\ & \left.\left.\boldsymbol{\xi}_i(k)\right]+g_i\left[\boldsymbol{x}_0(k)-\boldsymbol{\xi}_i(k)\right]\right\} \end{aligned} $

(8)

$ \boldsymbol{u}_i(k)=\boldsymbol{K}_{i \sigma(k)}\left[\boldsymbol{y}_i(k)-\boldsymbol{C}_i \boldsymbol{\varPhi}_i \boldsymbol{\xi}_i(k)\right]+\boldsymbol{\varPsi}_{i p(k)} \boldsymbol{\xi}_i(k) $

(9)

式中：N_i为第i个智能体的邻居智能体集合，F_σ(k)、K_iσ(k)为关于该异构系统待确定的时变控制器增益。

1.3 低阶闭环系统模型

定义输出误差、局部状态误差、参考同步误差为

$ \left\{\begin{array}{l} \boldsymbol{e}_i(k)=\boldsymbol{y}_i(k)-\boldsymbol{y}_0(k) \\ \boldsymbol{\delta}_i(k)=\boldsymbol{x}_i(k)-\boldsymbol{\varPhi}_i \boldsymbol{\xi}_i(k) \\ \boldsymbol{\chi}_i(k)=\boldsymbol{\xi}_i(k)-\boldsymbol{x}_0(k) \end{array}\right. $

(10)

由式(4)、(5)，可以得到：

$ \begin{aligned} \boldsymbol{x}_i(k+1)= & \boldsymbol{\delta}_i(k+1)+\boldsymbol{\varPhi}_i \xi_i(k+1)= \\ & \boldsymbol{\varPhi}_i \boldsymbol{M}_{\rho(k)} \boldsymbol{\xi}_i(k)+\boldsymbol{\varPhi}_i \boldsymbol{F}_{\sigma(k)}\left\{\sum _ { j \in {\bf { N }} _ { i } } a _ { i j } \left[\boldsymbol{\chi}_j(k)-\right.\right. \\ & \left.\left.\boldsymbol{\chi}_i(k)\right]-g_i \boldsymbol{\chi}_i(k)\right\} \end{aligned} $

(11)

$ \boldsymbol{y}_i(k)=\boldsymbol{e}_i(k)+\boldsymbol{y}_0(k)=\boldsymbol{C}_i \boldsymbol{x}_i(k) $

(12)

定义向量：

$ \left\{\begin{array}{l} \boldsymbol{e}(k)=\left[\boldsymbol{e}_1^{\mathrm{T}}(k), \cdots, \boldsymbol{e}_n^{\mathrm{T}}(k)\right]^{\mathrm{T}} \\ \boldsymbol{\delta}(k)=\left[\boldsymbol{\delta}_1^{\mathrm{T}}(k), \cdots, \boldsymbol{\delta}_n^{\mathrm{T}}(k)\right]^{\mathrm{T}} \\ \boldsymbol{\chi}(k)=\left[\boldsymbol{\chi}_1^{\mathrm{T}}(k), \cdots, \boldsymbol{\chi}_n^{\mathrm{T}}(k)\right]^{\mathrm{T}} \\ \boldsymbol{x}_n(k)=\left[\boldsymbol{\delta}^{\mathrm{T}}(k), \boldsymbol{\chi}^{\mathrm{T}}(k)\right]^{\mathrm{T}} \end{array}\right. $

(13)

进一步可得到如下高维系统：

$ \left\{\begin{array}{l} \boldsymbol{x}_n(k+1)=\mathit{\Delta} \boldsymbol{x}_n(k)+\left[\begin{array}{ll} \boldsymbol{D}_{\boldsymbol{\rho}(k)}^{\mathrm{T}} & 0 \end{array}\right]^{\mathrm{T}} \boldsymbol{w}(k) \\ \boldsymbol{e}(k)=\left[\begin{array}{ll} \boldsymbol{C} & \boldsymbol{I} \otimes \boldsymbol{R} \end{array}\right] \boldsymbol{x}_n(k) \end{array}\right. $

(14)

其中

$ \Delta=\left[\begin{array}{cc} \boldsymbol{A}_{\rho(k)}+\boldsymbol{B}_{\rho(k)} \boldsymbol{K}_{\sigma(k)} C & \boldsymbol{\varPhi}(\boldsymbol{L}+\boldsymbol{G}) \otimes \boldsymbol{F}_{\sigma(k)} \\ 0 & \boldsymbol{I} \otimes \boldsymbol{M}_{\rho(k)}-(\boldsymbol{L}+\boldsymbol{G}) \otimes \boldsymbol{F}_{\sigma(k)} \end{array}\right] $

需要指出的系统(12)是一个包含网络拓扑的高维度系统，直接设计控制器将带来巨大的计算负担。因此以下推导得到低阶的闭环控制系统。

根据拓扑结构假设可知，存在一个非奇异矩阵Z，使得：

$ \boldsymbol{Z}^{-1}(\boldsymbol{L}+\boldsymbol{G}) \boldsymbol{Z}=\left(\begin{array}{ccc} \lambda_1 & \cdots & * \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \lambda_n \end{array}\right) $

(15)

定义$ \overline{\boldsymbol{x}}_n(k)=\left[\begin{array}{cc} \boldsymbol{I} & 0 \\ 0 & \boldsymbol{Z} \otimes \boldsymbol{I} \end{array}\right] \boldsymbol{x}_n(k)$，代入式(12)中，得到：

$ \left\{\begin{array}{l} \overline{\boldsymbol{x}}_n(k+1)=\bar{\Delta} \overline{\boldsymbol{x}}_n(k)+\left[\begin{array}{ll} \boldsymbol{D}_{\rho(k)}^{\mathrm{T}} & 0 \end{array}\right]^{\mathrm{T}} \boldsymbol{w}(k) \\ \boldsymbol{e}(k)=\left[\begin{array}{ll} \boldsymbol{C} & \boldsymbol{Z}^{-1} \otimes \boldsymbol{R} \end{array}\right] \overline{\boldsymbol{x}}_n(k) \end{array}\right. $

(16)

其中

$ \bar{\Delta}=\left[\begin{array}{ll} \boldsymbol{A}_{\rho(k)}+\boldsymbol{B}_{\rho(k)} \boldsymbol{K}_{\sigma(k)} \boldsymbol{C} & \boldsymbol{\varPhi}(\boldsymbol{L}+\boldsymbol{G}) \boldsymbol{Z}^{-1} \otimes \boldsymbol{F}_{\sigma(k)} \\ 0 & \boldsymbol{I} \otimes \boldsymbol{M}_{\rho(k)}-\boldsymbol{Z}(\boldsymbol{L}+\boldsymbol{G}) \boldsymbol{Z}^{-1} \otimes \boldsymbol{F}_{\sigma(k)} \end{array}\right] $

由上述分析可知系统(14)的稳定性等价于系统(16)的稳定性。因此，将上述高维系统降维后得到如下n个低维系统：

$ \left\{\begin{array}{l} \tilde{\boldsymbol{x}}_n(k+1)=\widetilde{\Delta} \boldsymbol{x}_n(k)+\left[\begin{array}{ll} \boldsymbol{D}_{i \varphi(k)}^{\mathrm{T}} & 0 \end{array}\right]^{\mathrm{T}} \boldsymbol{w}_i(k) \\ \boldsymbol{e}_i(k)=\left[\begin{array}{ll} \boldsymbol{C}_i & \amalg \end{array}\right] \tilde{\boldsymbol{x}}_n(k) \end{array}\right. $

(17)

式中: $\tilde{\boldsymbol{x}}_n(k)=\left[\begin{array}{ll} \tilde{\boldsymbol{\delta}}_i^{\mathrm{T}}(k) & \tilde{\boldsymbol{\chi}}_i^{\mathrm{T}}(k) \end{array}\right]^{\mathrm{T}} \text {, }$$\widetilde{\mathit{\Delta}}=\left[\begin{array}{cc} \boldsymbol{A}_{i \rho(k)}+\boldsymbol{B}_{i \varphi(k)} \boldsymbol{K}_{i \sigma(k)} \boldsymbol{C}_i & \Pi \\ 0 & \boldsymbol{M}_{\rho(k)}-\lambda_i \boldsymbol{F}_{\sigma(k)} \end{array}\right], $∏与∏为系统分析的无关项。系统扰动$\boldsymbol{w}_i(k)$不会影响到参考同步误差$\boldsymbol{\chi}_i(k)$, 故在合适的增益$\boldsymbol{F}_{\sigma(k)}$下, 使得:

$ \boldsymbol{\chi}_i(k+1)=\left[\boldsymbol{M}_{\rho(k)}-\lambda_i \boldsymbol{F}_{\sigma(k)}\right] \tilde{\boldsymbol{\chi}}_i(k) $

(18)

渐近稳定，即$ \lim\limits _{k \rightarrow \infty} \tilde{\boldsymbol{\chi}}_i(k)=0$。

1.4 一致性问题分析

根据前述分析，本文所考虑的输出一致性问题可以描述为求解合适的控制增益K_iσ(k)、F_σ(k)，使得如下条件成立，即：

1) 在非零初始条件下，当系统无扰动时，即w_i(k)=0时，有

$ \left\{\begin{array}{l} \boldsymbol{E}\left\{\sum\limits_{k=0}^{\boldsymbol{\infty}}\left\|\tilde{\boldsymbol{\delta}}_i(k)\right\|^2\right\}<\boldsymbol{\infty} \\ \boldsymbol{E}\left\{\sum\limits_{k=0}^{\boldsymbol{\infty}}\left\|\tilde{\boldsymbol{\chi}}_i(k)\right\|^2\right\}<\boldsymbol{\infty} \end{array}\right. $

(19)

成立。

2) 在零初始条件下，当w_i(k)∈[0, ∞]时，有

$ \boldsymbol{E}\{\boldsymbol{J}(\boldsymbol{w}, \boldsymbol{e}, \boldsymbol{T})\}>\alpha\langle\boldsymbol{w}, \boldsymbol{w}\rangle_T $

(20)

成立。

2 问题分析与主要结论 2.1 基于Lyapunov理论的稳定性分析

本文采用有向图来描述异构多智能体系统中不同个体之间的信息交互, 因此拓扑矩阵的特征值$\lambda_n$可能为虚数。假设有$\operatorname{Re}\left(\lambda_1\right) \leqslant \operatorname{Re}\left(\lambda_2\right) \leqslant \cdots \leqslant$ $\operatorname{Re}\left(\lambda_n\right)$, 并定义任意复数特征值$\lambda$可分解为$\boldsymbol{\varUpsilon}_\lambda=$ $\left[\begin{array}{cc} \operatorname{Re}(\lambda) \boldsymbol{I} & -\operatorname{Im}(\lambda) \boldsymbol{I} \\ \operatorname{Im}(\lambda) \boldsymbol{I} & \operatorname{Re}(\lambda) \boldsymbol{I} \end{array}\right]$, $\bar{\lambda}_{1, 2}=\operatorname{Re}\left(\lambda_1\right) \pm \mathrm{j} \varphi, \bar{\lambda}_{3, 4}= $$\operatorname{Re}\left(\lambda_n\right) \pm \mathrm{j} \varphi $, 式中$ \varphi=\max \left\{\operatorname{Im}\left(\lambda_n\right)\right\}$。

定理1   若对于给定的控制器增益K_ip、F_p，存在一组正定对称矩阵P_m，使得对于所有i∈{1, 2, ⋯, n}，m∈J，p∈ N都有

$ \sum\limits_{p=1}^d \theta_{m p} \boldsymbol{M}_f^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{M}_f-\boldsymbol{P}_m <0 $

(21)

$ \sum\limits_{n=1}^d \theta_{m p} \boldsymbol{\varGamma}_{i m p}^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{\varGamma}_{i m p}-\boldsymbol{P}_m <0 $

(22)

成立，那么异构多智能体系统在异步问题下的协同一致性问题可以得到解决。式中：$\boldsymbol{M}_f=\left(\boldsymbol{M}_m-\boldsymbol{\varUpsilon}_\lambda \boldsymbol{F}_p\right) $，$ \sum\limits_{l=1}^s \pi_{m l} P_l=m, \boldsymbol{\varGamma}_{i m p}=\boldsymbol{A}_{i m}+\boldsymbol{B}_{i m} \boldsymbol{K}_{i p} \boldsymbol{C}_i$。

证明   1) 当w_i(k) =0时。首先，对于误差闭环系统(18), 设$\boldsymbol{z}_i(k)=\left[\operatorname{Re}\left[\tilde{\boldsymbol{\chi}}_i(k)\right]^{\mathrm{T}} \;\;\operatorname{Im}\left[\tilde{\boldsymbol{\chi}}_i(k)\right]^{\mathrm{T}}\right]^{\mathrm{T}}$, 闭环误差系统(15) 随机渐近稳定可以等价于系统:

$ \boldsymbol{z}_i(k+1)=\left(\boldsymbol{M}_m-\boldsymbol{\varUpsilon}_\lambda \boldsymbol{F}_p\right) \boldsymbol{z}_i(k) $

(23)

随机渐近稳定。

定义Lyapunov函数：

$ \boldsymbol{V}\left[\boldsymbol{z}_i(k), k\right]=\boldsymbol{z}_i^{\mathrm{T}}(k) \boldsymbol{P}_m \boldsymbol{z}_i(k) $

可以得到：

$ \begin{aligned} \boldsymbol{E}\left\{\Delta \boldsymbol{V}\left[\boldsymbol{z}_i(k), k\right]\right\}= & \boldsymbol{E}\left\{\boldsymbol{V}\left[\boldsymbol{z}_i(k+1), k+1\right]-\boldsymbol{V}\left[\boldsymbol{z}_i(k), k\right]\right\}= \\ & \sum\limits_{p=1}^d \theta_{m p} \boldsymbol{z}_i^{\mathrm{T}}(k)\left(\boldsymbol{M}_m- \boldsymbol{\varUpsilon}_\lambda \boldsymbol{F}_p\right)^{\mathrm{T}}\cdot \\ & \sum\limits_{l=1}^s \boldsymbol{P}_m\left(\boldsymbol{M}_m- \boldsymbol{\varUpsilon}_\lambda \boldsymbol{F}_p\right) \boldsymbol{z}_i(k)- \\ & \boldsymbol{z}_i^{\mathrm{T}}(k) \boldsymbol{P}_m \boldsymbol{z}_i(k) \end{aligned} $

(24)

设$\sum\limits_{l=1}^s \boldsymbol{P}_m=\boldsymbol{P}_m, \boldsymbol{M}_f=\left(\boldsymbol{M}_m- \boldsymbol{\varUpsilon}_\lambda \boldsymbol{F}_p\right) $，则

$ \boldsymbol{E}\left\{\Delta \boldsymbol{V}\left[\boldsymbol{z}_i(k), k\right]\right\}=\boldsymbol{z}_i^{\mathrm{T}}(k)\left(\sum\limits_{p=1}^d \theta_{m p} \boldsymbol{M}_f^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{M}_f-\boldsymbol{P}_m\right) \boldsymbol{z}_i(k) $

(25)

由式(21)，可知

$ \boldsymbol{E}\left\{\Delta \boldsymbol{V}\left[\boldsymbol{z}_i(k), k\right]\right\} \leqslant 0 $

设$ \boldsymbol{\varTheta} \triangleq \sum\limits_{p=1}^d \theta_{m p} \boldsymbol{M}_f^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{M}_f-\boldsymbol{P}_m, \boldsymbol{\varTheta}^{\prime} \triangleq-\boldsymbol{\varTheta}$，可得

$ \boldsymbol{E}\left\{\Delta \boldsymbol{V}\left[\boldsymbol{z}_i(k), k\right]\right\} \leqslant-\lambda \min \left\{\boldsymbol{\varTheta}^{\prime}\right\} \boldsymbol{z}_i^{\mathrm{T}}(k) \boldsymbol{z}_i(k) $

(26)

将不等式(25)从k=0累加至∞，可得

$ \begin{aligned} \boldsymbol{E}\{\boldsymbol{V}(\infty)\}-\boldsymbol{E}\{\boldsymbol{V}(0)\} \leqslant & -\lambda \min \{\boldsymbol{\varTheta}^{\prime}\} \boldsymbol{E}\left\{\sum\limits_{k=0}^\boldsymbol{\infty}\left\|\boldsymbol{z}_i(k)\right\|^2\right\} \leqslant \\ & \frac{1}{\lambda \min \left\{\boldsymbol{\varTheta}^{\prime}\right\}} \boldsymbol{E}\{\boldsymbol{V}(0)\} <\boldsymbol{\infty} \end{aligned} $

(27)

对于闭环误差系统(17)，定义Lyapunov函数：$ \boldsymbol{V}\left[\tilde{\boldsymbol{\delta}}_i(k), k\right]=\tilde{\boldsymbol{\delta}}_i^{\mathrm{T}}(k) \boldsymbol{P}_m \widetilde{\boldsymbol{\delta}}_i(k)$, 令$\sum\limits_{l=1}^s \boldsymbol{P}_l=\boldsymbol{P}_m $，$ \boldsymbol{\varGamma}_{i m p}=\boldsymbol{A}_{i m}+\boldsymbol{B}_{i m} \boldsymbol{K}_{i p} \boldsymbol{C}_i$，则

$\boldsymbol{E}\left\{\Delta \boldsymbol{V}\left[\tilde{\boldsymbol{\delta}}_i(k), k\right]\right\}=\\ \tilde{\boldsymbol{\delta}}_i^{\mathrm{T}}(k)\left[\sum\limits_{p=1}^d \theta_{m p} \boldsymbol{\varGamma}_{i m p}^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{\varGamma}_{i m p}-\boldsymbol{P}_m\right] \boldsymbol{\delta}_i(k) $

(28)

由式(22)可知，$\boldsymbol{E}\left\{\Delta \boldsymbol{V}\left[\tilde{\boldsymbol{\delta}}_i(k), k\right]\right\} \leqslant 0 $，由类似证明1)可得：

$ \boldsymbol{E}\left\{\sum\limits_{k=0}^{\boldsymbol{\infty}}\left\|\widetilde{\boldsymbol{\delta}}_i(k)\right\|^2\right\}<\boldsymbol{\infty} $

2) 当$\boldsymbol{w}_i(k) \neq 0$时。考虑存在扰动情况下的系统稳定性, 构建Lyapunov函数: $\boldsymbol{V}\left[\tilde{\boldsymbol{\delta}}_i(k), k\right]=$ $\tilde{\boldsymbol{\delta}}_i^{\mathrm{T}}(k) \boldsymbol{P}_m \widetilde{\boldsymbol{\delta}}_i(k)$, 可以得到:

$ \begin{aligned} \boldsymbol{E}\{\Delta \boldsymbol{V}(k)\}= & \tilde{\boldsymbol{\delta}}_i^{\mathrm{T}}(k+1) \sum\limits_{l=1}^s \pi_{m l} \boldsymbol{P}_l \widetilde{\boldsymbol{\delta}}_i(k+1)- \\ & \tilde{\boldsymbol{\delta}}_i^{\mathrm{T}}(k) \boldsymbol{P}_m \widetilde{\boldsymbol{\delta}}_i(k) \end{aligned} $

(29)

令$\boldsymbol{P}_m=\sum\limits_{l=1}^s \pi_{m l} \boldsymbol{P}_l, \boldsymbol{\varGamma}_{i m p}=\boldsymbol{A}_{i m}+\boldsymbol{B}_{i m} \boldsymbol{K}_{i p} \boldsymbol{C}_i $，则

$ \begin{aligned} \boldsymbol{E}\{\Delta V(k)\}= & \tilde{\boldsymbol{\delta}}_i^{\mathrm{T}}(k)\left(\sum\limits_{p=1}^d \theta_{m p} \boldsymbol{\varGamma}_{i m p}^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{\varGamma}_{i m p}-\boldsymbol{P}_m\right) \widetilde{\boldsymbol{\delta}}_i(k)+ \\ & \boldsymbol{h e}\left[\tilde{\boldsymbol{\delta}}_i^{\mathrm{T}}(k) \sum\limits_{p=1}^d \theta_{m p} \boldsymbol{\varGamma}_{i m p}^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{D}_{i m} \boldsymbol{w}_i(k)\right]+ \\ & \boldsymbol{w}_i^{\mathrm{T}}(k) \boldsymbol{D}_{i m}^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{D}_{i m} \boldsymbol{w}_i(k) \end{aligned} $

(30)

令$\left[\begin{array}{rr} \tilde{\boldsymbol{\delta}}_i(k) & \boldsymbol{w}_i(k) \end{array}\right]=\boldsymbol{\varLambda}_i(k) $，代入式(30)可得$\boldsymbol{E}\{\Delta \boldsymbol{V}(k)\}= $

$ \boldsymbol{\varLambda}_i^{\mathrm{T}}(k)\left[\begin{array}{cc} \sum\limits_{p=1}^d \theta_{m p} \boldsymbol{\varGamma}_{i m p}^T \boldsymbol{P}_m \boldsymbol{\varGamma}_{i m p}-\boldsymbol{P}_m & \sum\limits_{p=1}^d \theta_{m p} \boldsymbol{\varGamma}_{i m p}^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{D}_{i m} \\ * & D_{i m}^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{D}_{i m} \end{array}\right] \boldsymbol{\varLambda}_i(k) $

(31)

又因为

$ \begin{array}{l} \boldsymbol{J}(k) \triangleq \boldsymbol{e}_i^{\mathrm{T}}(k) \boldsymbol{D} \boldsymbol{e}_i(k)+2 \boldsymbol{e}_i^{\mathrm{T}}(k) \boldsymbol{E} \boldsymbol{w}_i(k)+\boldsymbol{w}_i^{\mathrm{T}}(k) \boldsymbol{F} \boldsymbol{w}_i(k)= \\ \;\;\;\;\;\;\;\;\;\;\;\boldsymbol{\varLambda}_i^{\mathrm{T}}(k)\left[\begin{array}{cc} \boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{D} \boldsymbol{C}_i & \boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{E} \\ * & \boldsymbol{F} \end{array}\right] \boldsymbol{\varLambda}_i(k) \end{array} $

(32)

那么

$ \boldsymbol{E}\left\{\Delta \boldsymbol{V}(k)-\boldsymbol{J}(k)+\alpha \boldsymbol{w}_i^{\mathrm{T}}(k) \boldsymbol{w}_i(k)\right\}=\boldsymbol{\varLambda}_i^{\mathrm{T}}(k)\left[\begin{array}{cc} \sum\limits_{p=1}^d \theta_{m p} \boldsymbol{I}_{i n p}^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{\varGamma}_{i m p}-\boldsymbol{P}_m-\boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{D} \boldsymbol{C}_i & \sum\limits_{p=1}^d \theta_{m p} \boldsymbol{\varGamma}_{i m p}^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{D}_{i m}-\boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{E} \\ * & \boldsymbol{D}_m^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{D}_{i m}-\boldsymbol{F}-\alpha \end{array}\right] \boldsymbol{\varLambda}_i(k) $

(33)

根据式(22)，可以得到$ \sum\limits_{p=1}^d \theta_{m p} \boldsymbol{\varGamma}_{i m p}^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{\varGamma}_{i m p}-$ $\boldsymbol{P}_m-\boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{D} \boldsymbol{C}_i <0 $，应用引理1可知：

$ \left[\begin{array}{cc} \sum\limits_{p=1}^d \theta_{m p} \boldsymbol{\varGamma}_{i m p}^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{\varGamma}_{i m p}-\boldsymbol{P}_m-\boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{D} \boldsymbol{C}_i & \sum\limits_{p=1}^d \theta_{m p} \boldsymbol{\varGamma}_{i m p}^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{D}_{i m}-\boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{E} \\ * & \boldsymbol{D}_{i m}^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{D}_{i m}-\boldsymbol{F}-\alpha \end{array}\right]<0 $

(34)

将$ \boldsymbol{E}\left\{\Delta \boldsymbol{V}(k)-\boldsymbol{J}(k)+\alpha \boldsymbol{w}_i^{\mathrm{T}}(k) \boldsymbol{w}_i(k)\right\}$从k=0累加至∞，有

$ \boldsymbol{E}\{\boldsymbol{V}(\infty)\}-\boldsymbol{E}\{\boldsymbol{J}(\boldsymbol{w}, \boldsymbol{e}, \boldsymbol{T})\}+\alpha\left\langle\boldsymbol{w}_i(k), \boldsymbol{w}_i(k)\right\rangle_T <0 $

(35)

因为$ \boldsymbol{E}\{\boldsymbol{V}(\boldsymbol{\infty})\}>0$，所以有

$ \boldsymbol{E}\{\boldsymbol{J}(\boldsymbol{w}, \boldsymbol{e}, \boldsymbol{T})\}>\alpha\left\langle\boldsymbol{w}_i(k), \boldsymbol{w}_i(k)\right\rangle_T $

(36)

证明完毕。

2.2 基于LMI的控制器增益求解

在前述章节中已经通过构建Lyapunov函数分析闭环误差系统的稳定性条件得到定理1，即设计控制器来解决异构多智能体系统在复杂网络攻击下与物理限制导致的系统与控制器异步问题，但是控制器参数与未知矩阵存在耦合问题，无法直接得到控制器参数。下面通过变量代换解耦合的方法来给出控制器增益K_ip、F_p的具体计算方法。

定理2   如果存在一系列的正定对称矩阵P_m、$\boldsymbol{G} 、\boldsymbol{Q} 、\boldsymbol{R}_{m p} 、\boldsymbol{R}_{i m p} 、\boldsymbol{\hbar}_p$和适维矩阵$\boldsymbol{\varepsilon}_{i p} 、\boldsymbol{L}_{i p} 、\boldsymbol{V}_{i p} 、\boldsymbol{Y}$, 使得下列矩阵不等式对于所有$i \in\{1, 2, \cdots, n\}, m \in \boldsymbol{J}, \boldsymbol{p} \in$ $\boldsymbol{N}$可解, 那么异构多智能体系统在复杂网络攻击下的系统模态与控制器模态异步问题下的一致性就可以得到保证。

$ \left[\begin{array}{ccccc} -\boldsymbol{P}_m & \sqrt{\theta_{m 1}} \boldsymbol{G}^{\mathrm{T}} & \sqrt{\theta_{m 2}} \boldsymbol{G}^{\mathrm{T}} & \cdots & \sqrt{\theta_{m d}} \boldsymbol{G}^{\mathrm{T}} \\ * & \boldsymbol{R}_{m 1}-\boldsymbol{G}-\boldsymbol{G}^{\mathrm{T}} & 0 & \cdots & 0 \\ * & * & \boldsymbol{R}_{m 2}-\boldsymbol{G}-\boldsymbol{G}^{\mathrm{T}} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ * & * & * & \cdots & \boldsymbol{R}_{m d}-\boldsymbol{G}-\boldsymbol{G}^{\mathrm{T}} \end{array}\right]<0 $

(37)

$ \left[\begin{array}{cc} -\boldsymbol{R}_{m p} & \rlap{-} \lambda \\ * & -\boldsymbol{H}-\boldsymbol{H}^{\mathrm{T}}+\boldsymbol{P}_m \end{array}\right]<0 $

(38)

$ \left[\begin{array}{cccc} \boldsymbol{P}_m-\boldsymbol{Q}-\boldsymbol{Q}^{\mathrm{T}} & * & * & * \\ \boldsymbol{A}_{i m}^{\mathrm{T}} \boldsymbol{Q}+\boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{L}_{i p} \boldsymbol{Y} & -\boldsymbol{R}_{i m p} & * & * \\ \boldsymbol{D}_{i m}^{\mathrm{T}} \boldsymbol{Q} & -\boldsymbol{E}^{\mathrm{T}} \boldsymbol{C}_i & -\boldsymbol{F}-\alpha & * \\ \boldsymbol{B}_{i m}^{\mathrm{T}} \boldsymbol{Q}-\boldsymbol{V}_{i p} \boldsymbol{Y} & \boldsymbol{\varepsilon}_{i p}^{\mathrm{T}} \boldsymbol{L}_{i p}^{\mathrm{T}} \boldsymbol{C}_i & 0 & -\boldsymbol{\varepsilon}_{i p} \boldsymbol{L}_{i p}-\boldsymbol{\varepsilon}_{i p}^{\mathrm{T}} \boldsymbol{L}_{i p}^{\mathrm{T}} \end{array}\right]<0 $

(39)

$ \left[\begin{array}{ccccc} -\boldsymbol{P}_m-\boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{D C}_i & \sqrt{\theta_{m 1}} \boldsymbol{G}^{\mathrm{T}} & \sqrt{\theta_{m 2}} \boldsymbol{G}^{\mathrm{T}} & \cdots & \sqrt{\theta_{m d}} \boldsymbol{G}^{\mathrm{T}} \\ * & R_{i m 1}-\boldsymbol{G}-\boldsymbol{G}^{\mathrm{T}} & 0 & \cdots & 0 \\ * & * & \boldsymbol{R}_{i m 2}-\boldsymbol{G}-\boldsymbol{G}^{\mathrm{T}} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ * & * & * & \cdots & \boldsymbol{R}_{i m d}-\boldsymbol{G}-\boldsymbol{G}^{\mathrm{T}} \end{array}\right]<0 $

(40)

式中：$ \boldsymbol{K}_{i p}=\left(\boldsymbol{L}_{i p} \boldsymbol{V}_{i p}^{-1}\right)^{\mathrm{T}}, \boldsymbol{F}_{i p}=\left(\boldsymbol{\hbar}_p \boldsymbol{H}^{-1}\right)^{\mathrm{T}}$，$\rlap{-} \lambda $= $\left[\begin{array}{cc} \boldsymbol{M}_m^{\mathrm{T}} \boldsymbol{H}-\operatorname{Re}\left(\lambda_q\right) \boldsymbol{\hbar}_p & -\operatorname{Im}\left(\lambda_q\right) \boldsymbol{\hbar}_p \\ \operatorname{Im}\left(\lambda_q\right) \boldsymbol{\hbar}_p & \boldsymbol{M}_m^{\mathrm{T}} \boldsymbol{H}-\operatorname{Re}\left(\lambda_q\right) \boldsymbol{\hbar}_p \end{array}\right] $，α、D、E、F、Y、ε_ip为可调节参数矩阵。

证明   1)若存在一个正定对称矩阵P_m，使得$\sum\limits_{p=1}^d \theta_{m p}\left(\boldsymbol{M}_m-\boldsymbol{\varUpsilon}_\lambda \boldsymbol{F}_p\right)^{\mathrm{T}} \boldsymbol{P}_m\left(\boldsymbol{M}_m-\boldsymbol{\varUpsilon}_\lambda \boldsymbol{F}_p\right)-\boldsymbol{P}_m <0 $，那么存在一个标量$ \partial$>0有

$ \sum\limits_{p=1}^d \theta_{m p}\left[\left(\boldsymbol{M}_m-\boldsymbol{\varUpsilon}_\lambda \boldsymbol{F}_p\right)^{\mathrm{T}} \boldsymbol{P}_m\left(\boldsymbol{M}_m-\boldsymbol{\varUpsilon}_\lambda \boldsymbol{F}_p\right)+\partial \boldsymbol{I}\right]-\boldsymbol{P}_m <0 $

(41)

令: $\boldsymbol{R}_{m p}=\left(\boldsymbol{M}_m-\boldsymbol{\varUpsilon}_\lambda \boldsymbol{F}_p\right)^{\mathrm{T}} \boldsymbol{P}_m\left(\boldsymbol{M}_m-\boldsymbol{Y}_\lambda \boldsymbol{F}_p\right)+\partial \boldsymbol{I} $, 则有

$ \sum\limits_{p=1}^d \theta_{m p} \boldsymbol{R}_{m p}-\boldsymbol{P}_m <0 $

(42)

$ \left(\boldsymbol{M}_m-\boldsymbol{\varUpsilon}_\lambda \boldsymbol{F}_p\right)^{\mathrm{T}} \boldsymbol{P}_m\left(\boldsymbol{M}_m-\boldsymbol{\varUpsilon}_\lambda \boldsymbol{F}_p\right)-\boldsymbol{R}_{m p}<0 $

(43)

将式(42)、(43)应用引理1，可以得到：

$ \left[\begin{array}{ccccc} -\boldsymbol{P}_m & \sqrt{\theta_{m 1}} & \sqrt{\theta_{m 2}} & \cdots & \sqrt{\theta_{m d}} \\ * & -\boldsymbol{R}_{m 1}^{-1} & 0 & \cdots & 0 \\ * & * & -\boldsymbol{R}_{m 2}^{-1} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ * & * & * & \cdots & -\boldsymbol{R}_{m d}^{-1} \end{array}\right]<0 $

(44)

$ \left[\begin{array}{cc} -\boldsymbol{R}_{m p} & * \\ \boldsymbol{M}_m-\boldsymbol{\varUpsilon}_\lambda \boldsymbol{F}_p & -\left(\boldsymbol{P}_m\right)^{-1} \end{array}\right]<0 $

(45)

在式(44)两边分别左乘和右乘对角矩阵diag$\{\boldsymbol{I}, \boldsymbol{G}, \boldsymbol{G}, \cdots, \boldsymbol{G}\}^{\mathrm{T}} $以及其转置，同时在式(45)两边分别左乘和右乘对角矩阵diag{I, H}^T以及其转置操作，可以得到：

$ \left[\begin{array}{ccccc} -\boldsymbol{P}_m & \sqrt{\theta_{m 1}}\boldsymbol{G}^{\mathrm{T}} & \sqrt{\theta_{m 2}} \boldsymbol{G}^{\mathrm{T}} & \cdots & \sqrt{\theta_{m d}} \boldsymbol{G}^{\mathrm{T}} \\ * & \boldsymbol{R}_{m 1}-\boldsymbol{G}-\boldsymbol{G}^{\mathrm{T}} & 0 & \cdots & 0 \\ * & * & \boldsymbol{R}_{m 2}-\boldsymbol{G}-\boldsymbol{G}^{\mathrm{T}} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ * & * & * & \cdots & \boldsymbol{R}_{m d}-\boldsymbol{G}-\boldsymbol{G}^{\mathrm{T}} \end{array}\right]<0 $

(46)

$ \left[\begin{array}{cc} -\boldsymbol{R}_{m p} & * \\ \boldsymbol{H}^{\mathrm{T}}\left(\boldsymbol{M}_m-\boldsymbol{\varUpsilon}_\lambda \boldsymbol{F}_p\right) & -\boldsymbol{H}-\boldsymbol{H}^{\mathrm{T}}+\boldsymbol{P}_m \end{array}\right]<0 $

(47)

定义$\boldsymbol{F}_{i p}=\left( \boldsymbol{\hbar}_p \boldsymbol{H}^{-1}\right)^{\mathrm{T}} $，并且令$\rlap{-} \lambda=H^{\mathrm{T}} $(M_m－$ \varUpsilon$_λF_p)，应用引理4，将$\rlap{-} \lambda $转换为

$ \rlap{-} \lambda=\left[\begin{array}{cc} \boldsymbol{M}_m^{\mathrm{T}} \boldsymbol{H}-\operatorname{Re}\left(\lambda_q\right) \boldsymbol{\hbar}_p & -\operatorname{Im}\left(\lambda_q\right) \boldsymbol{\hbar}_p \\ \operatorname{Im}\left(\lambda_q\right) \boldsymbol{\hbar}_p & \boldsymbol{M}_m^{\mathrm{T}} \boldsymbol{H}-\operatorname{Re}\left(\lambda_q\right) \boldsymbol{\hbar}_p \end{array}\right] $

(48)

2) 令

$ \begin{aligned} \boldsymbol{X}_{imp }= & \left(\boldsymbol{\varGamma}_{i m p}^n \boldsymbol{P}_m \boldsymbol{D}_{i m}-\boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{E}\right)^{\mathrm{T}}\left(\boldsymbol{D}_{i m}^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{D}_{i m}-\boldsymbol{F}-\alpha\right) \times \\ & \left(\boldsymbol{\varGamma}_{i m p}^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{D}_{i m}-\boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{E}\right) \end{aligned} $

则由式(35)应用引理1可得

$ \sum\limits_{p=1}^d\theta_{m p}\left(\boldsymbol{\varGamma}_{i m p}^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{\varGamma}_{i m p}-\boldsymbol{X}_{i m p}\right)-\boldsymbol{P}_m-\boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{D} \boldsymbol{C}_i <0 $

(49)

令$\boldsymbol{R}_{i m p}=\boldsymbol{\varGamma}_{i m p}^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{\varGamma}_{i m p}-\boldsymbol{X}_{i m p}+\partial \boldsymbol{I} $。类似上一个证明，存在$ \partial$>0，使得则有：

$ \sum\limits_{p=1}^d \theta_{m p} \boldsymbol{R}_{i m p}-\boldsymbol{P}_m-\boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{D} \boldsymbol{C}_i <0 $

(50)

$ \boldsymbol{\varGamma}_{i m p}^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{\varGamma}_{i m p}-\boldsymbol{X}_{i m p}-\boldsymbol{R}_{i m p}<0 $

(51)

应用引理1，将式(50)、(51)转换为：

$ \left[\begin{array}{ccccc} -\boldsymbol{P}_m-\boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{D} \boldsymbol{C}_i & \sqrt{\theta_{m 1}} & \sqrt{\theta_{m 2}} & \cdots & \sqrt{\theta_{m d}} \\ * & -\boldsymbol{R}_{i m 1}^{-1} & 0 & \cdots & 0 \\ * & * & -\boldsymbol{R}_{i m 2}^{-1} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ * & * & * & \cdots & -\boldsymbol{R}_{i m d}^{-1} \end{array}\right]<0 $

(52)

$ \left[\begin{array}{cc} \boldsymbol{\varGamma}_{i m p}^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{\varGamma}_{i m p}-\boldsymbol{R}_{i m p} & \boldsymbol{\varGamma}_{i m p}^{\mathrm{i}} \boldsymbol{P}_m \boldsymbol{D}_{i m}-\boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{E} \\ * & \boldsymbol{D}_{i m}^{\mathrm{T}} \boldsymbol{P}_m \boldsymbol{D}_{i m}-\boldsymbol{F}-\alpha \end{array}\right]<0 $

(53)

应用引理1，可以得到：

$ \left[\begin{array}{ccc} -\left(\boldsymbol{P}_m\right)-1 & \boldsymbol{\varGamma}_{i m p} & \boldsymbol{D}_{i m} \\ * & -\boldsymbol{R}_{i m p} & -\boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{E} \\ * & * & -\boldsymbol{F}-\alpha \end{array}\right]<0 $

(54)

对式(54)两边，分别左乘和右乘对角矩阵diag$\{\boldsymbol{I}, \boldsymbol{G}, \boldsymbol{G}, \cdots, \boldsymbol{G}\}^{\mathrm{T}} $及其转置，并应用引理2，可得

$ \left[\begin{array}{ccccc} -\boldsymbol{P}_m-\boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{D C}_i & \sqrt{\theta_{m 1}} \boldsymbol{G}^{\mathrm{T}} & \sqrt{\theta_{m 2}} \boldsymbol{G}^{\mathrm{T}} & \cdots & \sqrt{\theta_{m d}} \boldsymbol{G}^{\mathrm{T}} \\ * & \boldsymbol{R}_{i m 1}-\boldsymbol{G}-\boldsymbol{G}^{\mathrm{T}} & 0 & \cdots & 0 \\ * & * & \boldsymbol{R}_{i m 2}-\boldsymbol{G}-\boldsymbol{G}^{\mathrm{T}} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ * & * & * & \cdots & R_{i m d}-\boldsymbol{G}-\boldsymbol{G}^{\mathrm{T}} \end{array}\right]<0 $

(55)

对式(55)两边，分别左乘和右乘对角矩阵$\operatorname{diag}\{\boldsymbol{Q}, \boldsymbol{I}, \boldsymbol{I}\}^{\mathrm{T}} $及其转置，并应用引理2，可以得到：

$ \left[\begin{array}{ccc} \boldsymbol{P}_m-\boldsymbol{Q}-\boldsymbol{Q}^{\mathrm{T}} & \boldsymbol{Q }\boldsymbol { \varGamma } _ { i m p } & \boldsymbol{Q D _ { i m }} \\ * & -\boldsymbol{R}_{i m p} & -\boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{E} \\ * & * & -\boldsymbol{F}-\alpha \end{array}\right]<0 $

(56)

进一步，将式(56)拆分为

$\left[\begin{array}{ccc} \boldsymbol{P}_m-\boldsymbol{Q}-\boldsymbol{Q}^{\mathrm{T}} & \boldsymbol{Q}^{\mathrm{T}} \boldsymbol{A}_{i m} & \boldsymbol{Q}^{\mathrm{T}} \boldsymbol{D}_{i m} \\ * & -\boldsymbol{R}_{i m p} & -\boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{E}^{\mathrm{T}} \\ * & * & -\boldsymbol{F}-\alpha \end{array}\right]+\\ \boldsymbol{h e}\left(\left[\begin{array}{l} 0 \\ \boldsymbol{I} \\ 0 \end{array}\right] \boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{K}_{i p}^{\mathrm{T}} \boldsymbol{B}_{i m}^{\mathrm{T}} \boldsymbol{Q}\left[\begin{array}{lll} \boldsymbol{I} & 0 & 0 \end{array}\right]\right)<0 $

(57)

令$\boldsymbol{K}_{i p}=\left(\boldsymbol{L}_{i p} \boldsymbol{V}_{i p}^{-1}\right)^{\mathrm{T}}$, 并引人$\boldsymbol{\varepsilon}_{i p} 、\boldsymbol{Y}$两个可调节参数矩阵, 代人式(57), 可得:

$ \begin{aligned} & {\left[\begin{array}{ccc} \boldsymbol{P}_m-\boldsymbol{Q}-\boldsymbol{Q}^{\mathrm{T}} & \boldsymbol{Q}^{\mathrm{T}} \boldsymbol{A}_{i m}+\boldsymbol{Y}^{\mathrm{T}} \boldsymbol{L}_{i p}^{\mathrm{T}} \boldsymbol{C}_i & \boldsymbol{Q}^{\mathrm{T}} \boldsymbol{D}_{i m} \\ * & -\boldsymbol{R}_{i m p} & -\boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{E}^{\mathrm{T}} \\ * & * & -\boldsymbol{F}-\alpha \end{array}\right]+} \\ & \boldsymbol{h e}\left(\left[\begin{array}{l} 0 \\ \boldsymbol{I} \\ 0 \end{array}\right] \boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{L}_{i p} \boldsymbol{\varepsilon}_{i p} \boldsymbol{\varepsilon}_{i p}^{-1} \boldsymbol{V}_{i p}^{-1}\left(\boldsymbol{B}_{i m}^{\mathrm{T}} \boldsymbol{Q}-\boldsymbol{V}_{i p} \boldsymbol{Y}\right)\left[\begin{array}{lll} \boldsymbol{I} & 0 & 0 \end{array}\right]\right)<0 \end{aligned} $

(58)

$ \left\{\begin{aligned} &\boldsymbol{S}=\left[\begin{array}{ccc} \boldsymbol{P}_m-\boldsymbol{Q}-\boldsymbol{Q}^{\mathrm{T}} & \boldsymbol{Q}^{\mathrm{T}} \boldsymbol{A}_{i m}+\boldsymbol{Y}^{\mathrm{T}} \boldsymbol{L}_{i p}^{\mathrm{T}} \boldsymbol{C}_i & \boldsymbol{Q}^{\mathrm{T}} \boldsymbol{D}_{i m} \\ * & -\boldsymbol{R}_{i m p} & -\boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{E}^{\mathrm{T}} \\ & * & -\boldsymbol{F}-\alpha \end{array}\right] \\ &\boldsymbol{V}=\boldsymbol{\varepsilon}_{i p}^{-1} \boldsymbol{V}_{i p}^{-1}\left(\boldsymbol{B}_{i m}^{\mathrm{T}} \boldsymbol{Q}-\boldsymbol{V}_{i p} \boldsymbol{Y}\right)\left[\begin{array}{lll} \boldsymbol{I} & 0 & 0 \end{array}\right] \\ &\boldsymbol{W}=\left[\begin{array}{l} 0 \\ \boldsymbol{I} \\ 0 \end{array}\right] \boldsymbol{C}_i^{\mathrm{T}} \boldsymbol{L}_{i p} \boldsymbol{\varepsilon}_{i p}\\ &\boldsymbol{U}=\boldsymbol{V}_{i p} \boldsymbol{\varepsilon}_{i p} \end{aligned}\right. $

(59)

应用引理3，结合式(59)，可知定理2中的式(39)成立。证明完毕。

3 仿真

本文选取由一个领导者与3个跟随者组成的异构多智能体系统进行仿真研究，证明所提出方法的有效性。

领导者模型为

$ \left\{\begin{array}{l} \dot{\boldsymbol{x}}_0(t)=\left[\begin{array}{ll} 0 & 1 \\ 0 & 0 \end{array}\right] \boldsymbol{x}_0(t) \\ \boldsymbol{y}_0(t)=\left[\begin{array}{ll} 1 & 0 \end{array}\right] \boldsymbol{x}_0(t) \end{array}\right. $

(60)

跟随者模型为

$ \left\{\begin{array}{l} \dot{\boldsymbol{x}}_i(t)=\left[\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & c_i \\ 0 & -d_i & -a_i \end{array}\right] \boldsymbol{x}_i(t)+\left(\begin{array}{l} 0 \\ 0 \\ b_i \end{array}\right) \boldsymbol{u}_i(t)+\left(\begin{array}{l} 0 \\ 0 \\ e_i \end{array}\right) \boldsymbol{w}_i(t) \\ \boldsymbol{y}_i(t)=\left(\begin{array}{lll} 1 & 0 & 0 \end{array}\right) \boldsymbol{x}_i(t), i=1, 2, 3 \end{array}\right. $

(61)

$\left\{a_i, b_i, c_i, d_i, e_i\right\}$对于$i=1, 2, 3$分别取$\{2, 1, 1$, $10, 1\}, \{2, 1, 1, 3, 1\}, \{2, 2, 1, 10, 1\}$。

假设3个跟随者受到的外部扰动分别是0.5sin(k)，sin(k)，－sin(k)。求解可得输出调节器方程为

$ \left\{\begin{array}{l} \boldsymbol{\varPhi}_i=\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right]^{\mathrm{T}} \\ \boldsymbol{\varPsi}_{11}=\boldsymbol{\varPsi}_{12}=\boldsymbol{\varPsi}_{13}=\left[\begin{array}{ll} 0 & 10 \end{array}\right] \\ \boldsymbol{\varPsi}_{21}=\boldsymbol{\varPsi}_{22}=\boldsymbol{\varPsi}_{23}=\left[\begin{array}{ll} 0 & 3 \end{array}\right] \\ \boldsymbol{\varPsi}_{31}=\boldsymbol{\varPsi}_{32}=\boldsymbol{\varPsi}_{33}=\left[\begin{array}{ll} 0 & 5 \end{array}\right] \end{array}\right. $

(62)

假设在正常情况下，离散系统的固定采样周期为T=0.01。网络攻击持续时间可能为{0, T, 2T}，因此可以导致系统产生3种采样模态。

假设系统3个模态之间的转移概率矩阵为

$ \boldsymbol{A}=\left[\begin{array}{lll} 0.3 & 0.2 & 0.5 \\ 0.6 & 0.2 & 0.2 \\ 0.5 & 0.1 & 0.4 \end{array}\right] $

(63)

在不同系统模态下的控制器隐状态检测概率矩阵为

$ \boldsymbol{B}=\left[\begin{array}{lll} 0.4 & 0.4 & 0.2 \\ 0.2 & 0.7 & 0.1 \\ 0.1 & 0.3 & 0.6 \end{array}\right] $

(64)

异构多智能体之间的通讯拓扑结构图如图 1所示。

根据拓扑图计算得到λ₁=0.245 1，λ_{2, 3}=1.877 4±j0.744 9。

在仿真过程中，系统初始状态值设为

$ \left\{\begin{array}{l} x_0(0)=\left[\begin{array}{lll} 6.0 & 1.0 \end{array}\right]^{\mathrm{T}} \\ x_1(0)=\left[\begin{array}{lll} 7.8 & 1.0 & 1.0 \end{array}\right]^{\mathrm{T}} \\ x_2(0)=\left[\begin{array}{lll} 3.8 & 1.0 & 1.0 \end{array}\right]^{\mathrm{T}} \\ x_3(0)=\left[\begin{array}{lll} 4.6 & 1.0 & 1.0 \end{array}\right]^{\mathrm{T}} \\ \xi_1(0)=\left[\begin{array}{ll} -10 & -20 \end{array}\right] \\ \xi_2(0)=\left[\begin{array}{ll} 10 & 20 \end{array}\right] \\ \xi_3(0)=\left[\begin{array}{ll} -8 & -10 \end{array}\right] \end{array}\right. $

(65)

由定理2求得控制器增益K_ip、F_p为：

$ \left\{\begin{array}{l} \boldsymbol{K}_{11}=-1.646\;3, \boldsymbol{K}_{12}=-1.645\;7, \boldsymbol{K}_{13}=-1.598\;2 \\ \boldsymbol{K}_{21}=-1.605\;6, \boldsymbol{K}_{22}=-1.599\;8, \boldsymbol{K}_{23}=-1.598\;2 \\ \boldsymbol{K}_{31}=-1.631\;6, \boldsymbol{K}_{32}=-1.631\;4, \boldsymbol{K}_{33}=-1.632\;3 \end{array}\right. $

(66)

$ \left\{\begin{array}{l} \boldsymbol{F}_1=\left[\begin{array}{rlll} 0.426\;1 & 0.004\;3 \\ -0.001\;5 & 0.426\;1 \end{array}\right] \\ \boldsymbol{F}_2=\left[\begin{array}{rlll} 0.420\;8 & 0.005\;1 \\ -0.002\;6 & 0.421\;0 \end{array}\right] \\ \boldsymbol{F}_3=\left[\begin{array}{rlll} 0.421\;9 & 0.007\;2 \\ -0.003\;7 & 0.422\;1 \end{array}\right] \end{array}\right. $

(67)

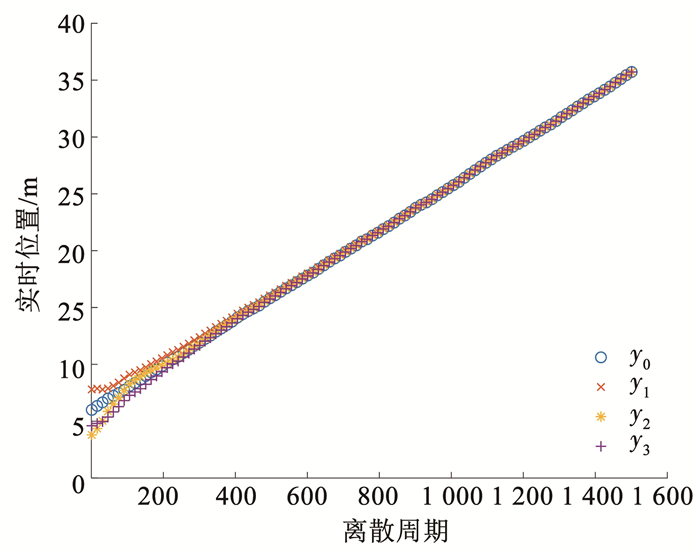
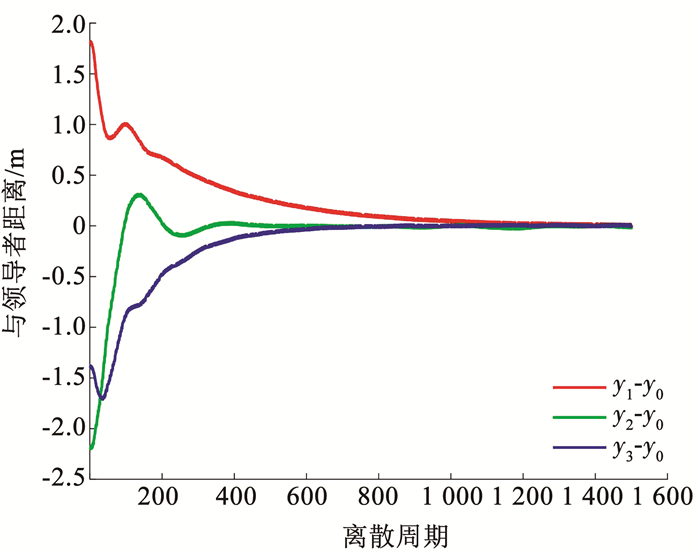
在仿真过程中，攻击行为和异步控制器模态按照给定的转移概率矩阵随机产生，具体如图 2所示。在该转移概率作用下得到了多智能体的输出以及输出误差曲线，如图 3、4所示。

由图 3、4可以看出，本文的异步控制器设计方法有效解决了复杂网络攻击行为影响下的多智能体系统一致性问题。

4 结论

1) 针对由隐蔽DoS攻击行为引起的系统模态与控制器模态异步现象，采用隐马尔可夫模型对这类现象进行建模; 利用隐马尔可夫模型对由隐蔽DoS攻击行为引起的系统模态与控制器模态的异步现象进行建模。

2) 设计了一个局部动态补偿器与输出反馈控制器，以保障异构多智能体系统具有耗散性能。

3) 利用调节方程和拓扑解耦方法，将异构多智能体系统的一致性问题转化为两个低维闭环控制系统的稳定性问题。

4) 利用Lyapunov稳定性定理结合系统耗散性控制，得到一组可用于求解控制器增益的线性矩阵不等式。本文通过一个三阶异构多智能体系统仿真实验，验证了所提方法的可行性与有效性。