提高载人密闭舱室的舒适度对于航天、航海等领域十分重要,作业人员的主观评价、操作舒适度、生理指标目前是评价舱室舒适度的重要因素。张帅等[1]通过虚拟仿真技术对潜水器任务中的潜航员生物力学参数及作业行为进行仿真,结合博弈论得到动态仿真数据,为提高舱室可靠性提出设计指导。初建杰等[2]通过构建三级民机客舱舒适度评估体系,研究主观与客观评估各级指标的赋权方法,提出了民机客舱舒适度评估方法并进行验证。李晓玲等[3]通过模拟驾驶环境实验,采集不同加速度振动的人体表面肌电信号,结合主观感受评分,提出了振动环境下基于SEMG的判定人体舒适性的客观评价方法。王文军等[4]采用遗传算法对飞行员人体姿势预测,通过快速上肢评估算法对所得姿势进行评估,获得舒适性参数, 最后以不同等级RGB值对舒适性参数进行直观可视化表示。Deng等[5]针对客舱人机界面布局设计的评价和决策问题,根据GEP(基因表达编程)提出操作舒适性预测模型,利用操作舒适性来评价布局方案。通过关节角度来描述上肢的手术姿势,将关节角度作为独立的变量来建立手术姿势的舒适模型。采用因子分析来减少可变维度,输出变量为运行舒适性得分。面向舱室的舒适度评价研究已涉及到各个领域,对于载人密闭舱室而言,设计一个通用准确的整体舒适度评价方法十分重要。本文提出基于故障树分析(Fault tree analysis,FTA)与模糊贝叶斯网络模型(Fuzzy bayesian networks,FBN)的载人密闭舱室舒适度评估方法,为舒适度评估提供方向,并指导改进舱室人机设计。
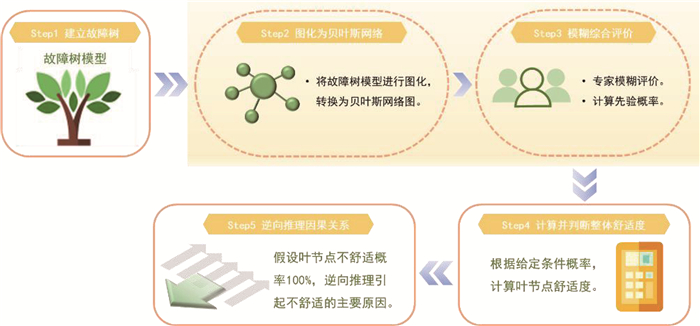
1 故障树模型构建 1.1 故障树研究方法现状目前密闭舱室人机设计和舒适度问题的分析研究还没有形成完整模式,仍然处在分类探索之中。FTA方法是安全系统工程中的主要分析方法,从一个最可能的事故开始自上而下逐层寻找引起顶事件的直接原因和间接原因,直到基本事件为止,并用逻辑门把事件之间的逻辑关系表达出来[6]。现已成熟应用于航空航天、制药、交通故障等高风险产业,并有完整的理论分析流程[7],也拓展出模糊故障树分析法、动态故障树分析法、T-S故障树分析法等多种方法。陶勇剑等[8]通过定性分析提取出故障树最小割集,转换成串并联结构模型进行系统可靠性估计,找出对系统可靠性估计不确定性影响大的组成单元,提高系统可靠性估计的准确性。Shu等[9]通过构建故障树研究了纯电动汽车中易受损伤部件电机控制器的可靠性,然后根据国际标准中提供的信息来估计电机控制器中单个部件的故障率,最后估计了整个电机控制器及其部件的可靠性指数与电动汽车使用寿命的偏向。但传统故障树分析法也有一定的局限性,比如故障概率无法精确获得,基于二态假设等,因此现有研究将故障树分析方法与其他方法融合分析解决实际问题。刘勇等[10]将T-S模糊故障树模型应用到多态导航系统性能分析中,以T-S模糊故障树表示系统的性能变量,映射为系统性能指标值,结合统计学中的期望思想,计算不同层次事件发生故障时系统的性能可靠性,通过实例研究验证评价系统的可靠性。冯蕴雯等[11]针对系统的故障树灵敏度分析缺乏统一评价指标的问题,将层次分析法引入故障树分析中,提出FTA-AHP方法生成系统综合灵敏度评价指标,结合案例验证其为系统可靠性提供了理论支撑。Sakar等[12]将故障树模型创建各因素之间的风险层次结构,映射到贝叶斯网络进行分析,来评估接地事故的风险等级。尹晓伟等[13]根据系统可靠性的框图建立FTA模型,然后将故障树直映射成为贝叶斯网络,结合条件概率表,运用贝叶斯网络的推理能力进行系统的可靠性评估,最后运用实例验证贝叶斯网络评估机械系统的有效性。为研究载人密闭舱室舒适度评价,本文引入故障树构建载人密闭舱室疲劳评估初步模型; 后结合模糊贝叶斯网络进行推理计算,评估流程如图 1所示。
|
图 1 载人密闭舱室舒适度评估流程图 Fig. 1 Flow chart of comfort evaluation for manned closed cabin |
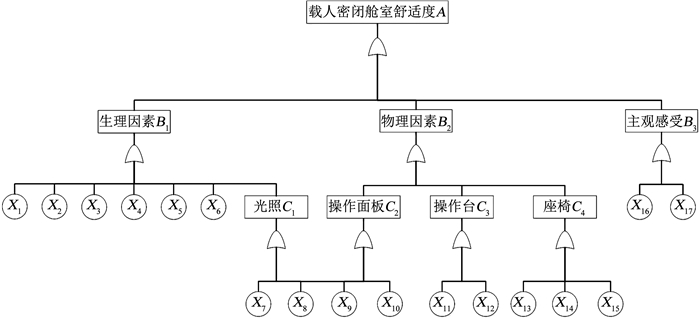
通过对现有文献整理,提取出影响密闭舱室舒适度的设计指标,进行故障树模型构建。需将顶事件定义为载人密闭舱室不舒适,逐级拓展寻找不舒适原因基本事件,用特定的逻辑门符号关联起来,以此来确定顶事件发生的所有不舒适的原因组合。根据对各领域舱室舒适度文献调研所收集指标构建载人密闭舱室舒适度评价FTA模型如图 2所示。基本事件含义见表 1。
|
图 2 载人密闭舱室舒适度故障树模型 Fig. 2 Comfort fault tree model of manned closed cabin |
| 表 1 基本事件含义表 Tab. 1 Table of basic event meanings |
贝叶斯网络是一个概率图模型,由Judea Pearl于1985年首次提出,可以模拟概率推理过程中因果关系的不确定性处理。它的网络拓扑是有向无环图(DAG)[14],贝叶斯网络的核心是贝叶斯公式,即:
| $ P(Y \mid X) P(X)=P(X \cap Y) $ | (1) |
| $ P(X \mid Y)=\frac{P(Y \mid X) P(X)}{P(Y)} $ | (2) |
| $ P(Y)=\sum\limits_{i=1}^n P\left(X_i\right) P\left(Y \mid X_i\right) $ | (3) |
式中:P(X)为事件X的先验概率,P(Y丨X)为在事件X发生的条件下,事件Y发生的概率,P(X丨Y)为在事件Y发生的条件下事件X发生的概率。
通过贝叶斯公式,可以由已知信息预测和推断未知信息。贝叶斯定理中事件相互之间的因果关系可以通过某种拓扑结构的贝叶斯网络来表现。贝叶斯网络由两个重要部分组成,一个是贝叶斯网络拓扑图,另一个是节点之间的条件概率表(Conditional probability table, CPT),用于表示各节点之间的连接强度。如果贝叶斯网络具有完整的条件概率值并可以计算特定的联合概率值,则可以认为它是可以计算和推理的。由于BN的节点彼此独立,因此联合概率分布可以表示为相关节点的概率的乘积。
| $ \begin{aligned} P\left(X_1, X_2, \cdots, X_n\right)= & \prod\limits_{i=1}^n P\left(X_i \mid X_{i-1}, X_{i-2}, \cdots, X_i\right)= \\ & \prod\limits_{i=1}^n P\left(X_i \mid \pi\left(X_i\right)\right) \end{aligned} $ | (4) |
式中:π(Xi)为Xi所有的根节点集合,P(Xi丨π(Xi))为其他中间节点的条件概率分布。BN中每一个节点都对应一个条件概率分布表。
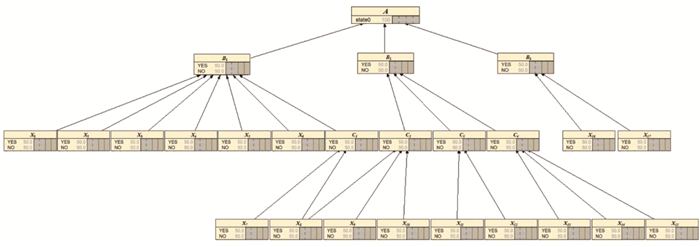
贝叶斯方法以贝叶斯理论为基础,对风险分析、事故分析、可靠性分析与安全管理等进行推论,已应用于各个研究领域[15-17]。在本文研究中,建立了载人密闭舱室舒适度FTA模型,因使用故障树方法进行评估时无法逆向推理,本文将故障树模型图形转化为贝叶斯网络模型,由贝叶斯网络来进行双向推理。图形转化是将FTA中的各级事件用相应的BN节点表示,逻辑符号由具体的条件概率代替[18]。将故障树模型图转化为贝叶斯网络,确定事件发生的网络构架; 通过BN分析进行因果关系的探究,确定顶事件发生的主要原因,揭示载人密闭舱室舒适性的影响因素,并提出对载人密闭舱室舒适度设计提出的重要建议。本文利用Netica软件构建初步BN模型,如图 3所示。
|
图 3 载人密闭舱室舒适度BN模型 Fig. 3 BN model of comfort of manned closed cabin |
贝叶斯网络具有很好的定量推论能力,数据获取是通过历史观测或实验获取,但很多时候事件的概率数据较少或不可用时,便需要引入专家评价方法来进行。模糊贝叶斯网络(FBN)是模糊理论与贝叶斯网络相结合的推理模型,在可靠性分析和故障问题中应用比较广泛。它在BN网络的现有基础上引入了模糊理论[19],将BN模型转换为模糊节点,能够对一些不确定的问题进行处理和预测。应用模糊变换原理及最大隶属度原则,通过考虑与被评估事件相关的各种因素,并在模糊数学中使用模糊概念来全面评估这些事件因素。首先定义一组评语,通过多个专家打分获取评价矩阵,再利用一组设定的隶属度函数生成隶属度权重矩阵,最后经过模糊运算得到具体的评价数值。三角模糊数运算简单、易理解,本文采用三角模糊数作为根节点事件的隶属度函数。
研究建立BN模型后将专家评分结合模糊综合评价法获取根节点先验概率和其他中间节点条件概率,再基于BN模型诊断顶层叶节点事件舒适度概率。专家定性语义表达对复杂情况与问题评估具有一定的意义,为量化专家的定性表达,建立语言变量和模糊数值的对应关系,本文设定评语等级集V ={非常不舒适(VN),不舒适(N),轻微不舒适(SN),中等(M),轻微舒适(SC),舒适(C),非常舒适(VC)},包含7个语言变量。这些语言变量可以转换为相应的三角模糊数,见表 2。
| 表 2 语言变量对应的三角模糊数 Tab. 2 Triangular fuzzy numbers corresponding to language variables |
通过专家打分评价,结合三角模糊综合评价法,计算底事件Xi的先验概率,同时获取中间节点的条件概率。将专家评价的自然语言转变为三角模糊概率,邀请多位专家对各个底事件节点舒适度进行等级评价,第n位专家对底事件指标节点Xi的评判意见通过三角模糊数转化,得到三角模糊概率为Pin=(ain, bin, cin)。假定各位专家权重相同,共有m位专家,将每位专家给出的评价结果进行平均处理,得到模糊均值概率为
| $ P_i^*=\frac{P_i^1+\cdots+P_i^n+\cdots P_i^m}{m}=\left(a_i^*, b_i^*, c_i^*\right) $ | (5) |
采用面积均值法把模糊均值概率转化成最能代表此模糊集合的概率值,表示为
| $ P_i^{* *}=\frac{a_i^*+2 b_i^*+c_i^*}{4} $ | (6) |
结合贝叶斯网络条件概率表,依次求得中间节点、叶节点的先验概率,对模糊贝叶斯网络进行因果推理,将舒适度评价集定义S ={S1, S2, S3, S4} ={很满意,满意,一般,不满意},其中S ∈[0.90, 1.00]为很满意, S ∈[0.80, 0.90)为满意, S ∈[0.70, 0.80)为一般, S ∈[0.70)为不满意。根据评价等级定义叶节点的舒适度,得出载人密闭舱室整体舒适度评价。同时可以结合条件概率分布,对模糊贝叶斯网络进行逆向诊断[20],假定叶节点不舒适概率为100%,推导其他节点的不舒适概率值,进一步找出影响目标节点A的关键指标因素。
3 实例分析与讨论 3.1 模糊综合评价选取西北工业大学学工业设计研究所密闭实验室为研究对象,实验室布局如图 4所示,运用构建的密闭舱室贝叶斯网络模型对其整体舒适性进行评价分析,本文采用专家评分法来确定贝叶斯网络节点的先验概率和条件概率分布。邀请4位对西北工业大学密闭实验室有1年以上使用经验的专家分别对每一个基本事件舒适程度给出评价意见,在此假定每位专家打分权重相同,专家对基本事件指标即根节点打分结果见表 3。

|
图 4 实验室载人密闭舱室布局图 Fig. 4 Layout of laboratory manned closed cabin |
| 表 3 根节点专家打分结果 Tab. 3 Root node expert scoring results |
根据式(5)、(6),可以计算出基本事件Xi的先验概率,见表 4。
| 表 4 根节点先验概率 Tab. 4 Prior probabilities of root nodes |
确定根节点与中间节点、叶节点的条件概率表,即可求出中间节点和叶节点的先验概率。由于数量较多,以中间节点C4为例,0为舒适,1为不舒适,列出条件概率表见表 5。
| 表 5 节点C4条件概率表 Tab. 5 Node C4 conditional probability table |
网络节点参数确定后,可以计算该贝叶斯网络。已知根节点X13、X14、X15对应的舒适度概率值,结合节点C4条件概率,根据式(3)可以得到P(C4)。
| $ \begin{aligned} P\left(C_4\right)= & P\left(C_4 \mid X_{13} X_{14} X_{15}\right) P\left(X_{13}\right) P\left(X_{14}\right) P\left(X_{15}\right)+ \\ & P\left(C_4 \mid X_{13} X_{14} \overline{X_{15}}\right) P\left(X_{13}\right) P\left(X_{14}\right) P\left(\overline{X_{15}}\right)+ \\ & P\left(C_4 \mid X_{13} \overline{X_{14}} X_{15}\right) P\left(X_{13}\right) P\left(\overline{X_{14}}\right) P\left(X_{15}\right)+ \\ & P\left(C_4 \mid X_{13} \overline{X_{14} X_{15}}\right) P\left(X_{13}\right) P\left(\overline{X_{14}}\right) P\left(\overline{X_{15}}\right)+ \\ & P\left(C_4 \mid \overline{X_{13}} X_{14} X_{15}\right) P\left(\overline{X_{13}}\right) P\left(X_{14}\right) P\left(X_{15}\right)+ \\ & P\left(C_4 \mid \overline{X_{13}} X_{14} \overline{X_{15}}\right) P\left(\overline{X_{13}}\right) P\left(X_{14}\right) P\left(\overline{X_{15}}\right)+ \\ & P\left(C_4 \mid \overline{X_{13} X_{14}} X_{15}\right) P\left(\overline{X_{13}}\right) P\left(\overline{X_{14}}\right) P\left(X_{15}\right)+ \\ & P\left(C_4 \mid \overline{X_{13} X_{14} X_{15}}\right) P\left(\overline{X_{13}}\right) P\left(\overline{X_{14}}\right) P\left(\overline{X_{15}}\right)=0.664 \end{aligned} $ | (7) |
本文将贝叶斯网络各个节点舒适概率值与条件概率输入Netica中进行计算,可求得到中间节点与叶节点概率因果推理结果见表 6,贝叶斯网络如图 5所示。
| 表 6 叶节点与中间节点全概率数值 Tab. 6 All probability values of leaf nodes and intermediate nodes |

|
图 5 载人密闭舱室舒适度贝叶斯网络计算图 Fig. 5 Bayesian network calculation diagram for comfort of manned closed cabin |
根据舒适度评价等级,可以确定西北工业大学工业设计研究所载人密闭舱室整体舒适度评价为“不满意”程度,仍需要进行调整; 在中间节点中,对于B1生理环境的满意度最高,B3主观感受的评价最不满意。进一步指导了舱室舒适性调整方案,应按照现有舒适度评价进行排序并改善设计。
3.4 舒适度评估验证为验证基于FTA-FBN载人密闭舱室舒适度评估方法有效性,面向16位初次使用该实验室的研究生进行问卷调研。要求被试人员在西北工业大学密闭实验室进行40 min的作业任务,并在任务结束后对故障树模型提出的3层舒适度指标进行主观评价,评价结果与FTA-FBN对比如图 6所示。

|
图 6 载人密闭舱室舒适度评价雷达图 Fig. 6 Radar chart for comfort evaluation of manned closed cabin |
通过调研结果可以得知,该密闭实验室舒适度评价得分为0.670, 为“不满意”水平,对于中间指标进行比较得出B3主观感受为最需要改进的指标,即空间大小与空间色彩为现有实验室评估最不舒适因素,B1生理因素最满意。底层基本指标评估数据与FTA-FBN评估结果不完全相同,但整体评估与本文提出的方法结果相符,能够验证此评估方法的合理性与适用性。
3.5 贝叶斯网络逆向推理通过贝叶斯网络逆向推理寻找出对载人密闭舱室不舒适影响突出的因素,假设顶节点A不舒适程度为100% 时,各个根节点后验概率见表 7。可以得知当载人密闭舱室不舒适程度为100% 时,由X16空间大小的不舒适概率最高为67.3%,舒适度概率为32.7%; 其次是X11台面高度,不舒适概率为59.6%,舒适度概率为40.4%,还有X17,X8,X1,X9等这些根节点是引起舱室不舒适的较为主要的原因,因此可以通过提高这些根节点的舒适度来优化设计方案。在舱室整体不舒适时,应首要检查这些前序节点的舒适性,以此来改善整体环境。
| 表 7 贝叶斯网络逆向推理根节点得分 Tab. 7 Bayesian network backward inference root node scores |
1) 提出基于FTA-FBN的舒适度评估方法,将故障树分析方法与贝叶斯网络、模糊理论相结合,对载人密闭舱室舒适度进行评估。
2) 构建载人密闭舱室舒适度故障树分析模型,将影响因素划分为3个中间层级,并构建17个基本事件。
3) 将故障树图化为贝叶斯模型,引入模糊理论进行评价,解决了故障树无法进行双向推理的缺点,扩展了故障树、模糊贝叶斯网络评估方法的适用范围。
4) 利用综合模糊评价得出专家对于根节点基本事件的舒适度评价,并结合条件概率表对中间节点、叶节点进行舒适度评估; 通过贝叶斯网络逆向推理得出因果关系,寻找造成整体不舒适性的主要原因。
5) 运用实例分析并探究验证了该方法的适用性与可靠性,为载人密闭舱室舒适度评估提供新的方法。
| [1] |
张帅, 何卫平, 陈登凯, 等. 载人潜水器舱室空间舒适性复合评估方法[J]. 哈尔滨工业大学学报, 2019, 51(10): 164. ZHANG Shuai, HE Weiping, CHEN Dengkai, et al. Compound evaluation method for the space comfort of manned submersible[J]. Journal of Harbin Institute of Technology, 2019, 51(10): 164. DOI:10.11918/j.issn.0367-6234.201810148 |
| [2] |
初建杰, 裴卉宁, 余隋怀, 等. 民机客舱舒适度评估指标体系及评估方法研究[J]. 人类工效学, 2017, 23(3): 51. CHU Jianjie, PEI Huining, YU Suihuai, et al. Research on evaluation index system and evaluation method of passenger Cabin comfort[J]. Ergonomic, 2017, 23(3): 51. DOI:10.13837/j.issn.1006-8309.2017.03.0010 |
| [3] |
李晓玲, 张翔, 张鄂, 等. 用肌电信号评价人体振动舒适性的方法研究[J]. 西安交通大学学报, 2009, 43(3): 23. LI Xiaoling, ZHANG Xiang, ZHANG E, et al. Evaluation of Human body to vibration comfortableness by surface electromyogram signals[J]. Journal of Xi'an Jiaotong University, 2009, 43(3): 23. DOI:10.3321/j.issn:0253-987X.2009.03.005 |
| [4] |
王文军, 余隋怀, 初建杰, 等. 飞机驾驶舱舒适性参数可视化技术[J]. 机械科学与技术, 2015, 34(4): 648. WANG Wenjun, YU Suihuai, CHU Jianjie, et al. The visualization technology of the comfort parameter in aircraft cockpit[J]. Mechanical Science and Technology for Aerospace Engineering, 2015, 34(4): 648. DOI:10.13433/j.cnki.1003-8728.2015.0431 |
| [5] |
DENG Li, WANG Guohua, CHEN Bo. Operating comfort prediction model of human-machine interface layout for Cabin based on GEP[J]. Computational Intelligence and Neuroscience, 2015, 2015: 11. DOI:10.1155/2015/896072 |
| [6] |
BIAN Haifeng, ZHANG Jun, LI Ruixue, et al. Risk analysis of tripping accidents of power grid caused by typical natural hazards based on FTA-BN model[J]. Natural Hazards, 2021, 106(3): 1771. DOI:10.1007/S11069-021-04510-5 |
| [7] |
陈紫起. 基于故障树方法的柴油机可靠性研究[D]. 大连: 大连理工大学, 2020 CHEN Ziqi. Research on reliability of diesel engine based on fault tree method[D]. Dalian: Dalian University of Technology, 2020. DOI: 10.26991/d.cnki.gdllu.2020.000450 |
| [8] |
陶勇剑, 董德存, 任鹏. 基于故障树的系统可靠性估计不确定性分析[J]. 同济大学学报(自然科学版), 2010, 38(1): 142. TAO Yongjian, DONG Decun, REN Peng. Uncertainty analysis of system reliability estimation based on fault tree[J]. Journal of Tongji University (Natural Science), 2010, 38(1): 142. DOI:10.3969/j.issn.0253-374x.2010.01.026 |
| [9] |
SHU Xiong, GUO Yingfu, YANG Huan, et al. Reliability study of motor controller in electric vehicle by the approach of fault tree analysis[J]. Engineering Failure Analysis, 2021, 121: 105165. DOI:10.1016/j.engfailanal.2020.105165 |
| [10] |
刘勇, 罗德林, 石翠, 等. 基于T-S模糊故障树的多态导航系统性能可靠性[J]. 北京航空航天大学学报, 2021, 47(2): 243. LIU Yong, LUO Delin, SHI Cui, et al. Performance reliability of multi-state system based on T-S fuzzy fault tree[J]. Journal of Beijing University of Aeronautics and Astronsutics, 2021, 47(2): 243. DOI:10.13700/j.bh.1001-5965.2020.0276 |
| [11] |
冯蕴雯, 宋祉岑, 路成, 等. 基于FTA-AHP的飞机系统综合灵敏度评价分析[J]. 西北工业大学学报, 2021, 39(5): 972. FENG Yunwen, SONG Zhicen, LU Cheng, et al. Analysis of comprehensive sensitivity evaluation of aircraft system based on FTA-AHP[J]. Journal of Northwestern Polytechnical University, 2021, 39(5): 972. DOI:10.1051/jnwpu/20213950971 |
| [12] |
SAKAR C, TOZ C A, BUBER M, et al. Risk analysis of grounding accidents by mapping a fault tree into a Bayesian network[J]. Applied Ocean Research, 2021, 113: 102764. DOI:10.1016/j.apor.2021.102764 |
| [13] |
尹晓伟, 钱文学, 谢里阳. 贝叶斯网络在机械系统可靠性评估中的应用[J]. 东北大学学报(自然科学版), 2008, 29(4): 560 YIN Xiaowei, QIAN Wenxue, XIE Liyang. Application of Bayesian network to reliability assessment of mechanical system[J]. Journal of Northeastern University (Natural Science), 2008, 29(4): 560. DOI: 10.3321j.issn:1005-3026.2008.04.026 |
| [14] |
徐磊, 李向阳, 黄湘岳. 基于贝叶斯网络的非常规突发事件灾情评估[J]. 上海交通大学学报, 2013, 47(5): 846. XU Lei, LI Xiangyang, HUANG Xiangyue. Unconventional emergencies assessment based on Bayesian network[J]. Journal of Shanghai Jiaotong University, 2013, 47(5): 846. DOI:10.16183/j.cnki.jsjtu.2013.05.030 |
| [15] |
SENOL E Y, YASLI F. A risk analysis study for chemical cargo tank cleaning process using Fuzzy Bayesian Network[J]. Ocean Engineering, 2021, 235: 109360. DOI:10.1016/j.oceaneng.2021.109360 |
| [16] |
LANDQUIST H, ROSÉN L, LINDHE A, et al. Bayesian updating in a fault tree model for shipwreck risk assessment[J]. Science of the Total Environment, 2017, 590/591: 82. DOI:10.1016/j.scitotenv.2017.03.033 |
| [17] |
RAMLI N, GHANI A N, AHMAD N, et al. Psychological response in fire: A Fuzzy Bayesian network approach using expert judgment[J]. Fire Technology, 2021, 2318. DOI:10.1007/S10694-021-01106-0 |
| [18] |
娄文忠, 赵悦岑, 冯恒振, 等. 基于贝叶斯网络的MEMS安全系统可靠性分析[J]. 北京理工大学学报, 2021, 41(9): 957. LOU Wenzhong, ZHAO Yuecen, FENG Hengzhen, et al. Reliability analysis of MEMS S&A based on Bayesian network[J]. Transactions of Beijing Institute of Technology, 2021, 41(9): 957. DOI:10.15918/j.tbit1001-0645.2020.065 |
| [19] |
耿秋. 基于模糊贝叶斯网络的航天器生存力评估专家系统研究[D]. 哈尔滨: 哈尔滨工业大学, 2019 GENG Qiu. Research of spacecraft survivability acessment expert system based on fuzzy Bayesian network[D]. Harbin: Harbin Institute of Technology, 2019. DOI: 10.27061/d.cnki.ghgdu.2019.001888 |
| [20] |
陈舞, 王浩, 张国华, 等. 基于T-S模糊故障树和贝叶斯网络的隧道坍塌易发性评价[J]. 上海交通大学学报, 2020, 54(8): 820. CHEN Wu, WANG Hao, ZHANG Guohua, et al. Evaluation of tunnel collapse susceptibility based on T-S fuzzy fault tree and Bayesian network[J]. Journal of Shanghai Jiaotong University, 2020, 54(8): 820. DOI:10.16183/j.cnki.jsjtu.2020.99.011 |
 2023, Vol. 55
2023, Vol. 55


