2. 中国空间技术研究院, 北京 100094;
3. 北京控制工程研究所, 北京 100094
2. China Academy of Space Technology, Beijing 100094, China;
3. Beijing Institute of Control Engineering, Beijing 100094, China
中国载人航天发展规划的第3步就是构建长期在轨载人空间站,空间科学载荷长期与空间站共轨飞行,并择机与空间站交会对接,以实现在轨加注、在轨维修等多项空间任务。在交会对接期间,两个甚至是多个航天器需要在预定的轨道位置上,完成导引、逼近、锁紧、对接等一系列动作,在过程中会产生相当的对接冲力以及推力器对目标的羽流冲击。为保证在交会对接阶段航天器的安全,尤其是对于柔性结构[1],需采用特定的空间可重复锁紧装置将其锁定,由该装置作为保护部件承受绝大部分的对接冲击载荷。空间可重复锁紧装置在轨需实现可分离部件与其他部件的多次锁紧与分离,受到航天器交会对接冲击和空间环境下性能退化的综合作用,并且具有高可靠、长寿命、小子样和高生产成本的特点,对其进行系统的可靠性评估研究具有非常重要的工程意义。
针对工程中常见的小子样、长寿命机械装置的可靠性评估问题,多采用基于性能退化的可靠性分析技术进行研究[2-3]。对于空间可重复锁紧装置,不仅经历装置自身的自然退化(磨损、疲劳、劣化等),还受到由交会对接、压紧释放等带来的冲击载荷[4-6]。Frostig等[7]推导了系统经历自然退化和基于泊松过程的累积冲击退化模型,Lehmann[8]提出了著名的DTS(degradation-threshold-shock)模型,Huynh等[9]在其基础上考虑了退化和冲击过程的相关性。Wang等[10]则根据退化路径的不同,引入了加法和乘法退化路径函数下的两过程组合模型。Tao等[11]针对轴颈轴承受自然退化和随机冲击作用下的竞争失效问题,开展冲击与退化试验对其进行可靠性评估。此外,对于长寿命产品在建模过程中还需要开展高应力水平下的加速退化试验[12]。Thomas等[13]概述了加速试验的性能退化建模方法。Pan等[14-15]提出了Gamma过程和多应力作用下Wiener过程的加速退化模型及相应的加速试验方法。王立志等[16]针对长寿命产品寿命数据不足的问题,提出了一种融合加速寿命数据、加速性能退化数据和外场数据的分析方法。王华伟等[17]利用贝叶斯模型实现了多源信息融合的剩余寿命预测。但是由于空间可重复锁紧装置的结构和工作特点,上述理论方法直接应用难度较大,且适用范围有限。
因此,本文紧扣空间可重复锁紧装置功能原理及在轨工况,考虑冲击环境对其自身性能退化的影响,建立一种冲击与退化相依竞争失效的可靠性模型,基于冲击承载及加速退化小子样试验数据,结合贝叶斯方法融合经验信息及相似产品历史试验数据进行模型参数估计,最后对某型号空间可重复锁紧装置的可靠性进行了评估。
1 功能、工作原理及可靠性特征量空间可重复锁紧装置在交付后要伴随航天器经历以下任务阶段:发射段、导引段、共轨飞行段、交会对接段、停靠段、分离撤离段和末期离轨段。入轨后共轨飞行段装置处于解锁断电状态,在航天器交会对接前执行锁紧动作,作为平台柔性结构的保护装置承受交会对接冲击载荷;航天器分离撤离后解锁,恢复平台工作状态。装置在轨经历多次交会对接工况,执行重复“锁紧-解锁-再锁紧”动作。
装置结构如图 1所示,由驱动组件(电机、减速器)、传动组件(滚珠丝杠副、导轨副)、测量组件(位移传感器、行程开关)、锁紧执行组件(移动手爪及其他连接件)组成。

|
图 1 空间可重复装置结构示意 Fig. 1 Schematic diagram of space reusable locking device |
装置工作原理如图 2所示,当装置锁紧及解锁时,驱动电路接受控制器指令驱动电机产生扭矩,通过减速器后驱动滚珠丝杠副将回转运动转化为移动手爪的直线运动,直到位移传感器和行程开关判断到达指定位置,完成对被锁紧件的锁紧或解锁。交会对接冲击载荷经由航天器本体传递至被锁紧件,再依次传递至移动手爪、导轨副、丝杠副及其他部件。装置断电贮存期间主要承受真空热环境载荷。

|
图 2 可重复锁紧装置工作原理图 Fig. 2 Principle diagram of space reusable locking device |
装置在轨期间需要承受交会对接冲击载荷,同时还需要保证锁紧和解锁动作的极致可靠。装置的主要故障模式有:1)装置结构受冲击断裂;2)锁紧或解锁不到位。因此,空间可重复锁紧装置的可靠性R为
| $ R=R_1 \times R_2 $ | (1) |
式中:R1为承受冲击载荷的可靠性,R2为锁紧及解锁可靠性。
R1可用“在规定的环境和工况条件下,装置受到的冲击强度A小于极限强度Af的概率”来表征,即R1=P(A < Af)。
装置的重复锁紧解锁过程从本质上是内部传动副驱动力矩和阻力矩综合作用的结果。基于上述装置结构组成和工作原理的描述,装置的可靠性模型为典型的串联模型,电机、减速器、丝杠副等部件相互独立且无冗余备份,装置的总阻力矩反映的是装置内部所有机械传动副的摩擦性能随服役时间变化的总和(包括润滑膜在空间环境下的劣化过程、冲击载荷导致部件卡滞等)。因此,R2可用“在规定的环境和工况条件下,阻力矩M小于失效阈值Mf的概率”来表征,即R2=P(M < Mf)。
2 冲击作用下的性能退化过程建模 2.1 冲击失效过程 2.1.1 极端冲击突发失效模型装置按照航天器交会对接的周期经历冲击过程,当某次冲击的强度大于其临界失效阈值Af时,装置发生突发失效。假设第j次冲击的强度为非负独立同分布随机变量{Aj},其累积分布函数为FA(a),当前时刻的总冲击次数为N(t),根据强度-应力干涉模型[18],装置在t时刻不发生失效的概率为
| $ P\left\{A_1 <A_f, \cdots, A_{N(t)}<A_f\right\}=\left(F_A\left(A_f\right)\right)^{N(t)} $ | (2) |
每次冲击的累积分布函数服从正态分布Aj~N(μA, σA2),则有
| $ F_A\left(A_f\right)={\mathit{\Phi}}\left(\frac{A_f-\mu_A}{\sigma_A}\right) $ | (3) |
当某次冲击的强度小于其临界失效阈值Af时,即发生非致命冲击。假设第j次冲击对性能退化的影响为Yj(j=0, 1, 2, …),且冲击的作用是累积可加的,{Yj}序列非负,且独立同分布[19],则t时刻冲击对装置造成的累积损伤量为
| $ Y(t)=\sum\limits_{j=0}^{N(t)} Y_j $ | (4) |
冲击导致的损伤量Yj服从正态分布N(μY, σY2),根据正态分布的可加性,多次冲击造成的累积损伤量Y(t)服从正态分布N(N(t)μY, N(t)σY2)。
2.2 性能退化过程 2.2.1 性能退化模型在非交会对接期,装置于解锁状态断电在轨贮存,由于润滑膜、非金属部件等在空间热、真空环境下发生老化,装置性能发生自然退化。装置的自然退化量X(t)是由很多微小损伤量所造成的均匀而平缓的过程,可视为服从Wiener过程:
| $ X(t)=\mu_X t+\sigma_X B(t) $ | (5) |
式中:B(t)为标准Wiener过程,μX为漂移系数,σX为扩散系数。由Wiener过程性质:X(0)=0;在任意时刻区间[t, t+Δt]内的增量X(t+Δt)-X(t)服从正态分布N(μXΔt, σX2Δt)。
2.2.2 加速模型由于装置在轨性能退化过程缓慢,因此需开展高应力水平下的加速退化试验获取性能退化数据。通过真空环境下的温度循环应力加速退化试验对在轨贮存期的性能退化过程进行模拟,采用Coffin-Manson模型描述:
| $ N_f=C(\Delta T)^{-q} $ | (6) |
式中:Nf为循环周期数,ΔT为温差范围,C为材料常数,q为Coffin-Manson指数,一般取3~5[20]。则相应的加速因子可定义为
| $ A=\left(\frac{\Delta T_{\text {test }}}{\Delta T_{\text {use }}}\right)^q $ | (7) |
式中:ΔTuse为实际工况温变范围,ΔTtest为加速试验温变范围。
基于加速因子不变原则[21],假设A为一个不随时间变化、只由应力水平ΔT决定的常数。因此,从退化增量的角度,装置的加速性能退化模型又可表示为
| $ X_l(t+\Delta t)-X_l(t) \sim N\left(\mu_X A \Delta t, \sigma_X^2 A \Delta t\right) $ | (8) |
由于模型参数估计过程受到试件数量和测试数据的限制,需采用贝叶斯方法,融合相似产品历史数据、经验信息以及试验测试数据,综合对模型参数进行估计。
首先,融合历史退化数据和经验信息获取先验分布,得到模型参数的先验分布π(q, μX, σX),假设模型参数相互独立,则可表示为π(q)π(μX)π(σX)。
然后,在给定模型参数q, μX, σX的条件下,假设性能退化增量之间相互独立且都服从正态分布。令Δxij表示试验中第i个装置第j次观测的性能退化增量, 其中i=1, …, n, j=1, …, m。则进一步建立X(t)的似然函数为
| $ L\left(X \mid q, \mu_X, \sigma_X\right)=\prod\limits_{i=1}^n \prod\limits_{j=2}^m \phi\left(\frac{\Delta x_{i j}-A \mu_X \Delta t_{i j}}{A \sigma_X^2 \Delta t_{i j}}\right) $ | (9) |
在获取加速性能退化模型参数的先验分布和性能退化数据的似然函数之后,采用贝叶斯公式建立模型参数联合后验分布:
| $ p\left(q, \mu_X, \sigma_X \mid X\right)=\frac{\pi\left(A, \mu_X, \sigma_X\right) L\left(X \mid A, \mu_X, \sigma_X\right)}{\int\limits_{c, q, \sigma_X>0} \pi\left(A, \mu_X, \sigma_X\right) L\left(X \mid A, \mu_X, \sigma_X\right) \mathrm{d} A \mathrm{~d} \mu_X \mathrm{~d} \sigma_X} \propto \pi\left(q, \mu_X, \sigma_X\right) \prod\limits_{i=1}^n \prod\limits_{j=2}^m \phi\left(\frac{\Delta x_{i j}-A \mu_X \Delta t_{i j}}{A \sigma_X^2 \Delta t_{i j}}\right) $ | (10) |
最后,结合式(9)、(10)即可得到相应的模型参数估计值
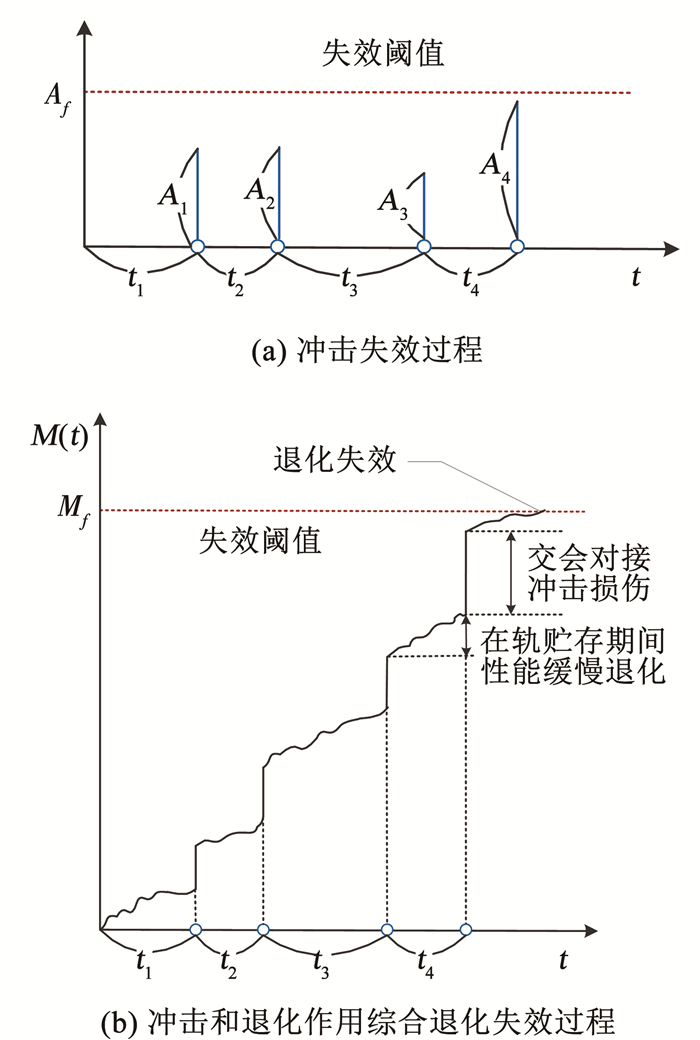
空间可重复锁紧装置的可靠性评估需对自然退化过程和冲击共同作用下的竞争失效过程进行研究,并考虑两者的相依性,如图 3所示。图 3(a)为装置的冲击失效过程,图 3(b)为受冲击和退化共同作用时的综合退化过程。当冲击载荷的量级超过冲击阈值,即遭受极端冲击,装置发生突发失效;否则该次冲击造成装置的累积损伤,即将损伤值计入性能退化量中,当总退化量超过失效阈值,装置发生退化失效。
|
图 3 冲击-退化竞争失效机制 Fig. 3 Shock - degradation competition failure mechanism |
假设装置在服役过程中的总性能退化M(t)是由服役期间的自然退化量X(t)和冲击的累积损伤Y(t)共同引起的,且两者具有叠加效应[10-11],即
| $ M(t)=X(t)+Y(t) $ | (11) |
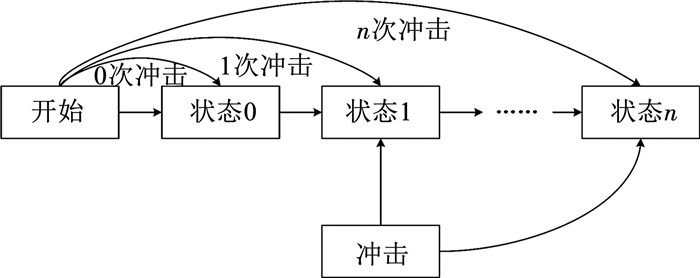
每发生一次交会对接冲击,产品性能就会随着损伤的累积作用而降低,从而将连续的性能退化过程分为多个状态[22],如图 4所示。
|
图 4 定时冲击下的状态转移过程 Fig. 4 State transition process under timed shock |
装置在各个状态下可靠工作的概率可表示为
| $ P_i= \begin{cases}P\left\{N(t)=0, X(t)<M_f\right\}, & i=0 \\ P\left\{N(t)=i, X(t)+Y(t)<M_f\right\} \times & \\ P\left\{A_1 <A_f, \cdots, A_i<A_f\right\}, & i \geqslant 1\end{cases} $ | (12) |
当发生n次冲击时,根据正态分布可加性,有
| $ X(t)+Y(t) \sim N\left(\mu_X(t)+n \mu_Y, \sigma_X^2(t)+n \sigma_Y^2\right) $ | (13) |
在确定的失效阈值Mf下,在轨t时刻的状态概率可表示为
| $ P\left\{X(t)+Y(t) \leqslant M_f\right\}={\mathit{\Phi}}\left(\frac{M_f-\mu_X(t)-N(t) \mu_Y}{\sqrt{\sigma_X^2(t)+N(t) \sigma_Y^2}}\right) $ | (14) |
因此,当i≥1时,装置处于可靠工作状态的概率Pi又可表示为
| $ \begin{aligned} P_i= & P\left\{X(t)+\sum\limits_{i=1}^{N(t)} Y_i <M_f\right\} F_A^{N(t)}\left(A_f\right)= \\ & \mathit{\Phi}\left(\frac{M_f-\mu_X(t)-N(t) \mu_Y}{\sqrt{\sigma_X^2(t)+N(t) \sigma_Y^2}}\right)\left(\mathit{\Phi}\left(\frac{A_f-\mu_A}{\sigma_A}\right)\right)^{N(t)} \end{aligned} $ | (15) |
由产品在t时刻的可靠度为:到达装置的N(t)次冲击的冲击量未超过冲击失效阈值Af (即R1)且性能退化总量不超过退化失效阈值Mf(即R2)的概率。综上所述,式(1)可靠度函数可进一步表示为
| $ R(t)= \begin{cases}\mathit{\Phi}\left(\frac{M_f-\mu_X(t)}{\sigma_X(t)}\right), & N(t)=0 \\ \mathit{\Phi}\left(\frac{M_f-\mu_X(t)-N(t) \mu_Y}{\sqrt{\sigma_X^2(t)+N(t) \sigma_Y^2}}\right) \times & \\ \left(\mathit{\Phi}\left(\frac{A_f-\mu_A}{\sigma_A}\right)\right)^{N(t)}, & N(t) \geqslant 1\end{cases} $ | (16) |
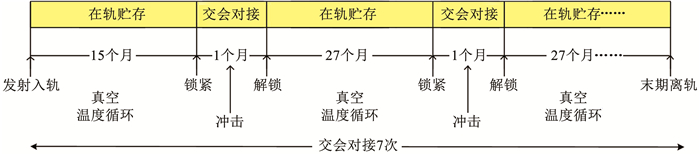
某型空间可重复锁紧装置在轨工况如图 5所示,计划入轨15个月后进行首次交会对接,交会对接期间装置锁紧并承受冲击载荷,航天器撤离分离后解锁,后续交会对接计划每隔27个月进行一次,共计7次。
|
图 5 某型号空间可重复锁紧装置在轨工况示意 Fig. 5 Schematic diagram of on-orbit working condition of a space reusable locking device |
模拟在轨实际冲击条件对试件进行承载试验,如图 6所示。

|
图 6 模拟交会对接承载试验 Fig. 6 Rendezvous and docking load simulation test |
1) 极端冲击突发失效建模。已知该型装置在轨承受交会对接冲击强度Aj~(3, 0.2562),采用承载力步进加载方式对装置的临界失效阈值进行摸底,得到装置承载临界值为Af=8 kN。
2) 累积冲击损伤建模。已知在轨交会对接冲击发生的时间和次数,以Yj表示试件发生第j次冲击的损伤值(性能退化量)。试验模拟在轨交会对接,取在轨冲击强度均值3 kN力对锁紧状态的装置进行受载模拟,卸载后测量解锁过程的阻力矩。
共计进行17次承载试验,对各次加载前后的阻力矩分别进行测试,将加载前后的阻力矩差值作为该次受载的损伤量,得到17组承载损伤值{Yj}={0.139 9, 0.176 3, 0.300 9, 0.443 5, 0.457 6, 0.494 9, 0.513 7, 0.522 7, 0.558 6, 1.124 1, 1.288 0, 1.306 3, 1.426 6, 1.526 7, 1.726 5, 1.980 0, 2.145 6},对数据进行正态性检验[23],检验结果为该组数据不拒绝正态性假设,并得到参数估计值
加速退化试验采用恒定应力加速试验方案。装置在轨温度为-5~5 ℃,综合考虑试验结果的区分度和试验效率,温度循环应力设定为-45~55 ℃,真空度6.65×10-3 Pa。共计进行13循环,每循环进行一次阻力矩测试,得到2台重复锁紧装置的加速退化曲线如图 7所示。

|
图 7 加速退化试验数据 Fig. 7 Accelerating degradation test data |
通过收集装置在设计、研制和试验阶段的多种信息源,结合开展的加速性能退化试验,综合进行基于贝叶斯方法的模型参数估计。可用于装置可靠性评估模型参数估计的信息包括:
1) 产品性能试验测试数据。装置研制过程中需进行性能测试,测试环境为真空常温环境,对测试所得的性能参数进行统计分析,得到μX的先验分布:
| $ \pi\left(\mu_X\right)=N\left(0.17, 1.15^2\right) $ | (17) |
2) 专家经验信息。针对参数q,由经验值取3~5区间的均匀分布,参数σX应用无信息先验分布,服从较大区间的均匀分布,有:
| $ \pi(q)=U(3, 5), \pi\left(\sigma_X\right)=U(0, 100) $ | (18) |
| $ A=(0.1 \Delta T)^q $ | (19) |
3) 相似产品历史性能退化数据。图 8所示为4台某型装置(相似产品)寿命试验中测试得到的性能退化数据。寿命试验条件为真空度6.65×10-3 Pa,温度范围-40~70℃。

|
图 8 相似产品历史性能退化数据 Fig. 8 Historical performance degradation data of similar products |
由式(9)可构建得到性能退化测试值的似然函数,该测试值由图 7加速退化试验数据和图 8相似产品性能退化数据组成,连同式(17)~(19)数据一并代入式(10),应用WinBUGS软件构建算例模型,采用软件中的MCMC(Markov Chain Monte Carlo)抽样方法进行参数估计[24],得到模型参数的均值、方差和区间估计值见表 1。
| 表 1 贝叶斯方法参数估计结果 Tab. 1 Results of parameter estimation by Bayesian method |
取贝叶斯后验均值作为各模型参数的估计值,得到重复锁紧装置的可靠度计算结果如图 9所示。
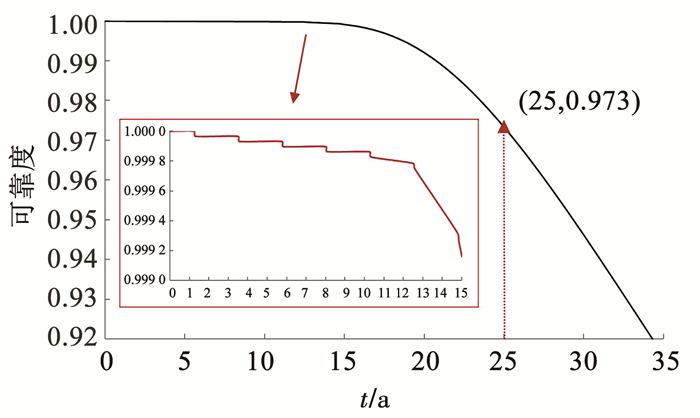
|
图 9 可靠度计算结果 Fig. 9 Reliability calculation results |
由图 9可知,该型号可重复锁紧装置在轨25 a内可靠度降低较慢,属于装置的稳定运行时期,在第25年时仍能以0.973的高可靠度运行。装置在轨期间承受的交会对接冲击除了会造成装置的累积损伤外,还会造成后续性能退化过程退化率的陡增。装置在第26年后可靠度开始呈线性下降趋势,进入寿命周期的后期。因此若需要在寿命末期以外对装置进行延寿,则需要加强对装置状态的监测并采取相应措施以预防故障的发生。
5 结论1) 考虑航天器交会对接冲击和空间环境下性能退化综合作用影响,从空间可重复锁紧装置的结构、功能、工作原理出发,分析在轨期间的主要故障模式,给出对应的可靠性特征量,具有较好的适用性和代表性。
2) 基于冲击与退化过程的相依竞争失效理论进行冲击作用下的性能退化过程建模,推导了空间可重复锁紧装置冲击-退化综合作用下的可靠性评估模型,可计算出装置可靠度随在轨时间的变化过程。
3) 通过承载模拟试验和加速退化试验建模求解装置可靠性模型,并融合装置研制、生产、测试过程中的多源信息进行模型参数估计,所得的可靠性评估结果符合工程实际,可为其他类似原理的不同类型航天器机构的可靠性评估提供参考。
| [1] |
叶田园, 庞贺伟, 周元子, 等. 航天器超静平台作动器发展及其关键技术综述[J]. 航天器环境工程, 2022, 39(1): 1. YE Tianyuan, PANG Hewei, ZHOU Yuanzi, et al. Overview of the development and key technologies of actuator for spacecraft ultra-quiet platform[J]. Space Craft Environment Engineering, 2022, 39(1): 1. DOI:10.12126/see.2022.01.001 |
| [2] |
周坤, 叶楠, 吴锦辉, 等. RV减速器高应力加速退化试验及可靠性分析[J]. 哈尔滨工业大学学报, 2022, 54(7): 37. ZHOU Kun, YE Nan, WU Jinhui, et al. High stress accelerated degradation test and reliability analysis of RV reducer[J]. Journal of Harbin Institute of Technology, 2022, 54(7): 37. DOI:10.11918/202112011 |
| [3] |
PANG Zhenan, SI Xiaosheng, HU Changhua, et al. Retracted: A review on modeling and analysis of accelerated degradation data for reliability assessment[J]. Microelectronics Reliability, 2020, 107: 113602-1. DOI:10.1016/j.microrel.2020.113602 |
| [4] |
王嘉, 张露予, 陶友瑞, 等. 基于时间和当前状态的退化与冲击模型[J]. 机械工程学报, 2019, 55(18): 180. WANG Jia, ZHANG Luyu, TAO Yourui, et al. Degradation and random shock model based on age and current state[J]. Journal of Mechanical Engineering, 2019, 55(18): 180. DOI:10.3901/JME.2019.18.180 |
| [5] |
孙富强, 李艳宏, 程圆圆. 考虑冲击韧性的退化-冲击相依竞争失效建模[J]. 北京航空航天大学学报, 2020, 46(12): 2195. SUN Fuqiang, LI Yanhong, CHENG Yuanyuan. Competing failure modeling for degradation-shock dependence systems with shock toughness[J]. Journal of Beijing University of Aeronautics and Astronautics, 2020, 46(12): 2195. DOI:10.13700/j.bh.1001-5965.2019.0628 |
| [6] |
李铭, 谢里阳, 张宇, 等. 齿轮的概率寿命预测与弯曲疲劳试验[J]. 机械工程学报, 2017, 53(18): 169. LI Ming, XIE Liyang, ZHANG Yu, et al. Probabilistic life prediction and bending fatigue test for gear[J]. Journal of Mechanical Engineering, 2017, 53(18): 169. DOI:10.3901/JME.2017.18.169 |
| [7] |
FROSTIG E, MOSHE K. Availability of inspected systems subject to shocks-a matrix algorithmic approach[J]. European Journal of Operational Research, 2009, 193(1): 168. DOI:10.1016/j.ejor.2007.10.052 |
| [8] |
LEHMANN A. Joint modeling of degradation and failure time data[J]. Journal of Statistical Planning and Inference, 2009, 139(5): 1693. DOI:10.1016/j.jspi.2008.05.027 |
| [9] |
HUYNH K T, BARROS A, BÉRENGUER C, et al. A periodic inspection and replacement policy for systems subject to competing failure modes due to degradation and traumatic events[J]. Reliability Engineering and System Safety, 2011, 96(4): 497. DOI:10.1016/j.ress.2010.12.018 |
| [10] |
WANG Yaping, PHAM H. Imperfect preventive maintenance policies for two-process cumulative damage model of degradation and random shocks[J]. International Journal of System Assurance Engineering and Management, 2011, 2(1): 66. DOI:10.1007/s13198-011-0055-8 |
| [11] |
TAO Yourui, ZHAO Jun, FENG Shizhe. A reliability assessment model for journal bearing based on natural degradation and random shocks[J]. Journal of Mechanical Science and Technology, 2020, 34(11): 4641. DOI:10.1007/s12206-020-1022-6 |
| [12] |
刘根, 王治华, 屈怀远, 等. 基于多变量优化的恒定应力加速退化试验设计[J]. 系统工程与电子技术, 2021, 43(1): 267. LIU Gen, WANG Zhihua, QU Huaiyuan, et al. Constant stress accelerated degradation test design based on multivariate optimization[J]. System Engineering and Electronics, 2021, 43(1): 267. DOI:10.3969/j.issn.1001-506X.2021.01.33 |
| [13] |
THOMAS E V, CASE H L, DOUGHTY D H, et al. Accelerated power degradation of Li-ion cells[J]. Journal of Power Source, 2003, 124(1): 254. DOI:10.1016/S0378-7753(03)00729-8 |
| [14] |
PAN Zhengqiang, BALAKRISHNAN N. Multiple-steps-stress accelerated degradation modeling based on Wiener and gamma processes[J]. Communications in Statistics-Simulation and Computation, 2010, 39(7): 1384. DOI:10.1080/03610918.2010.496060 |
| [15] |
潘正强, 周经伦, 彭宝华. 基于Wiener过程的多应力加速退化试验设计[J]. 系统工程理论与实践, 2009, 29(8): 64. PAN Zhengqiang, ZHOU Jinglun, PENG Baohua. Design of accelerated degradation tests with several stresses based on Wiener process[J]. System Engineering Theory & Practice, 2009, 29(8): 64. DOI:10.3321/j.issn:1000-6788.2009.08.008 |
| [16] |
王立志, 姜同敏, 李晓阳, 等. 融合加速试验及外场使用信息的寿命评估方法[J]. 北京航空航天大学学报, 2013, 39(7): 947. WANG Lizhi, JIANG Tongmin, LI Xiaoyang, et al. Lifetime evaluation method with integrated accelerated testing and field information[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(7): 947. DOI:10.13700/j.bh.1001-5965.2013.07.016 |
| [17] |
王华伟, 吴海桥. 基于信息融合的航空发动机剩余寿命预测[J]. 航空动力学报, 2012, 27(12): 2749. WANG Huawei, WU Haiqiao. Residual useful life prediction for aircraft engine based on information fusion[J]. Journal of Aerospace Power, 2012, 27(12): 2749. DOI:10.13224/j.cnki.jasp.2012.12.018 |
| [18] |
荣吉利, 宋乾强, 张涛. 一种预测航天火工装置可靠性的小样本方法[J]. 宇航学报, 2015, 36(3): 360. RONG Jili, SONG Qianqiang, ZHANG Tao. A small sample method for predicting reliability of space pyrotechnic devices[J]. Journal of Astronautics, 2015, 36(3): 360. DOI:10.3873/j.issn.1000-1328.2015.03.016 |
| [19] |
FAN Mengfei, ZENG Zhiguo, ZIO E, et al. Modeling dependent competing failure processes with degradation-shock dependence[J]. Reliability Engineering & System Safety, 2017, 165: 422. DOI:10.1016/j.ress.2017.05.004 |
| [20] |
COFFIN L F. Fatigue at high temperature-prediction and interpretation[M]. London: Proc. Inst. Mech. Eng., 1974: 109.
|
| [21] |
王浩伟, 周源, 滕飞, 等. 基于加速因子不变原则的加速退化试验优化设计[J]. 机械工程学报, 2018, 54(18): 212. WANG Haowei, ZHOU Yuan, TENG Fei, et al. Optimal design of accelerated degradation test based on acceleration factor constant principle[J]. Journal of Mechanical Engineering, 2018, 54(18): 212. DOI:10.3901/JME.2018.18.212 |
| [22] |
袁容. 基于性能退化分析的可靠性方法研究[D]. 成都: 电子科技大学, 2015 YUAN Rong. Research on reliability modeling and analysis methods based on the performance degradation[D]. Chengdu: University of Electronic Science and Technology of China, 2015 |
| [23] |
RAZALI N M, WAH Y B. Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests[J]. Journal of Statistical Modeling and Analytics, 2011, 2(1): 21. DOI:10.1515/bile-2015-0008 |
| [24] |
LUNN D J, THOMAS A, BEST N, et al. WinBUGS-A Bayesian modelling framework: Concepts, structure, and extensibility[J]. Statistics & Computing, 2000, 10(4): 325. DOI:10.1023/A:1008929526011 |
 2023, Vol. 55
2023, Vol. 55


