2. 航空制导武器航空科技重点实验室(中国空空导弹研究院), 河南 洛阳 471009
2. Aviation Key Laboratory of Science and Technology on Airborne Guided Weapons(China Airborne Missile Acodemy), Luoyang 471009, Henan, China
比例导引是应用最广泛的制导律形式,在接近速度为负的情况下,总是在控制导弹减少视线角速度的方向上运动,力图通过构建一个导弹-目标-命中点的碰撞三角形,实现对目标的毁伤。比例导引具有广泛的衍生形式,典型形式包括扩展比例导引、最优制导律和微分对策制导律。这些典型形式都包括一个比例导引部分或与视线角速度相关的部分,而由于考虑了目标的机动,导弹和目标的控制系统动态特性等,具有了不同的瞬时脱靶量组成形式。微分对策制导律是应对弹目追逃问题最为有效的形式,并不需要对目标的机动方式进行假设,且理论上可以提供设计指标下的导弹最优制导控制策略和目标最优逃逸策略,以及表征脱靶量或其他终端约束的鞍点解或对策解。文献[1]的研究结果表明,微分对策制导律具有一个保证较小脱靶量的捕获区域,且对目标信息的估计误差具有更强的鲁棒性。
先进的制导律,包括微分对策制导律通过对脱靶量的良好预测和制导增益的选取,实现良好的弹道特性,包括弹道的快速收敛、控制能量最优和弹道可成型等。但这些制导律的计算不可或缺的是对剩余飞行时间、目标加速度等信息的计算或估计。这些信息,特别是剩余飞行时间的准确程度会对期望的设计效果产生重要影响,如末制导尾端的控制量的大小,甚至符号,进而影响脱靶量。对于纯方位的量测情形,由于弹目距离未知,剩余飞行时间是不可观测的。纯方位量测可能是由于导弹加装的是被动导引头,或导引头受到干扰无法完成测距等现实原因导致的。
纯方位量测的情形下,改进弹目距离可观测性的方法是导弹通过机动打破导弹-目标-命中点的碰撞三角形,此时目标不再是位于视线上不可分辨的。文献[2]采用Cramer-Rao下界分析纯方位量测问题,发现在无机动的情况下,弹目距离是不可估计的,文献还对机动对估计精度的影响进行了分析。导弹通过机动提升了对目标的可观测性,但也破坏了碰撞三角形,从而带来了脱靶量,需要在可观测性和脱靶量之间进行折中,或者在特定的阶段或条件下实施机动。文献[3]在扩展比例导引的基础上,通过引入一个与弹目距离和视线角成比例的修正项,在弹目距离较远的情况下,通过驱动视线角速度的旋转,从而提高对弹目距离的可观测性,该修正项随着弹目距离减少所产生的修正效果会逐渐减小,从而保证最终的脱靶量。文献[4]通过量测方程的分析,给出了弹目距离可观测的充分条件,并基于Fisher信息矩阵和Cramer-Rao下界,提出了一种最大化弹目距离可观测性的近似性能衡量指标。
本文利用Kalman滤波器估计均方误差阵反应系统可观测性的特性,并与微分对策制导律的捕获区域的条件相结合,提出一种纯方位量测条件下可观测性增强的微分对策制导律。在捕获区域内,通过适当的机动,提升弹目距离等的可观测性,从而获取改进精度的目标相关信息,进一步提升制导性能。
1 问题描述及建模平面弹目相对运动关系如图 1所示。图中: q为视线角,r为弹目相对距离,a、v和γ分别为加速度、速度和航向角,下标m、t分别为导弹和目标的状态。

|
图 1 平面弹目相对运动关系 Fig. 1 Planar engagement geometry |
建立平面弹目相对运动的微分方程,如下所示:
| $ \left\{\begin{array}{l} \dot{r}=v_r=v_t \cos \left(\gamma_{\mathrm{t}}-q\right)-v_{\mathrm{m}} \cos \left(\gamma_{\mathrm{m}}-q\right) \\ \dot{q}=v_q / r=\left(v_t \sin \left(\gamma_{\mathrm{t}}-q\right)-v_{\mathrm{m}} \sin \left(\gamma_{\mathrm{m}}-q\right)\right) / r \\ \dot{a}_{\mathrm{m}}=\left(u_{\mathrm{mc}}-a_{\mathrm{m}}\right) / \tau_{\mathrm{m}} \\ \dot{\gamma}_{\mathrm{m}}=a_{\mathrm{m}} / v_{\mathrm{m}} \\ \dot{a}_{\mathrm{t}}=\left(u_{\mathrm{tc}}-a_{\mathrm{t}}\right) / \tau_{\mathrm{t}} \\ \dot{\gamma}_{\mathrm{t}}=a_{\mathrm{t}} / v_{\mathrm{t}} \end{array}\right. $ | (1) |
式中: 假设导弹和目标具有一阶控制系统动态特性,τm、τt分别为相应的时间常数, vr、vq分别为沿视线方向和视线法向上的弹目相对运动速度,umc、utc分别为导弹和目标的控制指令。
2 微分对策制导及其对策空间近年来,由于微分对策制导律对目标机动形式及加速度估计误差鲁棒性更强在机动目标拦截方面得到了较为深入的研究[5-13],包括多对象和多对象对抗的情形[5-6, 8-9, 12],对策双方分别追求性能指标的最大化和最小化。考虑导弹和目标的控制是有界的情况,所推导的微分对策制导律称为范数型微分对策制导律,包括DGL/0、DGL/1和DGL/S等多种典型形式[10-13]。范数型微分对策制导律以零控脱靶量z(t)作为性能指标,即J=|z(t)|,z(t)为对策双方t时刻起不施加任何控制,并以该瞬时参数飞行至命中时,所产生的脱靶量。范数型微分对策制导律的对策空间由飞行时间和零控脱靶量构建,包括捕获区和逃逸区两个部分。通过对这两个区域内制导策略的特性研究,并加以利用,可以改进纯方位测量情况下的可观测性。
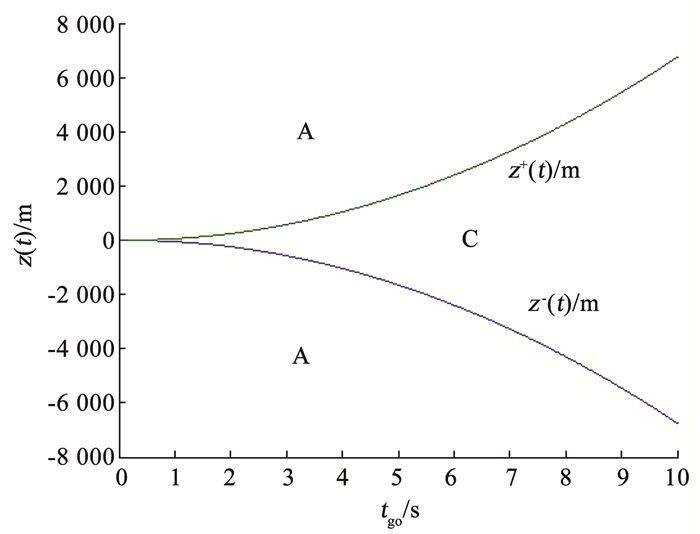
对于导弹和目标具有一阶控制系统动态特性的情况,相应的范数型微分对策制导律为DGL/1,其对策空间如图 2所示。对策空间由捕获区(C区)和逃逸区(A区)组成。在C区内,制导策略是任意的,不限于具体的形式,可以实现近零的脱靶量,而在A区内,最优制导策略为:
| $ \begin{aligned} & u_{\mathrm{mc}}^*(t)=a_{\mathrm{m}}^{\max } \cdot \operatorname{sign}(z(t)) \\ & u_{\mathrm{tc}}^*(t)=a_{\mathrm{t}}^{\max } \cdot \operatorname{sign}(z(t)) \end{aligned} $ | (2) |
|
图 2 对策空间 Fig. 2 Game space |
式中: umc*(t)、utc*(t)分别为导弹和目标的最优控制策略,相应的最大加速度为ammax和atmax,z(t)为零控脱靶量,表示导弹和目标在t时刻起不再施加任何控制,并以该时刻的参数飞行至拦截过程结束时的脱靶量。
在初始条件位于A区,目标采用式(2)所示的最优制导策略的情况下,导弹是无法完成目标的零脱靶量拦截的。文献[10]通过对策空间的分析给出了对策值为零的条件为
考虑导弹和目标具有一阶控制系统响应特性,z(t)可表示为
| $ \begin{gathered} z(t)=v_{\mathrm{c}} \dot{q} t_{\mathrm{go}}^2+a_{\mathrm{t}} \cos \left(\gamma_{\mathrm{t}}-q\right) \tau_{\mathrm{t}}^2 {\mathit{\Psi}}\left(t_{\mathrm{g}_0} / \tau_{\mathrm{t}}\right) \\ a_{\mathrm{m}} \cos \left(\gamma_{\mathrm{m}}-q\right) \tau_{\mathrm{m}}^2 {\mathit{\Psi}}\left(t_{\mathrm{go}} / \tau_{\mathrm{m}}\right) \end{gathered} $ | (13) |
式中:
假设末制导段视线角和对策双方的航向角不大,对式(3)两边关于时间t进行求导,并带入式(2),可以得到:
| $ \frac{\mathrm{d} z(t)}{\mathrm{d} t}={\mathit{\Gamma}} \cdot \operatorname{sign}(z(t)) $ | (4) |
其中
| $ \begin{array}{l} \mathit{\Gamma } = a_{\rm{t}}^{\max }\cos \left( {{\gamma _{{\rm{t}}0}} - {q_0}} \right){\tau _{\rm{t}}}\mathit{\Psi }\left( {{t_{{\rm{g}}0}}/{\tau _{\rm{t}}}} \right)\\ \;\;\;\;\; - a_{\rm{m}}^{\max }\cos \left( {{\gamma _{{\rm{m}}0}} - {q_0}} \right){\tau _{\rm{m}}}\mathit{\Psi }\left( {{t_{{\rm{go}}}}/{\tau _{\rm{m}}}} \right) \end{array} $ |
进一步对式(4)两边进行积分可以得到:
| $ \begin{aligned} z^{+}(t)= & a_{\mathrm{t}}^{\max } \cos \left(\gamma_{\mathrm{t} 0}-q_0\right) \tau_{\mathrm{t}}^2 \varphi\left(t_{\mathrm{go}} / \tau_{\mathrm{t}}\right)- \\ & a_{\mathrm{m}}^{\max } \cos \left(\gamma_{\mathrm{m} 0}-q_0\right) \tau_{\mathrm{m}}^2 \varphi\left(t_{\mathrm{go}} / \tau_{\mathrm{m}}\right) \end{aligned} $ | (5) |
式中: φ(α)=-exp(-α)+0.5α2-α+1。考虑式(4)中的符号函数,存在z-(t)=-z+(t)。如图 2所示,z+(t)和z-(t)构成了C区的边界,导弹和目标构成的对策双方关于该边界是互斥的。
3 估计器的设计弹上导引头所量测的都是表征弹目运动关系的相对信息,需要进行估计器的设计,从而提取闭合制导律计算所需要的参量,如剩余飞行时间、目标加速度等。利用弹上导航系统,导弹可以获取自身的飞行速度vm、加速度am和航向角γm等,这些量部分是可以直接量测的,部分是可以计算得出的,并不需要估计。
定义估计器的状态变量x为
| $ \boldsymbol{x}=\left[\begin{array}{llllll} r & q & \gamma_{\mathrm{t}} & a_{\mathrm{t}} & u_{\text {tc }} & v_{\mathrm{t}} \end{array}\right]^{\mathrm{T}} $ | (6) |
假设目标以最大机动能力作一个常值机动,开始时间在整个飞行过程中随机。采用功率波密度为(atmax)2/tf的随机噪声驱动的积分器来构建成型滤波器,从而建模目标机动命令。
基于定义的状态变量x,建立估计器的系统模型如下:
| $ \left\{\begin{array}{l} \dot{r}=v_{\mathrm{t}} \cos \left(\gamma_{\mathrm{t}}-q\right)-v_{\mathrm{m}} \cos \left(\gamma_{\mathrm{m}}-q\right) \\ \dot{q}=\left(v_{\mathrm{t}} \sin \left(\gamma_{\mathrm{t}}-q\right)-v_{\mathrm{m}} \sin \left(\gamma_{\mathrm{m}}-q\right)\right) / r \\ \dot{\gamma}_{\mathrm{t}}=a_{\mathrm{t}} / v_{\mathrm{t}} \\ \dot{a}_{\mathrm{t}}=\left(u_{\mathrm{tc}}-a_{\mathrm{t}}\right) / \tau_{\mathrm{t}} \\ \dot{u}_{\mathrm{tc}}=w \\ \dot{v}_{\mathrm{t}}=0 \end{array}\right. $ | (7) |
式中: 假设末制导段目标速度变化不大,采用近似常值建模,w为功率波密度为(atmax)2/tf的白噪声。
对于纯方位的量测情形,量测方程为
| $ y=\left[\begin{array}{llllll} 0 & 1 & 0 & 0 & 0 & 0 \end{array}\right] \cdot \boldsymbol{x}=\boldsymbol{H} \cdot \boldsymbol{x} $ | (8) |
由式(7)、(8)可以发现,该估计器是系统方程非线性,量测方程线性的非线性系统,本文采用扩展卡尔曼滤波(EKF)方法进行状态变量的估计。
在基于纯方位量测的制导问题当中,相对距离、相对速度和目标加速度等信息滤波效果的好坏除了与滤波器性能有关,在很大程度上还取决于系统可观测性的强弱。在纯方位测量的条件下,系统可观测性的强弱与飞行弹道紧密相关,因此制导律将直接影响弹上跟踪滤波器的估计效果。比例导引类的衍生制导律都会控制导弹向着减少视线角速度的方向上飞行,而趋于常值的视线角会造成导弹对目标的可观测性变差,进而目标信息的估计精度也会越来越差。估计性能越差,制导性能也会越差。制导方法和可观测性之间存在着矛盾。为了解决这一矛盾,可以进一步利用滤波器的输出参量的特性。文献[14]揭示了归一化后的滤波器估计均方误差阵Pk和滤波系统可观测性之间的关系,与Pk阵最大的特征值对应的状态变量的可观测性是最弱的,相反可观测性则是最强的。
对于EKF方法,Pk阵采用下式进行计算:
| $ \begin{gathered} \boldsymbol{P}_k=\left(\boldsymbol{I}-\boldsymbol{K}_k \boldsymbol{H}\right) \boldsymbol{P}_{k \mid k-1} \\ \boldsymbol{P}_{k \mid k-1}=\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \boldsymbol{P}_{k-1} \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\mathrm{T}}+\boldsymbol{Q}_{k-1} \end{gathered} $ | (9) |
式中: Pk|k-1为一步预测误差方差矩阵,Kk为滤波增益矩阵,Pk-1为k-1时刻的估计均方误差误差矩阵,Qk-1为k-1时刻的系统噪声矩阵,Φ为状态转移矩阵,采用系统(7)的雅克比矩阵进行计算:
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}=\exp (\boldsymbol{F} \cdot T) $ | (10) |
式中: T为滤波周期,与量测信息的输出周期保持一致,雅克比矩阵F为
| $ \boldsymbol{F}=\left[\begin{array}{cccccc} 0 & v_q & -v_{\mathrm{t}} \sin \left(\gamma_{\mathrm{t}}-q\right) & 0 & 0 & \cos \left(\gamma_{\mathrm{t}}-q\right) \\ -\frac{v_q}{r^2} & -\frac{v_r}{r} & \frac{v_{\mathrm{t}} \cos \left(\gamma_{\mathrm{t}}-q\right)}{r} & 0 & 0 & \frac{\sin \left(\gamma_{\mathrm{t}}-q\right)}{r} \\ 0 & 0 & 0 & 1 / v_{\mathrm{t}} & 0 & -a_{\mathrm{t}} / v_{\mathrm{t}}^2 \\ 0 & 0 & 0 & -1 / \tau_{\mathrm{t}} & 1 / \tau_{\mathrm{t}} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right] $ | (11) |
由于系统是非线性的,导弹的控制量umc改变了航向角γm,进而会造成vr和vq的变化,同时F阵发生改变,会进一步通过式(9)、(10)对Pk阵的特征值产生影响。不同的umc对F阵的改变不同,进而对Pk阵的特征值产生的影响也不同。Pk阵的特征值和umc之间的对应关系中存在一个对应最小特征值的umc。采用该umc进行控制来改进滤波系统的可观测性是最为有利的。
导弹的最大加速度为ammax,在[-ammax, ammax]范围内选取对应Pk阵最小特征值的控制量。在[-ammax, ammax]范围的控制量并不是都适用于导弹的控制,可能控制导弹向着脱靶的方向上飞行,产生对导弹-目标-碰撞点所构成的碰撞关系的严重破坏。而在微分对策对策的追击-逃逸框架内,可确定何时在增强可观测性的方向上控制,何时在减少脱靶量的方向上控制。
4 增强可观测性的微分对策制导律为闭合导弹制导律(2)的计算,需要采用所估计的目标的加速度
| $ u_{\mathrm{mc}}^*(t)=a_{\mathrm{m}}^{\max } \cdot \operatorname{sign}(\hat{z}(t)) $ | (12) |
这种基于确定性等价原理的制导律和滤波器独立运行方式并不是最优的。本文的增强可观测性的微分对策制导方法则将滤波器P阵特征值表征的可观测性和制导控制指令的选取结合起来。首先判断初始弹目相对运动关系所表征的脱靶量是位于对策空间的C区还是A区,如图 2所示,对于不同的分布,采取不同的制导策略。当位于C区时,则可以从增强可观测性的角度选取控制指令。所选取的控制指令会影响导弹-目标-碰撞点的碰撞几何关系,可能造成零控脱靶量的增加。根据对策空间的分析结果,零控脱靶量的门限为z+(t)和z-(t),这也决定了控制指令的选取范围,在零控脱靶量接近门限时,则沿着门限进行控制,保证制导性能。
在每一个滤波时间间隔内,首先采用式(3)和式(5)计算
在零控脱靶量位于C区的情况下,考虑控制系统延迟和外部其他不确定性因素的影响,对z+(t)和z-(t)乘以一个系数κz后作为边界值,用于
图 3给出了增强可观测性的微分对策制导律给出了的执行流程图。

|
图 3 制导律执行流程图 Fig. 3 Flow chart of guidance law execution |
仿真针对所设计的可观测性增强的微分对策制导律(DGL/E) 与典型范数型微分对策制导律DGL/1进行非线性仿真对比。主要针对一类迎面末端拦截情形进行了仿真研究,仿真参数见表 1。假设目标机动为具有一次随机时间切换的阶跃机动,其中r0为弹目初始距离,σq为视线角的量测噪声。
| 表 1 仿真参数 Tab. 1 Simulation parameters |
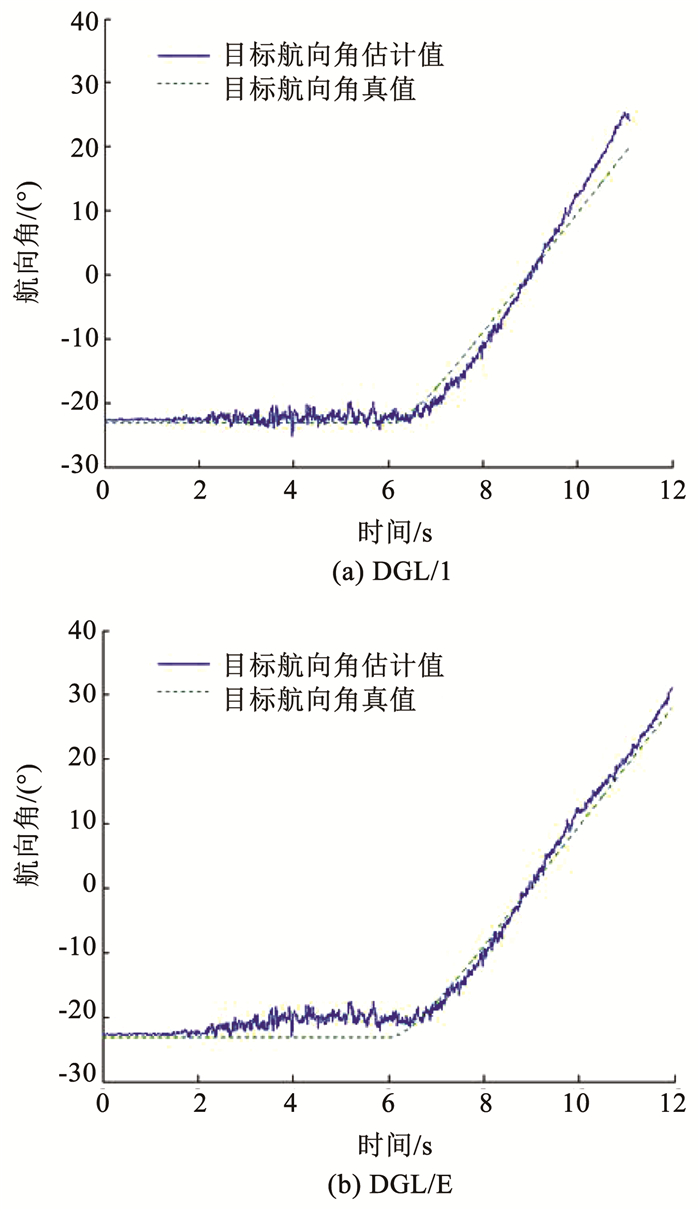
仿真中设定导弹控制指令的取值范围为umc=amaxm·[1.00 0.75 0.50 0 -0.50 -0.75 -1.00],典型仿真曲线如图 4~8所示。图 4为制导律DGL/1和DGL/E的飞行弹道曲线,DGL/1的弹道曲线较为平直,导弹始终在减少视线角速度的方向上飞行,而DGL/E的弹道则较为弯曲。DGL/E通过制导控制指令的适当取值,如图 5所示,调整了导弹的飞行轨迹,在接近目标的过程中,避免了视线角速度的过快收敛,如图 6所示。由于视线角速度的存在,视线角持续变化,增强了对目标的可观测性,从而改善了滤波器的性能,在末制导尾端获得了较好的目标加速度及其航向角的估计,如图 7、8所示,而DGL/1随着视线角速度的收敛,尾端的估计性能则较差,进而会带来较大的脱靶量。图 9为零控脱靶量的变化曲线,导弹采用制导律DGL/E将零控脱靶量保持在边界值附近,在保证脱靶量的同时,增强对目标的可观测性,达到了设计目的。

|
图 4 随机目标机动下的飞行弹道 Fig. 4 Flight trajectory for random target maneuver |

|
图 5 导弹控制指令 Fig. 5 Control commands of missile |

|
图 6 视线角速度 Fig. 6 Line of sight rate |

|
图 7 目标加速度 Fig. 7 Target accelerations |
|
图 8 目标航向角 Fig. 8 Flight path angles of target |

|
图 9 零控脱靶量 Fig. 9 Zero-effort miss distance |
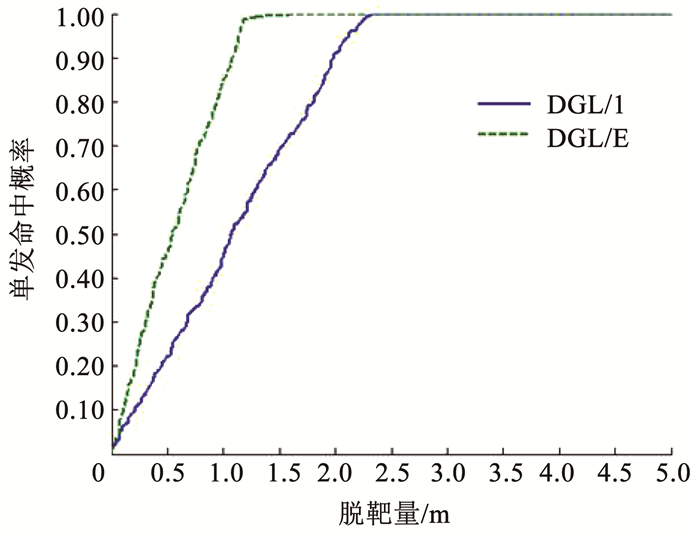
仿真基于Monte Carlo实验法,并采用单发命中概率[11, 15](Single shot kill probability, SSKP)作为性能的衡量指标,对DGL/1和DGL/E两种制导律的拦截性能进行了比较。两种制导律取相同的目标机动开始时间和视线角噪声随机数产生器种子,仿真次数为500次。如图 10所示,对于给定的SSKP,例如0.95,DGL/E所要求的弹头杀伤半径小于DGL/1,具有较好的目标拦截性能。
|
图 10 随机目标机动下的单发命中概率 Fig. 10 single shot kill probability for random target maneuver |
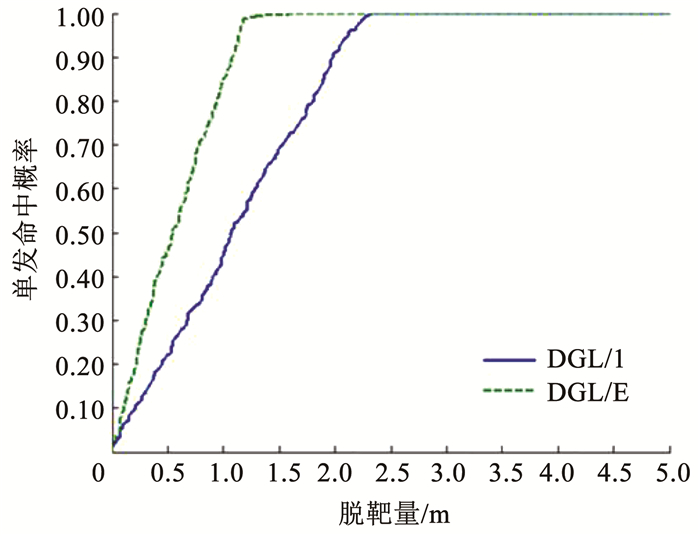
图 11、12进一步给出了目标采用式(2)所示的最优机动情况下的飞行弹道和SSKP。从图中可以看出,与随机目标机动的情况类似,在制导律DGL/E控制下,导弹向着增强可观测性的方向上飞行,且能够以更高的概率获得较小的脱靶量。

|
图 11 最优目标机动下的飞行弹道 Fig. 11 Flight trajectory for optimal target maneuver |
|
图 12 最优目标机动下的单发命中概率 Fig. 12 Single shot kill probability for optimal target maneuver |
1) 对于纯方位量测问题,提出了一种增强可观测性的微分对策制导方法。利用滤波器估计均方误差矩阵和系统可观测性的关系,在线对可观测性进行评估,在保证制导性能的前提下,选取适当的导弹控制指令。
2) 该设计方法超出了确定性等价原理的框架,将滤波和制导集成设计,在保证脱靶量的同时,通过主动改变飞行弹道来增强可观测性的方式促进滤波器的收敛,从而实现既提高可观测性,又命中目标的目的。
3) 基于Monte Carlo法的非线性系统仿真表明,DGL/E相比于DGL/1具有较好的目标信息估计性能和较高的SSKP。
| [1] |
SHINAR J, SHIMA T. Nonorthodox guidance law development approach forintercepting maneuvering targets[J]. AIAA Journal of Guidance, Control, and Dynamics, 2002, 25(4): 658. DOI:10.2514/2.4960 |
| [2] |
OSHMAN Y, DAVIDSON P. Optimization of observer trajectories for bearings-only targetlocalization[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(3): 892. DOI:10.1109/7.784059 |
| [3] |
SONG T L, UM T Y. Practical guidance for homing missiles with bearings-onlymeasurements[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(1): 434. DOI:10.1109/7.481284 |
| [4] |
ANJALY P, ASHWINI RATNOO A. Observability enhancement of maneuvering target with bearings-only information[J]. Journal of Guidance, Control, and Dynamics, 2018, 41(1): 184. DOI:10.2514/1.g003003 |
| [5] |
LI Liang, FANG Deng. A differential game for cooperative target defense with two slow defenders[J]. Science China(Information Sciences), 2020, 63(12): 265. DOI:10.1007/s11432-019-9895-4 |
| [6] |
GAO Qiuyue, WU Huici, ZHANG Yunfei, et al. Differential game-based analysis of multi-attacker multi-defender interaction[J]. Science China(Information Sciences), 2021, 64: 222302-1. DOI:10.1007/s11432-020-3228-8 |
| [7] |
LIANG Haizhao, WANG Jianying, WANG Yonghai, et al. Optimal guidance against active defense ballistic missiles via differential game strategies[J]. Chinese Journal of Aeronautics, 2020, 33(3): 978. DOI:10.1016/j.cja.2019.12.009 |
| [8] |
SUN Qilong, QI Naiming, XIAO Longxu, et al. Differential game strategy in three-player evasion and pursuit scenarios[J]. Journal of Systems Engineering and Electronics, 2018, 29(2): 352. DOI:10.21629/JSEE.2018.02.16 |
| [9] |
LIU Yanfang, QI Naiming, TANG Zhiwei. Linear quadratic differential game strategies with two-pursuit versus single-evader[J]. Chinese Journal of Aeronautics, 2012, 25: 896. DOI:10.1016/S1000-9361(11)60460-3 |
| [10] |
花文华, 孟庆龄, 张拥军. 寻的导弹范数型微分对策制导律[J]. 高技术通讯, 2013, 23(4): 392. HUA Wenhua, MENG Qingling, ZHANG Yongjun. Norm differential game guidance law for homing missiles[J]. Chinese High Technology Letters, 2013, 23(4): 392. DOI:10.3772/j.issn.1002-0470.2013.04.010 |
| [11] |
花文华, 孟庆龄, 张金鹏, 等. 有界双重控制导弹微分对策制导律[J]. 北京航空航天大学学报, 2016, 42(9): 1851. HUA Wenhua, MENG Qingling, ZHANG Jinpeng, et al. Differential game guidance law for dual and bounded controlled missiles[J]. Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(9): 1851. DOI:10.13700/j.bh.1001-5965.2015.0574 |
| [12] |
花文华, 张拥军, 张金鹏, 等. 双导弹拦截角度协同的微分对策制导律[J]. 中国惯性技术学报, 2016, 24(6): 838. HUA Wenhua, ZHANG Yongjun, ZHANG Jinpeng, et al. Differential game guidance law for double missiles with cooperative intercept angle[J]. Journal of Chinese Inertial Technology, 2016, 24(6): 838. DOI:10.13695/j.cnki.12-1222/o3.2016.06.025 |
| [13] |
BALHANCE N, WEISS M, SHIMA T. Cooperative guidance law for intrasalvo tracking[J]. Journal of Guidance, Control, and Dynamics, 2017, 40(6): 1441. DOI:10.2514/1.g002250 |
| [14] |
HAM F M, BROWN R G. Observability, eigenvalues, and Kalman filtering[J]. IEEE Transactions on Aerospace and Electronic Systems, 1983, AES-19(2): 269. DOI:10.1109/taes.1983.309446 |
| [15] |
SHINAR J, TURETSKY V, OSHMAN Y. Integrated estimation/guidance design approach for improved homing against randomly maneuvering targets[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(1): 154. DOI:10.2514/1.22916 |
 2023, Vol. 55
2023, Vol. 55


