2. 四川省水利水电勘测设计研究院有限公司, 成都 610031;
3. 国际小水电中心, 杭州 310002;
4. 水利部产品质量标准研究所, 杭州 310002;
5. 中国三峡建工(集团)有限公司, 成都 610041
2. Sichuan Water Resources and Hydroelectric Investigation & Design Institute Co., Ltd., Chengdu 610031, China;
3. International Center on Small Hydro Power, Hangzhou 310002, China;
4. Standard & Quality Control Research Institute, Ministry of Water Resources, Hangzhou 310002, China;
5. China Three Gorges Construction Engineering Corporation, Chengdu 610041, China
在输水管道系统中,阀门关闭、泵停机等情况均可能引起负压,当压强降低至水体汽化压强时,管道中会出现蒸汽空穴,其发生、增长、聚集、溃灭过程被称作水柱分离弥合水锤现象。蒸汽空穴溃灭引起水柱弥合极易产生异常高压,而导致管路振动、变形,甚至爆管事故[1]。因此,为保障输水管道系统的安全运行,准确地预测和模拟系统中可能发生的常规水锤及水柱分离弥合水锤现象至关重要。
国内、外学者针对输水管道内水柱分离弥合水锤现象进行了大量数值模拟研究。Streeter[2]首次提出离散蒸汽空穴模型(Discrete vapor cavity model, DVCM),并用于预测水柱分离过程中瞬变压力,此后许多学者[3-5]对该模型进行了研究和讨论,指出:该模型当网格数增加时,由于多个空穴溃灭相互作用而导致不真实的压力峰值。Brown[4]首次考虑滞留气体对水柱分离的影响,提出了离散气体空穴模型(Discrete gas cavity model, DGCM)。随后文献[3, 5]对DGCM模型进行了改进,假定小气泡和水柱分离的热力学过程分别为等温过程和趋于绝热过程;研究指出,对于自由气体体积分数为小于10-7或者更少时,可准确模拟水柱分离弥合水锤现象。Zhao等[6]指出在相同计算精度下,二阶Godunov格式比特征线法(Method of characteristics, MOC)方法效率更高,且在Cr < 1.0时更稳定。Zhou等[7]通过引入压强衰减系数,导出有限体积法(Finite volume method, FVM)的DGCM模型,成功消除了MOC-DGCM模型中出现的虚假数值振荡。然而,现有的水柱分离弥合水锤模型常采用恒定摩阻假定,低估了水锤压力的衰减,后续空穴的形成、弥合水锤压力的计算结果与实测值存在较大误差。
本文针对水柱分离弥合水锤现象,基于有限体积法二阶Godunov格式,建立了考虑动态摩阻的离散气体空穴模型(DGCM)。已有的水柱分离弥合水锤数学模型主要采用特征线法进行求解,并且很少考虑动态摩阻的影响。此外,与Zielke和Vardy and Brown原始加权类动态摩阻模型相比,本文采用Trikha-vardy-brown (TVB)[8]简化形式加权类动态摩阻模型,既能准确描述动态摩阻的影响,又能大大提高计算效率。本文将所建二阶Godunov-DGCM TVB模型的模拟结果与实验数据以及已有的稳态摩阻模型的计算结果进行比较,并对网格数、压力修正系数等参数敏感性进行分析。
1 数学模型及其求解 1.1 基本假定与MOC-DGCM模型一样,本文FVM-DGCM模型需要作相关基本假定[3]:小气泡的热力学过程为等温过程;两个气穴之间充满水体,波速保持恒定;在气体空穴处应用局部连续性方程来满足液体质量守恒。此外,为实现二阶Godunov-DGCM TVB还需做出如下假设[7, 9-10]:
1) 自由气体集中在控制体中心,称之为离散气体空穴,如图 1所示。

|
图 1 自由气体分布示意 Fig. 1 Schematic diagram of free gas distribution |
2) 为计算空穴体积,将每个控制单元平分为两个相等的计算单元。这样处理原因为:有限体积法中每个控制体内压力、流量处处相等,这与特征线法采用节点的计算方法是不同的;为计算气体空穴体积变化,需要将每个控制单元平分为两个相等的小计算单元,两个小计算单元的流量通过上、下游控制体计算得到,进而求出中间气体空穴体积变化。
3) 两个相同计算单元内的压强和流量均由FVM计算。
4) 气体空穴体积变化受相邻等分体内流量变化控制。
根据上述假设,管道内会出现纯水锤、水柱分离弥合水锤两种瞬变流状态。因此,描述管道内空穴瞬变流的数学模型包括:纯水体及空穴两部分的控制方程。
1.2 基本方程 1.2.1 水锤模型考虑动态摩阻的水锤连续方程和动量方程可以写成以下黎曼问题的形式:
| $ \frac{\partial \boldsymbol{U}}{\partial t}+\frac{\partial \boldsymbol{F}}{\partial x}=\boldsymbol{S} $ | (1) |
| $ \mathit{\boldsymbol{F}}{\rm{ = }}\mathit{\boldsymbol{A U}} $ | (2) |
其中:
在有限体积法中,对于任意一个计算单元Ii,其中心节点为i,边界界面为i-1/2和i+1/2。变量(H、V)定义在计算单元中心节点,并为计算单元的平均值,计算单元Ii的数值通量将在界面i-1/2和i+1/2处计算。
| $ \boldsymbol{U}_i^{n+1}=\boldsymbol{U}_i^n-\frac{\Delta t}{\Delta x}\left(\boldsymbol{F}_{i+1 / 2}-\boldsymbol{F}_{i-1 / 2}\right)+\frac{\Delta t}{\Delta x} \int_{i-1 / 2}^{i+1 / 2} \boldsymbol{S} \mathrm{d} x $ | (3) |
式中: Δx为计算单元长度, Δt为计算时间步长, 上标n表示t时刻,即计算的当前时步(已知), 上标n+1表示t+Δt时刻,即计算的下一时步(待求), U为在下一时步n+1的求解涉及计算单元界面处的数值通量并预估源项, Fi-1/2为i-1/2界面的离散通量,Fi+1/2为i+1/2界面的离散通量。
1.2.2 离散气体空穴模型采用理想气体方程描述气穴变化(当气体空隙率为0时,为纯水锤情况):
| $ M_{\mathrm{g}} R_{\mathrm{g}} T=p_{\mathrm{g}}^* \alpha \forall=p_0^* \alpha_0 \forall $ | (4) |
式中:Mg为气体质量,Rg为气体常数,T为绝对温度,∀为水气两相总体积,α、α0分别为气体在绝对压强pg*和参考压强p0*下气体空隙率,α=∀g/∀,∀g为气体体积。
气体空穴绝对压强pg*为
| $ p_{\mathrm{g}}^*=\rho g\left(H-z-H_v\right) $ | (5) |
式中:ρ为水体密度,z为管道中心线高程,Hυ为水体绝对汽化压力水头。
气体空穴体积的连续性方程如下:
| $ \frac{\mathrm{d} \forall_{\mathrm{g}}}{\mathrm{d} t}=Q-Q_u $ | (6) |
| $ H_{g(j)}^{n+1}=\frac{H_{u j}^{n+1}+H_j^{n+1}}{2} $ | (7) |
| $ \forall_{g(j)}^{n+1}=\frac{p_0^* \alpha_0 \forall}{\rho g\left(H_{g(j)}^{n+1}-z-H_v\right)} $ | (8) |
式中:Qu为计算步时内平均流入截面的流量,Q为计算步时内平均流出截面的流量,Hujn+1、Hjn+1为第j个控制单元空穴上游侧和下游侧在计算时刻的测压管水头,Hg(j)n+1为第j个控制单元平均测压管水头,z为计算节点高程。
1.2.3 简化加权类动态摩阻模型采用权函数来描述瞬变过程中的动态摩阻,可表示为
| $ J_U=\frac{4}{\rho g D} \tau_w=\frac{16 v}{g D^2} \int_0^t W(t-u) \frac{\partial V}{\partial t}(u) \mathrm{d} u $ | (9) |
式中:D为管道直径,τw为壁面剪切应力,v为运动黏度系数,u为在0~t之间积分的时间变量,W为关于量纲一的时间的函数。权函数是历史速度和历史加速度的函数,代表着历史速度和历史加速度对当前时刻瞬时摩阻的影响程度。在Trikha提出的简化权函数的基础上,文献[8]提出了一种更准确的壁面剪切应力方法,即Trikha-Vardy-Brown方法,动态剪切应力τu可表示为
| $ \begin{aligned} \tau_u(t+\Delta t) \approx & \frac{2 \rho v}{R} \sum\limits_{i=1}^N\left[Y_{a i}(t) \mathrm{e}^{-\left(n_i v/ R^2\right) \Delta t}+\right. \\ & \left.\frac{m_i R^2}{n_i v \Delta t}\left(1-\mathrm{e}^{-\left(n_i v / R^2\right) \Delta t}\right)(V(t+\Delta t)-V(t))\right] \end{aligned} $ | (10) |
式中:R为管道半径,Yai为历史速度对当前时刻壁面剪切应力的影响,mi、ni为系数,Vardy等[8]确定系数取值如下:[ni, i=1, …, 9]=[26.374 4; 102.0; 102.5; 103.0; 104.0; 105.0; 106.0; 107.0; 108.0]和[mi, i= 1, …, 9]=[1.000 0;2.183 0;2.714 0;7.545 5;39.006 6; 106.807 5;359.084 6;1 107.929 5;3 540.683 0]。
1.3 有限体积法Godunov求解格式 1.3.1 通量计算在Godunov方法中[6, 11],数值通量可通过计算单元Ii各个界面处的局部黎曼问题进行求解[12]。对于内部计算单元Ii,界面处i+1/2的通量为
| $ \begin{aligned} \boldsymbol{F}_{i+1 / 2}= & \boldsymbol{A}_{i+1 / 2} \boldsymbol{U}_{i+1 / 2}= \\ & \frac{1}{2} \boldsymbol{A}_{i+1 / 2}\left\{\left(\begin{array}{cc} 1 & a / g \\ g / a & 1 \end{array}\right) \boldsymbol{U}_{\mathrm{L}}^n-\left(\begin{array}{cc} -1 & a / g \\ g / a & -1 \end{array}\right) \boldsymbol{U}_{\mathrm{R}}^n\right\} \end{aligned} $ | (11) |
式中:ULn为单元体i在边界i+1/2左侧的平均值,URn为单元体i在边界i+1/2右侧的平均值。
1.3.2 二阶格式用MUSCL-Hancock[3]法进行线性重构得到二阶Godunov格式,步骤如下:
1) 数据重构。为避免虚假震荡,引入斜率限制器MINMOD函数:
| $ \operatorname{MINMOD}\left(\sigma_i^n, \sigma_{i-1}^n\right)= \\ \begin{cases}\sigma_i^n, & \left|\sigma_i^n\right| <\left|\sigma_{i-1}^n\right|, \sigma_i^n \sigma_{i-1}^n>0 \\ \sigma_{i-1}^n, & \left|\sigma_i^n\right|>\left|\sigma_{i-1}^n\right|, \sigma_i^n \sigma_{i-1}^n>0 \\ 0, & \sigma_i^n \sigma_{i-1}^n \leqslant 0\end{cases} $ | (12) |
式中,
| $ \boldsymbol{U}_i^{\mathrm{L}}=\boldsymbol{U}_i^n-0.5 \Delta x \operatorname{MINMOD}\left(\sigma_j^n, \sigma_{j-1}^n\right) $ | (13) |
| $ \boldsymbol{U}_i^{\mathrm{R}}=\boldsymbol{U}_i^n+0.5 \Delta x \operatorname{MINMOD}\left(\sigma_j^n, \sigma_{j-1}^n\right) $ | (14) |
式中:上角标L为x→xi-1/2且x>xi-1/2,上角标R为x→xi+1/2且x < xi+1/2。
2) 推进时间计算。即:
| $ \boldsymbol{U}_i^{\mathrm{L}^*}=\boldsymbol{U}_i^{\mathrm{L}}-\frac{\Delta t}{2 \Delta x}\left[\boldsymbol{F}\left(\boldsymbol{U}_i^{\mathrm{R}}\right)-\boldsymbol{F}\left(\boldsymbol{U}_i^{\mathrm{L}}\right)\right] $ | (15) |
| $ \boldsymbol{U}_i^{\mathrm{R} *}=\boldsymbol{U}_i^{\mathrm{R}}-\frac{\Delta t}{2 \Delta x}\left[\boldsymbol{F}\left(\boldsymbol{U}_i^{\mathrm{R}}\right)-\boldsymbol{F}\left(\boldsymbol{U}_i^{\mathrm{L}}\right)\right] $ | (16) |
3) Riemann问题的近似求解。即:
| $ \boldsymbol{U}_{\mathrm{L}}^n=\boldsymbol{U}^{\mathrm{R}^*}{ }_i, \boldsymbol{U}_{\mathrm{R}}^n=\boldsymbol{U}_{i+1}^{\mathrm{L} *} $ | (17) |
考虑TVB动态摩阻项,将其纳入源项,在源项求解中,采用二阶龙格-库塔法进行计算,其显式求解过程如下:
| $ \overline{\boldsymbol{U}}_i^{n+1}=\boldsymbol{U}_i^n-\frac{\Delta t}{\Delta x}\left(\boldsymbol{F}_{i+1 / 2}^n-\boldsymbol{F}_{i-1 / 2}^n\right) $ | (18) |
| $ \overline{\boldsymbol{U}}_i^{n+1}=\overline{\boldsymbol{U}}_i^{n+1}+\frac{\Delta t}{2} \boldsymbol{S}\left(\overline{\boldsymbol{U}}_i^{n+1}\right) $ | (19) |
| $ \boldsymbol{U}_i^{n+1}=\overline{\boldsymbol{U}}_i^{n+1}+\Delta t \boldsymbol{S}\left( {\overline{\overline U} _i^{n + 1}} \right) $ | (20) |
式中,
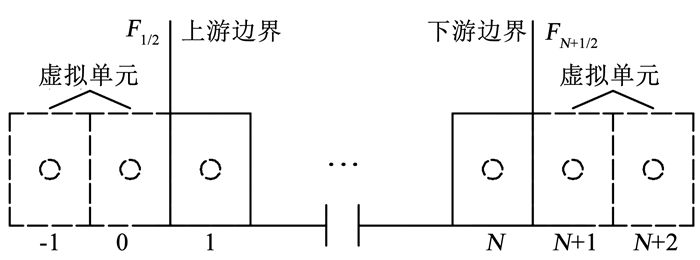
文献[6]中描述需要通过Riemann不变量方程单独计算边界处的通量值,然后计算其他单元控制体的通量值,文献[9, 13]提出了虚拟边界处理方法,可以使边界和所有单元控制体的通量值统一计算。由二阶Godunov格式可知,计算时需知道与之相邻上、下游各两个单元数值,在上、下游边界处各加入两个虚拟单元0、-1和虚拟单元N+1、N+2,如图 2所示。
|
图 2 计算区域与虚拟单元 Fig. 2 Computation area and virtual cells |
1) 上游边界为U-1=U0=U1/2。
由式(11)联立负特征线可得Riemann不变量方程:
| $ H_{1 / 2}-\frac{a}{g} V_{1 / 2}=H_1^n-\frac{a}{g} V_1^n $ | (21) |
2) 下游边界为UN+1=UN+2=UN+1/2。
由式(11)联立正特征线可得Riemann不变量方程:
| $ H_{N+1 / 2}+\frac{a}{g} V_{N+1 / 2}=H_N^n+\frac{a}{g} V_N^n $ | (22) |
根据Godunov方法,计算两个等分单元内测压管水头及流量,然后计算气体空穴处测压管水头和气穴的体积。根据两个等分单元内压强是否降低到或小于汽化压强有两种计算方法。
1.4.1 两等分单元内压强均大于汽化压强当两部分的压强高于汽化压强时,气体空穴处压强取两部分的算术平均,即
| $ H_{g(j)}^{n+1}=\left(H_{u j}^{n+1}+H_j^{n+1}\right) / 2 $ | (23) |
将式(8)代入式(5)可得到:
| $ \forall_{g(j)}^{n+1}=\left(p_0^* \alpha_0 \forall\right) /\left[\rho g\left(H_{g(j)}^{n+1}-z-H_v\right)\right] $ | (24) |
由于离散气体空穴会影响其相邻两个等分单元内的流量变化,因此,等分单元的压强需要考虑自由气体的影响而做出调整。根据气体压强,气体空穴的水头与相邻两部分单元内水头的线性关系为:
| $ H_{u j}^{n+1}=C_{-a p} H_{u j}^{n+1}+\left(1-C_{-a p}\right) H_{g(j)}^{n+1} $ | (25) |
| $ H_j^{n+1}=C_{-a p} H_j^{n+1}+\left(1-C_{-a p}\right) H_{g(j)}^{n+1} $ | (26) |
式中: C-ap为压力修正系数(0~1), C-ap=0时气体空穴的水头、相邻两部分单元内水头三者相等,C-ap=1.0意味着完全忽略气体空穴的影响,其取值将对瞬态水头计算结果有明显影响,这在后面将进行讨论。
1.4.2 任一等分单元内压强达到或低于液体汽化压强一旦任一个等分单元内压强降低达到或者低于液体汽化压强,空化初生,气体空穴内将同时包含自由气体和蒸汽,气体空穴体积变化根据连续方程(6)决定。
| $ \forall_{g(j)}^{n+1}=\forall_{g(j)}^n+\left(Q_j^{n+1}-Q_{u j}^{n+1}\right) \Delta t $ | (27) |
将式(27)代入式(4)、(5)得到关系式:
| $ H_{g(j)}^{n+1}=\frac{p_0^* \alpha_0 \forall}{\rho_l g \forall_{g(j)}^{n+1}}+z(j)+H_v $ | (28) |
此时,两个等分单元内压力均等于气体空穴内压力为
| $ H_{u j}^{n+1}=H_j^{n+1}=H_{g(j)}^{n+1} $ | (29) |
采用本文所建立数学模型分别对纯水锤和水柱分离弥合水锤两种情况进行模拟分析,并将计算结果与文献[14-15]中实测数据进行了对比(实验数据见表 1)。随后,对参数敏感性进行研究分析。
| 表 1 实验系统和工况参数 Tab. 1 Experimental system and operating parameters |
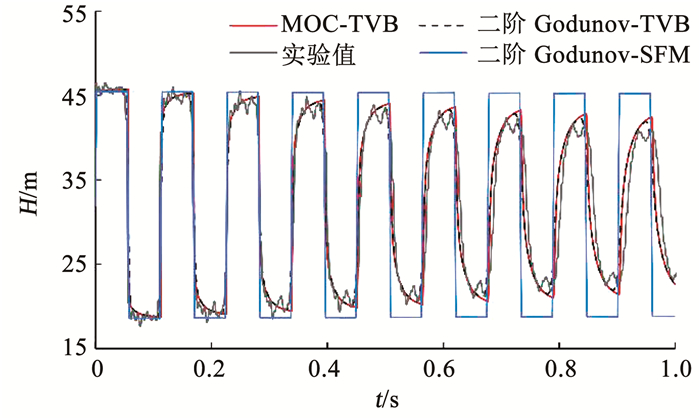
纯水锤现象验证采用实验工况1,数值模拟结果和实验结果对比如图 3所示。
|
图 3 计算结果与实验结果比较(工况1) Fig. 3 Comparison of calculated and experimental results(Case 1) |
图 3中,曲线Experiment和MOC-TVB分别是已有文献中的实验结果和文献中模型计算结果,本文采用二阶Godunov-SFM和二阶Godunov-TVB计算与之对比。采用MOC-TVB和二阶Godunov-TVB两种方法得到压力计算结果基本相同。对比稳态摩阻模型、二阶Godunov-TVB计算结果以及实验数据可知,稳态摩阻模型的模拟结果仅最大压力(第1峰值)与实验结果比较接近,随后压力值衰减较小,与实验数据相差较大;MOC-TVB和二阶Godunov-TVB两个模型能准确模拟出实验压力波动曲线的整个过程。
2.1.2 水柱分离弥合水锤现象验证水柱分离弥合水锤现象验证采用工况2、3,采用建议初始含气率10-7[16], 如图 4所示。

|
图 4 工况2、3下二阶Godunov格式稳态摩阻与动态摩阻结果与实验数据对比 Fig. 4 Comparison of steady and unsteady friction results of second-order Godunov scheme and experiment data (Cases 2 and 3) |
图 4给出了发生水柱分离工况2、3管道沿线的二阶Godunov-DGCM TVB计算结果与实验值、二阶Godunov-DGCM SFM计算结果的比较。从图 4中可以看出,考虑动态摩阻的数学模型能更为准确地模拟出实验的压力峰值、波动周期及压力衰减。
动态摩阻对第1峰值压力影响相对较小,但对后续压力波动衰减影响较大,这是因为在前期内,第1峰值压力为直接水锤压力,水锤波传递路径短,压力衰减小,动态摩阻的影响较小。随着瞬变过程进行,水锤波往返传播距离增大,导致衰减加大。
2.2 参数敏感性分析 2.2.1 库朗数影响图 5给出库朗数Cr分别取0.1、0.5和1.0时,MOC-TVB模型模拟的压力变化曲线。从图中可以看出,在MOC求解格式下,当Cr < 1.0时,压力波动曲线出现了明显的数值耗散。

|
图 5 在MOC-TVB中Cr的影响(工况1) Fig. 5 Effect of Cr in MOC-TVB (Case 1) |
图 6是工况1中二阶Godunov-TVB模型压力计算结果,其中Cr分别取0.9、0.5和0.1。由图中可知,Cr取0.1和0.5时压力波动曲线与Cr取0.9时压力波动曲线几乎一致,只产生了轻微的数值衰减。

|
图 6 在二阶Godunov-TVB中Cr的影响(工况1) Fig. 6 Effect of Cr in second-order Godunov-TVB (Case 1) |
综上所述,随着Cr减小,MOC-TVB和二阶Godunov-TVB计算结果均会产生数值衰减的现象。但二阶Godunov格式计算结果产生的衰减幅度远小于特征线法。这是因为经典的MOC方法计算精度为一阶精度,当Cr < 1.0时,一阶精度MOC会出现严重数值耗散情况;相关研究在文献[16]中做过分析。在Cr < 1.0时,二阶Godunov格式计算结果具有较高的稳定性和准确性。
2.2.2 网格数划分影响图 7是工况3在取不同网格数情况下,本文模型模拟压力结果与实验数据对比。从图中可以看出,当采用细密网格N=256时,压力波动峰值、周期均与实验值更接近。

|
图 7 在N=32、N=256时阀门计算结果曲线(工况3) Fig. 7 Calculation result at the valve when N=32 and N=256(Case 3) |
采用理论工况0分析压力修正系数C-ap对模型数值耗散的影响。此工况不考虑稳态和动态摩阻,计算结果的衰减均为数值耗散引起。图 8比较了当C-ap={1.0,0.9,0.5,0.1}时,精确解与模型计算结果。初始空隙率采用建议取值α0=10-7。

|
图 8 在二阶Godunov-DGCM TVB模型中C-ap取不同值时计算结果(工况0) Fig. 8 Effect of C-ap on calculated results in second-order Godunov-DGCM TVB model (Case 0) |
由图 8可知,当C-ap < 1.0时,计算压力结果存在数值耗散,C-ap越小数值耗散越严重。当C-ap取0.1时,计算结果的数值耗散最严重,压力幅值与理论值相差较大,这可能导致低估系统最大压力。综上所述,虽然C-ap的减小会导致计算结果发生数值耗散的情况,但是可以看出C-ap取0.5、0.9和1.0时,本文模型模拟的压力幅值与理论值基本保持一致。因此,二阶Godunov-DGCM TVB模型在对水锤现象进行分析时,建议C-ap在0.9~1.0范围内取值。
在工况3下,二阶Godunov-DGCM TVB模型计算阀门处压力结果曲线如图 9所示。从图 9中可以看出,当C-ap=1.0时,计算的结果出现了高频震荡,这在网格数取较小值时更明显。C-ap=0.9时拟合效果较好。

|
图 9 在二阶Godunov-DGCM TVB模型中C-ap取不同值时计算结果(工况3) Fig. 9 Effect of C-ap on calculated results in second-order Godunov-DGCM TVB model (Case 3) |
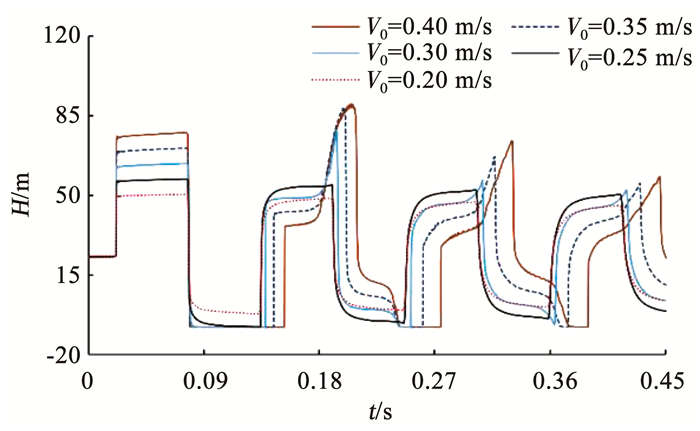
以工况3为例,水锤波速分别取为1 200、1 250、1 300、1 350、1 400 m/s;初始流速分别取为0.20、0.25、0.30、0.35、0.40 m/s,模型计算结果对比如图 10、11所示。

|
图 10 水锤波速对计算压力结果影响 Fig. 10 Effect of water hammer wave speed on calculated pressure results |
|
图 11 初始流速对计算压力结果影响 Fig. 11 Effect of initial velocity on calculated pressure results |
水锤波速受管径、壁厚、管材以及液体温度等影响,气泡也会对水锤波速以及水锤产生较大的影响[17]。由图中可知,水锤波速在1 200~1 400 m/s范围内,随着水锤波速增大,峰值压力增大,呈线性变化规律。
随着初始流速的增大,压力峰值增大。初始流速越大,水体初始能量越大,产生转换为压力的能量越大,而形成更大水锤压力。流速的增大加大了流体自身惯性力[18],使得发生水柱分离弥合时水体惯性增大,从而导致弥合水锤压力增大。
3 结论1) 本文建立的考虑动态摩阻的水柱分离弥合水锤Godunov模型能够准确模拟出纯水锤和水柱分离弥合水锤两种情况的瞬变压力,均与实验数据高度吻合。
2) 与已有的特征线模型相比,本文所建二阶Godunov模型具有更好的稳定性和准确性。这是因为,当Cr≤1.0时,特征线模型会产生严重的数值耗散现象,而二阶Godunov模型计算结果均与实验值吻合更好。
3) 模型中压力修正系数C-ap=0.9时,计算结果更准确、稳定;C-ap>0.9时,计算结果会产生震荡,C-ap<0.9时,会导致严重的数值耗散。
4) 随着水锤波速、初始流速的增大,压力峰值增大,并且与水锤波速呈现规律性关系。
5) 在水柱分离弥合水锤现象发生的瞬变过程中,水体的瞬态运动特性、空穴特征及管道形变或振动等多因素相互耦合作用,因此,若能综合考虑上述多因素动态耦合,将能更真实精准地描述水柱分离弥合现象。
| [1] |
姚青云, 李志敏. 事故停泵水锤对压力管道的影响[J]. 排灌机械, 2006, 24(6): 45. YAO Qingyun, LI Zhimin. Effect of water hammer to pressure pipes for pumping accidents[J]. Drainage and Irrigation Machinery, 2006, 24(6): 45. DOI:10.3969/j.issn.1674-8530.2006.06.012 |
| [2] |
STREETER V L. Water hammer analysis[J]. Journal of Hydraulic Division, 1969, 95: 1959. DOI:10.1061/JYCEAJ.0002199 |
| [3] |
WYLIE E B, STREETER V L, SUO Lisheng. Fluid transients in systems[M]. New York: Prentice Hall, 1993.
|
| [4] |
BROWN R J. Water-column separation at two pumping plants[J]. Journal of Basic Engineering, 1968, 90(4): 521. DOI:10.1115/1.3605184 |
| [5] |
DE VRIES A H. Cavitatie door waterslag in horizontale leidingen met enige hoge punten[R]. Delft, Netherlands: Delft Hydraulics Laboratory, 1973
|
| [6] |
ZHAO Ming, GHIDAOUI M S. Godunov-type solutions for water hammer flows[J]. Journal of Hydraulic Engineering, 2004, 130(4): 341. DOI:10.1061/(ASCE)0733-9429(2004)130:4(341) |
| [7] |
ZHOU Ling, WANG Huan, BERGANT A, et al. Godunov-type solutions with discrete gas cavity model for transient cavitating pipe flow[J]. Journal of Hydraulic Engineering, 2018, 144(5): 04018017. DOI:10.1061/(ASCE)HY.1943-7900.0001463 |
| [8] |
VARDY A, BROWN J. Efficient approximation of unsteady friction weighting functions[J]. Journal of Hydraulic Engineering, 2004, 130(11): 1097. DOI:10.1061/(ASCE)0733-9429(2004)130:11(1097) |
| [9] |
王欢. 管道内液柱分离-弥合瞬变流的动态特性研究[D]. 南京: 河海大学, 2018 WANG Huan. Investigation on dynamic behavior of transient flow with liquid column separation in pipelines[D]. Nanjing: Hohai University, 2018 |
| [10] |
赵越. 基于有限体积法Godunov格式的管道瞬变流数学建模及研究[D]. 南京: 河海大学, 2019 ZHAO Yue. Finite volume method Godunov-type scheme for transient flow in pipeline[D]. Nanjing: Hohai University, 2019 |
| [11] |
蒋明, 陈明. 求解管道耦合水力瞬变模型的Godunov格式[J]. 应用力学学报, 2013, 30(3): 406. JIANG Ming, CHEN Ming. Godunov scheme for solving coupling hydraulic transient model of thepipeline[J]. Chinese Journal of Applied Mechanics, 2013, 30(3): 406. DOI:10.11776/cjam.30.03.C039 |
| [12] |
GUINOT V. Riemann solvers for water hammer simulations by Godunov method[J]. International Journal for Numerical Methods in Engineering, 2000, 49(7): 851. DOI:10.1002/1097-0207(20001110)49:73.0.CO;2-# |
| [13] |
赵越, 周领, 刘德有, 等. 基于有限体积法Godunov格式的水锤计算模型[J]. 水利水电科技进展, 2019, 39(1): 76. ZHAO Yue, ZHOU Ling, LIU Deyou, et al. Water hammer model based on finite volume method and Godunov-type scheme[J]. Advances in Science and Technology of Water Resources, 2019, 39(1): 76. DOI:10.3880/j.issn.1006-7647.2019.01.013 |
| [14] |
BERGANT A, SIMPSON A R, VÌTKOVSK J. Developments in unsteady pipe flow friction modelling[J]. Journal of Hydraulic Research, 2001, 39(3): 249. DOI:10.1080/00221680109499828 |
| [15] |
SIMPSON A R. Large water hammer pressures due to column separation in sloping pipes[D]. Ann Arbor: University of Michigan, 1986
|
| [16] |
ZHOU Ling, WANG Huan, LIU Deyou, et al. A second-order finite volume method for pipe flow with water column separation[J]. Journal of Hydro-environment Research, 2016, 17: 47. DOI:10.1016/j.jher.2016.11.004 |
| [17] |
张彦光. 压力管道水锤波速影响因素的分析及其对长距离输水管道中水锤计算的影响研究[D]. 西安: 长安大学, 2011 ZHANG Yanguang. An analysis of influential factors of the water hammer's wave velocity in pressure pipeline and a study on its influencers upon the calculation of water hammer in the long-distance water delivery pipelines[D]. Xi'an: Chang'an University, 2011 |
| [18] |
魏闯, 李明思, 雷成霞, 等. 流速对管网水锤负压影响的试验研究[J]. 石河子大学学报(自然科学版), 2020, 38(3): 307. WEI Chuang, LI Mingsi, LEI Chengxia, et al. Experimental study on the effect of flow velocity on negative pressure of water hammer in pipe network[J]. Journal of Shihezi University (Natural Science), 2020, 38(3): 307. DOI:10.13880/j.cnki.65-1174/n.2020.21.060 |
 2023, Vol. 55
2023, Vol. 55


