2. 四川大学 物理学院, 成都 610065
2. College of Physics, Sichuan University, Chengdu 610065, China
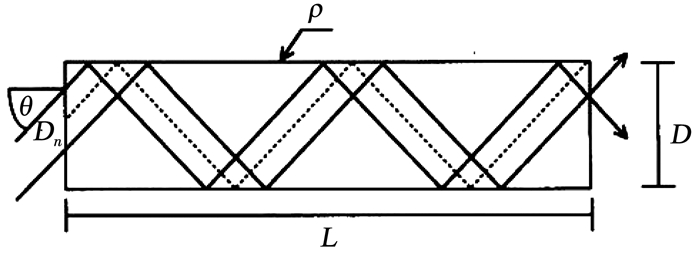
导光管采光系统是一种新型的绿色采光装置,通过具有良好光传输性能的圆筒式通道,可将室外天然光引入建筑深处或者无窗空间。实际使用中,常采用圆筒式镜面导光管与集光器、漫射器组成采光系统[1]。在技术与经济许可的情况下,导光管内壁应选用高反射率的镜面反射材料,以提高其光传输效率(Light transmission efficiency,LTE)。光纤利用“全反射”原理,可见光以大于全反射临界角(arcsin(n1/n2))的入射角,从光密介质射向光疏介质时,即两者折射率分别为n2和n1,且n2>n1,可以实现100%传输光能,比如从玻璃或水中射向空气中;而导光管需要依靠内壁对可见光的镜面反射能力,实现一定距离传输光能的功能,因此导光管内壁反射率是决定其光传输性能的最重要指标。但是,除了内壁反射率,管道形状、尺寸、弯头方式、光源等众多因素,共同影响着LTE数值,因此建立较为精确的导光管LTE预测模型,近30多年来一直是该领域的一个研究热点。
基于各种方法(理论分析、采光实验、光学模拟、数学解析等)获取的大量数据,众多学者建立了导光管LTE的计算模型。Zastrow等[2]提出了最早的导光管LTE计算式,即式(1),仅适用于低等效长度M(即管长L与管径D之比)、低入射角θ(即入射光线与管轴之间的夹角)和高反射率ρ的导光管。Swift等[3]采用光线追迹法,使用如图 1所示的圆筒式导光管的几何结构,并建立了导光管LTE的表达式,即式(2)。Edmonds等[4]开发了一种镜面导光管LTE的预测模型,即式(3),该式适用于M < 6的直导光管,其中x指光线进入管口的点与管轴心之间的距离。Jenkins等[5]针对内壁面反射率为0.95的直导光管,建立了导光管LTE与等效长度M之间的简单关系式,即式(4)。2006年国际照明委员会(International commission on illumination, CIE)提出了导光管LTE的计算式,即式(5)[6]。2019年Petržala[7]提出了全阴天环境下导光管LTE的简单解析公式,即式(6)。
| $ \mathrm{LTE}=\rho^{4 \times L \times \tan \theta /(\pi \times D)} $ | (1) |
| $ \begin{aligned} \mathrm{LTE}= & \frac{4}{\pi} \int_{D=0}^1 \frac{D^2}{\sqrt{1-D^2}} \rho^{\operatorname{int}\left(\frac{L \tan \theta}{D^2}\right)} \times \\ & \left\{1-(1-\rho)\left[\frac{L \tan \theta}{D^2}-\operatorname{int}\left(\frac{L \tan \theta}{D^2}\right)\right]\right\} \mathrm{d} D \end{aligned} $ | (2) |
| $ \text { LTE }=4 \int_0^{D / 2} \frac{\left((D / 2)^2-x^2\right)^{1 / 2}}{D / 2} \rho^N \mathrm{~d} x / \pi(D / 2)^2 $ | (3) |
| $ \mathrm{LTE}=0.82 \mathrm{e}^{\frac{-0.11 L}{D}} $ | (4) |
| $ \mathrm{LTE}=\frac{\mathrm{e}^{(L / D) \times \ln \rho \times \tan 30^{\circ}}}{\left[\left(1-(L / D) \times \ln \rho \times \tan 30^{\circ}\right)\right]^{1 / 2}} $ | (5) |
| $ \begin{aligned} \text { LTE } \approx & \frac{4.603 \rho^{1 / 2}}{1.16424[1.988-(L / D) \times \ln \rho]^2} \times \\ & \left\{1+\frac{0.498292 \times(L / D) \times \ln \rho}{1.988-(L / D) \times \ln \rho}+\right. \\ & \left.\frac{0.612324 \times[(L / D) \times \ln \rho]^2}{[1.988-(L / D) \times \ln \rho]^2}\right\} \end{aligned} $ | (6) |
|
图 1 平行光入射直导光管 Fig. 1 Parallel rays entering a straight light pipe |
从上述导光管LTE计算式,可知以往的研究均假定:导光管内壁反射率ρ是恒定不变的数值。对比实验数据发现,这些计算式只适合漫射光源下反射比较高、等效长度较小,或直射光源下太阳高度角较高(即直射光线入射角较小)的导光管LTE预测[2, 7-8]。这些情况下,光线在导光管内的反射次数少,故基于这些计算式的LTE预测结果精度较高,而随着反射率减小、等效长度增长或太阳高度角较低时,光线在导管内传输过程中的反射次数增多,实验与预测结果之间差距开始增大。
另外,也有一些学者开发利用了导光管采光性能模拟软件,如HOLIGILM[9-11]、SkyVision[12-13]等,或光学模拟软件TracePro[14-15]等,模拟计算不同规格的导光管LTE。这些文献和模拟计算软件在设置管内壁反射率时,也均将其设定为恒定不变的数值。
2008年Swift等[16]曾提出导光管内壁反射率会因光偏振而随反射次数而变化,并给出了单束i光线在管内LTE与反射次数和反射率的概念性关系式,即式(7),该式中ρn(i)为i光线第n次的内壁反射率。然而,并没有给出令人信服的相关理论,也无法深入分析非恒定的管内壁反射率对导光管LTE的影响。
| $ \begin{array}{l} {\rm{LT}}{{\rm{E}}_i} = {\mathit{\Phi} _{{\rm{out }}(i)}}/{\mathit{\Phi} _{{\rm{in}}(i)}} = {\mathit{\Phi} _{{\mathop{\rm in}\nolimits} (i)}}\\ \;\;\;\;\;\;\; \times \prod\limits_{n = 1}^{n(i)} {{\rho _{n(i)}}} /{\mathit{\Phi} _{{\rm{in}}(i)}} = \prod\limits_{n = 1}^{n(i)} {{\rho _{n(i)}}} \end{array} $ | (7) |
倘若光线在导光管内的传输过程中,光偏振的确会使内壁反射率随反射次数而不断变化。那么,上述基于恒定反射率的导光管LTE计算式(1)~(6)和相关模拟结果,必然是错误的,有很强的局限性。因此,本文根据光学理论,先确认光偏振对镜面反射材质反射率的影响,再进一步厘清导光管内壁反射率随反射次数的变化规律,最后分析内壁反射率的变化对导光管LTE的影响。
1 光偏振对金属表面反射率的影响光是横波,说明光波的电场矢量方向处于与光的传播方向垂直的平面。在这个平面上电场矢量的振动有多重状态,称为光波的偏振态[17]。偏振光最常见的来源之一,是从介电媒质反射这个无所不在的过程,如自然光照射到窗玻璃、纸张、光滑金属等上的反光,一般都是部分偏振光[18]。
金属电导率不为零,是有损耗电介质,其折射率为复数。当光照射光滑金属表面时,其反射仍遵循折射定律和菲涅尔反射定律。光线照射到金属表面的反射如图 2所示。那么,设n1、θ1为入射介质的折射率和入射角;
| $ a=\sqrt{\frac{1}{2}\left[n_2^2-n_2^2 k^2-n_1^2 \sin ^2 \theta_i+\sqrt{\left(n_2^2-n_2^2 k^2-n_1^2 \sin ^2 \theta_i\right)^2+4 n_2^4 k^2}\right]} $ | (8) |
| $ b=\sqrt{\frac{1}{2}\left[-\left(n_2^2-n_2^2 k^2-n_1^2 \sin ^2 \theta_i\right)+\sqrt{\left(n_2^2-n_2^2 k^2-n_1^2 \sin ^2 \theta_i\right)^2+4 n_2^4 k^2}\right]} $ | (9) |
| $ \rho_{\perp}=\sqrt{\frac{\left(n_1 \cos \theta_i-a\right)^2+b^2}{\left(n_1 \cos \theta_i+a\right)^2+b^2}} $ | (10) |
| $ \rho_{\|}=\sqrt{\frac{\left[n_2^2\left(1-k^2\right) \cos \theta_i-n_1 a\right]^2+\left(2 n_2^2 k \cos \theta_i-n_1 b\right)^2}{\left[n_2^2\left(1-k^2\right) \cos \theta_i+n_1 a\right]^2+\left(2 n_2^2 k \cos \theta_i+n_1 b\right)^2}} $ | (11) |

|
图 2 光滑金属表面的光线反射 Fig. 2 Light reflection on smooth metal surface |

|
图 3 光滑铝表面的S、P分量和整体的反射率曲线 Fig. 3 S- and P-components and overall reflectivity curve of smooth aluminum surface |
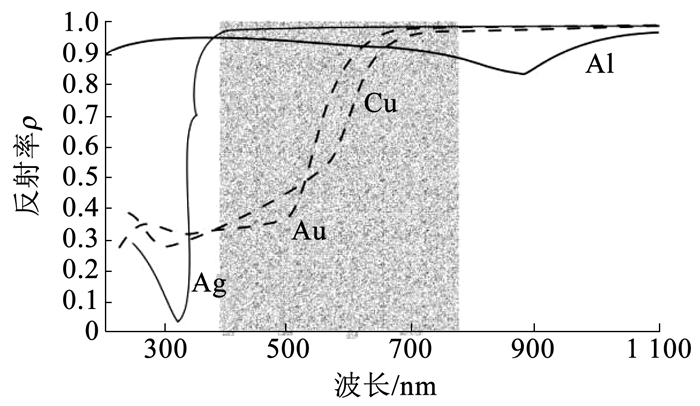
通常,导光管内壁面是表面非常光滑的金属镀膜,故当一束自然光线以某一角度投射到金属内壁面时,必然会发生一次镜面反射,并产生光偏振现象,且会在S、P分量产生如图 3所示的不同反射率,分别为ρ⊥和ρ‖,且ρ⊥总是大于ρ‖[21],而整体反射率为两者的平均值,即式(12)[18]。除了与管轴平行的光线,绝大多数进入足够长的圆筒式导光管内的光线,必然会发生多次镜面反射,那么导光管内壁面的整体反射率会出现什么样的变化?由于每一次反射的整体反射率会影响导光管内LTE,故需要厘清整体反射率随反射次数的变化规律。
| $ \rho=\frac{\rho_{\|}+\rho_{\perp}}{2} $ | (12) |
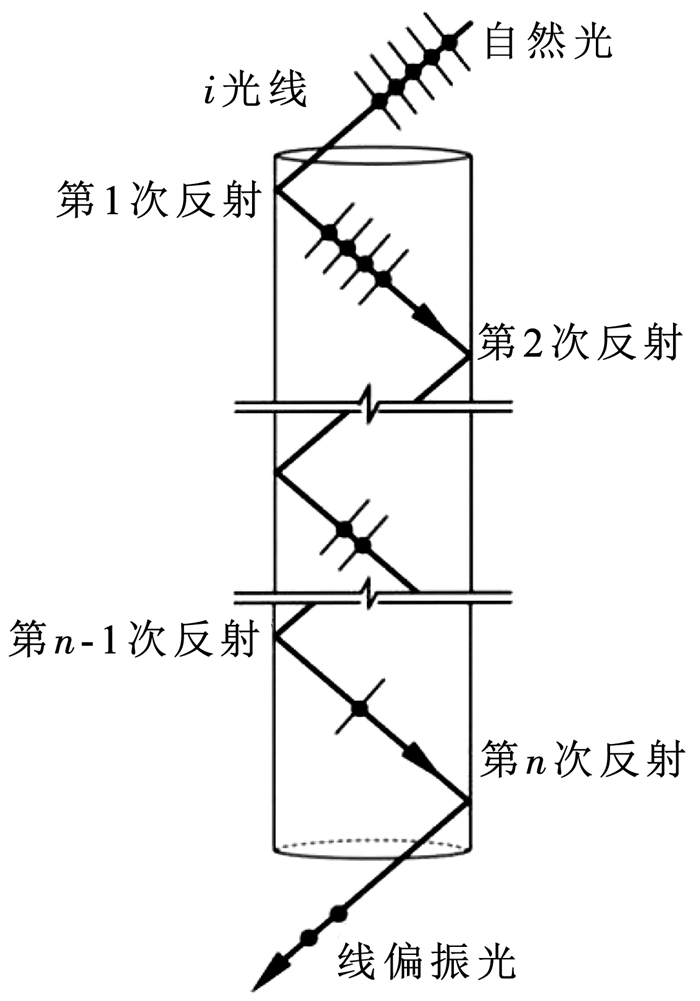
如图 4所示,以单束i自然光线为例,光线光通量设为Φin,以某一角度入射到一段导光管内壁面上,将遵循镜面反射定律,持续多次镜面反射;也将遵循菲涅尔反射定律,持续多次地发生光偏振现象。如图 5所示,自然光线在经过多层玻璃组成的玻璃堆后,透射光就成为几乎只有P分量的线偏振光[17, 22]。
|
图 4 圆筒式镜面导光管内i光线多次反射光路图 Fig. 4 Multiple reflections of i ray in a cylindrical mirror light pipe |

|
图 5 非偏振光透过多层玻璃堆后成为偏振光 Fig. 5 Generation of polarized lights of non-polarized light passing through multiple glasses |
与图 5类似,则可认为在导光管内的多次镜面反射过程中,i光线分解为相当于两条“孪生”线偏振光,即S分量和P分量。这两条光线在导光管内的光路完全相同、初始入射到壁面的光通量相同(均分为Φin/2),却会引起不同的反射率[17]。由于入射到壁面的角度相同,则S、P分量的每次反射率保持不变,即式(13)、(14),并从图 3中可以确定,ρ‖≤ρ⊥。那么,根据不断反射后的S、P分量光通量变化,就可计算出每一次反射的整体反射率,具体计算过程与结果详见表 1,并由表 1可推知,第n次反射的整体反射率ρn可采用式(15)表示。
| 表 1 导光管内i光线若干次反射中整体反射率ρn的计算 Tab. 1 Calculation of overall reflectivity ρn of i ray's multiple reflections in a cylindrical mirror light pipe |
由表 1和式(15)可推知,以往的研究文献中将第1次整体反射率ρ1作为后续若干次反射中恒定不变的反射率,忽视了光偏振引起整体反射率逐渐增大的事实,故导光管LTE计算式(1)~(6)存在明显的缺陷。
| $ \rho_{(1) \perp}=\rho_{(2) \perp}=\cdots=\rho_{(n) \perp}=\rho_{\perp} $ | (13) |
| $ \rho_{(1) \|}=\rho_{(2) \|}=\cdots=\rho_{(n) \|}=\rho_{\|} $ | (14) |
| $ \rho_n=\frac{\rho_{\|}^n+\rho_{\perp}^n}{\rho_{\|}^{n-1}+\rho_{\perp}^{n-1}} $ | (15) |
由图 3可知,1≥ρ⊥≥ρ‖≥0,故与S分量相比,P分量光损速率相对较大,则若干次反射后,P分量光通量占比不断减小,直至先降至几乎为零,而S分量方向光通量占比不断增大,直至几乎全部是S分量的偏振光。
| $ \begin{aligned} \rho_2= & \frac{\rho_{\|}^2+\rho_{\perp}^2}{\rho_{\|}+\rho_{\perp}} \geqslant \rho_1=\frac{\rho_{\|}+\rho_{\perp}}{2} \Rightarrow 2 \rho_{\perp}^2+2 \rho_{\|}^2 \geqslant \\ & \rho_{\perp}^2+\rho_{\|}^2+2 \rho_{\perp} \times \rho_{\|} \Rightarrow \rho_{\perp}^2+\rho_{\|}^2 \geqslant 2 \rho_{\perp} \times \rho_{\|} \Rightarrow \\ & \left(\rho_{\perp}-\rho_{\|}\right)^2 \geqslant 0 \end{aligned} $ | (16) |
| $ \begin{gathered} \rho_3=\frac{\rho_{\|}^3+\rho_{\perp}^3}{\rho_{\|}^2+\rho_{\perp}^2} \geqslant \rho_2=\frac{\rho_{\|}^2+\rho_{\perp}^2}{\rho_{\|}+\rho_{\perp}} \Rightarrow \frac{\rho_{\|}^2 \times \rho_{\|}+\rho_{\perp}^2 \times \rho_{\perp}}{\rho_{\|}^2+\rho_{\perp}^2} \geqslant \\ \frac{\rho_{\|}^2+\rho_{\perp}^2}{\rho_{\|}^2 \div \rho_{\|}+\rho_{\perp}^2 \div \rho_{\perp}} \Rightarrow\left(\rho_{\|}^2 \times \rho_{\|}+\rho_{\perp}^2 \times \rho_{\perp}\right)\left(\rho_{\|}^2 \div\right. \\ \left.\rho_{\|}+\rho_{\perp}^2 \div \rho_{\perp}\right) \geqslant\left(p_{\|}^2+\rho_{\perp}^2\right)^2 \Rightarrow \rho_{\|}^{2(2)}+\rho_{\perp}^2 \times \rho_{\|}^2 \times \frac{\rho_{\|}}{\rho_{\perp}}+ \\ \rho_{\perp}^2 \times \rho_{\|}^2 \times \frac{\rho_{\perp}}{\rho_{\|}}+\rho_{\perp}^{2(2)} \geqslant \rho_{\|}^{2(2)}+2 \rho_{\|}^2 \times \rho_{\perp}^2+\rho_{\perp}^{2(2)} \Rightarrow \frac{\rho_{\|}}{\rho_{\perp}}+ \\ \frac{\rho_{\perp}}{\rho_{\|}} \geqslant 2 \Rightarrow \rho_{\perp}^2+\rho_{\|}^2 \geqslant 2 \rho_{\perp} \times \rho_{\|} \Rightarrow\left(\rho_{\perp}-\rho_{\|}\right)^2 \geqslant 0 \end{gathered} $ | (17) |
| $ \begin{aligned} \rho_n= & \frac{\rho_{\|}^n+\rho_{\perp}^n}{\rho_{\|}^{n-1}+\rho_{\perp}^{n-1}} \geqslant \rho_{n-1}=\frac{\rho_{\|}^{n-1}+\rho_{\perp}^{n-1}}{\rho_{\|}^{n-2}+\rho_{\perp}^{n-2}} \Rightarrow \\ & \frac{\rho_{\|}^{n-1} \times \rho_{\|}+\rho_{\perp}^{n-1} \times \rho_{\perp}}{\rho_{\|}^{n-1}+\rho_{\perp}^{n-1}} \geqslant \frac{\rho_{\|}^{n-1}+\rho_{\perp}^{n-1}}{\left(\rho_{\|}^{n-1} \div \rho_{\|}+\rho_{\perp}^{n-1} \div \rho_{\perp}\right)} \Rightarrow \\ & \left(\rho_{\|}^{n-1} \times \rho_{\|}+\rho_{\perp}^{n-1} \times \rho_{\perp}\right)\left(\rho_{\|}^{n-1} \div \rho_{\|}+\rho_{\perp}^{n-1} \div \rho_{\perp}\right) \geqslant \\ & \left(\rho_{\|}^{n-1}+\rho_{\perp}^{n-1}\right)^2 \Rightarrow \rho_{\|}^{2(n-1)}+\rho_{\perp}^{n-1} \times \rho_{\|}^{n-1} \times \frac{\rho_{\|}}{\rho_{\perp}}+\rho_{\perp}^{n-1} \times \\ & \rho_{\|}^{n-1} \times \frac{\rho_{\perp}}{\rho_{\|}}+\rho_{\perp}^{2(n-1)} \geqslant \rho_{\|}^{2(n-1)}+2 \rho_{\|}^{n-1} \times \rho_{\perp}^{n-1}+\rho_{\perp}^{2(n-1)} \Rightarrow \\ & \frac{\rho_{\|}}{\rho_{\perp}}+\frac{\rho_{\perp}}{\rho_{\|}} \geqslant 2 \Rightarrow \rho_{\perp}^2+\rho_{\|}^2 \geqslant 2 \rho_{\perp} \times \rho_{\|} \Rightarrow\left(\rho_{\perp}-\rho_{\|}\right)^2 \geqslant 0 \end{aligned} $ | (18) |
由于ρ⊥≠ρ‖,则可证明式(16)~(18)成立,进而可证明整体反射率将随反射次数而逐渐增大,揭示了导光管内光偏振引起的整体反射率变化规律,并解释了导光管光损失速率减缓的现象。
3 光反射率的变化对导光管光传输效率影响的计算式理论上,圆筒状导光管LTE就是指管出口光通量与管入口光通量的比值,可用式(19)表示。
| $ \text { LTE }=\text { 管出口光通量 } / \text { 管人口光通量 }={\mathit{\Phi }_{{\rm{out }}}}/{\mathit{\Phi }_{{\rm{in }}}} $ | (19) |
由图 6可知,无论是漫射光源或直射光源,射入管内的光可分解为无数条光线。假定图 4中i光线为图 6中漫射光源中的一条光线。在i光线的光程中,每投射到管内壁一次,就会因光能被吸收而产生一次光损失,此次光能损失量由当次整体反射率决定。因此,在i光线贯穿某一导光管后,累积的光损失(或LTE),实质上只决定于反射次数与每次的整体反射率。故Swift等[16]提出的计算式(7),准确表达了单束光线在导光管内LTE变化的概念性规律。因此,考虑到光偏振引起的管内壁面整体反射率的变化,根据式(15)可进一步推导出i光线在管内的LTEi,即式(20),这将有利于建立科学的复杂光源下导光管LTE数学计算模型。若忽视整体反射率随反射次数而不断增大的变化规律,则i光线的LTE′i可用式(21)表示。

|
图 6 直射光源与漫射光源的光线分解、组合图 Fig. 6 Decomposition and combination of countless rays in direct and diffuse light sources |
根据式(16)~(18),可证明式(22)成立,则说明LTEi≥LTE′i。因此,这可在一定程度上解释以往研究文献中以恒定不变的反射率预测导光管LTE,会呈现随着反射次数增多而误差增大的趋势。
且由式(16)~(18)可知,ρ⊥与ρ‖之间的差异越大,LTEi与LTE′i之间的差异也会随之变大。当前,导光管采用高反射率的金属镜面反射材料制作,多在0.90以上,甚至0.99,接近1.00。如果整体反射率保持较高,则ρ⊥与ρ‖之间的差异程度、两者偏离整体反射率的程度也必然很微小,那么LTEi与LTE′i之间的差异就会很微小。这可以解释式(1)~(6)的导光管LTE计算结果的误差会随整体反射率的提高而减小。
| $ \begin{aligned} \operatorname{LTE}_i= & \prod\limits_{n=1}^{N_{(i)}} \rho_{n(i)}=\prod\limits_{n=1}^{N_{(i)}} \frac{\rho_{\|}^n+\rho_{\perp}^n}{\rho_{\|}^{n-1}+\rho_{\perp}^n}= \\ & \frac{\rho_{\|}+\rho_{\perp}}{2} \times \frac{\rho_{\|}^2+\rho_{\perp}^2}{\rho_{\|}+\rho_{\perp}} \times \frac{\rho_{\|}^3+\rho_{\perp}^3}{\rho_{\|}^2+\rho_{\perp}^2} \times \cdots \\ & \frac{\rho_{\|}^n+\rho_{\perp}^n}{\rho_{\|}^{n-1}+\rho_{\perp}^{n-1}}=\frac{\rho_{\|}^n+\rho_{\perp}^n}{2} \end{aligned} $ | (20) |
| $ \begin{aligned} \mathrm{LTE}_i^{\prime}= & \mathit{\Phi}_{\mathrm{out}(i)}^{\prime} / \mathit{\Phi}_{\mathrm{in}(i)}=\mathit{\Phi}_{\mathrm{in}(i)} \times\left(\frac{\rho_{\|}+\rho_{\perp}}{2}\right)^n / \mathit{\Phi}_{\mathrm{in}(i)}= \\ & \left(\frac{\rho_{\|}+\rho_{\perp}}{2}\right)^n \end{aligned} $ | (21) |
| $ \begin{aligned} \mathrm{LTE}_i= & \frac{\rho_{\|}^n+\rho_{\perp}^n}{2}=\frac{\rho_{\|}+\rho_{\perp}}{2} \times \frac{\rho_{\|}^2+\rho_{\perp}^2}{\rho_{\|}+\rho_{\perp}} \times \frac{\rho_{\|}^3+\rho_{\perp}^3}{\rho_{\|}^2+\rho_{\perp}^2} \times \cdots \times \\ & \frac{\rho_{\|}^n+\rho_{\perp}^n}{\rho_{\|}^{n-1}+\rho_{\perp}^{n-1}} \geqslant \frac{\rho_{\|}+\rho_{\perp}}{2} \times \frac{\rho_{\|}+\rho_{\perp}}{2} \times \\ & \frac{\rho_{\|}^2+\rho_{\perp}^2}{\rho_{\|}+\rho_{\perp}} \times \cdots \times \frac{\rho_{\|}^{n-1}+\rho_{\perp}^{n-1}}{\rho_{\|}^{n-2}+\rho_{\perp}^{n-2}} \geqslant \cdots \geqslant \frac{\rho_{\|}+\rho_{\perp}}{2} \times \\ & \frac{\rho_{\|}+\rho_{\perp}}{2} \cdots \frac{\rho_{\|}+\rho_{\perp}}{2}=\left(\frac{\rho_{\|}+\rho_{\perp}}{2}\right)^n=\operatorname{LTE}_i^{\prime} \end{aligned} $ | (22) |
倘若i光线的入射角约为60°,如图 3所示ρ⊥和ρ‖分别设为0.95和0.85,当只有1次反射时,LTEi=LTE′i;但当反射次数增多,就会出现一定的差距,比如当达到10次反射时,则由式(20)、(21)可计算出LTEi和LTE′i分别约为0.40和0.35,误差达到12.35%。因此,在预测导光管LTE时,应考虑光偏振的累积效应对管壁反射率的影响。
4 讨论由图 3可知,镜面反射材料的反射率还与光线入射角度有关,且ρ⊥与ρ‖之间的差异也会不同,那么漫射光源中不同入射角度的光线产生的整体反射率变化就会更加复杂,增加准确预测导光管LTE的难度。而且,由图 7可知,以同一角度入射同一镜面反射材料时,不同波长可见光会呈现不同的反射率,即光谱反射率[23],这也可能会影响导光管的采光性能。因此,文中以上主要研究结果并未考虑以上两个因素的影响,只是通过数学公式推导,理论分析了光偏振对导光管内壁反射率及其LTE的影响,所以,本研究结果尚有一定的局限性。
|
图 7 银、金、铜和铝的光谱反射率 Fig. 7 Spectral reflectance of silver, gold, copper and aluminum |
为了准确评价导光管的采光性能,有必要从以下方面进一步展开深入研究:1)采用光学实验方法,验证了以相同入射角度的若干次镜面反射后,光偏振是否导致反射光几乎只有S分量的线偏振光。2)依次探讨光线的入射角度、光谱反射率、光偏振等因素的影响后,还需要探讨这些因素对导光管内壁整体反射率及导光管LTE的耦合影响,并厘清这些因素的耦合关系,最终建立更科学的导光管LTE数学计算模型。3)由于导光管的前、后分别设置透光率很高的集光器和漫射器,那么光线透过这些透光材料,经折射也会产生光偏振[18]。同样,需要研究光偏振对整个导光管采光系统采光性能的影响。
5 结论1) 分析光偏振的原理,可以确定光线投射到圆筒式镜面导光管的内壁面上,必然会发生光偏振现象,从而会在S、P分量产生不同反射率。
2) 分析光偏振的累积效应,揭示了导光管内壁整体反射率的变化规律。由于光线在导光管内不断地镜面反射,因持续的光偏振,尽管S、P分量的反射率保持不变,却引起整体反射率会随反射次数而逐渐增大,进而使光能损失或导光管光传输效率衰减的速率不断减缓。
3) 根据光偏振的累积效应,进一步推导了单束光线在导光管中光传输效率表达式。这为建立科学的复杂光源下导光管光传输效率数学计算模型,奠定了理论基础。
| [1] |
中华人民共和国住房和城乡建设部. 导光管采光系统技术规程: JGJ/T 374-2015[S]. 北京: 中国建筑工业出版社, 2015 Ministry of Housing and Urban-Rural Development of the People's Republic of China. Technical specification for tubular daylighting system: JGJ/T 374-2015[S]. Beijing: China Architecture & Building Press, 2015 |
| [2] |
ZASTROW A, WITTWER V. Daylighting with mirror light pipes and with fluorescent planar concentrators[J]. Proceeding of SPIE, 1986, 692: 227. DOI:10.1117/12.936710 |
| [3] |
SWIFT P D, SMITH G B. Cylindrical mirror lightpipes[J]. Solar Energy Materials and Solar Cells, 1995, 36(2): 159. DOI:10.1016/0927-0248(94)00172-3 |
| [4] |
EDMONDS I R, MOORE G I, SMITH G B, et al. Daylighting enhancement with light pipes coupled to laser-cut light-deflecting panels[J]. Lighting Research & Technology, 1995, 27(1): 27. DOI:10.1177/14771535950270010101 |
| [5] |
JENKINS D, MUNEER T, KUBIE J. A design tool for predicting the performances of lightpipes[J]. Energy and Buildings, 2005, 37(5): 485. DOI:10.1016/j.enbuild.2004.09.014 |
| [6] |
Tubular Daylight Guidance Systems Commission Internationale de L'Eclairage. Tubular Daylight Guidance Systems, Technical Report: CIE 173-2006[S]. Vienna: CIE Central Bureau, 2006
|
| [7] |
PETRŽALA J. Simple analytic formula for the light-tube optical efficiency under overcast skyconditions[J]. Solar Energy, 2019, 194: 47. DOI:10.1016/j.solener.2019.10.032 |
| [8] |
DUTTON S, SHAO Li. Raytracing simulation for predicting light pipe transmittance[J]. International Journal of Low-Carbon Technologies, 2007, 2(4): 339. DOI:10.1093/ijlct/2.4.339 |
| [9] |
KOCIFAJ M, DARLA S, KITTLER R. HOLIGILM: Hollow light guide interior illumination method-An analytic calculation approach for cylindrical light-tubes[J]. Solar Energy, 2008, 82(3): 247. DOI:10.1016/j.solener.2007.07.003 |
| [10] |
高民东, 徐广强, 曹冠英, 等. 辽宁大连地区标准阴天条件下光导管效率与照度分布的模拟分析[J]. 太阳能学报, 2017, 38(8): 2303. GAO Mingdong, XU Guangqiang, CAO Guanying, et al. Simulation analysis of efficiency and illumination distribution of light guide under CIE overcast sky condition in dalian area, liaoning[J]. Acta Energiae Solaris Sinica, 2017, 38(8): 2303. DOI:10.19912/j.0254-0096.2017.08.038 |
| [11] |
盛夏, 曹冠英, 宣昂, 等. 不同天气模式下光导照明系统的效率分析[J]. 照明工程学报, 2017, 28(3): 66. SHENG Xia, CAO Guanying, XUAN Ang, et al. The efficiency analysis of hollow light guide system under different weather patterns[J]. China Illuminating Engineering Journal, 2017, 28(3): 66. DOI:10.3969/j.issn.1004-440X.2017.03.013 |
| [12] |
LO VERSO V R M, PELLEGRINO A, SERRA V. Light transmission efficiency of daylight guidance systems: An assessment approach based on simulations and measurement in a sun/sky simulator[J]. Solar Energy, 2011, 85(11): 2789. DOI:10.1016/j.solener.2011.08.017 |
| [13] |
李文忠, 冯永忠, 罗涛, 等. 天然光导光管系统的设计与模拟计算[J]. 照明工程学报, 2008, 19(4): 52. LI Wenzhong, FENG Yongzhong, LUO Tao, et al. Design and simulation of daylight light-pipe system[J]. China Illuminating Engineering Journal, 2008, 19(4): 52. DOI:10.3969/j.issn.1004-440X.2008.04.009 |
| [14] |
王书晓, 利岚, 张滨. 基于日光系数法的导光管效率计算方法研究[J]. 建筑科学, 2013, 29(8): 12. WANG Shuxiao, LI Lan, ZHANG Bin. Daylight coefficient computational method-based study on calculation method of tubular daylight device efficiency[J]. Building Science, 2013, 29(8): 12. DOI:10.3969/j.issn.1002-8528.2013.08.004 |
| [15] |
吴新汶, 王春苑, 欧阳金龙. 利用TracePro模拟分析导光管的传输效率[J]. 照明工程学报, 2020, 31(2): 145. WU Xinwen, WANG Chunyuan, OUYANG Jinlong. Analysis of transmission tube efficiency of light pipe based on TracePro[J]. China Illuminating Engineering Journal, 2020, 31(2): 145. DOI:10.3969/j.issn.1004-440X.2020.02.028 |
| [16] |
SWIFT P D, LAWLOR R, SMITH G B, et al. Rectangular-section mirror lightpipes[J]. Solar Energy Materials and Solar Cells, 2008, 92(8): 969. DOI:10.1016/j.solmat.2008.02.029 |
| [17] |
郑植仁, 吴文智, 李艾华. 光学[M]. 哈尔滨: 哈尔滨工业大学出版社, 2015. ZHENG Zhiren, WU Wenzhi, LI Aihua. Optics[M]. Harbin: Harbin Institute of Technology Press, 2015. |
| [18] |
HECHT E. Optics[M]. 4th ed. Edinburgh: McGraw-Hill Education, 2002.
|
| [19] |
鲜于子安, 侯立周. 金属镜面双反射消偏研究[J]. 航天返回与遥感, 2015, 36(5): 67. XIANYU Zi'an, HOU Lizhou. Research on eliminating polarizations characteristic of metal reflectors of Double reflection[J]. Spacecraft Recover & Remote Sensing, 2015, 36(5): 67. DOI:10.3969/j.issn.1009-8518.2015.05.009 |
| [20] |
杨雨迎, 崔占忠, 王玲, 等. 金属目标表面的反射激光偏振特性[J]. 科技导报, 2013, 31(11): 28. YANG Yuying, CUI Zhanzhong, WANG Ling, et al. Reflective laser polarizations characteristics of metal target surface in the short-range detection[J]. Science & Technology Review, 2013, 31(11): 28. DOI:10.3981/j.issn.1000-7857.2013.11.002 |
| [21] |
赵建林. 高等光学[M]. 北京: 国防工业出版社, 2001. ZHAO Jianlin. Advanced optics[M]. Beijing: National Defense Industry Press of China, 2001. |
| [22] |
GHATAKA. Optics[M]. 4th ed. New Delhi: McGraw-Hill Education, 2009.
|
| [23] |
NILSSON A M, JONSSON J C, ROOS A. Spectrophotometric measurements and ray tracing simulations of mirror light pipes to evaluate the color of the transmittedlight[J]. Solar Energy Materials and Solar Cells, 2014, 124: 172. DOI:10.1016/j.solmat.2014.01.049 |
 2023, Vol. 55
2023, Vol. 55


