整形偏移正交相移键控(shaped-offset quadrature phase-shift keying,SOQPSK)是一种高效的数字调制方案,其本质是一种连续相调制(continuous phase modulation,CPM)。由于其频谱效率和恒定包络性质,已被卫星通信标准MIL-STD-188-181[1]和串行遥测标准IRIG 106[2]采用。SOQPSK的新兴应用是通过时分多址网络, 即称为集成网络增强遥测(integrated network enhanced telemetry,iNET)的下一代航空遥测系统的突发模式传输[3]。在21世纪初,Hill[4]利用精心设计的整形脉冲来取代OQPSK信号相位上的脉冲δ(t),即脉冲整形概念,使得相位能在一个码元周期内平滑地过渡到下一个码元周期,从而得到了SOQPSK调制信号。目前SOQPSK的几种不同的信号形式已应用到航空遥测领域。因此从信号包络及带宽压缩方面来看,在带宽效率要求较高的场合,SOQPSK有更广阔的应用前景。
目前,SOQPSK信号的符号定时算法主要可以分为数据辅助(data aided,DA)算法[5]和非数据(non data aided,NDA)辅助算法[6-9]。数据辅助算法需要借助一个已知的训练序列,并对其进行信号处理来获得符号定时误差信息,从而对采样时钟进行反馈补偿。数据辅助算法的精度一般较高,但是具有两个缺点:首先该算法需要传输含有训练序列的同步头,占用了传输信息数据的时间,降低了信息传输效率;其次是由于信道是时变的,因此针对同步头估计出的定时误差对同步头后面的符号可能并不够精确。而非数据辅助算法则没有这两个问题,这类算法可分为面向判决的非数据辅助算法[6]以及非面向判决的非数据辅助算法[8-9]。这两类算法的主要区别是消除传递信息自干扰的手段不同。其中,面向判决的算法需要先对接收信号进行解调,将解调出的符号带入回原信号以消除符号的自干扰,然后再对定时误差进行估计;而非面向判决的算法则使用统计手段将似然方程对传输符号求期望,从而消除自干扰,然后再估计定时误差。对于SOQPSK信号来讲,由于其是CPM信号且码元之间具有关联性,因此SOQPSK信号的解调较为复杂,面向判决的估计算法较难施行,所以非面向判决的非数据辅助算法在这些算法中优势比较明显。
目前,非面向判决的非数据辅助算法主要有基于非线性4次方变换的算法[8]和基于最大似然的算法[9-10]。其中,文献[9]提出的基于最大似然(maximum likelihood,ML)的符号定时与相位误差联合估计算法性能最佳。该算法虽估计精度优秀,但实现复杂度高,本文主要分析该算法在不同简化程度下的性能区别,并给出一种复杂度方面的优化措施。由于SOQPSK-MIL信号提出最早且应用面也较为广泛,因此本文选择SOQPSK-MIL信号作为研究对象。
1 信号模型由于SOQPSK信号属于CPM类信号,因此具有如下形式:
| $ s(t ; \boldsymbol{\alpha})=\sqrt{\frac{E_{\mathrm{s}}}{T}} \exp \left\{\mathrm{j} 2 \pi h \sum\nolimits_i \alpha_i q(t-i T)\right\} $ | (1) |
式中:Es为符号能量; T为符号持续时间; α={αi}为M元符号的序列; h为调制指数,对于SOQPSK信号,h=1/2。通常将相位脉冲q(t)看作是面积为1/2且持续时间为LT的频率脉冲g(t)的时间积分。对于SOQPSK信号,传输符号{αi}不是独立同分布的,而是以某种方式相关,与普通CPM信号不同[3]。
SOQPSK与普通CPM不同的主要特征是预编码器的输出是三进制数据。预编码器根据关系将二进制数据an∈{0, 1}转换为三进制数据αn
| $ \alpha_n=(-1)^{n+1}\left(2 a_{n-1}-1\right)\left(a_n-a_{n-2}\right) $ | (2) |
预编码器在CPM信号上施加了类似于OQPSK信号的特性。三元符号具有以下约束条件:1)虽然αi被视为三元的,但在任意长度的相邻符号中,αi实际上都是从两个二进制码字集{0, +1}或{0, -1}中的一个选取的。2)当αi=0时,αi+1的二进制码字可以不继续使用αi所使用的二进制码字集; 当αi≠0时,αi+1所使用的二进制码字集不变。3)αi=+1的情况下, αi+1=-1的情况不存在,反之亦然。
定义相位函数
| $ \varphi(\boldsymbol{\alpha} ; t)=2 \pi h \sum\nolimits_i \alpha_i q(t-i T) $ | (3) |
则式(1)可写为
| $ s(t ; \boldsymbol{\alpha})=\sqrt{\frac{E_{\mathrm{s}}}{T}} \exp \{\mathrm{j} \varphi(\boldsymbol{\alpha} ; t)\} $ | (4) |
式(3)中的相位响应q(t)通常被认为是面积为1/2且持续时间为LT的频率脉冲g(t)的时间积分。从而,当t < 0时q(t)=0,对于t>LT的q(t)=1/2。当L=1时,SOQPSK信号称为完全响应;当L>1时,则称为部分响应。
SOQPSK信号形式的不同之处在于其各自的频率脉冲。目前SOQPSK大致上有4个信号形式,分别为SOQPSK-MIL、SOQPSK-A、SOQPSK-B、SOQPSK-TG。第一个军事标准的SOQPSK(SOQPSK-MIL)是矩形频率脉冲的完全响应SOQPSK信号,该频率脉冲由式(5)给出[6]:
| $ {g_{{\rm{MIL}}}}(t) = \left\{ \begin{array}{l} \frac{1}{{2T}}, 0 \le t < T\\ 0, {\rm{ 其他 }} \end{array} \right. $ | (5) |
本文的分析主要针对SOQPSK-MIL信号,后文的分析也将主要基于SOQPSK-MIL信号的表示形式。
2 基于ML的联合估计算法在加性高斯白噪声信道下,假设接收信号的频率偏移已被矫正,则离散化后可表示为
| $ x(k)=\sqrt{\frac{E_{\mathrm{s}}}{T}} \exp \left\{\mathrm{j}\left[\theta+\varphi\left(\boldsymbol{\alpha} ; k T_{\mathrm{s}}-\tau\right)\right]\right\}+\omega(k) $ | (6) |
式中:θ为载波相位偏移,τ为定时偏移,ω(k)为均值为零且功率谱密度为N0的离散复基带AWGN。
此时,接收信号关于符号、相位误差和定时误差的似然方程为
| $ \begin{array}{l} \ \ \ \ \ \ \ \ \Lambda (x\mid \tilde \alpha , \tilde \theta , \tilde \tau ) = \\ \exp \left\{ { - \frac{1}{{2\sigma _n^2}}\sum\limits_{k = 0}^{{N_0} - 1} {{{\left| {x(k) - \sqrt {\frac{{{E_{\rm{s}}}}}{T}} \exp \left\{ {{\rm{j}}\left[ {\tilde \theta + \varphi \left( {\tilde \alpha ;k{T_{\rm{s}}} - \tilde \tau } \right)} \right]} \right\}} \right|}^2}} } \right\} \end{array} $ | (7) |
式中:
| $ \begin{aligned} \Lambda(\tilde{\tau}, \tilde{\theta})= & \operatorname{Re}\left\{\mathrm{e}^{-\mathrm{j} 2 \tilde{\theta}} \mathrm{e}^{-\mathrm{j} \pi \tilde{\tau} / T} \sum\limits_{m=-\infty}^{\infty} Z_{2 m+1}^{+} \mathrm{e}^{-\mathrm{j} 2 \pi m \tilde{\tau} / T}\right\}+ \\ & \sum\limits_{m=-\infty}^{\infty} Z_m^{-} \mathrm{e}^{-\mathrm{j} 2 \pi m \tilde{\tau} / T} \end{aligned} $ | (8) |
其中:
| $ Z_{2 m+1}^{+}=\sum\limits_{k=0}^{N L_0-1}\left[x\left(k T_{\mathrm{s}}\right) \mathrm{e}^{j \pi(2 m+1) k / N}\right] y_{2 m+1}^{+}\left(k T_{\mathrm{s}}\right) $ | (9) |
| $ Z_m^{-}=\sum\limits_{k=0}^{N L_0-1}\left[x\left(k T_{\mathrm{s}}\right) \mathrm{e}^{\mathrm{j} 2 \pi m k / N}\right] y_m^{-}\left(k T_{\mathrm{s}}\right) $ | (10) |
| $ y_{2 m+1}^{+}\left(k T_{\mathrm{s}}\right)=\sum\limits_{i=0}^{N L_0-1} x\left(i T_{\mathrm{s}}\right) h_{2 m+1}^{+}\left[(k-i) T_{\mathrm{s}}\right] $ | (11) |
| $ y_m^{-}\left(k T_{\mathrm{s}}\right)=\sum\limits_{i=0}^{N L_0-1} x^*\left(i T_{\mathrm{s}}\right) h_m^{-}\left[(k-i) T_{\mathrm{s}}\right] $ | (12) |
式中:Ts为采样周期,N为每个周期内的采样点数,L0为观测符号数,h2m+1+(kTs)和hm-(kTs)是复值函数h2m+1+(t)和hm-(t)在kTs时刻的采样值,由下式给出:
| $ h_{2 m+1}^{+}(t)=\frac{1}{T} \int_0^T H^{+}(u, t) \mathrm{e}^{-\mathrm{j} \pi(2 m+1) u / T} \mathrm{~d} u $ | (13) |
| $ h_m^{-}(t)=\frac{1}{T} \int_0^T H^{-}(u, t) \mathrm{e}^{-\mathrm{j} 2 \pi m u / T} \mathrm{~d} u $ | (14) |
其中,对于u∈[0, T)
| $ \left\{\begin{aligned} H^{+}(u, t)= & \prod\limits_{i=-(2 L+1)}^{\bar{L}+1} \cos \{\pi[\bar{q}(u-i T)+ \\ & \bar{q}(u-t-i T)]\} \\ H^{-}(u, t)= & \prod\limits_{i=-(2 L+1)}^{\bar{L}+1} \cos \{\pi[\bar{q}(u-i T)- \\ & \overline{q(u-t-i T)]\}} \end{aligned}\right. $ | (15) |
式中: q(t)=0.5[q(t)+q(t-T)],q(t)为SOQPSK信号的相位响应函数,对式(5)给出的频率脉冲函数进行积分即可。
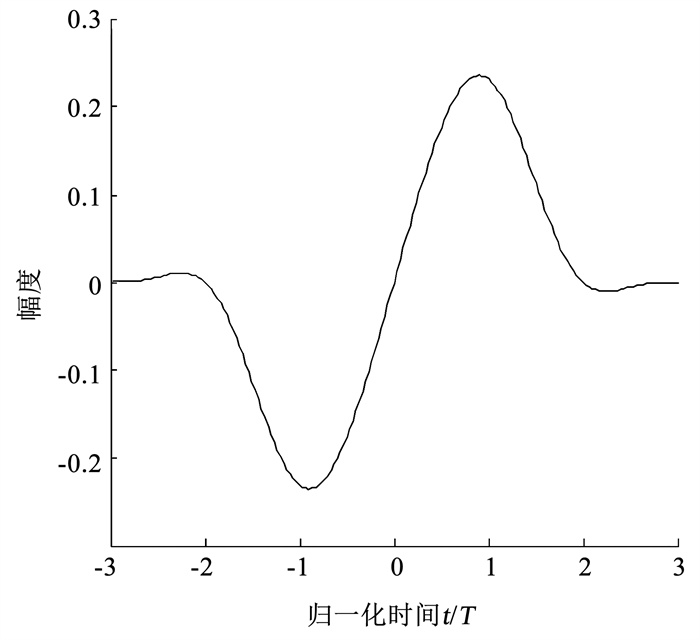
3 ML联合估计算法性能分析目前已不难看出,h函数对最终估计结果占有着至关重要的作用。因为接收到的离散采样信号需要与h函数卷积后再进行其他处理,因此h函数的能量大小对最终的估计精度有着重要影响。表 1给出了对于SOQPSK-MIL信号各项h函数与h1+(t)相比的能量比例大小。图 1~图 6则给出了这些h函数当中能量占比较大的3个h函数的实部与虚部。需要注意的是,各项h函数其下角标的正负与其能量无关,因为互为共轭关系。例如h1+与h-1+互为共轭,因此二者能量相同,h1-与h-1-以及其他h函数亦是如此。故表中h函数下角标均为正值,图 1~图 6的h函数也均给出的是下角标为正值时的情况。
| 表 1 h函数能量占比 Tab. 1 Energy ratio of h functions |
|
图 1 h1+函数的实部 Fig. 1 Real part of h1+ function |

|
图 2 h1+函数的虚部 Fig. 2 Imaginary part of h1+ function |
|
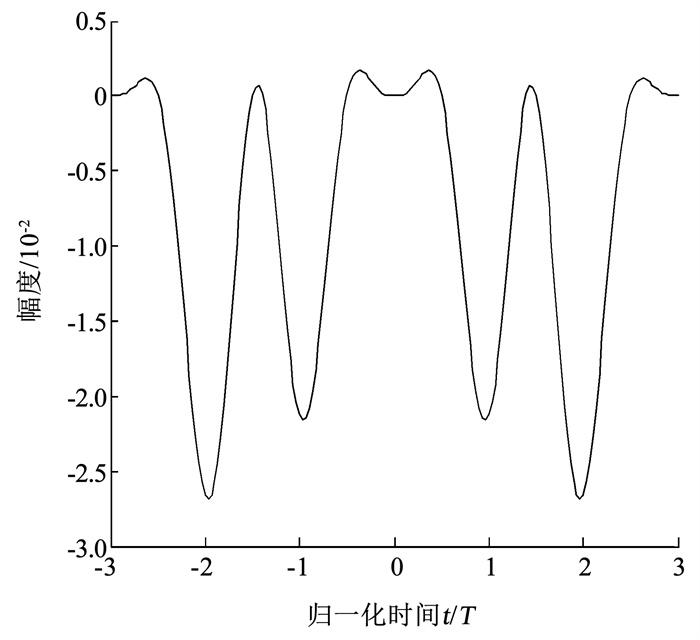
图 3 h1-函数的实部 Fig. 3 Real part of h1- function |
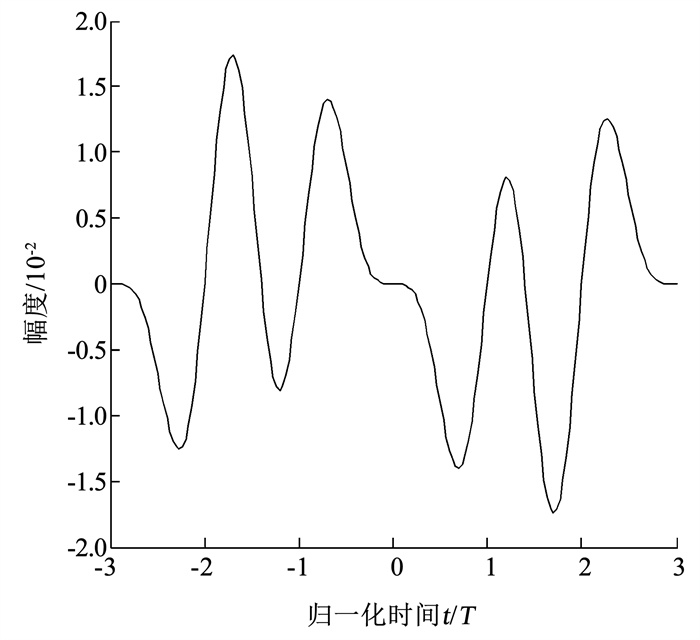
|
图 4 h1-函数虚部 Fig. 4 Imaginary part of h1- function |

|
图 5 h3+函数的实部 Fig. 5 Real part of h3+ function |

|
图 6 h3+函数的虚部 Fig. 6 Imaginary part of h3+ function |
文献[9]结果表明Z1+和Z-1+在所有参数中的能量占比最大(因为h±1+能量最大),从而可以忽略其他参数,而文献[10]中虽采用了与文献[9]不同的展开与化简手段对最大似然函数进行处理,但其结果与文献[9]中ML联合估计算法只采用Z1-和Z-1-参数时所获得的结果完全相同。为了更加全面地说明参数选取对最终定时误差估计精度的影响, 本文主要对比以下3种情况下估计精度的差异:1)只使用Z1+和Z-1+;2)使用Z1+、Z-1+、Z1-和Z-1-;3)使用Z1+、Z-1+、Z3+和Z-3+。
首先,化简后的最大似然函数见式(8), 在只使用Z1+和Z-1+两参数的情况下,式(8)可写为
| $ \Lambda(\tilde{\tau}, \tilde{\theta})=\operatorname{Re}\left\{\mathrm{e}^{-\mathrm{j}[2 \theta-\psi(\tilde{\tau})]} M(\tilde{\tau})\right\} $ | (16) |
式中
为使式(16)最大,显然应令指数项等于1,也即
为使
| $ \begin{gathered} M^2(\tilde{\tau})=|Z(\tilde{\tau})|^2=Z(\tilde{\tau}) Z^*(\tilde{\tau})= \\ \left(Z_1^{+} \mathrm{e}^{-\mathrm{j} \pi \tilde{\tau} / T}+Z_{-1}^{+} \mathrm{e}^{\mathrm{j} \pi \tilde{\tau} / T}\right)\left(Z_1^{+*} \mathrm{e}^{\mathrm{j} \pi \tilde{\tau} / T}+Z_{-1}^{+*} \mathrm{e}^{-\mathrm{j} \pi \tilde{\tau} / T}\right)= \\ Z_1^{+} Z_1^{+*}+Z_{-1}^{+} Z_{-1}^{+*}+Z_1^{+} Z_{-1}^{+*} \mathrm{e}^{-\mathrm{j} 2 \pi \tilde{\tau} / T}+Z_{-1}^{+} Z_1^{+*} \mathrm{e}^{\mathrm{j} 2 \pi \tilde{\tau} / T} \end{gathered} $ | (17) |
式(17)中前两项均为固定值,因此即令后两项和最大。令K=Z1+Z-1+*并对式(17)关于
| $ \frac{\mathrm{d} M^2(\tilde{\tau})}{\mathrm{d} \tilde{\tau}}=-\mathrm{j} \frac{2 \pi}{T} K \mathrm{e}^{-\mathrm{j} 2 \pi \tilde{\tau} / T}+\mathrm{j} \frac{2 \pi}{T} K^* \mathrm{e}^{\mathrm{j} 2 \pi \tilde{\tau} / T} $ | (18) |
令该导数等于零可求得极值点,结果为
| $ \begin{aligned} \frac{\mathrm{d} M^2(\tilde{\tau})}{\mathrm{d} \tilde{\tau}}= & \mathrm{j} \frac{2 \pi}{T}\left[\left(K-K^*\right) \cos (2 \pi \tilde{\tau} / T)-\right. \\ & \left.\left(K+K^*\right) \sin (2 \pi \tilde{\tau} / T)\right]=0 \end{aligned} $ | (19) |
即
| $ \tan \frac{2 \pi}{T} \tilde{\tau}=\frac{\operatorname{Im}\{K\}}{\operatorname{Re}\{K\}} $ | (20) |
因此估计结果
不难看出,在只使用Z1+和Z-1+两个参数的情况下,估计结果可直接由参数计算得出,使得算法能够开环实现。而在额外加上了Z1-和Z-1-两个参数之后,情况变得有些复杂。
再次回到式(8),在同时使用Z1+、Z-1+、Z1-和Z-1-共4个参数的情况下,似然方程可写为
| $ \begin{aligned} \Lambda(\tilde{\tau}, \tilde{\theta})= & \operatorname{Re}\left\{\mathrm{e}^{-\mathrm{j}[2 \theta-\psi(\tilde{\tau})]} M(\tilde{\tau})\right\}+ \\ & Z_1^{-} \mathrm{e}^{-\mathrm{j} 2 \pi \tilde{\tau} / T}+Z_{-1}^{-} \mathrm{e}^{\mathrm{j} 2 \pi \tilde{\tau} / T} \end{aligned} $ | (21) |
相位误差估计值的获取与上述方法相同,同样要使
| $ \Lambda_{\max }(\tilde{\tau}, \tilde{\theta})=M(\tilde{\tau})+Z_1^{-} \mathrm{e}^{-\mathrm{j} 2 \pi \tilde{\tau} / T}+Z_{-1}^{-} \mathrm{e}^{\mathrm{j} 2 \pi \tilde{\tau} / T} $ | (22) |
令式(22)与其共轭相乘,从而得到其模的平方
| $ \begin{aligned} & \left|\Lambda_{\max }(\tilde{\tau}, \tilde{\theta})\right|^2=A^* A+B^* B+A^* B \mathrm{e}^{\mathrm{j} 2 \pi \tilde{\tau} / T}+ \\ & A B^* \mathrm{e}^{-\mathrm{j} 2 \pi \tilde{\tau} / T}+C^2 \mathrm{e}^{-\mathrm{j} 4 \pi \tilde{\tau} / T}+D^2 \mathrm{e}^{\mathrm{j} 4 \pi \tilde{\tau} / T}+2 C D \end{aligned} $ | (23) |
为简化,令A=Z1+, B=Z-1+, C=Z1-, D=Z-1-。
令X=AB*, Y=C2,对式(23)关于
| $ \begin{aligned} & \operatorname{Im}\{X\} \cos (2 \pi \tilde{\tau} / T)+2 \operatorname{Im}\{Y\} \cos (4 \pi \tilde{\tau} / T)- \\ & \operatorname{Re}\{X\} \sin (2 \pi \tilde{\tau} / T)-2 \operatorname{Re}\{Y\} \sin (4 \pi \tilde{\tau} / T)=0 \end{aligned} $ | (24) |
注意此化简过程中使用了Z1-=Z-1-*这一性质,其原因参考文献[11]。
显然式(24)不再是能够采用简单手段直接求解的形式,因此本文通过式(20)先求出
对于同时使用Z1+、Z-1+、Z3+和Z-3+共4个参数对定时误差估计值求解的方法与前文类似,其形式较复杂,可以表示为
| $ \begin{aligned} \frac{\mathrm{d} M^2(\tilde{\tau})}{\mathrm{d} \tilde{\tau}}= & \operatorname{Im}\{X\} \cos (2 \pi \tilde{\tau} / T)+\operatorname{Re}\{X\} \sin (2 \pi \tilde{\tau} / T)+ \\ & 2 \operatorname{Im}\{Y\} \cos (4 \pi \tilde{\tau} / T)+2 \operatorname{Re}\{Y\} \sin (4 \pi \tilde{\tau} / T)+ \\ & 3 \operatorname{Im}\{Z\} \cos (6 \pi \tilde{\tau} / T)+3 \operatorname{Re}\{Z\} \sin (6 \pi \tilde{\tau} / T)+ \\ & \operatorname{Im}\{M\} \cos (2 \pi \tilde{\tau} / T)+\operatorname{Re}\{M\} \sin (2 \pi \tilde{\tau} / T)+ \\ & 2 \operatorname{Im}\{N\} \cos (4 \pi \tilde{\tau} / T)+2 \operatorname{Re}\{N\} \sin (4 \pi \tilde{\tau} / T)+ \\ & \operatorname{Im}\{P\} \cos (2 \pi \tilde{\tau} / T)+\operatorname{Re}\{P\} \sin (2 \pi \tilde{\tau} / T) \end{aligned} $ | (25) |
式中:X=Z-3+Z-1+*, Y=Z-3+Z1+*, Z=Z-3+Z3+*, M=Z-1+Z1+*, N=Z-1+Z3+*, P=Z1+Z3+*。
令式(25)计算的导数为零,并通过迭代手段可求得最终估计结果
图 7为上文所述3种情况下的定时误差估计性能,观测数据长度L0=200,每符号采样点数N=4。3种情况分别为:情况1只使用Z1+和Z-1+进行估计;情况2使用Z1+、Z-1+、Z1-和Z-1-进行估计;情况3使用Z1+、Z-1+、Z3+和Z-3+进行估计。可看出三者的曲线近乎完全重合。

|
图 7 3种情况下的定时误差估计性能 Fig. 7 Timing error estimation performance in three cases |
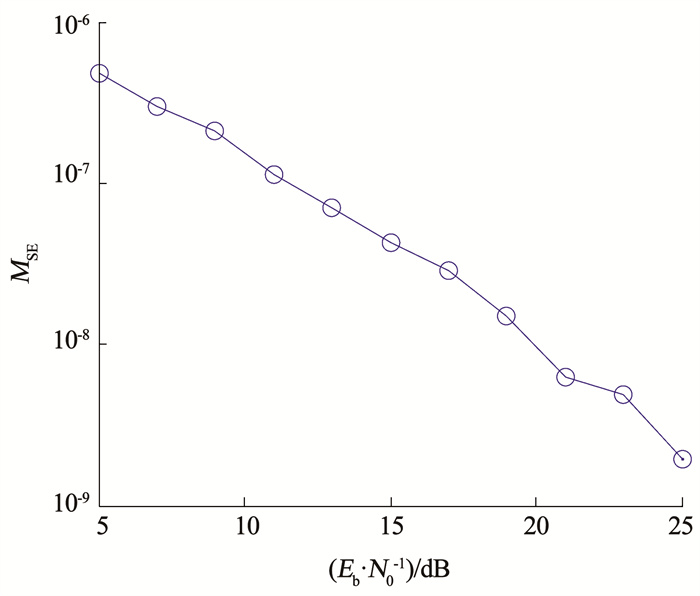
图 8为情况2与情况1的MSE差值,其MSE的差值小于MSE自身的1‰,即增加的Z1-和Z-1-参数对最终估计精度的影响完全可以忽略不计。至于情况3,由于h3+函数的自身能量过小,增加的Z3+和Z-3+已经无法再提高估计精度。
|
图 8 情况1与情况2的MSE差值 Fig. 8 MSE difference between case 1 and case 2 |
由图 7可知,该ML联合估计算法在只使用Z1+、Z-1+两参数时,就可实现高精度的估计,增加其他参数不会对性能产生显著提升,还会大量增加计算的复杂度。因此,考虑只使用Z1+和Z-1+进行联合估计的优化问题。
由式(8)~(14)可知,算法的主要计算量集中在Z1+和Z-1+两个参数的计算上,Z1+和Z-1+的计算框图见图 9。

|
图 9 Z1+和Z-1+的计算框图 Fig. 9 Calculation block diagram of Z1+ and Z-1+ |
h1(re)(k)为h1+(k)的实部,h1(im)(k)为h1+(k)的虚部,且使用了h1+(k)和h-1+(k)共轭的性质(参见文献[11]),从而分别将接收采样信号x(k)与h1(re)(k)和h1(im)(k)相卷积后相加或是相减便可分别得到x(k)与h1+(k)和h-1+(k)卷积的结果。注意x(k)与ejπk/N和e-jπk/N相乘的两路各需延迟ND个采样点,以使这两路数据与卷积后的数据对齐。N为每符号采样点数,D选取为h函数符号跨度的一半,见图 1和图 2,本文选取的h函数符号跨度为6,因此应取D=3。
图 9中的卷积过程是计算复杂度最高的部分,因此,本文主要针对卷积实现过程,提出了一种h函数的优化处理算法,该算法以保证h函数能量不变为准则,且在采样速率为4倍符号速率时每个周期保证能进行4点采样,将其拟合为一个离散的三值函数,将h函数的实部与虚部均化为三值函数,优化后的h1+(t)函数见图 10和图 11,该函数除零值外只存在某单一数值与其负数值。

|
图 10 优化h1+(t)函数的实部 Fig. 10 Optimization of real part of h1+(t) function |

|
图 11 优化h1+(t)函数的虚部 Fig. 11 Optimization of imaginary part of h1+(t) function |
具体实现过程如下:
1) 首先对h1(re)(t)和h1(im)(t)大于0的部分和小于0的部分分别进行积分。从图 10和图 11中可看出,h1(re)(t)为奇对称函数,h1(im)(t)为偶对称函数,定义h1(re)(t)两部分的积分结果均为S1,h1(im)(t)大于0部分的积分结果为S2+,小于0部分的积分结果S2-,其中S2+>S2-。
2) 之后进行离散量化过程。对于h1(re)(t),离散量化过程中共需以下几个参数,每符号采样点数N,量化幅度A(re),非零值量化长度L(re),两个非零值量化起始点n1+、n1-以及两个非零值量化截止点n2+、n2-,定义L(re)=n2+-n1++1=n2--n1-+1,令上述参数满足如下条件:
| $ \left\{\begin{array}{l} A^{(\mathrm{re})} L^{(\mathrm{re})}=S_1 \\ n_1^{-}+n_2^{+}=n_1^{+}+n_2^{-}=6 N \\ L^{(\mathrm{re})}=\left\lfloor N l_{\text {half }}^{(\mathrm{re})}\right\rfloor \end{array}\right. $ | (26) |
从而保证奇对称性以及函数能量不变的性质,式中lhalf(re)为连续函数h1(re)(t)非零部分一半能量所占长度,⌊·」为向下取整。最后根据上述约束条件对量化起始点进行手动调整选取性能最好的量化方案即可。
3) 对于h1(im)(t),离散量化方案与h1(re)(t)类似,需要以下参数: 每符号采样点数N,量化幅度A(im),正负两部分的非零值量化长度L(im)+和L(im)-,从左至右共3个非零值量化起始点n11-、n11+、n12-以及从左至右共3个非零值量化截止点n21-、n21+、n22-。这些参数应满足如下关系:
| $ \left\{\begin{array}{l} L^{(\mathrm{im})-}=n_2^{1-}-n_1^{1-}+1=n_2^{2-}-n_1^{2-}+1 \\ L^{(\mathrm{im})+}=n_2^{1+}-n_1^{1+}+1 \end{array}\right. $ | (27) |
令上述参数满足如下约束条件:
| $ \left\{\begin{array}{l} A^{(\mathrm{im})} L^{(\mathrm{im})-}=S_2^{-} \\ L^{(\mathrm{im})-}=\left\lfloor N l_{\mathrm{half}}^{(\mathrm{im})-}\right\rfloor \\ n_1^{1-}+n_2^{2-}=n_1^{2-}+n_2^{1-}=n_1^{1+}+n_2^{1+}=6 N \\ L^{(\mathrm{im})+}=\left\lfloor S_2^{+} / A^{(\mathrm{im})}\right\rfloor \end{array}\right. $ | (28) |
这一过程中需注意要先算出A(im),再计算L(im)+,若L(im)-计算结果为0则将其置1,lhalf(im)-为连续函数h1(im)(t) < 0部分一半能量所占长度。最后根据上述约束条件对量化起始点进行手动调整选取性能最好的量化方案即可。
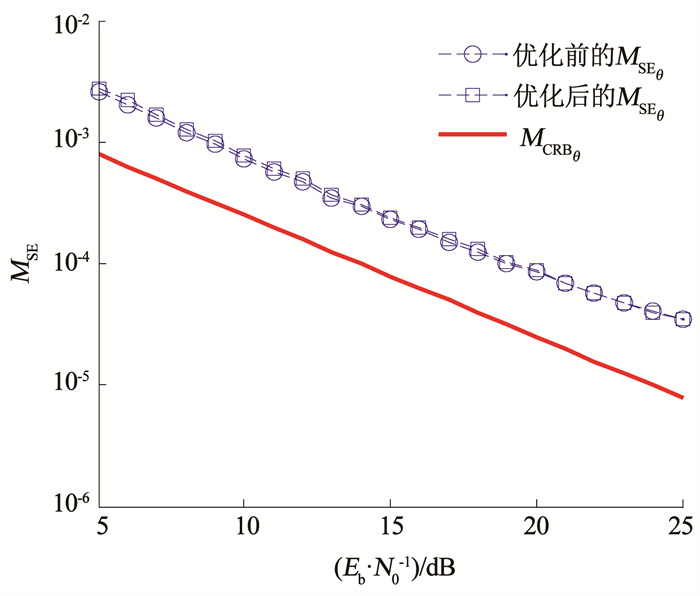
图 12和图 13分别给出观测长度L0=200,每符号采样点N=4情况下的卷积过程优化后ML联合估计算法符号定时性能差别和相位同步性能差别,以及它们与修正后的Cramer-Rao界的关系。

|
图 12 h函数优化前后符号定时性能比较 Fig. 12 Comparison of symbol timing performance before and after h function optimization |
|
图 13 h函数优化前后相位同步性能比较 Fig. 13 Comparison of phase synchronization performance before and after h function optimization |
修正后的Cramer-Rao界计算由文献[9]给出,其形式见式(29)和式(30):
| $ M_{\mathrm{CRB}_\tau}=\frac{4 T^2}{\pi^2 L_0} \times \frac{1}{E_{\mathrm{b}} / N_0} $ | (29) |
| $ M_{\mathrm{CRB}_\theta}=\frac{1}{2 L_0\left(E_{\mathrm{b}} / N_0\right)} $ | (30) |
可以看出,无论是符号定时还是相位同步的估计,使用优化后的h1+(t)函数进行估计对精度的影响都很小,算法的估计精度仍维持在一个较高的水平,因此本文所提出的h函数的优化算法精度高且更加易于实现。
在复杂度方面,假设采样率为N倍符号速率,观测长度为L0。优化前的算法从接收到采样后的信息到得到估计结果,共需计算(6N+3)NL0次复数乘法;优化后的算法由于在每个采样点只需计算一次复数乘法,其余操作只需加法就能实现,因此共需计算4NL0次复数乘法。算法的计算复杂度由O(N2L0)下降为O(NL0)。若以符号采样率为4倍符号速率为例,采样后的h函数共有24个点,因此每个卷积点需计算24次复数乘法,也即96次实数乘法。而使用如图 10和图 11所示的优化后的h函数后,每点的卷积过程只计算4次实数乘法,因此图 9中的卷积过程的实部与虚部除加法器外各只需1个乘法器即可实现,相当于卷积过程的计算复杂度缩小为原来的1/24,整体的计算复杂度下降为原来的14.8%。
对于简化前后的ML联合估计算法的精确度,由于推导过程过于复杂,因而无法从理论上证明h函数量化手段对于估计精度的具体影响,但本文的实际仿真已可充分证明该简化手段的有效性和可靠性。
5 结论本文对基于ML理论的符号定时与相位同步联合估计算法进行了分析研究。在SOQPSK信号模型及ML理论的基础上,基于目前研究针对不同参数选取对估计精度影响分析不足的现状,详细分析了联合算法中不同h函数的能量占比情况,及不同简化程度下算法的性能对比;通过以上分析给出了使用Z1+和Z-1+以外的参数进行估计时算法性能也已经无法显著提升的结论。同时,针对只采用Z1+和Z-1+参数进行估计的情况,围绕算法实现复杂度较高的问题,对h函数进行优化,使其变为一个三值函数,从而简化了算法的计算复杂度。仿真分析表明,在算法定时误差与相位误差估计精度近似不变的前提下,算法卷积过程计算复杂度由O(N2L0)下降为O(NL0),从而降低了算法的实现复杂度。
| [1] |
Interoperability standard for single-access 5-kHz and 25-kHz UHF satellite communications channels: MIL-STD-188-181B[S]. Fort Monmouth: Defense Information Systems Agency, 1999
|
| [2] |
Telemetry standards, IRIG standard 106-17[S]. White Sands Missile Range: Range Commanders Council, 2017
|
| [3] |
Integrated network enhanced telemetry (iNET) Radio Access Network Standards Working Group Radio access network (RAN) standard: Version 0.7.9 Tech. Rep. [S]. 2011. https://www.tena-sda.org/display/INET/iNET+Platform+Interface+Standards
|
| [4] |
HILL T J. A non-proprietary, constant envelope, variant of shaped offset QPSK (SOQPSK) for improved spectral containment and detection efficiency[C]//MILCOM 2000 Proceedings. 21st Century Military Communications. Los Angeles: IEEE, 2000: 347. DOI: 10.1109/MILCOM.2000.904973
|
| [5] |
HOSSEINI E, PERRINS E. Burst-mode synchronization for SOQPSK[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(6): 2707. DOI:10.1109/TAES.2019.2893816 |
| [6] |
CHANDRAN P, PERRINS E. Decision-directed symbol timing recovery for SOQPSK[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(2): 781. DOI:10.1109/TAES.2009.5089561 |
| [7] |
王启峰. SOQPSK信号同步与解调算法研究[D]. 武汉: 华中科技大学, 2016 WANG Qifeng. Research on synchronization and demodulation algorithm of SOQPSK candidate[D]. Wuhan: Huazhong University of Science & Technology, 2016 |
| [8] |
WANG Qifeng, HUANG Benxiong, XU Zhengguang. Joint phase and timing recovery for SOQPSK based on phase trajectory[C]//Proceedings of the 2015 International Conference on Wireless Communications & Signal Processing (WCSP). Nanjing: IEEE, 2015: 1. DOI: 10.1109/WCSP.2015.7341077
|
| [9] |
D'AMICO A A. Feedforward joint clock and phase estimation schemes for SOQPSK-Type signals[J]. IEEE Wireless Communications Letters, 2013, 2(6): 679. DOI:10.1109/WCL.2013.092813.130500 |
| [10] |
CHANDRAN P, PERRINS E S. Symbol timing recovery for CPM with correlated data symbols[J]. IEEE Transactions on Communications, 2009, 57(5): 1265. DOI:10.1109/TCOMM.2009.05.070091 |
| [11] |
D'AMICOA A, D'ANDREAA N, MENGALI U. Feedforward synchronization schemes for MSK-type signals[J]. European Transactions on Telecommunications, 1999, 10(6): 597. DOI:10.1002/ett.4460100605 |
 2023, Vol. 55
2023, Vol. 55


