自适应波束形成技术利用传感器阵列的接收数据计算加权系数，旨在使期望信号无失真通过的同时抑制空间干扰，其广泛应用于雷达、声呐以及无线通信领域^[1]。然而，传感器阵列不仅在制造、安装时产生位置误差，还有可能在使用过程中由于温度和压力等环境变化产生幅度、相位和阵列形状方面的误差^[2]。通常，这些误差会随着时间变化，因此在使用前无法预测，最终会导致传感器阵列的性能严重下降。

在过去几十年内，学者们提出了许多算法来降低各类误差对自适应波束形成器的影响。对角加载^[3]是其中最为著名的一种方法，其主要思想是将样本协方差矩阵与一个均匀对角矩阵相加，从而降低波束形成器对误差的敏感性，然而最优的加载系数一般难以准确取得^[4]。随着凸优化技术的发展，波束形成的稳健性约束被应用于对抗随机误差导致的性能下降问题，例如协方差矩阵拟合方法^[5-6]以及最差性能最优方法^[7-8]等。在此基础上，线性约束^[9]和迭代自适应方法^[10]进一步增强了主瓣指向的稳健性。然而，上述方法都基于样本协方差求逆，其主瓣指向稳健性提升的同时，也牺牲了一部分的干扰抑制能力^[11]。此外，一旦出现较大的导向向量失配，这些波束形成器仍有可能出现期望信号“自消”的现象。

针对上述问题，文献[12]指出，基于样本协方差矩阵求逆类波束形成器的性能下降的最直接原因为样本协方差矩阵内的期望信号成分与期望信号的导向向量出现了失配。因此，文献[13]提出了一种基于空域扇区重构的波束形成方法，该方法重构出了一个不含期望信号成分的干扰加噪声协方差矩阵，避免了高信噪比下的期望信号“自消”问题。在此之后，许多基于空域扇区重构的改进方法被提出，例如稀疏重构^[14-15]、不确定集重构^[16]以及投影重构^[17]等。然而，基于空域扇区重构的方法不仅仅依赖于准确的空间谱信息，也严重依赖于阵列参数的先验知识，当阵列出现误差时其难以准确抑制干扰，总体性能甚至差于传统的对角加载类方法。针对阵列参数的先验知识不准确的问题，文献[18]提出了基于加权子空间拟合的方法来克服传感器位置误差，得到了较好的结果。文献[19]针对幅度相位误差，也提出了一种重构自适应波束形成器，能够有效提高其在只存在幅度相位误差时的输出信干噪比。文献[18-19]采用了估计-补偿的手段，即估计误差后在空域扇区重构过程中对误差进行补偿，仍严重依赖准确的空间谱信息。针对这个问题，文献[20]提出了信号子空间基变换的协方差矩阵重构方法，不再需要空间谱信息。然而，该方法还存在诸多不足：一方面，其仅能克服阵元位置误差，当存在多种误差耦合时，难以对单个误差进行解耦并准确估计，从而降低了协方差矩阵重构的准确性；另一方面，重构的协方差矩阵仅仅利用了信号子空间的信息，噪声协方差矩阵仍假设为理想的对角矩阵；此外，该方法仅采用遗传算法对非线性优化问题进行求解，计算复杂度高。

为解决多种误差耦合时协方差矩阵重构的问题，提出了一种基于特征空间基变换的波束形成方法。该方法通过利用包含信号子空间和噪声子空间的特征空间，仅需要知道信号个数，就能对多种失配参数进行估计并构造出一种基变换矩阵，从而将期望信号分量从信号子空间内剔除。一系列的数值仿真验证了所提波束形成器能够在多种误差耦合时有效抑制空间干扰。

1 信号模型

考虑一个由m个全向传感器组成的阵列，该阵列从几个远场信源处接收窄带信号，则阵列观测到的第k个数据可以写为^[20]

$ \boldsymbol{X}(k)=\boldsymbol{a}_0 s_0(k)+\sum\limits_{q=1}^Q \boldsymbol{a}_q s_q(k)+\boldsymbol{n}(k) $

(1)

式中: a₀和a_q分别为期望信号的实际导向向量和第q个干扰的实际导向向量；s₀(k)、s_q(k)和n(k)分别为期望信号、第q个干扰和加性高斯白噪声。在这个阵列模型中，所有的信号、干扰和噪声都假设为两两互不相关。与文献[20]只考虑位置误差不同，本文考虑传感器位置误差和幅度相位误差耦合的情况，首先给出存在多种误差时的导向矢量为

$ \begin{aligned} \boldsymbol{a}\left(\boldsymbol{d}_{\mathrm{e}}, \boldsymbol{\varphi}_{\mathrm{e}}, \theta\right)= & \boldsymbol{\alpha} \odot \mathrm{e}^{\mathrm{j}\left[k_{\mathrm{w}}\left(\bar{\boldsymbol{d}}+\boldsymbol{d}_{\mathrm{e}}\right) \sin \theta+\boldsymbol{\varphi}_{\mathrm{e}}\right]}= \\ & \overline{\boldsymbol{a}}(\theta) \odot \boldsymbol{\alpha} \odot \mathrm{e}^{\mathrm{j}\left(k_{\mathrm{w}} \boldsymbol{d}_{\mathrm{e}} \sin \theta+\boldsymbol{\varphi}_{\mathrm{e}}\right)} \end{aligned} $

(2)

式中: d为假设的传感器位置向量，d_e为传感器位置误差向量，⊙为矩阵的哈达马积，k_w为波数。α和φ_e分别为传感器增益向量和相位误差向量，本文假设其均与角度无关。通常情况下，阵列的第一个传感器被视为参考阵元，即第一个阵元不存在任何误差。那么，参考传感器的传感器增益设为1。因此，d_e、α和φ_e可以定义为

$ \begin{aligned} & \boldsymbol{d}_{\mathrm{e}}=\left[0, d_2, \cdots, d_M\right]^{\mathrm{T}} \in \mathbb{R}^{M \times 1} \\ & \boldsymbol{\alpha}=\left[1, \alpha_2, \cdots, \alpha_M\right]^{\mathrm{T}} \in \mathbb{R}^{M \times 1} \\ & \boldsymbol{\varphi}_{\mathrm{e}}=\left[0, \varphi_2, \cdots, \varphi_M\right]^{\mathrm{T}} \in \mathbb{R}^{M \times 1} \end{aligned} $

(3)

可以看出，若对于任意阵元i满足d_i=0、φ_i=0、α_i=1，那么a(d_e, φ_e, θ)= a(θ)，即不存在任何误差。由样本协方差矩阵的定义可知，其包含了所有角度的入射信号信息和实际阵列参数信息。因此，可以直接对样本协方差矩阵进行特征分解，得到信号与噪声两部分^[20]为

$\hat{\boldsymbol{R}}_{\mathrm{x}}=\sum\limits_{m=1}^M \lambda_m \boldsymbol{v}_m \boldsymbol{v}_m^{\mathrm{H}}=\boldsymbol{V} \boldsymbol{\varLambda} \boldsymbol{V}^{\mathrm{H}}=\boldsymbol{V}_{\mathrm{S}} \boldsymbol{\varLambda}_{\mathrm{S}} \boldsymbol{V}_{\mathrm{S}}^{\mathrm{H}}+\boldsymbol{V}_{\mathrm{N}} \boldsymbol{\varLambda}_{\mathrm{N}} \boldsymbol{V}_{\mathrm{N}}^{\mathrm{H}} $

(4)

式中λ_m和v_m分别为降序排列的第m个特征值和对应的特征向量；Λ=diag{λ₁，λ₂，⋯, λ_M}是由M个特征值组成的对角矩阵; V是包含所有特征向量的矩阵，构成了特征空间的一组正交基; Λ_S=diag{λ₁, λ₂, ⋯, λ_L} 包含了L个主特征值; V_S是包含主特征值对应特征向量的信号子空间; Λ_N=diag{λ_L+1, ⋯, λ_M}由剩余的特征值组成; V_N为含对应特征向量的噪声子空间。

2 特征空间基变换波束形成方法 2.1 信号子空间和非正交基的估计

根据文献[20]，当阵列和入射信号的先验信息完全精确已知时，由期望信号和干扰对应的真实导向向量张成的空间和信号子空间是相同的，即

$ \operatorname{span}\left\{\boldsymbol{V}_{\mathrm{S}}\right\}=\operatorname{span}\{\boldsymbol{A}\} $

(5)

式中$\boldsymbol{A}=\left\lceil\boldsymbol{a}\left(\theta_0\right), \boldsymbol{a}\left(\theta_1\right), \cdots, \boldsymbol{a}\left(\theta_Q\right)\right\rceil $表示由1个期望信号和Q个干扰对应的真实导向向量组成的矩阵，可以被看作是信号子空间的一组角度相关的非正交基；相对的，V_S中的各列也可以被看作为信号子空间的一组正交基。值得注意的是，当干扰与期望信号相干，或者信号干噪比R_IN(interference-to-noise ratio, INR)远大于信噪比R_SN(signal-to-noise ratio, SNR)时，主特征值的数量L将不再等于入射信号的数量，L的个数将会小于实际的信号数量。此时，可以使用其他信源数估计的算法来估计入射信号的数量。

根据式(2)，增益误差与位置误差以及相位误差两两相互独立，且幅度误差只影响导向向量的幅度，那么第m个传感器的增益误差可以估计为

$ \hat{\alpha}_m=\sqrt{\frac{\hat{R}_{\mathrm{x}}(m, m)-\lambda_M}{\hat{R}_{\mathrm{x}}(1, 1)-\lambda_M}} $

(6)

式中$\hat{R}_{\mathrm{x}}(m, m) $为样本协方差矩阵中第m个对角线元素，λ_M是样本协方差矩阵(sample covariance matrix，SCM)中最小的特征值。

与文献[20]不同的是，本文不仅考虑了传感器的位置误差，额外的相位误差以及信号来波方向也都是耦合在一起的，它们都会影响导向向量的相位。由于参数的耦合效应，无法对位置误差相位误差以及来波方向3个参数进行解耦，也就无法对信号进行精确的方位估计。然而，波束形成与方位估计的原理不同，波束形成只需要估计位置误差、相位误差以及信号来波方向三者耦合后的相位矩阵，就可以对干扰进行精确的抑制。根据式(2)，当各个信号的入射方向未知且存在阵元位置误差和相位误差时，可以将导向向量写为矩阵形式，即

$ \begin{aligned} \boldsymbol{A}\left(\boldsymbol{d}_{\mathrm{e}}, \boldsymbol{\varphi}_{\mathrm{e}}, \boldsymbol{\varTheta}\right)= & {\left[\boldsymbol{a}\left(\boldsymbol{d}_{\mathrm{e}}, \boldsymbol{\varphi}_{\mathrm{e}}, \theta_0\right), \boldsymbol{a}\left(\boldsymbol{d}_{\mathrm{e}}, \boldsymbol{\varphi}_{\mathrm{e}}, \theta_1\right), \cdots, \right.} \\ & \left.\boldsymbol{a}\left(\boldsymbol{d}_{\mathrm{e}}, \boldsymbol{\varphi}_{\mathrm{e}}, \theta_Q\right)\right] \end{aligned} $

(7)

式中: Θ包含了所有信号的方位; 矩阵$\boldsymbol{A}\left(\boldsymbol{d}_{\mathrm{e}}, \boldsymbol{\varphi}_{\mathrm{e}}, \boldsymbol{\varTheta}\right) $是阵元位置误差向量d_e、阵元相位误差向量φ_e和方向向量Θ的函数。为了能够将导向向量集张成空间A(d_e, φ_e, Θ)与信号子空间span{V_S}进行拟合，根据文献[20]，两个子空间之间的空间距离D_S(space distance, SD)为

$ D_{\mathrm{S}}=\left\|\boldsymbol{V}_{\mathrm{S}} \boldsymbol{W}^{1 / 2}-\boldsymbol{A}\left(\boldsymbol{d}_{\mathrm{e}}, \boldsymbol{\varphi}_{\mathrm{e}}, \boldsymbol{\varTheta}\right) \boldsymbol{T}\right\|_{\mathrm{F}} $

(8)

式中: ‖·‖_F为求矩阵的Frobenius范数(F-范数); W为一个正定矩阵，在最小渐进方差最小的条件下可以取为W =(Λ_S-λ_MI)²Λ_S^-1。 T的最小二乘解可以写为

$ \begin{aligned} \hat{\boldsymbol{T}}= & \left(\boldsymbol{A}^{\mathrm{H}}\left(\boldsymbol{d}_{\mathrm{e}}, \boldsymbol{\varphi}_{\mathrm{e}}, \boldsymbol{\varTheta}\right) \boldsymbol{A}\left(\boldsymbol{d}_{\mathrm{e}}, \boldsymbol{\varphi}_{\mathrm{e}}, \boldsymbol{\varTheta}\right)\right)^{-1} \boldsymbol{A}^{\mathrm{H}}\left(\boldsymbol{d}_{\mathrm{e}}, \boldsymbol{\varphi}_{\mathrm{e}}, \boldsymbol{\varTheta}\right) \boldsymbol{V}_{\mathrm{S}}= \\ & \boldsymbol{A}^{+}\left(\boldsymbol{d}_{\mathrm{e}}, \boldsymbol{\varphi}_{\mathrm{e}}, \boldsymbol{\varTheta}\right) \boldsymbol{V}_{\mathrm{S}} \end{aligned} $

(9)

将式(9)代入式(8)，可以将空间距离改写为

$ D_{\mathrm{S}}=\left\|\boldsymbol{V}_{\mathrm{S}} \boldsymbol{W}^{1 / 2}-\boldsymbol{A}\left(\boldsymbol{d}_{\mathrm{e}}, \boldsymbol{\varphi}_{\mathrm{e}}, \boldsymbol{\varTheta}\right) \boldsymbol{T}\right\|_{\mathrm{F}}=\operatorname{tr}\left\{\boldsymbol{P}^{\perp} \boldsymbol{V}_{\mathrm{S}} \boldsymbol{W} \boldsymbol{V}_{\mathrm{S}}^{\mathrm{H}}\right\} $

(10)

此时，可以通过最小化两个空间的距离来估计真实的导向向量集为

$ \hat{\boldsymbol{A}}\left(\hat{\boldsymbol{d}}_{\mathrm{e}}, \hat{\boldsymbol{\varphi}}_{\mathrm{e}}, \hat{\boldsymbol{\varTheta}}\right)=\min\limits _{\boldsymbol{d}_{\mathrm{e}}, \boldsymbol{\varphi}_{\mathrm{e}}, \boldsymbol{\varTheta}} \operatorname{tr}\left\{\boldsymbol{P}^{\perp} \boldsymbol{V}_{\mathrm{S}} \boldsymbol{W} \boldsymbol{V}_{\mathrm{S}}^{\mathrm{H}}\right\} $

(11)

式中: $\boldsymbol{P}^{\perp}$是正交投影矩阵, 可以表示为$\boldsymbol{P}^{\perp}=\boldsymbol{I}-$ $\boldsymbol{A}\left(\boldsymbol{d}_{\mathrm{e}}, \boldsymbol{\varphi}_{\mathrm{e}}, \boldsymbol{\varTheta}\right) \boldsymbol{A}^{+}\left(\boldsymbol{d}_{\mathrm{e}}, \boldsymbol{\varphi}_{\mathrm{e}}, \boldsymbol{\varTheta}\right)$; 其中$\boldsymbol{A}\left(\boldsymbol{d}_{\mathrm{e}}, \boldsymbol{\varphi}_{\mathrm{e}}, \boldsymbol{\varTheta}\right) \in$ ^{M × (Q + 1)}代表了可能不匹配的导向向量集, $(\cdot)^{+}$为矩阵的伪逆, 为复数域, $\varTheta$中包含了所有信号的可能方向。$\boldsymbol{A}\left(\boldsymbol{d}_{\mathrm{e}}, \boldsymbol{\varphi}_{\mathrm{e}}, \boldsymbol{\varTheta}\right)$中的第$i$列表示第$i$个信号的导向向量, 可以表示为

$ \boldsymbol{a}\left(\boldsymbol{d}_{\mathrm{e}}, \boldsymbol{\varphi}_{\mathrm{e}}, \theta_i\right)=\hat{\boldsymbol{\alpha}} \odot \mathrm{e}^{\mathrm{j}\left[k_{\mathrm{w}}\left(\boldsymbol{d}+\boldsymbol{d}_{\mathrm{e}}\right) \sin \boldsymbol{\theta}_i+\boldsymbol{\varphi}_{\mathrm{e}}\right]} $

(12)

式中$\hat{\boldsymbol{\alpha}}=\left[1, \hat{\alpha}_2, \cdots, \hat{\alpha}_M\right]^{\mathrm{T}} $是增益误差向量，该最小化问题显然是一个包含2M+Q－1变量的非线性优化问题。该优化问题类似于文献[20]中的最优化问题，然而求解的变量增加了近一倍，如果直接采用文献[20]中所使用的遗传算法进行直接求解，其计算复杂度将大大超过可接收范围。本文使用名为BFGS方法的二阶优化方法，其收敛速度快但对初值敏感。因此，本文提出一种混合优化方案，即先进行几代遗传算法初始化提供一个较好的初始值，接着使用收敛速度快的BFGS方法来解决这个优化问题。

首先构造最小化问题的解向量为

$\boldsymbol{\delta}=\left[d_2, \cdots, d_M, \varphi_2, \cdots, \varphi_M, \theta_0^{\prime}, \cdots, \theta_Q^{\prime}\right]^{\mathrm{T}} $

(13)

式中θ_q^′, q=0, 1, ⋯, Q是以升序排列的所有信号的可能波达方向。θ₀^′不一定是期望信号的波达方向。此时，式(11)可以改写为

$ \hat{\boldsymbol{A}}(\hat{\boldsymbol{\delta}})=\min\limits _\boldsymbol{\delta} F(\boldsymbol{\delta}) $

(14)

式中F(δ)为目标函数。因此，BFGS方法的迭代算法可以表示为

$ \hat{\boldsymbol{\delta}}(l+1)=\hat{\boldsymbol{\delta}}_{(l)}-\beta_{(l)} \boldsymbol{B}_{l+1}^{-1} F^{\prime}\left(\hat{\boldsymbol{\delta}}_{(l)}\right) $

(15)

式中: $\dot{\boldsymbol{\delta}}_{(l)}$和$\beta_{(l)}$分别为第一次迭代的解向量和步长$; F^{\prime}(\boldsymbol{\delta})$为$F(\boldsymbol{\delta})$的一阶导数, 表示梯度$; \boldsymbol{B}$是用来近似二阶黑塞矩阵的正定矩阵, 其可以使用迭代的方式计算为

$ \begin{aligned} \boldsymbol{B}_{l+1}^{-1}= & \boldsymbol{B}_l^{-1}+\left(1+\frac{\Delta g_l^{\mathrm{T}} \boldsymbol{B}_l^{-1} \Delta g_l}{\Delta g_l^{\mathrm{T}} \Delta \boldsymbol{\delta}_l}\right) \frac{\Delta \boldsymbol{\delta}_l \Delta \boldsymbol{\delta}_l^{\mathrm{T}}}{\Delta \boldsymbol{\delta}_l^{\mathrm{T}} \Delta g_l}- \\ & \frac{\boldsymbol{B}_l^{-1} \Delta g_l \Delta \boldsymbol{\delta}_l^{\mathrm{T}}+\left(\boldsymbol{B}_l^{-1} \Delta g_l \Delta \boldsymbol{\delta}_l^{\mathrm{T}}\right)^{\mathrm{T}}}{\Delta g_l^{\mathrm{T}} \Delta \boldsymbol{\delta}_l} \end{aligned} $

(16)

式中: Δg_l为前后两次梯度的差值，Δδ_l为前后解的差值。梯度F′(δ)可以表示为

$ F^{\prime}(\boldsymbol{\delta})=\left[\frac{\partial F}{\partial d_m}, \cdots, \frac{\partial F}{\partial \varphi_m}, \cdots, \frac{\partial F}{\partial \theta_0^{\prime}}, \cdots, \frac{\partial F}{\partial \theta_Q^{\prime}}\right]^{\mathrm{T}} $

(17)

式(17)中梯度的目标函数F(δ)中含有矩阵求迹等算符，使得一阶偏导数的闭式解很难得到。利用F(δ)是光滑的，即对所有变量二阶可导的性质，可以采用中心差分来逼近一阶偏导数。例如，梯度可以近似为

$ \frac{\partial F\left(\hat{\boldsymbol{\delta}}_{(l)}\right)}{\partial d_2} \approx \frac{F\left(\hat{\boldsymbol{\delta}}_{(l)}+\Delta \boldsymbol{\delta}_{d_2}\right)-F\left(\hat{\boldsymbol{\delta}}_{(l)}-\Delta \boldsymbol{\delta}_{d_2}\right)}{2 \Delta d_2} $

(18)

式中Δδ_d2=[Δd₂, 0]^T，Δd₂是一个很微小的量，表示变量d₂的微元。在使用中心差分法后可以有效地计算目标函数的梯度。解决了梯度的数值计算问题后，就可以解得导向向量集为

$ \hat{\boldsymbol{A}}_{\mathrm{S}}=\hat{\boldsymbol{A}}\left(\hat{\boldsymbol{d}}_{\mathrm{e}}, \hat{\boldsymbol{\varphi}}_{\mathrm{e}}, \hat{\boldsymbol{\varTheta}}\right)=F(\hat{\boldsymbol{\delta}}) $

(19)

需要注意的是, 尽管空间$\operatorname{span}\left\{\hat{\boldsymbol{A}}_{\mathrm{S}}\right\}$和空间$\operatorname{span}\left\{\boldsymbol{V}_{\mathrm{S}}\right\}$的空间距离最小化, 由于阵元位置误差、相位向量误差和DOA误差耦合在一起, 导致估计出的$\hat{\boldsymbol{d}}_{\mathrm{e}} 、\hat{\boldsymbol{\varphi}}_{\mathrm{e}}$和$\hat{\boldsymbol{\varTheta}}$只能保证$\operatorname{span}\left\{\hat{\boldsymbol{A}}_{\mathrm{S}}\right\}$和$\operatorname{span}\left\{\boldsymbol{V}_{\mathrm{S}}\right\}$最大程度的拟合, 而并不一定是实际值。

2.2 基变换重构干扰和噪声协方差矩阵

为了避免直接估计干扰和噪声的功率, 可以通过使用特征空间基变换技术直接从样本协方差矩阵中消除期望信号分量, 从而重建干扰和噪声协方差矩阵。在估计得到$\hat{\boldsymbol{A}}_{\mathrm{S}}$后, 两个子空间近似相等, 即$\operatorname{span}\left\{\hat{\boldsymbol{A}}_{\mathrm{S}}\right\} \approx \operatorname{span}\left\{\boldsymbol{V}_{\mathrm{S}}\right\}$, 其中$\boldsymbol{V}_{\mathrm{S}}$可被视为信号子空间的一组正交基, 而$\hat{\boldsymbol{A}}_{\mathrm{s}}$可以被视为信号子空间中与角度相关的一组非正交基。

样本协方差矩阵在加性高斯白噪声情况下是一个典型的厄密特矩阵，将样本协方差矩阵进行特征分解后，可以根据特征值大小对子空间进行划分，这样就可以得到相互正交的信号子空间和噪声子空间。文献[20]中将信号子空间进行拟合后，直接在信号子空间中将期望信号分量剔除，从而得到干扰协方差矩阵，而噪声协方差矩阵仍然采用对角矩阵。在本文中，我们将信号子空间和噪声子空间组合为特征空间，并在特征空间中直接将期望信号分量剔除，从而剩余的干扰和噪声部分可以直接生成干扰加噪声协方差矩阵，避免了噪声功率的估计。由定义可知, $\hat{\boldsymbol{A}}_{\mathrm{S}}$中每一列均与噪声子空间正交, 可以表示为$\operatorname{span}\left\{\hat{\boldsymbol{A}}_{\mathrm{S}}\right\} \perp \operatorname{span}\left\{\boldsymbol{V}_{\mathrm{N}}\right\}$。此时, 在整个特征空间$\operatorname{span}\{\boldsymbol{V}\}$中, $\operatorname{span}\left\{\hat{\boldsymbol{A}}_{\mathrm{S}}\right\}$是$\operatorname{span}\left\{\boldsymbol{V}_{\mathrm{N}}\right\}$的正交补空间, 这表明：

$ \operatorname{span}\left\{\left[\hat{\boldsymbol{A}}_{\mathrm{S}} \boldsymbol{V}_{\mathrm{N}}\right]\right\} \approx \operatorname{span}\left\{\left[\boldsymbol{V}_{\mathrm{S}} \boldsymbol{V}_{\mathrm{N}}\right]\right\}=\operatorname{span}\{\boldsymbol{V}\} $

(20)

式中$\left[\hat{\boldsymbol{A}}_{\mathrm{S}} \;\boldsymbol{V}_{\mathrm{N}}\right]$是一个$M \times M$阶矩阵, 可以定义一个从$\left[\hat{\boldsymbol{A}}_{\mathrm{S}}\; \boldsymbol{V}_{\mathrm{N}}\right]$到$\boldsymbol{V}$的基变换矩阵为

$ \boldsymbol{T}=\left[\begin{array}{ll} \hat{\boldsymbol{A}}_{\mathrm{S}} & \boldsymbol{V}_{\mathrm{N}} \end{array}\right]^{+} \boldsymbol{V} $

(21)

因此，式(4)中样本协方差矩阵可以表示为

$ \hat{\boldsymbol{R}}_{\mathrm{x}}=\boldsymbol{V} \boldsymbol{\varLambda} \boldsymbol{V}^{\mathrm{H}}=\left[\hat{\boldsymbol{A}}_{\mathrm{S}}\; \boldsymbol{V}_{\mathrm{N}}\right] \boldsymbol{T} \boldsymbol{\varLambda} \boldsymbol{T}^{\mathrm{H}}\left[\hat{\boldsymbol{A}}_{\mathrm{S}}\; \boldsymbol{V}_{\mathrm{N}}\right]^{\mathrm{H}} $

(22)

式中信号子空间span{V}正交基V可以表示为V=$\left[\hat{\boldsymbol{A}}_{\mathrm{S}} \;\boldsymbol{V}_{\mathrm{N}}\right] \boldsymbol{T} $。此时可以直接从样本协方差矩阵中剔除期望信号成分，并重构干扰加噪声协方差矩阵为

$ \hat{\boldsymbol{R}}_{\mathrm{i}+\mathrm{n}}=\left[\hat{\boldsymbol{A}}_{\mathrm{S}} \;\boldsymbol{V}_{\mathrm{N}}\right] \boldsymbol{D} \boldsymbol{T} \boldsymbol{\varLambda} \boldsymbol{T}^{\mathrm{H}} \boldsymbol{D}^{\mathrm{H}}\left[\hat{\boldsymbol{A}}_{\mathrm{S}} \;\boldsymbol{V}_{\mathrm{N}}\right]^{\mathrm{H}} $

(23)

式中D是M×M的对角矩阵，表示为

$ \boldsymbol{D}=\operatorname{diag}\left\{\left[\mu, \boldsymbol{1}_{1 \times M-1}\right]\right\} $

(24)

式中μ是一个大于零的非常小的常数，是为了确保在样本协方差矩阵中将期望信号成分进行提出。当μ=0的情况下，虽然在理论上可以完全消除期望信号成分，但是也可能导致$\hat{\boldsymbol{R}}_{\mathrm{i}+\mathrm{n}} $产生零特征值或极小特征值，使得$\hat{\boldsymbol{R}}_{\mathrm{i}+\mathrm{n}} $不可逆，所以μ一般取值可以很小，但是不能直接取0。

2.3 波束形成器设计

在实际应用中，期望信号的真实导向向量是很难直接得到的，这就需要对导向向量进行估计或校正。上一小节中，已经估计出较为准确的干扰加噪声协方差矩阵，因此，期望信号的导向向量可以被估计为期望信号协方差矩阵的主特征向量，具体表达式为

$ \hat{\boldsymbol{a}}_0=\sqrt{M} P\left\{\hat{\boldsymbol{R}}_{\mathrm{x}}-\hat{\boldsymbol{R}}_{\mathrm{i}+\mathrm{n}}\right\} $

(25)

式中P{·}为协方差矩阵最大特征值对应的特征向量。因此，波束形成器的加权向量可以写为

$ \boldsymbol{w}=\frac{\hat{\boldsymbol{R}}_{\mathrm{i}+\mathrm{n}}^{-1} \hat{\boldsymbol{a}}_0}{\boldsymbol{a}_0^{\mathrm{H}} \hat{\boldsymbol{R}}_{\mathrm{i}+\mathrm{n}}^{-1} \hat{\boldsymbol{a}}_0} $

(26)

至此，能够得到所提波束形成器的加权向量，理论上该波束形成器在阵列存在误差时，仍能准确地抑制未知方位的干扰，并输出期望信号。所提波束形成器对误差稳健的理论机理主要可以概括为以下几点：

1) 充分考虑了不同类型的阵列误差对阵列流形向量影响，并将所有可能的误差作为未知参数纳入了信号模型;

2) 利用接收数据的信号子空间以及入射信号的阵列流形向量张成空间应当相同的特性，建立了包含所有误差参数的非线性优化方程，并采用混合优化的方式对其进行快速求解;

3) 利用了信号子空间的拟合只需要所有信号的导向向量，而不需要对误差参数精确求解的特性，避免了对耦合在一起的未知参数进行解耦;

4) 将拟合后的导向向量与噪声子空间组合为新的特征空间，直接在特征空间内剔除期望信号分量，最大限度保留了干扰和噪声的真实信息，从而能够在波束形成过程中精确地抑制干扰和噪声。

2.4 性能分析

本文所提算法的计算复杂度主要取体现在式(11) 中的信号子空间非正交基的估计过程，其待优化的变量数目为Q+2M－1个。因此，假设遗传算法初始化和BFGS的总迭代次数为μ，那么所提算法总体的复杂度就可以写为O(μM²(Q+2M－1)²)。作为对比，收缩不确定集的波束形成器^[20]的计算复杂度可以写为O(max(M³; M²[(I+J)L]))，式中的I、J以及L都是离散角度的数量，文章中的典型值分别为17、34以及171。INCM重构和SV估计波束形成器^[13]的计算复杂度为O(M^3.5)。

本文所提算法能够在阵元位置、幅相误差以及信号入射角度均未知的情况下对干扰进行抑制，从所实现的功能角度来说，所提算法已经接近于“盲”算法。然而，其与盲源分离(blind source separation, BSS)技术仍有很大的区别。从先验知识的角度来看，虽然所提算法和BSS都是在各个信号源以及阵列参数未知情况下的信号波形估计器, 然而所提算法仍需要信源个数作为先验知识。

许多文献都已经证明BSS方法和自适应波束形成方法是等效的，BSS方法的性能不会高于自适应波束形成的性能上限^[21]。此外，BSS方法存在两个主要缺陷。第一个是BSS方法的输出信号幅度信息可能是不准确的，即BSS方法做不到期望信号的无失真要求，难以用于准确估计信号的功率。BSS方法的另一个缺陷是如果不利用阵列结构信息，BSS的输出将不包含任何角度信息，BSS方法只能笼统地将各个源信号分离，但不能像所提算法一样提取出指定方向的信号。因此，本文所提算法的功能是BSS算法无法实现的。表 1给出了所提算法与BSS的区别^[21]。

3 数值仿真

利用数值仿真来评估所提出的波束形成器的稳健性，考虑一个包含10个无指向性阵元的均匀直线阵，此阵列接收3个远场源的窄带信号，阵元间距为信号的半波长。期望信号和干扰均从零均值高斯噪声中产生，干扰功率为20 dB，3个信号在时间和空间上是相互独立的。阵列噪声设置为高斯白噪声，功率为0 dB。在研究信干噪比R_SIN(signal-to-interference ratio, SINR)随R_SN变化的规律时，快拍数K=30；当研究R_SIN随快拍数的变化规律时，R_SN=10 dB。所有数值实验的结果如无特殊说明，均为200次蒙特卡洛模拟的平均值。在这些数值仿真中，假设除参考阵元外的校准误差部分由增益误差、相位误差以及阵元位置误差组成。其中，增益误差服从高斯分布N(0, 0.1²)，相位误差服从N(0, (0.1π)²)，阵元位置误差服从N(0, 0.1²)。混合优化过程中，用以提供初始化的遗传算法迭代次数为15次。

将所提算法与其他3个波束形成器进行对比，它们分别是稳健Capon波束形成器(记为RCB)、INCM重构和SV估计波束形成器(记为REB)、基于收缩不确定集的波束形成器(记为USS-REB)。假设REB和USS-REB的期望信号扇区为Θ=[10°, 20°]；对于USS-REB，不确定集约束参数为ε= $\sqrt{0.1} $，干扰扇区为Θ_int=[－30°, －20°]∪[30°, 40°]；RCB的约束参数为ε=3。

3.1 信号DOA精确已知时，但存在失配误差

在第一个数值仿真实例中，假定对于所有波束形成器来说3个信号的DOA都是精确已知的。假设期望信号来自15°，2个干扰信号分别从－25°和35°入射。由于信号的DOA已知，式(11)中的Θ参数固定，即将Θ从解空间向量中排除，再进行非正交基的估计。

图 1给出了DOA精确已知情况下的输出信干噪比随输入信噪比的变化情况，可以看出RCB的性能随着输入信噪比的升高而急剧降低，即使信号DOA精确已知，高信噪比下RCB对导向向量误差的敏感程度较高，导致其性能急剧降低。对于REB和USS-REB这两个基于空域扇区重构的波束形成器在不同的输入信噪比条件下，它们的输出信干噪比都要比最优上限低大约14 dB，性能甚至差于基于样本协方差矩阵的RCB。造成这种现象的原因是此次仿真使用的导向向量误差较大，导向向量失配情况较为严重，空域扇区重构的REB和USS-REB采用的重构协方差矩阵无论是在低信噪比还是高信噪比下，与真实的协方差矩阵一直存在较大差异。可以看出所提出算法的性能几乎贴近于最优上限，由于采用了特征子空间非正交基的联合估计以及基变换重构，所提算法能够较为稳健地将期望信号成分从样本协方差矩阵中直接剔除，从而保证了其拥有较好的干扰抑制性能的同时，能够避免期望信号“自消”。

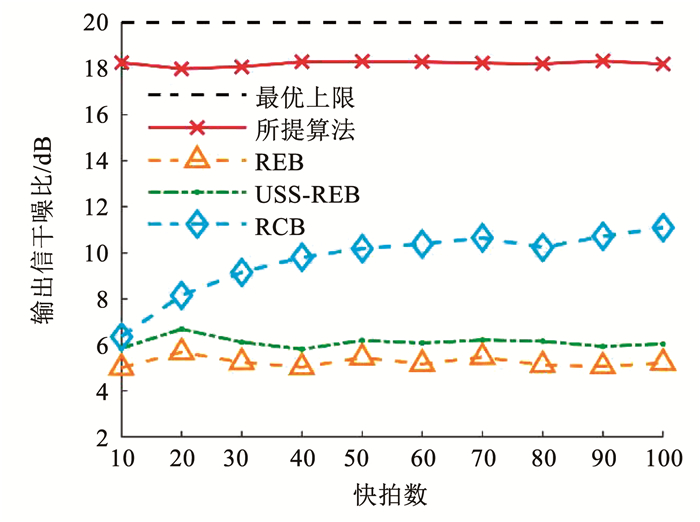
图 2为输出信干噪比随着快拍数的变化曲线。由于模型误差较大，REB和USS-REB已经失效。随着快拍数的增大，RCB所采用的样本协方差矩阵误差降低，性能逐步升高至10 dB左右。因为直接利用了重构协方差矩阵的理想特性，而不是样本协方差矩阵的统计特性，所提算法的性能基本不随快拍数而变化，对小快拍数也较为稳健。

3.2 信号DOA未知时的性能

在第二个仿真实例中，探究同时存在阵元位置误差以及信号DOA误差的情况下波束形成器的性能。除了上述阵元位置以及幅相误差外，所有信号的DOA误差都服从[－2°, 2°]的均匀分布，即期望信号从[13°, 17°]内随机射入，两个干扰的来波方向分别为[－27°, -23°]和[33°, 37°]内的随机值。由于DOA误差存在，所有信号精确的DOA都是未知的。

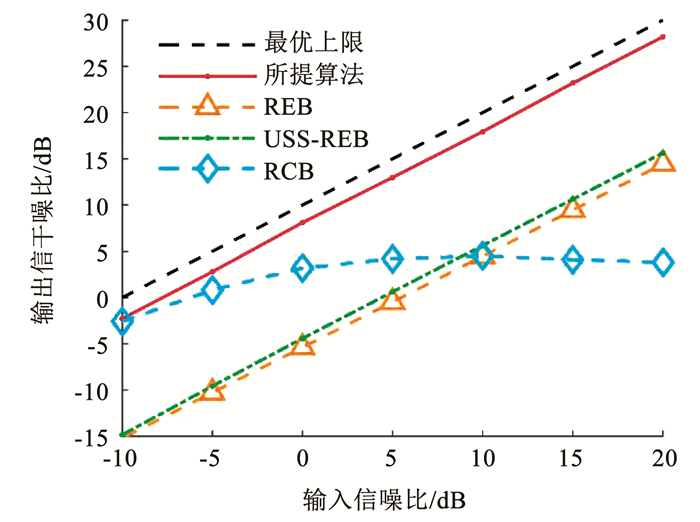
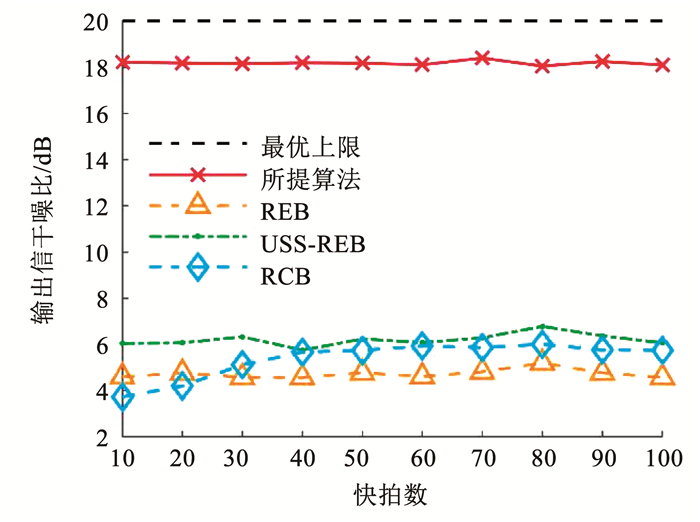
图 3展示了DOA未知时各算法的输出信干噪比随信噪比的变化情况，其中REB和USS-REB已经失效，其性能与图 1相比几乎没有变化。由于采用了三类误差与信号DOA的联合估计，所提算法可以给出精确的子空间非正交基，从而能够利用基变换技术重构出较为精确的干扰加噪声协方差矩阵，即使在DOA入射角度未知的情况下，也能有效地将样本协方差矩阵中的期望信号成分剔除，从而保证了波束形成器在信号DOA未知且存在阵元位置和幅相误差时的稳健性。图 4给出了不同的波束形成器在不同快拍数下的性能。与图 2类似，所提算法在不同的快拍数下都具有较为稳健的性能。RCB算法性能与图 2相比有较大差别，这是因为未知的DOA会加剧其对导向向量的敏感程度，造成期望信号“自消”。

3.3 算法的收敛性

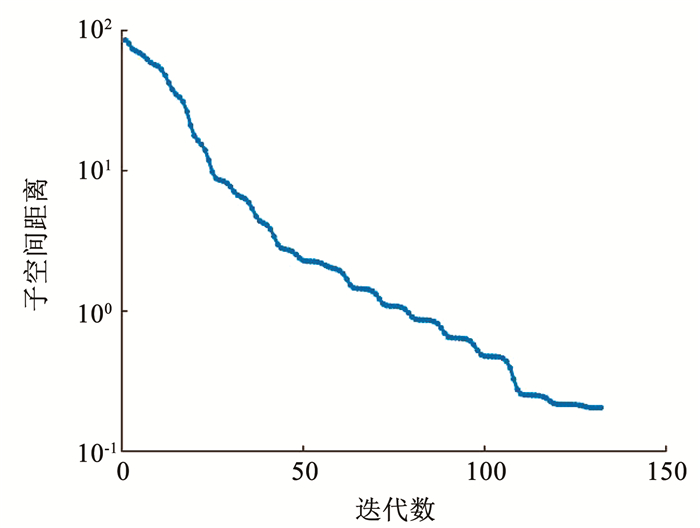
在第三个数值仿真研究混合优化算法的收敛性，该算法用以解决估计非正交基的非线性优化问题。在本例中，假设所有的参数设置与第二个数值仿真例子相同，从而观测估计出的子空间距离随迭代数的变化特性。图 5给出了估计的子空间距离随迭代数的变化曲线，在迭代数较小时，初始的子空间距离达到了近100，这是由于阵元位置、幅相误差以及DOA误差耦合的导向向量误差，引起导向向量张成的子空间与真实信号子空间的不匹配。随着迭代数的增加，子空间距离急剧下降，最终在130次迭代后达到收敛，子空间距离降低至0.2。此时，导向向量张成的子空间与信号子空间拟合程度高，通过本文所提算法，能够直接在样本协方差矩阵中剔除期望信号成分，从而保证了波束形成器的稳健性。

4 结论

针对传感器阵列的阵元位置误差与幅度相位误差共存且信号精确的来波方向未知的情况，提出了一种基于特征空间基变换重构干扰加噪声协方差矩阵的方法。该算法首先利用信号真实的导向向量张成的空间与信号子空间相同且与噪声子空间正交的特性，构建了一个用以估计信号子空间角度相关非正交基的联合优化问题。通过采用遗传算法与BFGS拟牛顿算法相结合的方法，使得此联合优化问题迅速收敛至最优解。最终，通过将导向向量拟合的信号子空间与观测噪声子空间结合为特征空间，并在特征空间内将期望信号成分剔除，从而直接重构出干扰加噪声协方差矩阵。数值仿真证明，所提波束形成算法在导向向量失配和信号方位未知的情况下稳健性较强，能够在保证期望信号无失真的同时，有效抑制未知方向的干扰。