2. 武汉工程大学 邮电与信息工程学院, 武汉 430073
2. The College of Post and Telecommunication, Wuhan Institute of Technology, Wuhan 430073, China
为了保证结构在使用周期内的安全,精确的安全检测与及时的诊断评估非常重要[1]。建立一个与实际结构响应相吻合的有限元模型是正确评估结构安全的前提。有限元模型修正是修正结构初始建模的有效方法。结构的有限元模型修正可分为确定性模型修正和随机模型修正。确定性有限元模型修正方法已经在土木、机械和航空航天等领域得到了成功应用[2-3]。该方法认为修正模型的参数为确定性值,通过实测结构静动力响应反向识别结构参数,使得有限元模型计算结果与实际结构响应一致。但是在实际工程中,由于结构建模存在着大量不确定的因素如材料特性、几何尺寸、边界条件以及外荷载等[4],以及测量的不确定性,这些不确定性因素会导致结构修正参数的不确定性。这种不确定性可用概率的概念来描述。随机有限元模型修正是在考虑上述不确定性因素条件下[5-6],通过含有随机误差的实测响应来估计结构参数的统计特性,从而使得修正后的有限元模型的响应统计特性与实测结果一致。并且可将获得的修正参数用于结构检测和损伤识别,为结构安全评估提供可靠的分析模型[7-10]。基于贝叶斯的有限元模型修正方法最早由Beck等[11]提出,该方法结合了先验信息、实测信息等多种信息,考虑了结构测量以及本身的不确定因素,已成为随机模型修正中的一个重要研究方法。由于该方法不仅需要进行确定性模型的迭代计算,且在每步迭代过程中,都需要进行基于马尔可夫链抽样的大量样本计算,所以计算耗时较长,当修正参数较多时往往不收敛。
为了提高贝叶斯模型修正的计算效率,运用代理模型(meta-model)替换有限元模型开展抽样计算是一个很有意义的方向。传统的代理模型一般是先通过一定量的样本计算已知的输入输出关系,然后选择一个数学模型(例如响应面)拟合结构的输入输出关系。在代理模型发展过程中,邓苗毅等[12]运用响应面代理模型进行了静力贝叶斯模型修正;马天政等[13]采用Kriging代理模型建立了结构输入和输出关系,提高了贝叶斯模型修正的效率;除此之外的代理模型还有人工神经网络代理模型[14]等,但这些代理模型的准确性非常依赖于拟合样本选取的合适性。与上述传统的代理模型不同,本文提出了一种新的同伦代理模型,利用同伦方法求解有限元静力平衡方程,不需要通过数据拟合建立输入输出或修正参数与响应之间的关系。进一步结合贝叶斯方法,建立了一种改进的贝叶斯随机模型修正方法。数值仿真与试验结果表明,该方法在保证贝叶斯模型修正精度的同时,极大地提高了计算效率。同时在先验信息误差及测量误差较大的情况下,具有很好的适用性。
1 贝叶斯模型修正 1.1 贝叶斯模型修正原理贝叶斯模型修正是通过结合先验信息和测量数据来更新初始模型的修正参数[15],这一过程可表示为
| $ \begin{aligned} p(\boldsymbol{\theta} \mid x)= & \frac{p(x \mid \boldsymbol{\theta}) \pi(\boldsymbol{\theta})}{\int_\boldsymbol{\theta} p(x \mid \boldsymbol{\theta}) \pi(\boldsymbol{\theta}) \mathrm{d} \boldsymbol{\theta}}= \\ & c \cdot p(x \mid \boldsymbol{\theta}) \pi(\boldsymbol{\theta}) \end{aligned} $ | (1) |
式中:θ为修正参数;x为结构响应;π(θ)为修正参数θ的先验分布;p(x| θ)为θ的条件分布,称为似然函数;c为常数因子。
在土木工程结构中,修正参数θ多选用单元的截面尺寸、材料特性、边界条件等,其先验分布通常是未知的。但这些参数有明确的物理意义,可大致确定其最大可能性范围,故贝叶斯先验信息可采用如下正态分布:
| $ \pi\left(\boldsymbol{\theta}_i\right)=N\left(\mu_{\boldsymbol{\theta}_i}, \operatorname{cov}\left(\boldsymbol{\theta}_i\right)\right), i=1, 2, \cdots, m $ | (2) |
式中: μθi为第i个修正参数的先验均值; cov(θi)为第i个修正参数的先验方差;m为修正参数的个数。假设实际结构的静力位移响由n个测点位移组成的向量为Z*,其与有限元模型的理论计算值Z(θ)之间符合如下的线性假设:
| $ \boldsymbol{Z}^*=\boldsymbol{Z}(\boldsymbol{\theta})+\boldsymbol{\varepsilon} $ | (3) |
式中: θ为所有修正参数θi, i=1, 2, …, m组成的向量;ε∈Rn表示测量误差、环境波动等不确定性因素产生的差值向量。假设共进行了s次位移测量,且每次试验相互独立,则似然函数可表示为
| $ \left\{\begin{array}{l} p\left(\boldsymbol{Z}^* \mid \boldsymbol{\theta}\right)=\frac{1}{(\sqrt{2 \pi \operatorname{cov}})^s} \exp \left\{-\frac{1}{2} \boldsymbol{J}(\boldsymbol{\theta})\right\} \\ \boldsymbol{J}(\boldsymbol{\theta})=\sum\limits_{i=1}^s\left[\boldsymbol{Z}_i^*-\boldsymbol{Z}(\boldsymbol{\theta})\right]^{\mathrm{T}} \operatorname{cov}^{-1}\left[\boldsymbol{Z}_i^*-\boldsymbol{Z}(\boldsymbol{\theta})_i\right] \end{array}\right. $ | (4) |
式中:Zi*为第i次实测位移向量,Zi*=[d1i*, d1i*, …, dni*];Z(θ)i为第i次有限元模型计算位移向量,Z(θ)i=[d1i(θ), d2i(θ), …, dni(θ)]; cov为测量样本的协方差矩阵。
从而得到后验概率密度函数:
| $ \left\{\begin{array}{l} p\left(\boldsymbol{\theta} \mid \boldsymbol{Z}^*\right)=c^{\prime} \cdot \exp \left[-\frac{1}{2} \boldsymbol{J}(\boldsymbol{\theta})\right] \\ \boldsymbol{J}^{\prime}(\boldsymbol{\theta})=\sum\limits_{r=1}^n \sum\limits_{i=1}^s\left\{\frac{\left[d_{r i}^*-d_{r i}(\boldsymbol{\theta})\right]^2}{\operatorname{cov}}\right\}+\frac{\left[\boldsymbol{\theta}-\boldsymbol{\mu}_{\boldsymbol{\theta}}\right]^2}{\operatorname{cov}_{\boldsymbol{\theta}}} \end{array}\right. $ | (5) |
式中:J′(θ)为目标函数;dri*为第i次测量的第r个测点位移;dri(θ)为第i次有限元计算的第r个测点位移;c′为常数;μθ为修正系数先验均值向量;covθ为修正系数先验均值的协方差矩阵。由于式(5)中静力位移的计算值是修正参数θ的函数,在实际结果中其显式表达式难以获取,故采用数值算法求解后验参数的分布。
1.2 DRAM算法在求解修正参数的后验概率密度时,通常采用蒙特卡洛马尔可夫链(MCMC)方法进行近似计算,生成修正参数Markov链,用以估计修正参数的统计特性。产生Markov链的最基本方法分为两种,分别是Gibbs抽样[16]和MH抽样[17]。考虑到当目标函数中的未知参数数量大幅增加时,样本的接受概率会大幅降低,造成马尔科夫链过于平滑,难以找到正确的参数样本。Haario等[18]提出了一种延缓拒绝自适应抽样(DRAM)方法来解决这个问题,其步骤如下:
1) 选择具有物理意义的初始参数θ0, 使得p(θ0| x)>0;
2) 利用当前θt值,根据第一层建议分布q(θ*, θt)产生一个候选样本θ*;
3) 根据式(5),计算参数接受概率
| $ \begin{aligned} \alpha_1= & \min \left[1, p\left(\boldsymbol{\theta}^* \mid \boldsymbol{x}\right) / p\left(\boldsymbol{\theta}^t \mid x\right)\right]= \\ & \min \left(1, \exp \left[\boldsymbol{J}^{\prime}\left(\boldsymbol{\theta}^t\right)-\boldsymbol{J}^{\prime}\left(\boldsymbol{\theta}^*\right)\right]\right) \end{aligned} $ | (6) |
4) 从[0, 1]均匀分布中随机产生一个变量u,当α1>u时,接受候选样本θ*,即θt+1=θ*;当α1 < u时,根据已经接受的样本θt和被拒绝的候选样本θ*,利用第二层建议分布q2再次产生新的候选样本θ**,然后计算候选样本θ**的接受概率α2
| $ \alpha_2=\min \left[1, \frac{\pi\left(\boldsymbol{\theta}^*\right) q\left(\boldsymbol{\theta}^* \mid \boldsymbol{\theta}^t\right) q_2\left(\boldsymbol{\theta}^{* *}, \boldsymbol{\theta}^*, \boldsymbol{\theta}^t\right)\left(1-\alpha_1\right)}{\pi\left(\boldsymbol{\theta}^t\right) q\left(\boldsymbol{\theta}^{\prime} \mid \boldsymbol{\theta}^*\right) q_2\left(\boldsymbol{\theta}^{\boldsymbol{t}}, \boldsymbol{\theta}^*, \boldsymbol{\theta}^{* *}\right)\left(1-\alpha_1\right)}\right] $ | (7) |
再次生成一个[0, 1]均匀分布的随机变量u,当α2>u时,接受候选样本θ**,即θt+1=θ**;当α2 < u时,拒绝候选样本θ**,即θt+1=θt。然后从第2步开始重新迭代;
5) 当迭代次数t大于非自适应阶段次数N0时,自适应阶段开始,更改建议分布的协方差矩阵Ct,并从第2步开始迭代。其中建议分布的协方差矩阵Ct如下:
| $ \boldsymbol{C}_t=\left\{\begin{array}{l} \boldsymbol{C}_0, t<N_0 \\ s_{\mathrm{d}} \operatorname{cov}\left(\boldsymbol{\theta}^0, \boldsymbol{\theta}^1, \cdots, \boldsymbol{\theta}^{t-1}\right)+s_{\mathrm{d}} \varepsilon_0 \boldsymbol{I}_{\mathrm{d}}, t \geqslant N_0 \end{array}\right. $ | (8) |
式中:ε0为较小的正数,以保证Ct的非奇异性,常取10-5;C0为初始协方差矩阵;sd为比例因子,按经验sd=5.76/m,m为修正参数的维数;Id是m维的单位矩阵;cov(θ0, θ1, …, θt-1)为历史样本的协方差矩阵。
6) 重复步骤1~5,达到设定迭代次数后终止。得到修正参数Markov链收敛段的统计特性用以估计后验概率密度函数。
2 同伦代理模型在贝叶斯模型修正方法中,若直接采用有限元模型进行样本响应计算工作量大、耗时长,所以许多代理模型(meta-model)应运而生,如响应面模型、Kriging模型、支持向量机、神经网络等。本文采用同伦分析方法拟合修正参数和响应之间的关系,这个新的代理模型能够高效精确地模拟复杂的输入输出非线性关系[19]。
考虑一个结构承受静力荷载F,其静力平衡控制方程可表达为
| $ \boldsymbol{K D}=\boldsymbol{F} $ | (9) |
式中: K为结构刚度矩阵,D为节点位移向量。
将结构划分为N个单元,由于初始模型与实际结构之间刚度存在偏差,所以结构单元刚度矩阵ki(i=1, 2, …, N)可以进一步表示为
| $ \boldsymbol{k}_i=\boldsymbol{k}_{0 i}+\alpha_i \boldsymbol{k}_{0 i} $ | (10) |
式中:k0i为初始模型第i单元的单元刚度矩阵;αi为第i单元的刚度修正系数。
根据同伦分析方法的思想,在确定性结构和修正参数之间建立一个同伦关系,结构节点位移向量D必然是随机修正系数α的函数,故构建一个函数ψ(α, h, p):
| $ \boldsymbol{\psi}(\boldsymbol{\alpha}, h, p)=\left\{\begin{array}{l} \boldsymbol{D}_0, p=0 \\ \boldsymbol{D}(\boldsymbol{\alpha}, h), p=1 \end{array}\right. $ | (11) |
式中D0为初始模型的初始解,即D0=k0-1F。同时,构造如下方程来寻求最终解D(α, h)与D0之间的关系:
| $ \begin{gathered} (1-p)\left[\boldsymbol{k}_0 \boldsymbol{\psi}(\boldsymbol{\alpha}, h, p)-\boldsymbol{k}_0 \boldsymbol{D}_0\right]= \\ p h\left[\left(\boldsymbol{k}_0+\sum\limits_{i=1}^N \alpha_i \boldsymbol{k}_i\right) \boldsymbol{\psi}(\boldsymbol{\alpha}, h, p)-\boldsymbol{F}\right] \end{gathered} $ | (12) |
由式(11)和式(12)可知,当p=0时,ψ(α, h, 0)= D0; 当p=1时,ψ(α, h, 1)=D(α, h)。因此建立了D0到D(α, h)的同伦关系,称式(12)为零阶变形方程。
将ψ(α, h, p)用麦克劳林公式在参数p处展开:
| $ \begin{aligned} \boldsymbol{\psi}(\boldsymbol{\alpha}, h, p)= & \boldsymbol{\psi}(\boldsymbol{\alpha}, h, 0)+\sum\limits_{l=1}^{\infty}\left[\frac{\boldsymbol{\psi}^{[l]}(\boldsymbol{\alpha}, h, 0)}{l !}\right] p^l= \\ & \boldsymbol{D}_0+\sum\limits_{l=1}^{\infty}\left[\frac{\boldsymbol{\psi}^{[l]}(\boldsymbol{\alpha}, h, 0)}{l !}\right] p^l \end{aligned} $ | (13) |
式中ψ[l](α, h, 0)为ψ(α, h, p)在p=0处关于p的l阶偏导数,其具体形式可以通过将零阶变形式(12)对参数p求l次偏导后,再令p=0得到。
为了便于简述,以下过程均将ψ(α, h, p)简写为ψ。
首先将零阶变形式(12)对p求一次偏导,并令p=0得到
| $ \boldsymbol{k}_0 \boldsymbol{\psi}^{[1]}=h\left[\left(\boldsymbol{k}_0+\sum\limits_{i=1}^N \alpha_i \boldsymbol{k}_i\right) \boldsymbol{D}_0-\boldsymbol{F}\right] $ | (14) |
由于D0=k0-1F,则有
| $ \boldsymbol{k}_0 \boldsymbol{\psi}^{[1]}=h\left(\sum\limits_{i=1}^N \boldsymbol{\alpha}_i \boldsymbol{k}_i\right) \boldsymbol{D}_0 $ | (15) |
即
| $ \boldsymbol{\psi}^{[1]}=(-h) \sum\limits_{i=1}^N \boldsymbol{D}_i \alpha_i $ | (16) |
式中Di=k0-1(-kiD0)。
由此类推,通过将零阶变形方程对参数p求l阶偏导,可得到ψ[l]代入式(13),具体步骤见文献[20]。然后令p=1,整理后有如下表达式:
| $ \begin{aligned} \boldsymbol{U}(\boldsymbol{\alpha}, h)= & \boldsymbol{\psi}(\boldsymbol{\alpha}, h, 1)= \\ & \boldsymbol{\psi}(\boldsymbol{\alpha}, h, 0)+\sum\limits_{k=1}^l\left(\frac{\boldsymbol{\psi}^{[k]}(\boldsymbol{\alpha}, h, 0)}{k !}\right)= \\ & \boldsymbol{U}_0+\gamma_{l, 1}(h) \sum\limits_{i_1=1}^N \boldsymbol{U}_{i_1} \alpha_{i_1}+\cdots+ \\ & \gamma_{l, k}(h) \sum\limits_{i_1=1}^N \sum\limits_{i_2=1}^{i_1} \cdots \sum\limits_{i_k=1}^{i_{k-1}} \boldsymbol{U}_{i_1 i_2 \cdots i_k} \alpha_{i_1} \alpha_{i_2} \cdots \alpha_{i_k}+\cdots+\\ &\gamma_{l, l}(h) \sum\limits_{i_1=1}^N \sum\limits_{i_2=1}^{i_1} \sum\limits_{i_3=1}^{i_2} \cdots \sum\limits_{i_m=1}^{i_{m-1}} \boldsymbol{U}_{i_1 i_2 \cdots i_m} \alpha_{i_1} \alpha_{i_2} \cdots \alpha_{i_m} \end{aligned} $ | (17) |
式中
| $ \gamma_{l, k}(h)=\left\{\begin{array}{l} 0, t>l \\ (-h)^t \sum\limits_{k=0}^{l-t}\left(\begin{array}{l} k+t-1 \\ k \end{array}\right)(1+h)^k, 1 \leqslant t \leqslant l \\ 1, t \leqslant 0 \end{array}\right. $ | (18) |
γl, k(h)称作趋近函数,此函数中含有一个待定参数h,其取值在-2~0。随机位移表达式(17)的收敛范围会直接被趋近函数式(18)直接影响,具体见文献[20-21]中详细说明。
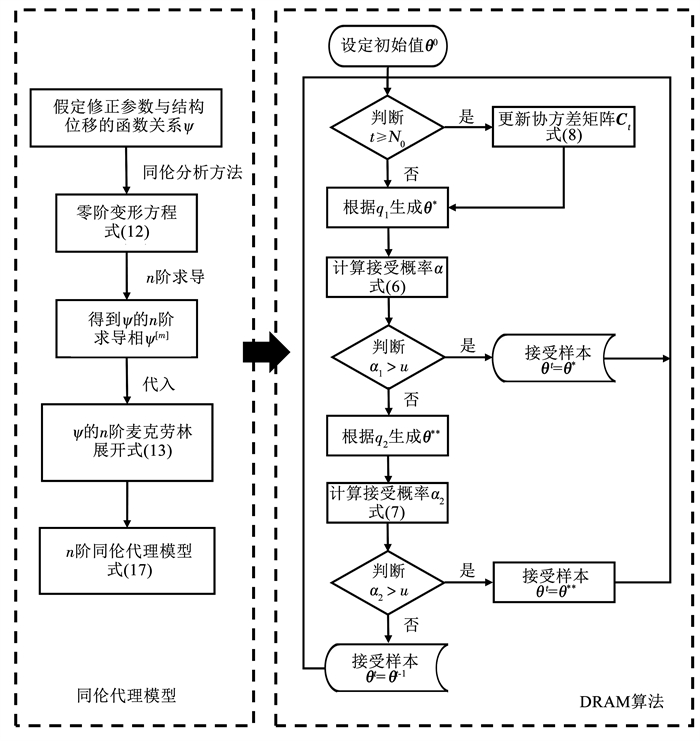
结合同伦代理模型的静力贝叶斯随机模型修正方法步骤见图 1。
|
图 1 结合同伦代理模型与贝叶斯方法的静力随机模型修正流程图 Fig. 1 Flow chart of static stochastic model updating based on homotopy meta-model and Bayesian method |
考虑一个混凝土简支梁,见图 2。梁的初始有限元模型截面惯性矩I=1.95×10-4 m4,梁长1.9 m,将梁划分为8个单元,其中单元1~4的初始弹性模量为E0,单元5~8的初始弹性模量为8E0, E0=2.80×1010 Pa。外力作用于2、6号测点,大小均为5 040 N。假定简支梁真实模型的弹性模量与初始有限元模型存在差异,各个单元的真实弹性模量Ei相对于单元初始弹性模量Ei0存在变化,即Ei=(1+αi)·Ei0, i=1, 2, …, 8。选定这8个单元的弹性模量的变化率αi为修正参数,预设某组修正参数下结构模型为真实模型,其计算位移作为仿真的测量位移均值,并假定测量位移为服从正态分布的相互独立随机变量,变异系数为0.03。修正参数的预设值见表 1。

|
图 2 简支梁有限元模型 Fig. 2 Finite element model of simply supported beam |
| 表 1 修正参数预设值 Tab. 1 Default values of updating parameters |
首先需要对同伦代理模型的精度进行检验。分别建立混凝土数值梁的有限元模型、同伦代理模型以及二次响应面代理模型。然后计算结构各单元参数与节点位移之间的关系。由于篇幅有限,以单元3为例,绘制出单元3的真实参数的修正参数为自变量,6号测点位移为因变量的函数见图 3。

|
图 3 三种模型的比较 Fig. 3 Comparison of three models |
从图 3中可以看出,该单元的修正参数与位移之间关系表现出非线性。当修正参数变化范围为(-0.2, 0.2)时,同伦代理模型和二次响应面代理模型计算的6测点的位移与有限元模型计算值相吻合;但当修正参数取值范围为(-0.6, 0.6)时,二次响应面代理模型的输出位移逐渐偏离有限元方法的计算值,相对误差达到11.8%。然而同伦代理模型的输出位移与有限元模型的计算值的相对差仍能控制在3%以内。这表明本文所提出的同伦代理模型在结构参数波动范围较大时,仍然能够准确拟合结构输入和输出之间的非线性关系。
本数值算例使用贝叶斯模型修正方法对该梁进行模型修正,在迭代过程中分别选取有限元模型、同伦代理模型以及响应面代理模型进行计算。
在贝叶斯模型修正过程中,修正参数的先验分布取N(0, 0.12)的正态分布,通过式(5)的目标函数进行马尔科夫链抽样,所使用的DRAM抽样方法中的采样次数设定为2万次,前5 000次为非自适应阶段,舍去前14 000个样本作为burn-in阶段,剩下的6 000个样本用来估计修正参数的后验概率密度函数。
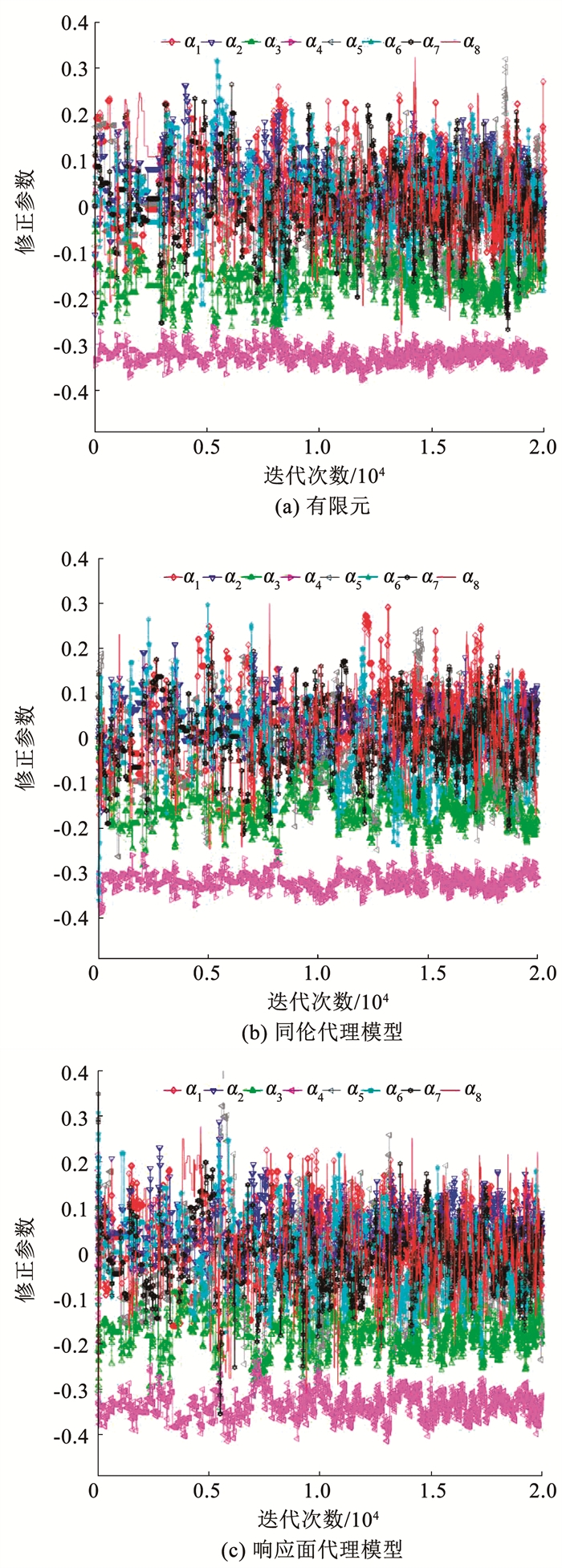
图 4(a)是采用有限元计算的马尔科夫链,图 4(b)和图 4(c)分别是采用同伦代理模型和响应面代理模型计算的修正参数马尔科夫链。从图 4中可以看出,3种计算模型下的修正参数均在迭代的后半段趋于稳定,表明本方法具有良好的收敛性。
|
图 4 三种模型的修正参数的Markov链 Fig. 4 Markov chain of three models updating parameters |
图 5是修正参数的均值和均方差图。从图中可看出,运用3种计算模型所修正的结果与预设值相符。但从图 5(a)修正参数的均值中可以看出,运用同伦代理模型的修正结果相比于响应面代理模型的修正结果更加靠近有限元模型的修正结果,例如在单元刚度修正较大的3、4单元处,同伦代理模型的计算结果与有限元模型的计算结果相对误差小于2%,响应面模型的计算结果相对误差达到了10%。说明同伦代理模型和响应面代理模型均能够有效地替代有限元模型进行贝叶斯模型修正中的迭代运算,但同伦代理模型在修正参数的修正精度上比响应面代理模型高。

|
图 5 简支梁修正参数 Fig. 5 Updating parameters of simply supported beam |
图 6是修正后的结构位移概率密度函数。对比图中7个测点修正位移的概率密度函数与仿真测量位移的概率密度函数可发现,有限元模型和同伦代理模型的计算结果与仿真位移概率密度函数完全一致,而响应面代理模型的计算结果与仿真位移概率密度函数存在着误差。说明了本文方法对结构响应修正的准确性。

|
图 6 测点位移概率密度函数 Fig. 6 Probability density function of displacement of measurement points |
表 2列出了不同方法的计算时间。由表 2可知,即使有限元模型仅有6个单元,同伦代理模型比有限元模型的计算效率提高了120%。虽然同伦模型与响应面的效率相当或略低,但图 6显示,同伦模型修正精度优于响应面。
| 表 2 计算时间 Tab. 2 Calculation time |
通过对一实际的铝合金简支梁进行模型修正,以验证本文提出方法的有效性。铝合金简支梁弹性模量为72 GPa,截面尺寸为10 cm×0.8 cm,梁的长度为1.30 m,如图 7所示。

|
图 7 铝合金简支梁静力位移测量试验 Fig. 7 Static displacement measurement test of aluminum alloy simply supported beam |
试验中,采用砝码悬挂在梁身作为静力荷载,外荷载加载位置与位移测量点见图 8。在采集实测位移样本时,取每一次加载后位移平稳段数据的平均值作为一次静力位移响应值,然后卸载再加载,读取数据。反复进行20次,得到20组静力位移数据作为试验数据的样本集。为了得到较为精确的有限元模型,计算过程中将梁分为60个有限元单元,同时将梁分为6个区域,6个区域的刚度相对于初始有限元刚度的变化量作为修正参数。考虑到在模拟简支梁支座处梁端存在搭接长度,所以根据试验实际搭接长度测量,区域1~5的计算长度为0.2 m,区域6的计算长度为0.19 m,计算简图见图 8。为了验证试验结构模型修正的效果,区域2和区域5的截面分别切除30%和40%来模拟刚度变化,作为对修正参数物理意义的验证标准。

|
图 8 铝合金简支梁模型 Fig. 8 Finite element model of aluminum alloy simply supported beam |
得到实测位移样本后,进行基于同伦代理模型的贝叶斯模型修正,抽样次数设定为2万次,修正参数的Markov链见图 9。从图 9可以看出,各修正参数的马尔科夫链很快趋于平稳。舍去5 000次的过渡样本,

|
图 9 修正参数的Markov链 Fig. 9 Markov chain of updating parameters |
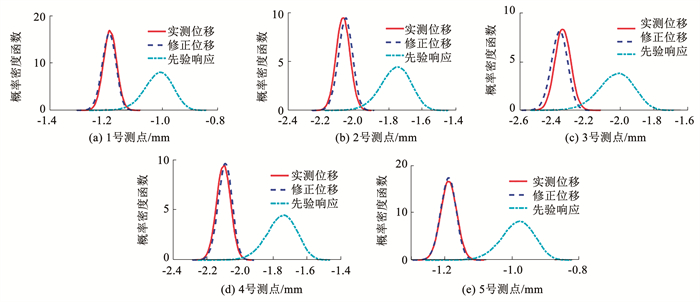
取后15 000组数据对修正参数的后验概率密度函数进行估计。修正后的结构计算位移的概率密度函数见图 10。从图 10中可以看出,虽然由修正参数先验信息得到的先验响应与实测结果相差较大,修正后模型能非常好地复现实测的结构静力位移概率密度函数,各测点位移概率密度函数的均值和均方差的相对误差均在1.5%以下。表 3列出修正参数后验均值。从表 3中可发现,修正参数均值与铝合金梁的实际刚度较为吻合。特别注意到,即使所给先验均值和实际结果相差较大(修正幅度40%),同伦代理模型的结果仍与真值较为符合。另外,还发现所有修正后区域的刚度均产生变化,这是因为实际测量位移的随机误差逆向传播到了铝合金梁的所有单元中,且由于测量的随机性,修正后的参数也为随机量,这正是随机有限元模型修正与确定性的模型修正的区别。测量结果的不确定性会导致修正参数只能在概率意义上与实际刚度吻合。即便如此,本文方法得到的修正结果能与结构物理意义上的刚度变化一致,且能高精度地预测结构响应。这说明本文提出的方法对于实际结构的随机模型修正是有效的。在计算效率方面,从表 4可以看出,同伦代理模型的计算效率比用有限元模型计算的效率提高了约17倍。可以预见,随着结构规模变大和自由度增加,同伦代理模型的计算效率会更高,为本文方法在实际结构中的应用提供了可能。另外,本文方法不限于静力问题,也可以用于动力模型修正中。
|
图 10 铝合金简支梁测点位移概率密度函数 Fig. 10 Probability density function of displacement of measurement points of aluminum alloy simply supported beam |
| 表 3 修正参数结果 Tab. 3 Updating parameter results |
| 表 4 模型修正计算时间 Tab. 4 Calculation time of updating model |
提出了一种结合同伦代理模型的静力贝叶斯随机模型修正方法。利用同伦随机有限元方法得到了高精度的代理模型,并被用于MCMC抽样过程,在保证计算精度的同时大幅提高了计算效率。数值算例和铝合金梁试验结果验证了该方法的有效性。得到了以下结论:
1) 结合同伦代理模型的静力贝叶斯模型修正在精度上与传统的基于有限元计算的静力贝叶斯模型修正保持一致,能够准确地修正结构参数,使之复现模型的实测静力响应,并且修正结构参数符合实际物理意义,保证了修正结果的有效性;
2) 相比于传统的二次响应面代理模型,同伦代理模型的修正精度更高;
3) 利用同伦代理模型替代传统的有限元模型,本文所提方法在保证计算精度的同时能够大幅提高计算效率,在结构单元划分为60个单元时效率提高了近17倍。
| [1] |
李惠, 鲍跃全, 李顺龙, 等. 结构健康监测数据科学与工程[J]. 工程力学, 2015, 32(8): 1. LI Hui, BAO Yuequan, LI Shunlong, et al. Data science and engineering for structural health monitoring[J]. Engineering Mechanics, 2015, 32(8): 1. DOI:10.6052/j.issn.1000-4750.2014.08.st11 |
| [2] |
张保强. 热结构不确定性动力学仿真及模型确认方法研究[D]. 南京: 南京航空航天大学, 2012 ZHANG Baoqiang. Uncertainty simulation of thermal structural dynamics and model validation method research[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012 |
| [3] |
SARMADI H, KARAMODIN A, ENTEZAMI A. A new iterative model updating technique based on least squares minimal residual method using measured modal data[J]. Applied Mathematical Modelling, 2016, 10323. DOI:10.1016/j.apm.2016.07.015 |
| [4] |
MOSAVI A A, SEDARAT H, O'CONNOR S M, et al. Calibrating a high-fidelity finite element model of a highway bridge using a multi-variable sensitivity-based optimization approach[J]. Structure and Infrastructure Engineering, 1997, 10(5): 627. DOI:10.1080/15732479.2012.757793 |
| [5] |
KUOK Y S C. Bayesian methods for updating dynamic models[J]. Applied Mechanics Reviews, 2011, 64(1): 3. DOI:10.1115/1.4004479 |
| [6] |
PRUDENCIO E E, CHEUNG S H. Parallel adaptive multilevel sampling algorithms for the Bayesian analysis of mathematical models[J]. International Journal for Uncertainty Quantifications, 2012, 2(3): 215. DOI:10.1615/Int.J.UncertaintyQuantification.2011003499 |
| [7] |
MOTTERSHEAD J E, FRISWELL M I. Model updating in structural dynamics: a survey[J]. Journal of Sound and Vibration, 1993, 167(2): 347. DOI:10.1006/jsvi.1993.1340 |
| [8] |
张令弥. 动态有限元模型修正技术及其在航空航天结构中的应用[J]. 强度与环境, 1994, 1(2): 10. ZHANG Lingmi. Dynamic finite element model updating and its application in aerospace structures[J]. Structure & Environment Engineering, 1994, 1(2): 10. |
| [9] |
郭勤涛, 张令弥, 费庆国. 结构动力学有限元模型修正的发展——模型确认[J]. 力学进展, 2006, 36(1): 38. GUO Qintao, ZHANG Lingmi, FEI Qingguo. From FE model updating to model validation: advances in modeling of dynamic structures[J]. Advances in Mechanics, 2006, 36(1): 38. DOI:10.3321/j.issn:1000-0992.2006.01.010 |
| [10] |
朱宏平, 徐斌, 黄玉盈. 结构动力模型修正方法的比较研究及评估[J]. 力学进展, 2002, 32(4): 513. ZHU Hongping, XU Bin, HUANG Yuying. Comparison and evaluation of analytical approaches to structural dynamic model correction[J]. Advances in Mechanics, 2002, 32(4): 513. |
| [11] |
BECK J L, AU S K. Bayesian updating of structural models and reliability using Markov chain Monte Carlo simulation[J]. Journal of Engineering Mechanics, 2002, 128(4): 380. DOI:10.1061/(ASCE)0733-9399(2002)128:4(380) |
| [12] |
邓苗毅, 任伟新, 王复明. 基于静力响应面的结构有限元模型修正方法[J]. 实验力学, 2008, 23(2): 7. DENG Miaoyi, REN Weixin, WANG Fuming. Structure finite element model (FEM) updating based on static-load response surface methodology[J]. Journal of Experimental Mechanics, 2008, 23(2): 7. |
| [13] |
马天政, 吕昊, 张义民. 一种基于Bayes方法的随机模型修正方法[J]. 工程设计学报, 2016, 23(3): 6. MA Tianzheng, LV Hao, ZHANG Yimin. Stochastic model updating based on Bayesian method[J]. Chinese Journal of Engineer Design, 2016, 23(3): 6. DOI:10.3785/j.issn.1006-754X.2016.03.002 |
| [14] |
SIMPON T W, PEPLINSKI J D, KOCH P N, et al. Meta-models for computer-based engineering design: survey and recommendations[J]. Engineering with Computers, 2001, 17: 129. DOI:10.1007/PL00007198 |
| [15] |
茆诗松, 汤银才. 贝叶斯统计[M]. 北京: 中国统计出版社, 2012: 15. MAO Shisong, TANG Yincai. Bayesian statistics[M]. Beijing: China Statistics Press, 2012: 15. |
| [16] |
GEMAN D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images[J]. Readings in Computer Vision, 1987, 20(5/6): 25. DOI:10.1080/02664769300000058 |
| [17] |
METOPOLIS N, ROSENBLUTH A W, TELLER A H, et al. Equations of state calculations by fast computing machines[J]. Journal of Chemical Physics, 1953, 21: 1087. DOI:10.2307/2342435 |
| [18] |
HAARIO H, LAINE M, MIRA A, et al. DRAM: efficient adaptive MCMC[J]. Statistics and Computing, 2006, 16(4): 339. DOI:10.1007/s11222-006-9438-0 |
| [19] |
张衡, 王鑫, 黄斌, 等. 基于同伦分析方法的随机结构静力响应求解[J]. 工程力学, 2019, 36(11): 27. ZHANG Heng, WANG Xin, HUANG Bin, et al. Solution for static response of structure with random parameters based on homotopy analysis method[J]. Engineering Mechanics, 2019, 36(11): 27. |
| [20] |
HUANG B, ZHANG H, PHOON K K. Homotopy approach for random eigenvalue problem[J]. International Journal for Numerical Methods in Engineering, 2018, 113(3): 450. DOI:10.1002/nme.5622 |
| [21] |
廖世俊. 广义泰勒原理: "同伦分析方法"之有效性的一个数理逻辑证明[J]. 应用数学和力学, 2003, 24(1): 47. LIAO Shijun. On a generalized Taylor theorem: a rational proof of the validity of the so-called homotopy analysis method[J]. Applied Mathematics and Mechanics, 2003, 24(1): 47. |
 2023, Vol. 55
2023, Vol. 55


