2. 移动通信技术重庆市重点实验室(重庆邮电大学), 重庆 400065
2. Chongqing Key Lab of Mobile Communications Technology (Chongqing University of Posts and Telecommunications), Chongqing 400065, China
随着互联网与物联网技术的飞速发展,无线通信服务在近几年内发展迅猛。为了适应数据流量的迅速增加、设备的连接、新兴业务和应用的需要,超密集网络应运而生[1]。超密集网络是5G技术中最具有发展前景的技术之一,它可以将低功率基站大规模部署到一些热点区域,从而提高系统的承载能力[2]。由于超密集网络具有密集化、异构化的特性并且移动用户业务呈现多样性,如何合理地选取合适的接入网络已成为一个值得深入探讨的问题[3]。为了保障用户服务质量(quality of service, QoS)和提高网络整体资源利用率,需要设计合适的接入选择算法。
针对异构网络中用户接入选择问题,国内外研究者进行了大量深入的研究。文献[4-7]以用户接收信号强度、信号干扰比或传输速率等作为判决因素,将用户接入到收益最大的网络中;但是这类方法考虑的因素层面单一,不能适应动态变化的超密集网络环境,用户接入的可能不是综合性能最好的网络。文献[8-11]从多个角度对网络选择的影响因素进行了研究,采用多属性决策判决法对用户的偏好和网络效用进行了分析,保证了用户的QoS;然而,此类算法过于注重用户QoS而忽略了网络的承受能力,可能会将大部分用户接入到同一个网络中,加重某些网络的负载,导致负载不均衡。文献[12-14]将选网问题建模为马尔可夫决策过程,利用Q学习[15]自主学习的特点,为用户选择长期收益最大的网络,在一定程度上减少了切换次数;然而,在Q学习过程中,由于网络数量和用户数量的增多,使得系统的状态维数迅速增长,运算量也随之剧增,从而影响了算法的运行效率。
针对以上问题,提出一种新的基于DQN的接入选择算法,该算法综合考虑网络、用户和业务3个层面的因素,从而确保用户的QoS,并有效地解决网络的高动态特性所造成的负载不均衡问题。同时,利用双Q学习[16]算法思想,将DQN中的目标函数进行优化,解决DQN算法在进行Q值估计时存在的过高估计问题,并且,针对传统的DQN算法由于收敛速度慢导致的算法处理时延过大的情况,采用优先级经验回放机制[17]加速了算法的收敛。
1 问题建模接入选择过程主要分为3个阶段:网络发现、选网决策和接入执行[18],研究重点集中在选网决策阶段。超密集网络场景中部署了多种不同类型的接入点,一个移动终端能够从各个网络中接收到基站发出的信号,并自由选择周围的网络。移动用户在时隙τ内保持连接,并且只选择一个网络进行传输。用户需要在每个时隙τ结束时做出决策,决策时段用
为保证基于改进DQN的接入选择算法顺利运行,首先需要建立强化学习模型,然后,运用深度学习的方法,来解决强化学习的问题。采用马尔可夫决策过程建立强化学习模型,用 < S, A, P, π, r>表示。其中,S为网络的离散状态空间,包含影响网络的各个参数、用户连接状态以及用户业务类型;A为动作空间,由候选网络集合表示;P表示网络状态由st转移到下一个状态st+1的概率;用户的动作策略π: S→ A表示动作A由状态S决定;奖励函数r: S×A→ R表示用户执行动作后接收到的来自超密集网络环境的反馈。强化学习过程见图 1,在每个决策时刻t,智能体根据观测到的环境状态st以及策略π来完成动作at,环境会向智能体回送奖励rt,然后环境进入一个新的状态st+1。

|
图 1 强化学习过程 Fig. 1 Reinforcement learning process |
1) 状态和动作空间。假设在每个决策时刻t,移动用户的候选网络数量为M。选择代表用户QoS和网络状态的5个参数作为决策因素,分别为可用带宽(Bm)、时延抖动(Dm)、丢包率(Lm)、价格(Cm)和安全性(Sm)。则某一时刻网络状态空间为
| $ \boldsymbol{S}=\left\{B_m, D_m, L_m, C_m, S_m, m, h, n\right\} $ | (1) |
式中:m为用户终端连接到的网络,h为业务类型,n为当前用户终端所连接的网络中服务的用户数。
移动用户的接入动作由a表示,则动作空间A为
| $ \boldsymbol{A}=\{a \mid a \in\{1, 2, \cdots, M\}\} $ | (2) |
2) 奖励函数。由于考虑到多个网络参数,为了更好地权衡用户偏好和网络实际状态,将奖励函数定义为
| $ R_t=r_{\text {load }_{i, t}}+\sum\limits_x \omega_x r_{x_{i, t}} $ | (3) |
式中:ωx为第x个网络参数的权重,该权重由层次分析法结合熵权法求出; rxi, t为t时刻候选网络i的参数x的归一化奖励; rloadi, t为t时刻候选网络i的负载的归一化奖励。
针对效益型参数,如可用带宽、安全性等,rxi, t定义为
| $ r_{x_{i, t}}=\left\{\begin{array}{l} 0, x_{i, t} \leqslant x_{\min } \\ \frac{x_{i, t}-x_{\min }}{x_{\max }-x_{\min }}, x_{\min }<x_{i, t}<x_{\max } \\ 1, x_{i, t} \geqslant x_{\max } \end{array}\right. $ | (4) |
针对代价型参数,如时延抖动、丢包率、价格等,rxi, t定义为
| $ r_{x_{i, t}}=\left\{\begin{array}{l} 1, x_{i, t} \leqslant x_{\min } \\ \frac{x_{\max }-x_{i, t}}{x_{\max }-x_{\min }}, x_{\min }<x_{i, t}<x_{\max } \\ 0, x_{i, t} \geqslant x_{\max } \end{array}\right. $ | (5) |
一个网络可同时为多个移动用户提供服务,但当连接用户超过负载上限时,接入请求失败,导致用户阻塞,设计负载均衡策略可以有效地减少阻塞率。t时刻网络i的负载情况可由负载系数li, t表示
| $ l_{i, t}=\frac{n_{i, t}}{N_i} $ | (6) |
式中:ni, t为t时刻接入网络i的用户数,Ni为网络i能够同时服务的最大用户数。
根据负载系数,将负载的归一化奖励定义为
| $ r_{\operatorname{load}_{i, t}}=\frac{1}{l_{i, t}+1} $ | (7) |
算法最终目标是获得使长期累积回报期望最大的动作,即选择长期综合效用最大的网络。因此,策略π下的动作-价值函数(Q函数)被定义为状态st下从状态空间S中执行动作at的期望累积回报,则Q函数为
| $ \begin{aligned} Q_\pi\left(s_t, a_t\right)= & E\left[R_{t+1}+\gamma Q_\pi\left(s_{t+1}, a_{t+1}\right)\right]=R\left(a_t \mid s_t\right)+ \\ & \gamma \sum\limits_{s_{t+1} \in S} P\left(s_{t+1} \mid s_t, a_t\right) \sum\limits_{a_{t+1} \in A} \pi\left(a_{t+1} \mid s_{t+1}\right) \cdot \\ & Q_\pi\left(s_{t+1}, a_{t+1}\right) \end{aligned} $ | (8) |
式中:Rt为t时刻的立即回报; γ为折扣因子,用来评价之后时刻立即回报的重要程度。
因此,贝尔曼方程为
| $ \begin{aligned} Q^*\left(s_t, a_t\right)= & \max _\pi Q_\pi\left(s_t, a_t\right)= \\ & R\left(a_t \mid s_t\right)+\gamma \sum\limits_{s_{t+1} \in S} P\left(s_{t+1} \mid s_t, a_t\right) \cdot \\ & \max _{a_{t+1} \in A} Q^*\left(s_{t+1}, a_{t+1}\right) \end{aligned} $ | (9) |
对于任何状态st∈S,其对应的最优动作就是使Q*(st, at)值最大的动作,则最优策略为
| $ \pi^* \equiv \underset{a_t \in A}{\arg \max } Q^*\left(s_t, a_t\right), \forall s_t \in \boldsymbol{S} $ | (10) |
在Q学习中,Q表中的每个状态-动作对(s, a)都对应一个Q值,Q值的更新公式为
| $ \begin{aligned} & Q\left(s_t, a_t\right) \leftarrow Q\left(s_t, a_t\right)+\alpha\left(R_{t+1}+\right. \\ & \left.\gamma \max _{a_{t+1} \in A} Q\left(s_{t+1}, a_{t+1}\right)-Q\left(s_t, a_t\right)\right) \end{aligned} $ | (11) |
式中α∈(0, 1)为学习率。
2.1 传统DQN算法Q学习中Q表的维护既要耗费大量的运算资源,又易发生维度爆炸,因此可以采用一种非线性函数近似器来近似Q函数。神经网络是一种常用的非线性函数近似器,利用DNN作为Q函数近似器的Q学习方法即为DQN。传统DQN算法重点有两部分,分别是构建目标网络和引入经验回放机制。
1) 构建目标网络。DQN使用神经网络(主网络)来逼近Q函数,其参数化表示为Qmain(st, at; θk),其中,θk为第k次迭代时神经网络的参数。主网络每次迭代的优化目标为
| $ y=R_{t+1}+\gamma \max\limits_a Q_t\left(s_{t+1}, a ; \theta_k^{-}\right) $ | (12) |
该优化目标由另一个与主网络结构相同的目标网络Qt(st+1, a; θk-)产生,其中a为当前状态下所有可能的动作,st+1为网络下一个时刻的状态,θk-由主网络参数经过G次迭代后复制而来。
在主网络的训练中,采用了一种基于随机梯度下降的算法,使损失函数最小,从而使神经网络的参数得到最大程度的更新,损失函数为
| $ L_k\left(\theta_k\right)=E\left[\left(y-Q_{\text {main }}\left(s_t, a_t ; \theta_k\right)\right)^2\right] $ | (13) |
由式(13)可得损失函数的梯度
| $ \square_{\theta_k} L_k\left(\theta_k\right)=E\left[\left(y-Q_{\text {main }}\left(s_t, a_t ; \theta_k\right)\right) \square_{\theta_k} Q_{\text {main }}\left(s_t, a_t ; \theta_k\right)\right] $ | (14) |
2) 经验回放机制。每个决策时刻智能体与环境的交互信息表示为一条经验e=(st, at, rt, st+1),将所有经验存储到序列D={e1, e2, …, eN}中,建立经验回放机制。每次从D中随机选取少量的经验样本进行训练。通过重复采样历史数据提高了数据的利用率,与此同时在一定程度上降低了数据之间的关联性。
2.2 改进DQN算法由式(12)可以看出,动作的选择和评价都基于同一个参数θk-,这将有一定几率造成Q值的过高估计,在进行网络选择时将有可能导致用户无法接入到综合性能最好的网络。为了解决这个问题,参考双Q学习算法思想,对DQN算法做出如下改进:将动作的评估由原来的主网络计算转为由目标网络计算,而动作的选择仍然由主网络操作。此时需要将DQN中优化目标进行改进,具体为
| $ y=R_{t+1}+\gamma Q_t\left(s_{t+1}, a_{\text {main }} ; \theta_k^{-}\right) $ | (15) |
式中:
传统DQN算法中经验转移从回放记忆中使用同等频率进行采样,对回放序列中经验的重要程度缺乏考虑,从而导致抽样随机性较大、学习效率低等情况,当网络状态维度增大时,网络选择算法可能会因为处理时延增大而失效。
针对此问题,引入求和树结构的优先经验回放机制。优先经验回放的基本理念是:打破平均抽样,给有较高学习效率的样本以较大的抽样权重。以时间差分(temporal difference, TD)误差作为优先级指标,误差越大,对梯度学习的影响越大,故应该优先取样。利用求和树结构,实现按照优先级为TD误差的抽样。具体表示为:将每个经验的优先级值视为一个叶节点,两个节点作为一组,向上叠加,形成一个二叉树,根节点的值即为所有经验的优先级值的和。在对训练数据进行采样时,先将样本划分为多个区间,区间的大小为根节点的总优先级值除以每个批次中的样本数,每个区间中随机抽取一个数,从根节点开始由上至下搜索叶节点,确定最终的采样数据。TD误差为
| $ \begin{aligned} \delta_t= & R_{t+1}+\gamma \max _a Q_t\left(s_{t+1}, \underset{a}{\arg \max } Q_{\text {main }}\left(s_{t+1}, a ; \theta\right) ; \theta^{-}\right)- \\ & Q_{\text {main }}\left(s_t, a_t ; \theta\right) \end{aligned} $ | (16) |
TD误差的绝对值越大,提取样本进行训练的可能性就越大,但是这样容易造成网络的过拟合,对此,将第i条经验样本被提取的概率为
| $ P(i)=\frac{p_i}{\sum p_i} $ | (17) |
式中:pi=|δt+ε|>0,ε是一个很小的值,用于保证TD误差为0的经验样本能被抽取到,从而避免神经网络的过拟合,保证算法的性能。
基于经验优先级采样的方法无需遍历经验池也能提取到优先级高的样本,减少运算资源,加快神经网络的学习速度。
针对以上两条对DQN的改进方法,设计基于改进DQN的接入选择算法的结构框图见图 2。
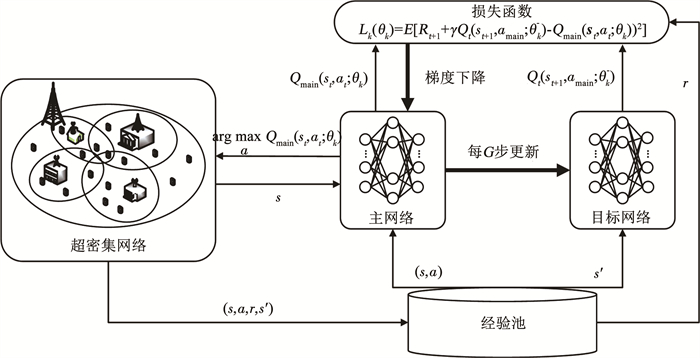
|
图 2 改进DQN接入选择算法结构框图 Fig. 2 Block diagram of improved DQN access selection algorithm |
整个网络接入选择算法主要分为离线训练与在线决策两部分。离线学习阶段,用户终端读取网络状态信息作为状态s,系统将状态s输入主网络,并在前向传播之后输出当前状态下所有状态-动作对的Q值,根据ε-greedy策略选择动作a,ε-greedy策略见式(18)。训练的每一步都更新ε-greedy策略,即
| $ \pi(a \mid s)=\left\{\begin{array}{l} 1-\varepsilon, a^*=\underset{a \in A}{\arg \max } Q(s, a) \\ \varepsilon, \text { 随机 } a \end{array}\right. $ | (18) |
动作选择结束后,用户终端在超密集网络环境中执行该动作,之后环境会返回一个奖励r和下一个状态s′,此时元组(s, a, r, s′)就作为一条经验存入经验池,重复这个过程直到经验条数满足训练要求为止。当经验池存满之后,利用优先经验回放机制,从经验池中随机采样,将采样得到的奖励r和下一个状态s′送入目标网络,计算优化目标y,并将y输入主网络计算损失值,从而更新主网络。之后用户终端再与环境交互,产生经验放入经验池,再从经验池中采样更新主网络,直到神经网络完全收敛。此外,训练过程中,每隔G步更新目标网络参数θ-=θ。
神经网络训练完成之后,进入在线决策阶段,用户终端可以根据当前业务类型以及超密集网络环境状态选择长期收益最大的网络接入,由于算法设计时考虑了网络、用户以及业务3个层面的因素,并且构建了负载均衡策略,可以实现用户QoS的提升以及负载均衡,降低用户阻塞率。
3 仿真实验及分析为了验证本文提出的改进DQN算法的性能,将其与DQN、Q学习以及SAW算法进行比较分析。首先对比改进DQN和传统DQN的Q值变化曲线和累积回报的收敛性,然后将这4种算法在相同条件下分别进行100轮仿真实验,并对这4种算法在平均用户接入阻塞率、系统吞吐量以及处理时延方面进行对比分析。
3.1 仿真参数设置仿真场景中考虑由一个家庭基站(femtocell base station, FeBS)、两个微微基站(picocell base station, PeBS)和两个WIFI热点组成的超密集异构网络。FeBS覆盖半径为200 m,带宽为15 MHz,有75个资源块可以分配;PeBS覆盖半径为120 m,带宽为5 MHz,有30个资源块可以分配,两种基站均采用64QAM调制,编码速率为0.93。每个FeBS用户可以分配5个资源块,每个PeBS用户可以分配3个资源块,每个资源块由12个连续子载波组成。WIFI热点覆盖半径为70 m,且遵循802.11n协议,最大数据速率为16 Mbit/s和12 Mbit/s,可以同时为5个用户提供服务。同时,用户的业务类型考虑会话类、流媒体类、背景类和交互类。在任意决策周期τ内,每个用户只选择一种网络和一种业务类型进行通信。考虑到实际场景中用户的移动性,设置每个用户在时隙τ内保持连接不变,并且随机产生移动方向,移动速度为3 m/s。候选网络的参数设置见表 1。
| 表 1 候选网络及其参数 Tab. 1 Candidate networks and parameters |
首先将改进后的DQN算法与传统DQN算法在Q值估计方面进行比较,通过在Q值变化趋势上的对比,表明所提改进DQN算法在离线训练过程中的优势。图 3为两种算法下Q值的变化趋势对比。由图 3可以看出, 在相同迭代次数下,传统DQN算法估计Q值起点较高,经过改进后的DQN算法由于对目标函数进行了优化,改善了Q值的高估问题。
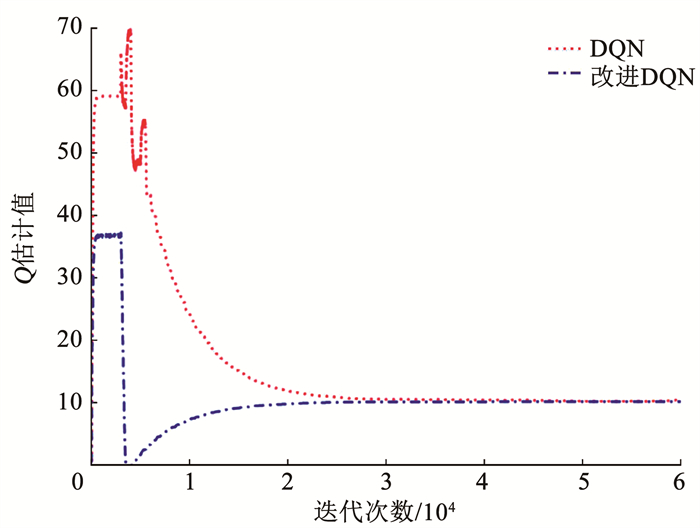
|
图 3 Q估计值变化趋势对比 Fig. 3 Comparison of variation trend of Q estimation value |
其次将改进DQN算法与传统DQN算法在累积回报方面进行比较,通过累积回报变化趋势对比,表明所提改进DQN算法在离线训练过程中的优势。图 4为两种算法下累积回报的变化趋势。由图 4可以看出, 在相同迭代次数下,传统DQN算法获得的累积回报低于改进DQN算法,并且收敛速度较慢,这是因为改进DQN算法引入了优先经验回放机制,算法收敛加快。
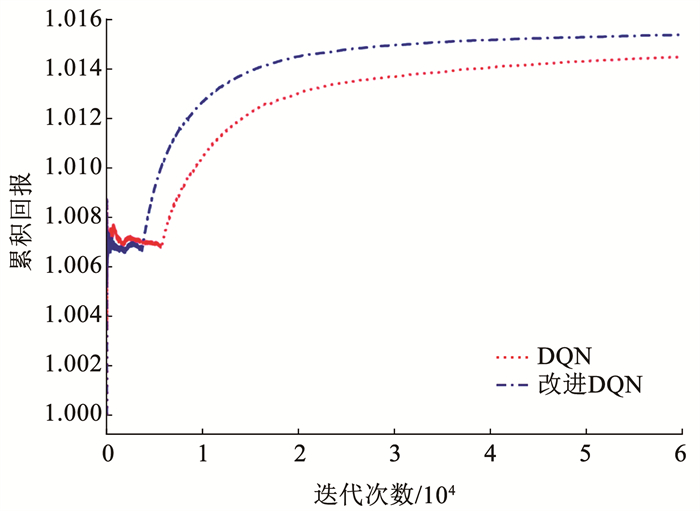
|
图 4 累积回报变化趋势对比 Fig. 4 Comparison of variation trend of cumulative return |
1) 用户接入阻塞率对比分析。图 5是在业务到达率为0~21时,改进DQN、DQN、Q学习和SAW这4种算法的接入阻塞率对比。从图中可以看出,当用户到达率小于6时,4条曲线的差异不明显,因为到达率较低时,网络中的用户数量少,资源足够所有用户使用。当到达率大于6时,改进DQN算法的接入阻塞率平均比DQN、Q学习和SAW分别降低了5.4%、23.4%、15.8%,这是因为SAW算法只根据网络的当前状态进行接入决策,没有考虑到网络的长期收益。
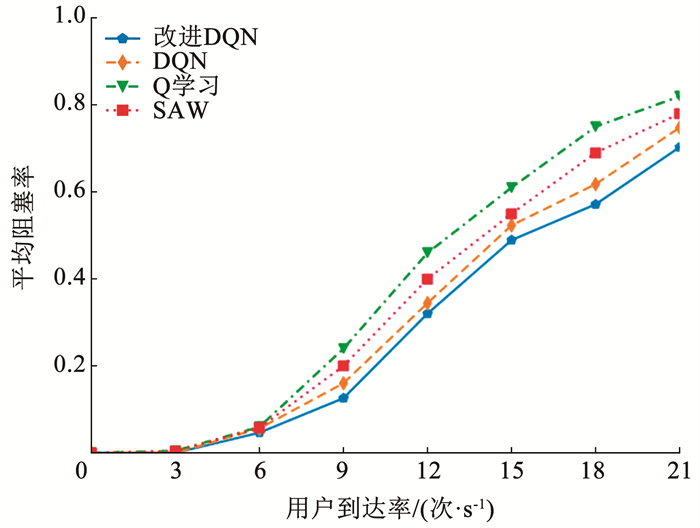
|
图 5 用户接入阻塞率对比 Fig. 5 Comparison of user access blocking rate |
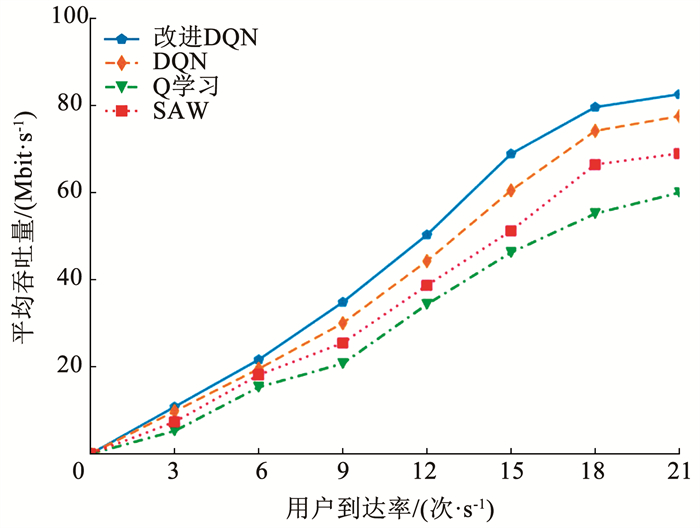
2) 系统吞吐量对比分析。图 6为在业务到达率为0~21时,改进DQN、DQN、Q学习和SAW这4种算法的系统吞吐量对比。从图中可以看出,改进DQN算法下系统的吞吐量平均比DQN、Q学习和SAW分别提高了10.4%、47.1%、26.2%,这是因为改进DQN算法具有自学习能力,能够通过自主学习自动调整接入策略,适应网络的动态变化。
|
图 6 系统吞吐量对比 Fig. 6 Comparison of system throughput |
3) 平均处理时延对比分析。图 7为改进DQN、DQN、Q学习和SAW这4种算法的平均处理时延对比。此处处理时延表示仿真实验过程中用户完成一次选网动作程序运行的时间。从图中可以看出,改进DQN对比Q学习处理时延显著降低了54.9%,这是因为Q学习的计算复杂度会随着状态空间的增加而急剧增大。DQN算法由于抛弃了Q学习的查表方式选择用神经网络逼近Q函数,相对于Q学习来说,DQN的计算复杂度受到状态空间维度的影响并不大,改进后的DQN在DQN基础上引入了优先经验回放机制,使算法的收敛性得到了一定的提高,降低了14.8%的处理时延。SAW算法只是对参数进行简单的加权,相比于SAW算法,改进DQN算法为了使用户QoS和网络性能得到提高,牺牲了一定的处理时延。

|
图 7 平均处理时延对比 Fig. 7 Comparison of average delay |
提出了一种基于改进DQN的超密集网络接入选择算法,该算法既能通过修改目标函数解决DQN算法高估问题,引入优先经验回放机制又能够加快传统DQN算法的收敛速度。仿真实验证明,相较于传统DQN、Q学习、SAW这3种算法,所提算法能够有效地提升系统吞吐量,同时确保用户QoS,降低接入阻塞率,并且在一定程度上降低时间复杂度。在之后的研究中,将考虑同一环境中其他用户的网络选择行为对当前用户选网的影响,设法解决多用户同时竞争网络资源时的选网问题。
| [1] |
ARBI A, O'FARRELL T. Energy efficiency in 5G access networks: small cell densification and high order sectorisation[C]//2015 IEEE International Conference on Communication Workshop. London: IEEE, 2015: 2806. DOI: 10.1109/ICCW.2015.7247604
|
| [2] |
LIU Junyu, SHENG Min, LI Jiandong. Improving network capacity scaling law in ultra-dense small cell networks[J]. IEEE Transactions on Wireless Communications, 2018, 17(9): 6218. DOI:10.1109/TWC.2018.2856766 |
| [3] |
DAI Linglong, WANG Bichai, YUAN Yifei, et al. Non-orthogonal multiple access for 5G: solutions, challenges, opportunities, and future research trends[J]. IEEE Communications Magazine, 2015, 53(9): 75. DOI:10.1109/MCOM.2015.7263349 |
| [4] |
CHANG C, HSIEH C, CHEN Y. A preference value-based cell selection scheme in heterogeneous wireless networks[C]//2010 IEEE Wireless Communication and Networking Conference. Sydney: IEEE, 2010: 2. DOI: 10.1109/WCNC.2010.5506518
|
| [5] |
BORST S, KAYA A Ö, CALIN D, et al. Dynamic path selection in 5G multi-RAT wireless networks[C]//IEEE INFOCOM 2017-IEEE Conference on Computer Communications. Atlanta: IEEE, 2017: 3. DOI: 10.1109/INFOCOM.2017.8057228
|
| [6] |
KAN Shanlei, CHEN Hongyuan, ZHU Yuanping, et al. Aggregation based cell selection methods for multi-RAT HetNet[C]//2016 8th International Conference on Wireless Communications & Signal Processing. Yangzhou: IEEE, 2016: 2. DOI: 10.1109/WCSP.2016.7752572
|
| [7] |
NGUYEN D D, NGUYEN H X, WHITE L B. Performance of adaptive RAT selection algorithms in 5G heterogeneous wireless networks[C]//2016 26th International Telecommunication Networks and Applications Conference. Dunedin: IEEE, 2016: 72. DOI: 10.1109/ATNAC.2016.7878785
|
| [8] |
YU Hewei, ZHANG Biao. A heterogeneous network selection algorithm based on network attribute and user preference[J]. Ad Hoc Networks, 2018, 72: 75. DOI:10.1016/j.adhoc.2018.01.011 |
| [9] |
YU Hewei, ZHANG Biao. A hybrid MADM algorithm based on attribute weight and utility value for heterogeneous network selection[J]. Journal of Network and Systems Management, 2019, 27(3): 765. DOI:10.1007/s10922-018-9483-y |
| [10] |
TANG Liangrui, JI Shiyu, YAN Jiangyu. A heterogeneous network access selection algorithm based on attribute dependence[J]. Wireless Personal Communications, 2017, 92(3): 1165. DOI:10.1007/s11277-016-3600-6 |
| [11] |
ZHU Anqi, MA Mingfang, GUO Songtao, et al. Adaptive multi-access algorithm for multi-service edge users in 5G ultra-dense heterogeneous networks[J]. IEEE Transactions on Vehicular Technology, 2021, 70(3): 2810. DOI:10.1109/TVT.2021.3060573 |
| [12] |
CHEN Jialing, YIN Mingxi, DUAN Xiaohui, et al. Q-learning based selection strategies for load balance and energy balance in heterogeneous networks[C]//2020 5th International Conference on Computer and Communication Systems. Shanghai: IEEE, 2020: 729. DOI: 10.1109/ICCCS49078.2020.9118518
|
| [13] |
KHODMI A, REJEB S B, NASSER N, et al. MDP-based handover in heterogeneous ultra-dense networks[C]//2021 International Conference on Information Networking. Jeju Island: IEEE, 2021: 350. DOI: 10.1109/ICOIN50884.2021.9334024
|
| [14] |
王月平, 徐涛. 基于演化博弈的用户接入机制[J]. 计算机应用, 2020, 40(5): 1394. WANG Yueping, XU Tao. User access mechanism based on evolutionary game[J]. Journal of Computer Applications, 2020, 40(5): 1394. DOI:10.11772/j.issn.1001-9081.2019112024 |
| [15] |
WATKINS C J C H, DAYAN P. Q-learning[J]. Machine Learning, 1992, 8(3): 280. DOI:10.1007/BF00992698 |
| [16] |
VANHASSELT H. Double Q-learning[J]. Advances in Neural Information Processing Systems, 2010, 23(2): 2615. |
| [17] |
SCHAUL T, QUAN J, ANTONOGLOU I, et al. Prioritized experience replay[C]//Proceedings of the 4th International Conference on Learning Representations. San Juan: [s. n. ], 2016: 325. DOI: 10.48550/arXiv.1511.05952
|
| [18] |
俞鹤伟, 梁根. 异构无线网络接入选择算法综述[J]. 哈尔滨工业大学学报, 2017, 49(11): 179. YU Hewei, LIANG Gen. Overview of access selection algorithms for heterogeneous wireless networks[J]. Journal of Harbin Institute of Technology, 2017, 49(11): 179. DOI:10.11918/j.issn.0367-6234.201605125 |
 2023, Vol. 55
2023, Vol. 55


