2. 北京交通大学 土木建筑工程学院, 北京 100044
2. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China
地震动序列中包含的信息、特征以及对结构造成的震害可以用地震动强度指标来衡量。对于特定结构,选择合适的地震动强度指标来评估结构的损伤以及结构的震后可恢复性可以有效地降低由于地震动之间的差异带来的结果离散性。既有研究表明,地震动强度指标与结构损伤具有关联性。在结构损伤分析时,理想的情况是所选择的地震动强度指标能最大程度地反映结构在地震动作用下的损伤情况。
近年来,国内外研究学者针对不同地震动强度参数与结构损伤之间的相关性开展了一系列研究。文献[1]研究了14种地震强度指标SSI与一座钢筋混凝土框架结构整体损伤之间的相关性,并得出基本周期谱加速度与结构整体损伤的相关性最高的结论。文献[2]开展了隧道衬砌结构损伤与地震动强度指标的相关性研究。结果表明,对于无速度脉冲的地震动,地面峰值速度(Vpg)和地面峰值位移(Dpg)具备较高的相关性。文献[3]基于中国汶川地震动数据,研究了长周期单自由度体系最大响应与12种地震强度指标的相关性,结果显示不同地震动强度指标与长周期单自由度体系最大响应的相关性差别显著。
文献[4]研究了远场地震动作用下23种地震动强度指标与一座三层钢筋混凝土框架结构损伤指标之间的相关性,研究表明,地震反应谱强度SI指标(SSI)与结构的最大层间位移角、Park - Ang损伤指标具有最高的相关性。文献[5]基于中国汶川地震动的实际震害资料,开展了结构的破坏情况与地面峰值加速度(Apg)、Vpg和SSI之间的相关性研究。结果表明,Vpg与近断层脉冲地震动作用下的结构损伤有较好关联性。文献[6]开展了在不同方向的地震动作用下,结构损伤与地震动强度指标之间的关联性,结果表明地面峰值速度Vpg、Arias强度和地震反应谱强度SSI与结构层间位移角和Park - Ang损伤指标关联性较高。
文献[7]开展了地震动强度指标与大跨度桥梁损伤的相关性研究,并建议使用Vpg进行大跨度钢桥的地震风险评估。文献[8]开展了地震动强度参数与地铁车站结构动力响应指标分析,结果表明加速度型地震动参数更适合用于预测单层双跨地铁车站结构在地震作用下的动力响应。文献[9]开展了地震动强度指标与框架结构响应的相关性研究。文献[10]研究了地震动多元强度参数主成分与结构损伤的相关性。文献[11]针对隔震结构,开展了地震动强度指标与结构损伤的相关性研究。文献[12]研究了钢框架结构最大层间位移角与地震动强度指标关联性情况,并建议使用地震动比能量密度(SED)作为分析钢框架结构抗震性能的强度指标。综上所述,目前地震动强度指标与损伤关联性的研究多针对于框架结构、高层结构、隧道和桥梁结构等,缺乏针对高耸结构的相关研究。
烟囱、电视塔等高耸结构在中国数量巨大、分布广泛,是基础设施的重要组成部分,与其他建筑物相比,由于不具备多道抗震防线,在强震作用下容易发生破坏。特别地,在近断层脉冲型地震动作用情况下,结构将产生更大的位移、变形等结构动力响应[13]。因此,有必要开展高耸结构损伤与近断层脉冲型地震动强度指标的相关性研究。
本文选择2座高度分别为120 m和240 m的烟囱结构,在近断层脉冲型地震动作用下,利用开源程序OpenSEES分析结构在近断层脉冲型地震动作用下的最大顶点位移、层间位移角、最大弯曲曲率、Park - Ang损伤、最大楼层加速度与地震动强度指标的相关性。为分析和评价高耸结构在脉冲型地震动作用下的抗震性能以及震后可恢复性时,结构损伤指标和地震动强度指标的选择提供参考。
1 一种新的复合型地震动强度指标基本周期对应的谱加速度Sa(T1)由于同时包含了地震动的频谱特征以及单自由度结构体系在地震动作用下的最大响应,而得到广泛的应用。然而随着结构高度的逐渐增加,以及结构延性设计概念的普及,Sa(T1)在评价长周期结构抗震性能上逐渐显示出局限性。一方面,仅仅考虑结构的基本周期的动力响应是不够的,对于高耸混凝土结构,高阶振型对于结构动力响应的贡献不容忽视;另一方面,延性设计概念允许结构材料进入塑性状态,结构损伤的积累宏观体现在结构刚度的退化,结构自振周期的延长。为了将结构高阶振型参与、周期延长效应以及频谱形状的特性从地震动强度指标的层面上加以反映,基于反应谱加速度改进的地震动强度指标得到了大量关注。
文献[14]提出一种考虑结构周期延长效应的双参数指数型地震动强度指标S*=Sa(T1)RαSa, 其中RSa=Sa(Tf)/Sa(T1),Tf是结构延长后的周期。文献[15]提出了2个指数型强度指标I12和I123,I12指标考虑了结构周期延长效应,适用于中低层建筑结的抗震性能评价,τa和τb可分别取结构基本周期以及延长后的周期。I123考虑结构的前3阶振型的参与,I12=Sa(τa, 5%)1-βSa(τb, 5%)β和I123= Sa · (τa, 5%)1-β-γSa(τb, 5%)βSa(τc, 5%)γ。文献[16-17]建议分别考虑结构周期延长效应的指标SN1=Sa(T1)0.5Sa(CT1)0.5和考虑结构前2阶振型的指标SN2=Sa(T1)0.75Sa(T2)0.25。
文献[18]基于超高层结构,提出了一种考虑高阶振型的地震动指标Sa,并认为在地震动强度指标层面上,结构各阶振型对结构响应的贡献相同。值得注意的是,该研究表明,在地震动指标中考虑的振型数量并不是越多越好。文献[19]使用指数组合形式提出了2种考虑高阶振型的地震动强度指标S12=Sa(T1)αSa(T2)β和S123=Sa(T1)αSa(T2)β · Sa(T3)γ,α、β和γ分别是结构振型质量与总质量的比值。
除了采用指数组合形式修正谱加速度外,也有学者使用线性组合的方式修正地震动强度指标,文献[20]采用结构前2阶和前3阶谱加速度值线性相加形式,提出了2个强度指标,Sa12*=0.8Sa(T1)+0.2Sa(T2)和Sa123*=0.8Sa(T1)+0.15Sa(T2)+0.05Sa(T3)。在此基础上,文献[21]使用结构振型质量参与系数作为组合因子,提出了一种考虑结构高阶振型参与的地震动强度指标Sa*=
| 表 1 基于加速度反应谱修正的地震动强度指标 Tab. 1 Ground motion intensity measures based on acceleration spectrum |
在强震作用下,结构由开始出现损伤到最终破坏可以看作是刚度不断退化的过程,宏观上出现结构周期延长现象。此外,对于多自由度结构体系,有必要考虑高阶振型对于结构响应的贡献,而现有的修正指标仅考虑了高阶振型或者周期延长效应,缺乏对这2种因素的综合体现。因此,本文基于加速度反应谱,在既有研究基础上提出了一种同时考虑周期延长效应和高阶振型贡献的地震动强度指标Sc*,其表达式为
| $ S_{\mathrm{c}}^*=\alpha_1 S_{\mathrm{a}}\left(T_1\right)^\beta S_{\mathrm{a}}\left(C T_1\right)^{1-\beta}+\sum\limits_{i=2}^n \alpha_i S_{\mathrm{a}}\left(T_i\right) $ | (1) |
式中:Sa(Ti)为第i阶的结构反应谱加速度; n为参与计算的振型数量; αi为第i阶的振型组合系数; β为周期延长效应权重系数; C为结构的周期延长系数。从定义可以看出,Sc*从理论构成上参考了振型分解反应谱法的概念,在首项以指数组合形式考虑了周期延长效应,从第2项开始以线性叠加形式考虑了高阶振型的参与。复合型的组合方式保证了指标的多用性,具体来说如果不考虑高阶振型效应(即仅有第1项),Sc*具备了和SN1、S*、I12等指数型强度指标相同的特征;而如果不考虑周期延长效应(周期延长系数C=1),Sc*则会“退化”成为仅考虑高阶振型效应的线性组合指标Sa*、Sa12*和Sa123*。从内容上,Sc*完善了现有的基于反应谱加速度指标的研究,使得结构在强震作用下的高阶振型效应以及周期延长效应在同一个地震动强度指标中同时得到体现,其组合形式也同时反映了现有指数型与线性叠加型指标的特点。
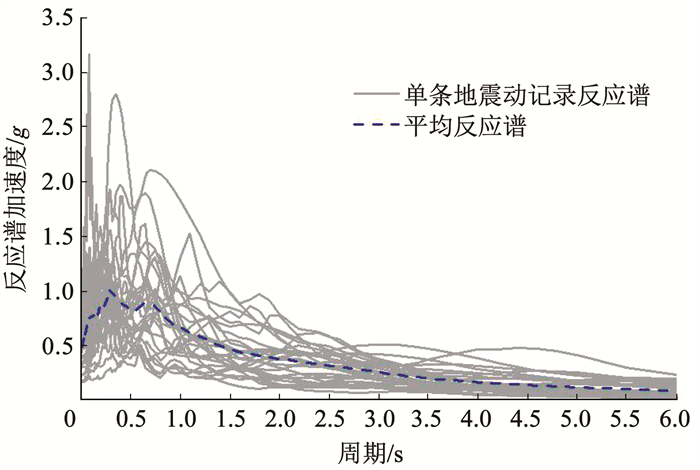
2 地震动记录与强度指标的选择 2.1 地震动记录的选择近断层地震动与远场地震动的特性有较大差异,近断层地震动作用下的结构相对于远场地震动作用破坏更为严重。近断层地震动中,有些地震动时程序列中具有明显的加速度脉冲或长周期速度脉冲,这种脉冲效应会引起结构更大的变形、位移和其他动力响应。为了研究脉冲型地震动作用下,高耸混凝土结构损伤指标与地震动强度指标相关性,本文选择FEMA[22]推荐的28条近断层脉冲型地震动记录输入结构。其加速度反应谱信息见图 1。
|
图 1 近断层脉冲效应地震动加速度反应谱 Fig. 1 Ground motion acceleration response spectrum with pulse-like effect |
合理的地震动强度指标是预测结构响应和评价结构地震功能可恢复能力的重要基础。理想的地震动强度指标需要综合反映地震动的3要素,即频谱、振幅和持时,这些特征与结构的响应有着密切的关系。一个合理的地震动强度指标理应准确反映结构在地震作用下的响应程度。本文选择了包括Sc*
在内的37个地震动强度指标,并将其按照类别划分为:幅值型地震动强度指标(Apg、Vpg、Dpg、Vpg/Apg、Dpg/Apg);频谱型地震动强度指标(Sc*、Sa(T1)、EEPA、EEPV),频谱积分型强度指标(AASI、VVSI)和Housner谱强度指标(SSI);持时型地震动强度指标(Td)。复合型地震动强度指标(Arias强度)、特征强度(Ic)、比能量密度(SSED)、累积绝对速度(CCAV)、累积绝对位移(CCAD)、Nau指标(Ea、Ev、Ed)、地震功率指标(Pa、Pv、Pd)、Riddell指标(Ia、Id、Iv)、Fajfar指标(If),以及部分指标对应的均方根类的指标(arms、vrms、drms、Ars、Vrs、Drs、aRMS、vRMS、dRMS)。详细信息见表 2。
| 表 2 本文选择的地震动强度指标 Tab. 2 Ground motion intensity measures selected in this paper |
结构的损伤指标是定量评估结构破坏程度的工具。常见的结构损伤指标有反映构件损伤的Park - Ang指标、结构最大层间位移角、最大楼层加速度、最大顶点位移等。
在高耸结构损伤指标的选择方面,文献[23-24]以混凝土受压应变为损伤参数对冷却塔和烟囱进行了地震易损性分析;文献[25]用层间位移角作为结构损伤指标对德黑兰电视塔进行了增量动力分析;文献[26]使用曲率延性系数作为损伤指标,分析了高耸烟囱的地震易损性和抗倒塌性能。
本文在研究高耸结构损伤指标与地震动强度指标关联性时,选择了5种损伤指标,分别是结构最大弯曲曲率、结构最大层间位移角、结构最大顶点位移、结构最大楼层加速度以及Park - Ang损伤指标。Park - Ang损伤指标是文献[27]在试验基础上提出的同时考虑钢筋混凝土构件变形和滞回耗能的双参数模型。该模型已经成为评价钢筋混凝土构件损伤时使用最为广泛的模型之一,其计算式如下:
| $ D=\frac{\delta_{\mathrm{m}}}{\delta_{\mathrm{u}}}+\beta \frac{\int \mathrm{d} E}{F_{\mathrm{y}} \delta_{\mathrm{u}}} $ | (2) |
式中:δm为截至计算点处构件的最大变形; δu为构件在荷载作用下的极限变形; β为耗能因子; ∫dE为计算点处的滞回耗能; Fy为构件的屈服力。
4 结构数值模型 4.1 结构概况本文选择高度分别为120 m和240 m的实际钢筋混凝土烟囱作为研究对象,这2座烟囱均建于20世纪90年代。主体结构由钢筋混凝土壳体、隔热层和内衬组成,其中120 m烟囱底部半径为5.86 m,混凝土材料标号为C30,钢筋采用HRB335,隔热层和内衬的密度分别为450 kg/m3和1 200 kg/m3;240 m烟囱底部半径为12.07 m,隔热层和内衬的密度分别为350 kg/m3和1 900 kg/m3。表 3和表 4分别为2座烟囱结构的截面尺寸,详细的结构配筋情况可参考文献[28],在此不再具体说明。
| 表 3 120 m烟囱结构截面尺寸 Tab. 3 Cross-sectional dimensions of the 120 m chimney |
| 表 4 240 m烟囱结构截面尺寸 Tab. 4 Cross-sectional dimensions of the 240 m chimney |
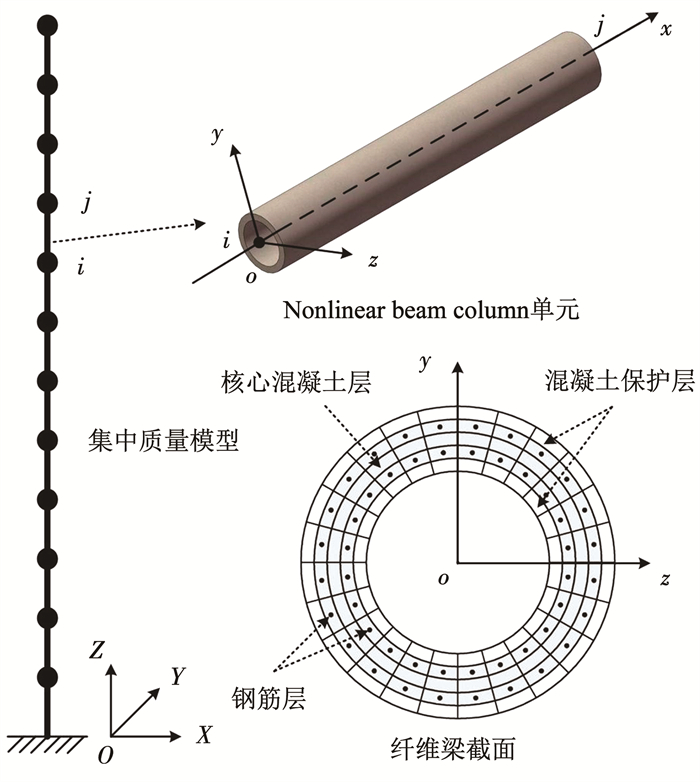
本文采用开源程序OpenSEES(Open System for Earthquake Engineering Simulation),基于分布塑性的纤维梁柱单元建立了2座烟囱结构的模型,见图 2。烟囱结构模型使用集中质量的长悬臂模型模拟,集中质量点之间使用非线性梁柱单元(nonlinear beam column, NBC)连接。由于烟囱隔热层和内衬在建造时分段堆砌在筒壁内侧环形梁上,在建模时将隔热层和内衬的质量以集中质量形式作用在单元节点处,可不考虑隔热层和内衬对结构侧向刚度的贡献。结构圆筒截面被离散为若干个纤维层,从外到内依次为外侧混凝土保护层、外排钢筋层、核心混凝土层、内排钢筋层以及内测混凝土保护层,各个纤维层被赋予对应的材料力学特性,结构的阻尼矩阵为瑞利阻尼模型,阻尼比取0.05。圆形筒身截面剪切、扭转效应的使用Section Aggregator命令进行模拟。
|
图 2 烟囱结构有限元模型 Fig. 2 Finite element model of the chimney in OpenSEES |
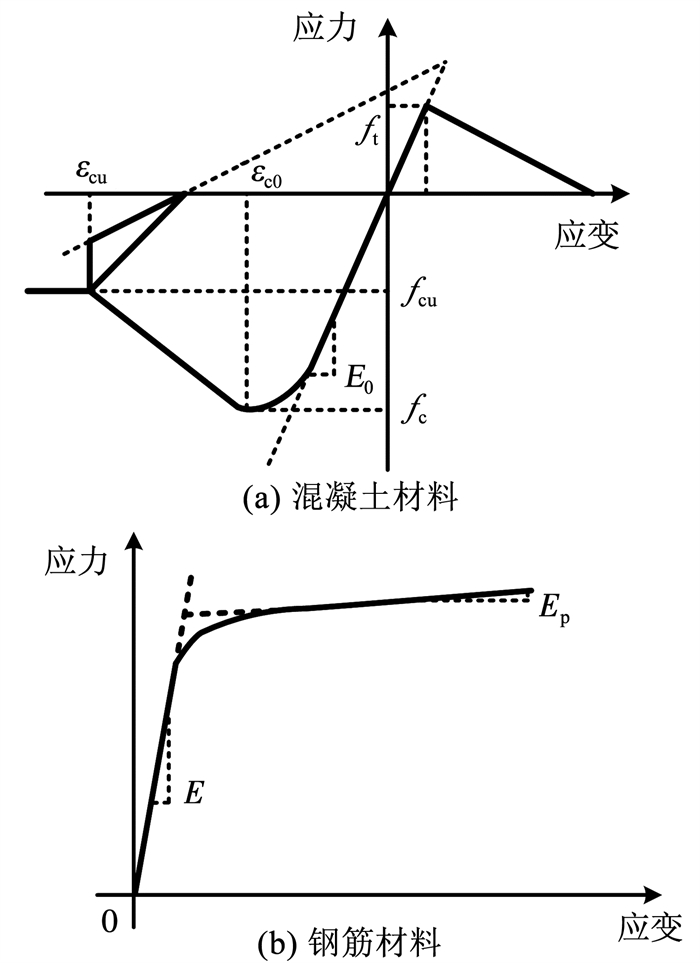
混凝土材料采用Concrete02模型模拟,其应力应变关系见图 3(a)。Concrete02模型可以考虑混凝土受拉软化的线性加、卸载规则,并且可以考虑混凝土的初始开裂等性能。钢筋材料使用OpenSEES中的Steel02模型模拟,其应力应变关系见图 3(b)。Steel02模型能较好地钢筋应变硬化现象,并考虑了Bauschinger效应。
|
图 3 材料应力应变模型 Fig. 3 Strain - stress model of materials |
本文烟囱结构模型的动力特征见表 5。2座烟囱结构总质量分别为12 590 t和3 650 t,240 m烟囱结构前3阶自振周期分别为3.33 s、0.98 s和0.45 s;120 m烟囱前3阶自振周期分别为1.92 s、0.36 s和0.14 s。文献[26]对本文的240 m烟囱进行了实际频率测量,以验证本文OpenSEES建立烟囱模型的准确性。结果显示,周期与实测周期在5%以内,这表明本文模型能够有效模拟烟囱结构的动力特征。
| 表 5 烟囱结构动力特征 Tab. 5 Dynamic properties of the chimneys |
本文在研究地震动强度指标和结构损伤指标相关性时,采用皮尔逊相关性系数ρPearson评价相关程度,其计算方法见式(3)。
| $ \rho_{\text {Pearson }}=\frac{\sum\limits_{i=1}^n\left(X_i-\bar{X}\right)\left(Y_i-\bar{Y}\right)}{\sqrt{\sum\limits_{i=1}^n\left(X_i-\bar{X}\right)^2 \sum\limits_{i=1}^n\left(Y_i-\bar{Y}\right)^2}} $ | (3) |
式中:Xi为结构响应值或者损伤指标样本值;Yi为地震动强度指标样本值;X和Y分别为样本点均值。当ρPearson越接近1时,表示评价的指标之间相关性越高。
图 4为240 m烟囱结构5种损伤指标与地震动强度指标Sc*、Sa(T1)散点图和线性相关系数情况。文献[29]详细介绍并讨论了在计算Sc*时,周期延长系数C以及振型参与数量n的取值,在此不再赘述。通过对比发现,不管选择何种结构损伤指标,Sc*和损伤指标相关性系数较Sa(T1)均得到了提高。这表明在高耸烟囱的地震动强度指标理论中,有必要在基本周期谱加速度的基础上,同时考虑更多模态的参与以及周期延长效应。

|
图 4 240 m烟囱损伤指标与Sc*指标关联性散点图 Fig. 4 Scatter plots of correlation between damage indices of 240 m chimney and Sc* |
图 5为37个地震动强度指标与脉冲型地震动作用下烟囱结构的Park - Ang损伤之间的线性相关系数情况。其中,横坐标为地震动强度指标,纵坐标为该指标与结构Park - Ang损伤指标的皮尔逊相关系数(ρPearson)情况,ρPearson值越接近1,表明2种指标的相关性越强。

|
图 5 Park - Ang损伤指标与地震动强度指标关联性 Fig. 5 Correlation between ground motion intensity measures and Park - Ang damage index |
如图 5(a)所示,对于120 m烟囱,在所有的地震动强度指标中,本文提出的同时考虑周期延长效应和高阶振型效应的Sc*指标与Park - Ang损伤指标的相关性最高,基本周期对应的谱加速度Sa(T1)、有效峰值速度(EEPV)和Housner谱强度(SSI)紧随其后。在240 m烟囱中,本文提出的Sc*指标与Park - Ang损伤指数仍然具备最高的相关性,vRMS、速度均方根vrms和VVSI分别位于相关性第2至4位。总体上,与速度相关的地震动强度指标(SSI、VVSI、EEPV、Vpg、vrms)显示出与烟囱Park - Ang损伤指数有较强的相关性。对于烟囱结构,表示地震动持时的指标Td与结构Park - Ang损伤相关性较低。此外,虽然Vpg/Apg和Dpg/Vpg都在一定程度上反映了地震动的频谱特性,但这2个指标与结构Park - Ang损伤的相关性却大不相同。在复合强度指标(Ia、Id、Iv、If)中,If和Iv具备相对较高的相关性。
对于烟囱结构,VVSI或SSI的较高相关性可以通过其定义来解释。一方面,速度型的地震动强度指标大多通过加速度时程曲线积分得到或者由位移时程曲线微分得到,因此速度型地震动强度指标与结构惯性力(加速度)和变形(位移)均有内在关联,而Park - Ang损伤指标本身即为考虑构件变形(位移)和滞回耗能的损伤指标;另一方面,VVSI或SSI采用反应谱和周期轴围成的面积定义速度谱强度,考虑了较为广泛的频谱特性,因此与结构的响应具有较高的关联性。
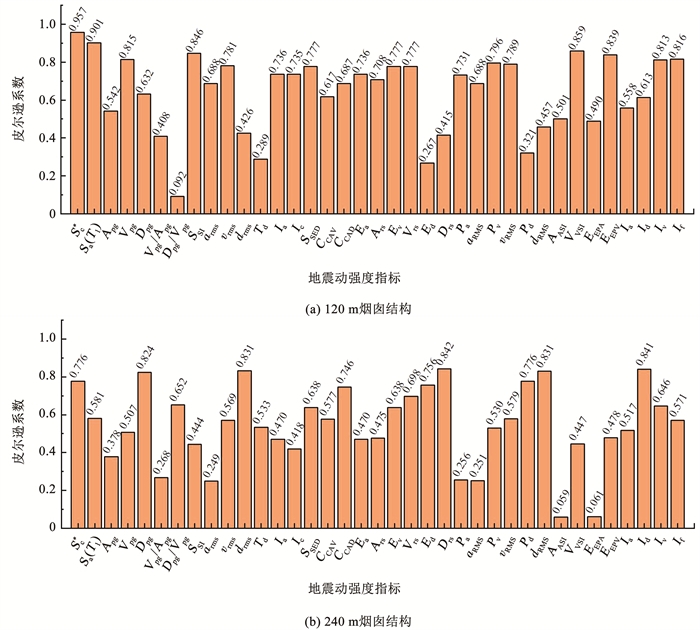
图 6为脉冲型地震动作用下地震动强度指标结构最大曲率之间的线性相关系数情况。对于120 m烟囱结构,本文提出的Sc*指标具备最高的相关性,相关系数高达0.957。采用频谱积分定义的速度型指标SSI、VVSI、EEPV具有相对较高的关联性。如图 5(b)所示,位移型的地震动强度指标与240 m烟囱最大曲率的相关性有较大增长,如Dpg、位移均方根drms、Drs、dRMS、Pd以及Id。此外,本文提出的Sc*指标是在Sa(T1)基础上,同时考虑了高阶振型效应和周期延长效应,通过对比Sc*和Sa(T1)的相关性系数,可以发现在表征结构最大曲率方面,在地震动强度指标包含的信息中考虑高阶振型和周期延长效应是非常有效和必要的。
|
图 6 结构最大曲率与地震动强度指标关联性 Fig. 6 Correlation between ground motion intensity measures and maximum structural curvature |
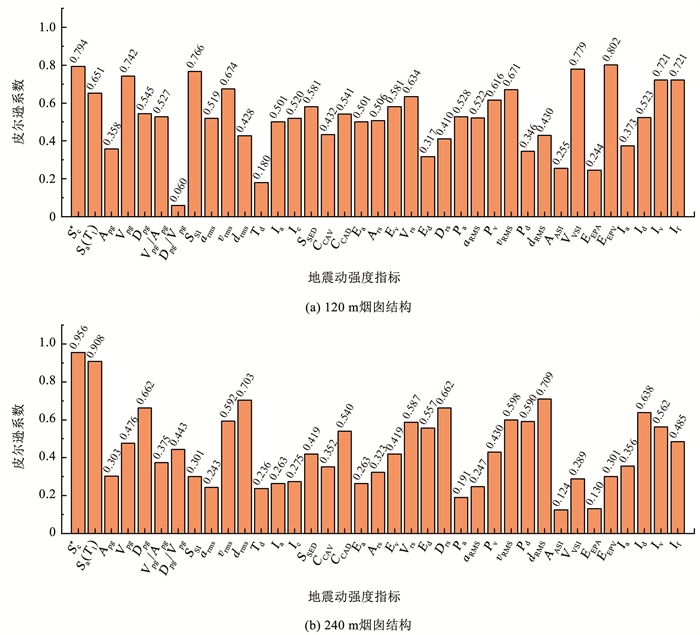
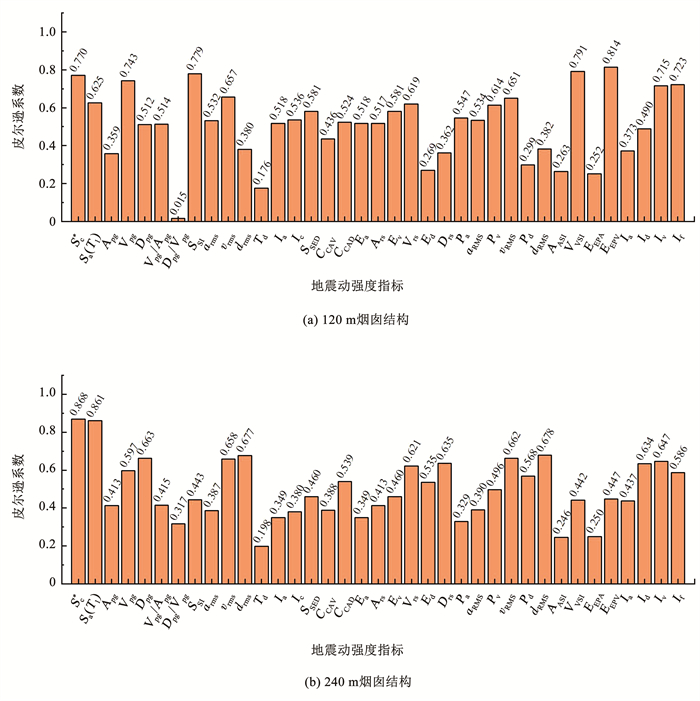
图 7和图 8分别为37个地震动强度指标结构最大顶点位移、最大层间位移角之间的线性相关系数情况。值得指出的是,本文提出的指标Sc*与240 m烟囱的层间位移角和最大顶点位移均具备最高的相关性。而对于120 m烟囱,EEPV与结构最大层间位移角、结构最大顶点位移之间具备最高的相关性。此外,对于速度相关的地面运动强度指标,特别是VVSI和SSI,其与结构最大层间位移角和结构最大顶点位移的相关性较强。此外,对比120 m烟囱,位移型的地震动强度指标与240 m烟囱损伤的相关性有较大增长,特别是Dpg、位移均方根drms、Drs和dRMS。位移型地震动指标一般认为与地震动的低频分量密切相关,由于结构周期的增长,结构的最大层间位移角和结构最大顶点位移对于位移型的地震动强度指标更加敏感。此外,图 6~8结果显示Apg的皮尔逊相关系数较低,这表明中国规范使用的Apg在表征近断层脉冲型地震动对于高耸烟囱的Park - Ang损伤、曲率、层间位移角以及顶点位移响应方面有一定局限性。
|
图 7 结构最大顶点位移与地震动强度指标关联性 Fig. 7 Correlation between ground motion intensity measures and maximum roof displacement |
|
图 8 结构最大层间位移角与地震动强度指标关联性 Fig. 8 Correlation between ground motion intensity measures and maximum inter-story drift ratio |
图 9为脉冲地震动作用下地震动强度指标和结构最大楼层加速度之间的线性相关情况。对于240 m烟囱,本文提出的指标Sc*在37个指标中具备最高的相关性。而对于120 m烟囱,Sc*有效性仅次于VVSI、SSI、EEPV、Vpg等速度型指标。此外,与图 5~7相比,图 8较显著的变化是与加速度有关的地震动强度指标(Apg、arms、Ea、Ars、Pa、aRMS、AASI、Ia)的相关系数有了一定提升。事实上,结构最大楼层加速度值可以看作对地面加速度的直接放大。因此,结构最大楼层加速度对加速度相关的地面运动参数很敏感,从而导致这类指标相关性的增长。此外,Vpg、VVSI、SSI和EEPV与结构最大楼层加速度依然保持较高的相关性。

|
图 9 结构最大楼层加速度与地震动强度指标关联性 Fig. 9 Correlation between ground motion intensity measures and maximum floor acceleration |
复合型地震动指标Ia、Id、Iv同时包含了地面峰值和地震动持时的信息,If同时考虑了地面峰值速度Vpg和地震动持时的信息。然而,由于高耸烟囱结构的地震响应对于地震动持时特征和部分幅值特征并不敏感(参考Dpg、Apg和Td的相关性系数),从相关性的角度上看,这些复合型地震动指标并未表现出明显的优势。
因此,在设计新的地震动强度指标时,并不是包含的信息越多越好。一方面,要结合结构动力响应特点,合理地反映地震动对于结构的震害;另一方面,在表征这些地震动特征时,也需要选择合理的组合形式。从本文的研究结果上看,选择加速度反应谱积分形式以及谱加速度幂乘积形式具有较好的效果。
6 结论基于加速度反应谱提出了一种同时考虑高阶振型和周期延长的地震动强度指标,以2座高耸烟囱为研究对象,使用OpenSEES分析了近断层脉冲型地震动作用下37种地震动指标与烟囱结构损伤指标的关联性。通过本文的研究,可以得出以下结论:
1) 对于2座烟囱结构,本文提出的Sc*在所有的37种指标中展示出与结构Park - Ang损伤最高的关联性,Sc*和其他损伤指标也具备相对较高的关联性。使用Sc*指标表征脉冲型地震动对于结构损伤的影响能有效减少地震动差异导致的离散性。
2) 整体上,速度型相关的地震动强度指标表现出与结构损伤指标的较高的相关性。随着结构周期的增大,位移型的地震动强度指标与损伤的关联性有增长的趋势。
3) 作为中国抗震规范规定的地震动强度指标,Apg与高耸烟囱结构的最大层间位移角、最大顶点偏移率、曲率以及Park - Ang损伤指标关联度较差。相比之下,Apg与结构的最大楼层加速度关联性较高。这表明Apg在表征高耸结构变形破坏方便存在局限性,但是可以用来分析非结构构件的抗震性能。
| [1] |
ELENAS A. Correlation between seismic acceleration parameters and overall structural damage indices of buildings[J]. Soil Dynamics and Earthquake Engineering, 2000, 20(1/2/3/4): 93. DOI:10.1016/S0267-7261(00)00041-5 |
| [2] |
CHEN Zhiyi, WEI Jianshu. Correlation between ground motion parameters and lining damage indices for mountain tunnels[J]. Natural Hazards, 2013, 65(3): 1683. DOI:10.1007/s11069-012-0437-5 |
| [3] |
韩建平, 周伟, 李慧. 基于汶川地震数据的地震动强度指标与中长周期SDOF体系最大响应相关性[J]. 工程力学, 2011, 28(10): 185. HAN Jianping, ZHOU Wei, LI Hui. Correlation between ground motion intensity indices and SDOF system responses with medium-to-long period based on the Wenchuan earthquake data[J]. Engineering Mechanics, 2011, 28(10): 185. |
| [4] |
CAO V V, RONAGH H R. Correlation between seismic parameters of far-fault motions and damage indices of low-rise reinforced concrete frames[J]. Soil Dynamics and Earthquake Engineering, 2014, 66(1): 2. DOI:10.1016/j.soildyn.2014.06.020 |
| [5] |
WANG Z J, ZHAO B M. Correlations between structural damage and ground motion parameters during the Ms8.0 Wenchuan Earthquake[J]. Soil Dynamics and Earthquake Engineering, 2015, 72(1): 29. DOI:10.1016/j.soildyn.2014.11.005 |
| [6] |
KOSTINAKIS K, ATHANATOPOULOU A, MORFIDIS K. Correlation between ground motion intensity measures and seismic damage of 3D R/C buildings[J]. Engineering Structures, 2015, 82(1): 51. DOI:10.1016/j.engstruct.2014.10.035 |
| [7] |
蒋崇文, 易伟建, 庞于涛. 地震动强度指标与大跨度刚构桥梁损伤的相关性[J]. 中国公路学报, 2016, 29(9): 97. JIANG Chongwen, YI Weijian, PANG Yutao, et al. Correlation between seismic intensity indices and damages of large span rigid frame bridges[J]. China Journal of Highway and Transport, 2016, 29(9): 97. DOI:10.19721/j.cnki.1001-7372.2016.09.012 |
| [8] |
钟紫蓝, 申轶尧, 甄立斌, 等. 地震动强度参数与地铁车站结构动力响应指标分析[J]. 岩土工程学报, 2020, 42(3): 486. ZHONG Zilan, SHEN Yiyao, ZHEN Libin, et al. Ground motion intensity measures and dynamic response indexes of metro station structures[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(3): 486. DOI:10.11779/CJGE202003010 |
| [9] |
陈健云, 李静, 韩进财, 等. 地震动强度指标与框架结构响应的相关性研究[J]. 振动与冲击, 2017, 36(3): 105. CHEN Jianyun, LI Jing, HAN Jincai, et al. Correlation between ground motion intensity indexes and seismic responses of frame structures[J]. Journal of Vibration and Shock, 2017, 36(3): 105. DOI:10.13465/j.cnki.jvs.2017.03.017 |
| [10] |
刘亭亭, 于晓辉, 吕大刚. 地震动多元强度参数主成分与结构损伤的相关性分析[J]. 工程力学, 2018, 35(8): 122. LIU Tingting, YU Xiaohui, LV Dagang. Analysis of correlation between principal components of multivariate earthquake intensity measures and structural damage[J]. Engineering Mechanics, 2018, 35(8): 122. DOI:10.6052/j.issn.1000-4750.2017.04.0289 |
| [11] |
杨参天, 解琳琳, 李爱群, 等. 适用于高层隔震结构的地震动强度指标研究[J]. 工程力学, 2018, 35(8): 21. YANG Cantian, XIE Linlin, LI Aiqun, et al. Intensity measures for seismically isolated tall buildings[J]. Engineering Mechanics, 2018, 35(8): 21. DOI:10.6052/j.issn.1000-4750.2017.07.0531 |
| [12] |
PINZON L A, VARGAS-ALZATE Y F, PUJADES L G, et al. A drift-correlated ground motion intensity measure: application to steel frame buildings[J]. Soil Dynamics and Earthquake Engineering, 2020, 132. DOI:10.1016/j.soildyn.2020.106096 |
| [13] |
MACRAE G A, MORROW D V, ROEDER C W. Near-fault ground motion effects on simple structures[J]. Journal of Structural Engineering, 2001, 127(9): 996. DOI:10.1061/(ASCE)0733-9445(2001)127:9(996) |
| [14] |
CORDOVA P P, DEIERLEIN G G, MEHANNY S S F, et al. Development of a two-parameter seismic intensity measure and probabilistic assessment procedure[C]//Proceedings of the Second U.S. -Japan Workshop on Performance-Based Earthquake Engineering Methodology for Reinforced Concrete Building Structures. Sapporo: [s. n. ], 2001
|
| [15] |
VAMVATSIKOS D, CORNELL C A. Developing efficient scalar and vector intensity measures for IDA capacity estimation by incorporating elastic spectral shape information[J]. Earthquake Engineering Structural Dynamics, 2005, 34(13): 1573. DOI:10.1002/eqe.496 |
| [16] |
LIN Lan, NAUMOSKI N, SAATCIOGLU M, et al. Improved intensity measures for probabilistic seismic demand analysis. Part 1:development of improved intensity measures[J]. Canadian Journal of Civil Engineering, 2010, 38(1): 79. DOI:10.1139/L10-110 |
| [17] |
LIN Lan, NAUMOSKI N, SAATCIOGLU M, et al. Improved intensity measures for probabilistic seismic demand analysis. Part 2:application of the improved intensity measures[J]. Canadian Journal of Civil Engineering, 2010, 38(1): 89. DOI:10.1139/L10-111 |
| [18] |
LU Xiao, YE Lieping, LU Xinzheng, et al. An improved ground motion intensity measure for super high-rise buildings[J]. Science China Technological Sciences, 2013, 56(6): 1525. DOI:10.1007/s11431-013-5234-1 |
| [19] |
周颖, 苏宁粉, 吕西林. 高层建筑结构增量动力分析的地震动强度参数研究[J]. 建筑结构学报, 2013, 34(2): 53. ZHOU Ying, SU Ningfen, LV Xilin. Study on intensity measure of incremental dynamic analysis for high-rise structures[J]. Journal of Building Structures, 2013, 34(2): 53. DOI:10.14006/j.jzjgxb.2013.02.011 |
| [20] |
SHOME N. Probabilistic seismic demand analysis of nonlinear structures[D]. Stanford: Stanford University, 1999
|
| [21] |
ZHANG Yantai, HE Zheng, LU Wengao, et al. A spectral-acceleration-based linear combination-type earthquake intensity measure for high-rise buildings[J]. Journal of Earthquake Engineering, 2018, 22(8): 1479. DOI:10.1080/13632469.2017.1286624 |
| [22] |
FEMA. FEMA P695: Quantification of building seismic performance factors[S]. Redwood City: Applied Technology Council, 2009
|
| [23] |
周长东, 田苗旺, 王朋国, 等. 考虑地震方向性的高耸RC烟囱结构易损性分析[J]. 湖南大学学报(自然科学版), 2017, 44(11): 11. ZHOU Changdong, TIAN Miaowang, WANG Pengguo, et al. Analysis on structural fragility of a high-rise RC chimney considering ground motion directionality[J]. Journal of Hunan University (Natural Sciences), 2017, 44(11): 11. DOI:10.16339/j.cnki.hdxbzkb.2017.11.002 |
| [24] |
周长东, 王朋国, 田苗旺, 等. 双曲线冷却塔在多维地震下的区域易损性评价[J]. 哈尔滨工业大学学报, 2017, 49(6): 156. ZHOU Changdong, WANG Pengguo, TIAN Miaowang, et al. Partitioned seismic vulnerability assessment of hyperbolic cooling tower under multi-dimensional earthquakes[J]. Journal of Harbin Institute of Technology, 2017, 49(6): 156. DOI:10.11918/j.issn.0367-6234.201604006 |
| [25] |
ASGARIAN B, MIRTAHERI M Y M, SAMANI H R, et al. Incremental dynamic analysis of high-rise towers[J]. Structural Design of Tall and Special Buildings, 2010, 19(8): 922. DOI:10.1002/tal.518 |
| [26] |
曾绪朗. 高耸钢筋混凝土烟囱结构抗震性能研究[D]. 北京: 北京交通大学, 2014 ZENG Xulang. Study on seismic performance of high-rise reinforced concrete chimney structure[D]. Beijing: Beijing Jiaotong University, 2014 |
| [27] |
PARK Y J, ANG A H S, WEN Y K. Seismic damage analysis of reinforced-concrete buildings[J]. Journal of Structural Engineering, 1985, 111(4): 740. DOI:10.1061/(ASCE)0733-9445(1985)111:4(740) |
| [28] |
邱意坤. 高耸混凝土结构地震动强度指标和整体损伤研究[D]. 北京: 北京交通大学, 2020 QIU Yikun. Study of ground motion intensity measures and global damage for high-rise stack-like concrete structures[D]. Beijing: Beijing Jiaotong University, 2020 |
| [29] |
QIU Yikun, ZHOU Changdong, SIHA A, et al. A spectral-acceleration-based combination-type earthquake intensity measure for high-rise stack-like structures[J]. Advances in Structural Engineering, 2019, 23(7): 1350. DOI:10.1177/1369433219894237 |
 2023, Vol. 55
2023, Vol. 55


