2. 地质灾害防治与地质环境保护国家重点实验室(成都理工大学),成都 610059
2. State Key Laboratory of Geohazard Prevention and Geoenvironment Protection (Chengdu University of Technology), Chengdu 610059, China
在水利、交通、油气等设施建设中存在大量隧道工程,实际又以水平地应力与竖向地应力存在明显差异的非静水应力场为主,研究非静水压力下非圆塑性区边界线、塑性区位移分布及围岩特征曲线对隧道支护设计具有重要意义。当围岩塑性区完全包围隧道时,非静水压力下圆形隧道的塑性区应力可联立围岩屈服条件和平衡微分方程获得,进而围岩弹性区应力计算成为确定隧道塑性区半径和位移的关键。基于Mohr-Coulomb准则和理想弹-塑性模型,已有学者采用Kastner法[1-7]、复变函数法[8-12]、摄动法[13-15]和总荷载不变法[16-18],探讨了非静水压力下圆形隧道的弹性区应力和非圆塑性区边界线。
Kastner[1]将非静水压圆形隧道纯弹性状态时的应力基尔希公式,直接代入Mohr-Coulomb准则建立隧道非圆塑性区的边界线方程。赵志强等[2-6]基于Kastner法提出隧道的蝶形塑性区理论,于学馥等[7]考虑应力重分布改进了Kastner法。需指出的是,Kastner法不计围岩弹塑性发展,也不顾非静水压隧道的塑性区边界线不是圆形,而使用内边界要求为圆形孔洞的应力基尔希公式。Detournay等[8-12]借助复变函数法将非圆形的隧道塑性区边界保角映射为圆形,难点在于如何有效确定隧道弹性区的应力复变函数形式及众多系数。魏悦广等[13-15]依据摄动法将隧道非圆塑性区边界和弹性区应力求解转化为泰勒级数展开式,获得了精度较高的围岩弹性区应力和类椭圆塑性区边界。严克强等[16-18]选择基尔希公式作为围岩弹性区应力表达式,由总荷载不变法推导隧道水平轴和竖向轴处的塑性区半径方程,并由几何相似原理给定其他方位角处的,但弹性区应力基尔希公式的内边界非圆问题依然存在。
总荷载不变法从基本的力平衡原理出发,理论基础简单,易于被工程接受及实用推广,同时,以简洁公式表达的围岩弹性区应力摄动解可逐阶逼近真实结果达到高精度。此外,峰后岩石强度常有一定跌落,弹-脆-塑性模型相比理想弹-塑性模型更适合描述岩石真实强度变化。因此,针对非静水压力作用下的圆形隧道,基于Mohr-Coulomb准则和弹-脆-塑性模型并引入围岩弹性区应力的摄动解,首先采用总荷载不变法建立水平轴与竖向轴处的塑性区半径方程,继而利用几何相似原理拓展至其他方位角处,对比文献总荷载不变法(以应力基尔希公式为基础)、Kastner法和复变函数法进行合理性与正确性验证,结合非关联流动法则推导塑性区位移解析解,探讨侧压力系数和脆性软化对隧道塑性区边界线、塑性区位移分布以及围岩特征曲线的影响规律。
1 总荷载不变法假定围岩为均匀、连续的各向同性材料,图 1为非静水压力下圆形隧道的平面应变力学模型,洞壁处作用均匀支护力pi,无穷远处作用竖向地应力q、水平地应力λq,λ为侧压力系数。另外,a为隧道半径;Rp为塑性区半径;r为某点到隧道中心的距离;θ为方位角,以水平右半轴为起点、逆时针旋转为正。

|
图 1 非静水压隧道力学模型(λ < 1) Fig. 1 Mechanical model of a non-hydrostatic pressure tunnel (λ < 1) |
对于非静水压力下圆形隧道的弹性区和塑性区,由地应力的双轴对称性知在水平轴和竖向轴处反对称的切应力恒为0[16-18],进而可对隧道开挖前/后的围岩环向正应力进行积分。总荷载不变法依据最基本的力平衡原理,对非静水压圆形隧道分为开挖前/后围岩的竖向总荷载不变、开挖前/后围岩的水平向总荷载不变,由方位角θ=0°处(θ面,存在环向正应力,切应力为零)围岩竖向总荷载不变可获得水平轴处塑性区半径RH的求解方程,同理,由方位角θ=90°处(θ面,存在环向正应力,切应力为零)围岩水平向总荷载不变可获得竖向轴处塑性区半径Rv的求解方程,下文将以沿水平轴的竖向总荷载不变为例分析。
图 2为非静水压力下圆形隧道在开挖前/后沿水平轴的围岩环向正应力分布,L为计算范围。隧道开挖前水平轴处围岩竖向作用均匀竖向地应力q,如图 2(a)所示;开挖后支护力pi均匀地作用在洞壁处,水平轴处塑性区存在环向正应力σθp|θ=0°(上标p代表塑性区,下同),弹性区存在环向正应力σeθ|θ=0° (上标e代表弹性区,下同),在弹-塑性交界处图 2(b)中理想弹-塑性模型的环向正应力连续,而图 2(c)中弹-脆-塑性模型的环向正应力不连续。
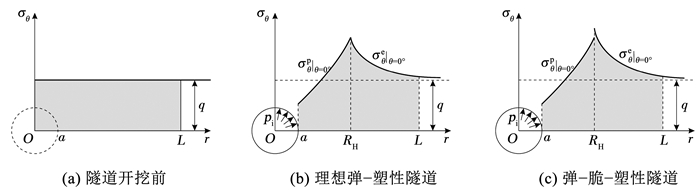
|
图 2 沿水平轴的围岩环向正应力 Fig. 2 Tangential normal stress of surrounding rock along horizontal axis |
依据竖向总荷载不变,得式(1a)中隧道开挖前沿水平轴的围岩竖向总荷载Q0与式(1b)中隧道开挖后的围岩竖向总荷载Q1相等。
| $ Q_0=q L $ | (1a) |
| $ \begin{gathered} Q_1=\int_0^{\frac{\pi}{2}} p_{\mathrm{i}} a \sin \theta \mathrm{d} \theta+\left.\int_a^{R_{\mathrm{H}}} \sigma_\theta^{\mathrm{p}}\right|_{\theta=0^{\circ}} \mathrm{d} r+\left.\int_{R_{\mathrm{H}}}^L \sigma_\theta^{\mathrm{e}}\right|_{\theta=0^{\circ}} \mathrm{d} r \end{gathered} $ | (1b) |
由式(1b)可知,计算隧道开挖后沿水平轴的围岩竖向总荷载Q1,需先求出水平轴处塑性区环向正应力σθp|θ=0°和弹性区环向正应力σeθ|θ=0°的表达式。
2.1 塑性区采用Mohr-Coulomb准则描述围岩强度的弹-脆-塑性特征,其中式(2)对应围岩初始强度,式(3)对应围岩峰后强度。
| $ \sigma_1=A_{\mathrm{i}} \sigma_3+B_{\mathrm{i}} \\ A_{\mathrm{i}}=\frac{1+\sin \varphi_{\mathrm{i}}}{1-\sin \varphi_{\mathrm{i}}}, B_{\mathrm{i}}=\frac{2 c_{\mathrm{i}} \cos \varphi_{\mathrm{i}}}{1-\sin \varphi_{\mathrm{i}}} $ | (2) |
| $ \sigma_1=A_{\mathrm{r}} \sigma_3+B_{\mathrm{r}} \\ A_{\mathrm{r}}=\frac{1+\sin \varphi_{\mathrm{r}}}{1-\sin \varphi_{\mathrm{r}}}, B_{\mathrm{r}}=\frac{2 c_{\mathrm{r}} \cos \varphi_{\mathrm{r}}}{1-\sin \varphi_{\mathrm{r}}} $ | (3) |
式中:σ1为第一主应力,σ3为第三主应力,并以压应力为正;Ai、Bi、Ar、Br为方程参数;ci、φi为围岩初始的黏聚力和内摩擦角(用于弹-塑性交界处弹性区一侧的围岩强度); cr、φr为围岩峰后的黏聚力和内摩擦角(用于隧道塑性区内的围岩强度)。
式(4)表示围岩主应力与各应力分量之间的关系[19],其中,σr、σθ、τrθ分别为径向正应力、环向正应力和切应力。
| $ \begin{aligned} \sigma_1=\frac{1}{2}\left(\sigma_r+\sigma_\theta\right)+\frac{1}{2} \sqrt{\left(\sigma_r-\sigma_\theta\right)^2+4 \tau_{r \theta}^2} \end{aligned} $ | (4a) |
| $ \sigma_3=\frac{1}{2}\left(\sigma_r+\sigma_\theta\right)-\frac{1}{2} \sqrt{\left(\sigma_r-\sigma_\theta\right)^2+4 \tau_{r \theta}^2} $ | (4b) |
将式(4)分别代入式(2)和(3)得非静水压力下隧道围岩初始/峰后的强度关系式为
| $ \begin{gathered} \left(1+A_{\mathrm{i}}\right) \sqrt{\left(\sigma_r-\sigma_\theta\right)^2+4 \tau_{r \theta}^2}= \\ \left(A_{\mathrm{i}}-1\right)\left(\sigma_r+\sigma_\theta\right)+2 B_{\mathrm{i}} \end{gathered} $ | (5) |
| $ \left(1+A_{\mathrm{r}}\right) \sqrt{\left(\sigma_r-\sigma_\theta\right)^2+4 \tau_{r \theta}^2}= \\ \left(A_{\mathrm{r}}-1\right)\left(\sigma_r+\sigma_\theta\right)+2 B_{\mathrm{r}} $ | (6) |
平衡微分方程为
| $ \begin{gathered} \frac{\partial \sigma_r}{\partial r}+\frac{1}{r} \frac{\partial \tau_{\theta r}}{\partial \theta}+\frac{\sigma_r-\sigma_\theta}{r}=0 \end{gathered} $ | (7a) |
| $ \frac{1}{r} \frac{\partial \sigma_\theta}{\partial \theta}+\frac{\partial \tau_{r \theta}}{\partial r}+\frac{2 \tau_{r \theta}}{r}=0 $ | (7b) |
联立式(6)和(7),并结合图 1隧道洞壁处的应力边界条件,即r=a时,σr=pi、τrθ=0,求得围岩塑性区的应力为[20]
| $ \sigma_r^{\mathrm{p}}=\left(p_{\mathrm{i}}+\frac{B_{\mathrm{r}}}{A_{\mathrm{r}}-1}\right)\left(\frac{r}{a}\right)^{A_{\mathrm{r}}-1}-\frac{B_{\mathrm{r}}}{A_{\mathrm{r}}-1} $ | (8a) |
| $ \sigma_\theta^{\mathrm{p}}=A_{\mathrm{r}}\left(p_{\mathrm{i}}+\frac{B_{\mathrm{r}}}{A_{\mathrm{r}}-1}\right)\left(\frac{r}{a}\right)^{A_{\mathrm{r}}-1}-\frac{B_{\mathrm{r}}}{A_{\mathrm{r}}-1} $ | (8b) |
| $ \tau_{r \theta}^{\mathrm{p}}=0 $ | (8c) |
式(8b)给出了水平轴处塑性区环向正应力σθp|θ=0°的精确表达式,在内边界非圆情况下弹性区应力表达式就决定了围岩竖向总荷载Q1的计算精度。严克强等[16-18]以不同方位角处的塑性区半径圆形化弹性区的非圆内边界,并按内边界作用径向压力σre|r=Rp,无穷远处地应力场分解为径向均匀压力λq和竖向压力(1-λ)q,求得以式(9)表示的基尔希公式作为非静水压力下圆形隧道的围岩弹性区应力表达式。
| $ \sigma_r^{\mathrm{e}}=\frac{q}{2}\left[(1+\lambda)\left(1-\frac{R_{\mathrm{p}}^2}{r^2}\right)-(1-\lambda)\left(1-4 \frac{R_{\mathrm{p}}^2}{r^2}+3 \frac{R_{\mathrm{p}}^4}{r^4}\right) \cos 2 \theta\right]+\left.\frac{R_{\mathrm{p}}^2}{r^2} \sigma_r^{\mathrm{e}}\right|_{r=R_{\mathrm{p}}} $ | (9a) |
| $\sigma_\theta^{\mathrm{e}}=\frac{q}{2}\left[(1+\lambda)\left(1+\frac{R_{\mathrm{p}}^2}{r^2}\right)+(1-\lambda)\left(1+3 \frac{R_{\mathrm{p}}^4}{r^4}\right) \cos 2 \theta\right]-\left.\frac{R_{\mathrm{p}}^2}{r^2} \sigma_r^{\mathrm{e}}\right|_{r=R_{\mathrm{p}}} $ | (9b) |
| $ \tau_{r \theta}^{\mathrm{e}}=\frac{q}{2}(1-\lambda)\left(1+2 \frac{R_{\mathrm{p}}^2}{r^2}-3 \frac{R_{\mathrm{p}}^4}{r^4}\right) \sin 2 \theta $ | (9c) |
需注意的是,非静水压圆形隧道的塑性区并非圆形,这与基尔希公式要求的圆形内边界不一致。
魏悦广等[13, 15]基于Mohr-Coulomb准则和理想弹-塑性模型,设摄动参数ε=1-λ,并采用摄动法将非圆塑性区边界求解转化为泰勒级数展开式,以逐阶逼近方式得到精度较高的围岩弹性区应力摄动解,又因2阶摄动解满足精度要求且表达较3阶简洁,引入式(10)表示的非静水压圆形隧道弹性区应力2阶摄动解,其中,(1-λ)、(1-λ)2项分别代表ε1阶摄动增量、ε2阶摄动增量。
| $ \begin{aligned} & \sigma_r^{\mathrm{e}}=q-(q \sin \varphi+c \cos \varphi) \frac{R_0^2}{r^2}-\frac{q(1-\lambda)}{2}\left[1-\frac{R_0^2}{r^2}+\left(1-4 \frac{R_0^2}{r^2}+3 \frac{R_0^4}{r^4}\right) \cos 2 \theta\right]- \\ & \frac{q^2(1-\lambda)^2(1-\sin \varphi)}{4(q \sin \varphi+c \cos \varphi)}\left[\frac{3}{2} \frac{R_0^2}{r^2}+\left(4 \frac{R_0^2}{r^2}-6 \frac{R_0^4}{r^4}\right) \cos 2 \theta+\left(-9 \frac{R_0^4}{r^4}+10 \frac{R_0^6}{r^6}\right) \cos 4 \theta\right] \end{aligned} $ | (10a) |
| $ \begin{aligned} & \sigma_\theta^{\mathrm{e}}=q+(q \sin \varphi+c \cos \varphi) \frac{R_0^2}{r^2}-\frac{q(1-\lambda)}{2}\left[1+\frac{R_0^2}{r^2}-\left(1+3 \frac{R_0^4}{r^4}\right) \cos 2 \theta\right]- \\ & \frac{q^2(1-\lambda)^2(1-\sin \varphi)}{4(q \sin \varphi+c \cos \varphi)}\left[-\frac{3}{2} \frac{R_0^2}{r^2}+6 \frac{R_0^4}{r^4} \cos 2 \theta+\left(3 \frac{R_0^4}{r^4}-10 \frac{R_0^6}{r^6}\right) \cos 4 \theta\right] \end{aligned} $ | (10b) |
| $\begin{gathered} \tau_{r \theta}^{\mathrm{e}}=-\frac{q(1-\lambda)}{2}\left(1+2 \frac{R_0^2}{r^2}-3 \frac{R_0^4}{r^4}\right) \sin 2 \theta+ \\ \frac{q^2(1-\lambda)^2(1-\sin \varphi)}{2(q \sin \varphi+c \cos \varphi)}\left[\left(\frac{R_0^2}{r^2}-3 \frac{R_0^4}{r^4}\right) \sin 2 \theta+\left(-3 \frac{R_0^4}{r^4}+5 \frac{R_0^6}{r^6}\right) \sin 4 \theta\right] \end{gathered} $ | (10c) |
式中:
对于弹-脆-塑性模型,弹-塑性交界处弹性区一侧采用围岩初始强度参数,塑性区采用围岩峰后强度参数,重新推导得非静水压力下弹-脆-塑性圆形隧道弹性区应力的2阶摄动解为
| $ \sigma_r^{\mathrm{e}}=q-\frac{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}}{A_{\mathrm{i}}+1} \frac{R_1^2}{r^2}-\frac{q(1-\lambda)}{2}\left[1-\frac{R_1^2}{r^2}+\left(1-4 \frac{R_1^2}{r^2}+3 \frac{R_1^4}{r^4}\right) \cos 2 \theta\right]-\\ \frac{q^2(1-\lambda)^2}{2 q\left(A_{\mathrm{i}}-1\right)+2 B_{\mathrm{i}}}\left[\frac{3 R_1^2}{2} \frac{r^2}{r^2}+\left(4 \frac{R_1^2}{r^2}-6 \frac{R_1^4}{r^4}\right) \cos 2 \theta+\left(-9 \frac{R_1^4}{r^4}+10 \frac{R_1^6}{r^6}\right) \cos 4 \theta\right] $ | (11a) |
| $\begin{aligned} \sigma_\theta^{\mathrm{e}}= & q+\frac{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}}{A_{\mathrm{i}}+1} \frac{R_1^2}{r^2}-\frac{q(1-\lambda)}{2}\left[1+\frac{R_1^2}{r^2}-\left(1+3 \frac{R_1^4}{r^4}\right) \cos 2 \theta\right]- \\ & \frac{q^2(1-\lambda)^2}{2 q\left(A_{\mathrm{i}}-1\right)+2 B_{\mathrm{i}}}\left[-\frac{3 R_1^2}{2} \frac{R^2}{r^2}+6 \frac{R_1^4}{r^4} \cos 2 \theta+\left(3 \frac{R_1^4}{r^4}-10 \frac{R_1^6}{r^6}\right) \cos 4 \theta\right] \end{aligned} $ | (11b) |
| $ \begin{aligned} \tau_{r \theta}^{\mathrm{e}}= & -\frac{q(1-\lambda)}{2}\left(1+2 \frac{R_1^2}{r^2}-3 \frac{R_1^4}{r^4}\right) \sin 2 \theta+ \\ & \frac{q^2(1-\lambda)^2}{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}}\left[\left(\frac{R_1^2}{r^2}-3 \frac{R_1^4}{r^4}\right) \sin 2 \theta+\left(-3 \frac{R_1^4}{r^4}+5 \frac{R_1^6}{r^6}\right) \sin 4 \theta\right] \end{aligned} $ | (11c) |
式中:
将式(8b)和(11b)代入式(1b),并令θ=0°得
| $ \begin{aligned} Q_1= & {\left[\frac{B_{\mathrm{r}}}{\left(A_{\mathrm{r}}-1\right) a^{A_{\mathrm{r}}-1}}+\frac{p_{\mathrm{i}}}{a^{A_{\mathrm{r}}-1}}\right] R_{\mathrm{H}}^{A_{\mathrm{r}}}-\left(q+\frac{B_{\mathrm{r}}}{A_{\mathrm{r}}-1}\right) R_{\mathrm{H}}+\left[\frac{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}}{A_{\mathrm{i}}+1}-\frac{q(1-\lambda)}{2}+\frac{3 q^2(1-\lambda)^2}{4 q\left(A_{\mathrm{i}}-1\right)+4 B_{\mathrm{i}}}\right] \frac{R_1^2}{R_{\mathrm{H}}}+} \\ & {\left[\frac{q(1-\lambda)}{2}-\frac{3 q^2(1-\lambda)^2}{2 q\left(A_{\mathrm{i}}-1\right)+2 B_{\mathrm{i}}}\right] \frac{R_1^4}{R_{\mathrm{H}}^3}+\frac{q^2(1-\lambda)^2}{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}} \frac{R_1^6}{R_{\mathrm{H}}^5}+\left[\frac{q(1-\lambda)}{2}-\frac{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}}{A_{\mathrm{i}}+1}-\frac{3 q^2(1-\lambda)^2}{4 q\left(A_{\mathrm{i}}-1\right)+4 B_{\mathrm{i}}}\right] \frac{R_1^2}{L}+} \\ & {\left[\frac{3 q^2(1-\lambda)^2}{2 q\left(A_{\mathrm{i}}-1\right)+2 B_{\mathrm{i}}}-\frac{q(1-\lambda)}{2}\right] \frac{R_1^4}{L^3}-\frac{q^2(1-\lambda)^2}{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}} \frac{R_1^6}{L^5}+q L } \end{aligned} $ | (12) |
依据沿水平轴的围岩竖向总荷载不变,将式(1a)和(12)代入Q1=Q0,化简得非静水压力下圆形隧道水平轴处的塑性区半径(RH)方程为
| $ A_1 R_{\mathrm{H}}^{A_{\mathrm{r}}}+B_1 R_{\mathrm{H}}+C_1+D_1 R_{\mathrm{H}}^{-1}+H_1 R_{\mathrm{H}}^{-3}+I_1 R_{\mathrm{H}}^{-5}=0 $ | (13) |
| $\begin{gathered} A_1=\frac{B_{\mathrm{r}}}{\left(A_{\mathrm{r}}-1\right) a^{A_{\mathrm{r}}-1}}+\frac{p_{\mathrm{i}}}{a^{A_{\mathrm{r}}-1}}, B_1=-q-\frac{B_{\mathrm{r}}}{A_{\mathrm{r}}-1} \\ C_1=\left[\frac{q(1-\lambda)}{2}-\frac{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}}{A_{\mathrm{i}}+1}-\frac{3 q^2(1-\lambda)^2}{4 q\left(A_{\mathrm{i}}-1\right)+4 B_{\mathrm{i}}}\right] \frac{R_1^2}{L}+ \end{gathered} $ |
| $\begin{gathered} {\left[\frac{3 q^2(1-\lambda)^2}{2 q\left(A_{\mathrm{i}}-1\right)+2 B_{\mathrm{i}}}-\frac{q(1-\lambda)}{2}\right] \frac{R_1^4}{L^3}-\frac{q^2(1-\lambda)^2}{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}} \frac{R_1^6}{L^5}} \\ D_1=\left[\frac{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}}{A_{\mathrm{i}}+1}-\frac{q(1-\lambda)}{2}+\frac{3 q^2(1-\lambda)^2}{4 q\left(A_{\mathrm{i}}-1\right)+4 B_{\mathrm{i}}}\right] R_1^2 \\ H_1=\left[\frac{q(1-\lambda)}{2}-\frac{3 q^2(1-\lambda)^2}{2 q\left(A_{\mathrm{i}}-1\right)+2 B_{\mathrm{i}}}\right] R_1^4 \\ I_1=\frac{q^2(1-\lambda)^2}{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}} R_1^6 \end{gathered} $ |
此外,弹-塑性交界处弹性区一侧的应力要满足围岩初始强度即式(5),且水平轴处的τrθe=0,结合式(11b)和塑性区半径RH得水平轴径向正应力为
| $ \left.\sigma_r^{\mathrm{e}}\right|_{\theta=0^{\circ}}=\frac{\left.\sigma_\theta^{\mathrm{e}}\right|_{r=R_{\mathrm{H}}}-B_{\mathrm{i}}}{A_{\mathrm{i}}} $ | (14) |
联立式(11a)(r=R′H,θ=0°)和式(14),化简得修正后的塑性区半径(R′H)方程为
| $ A^{\prime}{ }_1 R_{\mathrm{H}}^{\prime-2}+B_1^{\prime} R_{\mathrm{H}}^{\prime-4}+C_1^{\prime} R_{\mathrm{H}}^{\prime-6}+D_1^{\prime}=0 $ | (15) |
| $ \begin{gathered} A_1^{\prime}=\left[\frac{5 q(1-\lambda)}{2}-\frac{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}}{A_{\mathrm{i}}+1}-\frac{11 q^2(1-\lambda)^2}{4 q\left(A_{\mathrm{i}}-1\right)+4 B_{\mathrm{i}}}\right] R_1^2 \\ B_1^{\prime}=\left[\frac{15 q^2(1-\lambda)^2}{2 q\left(A_{\mathrm{i}}-1\right)+2 B_{\mathrm{i}}}-\frac{3 q(1-\lambda)}{2}\right] R_1^4 \\ C_1^{\prime}=-\frac{5 q^2(1-\lambda)^2}{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}} R_1^6, D_1^{\prime}{ }_1=\lambda q-\frac{\left.\sigma_\theta^{\mathrm{e}}\right|_{r=R_{\mathrm{H}}}-B_{\mathrm{i}}}{A_{\mathrm{i}}} \end{gathered} $ |
同理,根据沿竖向轴的围岩水平向总荷载不变,求得非静水压力下圆形隧道竖向轴处的塑性区半径(RV)方程为
| $ A_2 R_{\mathrm{V}}^{A_{\mathrm{r}}}+B_2 R_{\mathrm{V}}+C_2+D_2 R_{\mathrm{V}}^{-1}+H_2 R_{\mathrm{V}}^{-3}+I_2 R_{\mathrm{V}}^{-5}=0 $ | (16) |
| $ \begin{aligned} & A_2=\frac{B_{\mathrm{r}}}{\left(A_{\mathrm{r}}-1\right) a^{A_{\mathrm{r}}-1}}+\frac{p_{\mathrm{i}}}{a^{A_{\mathrm{r}}-1}}, B_2=-\lambda q-\frac{B_{\mathrm{r}}}{A_{\mathrm{r}}-1} \\ C_2= & {\left[\frac{q(1-\lambda)}{2}-\frac{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}}{A_{\mathrm{i}}+1}-\frac{3 q^2(1-\lambda)^2}{4 q\left(A_{\mathrm{i}}-1\right)+4 B_{\mathrm{i}}}\right] \frac{R_1^2}{L}+} \\ & {\left[\frac{q(1-\lambda)}{2}-\frac{q^2(1-\lambda)^2}{2 q\left(A_{\mathrm{i}}-1\right)+2 B_{\mathrm{i}}}\right] \frac{R_1^4}{L^3}-} \\ & \frac{q^2(1-\lambda)^2}{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}} \frac{R_1^6}{L^5} \end{aligned} $ |
| $ \begin{gathered} D_2=\left[\frac{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}}{A_{\mathrm{i}}+1}-\frac{q(1-\lambda)}{2}+\frac{3 q^2(1-\lambda)^2}{4 q\left(A_{\mathrm{i}}-1\right)+4 B_{\mathrm{i}}}\right] R_1^2 \\ H_2=\left[\frac{q^2(1-\lambda)^2}{2 q\left(A_{\mathrm{i}}-1\right)+2 B_{\mathrm{i}}}-\frac{q(1-\lambda)}{2}\right] R_1^4 \end{gathered} $ |
| $ I_2=\frac{q^2(1-\lambda)^2}{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}} R_1^6 $ |
在弹-塑性交界处弹性区一侧的应力同样要满足围岩初始强度即式(5),且竖向轴处的τrθe=0,结合式(11b)和塑性区半径RV得竖向轴径向正应力为
| $\left.\sigma_r^{\mathrm{e}}\right|_{\theta=90^{\circ}}=\frac{\left.\sigma_\theta^{\mathrm{e}}\right|_{r=R_{\mathrm{V}}}-B_{\mathrm{i}}}{A_{\mathrm{i}}} $ | (17) |
联立式(11a)(r=R′V,θ=90°)和式(17),化简得修正后的塑性区半径(R′V)方程为
| $ A_2^{\prime} R_{\mathrm{V}}^{\prime-2}+B_2^{\prime} R_{\mathrm{V}}^{\prime-4}+C_2^{\prime} R_{\mathrm{V}}^{\prime-6}+D_2^{\prime}=0 $ | (18) |
| $ \begin{gathered} A_2^{\prime}=\left[\frac{5 q^2(1-\lambda)^2}{4 q\left(A_{\mathrm{i}}-1\right)+4 B_{\mathrm{i}}}-\frac{3 q(1-\lambda)}{2}-\frac{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}}{A_{\mathrm{i}}+1}\right] R_1^2 \\ B_2^{\prime}=\left[\frac{3 q(1-\lambda)}{2}+\frac{3 q^2(1-\lambda)^2}{2 q\left(A_{\mathrm{i}}-1\right)+2 B_{\mathrm{i}}}\right] R_1^4 \\ C_2^{\prime}=-\frac{5 q^2(1-\lambda)^2}{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}} R_1^6, D_2^{\prime}=q-\frac{\left.\sigma_\theta^{\mathrm{e}}\right|_{r=R_{\mathrm{V}}}-B_{\mathrm{i}}}{A_{\mathrm{i}}} \end{gathered} $ |
蔡晓鸿等[21]基于Mohr-Coulomb准则和理想弹-塑性模型,根据弹-塑性交界处应力连续获得非静水压力下圆形隧道的非圆塑性区边界线,结果具有一般性,但理想弹-塑性模型难以反映围岩强度的脆性变化。董海龙等[17]基于Mohr-Coulomb准则和弹-脆-塑性模型,选择基尔希公式作为围岩弹性区应力表达式,依据总荷载不变法拓展了文献[21]的塑性区边界线方程。
仍以文献[21]的塑性区半径RC为基础,但选择弹-脆-塑性模型下的2阶摄动解即式(11)作为围岩弹性区应力表达式,这与文献[17]的围岩弹性区应力基尔希公式不同,继而结合3.1节所推导的塑性区半径R′H和R′V,根据几何相似原理拓展得非静水压力下圆形隧道的塑性区半径Rp为
| $ \begin{gathered} R_{\mathrm{p}}=\frac{R_{\mathrm{H}}^{\prime}}{R_{\mathrm{C}\left(\theta=0^{\circ}\right)}} R_{\mathrm{C}} \end{gathered} $ | (19a) |
| $ R_{\mathrm{p}}=\frac{R_{\mathrm{V}}^{\prime}}{R_{\mathrm{C}\left(\theta=90^{\circ}\right)}} R_{\mathrm{C}} $ | (19b) |
| $ R_{\mathrm{p}}=\alpha R_{\mathrm{C}} $ | (19c) |
| $ R_{\mathrm{C}}=a\left\{\frac{\left(1-\sin \varphi_{\mathrm{i}}\right)\left[0.5 q(1+\lambda)+q(1-\lambda) \cos 2 \theta+c_{\mathrm{i}} \cot \varphi_{\mathrm{i}}\right]}{p_{\mathrm{i}}+c_{\mathrm{i}} \cot \varphi_{\mathrm{i}}}\right\}^{\frac{1-\sin \varphi_{\mathrm{i}}}{2 \sin \varphi_{\mathrm{i}}}} $ |
| $ \alpha=\frac{\left(90^{\circ}-\theta\right) R_{\mathrm{H}}^{\prime}}{90^{\circ} R_{\mathrm{C}\left(\theta=0^{\circ}\right)}}+\frac{\theta R_{\mathrm{V}}^{\prime}}{90^{\circ} R_{\mathrm{C}\left(\theta=90^{\circ}\right)}} $ |
式中:RC(θ=0°)、RC(θ=90°)为文献[21]非静水压力下圆形隧道水平轴和竖向轴处的塑性区半径。
式(19a)表示仅用水平轴处的R′H拓展,式(19b)表示仅用竖向轴处的R′V拓展;式(19c)表示以系数α拓展,在第Ⅰ象限内由R′H/RC(θ=0°)和R′V/RC(θ=90°)线性插值系数α。其他3个象限的塑性区可由对称性确定。需指出的是,式(19)仅适用于塑性区完全包围隧道的情况,具体分为
1) RC(θ=0°)和RC(θ=90°)均不小于隧道半径a时,可按式(19)拓展,且λ < 1的塑性区短轴为RC(θ=90°),λ>1的塑性区短轴为RC(θ=0°),对应如下判定条件:
当λ≤1时
| $\left[\frac{\left(1-\sin \varphi_{\mathrm{i}}\right)\left(1.5 q \lambda-0.5 q+c_{\mathrm{i}} \cot \varphi_{\mathrm{i}}\right)}{p_{\mathrm{i}}+c_{\mathrm{i}} \cot \varphi_{\mathrm{i}}}\right]^{\frac{1-\sin \varphi_{\mathrm{i}}}{2 \sin \varphi_{\mathrm{i}}}} \geqslant 1 $ | (20) |
当λ>1时
| $\left[\frac{\left(1-\sin \varphi_{\mathrm{i}}\right)\left(1.5 q-0.5 q \lambda+c_{\mathrm{i}} \cot \varphi_{\mathrm{i}}\right)}{p_{\mathrm{i}}+c_{\mathrm{i}} \cot \varphi_{\mathrm{i}}}\right]^{\frac{1-\sin \varphi_{\mathrm{i}}}{2 \sin \varphi_{\mathrm{i}}}} \geqslant 1 $ | (21) |
2) RC(θ=0°)或(和)RC(θ=90°)小于隧道半径a,而R′H和R′V均不小于隧道半径a时,直接以长/短轴= R′H/R′V的类椭圆作为塑性区边界线。
3.3 拓展比较采用总荷载不变法拓展建立的非静水压力下圆形隧道塑性区半径解析解即式(19),引入了精度较高的围岩弹性区应力2阶摄动解,同时考虑了围岩强度的脆性软化,理想弹-塑性模型解答为其特例,具有一定的理论意义和工程应用前景。此外,所得解析解对侧压力系数λ < 1、λ=1和λ>1均适用,下文将针对λ < 1进行讨论,并对比λ=1时静水压力的结果。
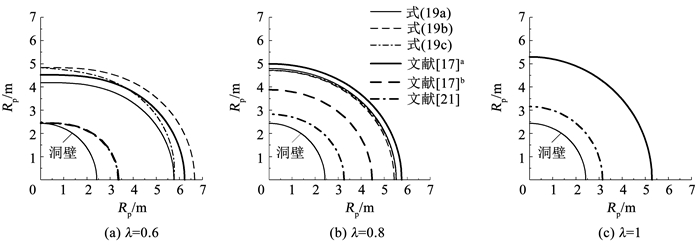
为说明本文解析解和文献[17]对文献[21]的拓展不同,以及总荷载不变法下2阶摄动解即式(11)与基尔希公式即式(9)作为弹性区应力表达式时塑性区边界线的差异,表 1和图 3给出了本文与文献[17, 21]的结果比较,其中,文献[17]以水平轴和竖向轴处的拓展分别记为文献[17]a和[17]b。隧道算例的参数为[17]: a=2.43 m,pi=0 MPa,q=21.78 MPa,L=∞;弹-脆-塑性围岩ci=4.8 MPa、φi=32°,cr=1.8 MPa、φr=20°;理想弹-塑性围岩cr=ci=4.8 MPa,φr=φi=32°。
| 表 1 塑性区半径的比 Tab. 1 Ratio of plastic zone radius |
|
图 3 塑性区边界线的不同拓展 Fig. 3 Different extensions of plastic boundary |
由表 1可知,本文水平轴处的塑性区半径是文献[21]的1.68~1.88倍,竖向轴处为1.68~1.99倍,这是由于文献[21]基于理想弹-塑性模型未考虑围岩强度的峰后下降。
另外,由图 3可以看出,λ=0.6时式(19a)较文献[17]a在水平轴和竖向轴处的塑性区半径小0.46、0.33 m,而式(19b)较文献[17]b在水平轴和竖向轴处的塑性区半径大3.29、2.38 m,表明弹性区应力表达式对非静水压隧道塑性区范围的影响显著,但随着侧压力系数λ的增大,弹性区应力表达式的影响在减小,λ=1时,式(19)与文献[17]的塑性区重合而无影响;λ=0.6时,文献[17]b与文献[21]的理想弹-塑性模型结果相差很小,表明文献[17]以基尔希公式作为围岩弹性区应力表达式有时难以体现围岩强度脆性软化对塑性区范围的不利扩展;λ < 1时,式(19a)与(19b)的塑性区边界线存在一定差异,按插值系数α的拓展即式(19c)简洁直观地兼顾了R′H和R′V,故下文统一采用式(19c) 探讨隧道塑性区边界线、塑性区位移及围岩特征曲线等问题。
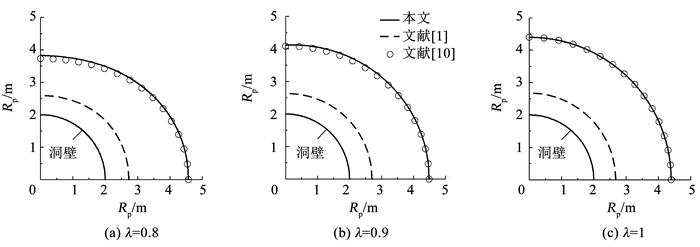
3.4 对比验证Kastner[1]直接将隧道纯弹性状态时的应力基尔希公式代入围岩强度准则,得到了非静水压力下圆形隧道塑性区半径的近似方程;吕爱钟等[10]推导了非静水压圆形隧道塑性区半径的复变函数解答。这2种方法均基于Mohr-Coulomb准则,且假定围岩为理想弹-塑性材料,即cr=ci、φr=φi,图 4为不同方法的隧道塑性区边界线对比。隧道算例的参数为[10]a=2 m,pi=0 MPa,q=15 MPa,L=∞,ci=cr=1 MPa,φi=φr=30°。
|
图 4 不同方法的塑性区边界线对比 Fig. 4 Comparison of plastic boundary for different methods |
由图 4可以看出,本文式(19c)与文献[10]的高精度复变函数解答吻合良好,验证了本文结果的正确性;Kastner法未考虑开挖后围岩的弹塑性发展与分区,简单地使用了纯弹性状态时的应力基尔希公式,使得文献[1]的塑性区范围小1.45~1.84 m。
3.5 实测验证文献[15]对TBM开挖的圆形煤矿巷道扰动范围开展现场实测,相关参数为a=2.25 m,pi=0 MPa,q=14.3 MPa,λ=1.33,ci=9 MPa,cr=3 MPa,φi=45°,φr=42°,方位角θ=5°、90°、162°处围岩的实测扰动区深度为2.98、3.31和2.89 m。
本文由理想弹-塑性模型所得塑性区范围为4.33~4.49 m,对应方位角θ=5°、90°、162°处围岩的计算塑性区深度为2.08、2.24和2.09 m,小于实测的扰动区深度;然而,由弹-脆-塑性模型所得塑性区范围为5.28~5.52 m,对应方位角θ=5°、90°、162°处围岩的计算塑性区深度为3.03、3.27和3.05 m,与实测的扰动区深度非常接近,表明弹-脆-塑性模型更适合求解此巷道的扰动范围。
文献[22]对淮南矿区某千米深井巷道松动圈范围进行了现场实测,相关参数为a=2.95 m(等效半径),pi=0.75 MPa,q=21.86 MPa,λ=0.8,ci=5.58 MPa,cr=0.72 MPa,φi=φr=27.83°,围岩帮部、顶部和底板中部的实测松动圈深度为2.80、2.39和3.84 m。
本文在弹-脆-塑性模型下所得塑性区范围为5.56~6.69 m,对应围岩帮部、顶部和底板中部的计算塑性区深度为4.15、2.61和4.06 m,可见计算塑性区深度稍大于实测松动圈深度而在其外侧,这符合深井巷道的开挖扰动规律。相反,由理想弹塑性模型计算所得围岩帮部、顶部和底板中部的计算塑性区深度为1.35、0.46和2.16 m,明显小于实测松动圈深度而不合理。
4 位移解答 4.1 弹性区弹性区围岩的几何方程为
| $ \begin{gathered} \varepsilon_r=\frac{\partial u_r}{\partial r}, \varepsilon_\theta=\frac{1}{r} \frac{\partial u_\theta}{\partial \theta}+\frac{u_r}{r} \end{gathered} $ | (22a) |
| $ \gamma_{r \theta}=\frac{\partial u_\theta}{\partial r}+\frac{1}{r} \frac{\partial u_r}{\partial \theta}-\frac{u_\theta}{r} $ | (22b) |
式中:εr、εθ、γrθ为弹性区的径向线应变、环向线应变和切应变,ur、uθ为对应的径向线位移和环向线位移。
将图 1中的水平/竖向初始地应力场转换为径向/环向初始地应力场[19],得初始径向正应力σr0、初始环向正应力σθ0和初始切应力τrθ0为
| $\left\{\begin{array}{l} \sigma_{r 0}=q-\frac{q(1-\lambda)(1+\cos 2 \theta)}{2} \\ \sigma_{\theta 0}=q-\frac{q(1-\lambda)(1-\cos 2 \theta)}{2} \\ \tau_{r \theta 0}=\frac{q(1-\lambda)(1+\sin 2 \theta)}{2} \end{array}\right. $ | (23) |
在平面应变状态下扣除初始地应力即式(23),由广义Hooke定律得弹性区围岩的物理方程为
| $ \varepsilon_r=\frac{1+\nu}{E}\left[(1-\nu)\left(\sigma_r^{\mathrm{e}}-\sigma_{r 0}\right)-\nu\left(\sigma_\theta^{\mathrm{e}}-\sigma_{\theta 0}\right)\right] $ | (24a) |
| $\varepsilon_\theta=\frac{1+\nu}{E}\left[(1-\nu)\left(\sigma_\theta^{\mathrm{e}}-\sigma_{\theta 0}\right)-\nu\left(\sigma_r^{\mathrm{e}}-\sigma_{r 0}\right)\right] $ | (24b) |
| $ \gamma_{r \theta}=\frac{2(1+\nu)}{E}\left(\tau_{r \theta}^{\mathrm{e}}-\tau_{r \theta 0}\right) $ | (24c) |
式中E、ν为围岩的弹性模量和泊松比。
联立式(11)、(22)~(24)得围岩弹性区位移为
| $\begin{aligned} u_r= & \frac{1-\nu^2}{E}\left\{\frac{q r(1-\lambda)(1+\cos 2 \theta)}{2}+\frac{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}}{A_{\mathrm{i}}+1} \frac{R_1^2}{r}-\frac{q(1-\lambda)}{2}\left[r+\frac{R_1^2}{r}+\left(r+4 \frac{R_1^2}{r}-\frac{R_1^4}{r^3}\right) \cos 2 \theta\right]-\right. \\ & \left.\frac{q^2(1-\lambda)^2}{2 q\left(A_{\mathrm{i}}-1\right)+2 B_{\mathrm{i}}}\left[-\frac{3 R_1^2}{2}+\left(-4 \frac{R_1^2}{r}+2 \frac{R_1^4}{r^3}\right) \cos 2 \theta+\left(3 \frac{R_1^4}{r^3}-2 \frac{R_1^6}{r^5}\right) \cos 4 \theta\right]\right\}- \\ & \frac{(1+\nu) \nu}{E}\left\{\frac{q r(1-\lambda)(1-\cos 2 \theta)}{2}-\frac{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}}{A_{\mathrm{i}}+1} \frac{R_1^2}{r}-\frac{q(1-\lambda)}{2}\left[r-\frac{R_1^2}{r}-\left(r-\frac{R_1^4}{r^3}\right) \cos 2 \theta\right]-\right. \\ & \left.\frac{q^2(1-\lambda)^2}{2 q\left(A_{\mathrm{i}}-1\right)+2 B_{\mathrm{i}}}\left[\frac{3 R_1^2}{2}-2 \frac{R_1^4}{r^3} \cos 2 \theta+\left(-\frac{R_1^4}{r^3}+2 \frac{R_1^6}{r^5}\right) \cos 4 \theta\right]\right\} \end{aligned} $ | (25a) |
| $ \begin{aligned} u_\theta= & \frac{1-\nu^2}{E}\left\{-\frac{q r(1-\lambda) \sin 2 \theta}{2}+\frac{q(1-\lambda)}{2}\left(r+2 \frac{R_1^2}{r}+\frac{R_1^4}{r^3}\right) \sin 2 \theta+\frac{q^2(1-\lambda)^2}{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}} \times\right. \\ & {\left.\left[-\left(\frac{R_1^2}{r}+\frac{R_1^4}{r^3}\right) \sin 2 \theta+\frac{R_1^6}{r^5} \sin 4 \theta\right]\right\}-\frac{(1+\nu) \nu}{E}\left\{\frac{q r(1-\lambda) \sin 2 \theta}{2}+\frac{q(1-\lambda)}{2}\left(-r+2 \frac{R_1^2}{r}-\frac{R_1^4}{r^3}\right) \sin 2 \theta+\right.} \\ & \left.\frac{q^2(1-\lambda)^2}{q\left(A_{\mathrm{i}}-1\right)+B_{\mathrm{i}}}\left[\left(-\frac{R_1^2}{r}+\frac{R_1^4}{r^3}\right) \sin 2 \theta+\left(\frac{R_1^4}{r^3}-\frac{R_1^6}{r^5}\right) \sin 4 \theta\right]\right\} \end{aligned} $ | (25b) |
由式(8)可知,非静水压圆形隧道的塑性区应力场属于与θ无关的绕轴对称,进而塑性区的切应变γrθ≡0、环向线位移upθ≡0,径向线应变εr和环向线应变εθ也只与r有关。于是,塑性区围岩的几何方程为
| $\varepsilon_r=\frac{\mathrm{d} u_r^{\mathrm{p}}}{\mathrm{d} r}, \varepsilon_\theta=\frac{u_r^{\mathrm{p}}}{r}, \gamma_{r \theta}=0 $ | (26) |
式中:urp为塑性区的径向线位移且为唯一存在的非零位移,下文简称塑性区位移。
在围岩塑性区内,将应变分解为式(27)中的弹性应变分量(对应于上标e)和塑性应变分量(对应于上标p),即
| $\varepsilon_\theta=\varepsilon_\theta^{\mathrm{e}}+\varepsilon_\theta^{\mathrm{p}}, \varepsilon_r=\varepsilon_r^{\mathrm{e}}+\varepsilon_r^{\mathrm{p}} $ | (27) |
采用非关联流动法则即式(28)描述围岩的剪胀特性[23]:
| $ \beta \varepsilon_\theta^{\mathrm{p}}+\varepsilon_r^{\mathrm{p}}=0 $ | (28) |
式中β为剪胀参数。
以弹-塑性交界处ur|r=Rp=upr|r=Rp为位移边界条件,联立式(8)、(23)和(26)得围岩塑性区位移urp为
| $ u_r^{\mathrm{p}}=\frac{(1+\nu)}{E r^\beta}\left[K_1\left(r^{\beta+A_{\mathrm{r}}}-R_{\mathrm{p}}^{\beta+A_{\mathrm{r}}}\right)+K_2\left(r^{\beta+1}-R_{\mathrm{p}}^{\beta+1}\right)\right]+\left.\left(\frac{R_{\mathrm{p}}}{r}\right)^\beta u_r\right|_{r=R_{\mathrm{p}}} $ | (29) |
| $\begin{gathered} K_1=\frac{[\beta(1-\nu)-\nu]\left(\frac{A_{\mathrm{r}} B_{\mathrm{r}}}{A_{\mathrm{r}}-1}+A_{\mathrm{r}} p_{\mathrm{i}}\right)+(1-\nu-\beta \nu)\left(\frac{B_{\mathrm{r}}}{A_{\mathrm{r}}-1}+p_{\mathrm{i}}\right)}{a^{A_{\mathrm{r}}-1}\left(\beta+A_{\mathrm{r}}\right)} \\ K_2=\frac{[\beta(1-\nu)-\nu]\left[\frac{q(1-\lambda)(1-\cos 2 \theta)}{2}-q-\frac{B_{\mathrm{r}}}{A_{\mathrm{r}}-1}\right]+(1-\nu-\beta \nu)\left[\frac{q(1-\lambda)(1+\cos 2 \theta)}{2}-q-\frac{B_{\mathrm{r}}}{A_{\mathrm{r}}-1}\right]}{\beta+1} \end{gathered} $ |
将r=a代入式(29),得隧道洞壁位移u0为
| $\begin{aligned} & u_0=\frac{(1+\nu)}{E a^\beta}\left[K_1\left(a^{\beta+A_{\mathrm{r}}}-R_{\mathrm{p}}^{\beta+A_{\mathrm{r}}}\right)+\right. \\ & \left.K_2\left(a^{\beta+1}-R_{\mathrm{p}}^{\beta+1}\right)\right]+\left.\left(\frac{R_{\mathrm{p}}}{a}\right)^\beta u_r\right|_{r=R_{\mathrm{p}}} \end{aligned} $ | (30) |
通过式(30)可构建围岩特征曲线即洞壁位移u0随支护力pi的变化,进而基于收敛约束法由围岩特征曲线(GRC)和支护特征曲线(SRC)的交点纵/横坐标确定支护压力和围岩稳定变形。
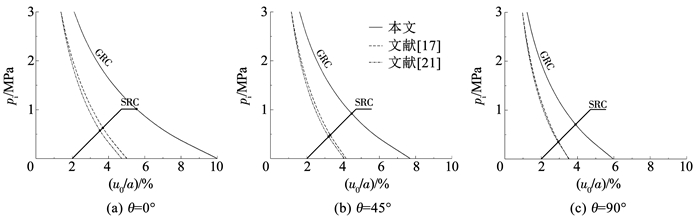
4.3 结果与讨论隧道算例同3.3节,并取λ=0.8。图 5、6给出了本文、文献[17](竖向轴拓展)和[21]的塑性区位移分布与收敛约束分析,其中,讨论塑性区位移分布时令支护力pi=0 MPa(下同),以虚线标出塑性区半径与隧道半径的比值。在收敛约束分析时,假定支护为均质等厚的圆环结构,并在u0/a=2%处施作。

|
图 5 塑性区位移分布 Fig. 5 Distribution of plastic zone displacement |
|
图 6 收敛约束分析 Fig. 6 Convergence-confinement analysis |
由图 5、6可以看出,本文的塑性区半径、塑性区位移、支护压力和围岩稳定变形均最大,最小的是文献[21](塑性区半径、洞壁位移比本文的分别小1.89~2.26、0.059~0.128 m),文献[17]的支护压力和围岩稳定变形稍大于文献[21],但明显小于本文的。在图 6(a)中本文对应的支护已到达承载极限,需提高支护承载能力或推后施作位置,而根据文献[17]或[21]所做的隧道设计将存在安全隐患。
5 影响因素分析结合本文采用总荷载不变法建立的隧道塑性摄动拓展解答即式(19c)、(29)和(30),探讨侧压力系数和脆性软化对塑性区边界线、塑性区位移分布和收敛约束分析的影响规律。
5.1 侧压力系数隧道算例同3.3节,并取E=2 GPa,ν=0.2,β=2,图 7为两种材料模型的塑性区边界线比较,其中,侧压力系数λ=0.6、0.8和1。可以看出,弹-脆-塑性模型的塑性区范围明显大于理想弹-塑性模型的,水平轴处的塑性区半径相差1.41~2.44 m,宜采用弹-脆-塑性模型分析隧道塑性发展。

|
图 7 塑性区边界线比较 Fig. 7 Comparison of plastic boundary |
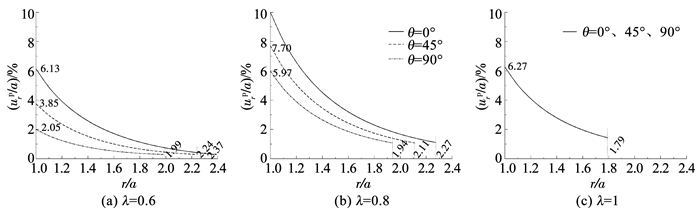
图 8、9给出了λ=0.6、0.8和1时弹-脆-塑性围岩的塑性区位移分布与收敛约束分析。
|
图 8 不同λ时塑性区位移分布 Fig. 8 Distribution of plastic zone displacement with different λ |

|
图 9 不同λ时收敛约束分析 Fig. 9 Convergence-confinement analysis with different λ |
由图 8(a)、(b)可以看出,λ=0.6、0.8时,在第Ⅰ象限内塑性区位移最大在θ=0°处,最小在θ=90°处,洞壁位移相差0.099 m;在λ=0.6的图 9(a)中,不同方位角处的围岩特征曲线及收敛约束存在显著差异,在θ=90°处施作支护时围岩位移已全部释放,支护将不再受荷与变形,而在θ=0°和45°处仍存在较大的支护压力,故非静水压力下需针对具体方位角进行收敛约束分析与支护设计;在λ=0.8的图 9(b)中,3个方位角处的支护压力和围岩稳定变形都明显不同,在θ=0°处支护已达到承载极限,这与静水压力λ=1的图 9(c)不同,依据理想静水压力条件开展的均匀支护设计将影响实际隧道后续施工和正常运维。
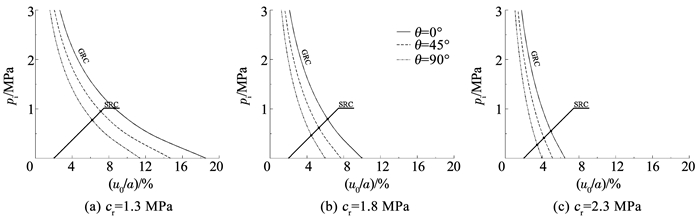
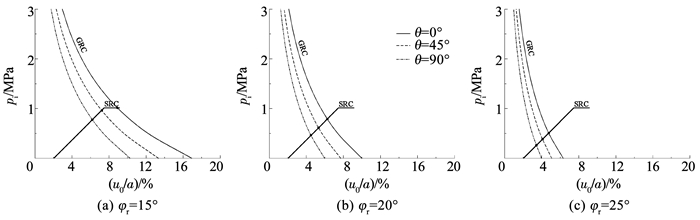
5.2 脆性软化隧道算例同3.3节,并取λ=0.8,E=2 GPa,ν=0.2,β=2,图 10~12给出了围岩不同峰后强度下的塑性区边界线和收敛约束分析。

|
图 10 脆性软化对塑性区边界线的影响 Fig. 10 Effect of brittle softening on plastic boundary |
|
图 11 不同cr时收敛约束分析 Fig. 11 Convergence-confinement analysis with different cr |
|
图 12 不同φr时收敛约束分析 Fig. 12 Convergence-confinement analysis with different φr |
由图 10可以看出,脆性软化幅度越大即围岩峰后强度越低,塑性区范围越大。峰后黏聚力cr每减小0.1 MPa,水平轴处的塑性区半径平均增加0.18 m、竖向轴处的增加0.15 m;峰后内摩擦角φr每减小1°,水平轴处的塑性区半径平均增加0.16 m、竖向轴处的增加0.14 m。
由图 11、12可以看出,支护压力和围岩稳定变形随峰后强度的增加明显减小,相应的支护可由达到承载极限过渡到安全储备充足,通过注浆、预应力锚杆等主动加固提高围岩的峰后强度,以改变支护类型或减小支护截面尺寸。
6 结论1) 采用总荷载不变法并引入围岩弹性区应力的2阶摄动解,所推导并由几何相似原理拓展建立的非静水压圆形隧道塑性区半径与塑性区位移的解析解,考虑了围岩强度的脆性软化,理想弹-塑性模型解答为其特例,结合收敛约束法可有效指导隧道支护初步设计,具有一定的理论意义和工程应用前景。
2) 弹性区应力表达式对非静水压圆形隧道的塑性区范围影响显著,通过对比文献总荷载不变法、Kastner法、复变函数法和实测数据,验证了本文按插值系数拓展解答的正确性与弹性区应力2阶摄动解的合理性;Kastner法的塑性区范围过小,采用应力基尔希公式所得支护压力和围岩稳定变形都偏小。
3) 非静水压力下不同方位角处的塑性区半径、塑性区位移分布与围岩特征曲线存在较大差异,需根据收敛约束法确定沿洞周最大的支护压力和围岩稳定变形,这有别于静水压力下圆形塑性区时的均匀支护设计;围岩峰后强度全面而明显地影响隧道塑性发展,可使支护处于承载极限、安全储备等状态。
| [1] |
KASTNER H. 隧道与坑道静力学[M]. 同济大学, 译. 上海: 上海科学技术出版社, 1980 KASTNER H. Statik destunnel-und stollenbaues[M]. Tongji University, translate. Shanghai: Shanghai Science and Technology Publishers, 1980 |
| [2] |
赵志强, 马念杰, 刘洪涛, 等. 巷道蝶形破坏理论及其应用前景[J]. 中国矿业大学学报, 2018, 47(5): 969. ZHAO Zhiqiang, MA Nianjie, LIU Hongtao, et al. A butterfly failure theory of rock mass around roadway and its application prospect[J]. Journal of China University of Mining and Technology, 2018, 47(5): 969. DOI:10.13247/j.cnki.jcumt.000922 |
| [3] |
郭晓菲, 郭林峰, 马念杰, 等. 巷道围岩蝶形破坏理论的适用性分析[J]. 中国矿业大学学报, 2020, 49(4): 646. GUO Xiaofei, GUO Linfeng, MA Nianjie, et al. Applicability analysis of the roadway butterfly failure theory[J]. Journal of China University of Mining and Technology, 2020, 49(4): 646. DOI:10.13247/j.cnki.jcumt.001169 |
| [4] |
李季, 强旭博, 马念杰, 等. 巷道围岩蝶形塑性区蝶叶方向性形成机制及工程应用[J]. 煤炭学报, 2021, 46(9): 2838. LI Ji, QIANG Xubo, MA Nianjie, et al. Formation mechanism and engineering application of the directionality of butterfly leaf in the butterfly plastic zone of roadway rock surrounded[J]. Journal of China Coal Society, 2021, 46(9): 2838. DOI:10.13225/j.cnki.jccs.2021.1150 |
| [5] |
袁超, 张建国, 王卫军, 等. 基于塑性区分布形态的软弱破碎巷道围岩控制原理研究[J]. 采矿与安全工程学报, 2020, 37(3): 451. YUAN Chao, ZHANG Jianguo, WANG Weijun, et al. Controlling principles of surrounding rock in soft and broken roadway based on the distribution pattern of plastic zone[J]. Journal of Mining and Safety Engineering, 2020, 37(3): 451. DOI:10.13545/j.cnki.jmse.2020.03.003 |
| [6] |
王卫军, 韩森, 董恩远. 考虑支护作用的巷道围岩塑性区边界方程及应用[J]. 采矿与安全工程学报, 2021, 38(4): 749. WANG Weijun, HAN Sen, DONG Enyuan. Boundary equation of plastic zone in roadway surrounding rocks considering supporting effect and its application[J]. Journal of Mining and Safety Engineering, 2021, 38(4): 749. DOI:10.13545/j.cnki.jmse.2020.0488 |
| [7] |
于学馥, 郑颖人, 刘怀恒, 等. 地下工程围岩稳定性分析[M]. 北京: 煤炭工业出版社, 1983. YU Xuefu, ZHENG Yingren, LIU Huaiheng, et al. The stability analysis of the surrounding rock mass in underground engineering[M]. Beijing: China Coal Industry Publishing House, 1983. |
| [8] |
DETOURNAY E, FAIRHURST C. Two-dimensional elastoplastic analysis of a long, cylindrical cavity under non-hydrostatic loading[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1987, 24(4): 197. DOI:10.1016/0148-9062(87)90175-6 |
| [9] |
饶军应. 岩溶介质中深埋洞室围岩应力弹性解析及应用研究[D]. 长沙: 中南大学, 2014 RAO Junying. Analytical solutions and application for stress around deeply buried holes in karst with elastic theory[D]. Changsha: Central South University, 2014 |
| [10] |
吕爱钟, 张晓莉, 王少杰. 两向不等压圆形隧洞弹塑性解析分析[J]. 岩石力学与工程学报, 2018, 37(1): 14. LV Aizhong, ZHANG Xiaoli, WANG Shaojie. Analytic method for elasto-plastic analysis of circular tunnels under non-axisymmetric stresses[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(1): 14. DOI:10.13722/j.cnki.jrme.2017.1307 |
| [11] |
LV A Z, WANG S J, ZHANG X L. Solution of the elasto-plastic interface of circular tunnels in Hoek-Brown media subjected to non-hydrostatic stress[J]. International Journal of Rock Mechanics and Mining Sciences, 2018, 106(6): 124. DOI:10.1016/j.ijrmms.2018.04.013 |
| [12] |
MA Y, LV A Z, CAI H. An analytical method for determining the non-enclosed elastoplastic interface of a circular hole[J]. Mathematics and Mechanics of Solids, 2020, 25(5): 1. DOI:10.1177/1081286520909489 |
| [13] |
魏悦广. 两向不等压作用下圆形巷道弹塑性分析摄动解[J]. 岩土工程学报, 1990, 12(4): 11. WEI Yueguang. Perturbation solution for elasto-plastic analysis of circular tunnel under unequal compression in two directions[J]. Chinese Journal of Geotechnical Engineering, 1990, 12(4): 11. DOI:10.1007/BF03008874 |
| [14] |
侯公羽, 李晶晶, 赵伟伟, 等. 两向不等压圆形巷道弹塑性摄动解[J]. 岩石力学与工程学报, 2014, 33(增刊2): 3639. HOU Gongyu, LI Jingjing, ZHAO Weiwei, et al. Perturbation solutions for elasto-plastic problems of circular tunnel under unequal compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(Sup.2): 3639. DOI:10.13722/j.cnki.jrme.2014.s2.031 |
| [15] |
TANG B, CHENG H, TANG Y Z, et al. Excavation damaged zone depths prediction for TBM-excavated roadways in deep collieries[J]. Environmental Earth Sciences, 2018, 77(5): 165. DOI:10.1007/s12665-018-7358-x |
| [16] |
严克强. 不对称荷载作用下圆洞围岩塑性区的估算方法[J]. 岩土工程学报, 1980, 2(2): 74. YAN Keqiang. Estimation method for plastic zone of circular tunnel under unsymmetrical load[J]. Chinese Journal of Geotechnical Engineering, 1980, 2(2): 74. |
| [17] |
董海龙, 高全臣. 考虑流变特性的两向不等压巷道围岩塑性区近似解[J]. 煤炭学报, 2019, 44(2): 419. DONG Hailong, GAO Quanchen. Approximate solution on plastic zone of roadway surrounding rock under unequal compression in two directions by considering rheology[J]. Journal of China Coal Society, 2019, 44(2): 419. DOI:10.13225/j.cnki.jccs.2018.1660 |
| [18] |
董海龙, 高全臣, 经纬, 等. 考虑流变的两向不等压深埋软岩巷道围岩塑性区近似解[J]. 煤炭学报, 2019, 44(增刊1): 74. DONG Hailong, GAO Quanchen, JING Wei, et al. Approximate solution of plastic zone in deep soft roadway surrounding rock under unequal stress field in two directions considering rheology[J]. Journal of China Coal Society, 2019, 44(Sup.1): 74. DOI:10.13225/j.cnki.ccjs.2018.1245 |
| [19] |
徐芝纶. 弹性力学[M]. 北京: 高等教育出版社, 2006. XU Zhilun. Elastic mechanics[M]. Beijing: Higher Education Press, 2006. |
| [20] |
MA Y, LV A Z, CAI H, et al. Analytical solution for determining the plastic zones around two unequal circular tunnels[J]. Tunnelling and Underground Space Technology, 2022, 120: 104267. DOI:10.1016/j.tust.2021.104267 |
| [21] |
蔡晓鸿, 蔡勇平. 水工压力隧洞结构应力计算[M]. 北京: 中国水利水电出版社, 2004. CAI Xiaohong, CAI Yongping. Structural stress calculation for hydraulic pressure tunnel[M]. Beijing: China Water and Power Press, 2004. |
| [22] |
经纬. 圆形巷道围岩变形分区的理论与试验研究[D]. 淮南: 安徽理工大学, 2017 JING Wei. Theoretical and experimental research on deformation partition of circular roadway[D]. Huainan: Anhui University of Science and Technology, 2017 |
| [23] |
张常光, 范文, 赵均海. 深埋圆形巷道围岩塑性区位移及特征曲线新解和参数分析[J]. 岩土力学, 2016, 37(1): 12. ZHANG Changguang, FAN Wen, ZHAO Junhai. New solutions of rock plastic displacement and ground response curve for a deep circular tunnel and parametric analysis[J]. Rock and Soil Mechanics, 2016, 37(1): 12. DOI:10.16285/j.rsm.2016.01.002 |
 2023, Vol. 55
2023, Vol. 55


