2. 上海工程技术大学 机械与汽车工程学院,上海 201620
2. School of Mechanical and Automotive Engineering, Shanghai University of Engineering Science, Shanghai 201620, China
从航空航天、汽车和土木结构到生物工程,聚合物基复合材料得到了广泛的应用[1-2]。在很多情况下,复合材料结构的服役寿命达到几年甚至几十年,因此在设计时需要考虑材料的长期力学性能[3-4]。大多数聚合物在载荷和环境因素作用下表现出显著的蠕变和应力松弛(即黏弹性)现象。为了设计耐久的复合材料部件和结构,需要充分研究这些现象并预测结构构件的长期力学行为。对于聚合物基复合材料,其黏弹性不仅受到基体材料分子松弛过程的影响,还受到复合材料的组份比例、微观结构形态以及纤维-基体之间黏结作用等因素的影响,使得复合材料及其结构的黏弹性力学行为变得十分复杂[5-6]。
纤维复合材料在制造和服役过程中,界面的黏结情况对复合材料的宏/细观力学性能发挥着重要的作用[7]。由于界面两侧组分的材料性能往往相差较大,所以在外载荷作用下,复合材料系统微结构界面处往往产生应力集中现象进而引起界面损伤与断裂[8]。这种界面处微结构的损伤破坏也将导致结构宏观性能的退化。然而现有文献中针对复合材料均匀化的多尺度模型大都基于唯象理论,无法根据材料的微结构应力变形情况对材料宏观力学性能退化进行有效预测。因此本文引入了考虑不完美界面的LEHT(locally exact homogenization theory)模型对材料进行性能模拟,该方法不仅可以有效预测纤维复合材料的宏观模量,还可以有效还原微元体晶胞内的界面刚度所引起的应力重分布情况。
目前的细观力学数值分析中对于不完美界面的建模方法除了将界面等效为一层具有较小弹性模量的薄厚度的物理夹层[7, 9]外,还可以通过引入一层零厚度的内聚力弹簧界面,该界面可以假想为均匀分布的有一定刚度的弹簧。当界面刚度接近无穷大时,界面完美结合,而完全脱黏的界面可以通过零界面刚度来模拟。这种柔性界面模型已被广泛用于研究部分作用的界面对材料有效性能的影响[10-11],以及界面损伤对纤维局部增强作用的影响[7]。
然而,目前文献中针对界面损伤对聚合物基复合材料黏弹性力学行为的研究相对较少[1-6, 12-17]。另外,缺乏复杂材料系统界面对微元体内应力分布的研究。基于上述原因,本文在前期推导的横观各向同性单向纤维复合材料细观模型[1]的基础上,运用对应性原理,将材料的黏弹性本构转换到Carson-Laplace域中求解具有不完美界面的周期性纤维增强复合材料的黏弹性问题,并得到材料的宏观模量系数。再利用Zakian[18-19]提出的反演方法将求得的宏/细观响应转化到时域中,其中基体黏弹性材料通过各向同性四参数流变模型模拟。最终结果与文献中的数值方法进行了对比,得到了良好的一致性。
1 黏弹性体的本构方程和材料性能本文采用最近开发的LEHT模型[1, 7]和弹性-黏弹性对应性原理对横观各向同性单向复合材料黏弹性问题进行分析,即将微元体的边值问题以及均匀化本构关系转化到Laplace域中进行求解,然后采用Zakian于1969年所提出的方法[18]将相应公式逆转化到时域当中,详情如图 1所示。
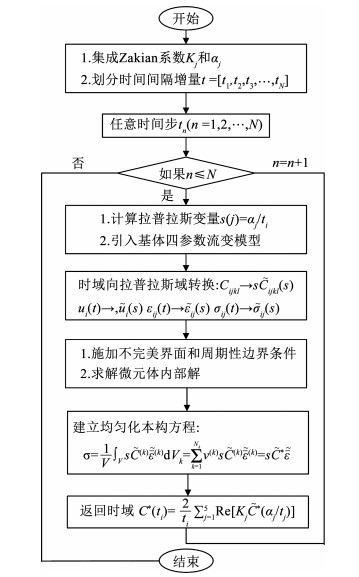
|
图 1 黏弹性问题求解流程 Fig. 1 Solution process of viscoelastic problems |
在时域和Laplace域之间的相互转化涉及到位移、应变和应力的转换, 即
| $\sigma_{i j}(t)=\int_0^t C_{i j k l}(t-\tau) \frac{\partial \varepsilon_{k l}(\tau)}{\partial \tau} \mathrm{d} \tau $ | (1) |
而通过转换后Carson-Laplace域内的本构关系变为
| $ \tilde{\sigma}_{i j}(s)=s \tilde{C}_{i j k l}(s) \tilde{\varepsilon}_{k l}(s) $ | (2) |
很明显,Laplace域里的本构关系由于避免了复杂的积分形式,因此比时域中的积分本构更为简单。只需将弹性问题中的弹性刚度矩阵与Laplace域中的刚度矩阵对应即可:
| $ \tilde{C}_{i j k l}(s)=\int_0^s C_{i j k l}(t) \mathrm{e}^{-s t} \mathrm{~d} t $ | (3) |
将Laplace域内的关系代入到由Wang等[7]开发的细观力学模型当中,在Laplace-Carson域内应用周期边界条件求解内部位移和应力场,并建立均匀化本构方程:
| $ \begin{aligned} \widetilde{\widetilde{\sigma}}= & \frac{1}{V} \int_V s \tilde{C}^{(k)} \widetilde{\bar{\varepsilon}}^{(k)} \mathrm{d} V_k=\sum\limits_{k=1}^{N_k} v^{(k)} s \tilde{C}^{(k)} \widetilde{\bar{\varepsilon}}^{(k)}= \\ & \tilde{S}^* \tilde{\bar{\varepsilon}} \quad(k=f, m) \end{aligned} $ | (4) |
式中vf和vm分别为纤维和基体的体积分数,并且有vf+vm=1。最后文献中有很多方法可以实现从Laplace域到时域的逆转换。本文选用了早期由Zakian提出的数值算法[18-19],通过以下步骤完成从Laplace域到时域解的转换:1)将研究时间划分为时间间隔增量:t =[t1, t2, t3, …, tN];2)赋值拉普拉斯变量为s(j)=αj/ti,αj取值见表 1;3)每一次增量ti,将拉普拉斯变量s引入到当前细观力学模型当中,得到拉普拉斯域中微元体边界值问题的最终解和均匀化刚度矩阵的表达式;4)最后,采用Zakian公式进行反演,即
| $ C^*\left(t_i\right)=\frac{2}{t_i} \sum _{j=1}^5 \operatorname{Re}\left[K_j \tilde{C}^*\left(\alpha_j / t_i\right)\right] $ | (5) |
| 表 1 从拉普拉斯域变换到时域的Zakian反演公式中采用的复系数[18-19] Tab. 1 Complex coefficients employed in Zakian′s inversion formula from Laplace transform to time domain [18-19] |
式中Kj取值见表 1。
2 考虑不完美界面的复合材料细观力学模型根据上节描述,本节回顾前期推导的考虑不完美界面的复合材料细观力学模型,具体推导见文献[7]。复合材料的细观结构可假设为在基体中呈周期性分布的纤维系统,本文针对图 2所示的具有周期性分布的正方形代表性单胞进行研究,该单胞符合周期性边界条件约束。为了满足约束本文采用了弱形式的变分原理:
| $ \int_{S_T} \delta \tilde{u}_i\left(\tilde{T}_i-\tilde{T}_i^0\right) \mathrm{d} S+\int_{S_u} \delta \tilde{T}_i\left(\tilde{u}_i-\tilde{u}_i^0\right) \mathrm{d} S=0 $ | (6) |
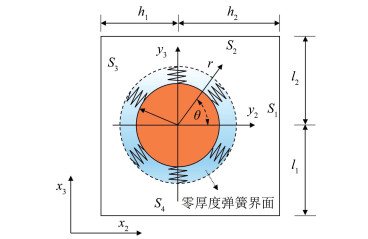
|
图 2 考虑非完美界面的复合材料周期性晶胞 Fig. 2 A periodic unitcell of composite considering imperfect interface |
式中Ti和ui分别为微元体ST和Su边界上的力和位移。
为了区分宏观尺度和细观尺度的影响,本文定义了两个坐标体系,即宏观坐标系统xi(i=1, 2, 3)和微元体坐标系统yi(i=1, 2, 3),并将微元体内部的位移分为平均位移和扰动位移[20]:
| $ \tilde{u}_i^{(k)}(x, y)=\bar{\varepsilon}_{i j} x_j+\tilde{u}_i^{\prime(k)}(y) $ | (7) |
式中k=f、m,f和m分别代表纤维和基体相。值得注意的是平均项中的平均应变
| $\left\{\begin{aligned} \tilde{u}_z^{\prime(k)}= & \sum\limits_{n=1}^{\infty} a\left[\left(\xi^n H_{n 1}^{(k)}+\xi^{-n} H_{n 3}^{(k)}\right) \cos n \theta+\right. \\ & \left.\left(\xi^n H_{n 2}^{(k)}+\xi^{-n} H_{n 4}^{(k)}\right) \sin n \theta\right] \\ \tilde{u}_r^{\prime(k)}= & F_{01}^{(k)} a \xi+F_{02}^{(k)} \alpha \xi^{-1}+ \\ & \sum\limits_{n=1}^{\infty} \sum\limits_{j=1}^4 a \xi^{e_{j j}}\left[F_{n j}^{(k)} \cos n \theta+s G_{n j}^{(k)} \sin n \theta\right] \\ \tilde{u}_\theta^{\prime(k)}= & \sum\limits_{n=1}^{\infty} \sum\limits_{j=1}^4 a \beta_{n j}^{(k)} \xi^{e_{n j}}\left[F_{n j}^{(k)} \sin n \theta-s G_{n j}^{(k)} \cos n \theta\right] \end{aligned}\right. $ | (8) |
式中: a表示纤维半径,无量纲径向坐标ξ=r/a在调节方程的条件数方面起着重要作用, Hnj(k)、Fnj(k)、Gnj(k)(j=1, 2, 3, 4)是待求的未知系数,特征值enj分别为en1=n+1,en2=n-1,en3=-(n+1),en4=-(n-1),βnj(k)是其对应的特征向量。
根据式(8),以及应变-位移和应力-应变关系,可得应力分量的解析表达:
| $ \left\{\begin{aligned} \tilde{\sigma}_{z r}^{(k)}= & 2 s \tilde{G}_A^{(k)} \bar{\varepsilon}_{z r}+s \tilde{G}_A^{(k)} \sum\limits_{n=1}^{\infty} n\left[\left(\xi^{n-1} H_{n 1}^{(k)}-\xi^{-n-1} H_{n 3}^{(k)}\right) \cos n \theta+\left(\xi^{n-1} H_{n 2}^{(k)}-\xi^{-n-1} H_{n 4}^{(k)}\right) \sin n \theta\right] \\ \tilde{\sigma}_{r r}^{(k)}= & s\left(k_T^{(k)}+G_T^{(k)}\right) \bar{\varepsilon}_{r r}+s\left(k_T^{(k)}-G_T^{(k)}\right) \bar{\varepsilon}_{\theta \theta}+2 s k_T^{(k)} \nu_A^{(k)} \bar{\varepsilon}_{z z}+ \\ & 2 s k_T^{(k)} F_{01}^{(k)}-2 s \mu_T^{(k)} F_{02}^{(k)} \xi^{-2}+\sum\limits_{n=1}^{\infty} \sum\limits_{j=1}^4 s P_{n j}^{(k)} \xi^{e_{n j}-1}\left(F_{n j}^{(k)} \cos n \theta+s G_{n j}^{(k)} \sin n \theta\right) \\ \tilde{\sigma}_{r \theta}^{(k)}= & 2 s \mu_T^{(k)} \bar{\varepsilon}_{r \theta}+\sum\limits_{n=1}^{\infty} \sum\limits_{i=1}^4 s R_{n j}^{(k)} \xi^{e_{n j}-1}\left(F_{n j}^{(k)} \sin n \theta-s G_{n j}^{(k)} \cos n \theta\right) \end{aligned}\right. $ | (9) |
其中:
为了精确满足不完美界面条件,采用了弹簧模型[21]用于描述纤维基体之间的损伤情况:
| $\left\{\begin{array}{l} \tilde{{\sigma}}_{z r}^{(m)}=\tilde{{\sigma}}_{z r}^{(f)}=s k_{z r}\left[\tilde{u}_z^{\prime(m)}-\tilde{u}^{\prime}(f)_z\right] \\ \tilde{{\sigma}}_{r r}^{(m)}=\tilde{{\sigma}}_{r r}^{(f)}=s \hat{k}_{r r}\left[\tilde{u}_r^{\prime(m)}-\tilde{u}^{\prime}(f)_r\right] \\ \tilde{{\sigma}}_{r \theta}^{(m)}=\tilde{{\sigma}}_{r \theta}^{(f)}=s \hat{k}_{r \theta}\left[\tilde{u}_\theta^{\prime(m)}-\tilde{u}^{\prime}(f)_\theta\right] \end{array}\right. $ | (10) |
式(10)表明由于已经发生破坏,纤维基体之间的位移并不连续,但是其差值与界面处仍保持连续的应力分量具有一定的比例关系。其中kzr、krr、krθ分别为弹簧在不同方向上的刚度,大小在零到无穷之间。当刚度为无穷大时,式(10)可以退化到完美界面情况。
最后式(8)、(9)中的未知系数可以通过施加不完美界面条件(10)和周期性边界条件(6)得到。对代表性单元求解后,可以有效还原材料内部的应力分布情况。最后通过对晶胞建立均匀化本构模型式(4),可以得到材料在Laplace域内的有效模量。
3 算例分析本文所研究的聚合物基复合材料,基体表现出黏弹性特性,而纤维仍属于弹性范围[5]。本文首先研究了玻璃纤维/环氧树脂基复合材料的宏观有效模量和微元体内局部响应。材料的弹性瞬时参数如表 2所示。另外,为了更好地描述基体的黏弹性力学本构,本文采用由Maxwell和Kelvin模型串联组成的四参数流变模型,如图 3所示,其蠕变柔度可表示为
| $ \begin{aligned} S_{11}(t)= & 1 / E+1 / E_1 \cdot\left[1-\exp \left(-E_1 / \eta_1 \cdot t\right)\right]+ \\ & t / \eta_2 \end{aligned} $ | (11) |
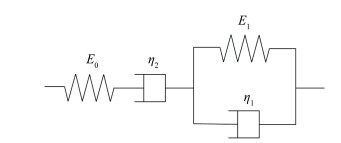
|
图 3 描述黏弹性基体的四参数模型 Fig. 3 Four-parameter model of viscoelastic matrix |
拉普拉斯域下的蠕变柔度可表示为
| $\begin{aligned} \tilde{S}_{11}(s)= & 1 /(s E)+1 /\left(s E_1\right)-1 /\left(E_1\left(s+E_1 / \eta_1\right)\right)+ \\ & 1 /\left(s^2 \eta_2\right) \end{aligned} $ | (12) |
其中: E1=1.8 GPa, η1=300 GPa · h, η2=8 000 GPa · h[1]。
3.1 宏观模量预测如图 4所示,本节首先给出了纤维半径为71 μm、体积分数为vf=0.3的复合材料的有效松弛模量。另外,为了验证界面损伤对材料宏观性能的影响,本节引入了不同的界面刚度,分别为k=3×1014 MPa/m、3×107 MPa/m、3 MPa/m,分别表示完美黏结、部分黏结以及完全脱黏。为了验证本方法的正确性,引入基于有限体积思想的FVDAM模型对完全黏结和完全破坏的复合材料系统进行验证,并取得了较好的对比结果。另外,由图 4也可以看出界面损伤对材料的宏观黏弹性特性影响较大。对于不完美界面情况,材料的有效松弛模量均小于完美黏结的情况;当界面完全破坏时,纤维不承担任何荷载,只有基体承受外力作用,因此有效模量最小。
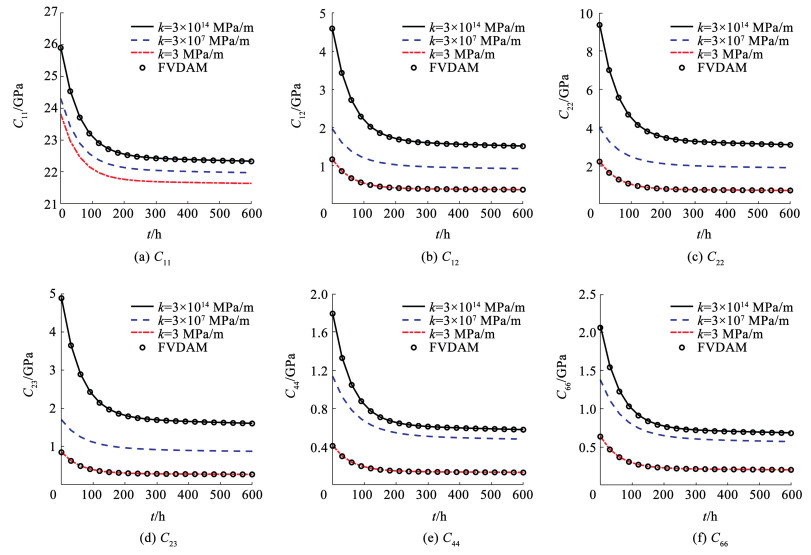
|
图 4 纤维半径为71 μm、体积分数为30%的玻璃纤维增强环氧复合材料的宏观有效模量 Fig. 4 The relaxation functions of a unidirectional glass/epoxy composite with 71 μm fiber radius and 30% fiber volume fraction |
此外,本文还给出了代表性单元在宏观荷载作用下微元体的应力松弛过程。图 5还原了微元体在面内荷载
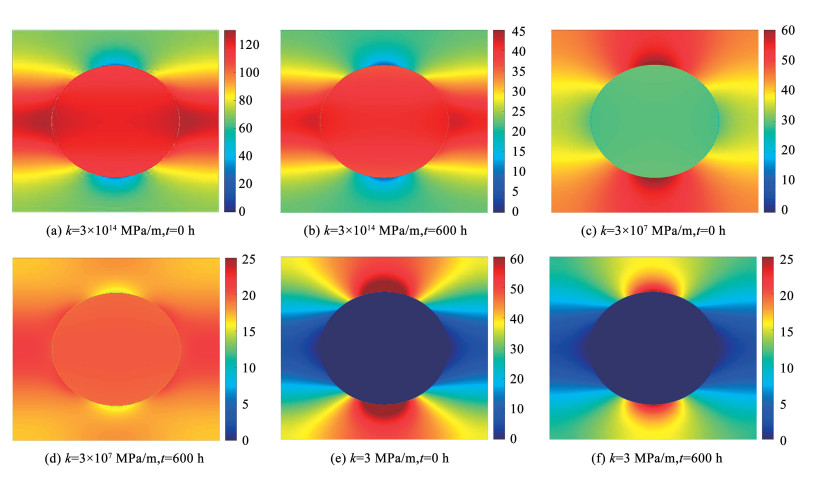
|
图 5 不同界面刚度下纤维复合材料晶胞在初始时刻(t=0 h)以及t=600 h的应力分量σ22(y2, y3)(MPa)分布情况 Fig. 5 The distribution of σ22(y2, y3)(MPa) at the initial moment (t=0 h) and t=600 hours of the unit cell of fiber composite under different interface stiffness |
针对纤维增强复合材料的黏弹性力学行为进行研究,采用了弹性-黏弹性对应性原理将细观力学模型转化到Laplace域内进行求解,然后将材料的宏/细观响应通过Zakian反演方法转换回时域内。同时为了模拟界面破坏对材料宏/细观力学性能的影响,引入了前期开发的考虑界面损伤效应的LEHT模型。该模型的优势在于精确求解代表性晶胞内的位移和应力表达式,进而可以实现不完美界面在数学上的精确满足,与FVDAM模型对完全黏结和完全破坏的复合材料系统预测的一致性验证了方法的正确性。由于该模型避免了其他数值计算方法中大规模的网格划分和对时间增量的分步迭代,因此可以实现材料性能退化的高效预测。另外,本文不仅研究了界面效应对材料宏观黏弹性特性退化的影响,还从细观结构应力重分布解释了宏观模量退化的影响,为评估具有不完美界面的聚合物基纤维复合材料的长期性能提供了一种有效的途径。
| [1] |
WANG G, PINDERA M J. Locally-exact homogenization of viscoelastic unidirectional composites[J]. Mechanics of Materials, 2016, 103(12): 95. |
| [2] |
许飞, 李磊, 杨胜春. 单向复合材料横向裂纹黏弹性损伤演化模型[J]. 复合材料学报, 2020, 37(6): 124. XU Fei, LI Lei, YANG Shengchun. A damage evolution law for transverse cracking in unidirectional composites of linear viscoelastic behavior[J]. Acta Materiae Compositae Sinica, 2020, 37(6): 124. |
| [3] |
孙同生, 于存贵, 杨文超, 等. 玻纤/环氧树脂复合材料非线性粘弹性响应[J]. 哈尔滨工业大学学报, 2020, 52(7): 139. SUN Tongsheng, YU Cungui, YANG Wenchao, et al. Nonlinear viscoelastic response of E-glass fiber /epoxy resin composites[J]. Journal of Harbin Institute of Technology, 2020, 52(7): 139. |
| [4] |
张小玉, 黄乾钰, 陈建中, 等. 聚合物基复合材料单向板黏弹性模型[J]. 华中科技大学学报(自然科学版), 2015(43): 30. ZHANG Xiaoyu, HUANG Qianyu, CHEN Jianzhong, et al. The viscoelastic model of PMC unidireectional plate[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2015(43): 30. |
| [5] |
梁军, 杜善义. 粘弹性复合材料力学性能的细观研究[J]. 复合材料学报, 2001, 18(1): 97. LIANG Jun, DU Shanyi. Study of mechanical properties of viscoelastic matrix composites by micromechanics[J]. Acta Materiae Compositae Sinica, 2001, 18(1): 97. |
| [6] |
任超, 陈建钧, 潘红良. 纤维增强复合材料黏弹性行为的预测模型[J]. 复合材料学报, 2012, 29(1): 162. REN Chao, CHEN Jianjun, PAN Hongliang. Prediction model for visco-elastic behavior of fiber reinforced composites[J]. Acta Materiae Compositae Sinica, 2012, 29(1): 162. |
| [7] |
WANG G, TU W, CHEN Q. Homogenization and localization of imperfectly bonded periodic fiber-reinforced composites[J]. Mechanics of Materials, 2019, 139(12): 103178. |
| [8] |
杨绘峰, 高存法. 功能梯度界面相对周期分布纤维增强复合材料反平面剪切的影响[J]. 固体力学学报, 2021, 42(1): 53. YANG Huifeng, GAO Cunfa. Influence of a functionally graded layer on the anti-plane shear behavior of a periodic fibrous composite[J]. Chinese Journal of Solid Mechanics, 2021, 42(1): 53. |
| [9] |
CHEN Q, WANG G. Homogenized and localized responses of coated magnetostrictive porous materials and structures[J]. Composite Structures, 2017, 187(3): 102. |
| [10] |
HASHIN Z. Thermoelastic properties of fiber composites with imperfect interface[J]. Mechanics of Materials, 1990, 8(4): 333. |
| [11] |
WANG X, SCHIAVONE P. A circular inhomogeneity with a mixed-type imperfect interface in anti-plane shear[J]. Applied Mathematical Modelling, 2017, 43(3): 538. |
| [12] |
刘文辉, 张新明, 张淳源. 均匀化方法在粘弹性多层复合材料中的应用[J]. 计算力学学报, 2005, 22(6): 722. LIU Wenhui, ZHANG Xinming, ZHANG Chunyuan. Applicatin of homogenization theory to viscoelastic multilayered composites[J]. Chinese Journal of Computational Mechanics, 2005, 22(6): 722. |
| [13] |
刘文辉, 张新明, 张淳源. 粘弹性复合材料中的渐近均匀化方法[J]. 工程力学, 2005(6): 63. LIU Wenhui, ZHANG Xinming, ZHANG Chunyuan. Asymptotic homogenization of viscoelastic composites[J]. Engineering Mechanics, 2005(6): 63. |
| [14] |
常崇义, 刘书田, 王成国. 单向纤维复合材料粘弹性性能预测[J]. 计算力学学报, 2006, 23(4): 414. CHANG Chongyi, LIU Shutian, WANG Chengguo. Prediction of visco-elastic property of unidirectional fiber reinforced composite materials[J]. Chinese Journal of Computational Mechanics, 2006, 23(4): 414. |
| [15] |
于航, 周储伟. 纤维复合材料粘弹性动态性能的细观力学分析[J]. 振动工程学报, 2011, 24(4): 359. YU Hang, ZHOU Chuwei. Meso-mechanical analysis on dynamic viscoelasticity of fiber-reinforced composites[J]. Journal of Vibration Engineering, 2011, 24(4): 359. |
| [16] |
VIET H N, PASTOR J, MULLER D. A method for predicting linear viscoelastic mechanical behavior of composites, a comparison with other methods and experimental validation[J]. European Journal of Mechanics A: Solids, 1995, 14(6): 939. |
| [17] |
SHIBUYA Y. Evaluation of creep compliance of carbon-fiber-reinforced composites by homogenization theory[J]. JSME International Journal: Series A, 1997, 40(3): 313. |
| [18] |
ZAKIAN V. Numerical inversion of laplace transform[J]. Electronics Letters, 1969, 5(6): 120. |
| [19] |
ZAKIAN V. Rational approximation to transfer-function matrix of distributed system[J]. Electronics Letters, 1970, 6(15): 474. |
| [20] |
CHARALAMBAKIS N. Homogenization techniques and micromechanics: a survey and perspectives[J]. Applied Mechanics Reviews, 2010, 63(3): 651. |
| [21] |
HASHIN Z. Thermoelastic properties of fiber composites with imperfect interface[J]. Mechanics of Materials, 1990, 8(4): 333. |
 2023, Vol. 55
2023, Vol. 55


