车辆的微观交通行为是交通流理论的核心研究对象。随着车联网和自动驾驶的普及,车辆的微观行为研究日益受到重视,并为自动驾驶车辆在混合交通流中的感知、决策规划提供基础信息。一般而言,车辆的微观交通行为可以分解为纵向行为和侧向行为。前者主要由跟驰模型描述、后者主要由换道模型刻画。跟驰模型是从车辆运动学的角度,研究前车的运动状态变化所引起的跟驰车辆的相应行为[1],如:文献[2]考虑车辆自由状态下的加速趋势和与前车碰撞的减速趋势提出了智能驾驶模型(intelligent driver model, IDM),能有效地描述车辆的驾驶状态;文献[3-4]通过研究车辆的跟驰行为,对智能网联环境下混合交通流的稳定性进行分析。换道行为是根据驾驶员特性,针对周围车辆的驾驶状态和周围环境信息的综合考量完成自身驾驶目标的复杂过程,如:文献[5]则提出了深度确定性策略算法,为换道行为提供决策依据;文献[6]考虑到车辆在换道过程中周围车辆的影响,提出了与时间相关的动态换道轨迹规划模型,并使用NGSIM数据验证了模型的有效性;文献[7]基于机器学习的方法为目标车辆的周围车辆建立了换道预测模型,能够准确地预测车辆轨迹;文献[8]则提出了一种用于联网的高级驾驶员辅助系统的集成变道轨迹规划方法,能够实现安全快速的换道。
近些年来,一些学者同时考虑车辆跟驰和换道行为,发展出二维车辆跟驰模型。文献[9]考虑连续的侧向距离提出了二维车辆跟驰模型,能够解决二维的交通流问题;文献[10]通过限制期望时间间隔的变化率,避免了在二维IDM模型中车辆会出现过高的减速度现象;文献[11]针对混合交通下自动驾驶车辆的运动,既考虑周围车辆对自动驾驶车辆的刺激作用,又考虑了车辆的横向和纵向运动,提出了增强型二维IDM模型;文献[12]也考虑了多个前后车辆的信息,提出了一种改进IDM模型来描述车辆的跟驰行为;文献[13]利用真实车辆数据标定IDM的参数提出了适应性IDM模型,提高道路交通稳定性;文献[14]将IDM与径向基函数神经网络结合研究低速车辆的跟驰驾驶行为。
还有一些学者认为周围运动物体和道路环境通过矢量场对行驶车辆的安全产生影响,发展了交通场理论。文献[15]建立了基于安全场势理论的换道模型,有效描述了车联网环境下车辆在换道过程中面临的驾驶风险。文献[16]则充分考虑混合交通流环境,建立了基于安全势场的车辆跟驰模型描述微观车辆驾驶行为。之后,文献[17]又考虑车辆加速度和转角的影响,提出一种动态驾驶风险潜在场模型。文献[18]针对智能车辆的路径规划,介绍一种基于势场模型的自主道路车辆预测路径规划控制器。文献[19]在此基础上,充分考虑交通环境各种因素的影响建立复合交通场模型。
从已有的研究成果来看,现有的二维IDM模型和交通场理论只能适用于均质道路和均质交通流,无法适用于匝道处等不同方向车辆复杂的相互作用及衍生的驾驶行为。基于此,本文提出了基于虚拟边界场的二维IDM模型,通过虚拟边界场和周围运动物体对车辆的作用,构建车辆在混合交通流场景下的轨迹运行模型。
本文首先介绍虚拟边界场的概念,从微观层面上分析边界场影响车辆的驾驶行为的机理,并对虚拟边界场建模。同时考虑周围车辆的影响,提出了基于虚拟边界场的二维IDM模型。接着介绍了基于动态时间规整(dynamic time warping, DTW)的边界场优化方法,为边界场的优化提供理论指导。基于开源数据集(Mirror-Traffic和NGSIM),利用粒子群算法求解出最优的虚拟边界场位置,对直行轨迹和出匝道轨迹进行预测并进行误差分析,最后给出文章的结论。
1 虚拟边界建模 1.1 基本概念和参数说明本文研究的虚拟边界场,是对目前研究的车辆二维微观交通行为的拓展和补充。目前诸多学者研究对象主要是后车对前车的跟驰行为,或者是周围车辆对目标车辆的影响作用。在匝道出入口处,车辆会考虑自身的行进方向。除了周围其他车辆的影响,车辆还会考虑道路拓扑因素。例如驶离匝道的车辆为了平顺驶离主线,会在到达出口匝道前依次换道至最外侧车道。为了刻画这种行为,本文引入了“虚拟边界场”的概念。如果车辆处于边界场中,它的驾驶行为都会受到虚拟边界场的作用,虚拟边界场由虚拟边界场线产生。虚拟边界场线界定了车辆驾驶范围,是车辆边界点可以到达的边界范围(理论上不允许超过)。如图 1所示,在界定的虚拟边界场线(图中的黄色粗虚线)生成的边界场(图 1中黄色的阴影)的作用下,红色车辆逐渐从Lane 1到Lane 5,最终从匝道驶离高速公路。下面分别论述虚拟边界线模型、边界场对车辆的作用,并构建二维智能驾驶模型。

|
图 1 虚拟边界场下的车辆驾驶行为 Fig. 1 Driving behaviors of vehicle under the virtual boundary fields |
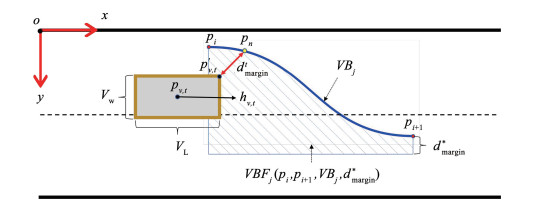
文中所用到参数及其解释如下:pi, pi+1表示虚拟边界场线的起始和终止点,pi=[xi, yi], pi+1=[xi+1, yi+1];VBj表示第j虚拟边界场线,它是根据Bezier曲线生成的;pn表示虚拟边界场线上的任意一点,pn=[xn, yn], pn∈VBj;VBFj表示第j个虚拟边界场;Vw表示车辆的宽度;VL表示车辆的长度;pv, t表示t时刻,车辆的中心坐标,pv, t=[xv, t, yv, t];pv, t′表示t时刻,车辆的边界坐标,pv, t′=[xv, t-0.5Vw, yv, t+0.5VL];hv, t表示t时刻,车辆的行驶方向,
根据前文的讨论,只有当车辆边界点pv, t′处于边界场中VBFj,车辆的驾驶行为才会受到影响。由于贝塞尔曲线具有易优化和曲率变化连续性等优点,通过选取适当的参数,能最大限度地提高乘客的舒适度,在轨迹规划和道路设计中得到了很多成功的应用[20-21]。本文利用贝塞尔曲线对虚拟边界线进行刻画。如图 2所示,边界场指图 2中蓝色阴影区域,它由4部分构成:虚拟边界场线的起始控制点(pi)、终止控制点(pi+1)、边界场线(VBj)和理想距离(dmargin*)。边界场线(VBj)根据三阶贝塞尔曲线[22](Bezier Curve)生成,由4个点决定,其中的两个点决定它的位置,另外两个点决定曲线的形状和方向。只要选取合适的位置,生成的曲线就能形象地刻画车辆的运动轨迹。本文中,自动驾驶车辆从匝道驶离高速道路过程的行驶轨迹,可以分为两部分:1)高速路上的换道过程,如图 1车辆从Lane 1到Lane2再到Lane 3的过程,车辆轨迹在起止点的斜率均为“0”;2)从高速路驶向匝道,如图 1车辆从Lane 4到Lane5的过程,车辆轨迹在起止点的斜率不为“0”,取决于匝道的几何位置。所以通过pi和pi+1,可以计算另外两个与形状和方向相关控制点pi, 1control, pi, 2control的坐标:
|
图 2 微观下的边界场对车辆的作用 Fig. 2 The effect of the boundary field on the vehicle at the microscopic level |
情景1)高速道路上的换道过程:
| $ \left\{\begin{array}{l} p_{i, 1}^{\text {control }}=\left[0.5\left(x_i+x_{i+1}\right), y_i\right] \\ p_{i, 2}^{\text {control }}=\left[0.5\left(x_i+x_{i+1}\right), y_{i+1}\right] \end{array}\right. $ | (1) |
情景2)从高速道路驶向匝道:
| $\left\{\begin{array}{l} p_{i, 1}^{\text {control }}=\left[0.5\left(x_i+x_{i+1}\right), y_i\right] \\ p_{i, 2}^{\text {control }}=\left[\alpha\left(x_i+x_{i+1}\right), \beta\left(y_i+y_{i+1}\right)\right] \end{array}\right. $ | (2) |
其中α, β∈(0, 1)。根据这4个点,可以计算边界场线:
| $ \begin{aligned} V B_j= & (1-\lambda)^3 p_i+3 \lambda(1-\lambda)^2 p_{i, 1}^{\text {control }}+ \\ & 3 \lambda^2(1-\lambda) p_{i, 2}^{\text {control }}+\lambda^3 p_{i+1}, \lambda \in[0, 1] \end{aligned} $ | (3) |
不同时刻下,边界场对车辆的作用是通过车辆边界坐标pv, t′与边界坐标场线VBj之间的实际最短距离dmargint和车辆的加速度实现的, 其中dmargint的大小为
| $ \begin{gathered} d_{\text {margin }}^t=\left\|\overrightarrow{p_{v, t}^{\prime} p_n}\right\|=\left[\left(x_n-x_{v, t}+0.5 V_{\mathrm{w}}\right)^2+\right. \\ \left.\left(y_n-y_{v, t}-0.5 V_{\mathrm{L}}\right)^2\right]^{1 / 2}, \left(x_n, y_n\right) \in V B_j \end{gathered} $ | (4) |
等式(4)中的xv, t, yv, t分别为
| $ \left\{\begin{array}{l} x_{v, t}=x_{v, 0}+\sum\limits_t v_t^{\mathrm{Long}} \cdot t+0.5 \cdot a_{\mathrm{Long}}^{\mathrm{Eff}} \cdot t^2 \\ y_{v, t}=y_{v, 0}+\sum\limits_t v_t^{\mathrm{Lat}} \cdot t+0.5 \cdot a_{\mathrm{Lat}}^{\mathrm{Eff}} \cdot t^2 \end{array}\right. $ | (5) |
其中[xv, 0, yv, 0]表示车辆在初始时刻时分别沿横向和侧向的速度。
假设车辆在边界场的作用下,与边界场线之间的理想距离为dmargin*,如果dmargint大于dmargin*,在横向方向上(图 2中的ox方向),车辆需要加速,但是在纵向方向上(图 2中的oy方向)车辆需要减速;反之,在横向方向上减速,在纵向方向上加速。如果dmargint等于dmargin*时,车辆既不需要加速也不需要减速。所以计算出横向和纵向的加速度分别为
| $ a_{\text {Long }}^{\text {Eff }}=a_{\text {Long }}\left[1-\left(\frac{d_{\text {margin }}^*}{d_{\text {margin }}^t}\right)^2\right] $ | (6) |
| $ a_{\text {Lat }}^{\mathrm{Eff}}=a_{\text {Lat }}\left[1-\left(\frac{d_{\text {margin }}^t}{d_{\text {margin }}^*}\right)^2\right] $ | (7) |
在实际的驾驶环境中,车辆的驾驶行为还受到周围车辆的影响,文献[11]综合考虑周围车辆对自动驾驶车辆的作用,提出了增强型二维IDM模型, 有效地刻画了车辆沿横向和纵向方向的运动。本文同时考虑了虚拟边界场和环境车辆,提出了基于虚拟边界场的二维IDM模型。
车辆的横向运动可以表示为
| $ a_{\text {Long }}^{\text {Eff }}=\left\{\begin{array}{l} a_{\text {Long }}\left\{1-\left(\frac{v_o^{\text {Long }}}{v_{\text {dong }}^{\text {Long }}}\right)^4-\left[\left(\frac{s_{\text {Long }}^*}{s_{\text {Front }}^{\text {Eff }}}\right)^2-\left(\frac{s_{\text {Long }}^*}{s_{\text {Rear }}^{\text {Eff }}}\right)^2\right]+\left[1-\left(\frac{d_{\text {margin }}^*}{d_{\text {margin }}^t}\right)^2\right]\right\}, p_{v, t}^{\prime} \in V B F_j \\ a_{\text {Long }}\left\{1-\left(\frac{v_o^{\text {Long }}}{v_{\mathrm{d}}^{\text {Long }}}\right)^4-\left[\left(\frac{s_{\text {Long }}^*}{s_{\text {Front }}^{\text {Eff }}}\right)^2-\left(\frac{s_{\text {Long }}^*}{s_{\text {Rear }}^{\text {Eff }}}\right)^2\right]\right\}, p_{v, t}^{\prime} \notin V B F_j \end{array}\right. $ | (8) |
其中
| $ s_{\text {Long }}^*=s_O^{\text {Long }}+\max \left(0, v_O^{\text {Long }} T^{\text {Long }}+\frac{v_O^{\text {Long }} \Delta v^{\text {Long }}}{2 \sqrt{a_{\text {Long }} b_{\text {Long }}}}\right) $ | (9) |
式(8)、(9)中的sLong*表示车辆沿横向方向的理想动态间隙;sFrontEff表示车辆前方方向与其他车辆的有效间隙;sRearEff车辆后方方向与其他车辆的有效间隙;vdLong表示车辆沿横向方向的理想速度;vOLong表示车辆沿横向方向的实际速度;ΔvLong表示车辆沿横向方向与其他车辆的平均速度差;TLong表示车辆沿横向方向的时距;aLong′, bLong分别表示车辆沿横向方向最大加速度和理想加速度。
车辆的纵向运动可以表示为
| $ a_{\text {Lat }}^{\text {Eff }}=\left\{\begin{array}{l} a_{\text {Lat }}\left\{\left(\frac{s_{\text {Lat }}^*}{s_{\text {Right }}^{\text {Eff }}}\right)^2-\left(\frac{s_{\text {Lat }}^*}{s_{\text {Left }}^{\text {Eff }}}\right)^2+\left[1-\left(\frac{d_{\text {margin }}^t}{d_{\text {margin }}^*}\right)^2\right]\right\}, \\ p_{v, t}^{\prime} \in V B F_j \\ a_{\text {Lat }}\left[\left(\frac{s_{\text {Lat }}^*}{s_{\text {Right }}^{\text {Eff }}}\right)^2-\left(\frac{s_{\text {Lat }}^*}{s_{\text {Left }}^{\text {Eff }}}\right)^2\right], p_{v, t}^{\prime} \notin V B F_j \end{array}\right. $ | (10) |
其中
| $ s_{\text {Lat }}^*=s_O^{\text {Lat }}+\max \left(0, v_O^{\text {Lat }} T^{\text {Lat }}+\frac{v_O^{\text {Lat }} \Delta v^{\text {Lat }}}{2 \sqrt{a_{\text {Lat }} b_{\text {Lat }}}}\right) $ | (11) |
式(10)、(11)中的sLat*表示车辆沿纵向方向的理想动态间隙;sRightEff表示车辆右侧方向与其他车辆的有效间隙;sLeftEff表示车辆左侧方向与其他车辆的有效间隙;vdLat表示车辆沿纵向方向的理想速度;vOLat表示车辆沿纵向方向的实际速度;ΔvLat表示车辆沿纵向方向与其他车辆的平均速度差;TLat表示车辆沿纵向方向的时距;aLat, bLat分别表示车辆沿纵向方向最大加速度和理想加速度。
式(8)~(11)中的sRearEff, sRightEff, sLeftEff,ΔvLat, ΔvLong, sFrontEff, 是由自动驾驶车辆和周围车辆的当前状态共同决定的,通过如图 3所示的伪代码算法流程图可以计算出它们的具体值。

|
图 3 伪代码 Fig. 3 Pseudocode |
本文的模型能够在混合交通流场景下,对不同车辆的行驶轨迹进行预测,通过对比理论轨迹与实际轨迹的相似性,验证模型的有效性。但是,两段轨迹的时间序列长度可能并不相等,而传统的欧几里得距离无法有效地求出两者之间的相似性。因此,本文采用动态时间规整DTW[23],它可以计算两个时间序列的相似度,尤其适用于不同长度、不同节奏的时间序列,具体公式为
| $ \begin{gathered} \operatorname{DTW}(i, j)=\operatorname{dist}\left(q_i\left(x_i, y_i\right), c_j\left(x_j, y_j\right)\right)+ \\ \min \{\operatorname{DTW}(i, j-1), \operatorname{DTW}(i-1, j), \operatorname{DTW}(i-1, j-1)\} \end{gathered} $ | (12) |
| $ \gamma(Q, C)=\sum\limits_{i=0}^n \sum\limits_{j=0}^m \operatorname{DTW}(i, j) $ | (13) |
其中:Q和C分别是两个时间序列,它们是由一系列坐标时间序列构成;qi(xi, yi),cj(xj, yj)分别是两个时间序列的一个坐标点;dist是求解两个坐标点之间的直线距离,从(0, 0)点开始匹配这两个序列Q和C,每到一个点,累加之前所有的点计算的距离,到达终点(n, m)后,这个累积距离就是γ(Q, C),即为序列Q和C的相似度。
3.2 参数标标定对模型的关键参数进行标定,分别选取直行车道最靠近道路内侧的边界起始点坐标(0,-0.1),和沿车辆行驶方向直行车道与匝道的交界点的最外侧坐标(145, 7.6),作为虚拟边界场线的起始和终止控制点。终止控制点的坐标在其他匝道处也容易确定。随机选取数据集中一条车辆轨迹的初始时刻坐标(6.05, 1.05)和速度20.1 m/s,作为车辆的初始坐标和初始速度。车长和车宽参考私家车的车型分别为4.0 m和1.8 m,其他的一些关键参数参考文献[9]工作,分别为:aLong=2.95 m/s2, aLat=0.63 m/s2, bLong=2.21 m/s2, vdLong=12.1 m/s, bLat=2.66 m/s2, TLong=1.3 s, TLat=1.18 s。在文献[9]的研究中,通过使用1 050条不同NGSIM数据对上述参数进行标定,并给出了它们的均值和标准差,所以在本文的研究中,只需要对车辆的边界坐标与虚拟边界场线的理想距离dmargin*进行标定。
考虑到dmargin*的物理意义,它的取值要根据车辆具体的驾驶场景确定。比如对于从Lane 1到Lane 3这一驾驶场景,dmargin*的取值为[0, 01 m, 1.00 m],本文设置仿真步长为0.01 m,不改变其他参数,代入到模型中进行仿真求解,得到理论轨迹,接着采用DTW算法计算出与实际之间的差值,通过计算可以确定dmargin*的取值为0.31 m。
3.3 PSO优化方法为了确定最优虚拟边界场线的坐标,本文采用粒子群算法(PSO)[24]来确定最优的坐标点,PSO是通过模拟鸟群觅食行为发展起来的一种基于群体协作的随机搜索算法。目标函数是利用前文的模型对75%的Mirror-Traffic数据库中出匝道轨迹进行预测,之后利用DTW求出它们之间的差异性,并取均值。设置粒子群数为50,迭代次数为500,两个学习因子参数和惯性权重参数分别为0.5,0.3和1.5。
4 模型分析 4.1 数据来源及描述为了验证模型的有效性,本文采用开源数据集(Mirror-Traffic)中高速公路汇出数据。其交通场景如图 4所示,其中Lane 1和Lane 2为直行车道,Lane 3和Lane 4为出口匝道。该数据集共有556条车辆轨迹,其中直行车辆轨迹为246条,出匝道车辆轨迹有290条。

|
图 4 Mirror-Traffic中的高速公路汇出交通场景 Fig. 4 Traffic scenario of highway in the Mirror-Traffic dataset |
在图 4中的驾驶环境中,针对“从Lane 1到Lane 3”的驾驶场景,需要确定出最优的虚拟边界场线的位置。根据上文的理论分析,虚拟边界场线的位置是由pi, pi+1, dmargin*3个参数唯一确定,其中该场景下的dmargin*标定为0.31 m,pi+1的坐标为Lane 2和Lane 3的交点(145, 7.6)。唯一不确定的值为虚拟边界线的起始控制点p0,所以通过确定它的坐标,边界场的位置就被唯一确定。利用前文提到的PSO算法,进行优化求解。优化迭代曲线如图 5所示,求解出最优的起始控制点p0坐标为(21.58, 0),并绘制出虚拟边界场线如图 6所示。

|
图 5 PSO求解最优边界场位置的曲线图 Fig. 5 The PSO curve to solve the optimal location of virtual boundary |

|
图 6 最优的边界场线位置和75%出匝道的车辆轨迹 Fig. 6 The optimal location of virtual boundary and 75% off-ramp trajectories |
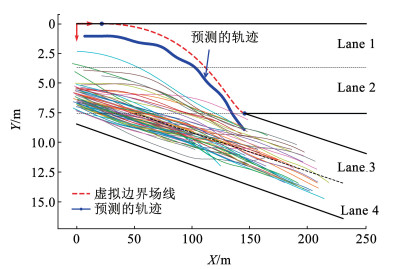
根据前文4.2节,已经求出最优边界场的起止控制点坐标和车辆的边界坐标pv, t′与虚拟边界场线VBj的理想距离,dmargin*。接下来对出匝道车辆的轨迹进行预测。结果如图 7所示。并将预测的轨迹与剩下25%的出匝道车辆轨迹进行比较。
|
图 7 最优边界场线下的预测轨迹 Fig. 7 Prediction trajectory based on the optimal virtual boundary |
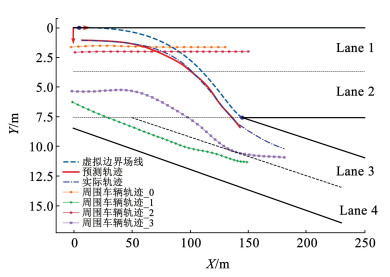
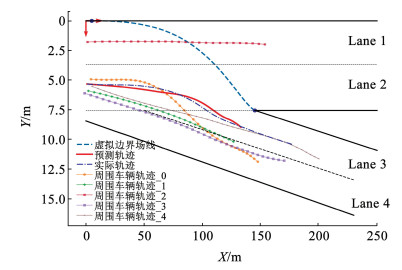
为进一步验证模型的准确性,利用本文的模型对Mirror数据集中的4种不同类型的出匝道车辆轨迹进行预测,另外选取目标车辆的周围车辆作为障碍车辆。将所有参数代入到模型中,进行仿真计算,并绘制出车辆轨迹如图 8所示。接着进行另外两组实验,结果如图 9、10所示。
|
图 8 仿真实验验证1 Fig. 8 Simulation experimental validation 1 |
|
图 9 仿真实验验证2 Fig. 9 Simulation experimental validation 2 |

|
图 10 仿真实验验证3 Fig. 10 Simulation experimental validation 3 |
图 8~10的实验结果分别验证了从Lane 1到Lane 2,从Lane 2到Lane 3和Lane 2到Lane 4三种不同的车辆从高速路驶出匝道的场景。上述3个场景结果图中,深绿色的虚线表示虚拟边界场线,蓝色曲线为实际的车辆轨迹,红色曲线表示根据前文的模型预测的车辆轨迹,通过比较蓝色和红色曲线,它们有着极高的相似度和趋势。
本文的模型除了对驶离匝道的车辆适用,对直行车辆同样适用。为此本文进行了仿真验证4,结果如图 11所示。在图 11中,黄色曲线是根据模型预测出来的一条出匝道轨迹,红色虚线是根据黄色虚线和其他周围障碍车辆预测出来的直行的轨迹,蓝色曲线为实际的车辆轨迹,通过比较发现两者基本上重合在一起,这说明了本文提出的模型对直行车辆也同样适用。

|
图 11 仿真实验验证4 Fig. 11 Simulation experimental validation 4 |
Mirror-Traffic数据针对是中国的道路环境,考虑到不同国家的交通环境,驾驶员特性等因素与国内情况不尽相同,本文又选取了美国高速公路数据集NGSIM,对本文的模型进行验证。数据经过处理以后,利用模型对其中的一条轨迹进行预测,结果如图 12所示,图中的红色曲线与蓝色曲线基本上重合在一起。另外选取其他多组数据分别进行验证,最终预测结果说明本文模型对美国的交通环境同样适用。

|
图 12 仿真实验验证5 Fig. 12 Simulation experimental validation 5 |
前文通过5次仿真实验对本文提出的基于虚拟边界场的二维IDM模型进行了验证,证明模型的有效性和准确性,但是预测轨迹与实际轨迹之间仍存在一定的误差,需要对误差进行分析。本文的误差分两类:1)YError,指的是车辆轨迹随着X轴变化,实际轨迹与预测轨迹在Y方向上的差值,即YError=Yreal-Ypredict;2)YAbsolute Error,指的是车辆轨迹随着X轴变化,实际轨迹与预测轨迹在Y方向上的绝对差值,即YAbsolute Error=abs(YError)。接着计算Mirror数据4次仿真实验的误差,如图 13所示。

|
图 13 4个仿真实验(Mirror数据)的纵向方向Y的预测轨迹与实际轨迹绝对误差随X的变化 Fig. 13 The YAbsolute Error between simulated values and actual values of four different simulation experiments |
在图 13中,4次实验随着X的变化,YAbsolute Error的值都处于[0 m, 0.8 m],其中对直行场景轨迹预测的误差最小。接着对Mirror-Traffic数据中所有的出匝道轨迹(共有290条)进行预测,并求出每条轨迹的平均YError和YAbsolute Error,分别绘制出它们的频数直方分布图如图 14、15所示。在图 14中,大约有95.5%的数据的误差处于[-1.0 m, 1.0 m],在图 15中大概有94.8%的数据的误差处于[0 m, 1.0 m],进一步表明了本文提出的基于虚拟边界场的二维IDM模型能够高精度地预测车辆驶离匝道的轨迹。
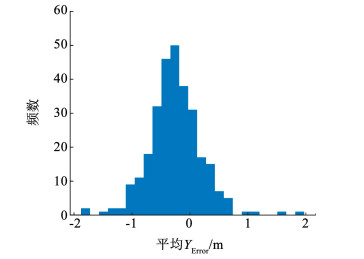
|
图 14 平均YError的频数分布直方图 Fig. 14 Frequency distribution histogram of the YError |
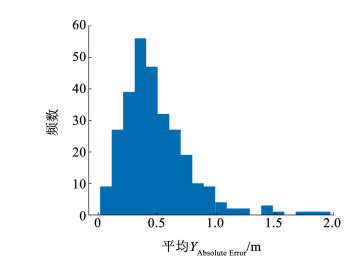
|
图 15 平均YAbsolute Error频数分布直方图 Fig. 15 Frequency distribution histogram of the YAbsolute Error |
为进一步验证模型预测的精度, 本文定义了广泛应用的精度评价指标:平均绝对误差(MAE)、均方误差(MSE)、均方根误差(RMSE)、平均绝对百分比误差(MAPE), 如式(14)所示。
| $\left\{\begin{array}{l} \text { MAE }=\frac{1}{m \cdot n} \sum\limits_{i=1}^n \sum\limits_{j=1}^m Y_{\text {Absolute Error }, j}^i \\ \text { MSE }=\frac{1}{m \cdot n} \sum\limits_{i=1}^n \sum\limits_{j=1}^m\left(Y_{\text {Error }, j}^i\right)^2 \\ \text { RMSE }=\sqrt{\frac{1}{m \cdot n} \sum\limits_{i=1}^n \sum\limits_{j=1}^m\left(Y_{\text {Error }, j}^i\right)^2} \\ \text { MAPE }=\frac{100 \%}{m \cdot n} \sum\limits_{i=1}^n \sum\limits_{j=1}^m\left(\frac{Y_{\text {Absolute Error }, j}^i}{Y_{\text {real }, j}^i}\right) \end{array}\right. $ | (14) |
其中:m表示数据集中的轨迹数;n表示每条轨迹的数据点个数;YError, ji表示第i条轨迹的第j实际轨迹点与预测轨迹点在Y方向上的差值;YAbsolute Error, ji表示第i条轨迹的第j实际轨迹点与预测轨迹点在Y方向上的绝对差值;Yreal, ji表示第i条轨迹的第j实际轨迹点在Y方向上的值。
利用模型分别随机选取30条Mirror-Traffic数据和45条NGSIM数据针对不同的时间尺度(短期、中期和中期)进行预测,利用式(14)分别计算预测评价指标,如表 1所示。在表 1中,30条Mirror数据的MAE、MSE、RMSE数值均小于1,此结果与前文图 14的直方分布图的结果相吻合,这充分说明了本文模型具有很高的精度。另外,45条NGSIM轨迹的计算结果也都在可接受的范围内,但是它们的值远大于Mirror的计算结果,主要是由于NGSIM数据在15年前采集,受限于当时的技术水平,所以NGSIM的数据噪音比较大,导致预测轨迹的误差相对比较大。
| 表 1 Mirror-Traffic和NGSIM数据不同时间尺度预测评价分析表 Tab. 1 Evaluation analysis of different time-scale trajectory prediction in Mirror-Traffic and NGSIM datasets |
针对两个数据集的时间特点,选取Mirror-Traffic数据和NGSIM数据中最长的车辆轨迹时间尺度作为参考(Mirror-Traffic: 13.16 s;NGSIM:99.2 s),分别用它们的20%、50%和70%作为短期、中期和长期的时间尺度,最终确定的3个时间尺度分别为3、6、9 s(Mirror-Traffic)和20、45、70 s(NGSIM)。从表 1中可以看到,针对这两个数据集,随着时间尺度不断增加,预测轨迹的误差也随之增加,但都在一定的范围内。
5 结论1) 针对现有的二维IDM模型的不足,提出了虚拟边界场方法,并将两者结合提出了基于虚拟边界场的二维IDM模型,从微观层面上分析了边界场在高速公路匝道处对车辆的作用。
2) 利用Mirror-Traffic和NGSIM开源数据集,通过仿真验证了模型的有效性,并对模型的一些关键参数进行标定,利用PSO算法求解出最优的边界场位置,并利用模型对出匝道车辆的轨迹进行预测,最后又进行了误差分析。
3) 研究成果能够描述传统车辆在匝道处混合交通流环境下的侧向和横向的二维运动,同时预测车辆的轨迹,也能够为自动驾驶车辆在混合交通流中的轨迹规划提供环境交通流预测信息。
4) 本文提出的模型是确定型模型。由于道路交通流存在相当大的随机性,因而,需要将随机性和二维运动模型相结合,构建的模型应能更符合实际;此外,车辆的运动轨迹由驾驶员操控车辆而形成,因此,需要进一步考虑车辆动力学特性。
| [1] |
王殿海, 金盛. 车辆跟驰行为建模的回顾与展望[J]. 中国公路学报, 2012, 25(1): 115. WANG Dianhai, JIN Sheng. Review and outlook of modeling of car following behaviour[J]. China Journal of Highway and Transport, 2012, 25(1): 115. |
| [2] |
TREIBER M, HENNECKE A, HELBING D. Congested traffic states in empirical observations and microscopic simulations[J]. Physical Review E, 2000, 62(2): 1805. DOI:10.1103/PhysRevE.62.1805 |
| [3] |
秦严严, 胡兴华, 李淑庆, 等. 智能网联环境下混合交通流稳定性解析[J]. 哈尔滨工业大学学报, 2021, 53(3): 152. QIN Yanyan, HU Xinghua, LI Shuqing, et al. Stability analysis of mixed traffic flow in connected and autonomous environment[J]. Journal of Harbin Institute of Technology, 2021, 53(3): 152. |
| [4] |
王昊, 秦严严. 网联车混合交通流渐进稳定性解析方法[J]. 哈尔滨工业大学学报, 2021, 51(3): 88. WANG Hao, QIN Yanyan. Asymptotic stability analysis of traffic flow mixed with connected vehicles[J]. Journal of Harbin Institute of Technology, 2021, 51(3): 88. |
| [5] |
HU Hongyu, LU Ziyang, QI Wang, et al. End-to-end automated lane-change maneuvering considering driving style using a deep deterministic policy gradient algorithm[J]. Sensors, 2020, 20(18): 5443. DOI:10.3390/s20185443 |
| [6] |
YANG Da, ZHENG Shiyu, WEN Cheng, et al. Adynamic lane-changing trajectory planning model for automated vehicles[J]. Transportation Part C: Emerging Technologies, 2018, 95: 228. DOI:10.1016/j.trc.2018.06.007 |
| [7] |
WANG Jinghua, ZHANG Zhao, LUO Guangquan. A bayesian inference based adaptive lane change prediction model[J]. Transportation Research Part C: Emerging Technologies, 2021, 132: 103363. DOI:10.1016/j.trc.2021.103363 |
| [8] |
DING Yang, ZHUANG Wenchao, WANG Liangmo, et al. Safe and optimal lane-change path planning for automated driving[J]. Proceedings of the Institution of Mechanical Engineers Part D: Journal of Automobile Engineering, 2021, 235(4): 1070. DOI:10.1177/0954407020913735 |
| [9] |
DELPIANO R, HERRERA J C, LAVAL J, et al. A two-dimensional car-following model for two-dimensional traffic flow problems[J]. Transportation Research Part C: Emerging Technologies, 2020, 114: 504. DOI:10.1016/j.trc.2020.02.025 |
| [10] |
XIONG Bangkai, JIANG Rui, TIANG Junfang. Improving two-dimensional intelligent driver models to overcome overly high deceleration in car-following[J]. Physica A: Statistical Mechanics and Its Applications, 2019, 534: 122313. DOI:10.1016/j.physa.2019.122313 |
| [11] |
SHARATH M N, VELAGA N R. Enhanced intelligent driver model for two-dimensional motion planning in mixed traffic[J]. Transportation Part C: Emerging Technologies, 2020, 120: 102780. DOI:10.1016/j.trc.2020.102780 |
| [12] |
ZONG Fang, WANG Meng, TANG Ming, et al. An improved intelligent driver model considering the information of multiple front and rear vehicles[J]. IEEE Access, 2021, 9: 66241. DOI:10.1109/ACCESS.2021.3072058 |
| [13] |
ALHARIQI A, GU Ziyuan, SABERI M. Calibration of the intelligent driver model (IDM) with adaptive parameters for mixed autonomy traffic using experimental trajectory data[J]. Transportmetrica B: Transport Dynamics, 2022, 10(1): 421. DOI:10.1080/21680566.2021.2007813 |
| [14] |
罗颖, 秦文虎. 基于IDM与RBFNN的组合型车辆低速跟驰模型[J]. 计算机应用研究, 2021, 37(8): 2354. LUO Ying, QIN Wenhu. Combination low-speed car-following model based on IDM and RBFNN[J]. Application Research of Computers, 2021, 37(8): 2354. |
| [15] |
李林恒, 甘婧, 曲栩, 等. 智能网联环境下基于安全势场理论的车辆换道模型[J]. 中国公路学报, 2021, 35(6): 184. LI Linheng, GAN Jing, QU Xu, et al. Lane-changing model based on safety potential field theory under the connected and automated vehicles environment[J]. China Journal of Highway and Transport, 2021, 35(6): 184. |
| [16] |
LI Linheng, JI Xinkai, GAN Jing, et al. A macroscopic model of heterogeneous traffic flow based on the safety potential field theory[J]. IEEE Access, 2021, 9: 7460. DOI:10.1109/ACCESS.2021.3049393 |
| [17] |
LI Linheng, JI Xinkai, GAN Jing, et al. Dynamic driving risk potential field model under the connected and automated vehicles environment and its application in car-following modeling[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 23(1): 122. DOI:10.1109/TITS.2020.3008284 |
| [18] |
RASEKHIPOUR Y, KHAJEPOUR A, CHENS K, et al. A potential field-based model predictive path-planning controller for autonomous road vehicles[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 18(5): 1255. DOI:10.1109/TITS.2016.2604240 |
| [19] |
LUO Yutao, DAI Jinkun, LI Hongluo. Research on intelligent decision based on compound traffic field[J]. International Journal of Automotive Technology, 2021, 22(4): 1023. DOI:10.1007/s12239-021-0092-5 |
| [20] |
KORZENIOWSKI D, SLASKI G. Method of planning a reference trajectory of a single lane change manoeuver with Bezier curve[C]//IOP Conference Series: Materials Science and Engineering. Bristol: IOP Publishing, 2016: 012012. DOI: 10.1088/1757-899X/148/1/012012
|
| [21] |
ZAKARIA W, RAMLI A, ALI J M. Bezier curves interpolation with end point constraints on road map[C]//AIP Conference Proceedings. Maryland: AIP Publishing LLC, 2019: 060060. DOI: 10.1063/1.5136492
|
| [22] |
WANG Lukun, ZHAO Xiaoying, SUN Hao, et al. Lane changing trajectory planning and tracking control for intelligent vehicle on curved road[J]. SpringerPlus, 2016, 5: 150. DOI:10.1186/s40064-016-2806-0 |
| [23] |
SUN Lifa, LI Kun, WANG Hao, et al. Phonetic posteriorgrams for many-to-one voice conversion without parallel data training[C]//2016 IEEE International Conference on Multimedia and Expo (ICME). Seattle: IEEE, 2016: 1. DOI: 10.1109/ICME.2016.7552917
|
| [24] |
BRATTON D, KENNEDY J. Defining a standard for particle swarm optimization[C]//2007 IEEE swarm intelligence symposium. Honolulu: IEEE, 2007: 120. DOI: 10.1109/SIS.2007.368035
|
 2023, Vol. 55
2023, Vol. 55


