2. 江苏省桥梁防撞系统工程技术研究中心,江苏 常州 201213
2. Jiangsu Province Bridge Collision Avoidance System Engineering Technology Research Center, Changzhou 201213, Jiangsu, China
近年来,中国经济的快速发展使得交通运输业需求增大,内河水运行业发展推动着船舶大型化和航道等级提升,但是水运行业繁忙也导致航道中船舶撞击桥梁事故频发并造成了严重的生命财产损失[1],船桥碰撞问题变得日益突出,亟待进一步研究。
船桥碰撞是一个在极短时间内由船舶结构、桥梁结构、桥梁防撞装置以及水的流体作用中发生巨大的能量转换的复杂的非线性动态响应过程。早期碰撞研究主要以船舶相互撞击和船舶撞击其他结构为主,研究形成的经典碰撞理论为后续的船桥碰撞研究奠定了理论基础。其中,Minorsky碰撞理论假定完全非弹性碰撞,通过附加质量模拟水流作用,应用动量定理和动能原理,由于假定的局限性且不考虑摩擦,应用范围受到限制[2]。Woisin碰撞理论在其基础上通过引入破损长度的概念进行修正,考虑能量及损耗进一步推动碰撞理论的发展[3-4]。Heins-Derucher理论和能量交换原理均采用能量守恒定理进行简单模型分析,其中能量交换原理考虑了简单桩土效应简化系统。该理论考虑了应力波传播,重点分析了碰撞时船桥响应,但对于大型防撞装置的设计过于保守[5-7]。在早期碰撞理论的基础上,各国在桥梁设计规范中加入桥梁防撞设计的内容。
为确保桥梁在运营阶段有足够的强度抵抗船舶撞击,各国规范通常在设计阶段均采用概率方式考虑船桥碰撞效应。按照中国的《公路桥梁抗撞设计规范》(JTG/T 3360-02—2020)规定,船舶撞击力作用在桥墩时,桥梁结构的内力、变形等响应按照等效静力法计算确定[8-9],该方法虽然简单,但在一定程度上可能产生较大的计算误差。现行规范中同时提出将动力学理论运用到桥梁结构撞击计算分析中,如强迫振动法、质点碰撞法等等,由此得到船撞效应结果更为合理。在使用质点碰撞法时,通常需要考虑规范规定的不同船舶撞击力-撞深曲线,采用有限元方法进行船撞力计算。此外,国内外学者也通过碰撞试验和有限元仿真对撞击力-撞深曲线进行了理论研究和验证。文献[10]利用圆柱形锤和直角尖端锤对缩尺驳船模型进行静态压缩试验和动态试验,试验结果表明,驳船船艏模型撞深与撞击力存在单调递增关系。文献[11]在已废弃的桥梁上进行驳船撞击实验,并量化分析实测得到的撞击力-驳船撞深变形。文献[12]基于船艏正撞刚性墙的有限元碰撞计算结果,提出撞击力-撞深关系的基本简化公式,即采用幂函数近似描述加载段撞击力-撞深关系,卸载段则采用直线关系近似描述。文献[13]建立考虑不同质量和速度的轮船撞击刚性墙有限元模型,将仿真得到的撞击力-撞深曲线量纲化,进而建立了撞击力-撞深曲线的概率统计模型。文献[14]建立船艏与刚性墙碰撞有限元模拟,分析船艏撞击力-撞深曲线整体与局部特征,并通过船桥碰撞实例验证。文献[15]进行了驳船船艏模型摆锤冲击试验,按照缩尺比1∶ 0.4制作缩尺驳船船艏模型并通过钢制框架固定于地基上作为被撞物,选取圆形与矩形两种截面形状的桥墩作为冲击锤头,开展累积撞击试验,验证船桥碰撞中桥墩形状对驳船船艏变形的影响,其研究中论证了小质量累次冲击试验与大质量单次冲击试验的一致性。国内外的上述研究工作已在船桥碰撞中撞击力-撞深曲线上取得一定进展。
目前船桥碰撞研究工作中,船舶撞击桥梁碰撞过程及撞击力-撞深模型是研究核心问题,足尺船艏模型碰撞试验成本高、难以实现,且船艏要达到更大变形时难以提供巨大的冲击能量,相关船桥碰撞试验较少。因此本文拟在大质量水平冲击试验装置的基础上,利用缩尺船艏模型和累积撞击等方式开展进一步的研究,以探讨船艏模型在发生大变形时撞击力-撞深问题。
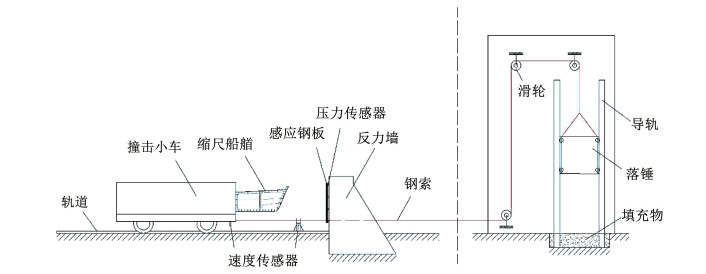
1 船艏碰撞试验 1.1 碰撞试验装置与试验方法为研究船艏在发生大变形时撞击力与撞深关系,并验证碰撞有限元数值模拟方法的正确性,基于江苏省桥梁防撞系统工程技术研究中心的大型碰撞试验装置开展了大质量水平冲击试验。该装置通过钢索和一系列定滑轮组将竖向装置和水平装置联动的方式,将常规竖向落锤装置与水平牵引碰撞装置相结合,实现垂直方向落锤下降带动水平方向的撞击加载,试验装置示意见图 1[16]。装置的最大落锤重量为2 t,最大提升高度30 m。撞击车自身重12 t,还可通过增加配重改变其质量,最大可达50 t。撞击车采用钢板、槽钢和工字钢整体焊接而成,撞击船艏模型通过高强螺栓与撞击车头部相连。通过控制落锤的提升高度,可调整模型车撞击试件时的水平速度。通过调整落锤的高度和撞击车的配重可获得撞击车的水平撞击动能。
|
图 1 碰撞试验装置示意 Fig. 1 Schematic of impact test setup |
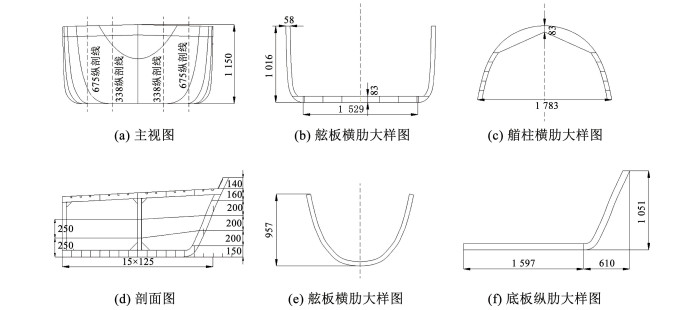
在上述试验装置提供的冲击能量下,仍难以完成一个足尺寸的复刻船艏模型碰撞试验,因此本文采用了缩尺船艏模型的方式进行碰撞试验。缩尺船艏碰撞试验的结果是否可靠取决于试验中模型能否比较真实地反映原型结构体系的实际工作状态。为了使模型试验的结果尽量真实地反映原型船头的结构特性,模型设计中考虑了模型与原型的相似性,根据试验的目的抓住主要相似因素。本文研究中选取长江航道中常见船舶等级为500 DWT的无球鼻艏船型,按照1∶ 10比例在几何尺度上进行缩放,试件所用材料与原型船保持一致,即采用Q235钢材,其余物理量相似关系见表 1。碰撞试验缩尺船艏模型设计图与实物图分别参见图 2与图 3。
| 表 1 缩尺船艏模型主要物理量相似关系 Tab. 1 Physical quantity similarity of the ship bow model |
|
图 2 缩尺船艏模型设计图(mm) Fig. 2 Details of the sizes of the ship bow model (mm) |

|
图 3 碰撞试验缩尺船艏模型实物照片 Fig. 3 Reduced-scale ship bow model of impact test |
考虑到缩尺船艏模型在碰撞过程中应与原型结构同样会受到动态屈曲和应变率效应的影响,结合有限元准静态压缩模拟结果,将船艏内部复杂龙骨和加劲肋构件中的角钢用带钢代替,降低了因长度缩尺带来的刚度增强影响。尽管通过建立缩尺船艏模型方式降低碰撞试验所需的撞击能量,仍难以通过一次碰撞试验来达到试验最终所需的撞深,在驳船船艏模型摆锤冲击试验中,通过累积冲击的方式以达到驳船船艏模型所需撞深,其研究中论证了小质量累次冲击试验与大质量单次冲击试验的一致性[15]。在本次碰撞试验中采用了4次连续累积的水平撞击荷载。
试验装置中钢索通过一系列定滑轮组将撞击车车头下部与落锤顶部相连。提升落锤到预定的高度后,释放落锤,钢索拉动撞击车向前运动,落锤的自由落体得到的重力势能转换为撞击车的水平撞击动能,从而实现水平撞击加载。在撞击车前端的缩尺船艏与刚性墙接触前,钢索与撞击车相互脱离。为减小撞击过程中的动能损失,模型车底部安装有4个车轮,车轮支撑在两条平行的水平导轨之上,为撞击车提供加速距离。
试验测试的主要内容包括:缩尺船艏与刚性墙的撞击速度,缩尺船艏与刚性墙间的撞击力的时程曲线。撞击速度测量采用光电门激光测速系统,当撞击车上的遮光板通过测速激光时,系统中会产生一个矩形脉冲电压信号,根据遮光板宽度和矩形脉冲电压信号的时间宽度可得撞击车的撞击速度。撞击力采用栓接在感应钢板和反力墙之间压电式压力传感器进行测量,通过实测电压信号的转换得到撞击力数据。
在碰撞试验开始前进行了缩尺船艏碰撞数值模拟,作为碰撞试验前期工作的一环。在碰撞试验完成后,通过在碰撞试验中测得到物理量对有限元仿真模型的试验条件进行修正,例如在碰撞试验中测得的撞击车实际碰撞速度,替代数值模拟中的冲击速度,通过对比碰撞试验和数值模拟结果,验证有限元仿真的模型和计算结果的正确性。
本次试验中,4次连续的水平撞击荷载及控制参数为相近的碰撞速度,撞击能量,以及落锤下降的高度,具体试验控制参数见表 2。
| 表 2 船艏碰撞试验控制参数 Tab. 2 Control parameters of impact test |
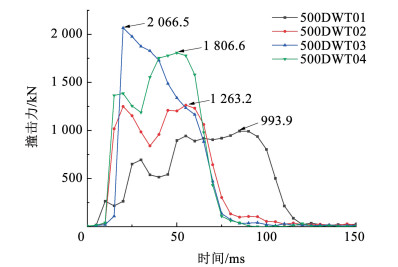
碰撞试验中通过设置在钢板后面的16个压力传感器实测得到电压信号,将其转换成压力数据并求出撞击力的合力。为去除数据中不相关的高频信号,采用低通滤波器技术,同时去除因初始传感器调零引起的负值数据。实测的撞击力时程曲线如图 4所示。
|
图 4 碰撞试验撞击力时程曲线 Fig. 4 Force time-history data of impact test |
从撞击力时程曲线中可以发现,尽管4次连续累积的水平撞击参数基本一致,但是撞击力曲线相差较大。随着撞击次数的不断累加,单次撞击力峰值逐步加大,分别为993.9、1 263.2、1 806.6、2 066.5 kN;碰撞时间逐步缩短,究其原因是累次撞击使得缩尺船艏模型塑性变形不断加大,引起船艏刚度不断增加。此外,4次碰撞试验的撞击力时程曲线中每一个局部峰值后的下降,都对应着缩尺船艏的内部结构中有新的局部构件参与变形耗能。
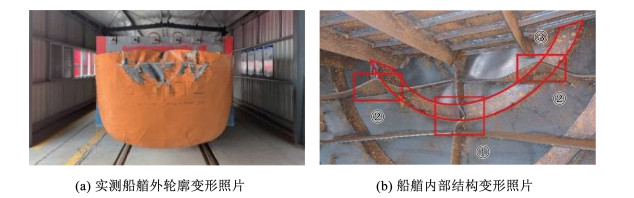
从图 5实测船艏变形状况可以看出,船艏外轮廓变形主要集中于前部,整体变形趋于平面,但在其局部结构中由于钢材屈曲出现凸凹不平。船艏对撞击力的抗力主要来自船艏的内部结构。从图 5(b)中可以看出,当船艏外轮廓发生变形时,主要涉及三部分结构发生变形:一是内部结构中的底板纵肋龙骨结构,即图中①所示位置;二是艏柱横肋发生变形,对应图中②所示位置;三是当船艏撞深达到一定深度时,圆环形③所示舷板横肋部分参与到变形中。每当船艏内部结构有新的构件参与变形都对应着船艏结构刚度的变化,继而引起撞击力发生变化。
|
图 5 500DWT01碰撞试验船艏变形情况 Fig. 5 Deformation pattern of ship bow following Test 500DWT01 |
本文采用通用非线性显式有限元软件LS-DYNA对缩尺船艏模型与刚性墙碰撞试验进行了数值模拟,并与碰撞试验结果进行比较分析,以检验数值模拟的正确性。根据船艏结构特征,船壳板厚度方向尺寸远小于其他方向尺寸,故采用壳单元建立船艏撞击模型。
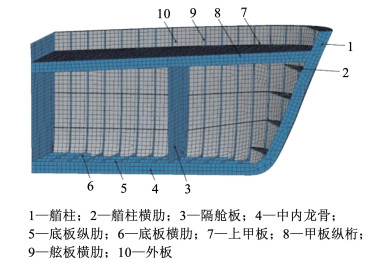
船艏结构是与刚性墙直接接触部位,船艏在船桥碰撞过程中会发生复杂的弹塑性变形,且在碰撞过程中一直存在相互接触和能量转换,船艏结构内部也会发生屈曲、压溃等破坏形式,因此需要建立多尺度和高精度的有限元模型。本文分析中的船艏网格尺寸取为15 mm,而船体中后部的船身结构远离撞击区域,采用了网格尺寸较大的刚性实体模拟船身结构,其网格尺寸为500 mm。船艏和船身之间通过过渡单元相连接。船舶结构与刚性墙共计29 490个单元,31 019个节点,其中缩尺船艏采用壳单元24 468个,节点26 094个。缩尺船艏有限元模型参见图 6。
|
图 6 缩尺船艏有限元模型 Fig. 6 Finite-element model of reduced-scale ship bow |
考虑缩尺船艏模型与原型结构同样受到动态屈曲和应变率效应的影响,缩尺船艏结构的Q235钢材采用了弹塑性材料本构模型,对应于LS-DYNA中的003号材料,并采用Cowper-Symonds公式作为船艏模型的本构关系,该本构的屈服应力公式[17]为
| $ \sigma_y=\left[1+\left(\frac{\dot{\varepsilon}}{C}\right)^{\frac{1}{P}}\right]\left(\sigma_0+\beta E_p \varepsilon_p^{\text {eff }}\right) $ | (1) |
式中:σy为考虑了应变率后材料的屈服强度;C、P为该本构的参数;
船艏钢材Q235的材料参数见表 3。缩尺船艏和刚性墙之间的接触以及缩尺船艏内部各构件之间的接触都采用基于罚函数界面摩擦的检测接触算法[18]。在碰撞有限元模型中设置3种接触模式: 一是缩尺船艏和刚性墙之间采用面面接触的形式;二是船艏内部加劲肋和外层钢壳的面面接触形式;三是考虑到本文缩尺船艏模型会出现因变形较大并导致内部加劲肋相互接触情况,对内部加劲肋也设置接触模式。前两种接触形式采用*CONTACT_SURFACE_TO_SURFACE的接触算法,第3种接触方式则采用*CONTACT_ SINGLE_SURFACE的接触算法[19]。
| 表 3 船艏钢材Q235材料参数 Tab. 3 Material parameters of Q235 used in reduced-scale ship bow |
对于缩尺500 DWT船艏模型,进行4次与试验条件相对应的有限元碰撞模拟计算。第一次模拟时,将缩尺船艏置于刚性墙前初始接触位置,并给定与试验测量值相等的初始碰撞速度(见表 1)。与刚性墙发生碰撞后,缩尺船艏模型逐渐产生塑性变形,每次碰撞模拟都以缩尺船艏速度达到零时,并开始反弹作为结束点。后续的有限元碰撞模拟,即在500 DWT02-500DWT04碰撞模拟中,采用LS-DYNA中的重启动功能。在重启动模拟中,缩尺船艏碰撞后产生的几何变形、单元应变和单元应力都由上一步的分析中计算得到,并作为下一次碰撞模拟的初始条件[19]。此外在每次重启动模拟之前,都将缩尺船艏置于刚性墙前接触点处,并重新赋予缩尺船艏与试验测量值对应的碰撞速度。
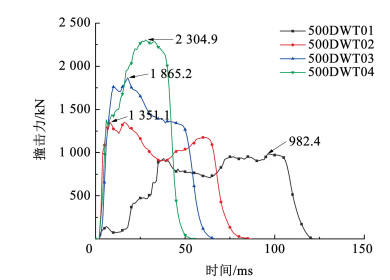
2.2.2 撞击力仿真结果通过缩尺船艏与刚性墙之间的传感器记录有限元碰撞模拟中的撞击力,且以撞击力降为零时表明缩尺船艏与刚性墙脱离接触并开始反弹,记录碰撞模拟结束时间点。4次有限元碰撞模拟的撞击力时程曲线如图 7所示。
|
图 7 有限元碰撞模拟撞击力时程曲线 Fig. 7 Force time-history data of finite element simulation |
从图 7中可以看出,与碰撞试验结果相一致,由于缩尺船艏中内部结构在碰撞过程中不断有新构件参与变形耗能,尽管4次连续累积的水平撞击荷载基本一致,但撞击力曲线相差较大,且随着撞击次数的不断累加,每次撞击力峰值逐步加大,依次为982.4、1 351.1、1 865.2、2 304.9 kN,而碰撞时间逐步缩短。
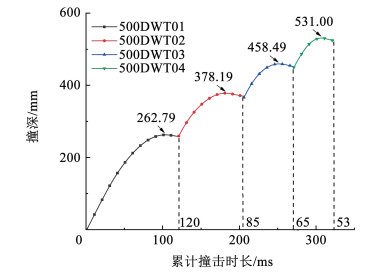
2.2.3 撞深仿真结果有限元仿真Mises应力及变形如图 8所示,通过记录船艏前部的节点群的位移,计算得到缩尺船艏撞深时程曲线,为便于观察,将缩尺船艏撞深曲线首尾相连绘制在同一图中,如图 9所示。

|
图 8 有限元碰撞模拟Mises应力云图 Fig. 8 Mises stress cloud of finite element simulation |
|
图 9 有限元碰撞模拟船艏撞深曲线 Fig. 9 Deformation time-history data of finite element simulation |
从图 9中可以看出,随着4次连续累积水平撞击荷载的加载,缩尺船艏模型的累积撞深逐步加大,依次达到262.79,378.19、458.49、531.00 mm,但每次撞深增量和碰撞时间均逐步减小。此外,缩尺船艏的每次撞深时程曲线趋势基本一致,前半段为增速不断减小的单调递增曲线,在达到峰值以后有略有回落,回弹是由于船艏模型在碰撞后钢材释放掉一部分弹性变形所致。
3 试验结果与有限元仿真的对比分析 3.1 撞击力对比分析对有限元碰撞模拟结果的后处理可得到4次累计碰撞试验的撞击力时程曲线,并与相对应的碰撞试验实测撞击力进行了对比,如图 10所示。

|
图 10 有限元仿真和试验测量的撞击力时程曲线对比图 Fig. 10 Comparison of simulated and experimental force time-history data |
由图 10可见,4次累计碰撞中有限元仿真和试验得到撞击力时程曲线基本一致,从而验证了有限元仿真的有效性。前3次有限元碰撞模拟得到撞击力时程曲线趋势与试验非常吻合,且最大撞击力相差较小。在第4次碰撞中,有限元仿真得到的撞击力峰值较试验值更大,且试验得到撞击力曲线在达到第一个峰值后有简短的回落。对比有限元仿真和试验的变形结果,发现回落为试验中缩尺船艏模型在第4次碰撞中舷板横肋和艏柱横肋焊接处发生断裂,吸收一部分能量并使得撞击力下降,而在有限元仿真中并没有考虑出现断裂情况。
3.2 撞击力-撞深曲线分析研究表明,碰撞试验和有限元仿真的撞击力时程曲线较为相似,包括撞击力峰值大小和碰撞持续时间,这表明缩尺船艏模型存在渐进性塑性破坏的特点。为进一步描述并可视化整个缩尺船艏模型碰撞过程,可通过记录500DWT01~500DWT04有限元仿真数据,形成一组单一系列的船艏模型撞深数据,将每次增量撞深数据相加,得到船艏累积撞深时程曲线,并同步到相对应的撞击力时程曲线。去掉曲线中卸载和重新加载部分,即可形成缩尺船艏模型整体的撞击力-撞深曲线。
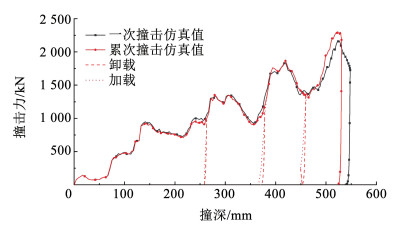
为验证4次连续累积水平撞击荷载的有效性,根据能量等效原则推算得到大质量缩尺船舶有限元碰撞模拟时碰撞速度为4.201 7 m/s,船舶大质量只需调整后半段船身材料容重即可,其余材料本构和接触方式设置与累次碰撞模拟保持一致,计算得到撞击力时程曲线与撞深曲线,形成一次撞击的缩尺船艏撞击力-撞深曲线与累次撞击的曲线绘于同一图中,如图 11所示。
|
图 11 缩尺船艏的撞击力-撞深曲线图 Fig. 11 Force-deformation relationship of reduced-scale ship bow |
由图 11可知,船艏的撞击力-撞深曲线整体呈逐步上升趋势,船艏结构在碰撞过程中随着撞深不断增加,撞击力也逐步增大。该曲线出现多个峰值,每次峰值表明船艏结构都有一组舷板横肋或艏柱横肋构件发生屈曲,参与变形耗能。同时,引起船艏接触刚度发生变化且撞击力-撞深曲线的斜率不断加大。对比一次撞击和累次撞击得到的撞击力-撞深曲线可以发现,船艏结构碰撞损伤深度与吸收的能量有基本确定的对应关系,小质量的碰撞曲线基本上属于大质量碰撞曲线的一部分。
参考《公路桥梁抗撞设计规范》(JTG/T 3360-02—2020)规定,将撞击力-撞深模型按下式进行无量纲化处理:
| $ \begin{aligned} F(\delta) & =\frac{E_0}{d_{\max }} \cdot f(\delta) \end{aligned} $ | (2) |
| $ \begin{aligned} \delta & =d / d_{\max } \end{aligned} $ | (3) |
式中:E0为初始动能;dmax为最大撞深;f(δ)为无量纲撞击力-撞深参数;δ为无量纲撞深,0≤δ≤1;d为撞深。
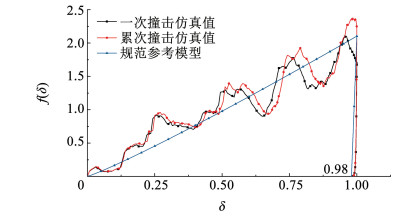
将一次撞击和累积撞击仿真得到的撞击力-撞深模型无量纲化,并与规范中附录D推荐的轮船无量纲撞击力-撞深模型进行比较,绘于图 12中。
|
图 12 无量纲撞击力-撞深模型 Fig. 12 Dimensionless force-deformation relationship model |
由上图 12可见,累次撞击下的无量纲撞击力-撞深曲线与一次撞击下相比存在滞后现象,且无量纲撞击力-撞深参数f(δ)峰值更高,这与图 11所示的撞击力-撞深曲线一致。规范附录中推荐的无量纲撞击力-撞深模型为分段函数模型,由一段幂函数和一段一次函数组成。仿真结果与规范参考模型相比,由于考虑缩尺船艏模型的内部结构,曲线存在起伏波动部分,而规范模型将不同船舶等级的船舶模型相统一以便于计算。此外规范模型中当撞深达到最大,即无量纲撞深值为1时,得到撞击力-撞深参数最大;但在仿真结果中存在撞击力-撞深参数达到峰值后,撞深仍存在小范围的增大现象。
4 结论本文基于缩尺船艏模型与刚性墙的碰撞试验和数值模拟,研究了船艏模型在发生弹塑性变形时撞击力与撞深关系,并得出以下结论:
1) 采用大质量水平冲击试验装置,对缩尺船艏模型进行4次连续、累积的水平撞击试验时,随着撞击次数的累加,单次撞击力峰值逐步加大,且碰撞时间逐渐缩短。试验结果表明, 累次撞击使得缩尺船艏模型塑性变形不断加大,引起船艏刚度不断增加。
2) 利用LS-DYNA软件对4次连续累积水平碰撞试验进行数值模拟,随着4次连续累积水平撞击荷载的施加,缩尺船艏模型的单次撞击力峰值和累积撞深均逐步加大,而每次撞深增量和碰撞时间均逐步减小。有限元模拟值与碰撞试验的结果吻合较好。
3) 为验证4次连续累积水平撞击荷载的有效性,调整船舶质量后进行一次碰撞数值模拟,对比撞击力-撞深曲线,可发现船艏结构碰撞损伤深度与吸收的能量有明显的对应关系,可认为小质量碰撞的碰撞力-撞深曲线基本上属于大质量碰撞曲线的一部分。
4) 将缩尺船艏模型的撞击力撞深曲线与规范参考模型对比分析,缩尺船艏模型考虑其内部结构非线性变形,撞击力撞深曲线存在起伏波动部分,而规范模型采用分段函数形式,将不同船舶等级的船舶模型相统一,以便于开展桥梁防撞设计计算。此外,与缩尺船艏模型不同,规范模型中撞击力-撞深参数与撞深同时达到峰值,在桥梁防撞设计计算中趋于保守。
| [1] |
项海帆, 范立础, 王君杰. 船撞桥设计理论的现状与需进一步研究的问题[J]. 同济大学学报(自然科学版), 2002, 30(4): 386. XIANG Haifan, FAN Lichu, WANG Junjie. Current status of ship-crash bridge design theory and issues for further research[J]. Journal of Tongji University (Natural Science Edition), 2002, 30(4): 386. |
| [2] |
MINORSKY V U. An analysis of ship collision with reference to protection of nuclear power ship[J]. Journal of Ship Research, 1959, 3(1): 1. DOI:10.5957/jsr.1959.3.1.1 |
| [3] |
WOISIN G. The collision tests of the GKSS[J]. Jahrbuch der Schiffbautechnischen Gesellschaft, 1976, 17(1): 465. |
| [4] |
WOISIN G. Ship-structural investigation for the safety of nuclear powered trading vessels[C]//International Seminar on Extreme Load Conditions and Limit Analysis Procedures for Structural Reactor Safeguards and Containment Structures. Berlin: [s. n. ], 1971: 225
|
| [5] |
DE RUCHER K N. Analysis of concrete bridge piers for vesselimpact[J]. Proceedings of Sino-American Symposium on Bridge and Structural Engineering, 1982(1): 13. |
| [6] |
DERUCHER K N. Bridge pile damage upon vessel impact[J]. Computers & Structures, 1984, 18(5): 931. |
| [7] |
DERUCHER K N. Proposed AASHTO standards for the design of bridge protectionsystem[J]. Civil Engineering for Practice and Design Engineering, 1982, 1(1): 131. |
| [8] |
中华人民共和国交通运输部. 公路桥梁抗撞设计规范: JTG/T 3360-02—2020[S]. 北京: 人民交通出版社, 2020 Ministry of Transport of the People's Republic of China. Design specification for highway bridge collision resistance: JTG/T 3360-02—2020[S]. Beijing: People's Traffic Publishing Press, 2020 |
| [9] |
FAN W, ZHOU G, YUAN W. Limitations and improvement thinking of code-prescribed static analysis method for vessel impact design of bridge structures[C]//The 3rd International Conference on Smart City and Systems Engineering (ICSCSE). Xiamen: ICSCSE, 2018: 42
|
| [10] |
MEIR-DORNBERG K E. Ship collisions, safety zones, and loading assumptions for structures in inland waterways[J]. VDI-Berichte, 1983, 496(1): 1. |
| [11] |
CONSOLAZIO G R, COWAN D R, BIGGS A, et al. Full-scale experimental measurement of barge impact loadson bridge piers[J]. Transportation Research Record Journal of the Transportation Research Board, 2005, 1936(1): 80. DOI:10.1177/0361198105193600110 |
| [12] |
孟德巍, 王君杰. 船艏正撞刚性墙力-撞深关系的简化公式研究[J]. 防灾减灾工程学报, 2011, 31(2): 160. MENG Dewei, WANG Junjie. A simplified formulation of the force-impact depth relationship for positive bow impact rigid walls[J]. Journal of Disaster Prevention and Mitigation Engineering, 2011, 31(2): 160. |
| [13] |
王君杰, 宋彦臣, 卜令涛. 船舶与桥墩撞击力-撞深关系概率模型[J]. 中国公路学报, 2014, 27(6): 59. WANG Junjie, SONG Yanchen, BU Lingtao. Probabilistic model of ship-bridge pier impact force-impact depth relationship[J]. Chinese Journal of Highways, 2014, 27(6): 59. |
| [14] |
FAN W, YUAN W. Ship bow force-deformation curves for ship-impact demand of bridges considering effect of pile-capdepth[J]. Shock and Vibration, 2014, 25(1): 1. |
| [15] |
KANTRALES G C, CONSOLAZIO G R, WAGNER D, et al. Experimental and analytical study of high-level barge deformation for barge-bridge collision design[J]. Journal of Bridge Engineering, 2016, 21(2): 04015039. |
| [16] |
曹家铖, 黄侨, 宋晓东, 等. 船桥碰撞中的船艏简化模型影响因素研究[C]//中国公路学会桥梁和结构工程分会2021年全国桥梁学术会议论文集. 北京: 中国公路学会桥梁和结构工程分会, 2021: 750 CAO Jiazheng, HUANG Qiao, SONG Xiaodong, et al. Study on the influencing factors of simplified model of ship bow in ship bridge collision[C]//Proceedings of the 2021 National Bridge Academic Conference of Bridge and Structural Engineering Branch of Chinese Highway Society. Beijing: Bridge and Structural Engineering Branch of Chinese Highway Society, 2021: 750 |
| [17] |
王君杰, 颜海泉, 钱铧. 基于碰撞仿真的桥梁船撞力规范公式的比较研究[J]. 公路交通科技, 2006, 23(2): 68. WANG Junjie, YAN Haiquan, QIAN Hua. Comparative study of bridge ship impact force specification formulae based on collision simulation[J]. Highway Traffic Science and Technology, 2006, 23(2): 68. |
| [18] |
ZHANG A, SUZUKI K. Numerical simulation the bottoms struc-tures grounding test by LS-DYNA[C]//The 5th European LS-DYNA Users Conference. Birmingham: Methods and Techniques Press, 2005
|
| [19] |
赵海鸥. LS-DYNA动力分析指南[M]. 北京: 兵器工业出版社, 2003. ZHAO Haiou. LS-DYNA power analysis guide[M]. Beijing: Weapon Industry Press, 2003. |
 2023, Vol. 55
2023, Vol. 55


