2. 中国市政工程西北设计研究院有限公司,兰州 730030;
3. 中国铁路设计集团有限公司,天津 300308
2. CSCEC AECOM Consultants Co., Ltd., Lanzhou 730030, China;
3. China Railway Design Corporation, Tianjin 300308, China
目前国内外研究学者对桥上无砟轨道在温度荷载、列车竖向荷载以及制动荷载作用下桥梁和无砟轨道相互作用有了深入的研究[1-3],对路基、简支梁上无砟轨道疲劳特性有了初步的探讨,相关研究成果对丰富无砟轨道理论和指导工程实践有一定的意义,如文献[4]建立了高速铁路简支梁桥上的纵连板式无砟轨道模型,考虑了无砟轨道混凝土裂缝的开裂和闭合效应等,对武汉、哈尔滨和广州地区气候条件下的无砟轨道结构寿命进行了预测;文献[5]基于车-桥耦合振动理论,建立了的64 m简支钢桁梁桥的车-桥动力学模型,分析了不同列车类型和行车速度对桥梁疲劳损伤的影响;文献[6]以CRTS Ⅰ型板式无砟轨道为研究对象,考虑了在列车荷载及环境温度共同作用下路基上无砟轨道结构的疲劳特性,得出在无砟轨道要求服役期间内,轨道板、底座板和凸形挡台几乎不会出现疲劳破坏,CA砂浆需要在服役期间加强养护;文献[7]研究了在典型软土地区中,轨道板在路基不均匀沉降、列车荷载及温度场作用下的损伤特性,指出路基不均匀沉降是造成轨道板损伤的关键性因素,并给出了路基不均匀沉降的限值;文献[8]借鉴复合材料界面损伤的研究方法,引入了内聚本构模型研究无砟轨道结构界面损伤,探讨了双线性、多项式及指数内聚本构模型的无砟轨道在温度梯度载荷下的界面损伤演化,结果表明对于无砟轨道界面损伤分析推荐使用指数内聚本构模型,而多项式内聚本构模型可以用来预测不对称损伤;文献[9]采用数字信号处理方法,将频率幅值分配随机相位,从大量实测列车荷载组合中筛选出了最不利的情况,基于该荷载工况,对轨道板的压缩损伤进行了评估,并给出了优化轨道板疲劳寿命的建议。
既有研究中对于无砟轨道的疲劳损伤研究多集中于路基或简支梁上,连续梁桥上无砟轨道系统疲劳损伤特性尚不明确。本文结合实验数据与相关经典文献,以昌景黄铁路上某(40+64+40)m连续梁为研究对象,采用有限元法建立了连续梁桥上CRTS双块式无砟轨道系统仿真模型。研究了列车静活载作用下桥梁、道床板、底座板及钢轨的动力响应特性与无缝线路纵向力分布规律,基于Miner准则和混凝土S-N曲线,分析了连续梁桥上无砟轨道结构疲劳特性。
1 连续梁桥上双块式无砟轨道系统仿真模型 1.1 无砟轨道结构钢轨采用CHN60轨,截面面积为77.45 cm2,对水平轴的惯性矩为3 217 cm4。扣件为WJ-8B型扣件,常阻力扣件的纵向变形-阻力关系表达式[10]为
| $ r_1=\left\{\begin{array}{l} 11.625 x, |x| \leqslant 2 \mathrm{~mm} \\ 23.25 \operatorname{sign} x, |x|>2 \mathrm{~mm} \end{array}\right. $ | (1) |
其中:r1为扣件纵向阻力,kN;x为钢轨相对承轨台的纵向位移,mm。
扣件横向变形-阻力关系的表达式为
| $ r_3=\left\{\begin{array}{l} 4.5 x, |x| \leqslant 2 \mathrm{~mm} \\ 9 \operatorname{sign} x, |x|>2 \mathrm{~mm} \end{array}\right. $ | (2) |
其中:r3为扣件横向阻力,kN;x为钢轨相对承轨台的横向位移,mm。
采用线性弹簧单元模拟垫板和弹条竖向刚度,扣件的竖向刚度取值为35 kN/mm。桥上CRTS双块式无砟轨道结构采用C40砼,道床板、底座板分块铺设。每块道床板和底座板之间有两个限位凹槽,限位凹槽四周均放置弹性垫板。道床板高度为260 mm、底座板高度为210 mm,长度×宽度均为5 940 mm×2 800 mm;道床板和底座板间设置弹性垫层,弹性垫层的纵、横向取为91 kN/mm[11],竖向刚度为0.1 N/mm3,采用只受压弹簧模拟竖向刚度;限位凹槽四周弹性垫板的刚度采用非线性弹簧模拟,顺桥向刚度取为14.3 kN/mm,横桥向刚度取为9.8 kN/mm,当道床板和底座板之间顺、横向相对位移超过弹性垫层厚度时,弹性垫层顺、横桥向刚度取为10 000 kN/mm;底座板和梁体之间通过剪力钉连接,采用刚度为10 000 kN/mm的弹簧模拟,使底座板和桥梁形成一个整体[12]。
1.2 桥梁结构简支梁梁体采用双线无砟轨道32 m预应力混凝土简支箱梁,如图 1所示。

|
图 1 简支箱梁横截面示意图(mm) Fig. 1 Schematic diagram of cross-section of simply supported box girder(mm) |
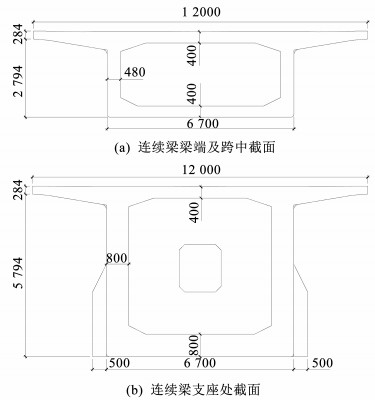
连续梁采用昌景黄铁路某(40+64+40)m连续梁,梁端、跨中及支座处梁截面,如图 2所示。根据梁端和支座处截面的截面属性,采用线性内插的方式模拟支座到连续梁跨中的渐变段截面属性。连续梁固定支座处桥墩纵向刚度取为1 000 kN/cm,简支梁固定支座处桥墩纵向刚度取为500 kN/cm[13]。
|
图 2 连续梁横截面示意图(mm) Fig. 2 Schematic diagram of continuous beam(mm) |
桥梁-双块式无砟轨道一体化空间分析模型充分考虑桥梁、支座、底座板、道床板、扣件和钢轨等构件及结构层间非线性约束,其中钢轨、道床板、底座板和桥梁用梁单元模拟,扣件、弹性垫层等连接方式采用非线性弹簧单元模拟,简支梁外侧两端考虑100 m的路基段,连续梁-无砟轨道系统有限元模型示意如图 3所示。

|
图 3 连续梁-无砟轨道系统模型示意图 Fig. 3 Diagram of continuous bridge-ballastless track system mode |
模型整体阻尼采用Rayleigh阻尼,阻尼比h取0.05,阻尼系数α和β分别为
| $ \alpha=2 h \frac{w_1 w_2}{w_1+w_2}, \beta=2 h \frac{1}{w_1+w_2} $ | (3) |
式中w1和w2为对结构竖向振型贡献最大的前2阶频率。
1.4 有限元模型验证本文采用鱼骨刺模型模拟简支梁和连续梁,利用刚臂模拟底座板和支座的空间位置,利用弹簧单元模拟桥梁、底座板、道床板和钢轨之间的约束。本文基于该建模方法建立了与UIC 774-3附录C.2[14]中单跨单线60 m简支梁一致的算例,计算伸缩力时按梁体升温35 ℃考虑;制动力按20 kN/m取值,满跨加载;挠曲作用下梁端发生转动,梁端上缘至桥台处纵向相对位移为8 mm,计算结果与UIC算例C.2进行对比,结果见表 1。
| 表 1 计算结果与UIC算例对比 Tab. 1 Comparison of calculated results and UIC case |
各计算结果与UIC算例较为吻合,其中挠曲力误差为4.72%,这是由于UIC采用的是解析算法,本文采用的是有限元方法,因此结果会产生一些误差,但该误差较小,证明本文所用的建模方法能正确模拟梁轨之间的相互作用,且本文计算出的钢轨纵向附加力符合大跨度桥上无缝线路纵向力的一般分布规律[15]。本文计算得出的在列车荷载作用下32 m简支梁跨中及钢轨最大位移分别为1.8 mm和0.8 mm,与文献[16]中32 m简支梁在列车荷载作用下简支梁跨中及钢轨最大位移分别为1.1 mm和0.7 mm相比偏大,这是因为参考文献中列车行车速度取值为250 km/h,而本文列车行车速度取值为350 km/h,由于计算结果受限于列车荷载取值、分析方法以及模型中各个构件的参数取值等因素的影响,总体上本文计算结果与参考文献中结果基本吻合。综上所述,本文所建立的连续梁-CRTS双块式无砟轨道模型是正确的。
2 连续梁上钢轨纵向附加力为研究大跨度连续梁轨相互作用规律,对连续梁-无砟轨道模型的纵向附加力进行计算,主要针对限制结构钢轨进行伸缩力、挠曲力和制动力的计算。根据铁路无缝线路设计规范[17],计算伸缩力时,梁体升温取为30 ℃;计算挠曲力时,由于集中荷载对附加力计算影响不大,因此只考虑竖向均布荷载,取为64 kN/m[15],加载长度根据列车重量除以均布荷载值得到,取为300 m;制动力率通常通过轮轨黏着系数计算,中国规范中常取为0.164,德国和UIC规范中规定的计算方法换算为轮轨黏着系数为0.25。为安全考虑,本文的黏着系数取0.25,计算制动力时,纵向荷载取为16 kN/m[15],加载长度取为300 m。挠曲、制动荷载示意如图 4所示。

|
图 4 荷载工况加载示意图 Fig. 4 Schematic diagram of loading under load cases |
根据以上计算工况,钢轨伸缩力、挠曲力和制动力包络如图 5所示。

|
图 5 钢轨结构应力包络图 Fig. 5 Stress envelope diagram of rail |
由图 5可知,桥上无砟轨道系统其钢轨结构伸缩压应力极大值约为143.1 MPa,位置位于简支梁和连续梁两端,拉应力极大值约为61.1 MPa,出现在简支梁和连续梁跨中;钢轨挠曲拉应力极值出现在简支梁和连续梁桥墩附近位置,最大值约为6.6 MPa,压应力极值出现在桥梁跨中附近位置,最大值约为5.0 MPa;钢轨制动力拉、压应力极值均出现在简支梁和连续梁桥墩附近位置,且简支梁处拉、压应力极值远大于连续梁处,最大拉应力为85.4 MPa,最大压应力为86.8 MPa。
3 桥上无砟轨道系统动力特性 3.1 交通荷载谱高速列车车辆主要为CRH系列高速列车,中国各铁路桥梁设计规范中没有规定相应的标准疲劳车,铁路桥梁设计规范[18]的中-活载已不适用于列车动载下结构疲劳强度设计与检算,动力计算采用CRH380B列车,列车行车速度取为350 km/h。
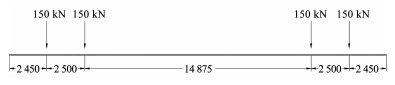
根据铁路轨道设计规范[19],轴重取1.5倍静荷载,高速列车交通荷载如图 6所示。考虑高速列车载客重量较小,动车和拖车重量基本一致,采用8节列车编组。
|
图 6 交通荷载谱(mm) Fig. 6 Traffic load spectrum(mm) |
选取典型截面,简支梁跨中、连续梁跨中处无砟轨道结构位移分别如图 7所示。

|
图 7 桥梁-无砟轨道系统动位移(mm) Fig. 7 Dynamic displacement of bridge-ballastless track system(mm) |
由图 7可知,在列车动载作用下,简支梁和连续梁跨中位置处钢轨、道床板最大位移基本相同,桥梁结构型式对轨道结构动位移影响较小。对于同一桥上轨道结构,钢轨、道床板竖向位移分别为0.8 mm和0.3 mm。由于连续梁跨度较简支梁大,相对较柔,因此连续梁跨中处竖向位移比简支梁跨中处大,连续梁跨中处最大竖向位移为3.1 mm,简支梁跨中处最大竖向位移为1.8 mm,增幅约72%。
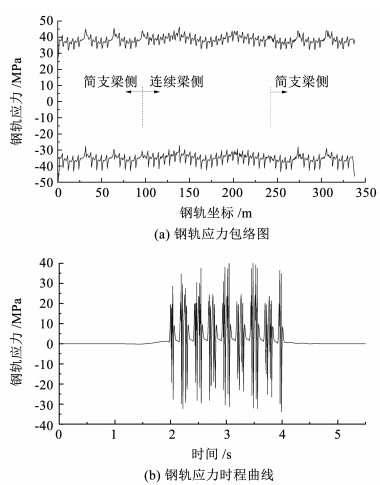
3.3 无砟轨道结构动应力列车动荷载作用下结构最不利跨中位置处钢轨应力曲线如图 8所示。
|
图 8 钢轨动应力 Fig. 8 Dynamic stress of rail |
由图 8可知,列车荷载作用下简支梁和连续梁上钢轨最大拉、压应力基本相同,分别为45.1 MPa和42.8 MPa。列车荷载作用使钢轨出现了8组规律基本相同的应力循环,最大拉、压应力分别为40.7 MPa和33.7 MPa。
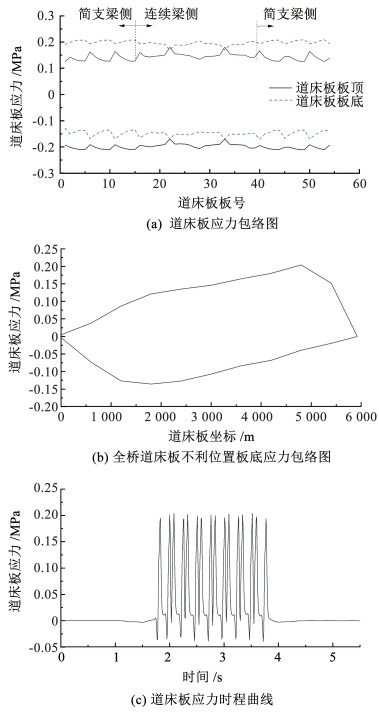
取每块道床板最易破坏处的进行分析,得到的54块道床板应力包络图、全桥道床板最不利位置处板底应力包络图以及典型位置处道床板应力时程曲线如图 9所示。
|
图 9 道床板动应力 Fig. 9 Dynamic stress of track plate |
由图 9可知,全桥范围内,道床板板底的最大拉应力大于板顶处,约0.22 MPa,压应力呈现相反规律,最大约0.21 MPa,由于混凝土抗拉强度较弱,道床板板底相对板顶受力状态更为不利。道床板分块铺设,因此在道床板两端应力为0 MPa,对于连续梁跨中位置处道床板,最大拉应力出现在道床板右侧限位凹槽附近,为0.22 MPa,最大压应力出现在道床板左侧限位凹槽附近,为0.13 MPa。列车荷载作用下道床板板底出现了8个应力循环,拉应力峰值基本相同,为0.22 MPa。
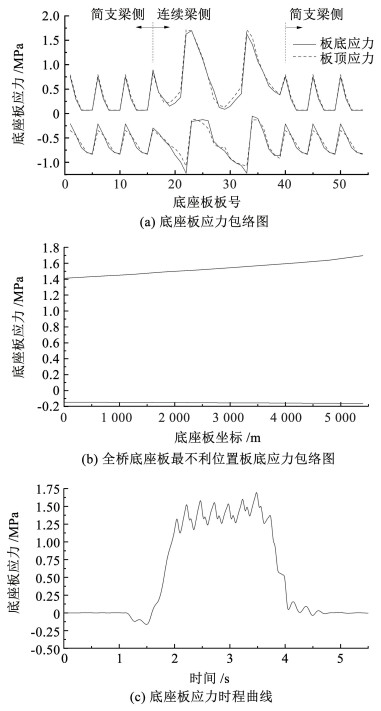
取每块底座板最易破坏处进行分析,得到的54块底座板应力包络图、全桥底座板受力最不利位置处板底应力包络图以及典型位置处底座板应力时程曲线如图 10所示。
|
图 10 底座板动应力 Fig. 10 Dynamic stress of baseplate |
由图 10可知,列车荷载作用下底座板板顶、板底的最大拉、压应力基本相同,分别为1.71 MPa和1.22 MPa,最大拉应力出现在连续梁主墩附近。列车荷载作用下连续梁跨中产生挠曲变形,使得其上底座板结构受压,因此桥梁跨中处底座板受到的压应力较大,拉应力较小。同时由于跨中桥梁的挠曲,使得桥墩附近梁体受拉,相应地其上底座板受拉应力较大,压应力较小。
4 桥上无砟轨道结构疲劳特性 4.1 结构疲劳寿命计算方法对于无砟轨道混凝土结构,通过雨流法可计算出列车荷载作用下其应力循环次数和应力幅值,结合Miner法则和材料的S-N曲线,可以得到在多级循环应力作用下结构的损伤,当损伤数总和达到某一临界值时(根据Miner法则,临界值通常取1),即满足D≥1时,便可判断结构发生了疲劳破坏
| $ D=\sum\limits_i D_i=\sum\limits_i \frac{n_i}{N_{i j}} $ | (4) |
式中:Di为在应力水平Si下的损伤数;ni为应力Si下试件的实际循环次数;Nij为应力Si下试件破坏时循环次数。
采用Tepfer混凝土结构单对数抗拉S-N疲劳方程:
| $ \frac{\sigma_{\max }}{f_{\mathrm{t}}}=1-b\left(1-\frac{\sigma_{\max }}{\sigma_{\min }}\right) \lg N $ | (5) |
式中:b为抗拉疲劳强度折减系数,b取为0.061 1[4];ft为混凝土静载作用下的轴心抗拉强度,在列车荷载作用下考虑到无砟轨道结构处于弯拉状态,混凝土弯拉强度约为轴拉强度的1.5~2倍[20],本文ft取1.5;σmax、σmix分别为混凝土应力的最大和最小值;N为混凝土疲劳寿命。
对于钢轨结构,采用日本铁道总研推导的60 kg/m钢轨焊接部位S-N曲线,即Miner组合法:
| $ S=a-b \lg N $ | (6) |
式中:S为钢轨弯曲应力幅值,MPa;N为钢轨达到失效所需的循环次数;系数a、b随着破坏概率而变化,根据文献[21]可知,当破坏概率为0.01%时,a取472.01,b取48.08。
4.2 无砟轨道结构疲劳寿命假定列车日通过量为220辆列车,计算可得全桥范围内钢轨疲劳寿命曲线以及每块道床板和底座板最不利位置处的疲劳寿命曲线,如图 11所示。

|
图 11 无砟轨道结构疲劳寿命 Fig. 11 Fatigue life of ballastless track structure |
由图 11可知,简支梁和连续梁上钢轨和道床板寿命曲线较为平滑,寿命基本相同,其中钢轨最不利位置处寿命为27.1 a,道床板在服役期内不会发生疲劳破坏。由于底座板通过剪力钉与梁面固结,其疲劳寿命与桥梁有关,桥梁跨中在列车荷载作用下弯曲,而其上的底座板由于弯压使得底座板的压应力较大、拉应力较小,因此跨中部分的底座板寿命较大。桥梁跨中的弯曲会导致桥墩附近桥梁拉长,从而使桥墩附近的底座板受拉,因此桥墩附近底座板寿命相较略小。桥梁跨中处底座板寿命较大,桥墩附近的底座板寿命相较略小,底座板在服役期内不会发生疲劳破坏。
相对于简支梁,连续梁跨度更大,结构体系性对较柔,在列车荷载作用下连续梁跨中的竖向位移比简支梁更大,因此连续梁主墩处底座板寿命小于简支梁桥墩处。
5 结论本文通过建立考虑了桥梁、支座、底座板、道床板、扣件和钢轨等构件及结构层间非线性约束的连续梁-CRTS双块式无砟轨道的一体化空间分析模型,研究了大跨度连续梁-无砟轨道系统梁轨相互作用规律,基于Miner准则和S-N曲线,得出了无砟轨道结构在列车荷载作用下的疲劳特性,主要结论如下:
1) 温度荷载作用下,钢轨压应力极值位于简支梁和连续梁两端,拉应力极值位于桥梁跨中;挠曲荷载作用下,钢轨拉应力极值位于简支梁和连续梁桥墩附近,压应力极值位于桥梁跨中;制动荷载作用下,钢轨拉、压应力极值均位于简支梁和连续梁桥墩附近。钢轨纵向力由温度荷载控制,最大应力为143.1 MPa,满足规范要求。
2) 列车动载作用下,简支梁和连续梁上钢轨最大拉、压应力基本相同,钢轨寿命曲线较为平滑,钢轨最易破坏处寿命为27.1 a。
3) 列车动载作用下,道床板板底最大拉应力大于板顶处,位于道床板右侧限位凹槽附近,全桥范围内最大动拉应力出现在连续梁跨中位置,道床板寿命曲线较为平滑,在服役期内道床板不会发生疲劳破坏。
4) 底座板最大动拉应力出现在连续梁主墩附近,且该处底座板结构最大拉、压应力基本相同。底座板寿命曲线与桥梁有关,寿命极小值出现在简支梁和连续梁桥墩附近,在服役期内底座板不会发生疲劳破坏。
| [1] |
戴公连, 葛浩, 邱远喜, 等. 高铁大跨度连续梁桥上无砟轨道断板受力研究[J]. 华中科技大学学报(自然科学版), 2015, 43(9): 100. DAI Gonglian, GE Hao, QIU Yuanxi, et al. Study on broken plate force of ballastless track on high-speed railway long-span continuous beam bridge[J]. Journal of Huazhong University of Science and Technology (Nature Science Edition), 2015, 43(9): 100. |
| [2] |
LI Yongle, SU Yang, XIA Feilong, et al. Vertical dynamic response of the ballastless track on long-span plate-truss cable-stayed bridges[J]. Science China-Technological Sciences, 2015, 58(2): 236. DOI:10.1007/s11431-014-5750-7 |
| [3] |
WENNER M, MARX S, KOCA M. Additional rail stresses due to long-term deformations of railway viaducts with ballastless track-model and reality[J]. Bautechnik, 2019, 96(9): 674. DOI:10.1002/bate.201900025 |
| [4] |
徐庆元, 林青腾, 方子匀, 等. 组合荷载下桥上纵连板式无砟轨道疲劳特性[J]. 中国铁道科学, 2017, 38(6): 37. XU Qingyuan, LIN Qingteng, FANG Ziyun, et al. Fatigue characteristics of longitudinally connected slab ballastless track on bridge under combined load[J]. China Railway Science, 2017, 38(6): 37. |
| [5] |
朱志辉, 冯乾朔, 龚威, 等. 考虑车-桥耦合的重载铁路钢桥局部疲劳分析[J]. 铁道工程学报, 2019, 36(9): 36. ZHU Zhihui, FENG Qianshuo, GONG Wei, et al. Local fatigue analysis of heavy-haul railway steel bridge based on train-bridge coupled vibration[J]. Journal of Railway Engineering Society, 2019, 36(9): 36. |
| [6] |
李思云, 杨荣山. CRTS-Ⅰ型板式无砟轨道疲劳寿命研究[J]. 铁道标准设计, 2016, 60(3): 34. LI Siyun, YANG Rongshan. Research on fatigue life of CRTS-Ⅰ slab ballastless track[J]. Railway Standary Design, 2016, 60(3): 34. |
| [7] |
SHAN Yao, WANG Binglong, ZHANG Jiawei, et al. The influence of dynamic loading and thermal conditions on tram track slab damage resulting from subgrade differential settlement[J]. Engineering Failure Analysis, 2021, 128: 105610. DOI:10.1016/j.engfailanal.2021.105610 |
| [8] |
ZHANG Jiawei, ZHU Shengyang, CAI Chengbiao, et al. Experimental and numerical analysis on concrete interface damage of ballastless track using different cohesive models[J]. Construction and Building Materials, 2021, 263: 120859. |
| [9] |
POVEDA E, RENA C, LANCHA J, et al. A numerical study on the fatigue life design of concrete slabs for railway tracks[J]. Engineering Structures, 2015, 100: 455. |
| [10] |
曲村. 高速铁路长大桥梁无砟轨道无缝线路设计理论及方法研究[D]. 北京: 北京交通大学, 2013: 42 QU Cun. Study on the design theory and method of ballastless continuous welded rail on long-span bridge in high-speed railway[D]. Beijing: Beijing Jiaotong University, 2013: 42 |
| [11] |
任娟娟. 桥上无砟轨道设计与维修理论[M]. 北京: 科学出版社, 2015: 79. REN Juanjuan. Structural design and maintenance theory of slab track on bridge[M]. Beijing: Science Press, 2015: 79. |
| [12] |
闫斌, 闫晗, 黄杰, 等. 高速铁路大跨斜拉桥上无砟轨道系统疲劳特性[J]. 铁道工程学报, 2020, 37(11): 44. YAN Bin, YAN Han, HUANG Jie, et al. Fatigue characteristics of ballastless track system on the long-span cable-stayed bridge of high-speed railway[J]. Journal of Railway Engineering Society, 2020, 37(11): 44. |
| [13] |
张鹏飞, 桂昊, 雷晓燕. 多跨简支梁桥上Ⅲ型板式无砟轨道制动力传递规律研究[J]. 铁道标准设计, 2019, 63(10): 12. ZHANG Pengfei, GUI Hao, LEI Xiaoyan. Dynamic transfer law of braking force for CRTS Ⅲ ballastless slab track on multi-span simply supported beam bridge[J]. Railway Standard Design, 2019, 63(10): 12. |
| [14] |
International Union of Railways. Track/bridge interaction recommendations for calculations: UIC 774-3[S]. Paris: International Union of Railways, 2001: 48
|
| [15] |
闫斌. 高速铁路中小跨度桥梁与轨道相互作用研究[D]. 长沙: 中南大学, 2013: 24 YAN Bin. Interaction between continuously welded rail and medium/small bridges of high-speed railway[D]. Changsha: Central South University, 2013: 24 |
| [16] |
翟婉明, 夏禾. 列车-轨道-桥梁动力相互作用理论与工程应用[M]. 北京: 科学出版社, 2011: 174. ZHAI Wanming, XIA He. Train-track-bridge dynamic interaction: theory and engineering application[M]. Beijing: Science Press, 2011: 174. |
| [17] |
中华人民共和国铁道部. 铁路无缝线路设计规范: TB 10015—2012[S]. 北京: 中国铁道出版社, 2013: 59 Ministry of Railways of the People's Republic of China. Code for design of railway continuous welded rail structures: TB 10015—2012[S]. Beijing: China Railway Publishing House, 2013: 59 |
| [18] |
国家铁路局. 铁路桥涵设计规范: TB 10002—2017[S]. 北京: 中国铁道出版社, 2017: 132 National Railway Administration of the People's Republic of China. Code fordesign on railway bridge and culvert: TB 10002—2017[S]. Beijing: China Railway Publishing House, 2017: 132 |
| [19] |
国家铁路局. 铁路轨道设计规范: TB 10082—2017[S]. 北京: 中国铁道出版社, 2017: 26 National Railway Administration of the People's Republic of China. Code for design of railway track: TB 10082—2017[S]. Beijing: China Railway Publishing House, 2017: 26 |
| [20] |
贡金鑫. 现代混凝土结构基本理论及应用[M]. 北京: 中国建筑工业出版社, 2009: 4. GONG Jinxin. Basic theory and application of modern concrete structure[M]. Beijing: China Architecture & Building Press, 2009: 4. |
| [21] |
刘建锋, 魏庆朝. 高速铁路钢轨疲劳寿命预测[J]. 铁道工程学报, 2000(2): 31. LIU Jianfeng, WEI Qingchao. Prediction of fatigue service life for rails of high-speed railway[J]. Journal of Railway Engineering Society, 2000(2): 31. |
 2023, Vol. 55
2023, Vol. 55


