2. 四川省公路规划勘察设计研究院有限公司,成都 610041
2. Sichuan Highway Planning, Survey, Design and Research Institute Ltd., Chengdu 610041, China
在高度城市化地区,桥梁施工带来的环境影响与交通中断,其所造成的直接或间接经济损失可能会超过结构本身的实际成本。为了缩短建设周期,先工厂预制再现场拼装的工业化建造技术被广泛用于桥梁建设中[1-5]。然而,由于构件在安装前已预制完成,故无法利用现场实测信息来修正不可避免的制造偏差和装配误差[6],进而可能引发装配失效。因此,能够适应并包容误差干扰的装配容差能力对预制装配结构尤为重要,成为提高其可施工性的主要途径[7]。
对具有复杂空间构型的城市地标性斜拉桥而言,工业化建造过程通常先在工厂预制主梁和桥塔节段,再采用现场拼装、顶推或转体等工艺快速就位成型,最后装配张拉斜拉索完成体系转换[8]。在多源不确定干扰下,该工序中作为装配接口构件的斜拉索,能否适应并包容主梁、桥塔两端不可避免的制造与定位误差[9-11],直接关系到现场装配进度,进而决定施工对城市环境和既有交通的影响程度。因此,量化评估不确定性并确定误差极端干扰下斜拉索装配的最大容差区间是桥梁工业化建造技术的重要内涵。
可靠性分析与优化设计(reliability-based design optimization, RBDO)的相关研究为上述不确定性问题的解决提供了可能。文献[12]针对地震作用与结构性能的随机性,将均匀设计与响应面方法相结合,对钢框架进行抗震可靠度分析;文献[13]对高大模板支架开展容错规划,以概率描述不确定干扰,并借助RBDO实现安全、适用、经济等设计目标;文献[14]进一步以区间变量描述材料参数和外荷载的不确定性,建立了概率-区间混合不确定下复合材料波纹板的RBDO模型。尽管上述研究能辅助不确定干扰下的决策过程,但寻优结果是一组确定值,只能提供标称设计参数,其能够适应并包容的不确定性范围是未知的,甚至在误差干扰最强烈的方向可能会严重破坏设计最优性及结构可靠性。
目前,针对这一难题的直接研究实属少见,但一些对称性研究为解决该问题带来了有益启发。文献[15]发展了一种考虑构件公差的区间优化方法,其中,区间中点与半径同时视为设计变量;文献[16]提出基于双层嵌套寻优策略的火炮动力响应区间优化方法,兼顾了结构鲁棒性和区间经济性;文献[17]针对具有显式功能函数表达的复合材料加劲板,建立了考虑区间边界影响的可靠性约束优化框架。然而,不同于上述研究中的构件或简单系统,真实的斜拉桥工业化建造过程中复杂结构响应的预测仍依赖于隐式的全过程非线性有限元;而在反演寻优过程中反复调用有限元分析(finite element analysis, FEA),将不可避免地面临路径冗长、耗时过高,进而不可工程实用的难题。
解决上述问题的一种可行思路是借助机器学习方法来减少有限元调用次数。文献[18]将代理模型技术与蒙特卡洛模拟(Monte-Carlo simulation, MCS)相结合,建立了直立锁缝屋面系统的抗风揭可靠度分析模型;文献[19]开发了一种基于元启发式算法的过滤策略,大幅减少了大规模结构优化过程中约束函数评估次数;文献[20]在斜拉桥施工索力调整时引入多层感知深度学习方法,建立了目标响应与索力调整量之间的准确映射关系。
因此,本文以可靠度区间下界(即最不利可靠度指标)量化施工误差的极端干扰,提出一种基于机器学习的斜拉索装配容差区间反演方法,旨在从相互耦合的多项结构性能指标中按需提取容差能力:构建了基于可靠性约束下多目标优化过程的反演模型,求解装配可调参量的最大容差区间;开发了基于主动学习克里金(active-learning Kriging, AL-Kriging)模型与遗传算法优化BP神经网络(genetic algorithm optimized back propagation neural networks, GA-BPNN)的最不利可靠度解耦式评估算法,显著降低了结构非线性响应预测、可靠度边界计算与多层嵌套寻优所带来的巨大算力消耗。
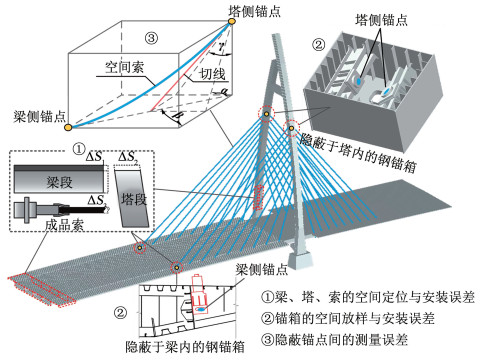
1 斜拉索的装配容差区间反演模型在考虑多源不确定性的典型斜拉桥工业化建造场景下,作为接口构件的斜拉索,在装配过程中不可避免地面临着施工误差干扰,如图 1所示。如何量化其能适应的最大误差范围,以提升装配过程抑制干扰的能力,是提升斜拉桥工业化建造的可施工性、避免部件返工和进度延误的重要举措。
|
图 1 复杂空间构型斜拉桥的斜拉索装配误差 Fig. 1 Assembly error of cable-stayed bridge with complex spatial configurations |
与传统RBDO不同,本文建立的区间反演模型以斜拉索的施工张拉力区间为装配可调参量,其中不确定区间中点和半径同时视为优化变量;同时,设计一非负无量纲指标W来反映所有设计变量的总不确定度,将其作为独立寻优目标整合入反演模型,并以多个目标与约束函数来描述结构各项性能指标,旨在实现设计目标的最优性、结构性能的可靠性、建造过程的可施工性三者之间的平衡。其中,设计变量为
| $ \boldsymbol{D}^{\mathrm{I}}=\left[d_1^{\mathrm{I}}, \cdots, d_i^{\mathrm{I}}, \cdots, d_{n_{\mathrm{D}}}^{\mathrm{I}}\right]^{\mathrm{T}} $ | (1) |
式中
目标函数:
| $ \min \left(-f_j\left(\boldsymbol{X}, \boldsymbol{Y}^{\mathrm{I}}, \boldsymbol{D}^{\mathrm{I}}\right)\right), j=1, 2, \cdots, l $ | (2) |
| $ \min (-W) $ | (3) |
约束条件:
| $ \beta^{\mathrm{L}}\left(\boldsymbol{X}, \boldsymbol{Y}^{\mathrm{I}}, \boldsymbol{D}^{\mathrm{I}}\right) \geqslant \beta^A $ | (4) |
| $ \boldsymbol{D}^{\mathrm{L}} \leqslant \boldsymbol{D}^{\mathrm{I}} \leqslant \boldsymbol{D}^{\mathrm{U}} $ | (5) |
式中:DI为nD对待优化斜拉索的施工张拉力;DU与DL构成设计域上下界。引入区间数学思想[21],视张拉力为区间数,采用区间中点dic与区间半径diw来描述,从而将设计变量总维度扩展为2nD;fj(X, YI, DI), j=1, 2, …, l,描述了装配过程中l个待达成的性能目标,W则反映了可施工性。显然,由于随机干扰向量X、区间干扰向量YI、区间设计向量DI的存在,可靠度指标β并非一定值,而是在[βL, βR]内波动,本文以其下界βL建立最不利可靠度约束来量化极端干扰,并保证其大于容许值βA。
无量纲指标W表达式[15]为
| $ W=\sqrt[n_{\mathrm{D}}]{\prod\nolimits_{k=1}^{n_{\mathrm{D}}} \frac{d_k^{\mathrm{w}}}{d_k^{\mathrm{c}}}} $ | (6) |
上节所述的装配容差区间反演模型,在计算最不利可靠度指标时将形成“外层多目标优化→中层可靠性分析→内层极值响应求解”的三重嵌套寻优格式;此外,对于需要基于大量非线性结构响应预测来执行密集可靠度计算的斜拉桥工业化建造过程,反复隐式有限元调用所导致的计算代价将十分昂贵而不可行。因此,突破上述瓶颈的关键是如何高效预测概率-区间联合表征下的最不利可靠度指标βL。
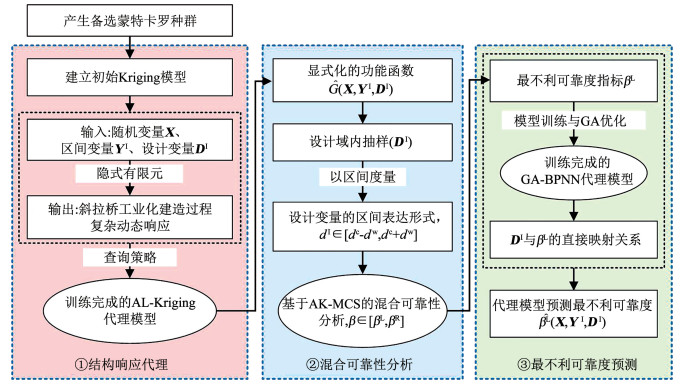
2.1 最不利可靠度的解耦式求解框架为解决上述难题,本文首先借助AL-Kriging模型显式化非线性响应,再以GA-BPNN建立设计变量与最不利可靠度指标的直接映射关系,以双层代理模型实现三重嵌套问题的层层解耦。流程如图 2所示,主要包括以下4个步骤:
|
图 2 基于机器学习的最不利可靠度解耦式求解框架 Fig. 2 Machine learning-based decoupling framework for calculating worst-case reliability index |
步骤1 立基于抗力R与效应S关系的功能函数G=R-S,通过有限元分析计算效应S。
步骤2 建立AL-Kriging模型仅在局部(即极限状态超平面G(X, YI, DI) = 0附近)逼近功能函数。
步骤3 引入设计变量的区间特性,以区间中点dic和区间半径diw度量;在设计域内抽样,对于每一组抽出的设计变量样本DI,计算对应的最不利可靠度指标βL。
步骤4 以步骤3中计算结果为训练样本,建立GA-BPNN模型实现DI与βL的直接映射,约束函数转化为
| $ \hat{\beta}^{\mathrm{L}}\left(\boldsymbol{X}, \boldsymbol{Y}^{\mathrm{I}}, \boldsymbol{D}^{\mathrm{I}}\right) \geqslant \beta^A $ | (7) |
式中
真实的斜拉桥工业化建造是具有非线性时滞特性的动态过程,为其复杂的结构响应快速构建代理模型,需要保证训练样本的优质性。这就要求不仅根据已有信息来预测未知点的动态和趋势,还需要获得预测误差来评价训练样本价值,以减少不必要采样次数、提高采样效率。为此,本文将Kriging模型与基于池的主动学习策略相结合,凭借高效的查询策略来构建“逐步逼近”机制,形成基于学习函数U的AL-Kriging结构响应代理模型。主要步骤如下:
步骤1 确定初始的实验设计(design of experiment, DoE):由拉丁超立方抽样(Latin hypercube sampling, LHS)方法在不确定空间抽取初始样本并计算对应的功能函数值G。
步骤2 生成备选蒙特卡罗样本集:对于随机变量,根据其概率分布抽样;对于区间变量,在上下界内均匀抽样;此外,备选样本数目应足够大,以遍布整个不确定空间。
步骤3 根据DoE建立Kriging模型,上述过程在MATLAB DACE工具箱中进行。
步骤4 Kriging模型预测并识别高价值样本:计算备选蒙特卡罗样本集中所有点的预测值与方差,根据下式[22]计算U值并定位Umin所对应的优质样本x*,即
| $ U(x)=\frac{\left|\mu_{\hat{G}}(x)\right|}{\sigma_{\hat{G}}(x)} $ | (8) |
| $ x^*=\arg \min\limits _x U(x) $ | (9) |
式中:x为未知点的输入值,
步骤5 判断收敛条件。当满足Umin≥2,即对于蒙特卡罗样本集内所有点,都有Φ[U(x)]≥0.977,这保证了功能函数符号的预测正确率高于97.7%,可认为模型精度已满足要求,迭代停止;否则,继续下一步。
步骤6 更新DoE。计算x*对应的功能函数值G,并添加至DoE,返回步骤3。
2.3 基于GA-BPNN的最不利可靠度预测模型上述训练完成的AL-Kriging模型实现了结构响应的精确预测,避免了非线性有限元的反复调用。即便如此,概率-区间混合不确定下的最不利可靠度预测仍然是一个双环嵌套搜索过程[23],仍然不可避免地面临着计算资源消耗高、求解耗时过长的问题。
为此,本文借助非线性拟合能力强的BPNN,搭建设计变量DI与最不利可靠度指标βL的直接映射关系;同时,为了降低由于网络参数定义不当而引起的拟合误差[24],将遗传算法应用于网络构建过程,形成GA-BPNN框架来寻优最佳网络参数。步骤如下:
步骤1 获得网络训练样本。抽取设计变量样本DI,采用基于AK-MCS的混合可靠性分析方法[23]求解每组样本对应的最不利可靠度指标βL。
步骤2 网络初始化。建立3层神经网络,隐藏层神经元采用S型传递函数,输出层神经元采用线性传递函数。其他网络超参数如隐藏神经元的数量、学习率等,首先由经验确定,然后通过后续试算调整。
步骤3 GA优化网络。以遗传种群中每个个体对应一组网络参数,将网络预测误差平方和Esum作为个体适应度,通过选择、交叉、变异操作,完成网络参数的寻优过程:
步骤4 训练并测试网络。根据步骤3中获得的最优网络阈值与权值建立网络,并对其进行训练和测试。本文将预测的最大相对误差Emax与拟合优度R2作为网络性能的衡量指标,其表达式分别为
| $ E_{\max }=\max \frac{\hat{y}_i-y_i}{\hat{y}_i}\square $ | (10) |
| $ R^2=1-\frac{\sum\nolimits_{i=1}^k\left(\hat{y}_i-y_i\right)^2}{\sum\nolimits_{i=1}^k\left(\bar{y}-y_i\right)^2} $ | (11) |
式中:
考虑外荷载F1、F2、P、T共同作用下的悬臂管结构,该结构的几何尺寸与受载情况如图 3所示,图中L1、L2、θ1、θ2描述了外力作用位置。采用上述区间反演模型对其进行尺寸优化,以验证本文方法的准确性与高效性。各不确定参数统计特性与功能函数表达同文献[25]。作为一典型算例,文献[17, 23, 26]均对该结构进行了可靠性研究。
此处引入容差思想来充分考虑管件的制造误差,将管厚t、直径d及其容差区间视为设计变量,以区间中点tc, dc和半径tw, dw描述。显然,当区间半径取0时,即退化为传统的RBDO问题,其表达式为
| $ \boldsymbol{D}^{\mathrm{I}}=\left[t^{\mathrm{I}}, d^{\mathrm{I}}\right]^{\mathrm{T}} $ | (12) |
式中:
以悬臂管体积V与容差指标W建立目标函数:
| $ \min V=\pi\left(d^{\mathrm{c}}-t^{\mathrm{c}}\right) t L_1 $ | (13) |
| $ \min -W $ | (14) |
约束条件:
| $ \hat{\beta}^{\mathrm{L}} \geqslant \beta^{\mathrm{A}} $ | (15) |
| $ t^{\mathrm{c}} \in[3, 6], d^{\mathrm{c}} \in[38, 46] $ | (16) |
| $ t^{\mathrm{w}} \in[0, 0.5], d^{\mathrm{w}} \in[0, 2] $ | (17) |
式中约束可靠度指标βA取3.0。
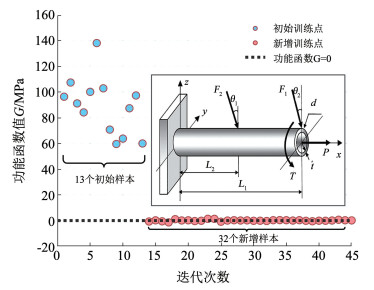
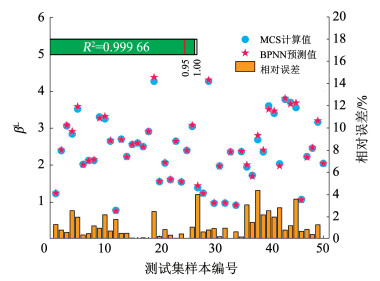
按本文思路,首先构建AL-Kriging模型代理结构的功能函数,如图 3所示,初始DoE包含13个训练样本,仅经过32次迭代便可获得满足精度需求的AL-Kriging模型,显然,由查询策略选择的新增训练点多位于极限状态(G=0)附近,将其加入DoE可以显著提升模型的可靠度预测精度,从而大幅提高了采样效率。接着,以GA-BPNN直接映射最不利可靠度指标,图 4展示了该代理模型在50个测试样本处的预测效果,其拟合优度R2达到0.999 66,最大误差仅为4.38%,表现出很高的预测精度。
|
图 3 AL-Kriging模型的DoE分布 Fig. 3 DoE distribution of AL-Kriging model |
|
图 4 最不利可靠度βL的GA-BPNN模型精度验证 Fig. 4 Accuracy verification of GA-BPNN model for worst-case reliability index βL |
在上述代理模型协助下,采用NSGA-Ⅱ算法执行区间反演过程,部分反演结果列于表 1。可见,随着容差能力提高,悬臂管的体积也有所增大,二者存在一定的冲突特性。同时注意到,反演所得悬臂管尺寸参数不再是确定值,而是一个区间数。
| 表 1 悬臂管算例的部分Pareto解集 Tab. 1 Partial Pareto solutions of the cantilever tube |
表 2对比了本文与文献[17, 25]方法在设计点[5, 0, 42, 0]处的最不利可靠度指标计算结果。对比表明,本文方法能在较少次调用功能函数的同时实现较高的可靠度预测精度。
| 表 2 最不利可靠度的求解精度与效率对比 Tab. 2 Comparison of calculation accuracy and efficiency for worst-case reliability index |
选择表 1中第2个结果为最优解,表 3对比了本文方法与文献[16]嵌套寻优方法以及传统无容差能力的多重嵌套RBDO方法的寻优结果。对比表明,容差设计后的平均体积虽然略有增加,但为构件的制造提供了较大的安全冗余,可见在保证结构可靠性和设计最优性的前提下,区间反演量化了构件的最大容差能力。耗时方面,对于该数值算例,传统RBDO过程求解需要4 479 min,文献[16]方法由于解耦不完全,也达到了615 min,这对于需要集成大量有限元分析的复杂工程问题是无法接受的;相比而言,本文方法174 min的耗时非常少,能够实用于复杂的斜拉桥工业化建造过程。
| 表 3 不同求解方法的寻优结果与耗时对比 Tab. 3 Comparison of optimal results and calculation time using different methods |
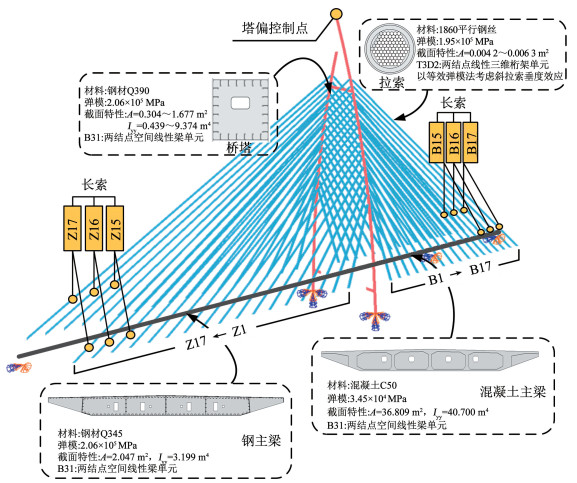
某跨径为151.1 m+91.1 m的空间索面独塔斜拉桥,采用弧形变截面钢箱桥塔和STC轻型钢混组合梁;全桥34对拉索呈空间非对称布置。该桥的立面布置如图 5所示,其工业化建造流程为:工厂预制钢梁、钢塔节段和斜拉索;现场拼接顶推主梁就位,同步吊装拼接主塔;张拉斜拉索完成体系转换,拆除主梁临时支架;二期铺装施工。由于跨径较小,本文采用简单的等效弹模法来近似模拟斜拉索的非线性力学行为,建立考虑施工阶段的有限元模型如图 6所示。为了保障先预制后装配的工业化建造流程顺利实施,避免因多源不确定性干扰下的施工误差延误现场装配工期,采用本文方法为体系转换制定斜拉索装配容差策略,并通过与传统的标称策略比较,分析装配容差能力的重要性和实用性。

|
图 5 算例斜拉桥的立面布置 Fig. 5 Elevation layout of the cable-stayed bridge in case study |
|
图 6 算例斜拉桥的非线性有限元模型 Fig. 6 Nonlinear finite element model of the cable-stayed bridge in case study |
以Z15、Z16、Z17、B15、B16、B17这6对长索的施工张拉力区间DI为装配可调参量,其区间中点和半径同为优化变量。设计3个目标函数:
| $ \begin{matrix} \text{find} & {{\boldsymbol{D}}^{\text{I}}}={{\left[ d_{1}^{\text{I}},d_{2}^{\text{I}},\cdots ,d_{6}^{\text{I}} \right]}^{\text{T}}},d_{i}^{\text{I}}\in \left[ d_{i}^{\text{c}}-d_{i}^{\text{w}},d_{i}^{\text{c}}+d_{i}^{\text{w}} \right],i=1,2,\cdots ,6 \\ \text{obj}\text{.} & {{{\hat{f}}}_{1}}=\min \{\max (\Delta Z)\} \\ {} & {{f}_{2}}=\min \square \sum\nolimits_{i=1}^{6}{\left( \left| d_{i}^{\text{c}}-d_{i}^{*} \right|+\max \left( \left| d_{i}^{\text{c}}-d_{i}^{\text{w}}-d_{i}^{*} \right|,\left| d_{i}^{\text{c}}+d_{i}^{\text{w}}-d_{i}^{*} \right| \right) \right)}\square \\ {} & {{f}_{3}}=\min \{-W\} \\ \text{s}\text{.t}\text{.} & {{{\hat{\beta }}}^{\text{L}}}\ge {{\beta }^{\text{A}}} \\ {} & d_{i}^{\text{c}}\in \left[ 0.95d_{i}^{*},1.05d_{i}^{*} \right],d_{i}^{\text{w}}\in \left[ 0,0.10d_{i}^{*} \right] \\ \end{matrix} $ | (18) |
式中:
| $ G\left(\boldsymbol{X}, \boldsymbol{D}^{\mathrm{I}}\right)=a^{\mathrm{A}}-a\left(\boldsymbol{X}, \boldsymbol{D}^{\mathrm{I}}\right) $ | (19) |
式中:参考其他学者的研究[28-32],用随机变量X表示不确定性干扰下的斜拉索张拉力,认为其服从正态分布,其变异系数统一取2%,部分代表性斜拉索的概率统计特性列于表 4;aA为塔顶最大容许偏位,根据《公路斜拉桥设计规范》[33],取30 mm;a(X, DI)为塔顶实际位移,当超过限值时则失效,这在施工过程中是不允许的。
| 表 4 部分斜拉索的张拉力概率分布特性 Tab. 4 Probability distributions of partial cable tensions |
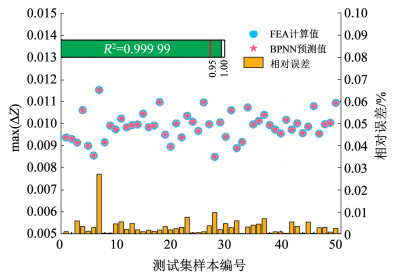
采用本文方法,通过代理模型拟合上述无显式表达的目标与约束函数。对于
|
图 7
目标函数 |
|
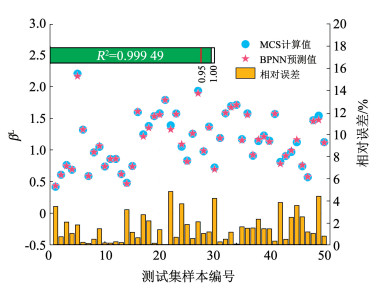
图 8
最不利可靠度 |
以NSGA-Ⅱ算法驱动求解式,图 9展示了所得的Pareto前沿,选取其中有代表性的8个策略列于表 5。显然,不同设计目标存在一定冲突,即伴随着容差能力(f3)的提高,设计最优性(

|
图 9 张拉力区间反演的Pareto前沿 Fig. 9 Pareto fronts of interval inversion for cable tensions |
| 表 5 部分反演结果的Pareto前沿 Tab. 5 Pareto fronts of partial inversion results |
以策略S8#为例,表 6表明,不同于传统方法只能给出标称值,本文方法同时明确了张拉力控制值和抗误差干扰区间;显然,将不确定性合理量化后,在保障结构可靠性和设计最优性的前提下,斜拉索B17能包容的张拉力偏差量较小,为217.4 kN,相应的张拉长度容差量为2.1 cm;而斜拉索Z15能包容的张拉力偏差量最大,为317.3 kN,相应的张拉长度容差量为4.9 cm;斜拉索Z15~Z17与B15~B17的抗误差干扰率在7.29%~12.98%之间。其中,容差量采用
| 表 6 策略S8#张拉力与张拉长度的容差区间 Tab. 6 Fault-tolerant interval of cable tensions and stretching lengths for strategy S8# |
可见,当斜拉索的装配容差能力被量化明确后,误差干扰下现场张拉过程的兼容性和控制能力都将有效提升,避免了现场进度延误甚至返工。同时,以上述区间中点为最优控制值,对目标斜拉索进行张拉调控后,将实际成桥索力与合理成桥状态索力的偏差情况列于表 7。两表对比可见,本文的容差控制策略在尽量包容施工误差干扰的同时,有效限制了成桥后索力与预期值的偏离程度(本例中最大为4%,出现在Z17处,满足《公路斜拉桥设计规范》[33]中±5%的要求),这保证了成桥后最优的塔梁线形及索力均匀性等目标。此外,本文方法还提供了多组可行的Pareto解集,决策者可以根据现场施工管理精度和技术控制水平来择优选择。
| 表 7 策略S8#的容差控制后索力与合理成桥索力对比 Tab. 7 Comparison between fault-tolerant cable force in strategy S8# and cable force of reasonable finished bridge |
为了应对施工误差干扰,区别于确定标称值的传统方法,本文提出一种基于机器学习的斜拉索装配容差区间反演方法,高效精确地量化了斜拉索抗误差干扰的装配容差性能。验证算例和工程应用结果表明:
1) 本文为传统标称优化策略提供了有益补充,在保证结构可靠性和设计最优性的前提下,不仅提供了目标斜拉索的最优张拉力控制值,还明确了容差区间。经容差反演,斜拉索Z15~Z17与B15~B17能包容的张拉力偏差量为217.4~317.3 kN,其抗误差干扰率达到7.29%~12.98%。以上述容差区间指导现场施工决策,对误差累积有更好的包容性,提升了斜拉桥工业化建造过程的可施工性。
2) 本文采用AL-Kriging模型显式化斜拉桥工业化建造过程的复杂动态响应,并借助GA-BPNN模型直接映射误差干扰下的结构最不利可靠度指标。通过机器学习克服了传统多重嵌套搜索架构引起的巨量算力消耗难题,推进了桥梁等大型复杂结构分析与控制的实用化。
3) 通过与现有的精确非线性分析理论与建模方法相结合,本文的区间反演策略可满足对大跨缆索承重桥梁进行施工容错控制的迫切需求。
4) 本文为预制装配工艺提供了一套抗误差干扰的容差控制策略,有助于提高工业化建造过程的施工韧性。在未来的研究中,该方法可推广于各类并行工程的建造容差控制,以及复杂结构系统的容错设计。
| [1] |
石雪飞, 刘志权, 胡可, 等. 全体外预应力节段预制拼装连续梁桥承载能力足尺模型试验[J]. 中国公路学报, 2018, 31(12): 163. SHI Xuefei, LIU Zhiquan, HU Ke, et al. Full-scale test of bearing capacity of a complete external prestressed segmental precast continuous girder bridge[J]. China Journal of Highway and Transport, 2018, 31(12): 163. DOI:10.3969/j.issn.1001-7372.2018.12.016 |
| [2] |
徐亚洲, 王志鹏, 谢启芳, 等. 螺纹钢法兰连接预制装配桥墩抗震性能研究[J]. 土木工程学报, 2021, 54(5): 65. XU Yazhou, WANG Zhipeng, XIE Qifang, et al. Research on seismic performance of fabricated assemble bridge piers connected with screw thread steel bar and flange[J]. China Civil Engineering Journal, 2021, 54(5): 65. DOI:10.15951/j.tmgcxb.2021.05.007 |
| [3] |
TAZARV M, SAⅡDI M S. UHPC-filled duct connections for accelerated bridge construction of RC columns in high seismic zones[J]. Engineering Structures, 2015, 99(15): 413. DOI:10.1016/j.engstruct.2015.05.018 |
| [4] |
KIM D, KWAK Y, SOHN H. Accelerated cable-stayed bridge construction using terrestrial laser scanning[J]. Automation in Construction, 2020, 117: 103269. DOI:10.1016/j.autcon.2020.103269 |
| [5] |
胡志坚, 姚鹏飞, 周知. 预制拼装混凝土桥梁连接钢筋粘结锚固性能[J]. 哈尔滨工业大学学报, 2021, 53(3): 82. HU Zhijian, YAO Pengfei, ZHOU Zhi. Bonding and anchoring properties of connecting steel bars of prefabricated concrete bridges[J]. Journal of Harbin Institute of Technology, 2021, 53(3): 82. DOI:10.11918/202002060 |
| [6] |
周凌宇, 郑恒. 基于坐标变换的短线预制梁段匹配误差调整[J]. 桥梁建设, 2016, 46(5): 71. ZHOU Lingyu, ZHENG Heng. Matching error adjustment of girder segments precast by short line match method based on coordinate transformation[J]. Bridge Construction, 2016, 46(5): 71. |
| [7] |
WANG Xiaoming, WANG Huan, SUN Yuan, et al. Fault-tolerant interval inversion for accelerated bridge construction based on geometric nonlinear redundancy of cable system[J]. Automation in Construction, 2022, 134: 104093. DOI:10.1016/j.autcon.2021.104093 |
| [8] |
LOZANO-GALANT J A, PAYÁ-ZAFORTEZA I, XU D, et al. Analysis of the construction process of cable-stayed bridges built on temporary supports[J]. Engineering Structures, 2012, 40: 95. DOI:10.1016/j.engstruct.2012.02.005 |
| [9] |
崔巍, 傅新军, 陈相, 等. 商合杭铁路芜湖长江公铁大桥2号墩桥塔钢锚梁定位测量技术[J]. 桥梁建设, 2020, 50(2): 110. CUI Wei, FU Xinjun, CHEN Xiang, et al. Positioning and measuring techniques for steel anchor beams in pylon at pier No.2 of Wuhu Changjiang River Rail-cum-Road Bridge on Shangqiu-Hefei-Hangzhou Railway[J]. Bridge Construction, 2020, 50(2): 110. |
| [10] |
郝超. 大跨度钢斜拉桥施工误差调整方法研究[J]. 浙江大学学报(工学版), 2003, 37(3): 54. HAO Chao. Study on construction error adjustment method of long-span steel cable-stayed bridge[J]. Journal of Zhejiang University (Engineering Science), 2003, 37(3): 54. |
| [11] |
杜蓬娟, 张哲, 黄才良. 斜拉桥成桥后误差调整的优化方法[J]. 哈尔滨工业大学学报, 2005, 37(7): 1016. DU Pengjuan, ZHANG Zhe, HUANG Cailiang. Optimization method of error adjustment of cable stayed bridge in finished state[J]. Journal of Harbin Institute of Technology, 2005, 37(7): 1016. DOI:10.3321/j.issn:0367-6234.2005.07.048 |
| [12] |
吕大刚, 贾明明, 李刚. 基于均匀设计响应面法的钢框架结构抗震可靠度分析[J]. 哈尔滨工业大学学报, 2011, 43(4): 1. LÜ Dagang, JIA Mingming, LI Gang. Seismic reliability analysis of steel frame structures based on uniform design response surface method[J]. Journal of Harbin Institute of Technology, 2011, 43(4): 1. DOI:10.11918/j.issn.0367-6234.2011.04.001 |
| [13] |
谢楠, 赵凯, 胡杭, 等. 高大模板支架的容错优化设计研究[J]. 工程力学, 2018, 35(增刊1): 101. XIE Nan, ZHAO Kai, HU Hang, et al. Error-tolerant optimization design of high false work[J]. Engineering Mechanics, 2018, 35(Sup.1): 101. DOI:10.6052/j.issn.1000-4750.2017.05.S018 |
| [14] |
郑宇宁, 邱志平, 苑凯华. 复合材料波纹板在剪切载荷下的屈曲特性分析与可靠性优化[J]. 振动与冲击, 2016, 35(19): 7. ZHENG Yuning, QIU Zhiping, YUAN Kaihua. Buckling performance analysis and reliability optimization of composite corrugated plates under shear loading[J]. Journal of Vibration and Shock, 2016, 35(19): 7. DOI:10.13465/j.cnki.jvs.2016.19.002 |
| [15] |
JIANG Chao, XIE H C, ZHANG Z G, et al. A new interval optimization method considering tolerance design[J]. Engineering Optimization, 2015, 47(12): 1637. DOI:10.1080/0305215X.2014.982632 |
| [16] |
WANG Liqun, YANG Guolai, XIAO Hui, et al. Interval optimization for structural dynamic responses of an artillery system under Uncertainty[J]. Engineering Optimization, 2020, 52(2): 343. DOI:10.1080/0305215X.2019.1590563 |
| [17] |
LIU Yan, JEONG H K, COLLETTE M. Efficient optimization of reliability-constrained structural design problems including interval uncertainty[J]. Computers & Structures, 2016, 177: 1. DOI:10.1016/j.compstruc.2016.08.004 |
| [18] |
李正良, 王成, 王涛, 等. 基于主动学习Kriging模型的直立锁缝屋面系统抗风揭可靠度分析[J]. 工程力学, 2021, 39(10): 9. LI Zhengliang, WANG Cheng, WANG Tao, et al. Reliability analysis of wind-resistance of standing seam roof system based on active learning Kriging model[J]. Engineering Mechanics, 2021, 39(10): 9. DOI:10.6052/j.issn.1000-4750.2021.06.0430 |
| [19] |
CAO Hongyou, QIAN Xudong, ZHOU Yunlai. Large-scale structural optimization using metaheuristic algorithms with elitism and a filter strategy[J]. Structural and Multidisciplinary Optimization, 2018, 57(2): 799. DOI:10.1007/s00158-017-1784-3 |
| [20] |
单德山, 张潇, 顾晓宇, 等. 基于多层感知深度学习的大跨度斜拉桥索力调整[J]. 桥梁建设, 2021, 51(1): 14. SHAN Deshan, ZHANG Xiao, GU Xiaoyu, et al. Cable force adjustment for long-span cable-stayed bridge based on multilayer perceptron deep learning[J]. Bridge Construction, 2021, 51(1): 14. DOI:10.3969/j.issn.1003-4722.2021.01.003 |
| [21] |
姜潮, 韩旭, 谢慧超. 区间不确定性优化设计理论[M]. 北京: 科学出版社, 2017: 24. JIANG Chao, HAN Xu, XIE Huichao. Theory and method of interval uncertain optimal design[M]. Beijing: China Science Press, 2017: 24. |
| [22] |
ECHARD B, GAYTON N, LEMAIRE M. AK-MCS: an active learning reliability method combining Kriging and Monte Carlo simulation[J]. Structural Safety, 2011, 33(2): 145. DOI:10.1016/j.strusafe.2011.01.002 |
| [23] |
YANG Xufeng, LIU Yongshou, GAO Yi, et al. An active learning kriging model for hybrid reliability analysis with both random and interval variables[J]. Structural and Multidisciplinary Optimization, 2015, 51(5): 1003. DOI:10.1007/s00158-014-1189-5 |
| [24] |
CHATTERJEE S, BANDOPADHYAY S. Reliability estimation using a genetic algorithm-based artificial neural network: an application to a load-haul-dump machine[J]. Expert Systems with Applications, 2012, 39(12): 10943. DOI:10.1016/j.eswa.2012.03.030 |
| [25] |
DU Xiaoping. Interval reliability analysis[C]//International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Las Vegas: ASME, 2007: 1103
|
| [26] |
ZHANG Xufang, WU Zhenguang, MA Hui, et al. An effective Kriging-based approximation for structural reliability analysis with random and interval variables[J]. Structural and Multidisciplinary Optimization, 2021, 63(10): 2473. DOI:10.1007/s00158-020-02825-8 |
| [27] |
WANG Xiaoming, WU Wentao, LIU Yan, et al. Surrogate-assisted two-phase tensioning strategy optimization for the system transformation process of a cable-stayed bridge[J]. Engineering Optimization, 2019, 52(4): 615. DOI:10.1080/0305215X.2019.1610947 |
| [28] |
陈兆栓. 预应力混凝土斜拉桥施工监控概率方法研究[D]. 广州: 华南理工大学, 2012 CHEN Zhaoshuan. Rearch on probabilistic method of construction monitoring and control of prestressed concrete cable-stayed bridges[D]. Guangzhou: South China University of Technology, 2012 |
| [29] |
梁鹏. 超大跨度斜拉桥几何非线性及随机模拟分析[D]. 上海: 同济大学, 2004 LIANG Peng. Geometric nonlinear and stochastic simulation analysis of super long span cable-stayed bridge[D]. Shanghai: Tongji University, 2004 |
| [30] |
梁鹏, 肖汝诚, 徐岳. 超大跨度斜拉桥施工过程随机模拟分析[J]. 中国公路学报, 2006, 19(4): 54. LIANG Peng, XIAO Rucheng, XU Yue. Random simulation analysis of construction process for super-long-span cable-stayed bridges[J]. China Journal of Highway and Transport, 2006, 19(4): 54. DOI:10.3321/j.issn:1001-7372.2006.04.010 |
| [31] |
王立彬, 李爱群, 靳慧. 考虑索力随机的斜拉桥结构分析[J]. 中国公路学报, 2010, 23(4): 45. WANG Libin, LI Aiqun, JIN Hui. Structural analysis of cable-stayed bridge under random cable force[J]. China Journal of Highway and Transport, 2010, 23(4): 45. DOI:10.19721/j.cnki.1001-7372.2010.04.008 |
| [32] |
孙宗光, 陈一飞, 邵元. 基于概率统计的运营状态下索力变异性分析与评价[J]. 桥梁建设, 2018, 48(3): 79. SUN Zongguang, CHEN Yifei, SHAO Yuan. Analysis and evaluation of stay cable tension variability of operation conditions based on probability and statistics[J]. Bridge Construction, 2018, 48(3): 79. DOI:10.3969/j.issn.1003-4722.2018.03.015 |
| [33] |
中华人民共和国交通部. 公路斜拉桥设计规范: JTG/T 3365-01—2020[S]. 北京: 人民交通出版社, 2020 Ministry of Transport of the People's Republic of China. Specifications for design of highway cable-stayed bridge: JTG/T 3365-01—2020[S]. Beijing: China Conmunications Press, 2020 |
 2023, Vol. 55
2023, Vol. 55


