2. 长安大学 建筑工程学院,西安 710061;
3. 中铁工程设计咨询集团郑州设计院,郑州 450000
2. School of Civil Engineering, Chang′an University, Xi′an 710061, China;
3. China Railway Engineering Design and Consulting Group Co., Ltd., Zhengzhou 450000, China
钢筋混凝土结构经常带裂缝工作,导致混凝土内部钢筋更加容易遭受锈蚀,从而影响结构的耐久性和安全性[1-2]。纤维增强复材筋(fiber reinforced polymer bars,FRP筋)具有轻质、高强、耐腐蚀和易加工等优点,因此,FRP筋被普遍认为可以代替普通钢筋服役[3-4]。另外,鉴于玄武岩纤维增强复材筋(basalt fiber reinforced polymer bars,BFRP筋)与其他FRP筋相比更加环保且制作成本低,BFRP筋已逐渐成为其他种类FRP筋的替代品[5-6]。BFRP筋的弹性模量较低,其配筋结构在服役时平均裂缝宽度远大于普通钢筋混凝土,同时BFRP筋的本构关系为线弹性,没有屈服点,导致BFRP筋增强混凝土梁呈现脆性破坏的特征,缺少安全性能[7]。因此,有必要采用高延性的混凝土改善FRP筋混凝土结构的脆性特性。
聚乙烯醇纤维增强工程水泥基复合材料(polyvinyl alcohol fiber reinforced engineered cementitious composites,PVA-ECC)具有高延性、多裂缝发展特性和微小裂缝宽度优点[8]。PVA-ECC代替普通混凝土可以有效弥补BFRP筋与混凝土复合结构裂缝多且宽度大的缺陷。鉴于PVA-ECC多裂缝发展和BFRP筋抗拉强度高等特性,采用PVA-ECC与BFRP筋复合结构,可以将两种材料的优势互补,解决传统钢筋混凝土结构易开裂且耐久性差的缺陷,同时可以提高结构的延性,提高结构抗震性能[9]。工程结构中,为保证PVA-ECC与BFRP筋之间协同工作,两者之间必需有足够的黏结强度。若PVA-ECC与BFRP筋的黏结强度不足,则结构将缺乏足够的承载力,影响结构安全性。因此,研究PVA-ECC与BFRP筋之间的黏结性能尤为重要。
FRP筋与PVA-ECC黏结滑移性能不同于钢筋与普通混凝土,不少学者对FRP筋与ECC的黏结性能开展了研究。Zhao等[10]研究了ECC与玻璃纤维增强复材筋(glass fiber reinforced polymer bars,GFRP筋)、碳纤维增强复材筋(carbon fiber reinforced polymer bars,CFRP筋)和普通钢筋的黏结性能,结果表明,黏结强度与ECC强度成比例增加,高肋钢筋比低肋钢筋表现出更高的黏结强度。吴丽丽等[11]研究了GFRP筋与ECC的黏结性能,结果表明,增加GFRP筋表面复杂程度,或增加ECC的强度、基体保护层厚度,有助于提高两者的黏结强度。Li等[12]在加固钢筋混凝土梁试验研究中发现,与BFRP筋增强聚合物砂浆加固梁相比,BFRP筋增强ECC基体加固梁具有更高的屈服强度和极限荷载。Hossain等[13]通过GFRP筋与ECC和普通混凝土拔出试验研究发现,ECC黏结强度高于普通混凝土,高弹性模量GFRP筋黏结强度低于低弹性模量GFRP筋。
综上,PVA-ECC与FRP筋结构相比传统钢筋混凝土结构具有非常显著的优势,但是目前关于PVA-ECC与FRP筋的黏结性能研究多集中于其他FRP筋。因此,需要进一步研究PVA-ECC与BFRP筋之间的黏结性能和黏结滑移本构模型。本文考虑BFRP筋表面形式、直径、锚固长度和PVA-ECC保护层厚度、强度5个因素,制作了28个PVA-ECC与BFRP筋的黏结锚固试件进行拔出试验,分析其破坏形态和破坏特征,揭示PVA-ECC与BFRP筋黏结破坏机理,探讨各因素对PVA-ECC与BFRP筋黏结性能影响规律,建立PVA-ECC与BFRP筋的黏结滑移本构模型。
1 试验 1.1 试验材料 1.1.1 BFRP筋试验采用的BFRP筋由树脂和玄武岩纤维通过拉挤成型工艺制成,且喷砂BFRP筋经过人工表面喷砂处理,具体BFRP筋参数及实测力学性能见表 1。其中,BFRP筋直径包括肋高,B表示缠绕带肋BFRP筋,BS表示喷砂缠绕带肋BFRP筋。BFRP筋表面形式如图 1所示,无喷砂BFRP筋表面光滑,喷砂BFRP筋表面粗糙,不同直径筋材的肋高有所不同,但相对肋高(肋高/直径)均约为6.7%。
| 表 1 BFRP筋的物理力学性能参数 Tab. 1 Physical and mechanical properties of BFRP bars |

|
图 1 BFRP筋表面特性 Fig. 1 Surface characteristics of BFRP bars |
本试验采用的PVA-ECC强度等级为C50和C80,配合比见表 2,两种强度的PVA-ECC均采用聚乙烯醇纤维,且纤维体积率均为2%。按照JC/T 2461—2018《高延性纤维增强水泥基复合材料力学性能试验方法》[14]进行了PVA-ECC的单轴拉伸试验和立方体抗压试验。PVA-ECC拉伸强度超过了4.5 MPa,极限拉伸应变超过3%。两种类型PVA-ECC的实测抗压强度为50.5 MPa和81.7 MPa。
| 表 2 PVA-ECC配合比 Tab. 2 PVA-ECC Mixture proportions |
为探究PVA-ECC与BFRP筋黏结性能的影响因素,设置锚固长度(5d、7d、9d,d表示筋材直径)、直径(8、10、12 mm)及PVA-ECC强度(C50、C80)、保护层厚度(70、25、15、5 mm)为变量,对28个PVA-ECC与BFRP筋拔出试件开展试验。试验参考《混凝土结构试验方法标准》(GB/T 50152—2012)[15]和ACI 440.3R-04规范[16],采用边长为150 mm的单向拔出立方体试件。根据锚固长度的不同,将BFRP筋截取为500 mm并划分成黏结段、非黏结段、外伸段。锚固长度即筋材在PVA-ECC中黏结段的长度。其中,非黏结段BFRP筋表面缠绕胶布并套上PVC管,防止PVA-ECC浆体进入PVC管中产生黏结应力影响试验结果。由于BFRP筋属于各向异性材料,抗剪强度低,因此,在BFRP筋外伸段套上无缝钢管,采用环氧树脂填充使二者黏结可靠,避免试验机夹具对BFRP筋端部造成剪切破坏,影响试验结果。此外,为了方便养护脱模,试件采用可拆卸木制模具,并根据试件设计需要的保护层厚度,在木模具前后相应位置进行打孔。具体试件结构如图 2所示。

|
图 2 试件结构 Fig. 2 Specimen structure |
试验采用量程为100 kN电伺服万能试验机进行加载,试验加载速率为0.5 mm/min,加载装置如图 3所示。反力架下层T形钢板用夹具夹紧并进行调平,将拔出试件穿入反力架上层钢板中,试验机上夹具夹住筋材,当试验机横梁移动时,荷载即施加于试件上。BFRP筋自由端和加载端位移采用量程为30 mm的电子式位移计测量,使用东华DH3816N采集数据,采样频率5 Hz。自由端滑移量Sz由自由端位移计测量得出,由于BFRP筋的弹性模量较低,试件脱黏部分至加载端位移计处的BFRP筋的弹性变形不可忽略,则加载端滑移量计算公式为
| $ S_{\mathrm{j}}=S_{\mathrm{w}}-S_{\mathrm{b}}=S_{\mathrm{w}}-\frac{F l_{\mathrm{b}}}{E_{\mathrm{b}} A_{\mathrm{b}}} $ | (1) |

|
图 3 拔出试验装置 Fig. 3 Pull out test device |
式中:Sj为加载端滑移量,Sw为加载端位移计的数值(取两个加载端位移计读数的平均值),Sb、lb分别为试件脱黏部分至加载端位移计处BFRP筋的伸长量和长度,F为外荷载,Eb、Ab分别为BFRP筋的弹性模量和有效横截面积。
PVA-ECC与BFRP筋平均黏结应力计算见式(2),最大平均黏结应力称为黏结强度。
| $ \tau=F / \pi d l $ | (2) |
式中:τ为平均黏结应力;d为BFRP筋直径;l为黏结长度。
2 试验结果与分析 2.1 试验破坏形态本次试验只有保护层厚度为5 mm的试件发生PVA-ECC劈裂破坏,其余试件均发生BFRP筋拔出破坏,并未出现筋材拉断现象。
1) 拔出破坏。试件发生拔出破坏时,BFRP筋随着外荷载增加从PVA-ECC中缓慢拔出,加载至结束PVA-ECC表面无明显裂缝。加载结束后观察黏结界面,无喷砂BFRP筋肋表面磨损严重,破坏主要发生在BFRP筋树脂层,PVA-ECC黏结滑移段处有BFRP筋表面树脂材料残留,如图 4(a)和图 4(b)所示。该现象与普通钢筋与PVA-ECC发生黏结破坏时不同。普通钢筋发生黏结破坏时,筋肋剪碎黏结界面附近的PVA-ECC材料,黏结界面发生破坏[12]。这是由于BFRP筋肋抗剪强度远小于普通钢筋。喷砂BFRP筋表面磨损程度较小,筋表面覆盖一层PVA-ECC,筋表面PVA-ECC覆盖层与周围PVA-ECC发生剪切破坏,如图 4(c)所示。

|
图 4 黏结破坏形态 Fig. 4 Bond failure pattern |
2) 劈裂破坏。加载过程中发生劈裂破坏时,试验机荷载曲线出现骤降,伴随有PVA-ECC的开裂声,裂缝出现在试件表面黏结段区域并向非黏结段延伸,最终贯穿试件表面。在卸载后,PVA-ECC表面两端非黏结段裂缝收缩,如图 4(d)所示。只有保护层厚度为5 mm的试件发生PVA-ECC劈裂破坏,这主要是因为BFRP筋肋与PVA-ECC相互挤压,使PVA-ECC一定范围内环向受拉,当环向拉应力大于PVA-ECC的开裂强度时,PVA-ECC出现裂纹,并且裂纹随着拉应力的增大而逐渐向外扩展,当保护层厚度较小时,裂纹容易扩展到PVA-ECC表面而发生劈裂破坏。
2.2 黏结强度结果PVA-ECC与BFRP筋拔出试件加载结果见表 3。其中,P为拔出破坏,S为劈裂破坏。试件编号含义为:PVA-ECC强度和BFRP筋表面形式-保护层厚度-锚固长度-BFRP筋直径,如E50BS-70-D5-10表示直径为10 mm,锚固长度为5倍直径,表面喷砂的BFRP筋,PVA-ECC保护层厚度为70 mm且强度为C50的拔出试件。
| 表 3 PVA-ECC与BFRP筋拔出试验结果 Tab. 3 Result of pull-out test of PVA-ECC and BFRP bars |
筋材与基体材料之间的黏结应力主要由化学胶结力、摩擦力及机械咬合力组成。根据试验结果分析,PVA-ECC与BFRP筋拔出破坏过程可分为微滑移阶段、滑移阶段、下降阶段及残余应力阶段,BFRP筋与PVA-ECC拔出破坏黏结滑移曲线如图 5所示。

|
图 5 拔出破坏黏结滑移曲线 Fig. 5 Bond-slip curves of pull-out failure |
1) 微滑移阶段(OA段)。加载初期,加载端滑移量非常小,自由端不发生滑移。此时,试件处于线弹性阶段,黏结滑移曲线斜率较大,接近直线。此时试件的黏结强度主要来自BFRP筋与PVA-ECC之间的化学胶结力。
2) 滑移阶段(AB段)。随着荷载增大,局部脱黏首先发生在BFRP筋与PVA-ECC的加载端附近,然后逐渐向自由端发展。脱黏界面上的化学胶结力在埋置长度上从加载端向自由端递减,BFRP筋与PVA-ECC产生相对滑移。黏结滑移曲线斜率逐渐减小,呈非线性。随着黏结应力继续增加至峰值,黏结滑移曲线逐渐平缓。此时,黏结强度主要由PVA-ECC与BFRP筋肋的机械咬合力和摩擦力提供。
3) 下降阶段(BC段)。黏结应力达到峰值后,随着滑移量的增加,BFRP筋肋磨损愈发严重,机械咬合力减小,黏结应力开始逐渐下降。
4) 残余应力阶段(CD段)。此阶段随着滑移量的增加,无喷砂的BFRP筋的黏结应力存在波动性变化,整个黏结滑移曲线近似于周期递减的正弦曲线。然而喷砂BFRP黏结滑移曲线在此阶段没有表现出明显的波动性变化,这是由于残余应力阶段的黏结强度主要靠界面残余摩擦力提供,而喷砂BFRP筋材表面的PVA-ECC覆盖层已发生层间剥离,导致黏结强度呈现一直下降趋势。
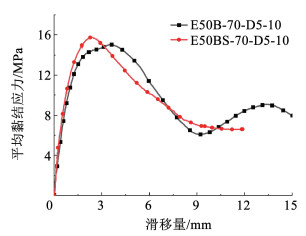
2.4 黏结性能影响因素研究 2.4.1 BFRP筋表面形式表面喷砂及无喷砂BFRP筋的自由端黏结滑移曲线如图 6所示。在外荷载作用下,表面喷砂BFRP筋达到黏结应力峰值时对应的滑移值比无喷砂BFRP筋更小。与无喷砂BFRP筋相比,喷砂BFRP筋在PVA-ECC中黏结强度提高约32.8%。喷砂BFRP筋发生黏结破坏时,BFRP筋表面的PVA-ECC覆盖层发生剪切破坏而拔出,并且BFRP筋表面喷砂层磨损程度较小,可见砂颗粒与BFRP筋表面黏结可靠。高超等[17]采用人工喷砂的BFRP筋与混凝土,其黏结强度提高约12%左右,发生黏结破坏时,BFRP筋表面喷砂层磨损严重。由此可见,喷砂对黏结强度的提高大小是受到砂颗粒和筋材表面黏结的牢固程度的影响,当砂颗粒黏结更牢固时,BFRP筋与PVA-ECC的黏结强度提升越高。
|
图 6 不同表面形式下自由端黏结滑移曲线 Fig. 6 Bond-slip curves of free ends with different surface forms |
BFRP筋黏结强度随锚固长度增加而降低。相比锚固长度为5d的试件,7d、9d试件黏结强度分别降低了11.57%和20.3%,黏结强度变化与锚固长度之间存在线性关系。黏结强度随锚固长度增加而降低是由黏结应力沿黏结段的非线性分布和泊松效应引起的。锚固长度越长,非线性分布越明显。当锚固长度较小时,高黏结应力分布区域较大,筋材锚固长度上的应力分布比较均匀,平均黏结应力较大;而当锚固长度较大时,高黏结应力分布区域较窄,筋材埋置长度上的应力分布不均匀,平均黏结应力较小。此外泊松效应的存在使筋材在拉伸过程中直径降低,进而导致BFRP筋与PVA-ECC间的摩擦力降低。
图 7为锚固长度为5d、7d、9d条件下BFRP筋的加载端和自由端黏结滑移曲线。3种不同锚固长度下试件达到黏结应力峰值时,自由端滑移量均在3 mm左右,加载端滑移量则随锚固长度增加而提高。

|
图 7 不同锚固长度下黏结滑移曲线 Fig. 7 Bond-slip curves under different anchorage lengths |
本试验中BFRP筋肋宽、肋间距保持不变,肋高随BFRP筋直径增加而增加,但相对肋高随筋材直径的增大而保持不变。3种直径BFRP筋的黏结滑移曲线如图 8所示,当BFRP筋的相对肋高均为6.7%时,试件的黏结强度表现出随着直径的增大而增大。黏结段FRP筋的应力呈现非线性分布的特点,当FRP筋的直径越大,其非线性应力分布越不均匀[18],在筋材的肋参数不变的情况下,较大直径的FRP筋需要更大的锚固长度才能获得相同法向黏结应力。因此,在其他条件不变时,FRP筋与混凝土的黏结强度应随着FRP筋直径的增大而降低[11, 18]。这不同于本试验的结论,其主要原因是本试验采用筋材的相对肋高保持不变,当增加BFRP筋的直径时,筋肋高度变高,则筋肋与PVA-ECC的接触面积增加,进而提高了二者之间的机械咬合力,使黏结强度增大。因此,增加BFRP筋肋高可以有效避免筋材直径增大对黏结强度的不利影响。

|
图 8 不同直径下自由端黏结滑移曲线 Fig. 8 Bond-slip curves of free ends with different diameters |
本试验通过设置不同的保护层厚度来模拟实际工程中保护层厚度不足带来的影响。对于保护层厚度为25、15、5 mm的试件,BFRP筋黏结强度随着保护层厚度的降低而降低,呈正相关。当保护层厚度为5 mm时,黏结强度为6.03 MPa,仅为保护层厚度为25 mm时的39.59%。实际工程中需要足够的保护层厚度对筋材产生约束,而保护层厚度的不足或漏筋会严重影响BFRP筋与PVA-ECC的黏结强度,继而影响结构的承载力。
根据图 9可知,保护层厚度为70 mm和25 mm的试件黏结应力峰值出现时,BFRP筋滑移量约3 mm。保护层厚度为15、5 mm试件的黏结应力达到峰值时,BFRP筋滑移量比保护层厚度70、25 mm的试件小。当保护层厚度不足发生黏结破坏时,黏结滑移曲线会发生骤降,试件覆盖层出现裂缝。通过判断黏结强度峰值出现时的黏结滑移值可以有效判断保护层厚度是否满足要求。对于直径不超过10 mm的BFRP筋,保护层厚度建议25 mm以上。

|
图 9 不同保护层厚度下自由端黏结滑移曲线 Fig. 9 Bond-slip curves of free ends under different protective layer thicknesses |
当PVA-ECC强度从C50提高到C80时,BFRP筋黏结强度从13.31 MPa提高到19.37 MPa,强度提高45.53%。已有研究[19]表明,FRP筋在普通混凝土中的黏结破坏是由于二者之间的黏结界面产生滑移而破坏;高强混凝土中,黏结破坏主要由FRP筋树脂与纤维剪切破坏造成的。在高强度PVA-ECC中,黏结强度由BFRP筋中树脂与纤维之间的剪切力控制,继续增加PVA-ECC强度并不能大幅提高黏结强度。
对比BFRP筋在两种强度的PVA-ECC中加载端和自由端的黏结滑移曲线图 10可知,高强度PVA-ECC中在黏结滑移曲线进入非线性阶段后,自由端的滑移量滞后于加载端,黏结损伤从加载端开始,然后逐渐转移到自由端,黏结应力在黏结滑移段呈不均匀分布。

|
图 10 不同PVA-ECC强度下黏结滑移曲线 Fig. 10 Bond-slip curves of under different PVA-ECC strengths |
PVA-ECC与BFRP筋黏结滑移本构是设计PVA-ECC与BFRP筋结构和进行有限元模拟的重要理论依据。目前国内外学者已经在FRP筋与混凝土黏结滑移本构研究方面建立了多种模型[20-23]。其中Malvar模型表达式[20]为
| $ \tau=\tau_{\mathrm{u}} \frac{F\left(s / s_{\mathrm{u}}\right)+(G-1)\left(s / s_{\mathrm{u}}\right)^2}{1+(F-2)\left(s / s_{\mathrm{u}}\right)+G\left(s / s_{\mathrm{u}}\right)^2} $ | (3) |
改进BPE模型表达式[21]为
| $ \tau=\left\{\begin{array}{l} \tau_{\mathrm{u}}\left(s / s_{\mathrm{u}}\right)^\alpha, 0 \leqslant s \leqslant s_{\mathrm{u}} \\ \tau_{\mathrm{u}}-\tau_{\mathrm{u}} p\left(s / s_{\mathrm{u}}-1\right), s_{\mathrm{u}} \leqslant s \leqslant s_{\mathrm{r}} \\ \tau_{\mathrm{r}}, s_{\mathrm{r}} \leqslant s \end{array}\right. $ | (4) |
连续曲线模型表达式[22]为
| $ \tau=\left\{\begin{array}{l} 2 \tau_{\mathrm{u}} \sqrt{\frac{s}{s_{\mathrm{u}}}}-\tau_{\mathrm{u}} \frac{s}{s_{\mathrm{u}}}, 0 \leqslant s \leqslant s_{\mathrm{u}} \\ \tau_{\mathrm{u}} \frac{\left(s_{\mathrm{r}}-s\right)^2\left(2 s+s_{\mathrm{r}}-3 s_{\mathrm{u}}\right)}{\left(s_{\mathrm{r}}-s_{\mathrm{u}}\right)^3}+ \\ \;\;\;\;\;\;\tau_{\mathrm{r}} \frac{\left(s-s_{\mathrm{u}}\right)^2\left(3 s_{\mathrm{r}}-2 s-s_{\mathrm{u}}\right)}{\left(s_{\mathrm{r}}-s_{\mathrm{u}}\right)^3}, s_{\mathrm{u}} \leqslant s \leqslant s_{\mathrm{r}} \end{array}\right. $ | (5) |
式中:τu、su为峰值黏结应力及对应滑移值,τr、sr为残余应力及对应滑移值,F、G、α、p均为试验结果确定的常数。
Malvar模型、改进BPE模型以及连续曲线模型均不是以PVA-ECC与BFRP筋的黏结滑移曲线构造的本构模型。因此,本文仅考虑以上3种模型来讨论PVA-ECC与BFRP筋黏结滑移本构模型。3种本构模型曲线与试验曲线拟合结果如图 11所示。另外,由于实际工程中为避免筋材保护层厚度不足的现象,配置了一定量的箍筋,结构不会发生劈裂破坏。因此,本研究并未选择劈裂破坏试件的数据来探讨PVA-ECC与BFRP筋的黏结滑移本构模型。

|
图 11 各本构模型与试验结果对比 Fig. 11 Comparison of constitutive models with the experimental results |
3种本构模型中,Malvar模型在上升段能较好的描述PVA-ECC与BFRP筋的黏结滑移变化规律,但结构式含有两个参数且较为复杂;改进BPE模型在上升段与PVA-ECC与BFRP筋黏结滑移曲线差异较大,且下降段为直线;连续曲线模型表达形式简单,但在上升段,连续曲线模型的黏结应力要高于试验的黏结应力。
3.2 PVA-ECC与BFRP筋黏结滑移本构模型本文依据连续曲线模型,改进上升段,获得适用于PVA-ECC与BFRP筋黏结滑移的本构模型。构造函数为
| $ \tau=a\left(\frac{s}{s_{\mathrm{u}}}\right)^k \tau_{\mathrm{u}}+b\left(\frac{s}{s_{\mathrm{u}}}\right) \tau_{\mathrm{u}} $ | (6) |
根据连续曲线模型思想,有约束条件:
| $ \left\{\begin{array}{l} \tau=0, s=0 \\ \tau=\tau_{\mathrm{u}}, \frac{\mathrm{d} \tau}{\mathrm{d} s}=0, s=s_{\mathrm{u}} \end{array}\right. $ | (7) |
将式(7)代入式(6), 求解可得
| $ k=\frac{a-1}{a}, b=1-a $ | (8) |
将式(8)代入式(6), 可得
| $ \frac{\tau}{\tau_{\mathrm{u}}}=a\left(\frac{s}{s_{\mathrm{u}}}\right)^{\frac{a-1}{a}}+(1-a)\left(\frac{s}{s_{\mathrm{u}}}\right) $ | (9) |
式中a是反映试验筋材和基体材料特性的常数,当筋材与基体材料确定时,a为定值。a越小,黏结滑移曲线上升段斜率越大。对于BFRP筋与PVA-ECC材料,根据试验数据,a值建议取7,改进后的本构模型黏结滑移曲线如图 12所示,同连续曲线模型相比,本文模型与试验结果吻合更好。因此最终可得到适用于PVA-ECC与BFRP筋黏结滑移本构模型:
| $ \left\{\begin{array}{l} \frac{\tau}{\tau_{\mathrm{u}}}=7\left(\frac{s}{s_{\mathrm{u}}}\right)^{\frac{6}{7}}-6\left(\frac{s}{s_{\mathrm{u}}}\right), 0 \leqslant s \leqslant s_{\mathrm{u}} \\ \tau=\tau_{\mathrm{u}} \frac{\left(s_{\mathrm{r}}-s\right)^2\left(2 s+s_{\mathrm{r}}-3 s_{\mathrm{u}}\right)}{\left(s_{\mathrm{r}}-s_{\mathrm{u}}\right)^3}+\tau_{\mathrm{r}} \frac{\left(s-s_{\mathrm{u}}\right)^2\left(3 s_{\mathrm{r}}-2 s-s_{\mathrm{u}}\right)}{\left(s_{\mathrm{r}}-s_{\mathrm{u}}\right)^3}, s_{\mathrm{u}} \leqslant s \leqslant s_{\mathrm{r}} \end{array}\right. $ | (10) |

|
图 12 本构模型与试验结果对比 Fig. 12 Comparison of the constitutive model with the experimental results |
设计28个PVA-ECC与BFRP筋拉拔试件进行拔出试验,通过分析破坏形态与破坏特征,揭示黏结滑移破坏机理,探究PVA-ECC及BFRP筋参数对黏结强度的影响规律,根据试验结果建立PVA-ECC与BFRP筋本构模型,得出以下结论:
1) 除保护层厚度为5 mm的试件发生劈裂破坏外,其余试件均为拔出破坏。无喷砂BFRP筋肋在外荷载作用下被PVA-ECC剪切破坏而丧失机械咬合力,可以通过提高BFRP筋肋的强度来提高筋材在PVA-ECC中的黏结强度。黏结滑移曲线可分为微滑移阶段、滑移阶段、下降阶段和残余应力阶段,在残余应力阶段无喷砂BFRP筋的黏结应力曲线有上下波动,而喷砂BFRP筋的黏结滑移曲线无明显波动。
2) 对BFRP筋表面进行喷砂处理可以提高筋材在PVA-ECC中黏结强度;BFRP筋黏结强度随锚固长度的增加而降低,近似呈线性关系;增大筋材直径的同时保证相对肋高不变可以有效避免因BFRP筋直径增大造成的黏结强度降低。
3) 当PVA-ECC保护层厚度从25 mm降至5 mm时,BFRP筋黏结强度随保护层厚度降低而降低,两者呈正相关,保护层厚度5 mm时黏结强度仅为正常试件的39.59%;PVA-ECC强度从50.5 MPa提高至81.3 MPa时,黏结强度提高了45.53%。
4) 提出了PVA-ECC与BFRP筋的黏结滑移本构模型,与试验结果吻合良好,且模型物理意义明确,可为PVA-ECC与BFRP筋结构数值模拟提供理论参考。
| [1] |
SHANG Huaishuai, ZHOU Junhao, FAN Guoxi, et al. Study on the bond behavior of steel bars embedded in concrete under the coupling of sustained loads and chloride ion erosion[J]. Construction and Building Materials, 2021, 276(Sup.2): 121684. DOI:10.1016/j.conbuildmat.2020.121684 |
| [2] |
RUI M F. Optimization of RC structure performance in marine environment[J]. Engineering Structures, 2010, 32(5): 1489. DOI:10.1016/j.engstruct.2010.02.011 |
| [3] |
TORRESACOSTA A A, NAVARROGUTIERREZ S, TERANGUILLEN J. Residual flexure capacity of corroded reinforced concrete beams[J]. Engineering Structures, 2007, 29(6): 1145. DOI:10.1016/j.engstruct.2006.07.018 |
| [4] |
NKURUNZIZA G, DEBAIKY A, COUSIN P, et al. Durability of GFRP bars: a critical review of the literature[J]. Progress in Structural Engineering and Materials, 2005, 7(4): 194. DOI:10.1002/pse.205 |
| [5] |
SIM J, PARK C. Characteristics of basalt fiber as a strengthening material for concrete structures[J]. Composites Part B: Engineering, 2005, 36(6/7): 504. DOI:10.1016/j.compositesb.2005.02.002 |
| [6] |
TAHA A, ALNAHHAL W, ALNUAIMI N. Bond durability of basalt FRP bars to fiber reinforced concrete in a saline environment[J]. Composite Structures, 2020, 243: 112277. DOI:10.1016/j.compstruct.2020.112277 |
| [7] |
URBANSKI M, LAPKO A, GARBACZ A. Investigation on concrete beams reinforced with basalt rebars as an effective alternative of conventional R/C structures[J]. Procedia Engineering, 2013, 57: 1183. DOI:10.1016/j.proeng.2013.04.149 |
| [8] |
LI V C, WANG Shuxin, WU C. Tensile strain-hardening behavior of polyvinyl alcohol engineered cementitious composite PVA-ECC[J]. Materials Journal, 2001, 98(6): 483. |
| [9] |
余江滔, 史天成, 郁颉, 等. 高性能纤维增强混凝土与筋材复合体系拉伸性能研究[J]. 同济大学学报(自然科学版), 2021, 49(6): 825. YU Jiangtao, SHI Tiancheng, YU Jie, et al. Experimental study of tensile properties of composite system of high performance concrete and reinforcements[J]. Journal of Tongji University (Natural Science), 2021, 49(6): 825. DOI:10.11908/j.issn.0253-374x.20293 |
| [10] |
ZHAO Debo, ZHOU Yingwu, XING Feng, et al. Bond behavior and failure mechanism of fiber-reinforced polymer bar-engineered cementitious composite interface[J]. Engineering Structures, 2021, 243: 112520. DOI:10.1016/j.engstruct.2021.112520 |
| [11] |
吴丽丽, 王云飞, 谢灵慧, 等. 玻璃纤维增强聚合物复合材料筋与工程水泥基复合材料黏结性能[J]. 复合材料学报, 2020, 37(3): 696. WU Lili, WANG Yunfei, XIE Linghui, et al. Bonding behavior between glass fiber reinforced polymer composite bars and engineered cementitious composite[J]. Acta Materiae Compositae Sinica, 2020, 37(3): 696. DOI:10.13801/j.cnki.fhclxb.20190729.001 |
| [12] |
LI Zhiqiang, HOU Wei, LIN Guan. Flexural strengthening of RC beams with BFRP or high strength steel bar-reinforced ECC matrix[J]. Construction and Building Materials, 2021, 303: 124404. DOI:10.1016/j.conbuildmat.2021.124404 |
| [13] |
HOSSAIN K M A. Bond strength of GFRP bars embedded in engineered cementitious composite using RILEM beam testing[J]. International Journal of Concrete Structures and Materials, 2018, 12(1): 1. |
| [14] |
高延性纤维增强水泥基复合材料力学性能试验方法: JC/T 2461—2018[S]. 北京: 中国建材工业出版社, 2018 Standard test method for the mechanical properties of ductile fiber reinforcedcementitious composites: JC/T 2461—2018[S]. Beijing: China Building Materials Press, 2018 |
| [15] |
混凝土结构试验方法标准: GB/T 50152—2012[S]. 北京: 中国建筑工业出版社, 2012 Standard for test method of concrete structures: GB/T 50152—2012[S]. Beijing: China Architecture & Building Press, 2012 |
| [16] |
ACI 440 Committee. Guide test methods for fiber-reinforced polymers (FRPs) for reinforcing or strengthening concrete structure: ACI 440.3R-04[S]. Farmington Hills: American Concrete Institute, 2004
|
| [17] |
高超, 董伟伟, 陈杰, 等. BFRP筋与纤维混凝土粘结性能研究[J]. 低温建筑技术, 2019, 41(10): 19. GAO Chao, DONG Weiwei, CHEN Jie, et al. Research on the bonding properties of BFRP bars and fiber reinforced concrete[J]. Low Temperature Architecture Technology, 2019, 41(10): 19. DOI:10.13905/j.cnki.dwjz.2019.10.006 |
| [18] |
杨超, 杨树桐, 戚德海. BFRP筋与珊瑚混凝土粘结性能试验研究[J]. 工程力学, 2018, 35(增刊1): 172. YANG Chao, YANG Shutong, QI Dehai. Experimental study on bonding properties of BFRP bars and coral concrete[J]. Engineering Mechanics, 2018, 35(Sup.1): 172. DOI:10.6052/j.issn.1000-4750.2017.06.S034 |
| [19] |
ROLLAND A, ARGOUL P, BENZARTI K, et al. Analytical and numerical modeling of the bond behavior between FRP reinforcing bars and concrete[J]. Construction and Building Materials, 2020, 231: 117160. DOI:10.1016/j.conbuildmat.2019.117160 |
| [20] |
孙晓燕, 姚晨纯, 王海龙, 等. FRP筋与混凝土粘结性能的研究进展[J]. 低温建筑技术, 2012, 34(6): 49. SUN Xiaoyan, YAO Chenchun, WANG Hailong, et al. Research on bond properties between fiber reinforces polymer (FRP) bar and concrete[J]. Low Temperature Architecture Technology, 2012, 34(6): 49. DOI:10.3969/j.issn.1001-6864.2012.06.021 |
| [21] |
张望喜, 胡彬彬, 王冠杰, 等. FRP筋与混凝土粘结性能研究进展及本构模型改进[J/OL]. 土木与环境工程学报(中英文). (2021-06-03).http://qks.cqu.edu.cn/cqdxxbcn/article/abstract/202302010 ZHANG Xiwang, HU Binbin, WANG Guanjie, et al. Research progress on bond behavior between FRP bars and concrete and improvement of constitutive model[J/OL]. Journal of Civil and Environmental Engineering. (2021-06-03). http://qks.cqu.edu.cn/cqdxxbcn/article/abstract/202302010 |
| [22] |
高丹盈, 朱海堂, 谢晶晶. 纤维增强塑料筋混凝土粘结滑移本构模型[J]. 工业建筑, 2003, 33(7): 41. GAO Danying, ZHU Haitang, XIE Jingjing. The constitutive models for bond slip relation between FRP rebars and concrete[J]. Industrial Construction, 2003, 33(7): 41. DOI:10.3321/j.issn:1000-8993.2003.07.011 |
| [23] |
郝庆多, 王言磊, 侯吉林, 等. GFRP带肋筋粘结性能试验研究[J]. 工程力学, 2008, 25(10): 158. HAO Qingduo, WANG Yanlei, HOU Jilin, et al. Experimental study on bond behavior of GFRP ribbed rebars[J]. Engineering Mechanics, 2008, 25(10): 158. |
 2023, Vol. 55
2023, Vol. 55


