采空区垮塌是地面塌陷、地裂缝等人为地质灾害的主要诱因^[1-2]。采空区群由多个单元采空区组成，不同采空区按照一定规律在中段(盘区)间排列，形成类似于多层框架结构的地下构筑体^[3-4]。采空区群整体垮塌通常是由某一个薄弱单元失稳，或其失稳诱发相邻采空区连锁失稳引起^[5]。如何甄别出采空区群中的薄弱单元，搜寻结构劣化、抗外力扰动能力弱的单元采空区，或某一单元采空区内部的薄弱顶板、间柱等构成元素，并采取强力支护手段或有效监控等防范措施，是防止此类工程事故的关键^[6-7]。长期以来，地下矿山工程技术人员主要采用人工巡查或经验判断方法，判别复杂采空区群中的薄弱单元，难免存在误判、漏查等问题，严重危及生产安全。

在长期重力作用及其他外力扰动下，空间结构体内部构件损伤是工程界的常见现象，由此改变其自振频率和振型等结构模态参数值。对比分析模态参数值变化，是甄别桥梁、高层建筑、体育场馆等地表复杂构筑物结构损伤的常用方法^[8-11]。20世纪70年代，文献[8]最早提出利用单元结构的固有频率来确定工程结构体中的损伤位置；文献[9]利用前几阶自振频率变化情况检测悬臂梁的损伤问题，并通过悬臂梁理论计算方法验证甄别结果的正确性；文献[10]基于结构振型变化值与刚度变化值的关系，成功地识别了两跨简支梁的损伤位置；文献[11]基于动态应变响应形成新的损伤指标，检测地震激励发生后某钢梁结构的安全性。

由于地下工程结构复杂、可视化程度低，模态损伤识别方法尚处于探索阶段，相关研究成果较少^[12-14]。文献[12]运用AHP和联系结构损伤“熵”法，对凡口铅锌矿采空区稳定性进行了评价分类；文献[13]利用地下隧道结构的动力响应特性，提出了一种基于小波分析的残余矢量识别技术，识别隧道侧壁损伤程度; 文献[14]以太白金矿为例，利用结构损伤理论，通过分析单元采空区的结构损伤“熵”值，甄别空区群内的短板单元，并与数值分析方法结果进行比较。

综上，已有成果尚未涉及地下矿山采空区群内部薄弱单元的损伤识别问题。本文拟利用动力学损伤模态参数方法，开展采空区群内部薄弱单元甄别领域的探索性研究, 借鉴结构损伤识别理论与方法，建立地下矿山采空区群离散振动力学模型，创新地提出地下复杂采空区群中薄弱单元的损伤模态识别法，基于结构单元的自振频率及应变模态指标进行比较、甄别，并给出甄别流程。以某地下石灰石矿为例，分别利用数值模拟结果和现场试验结果验证该方法的可靠性。该方法可为采空区工程地质灾害防控提供一条新思路。

1 空区单元损伤模态识别法 1.1 基本原理

采空区群具有鲜明的结构动力学性征，在外力扰动下，将发生结构动力响应^{[3-4, 15]}。由于每个采空区单元空间结构不同、赋存环境不同，导致各自拥有不同的卓越周期和差异性的承载极限阈值；同一荷载作用下，各单元体动力响应不同，损伤程度不同^[14]。

当采空区群内部单元受到外载荷作用发生损伤反应后，单元的自振频率、振型等模态参数值也随之改变^[16-17]，损伤程度不同，模态参数值变化的幅度也将不同。因此，应用离散分析方法，建立复杂采空区群离散振动力学模型，研究空区单元损伤前后模态参数值变化特性，可以有效识别采空区群内部薄弱单元。

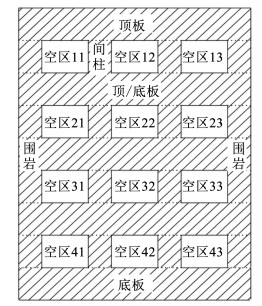
1.2 离散振动力学模型构建

以某地下石灰石矿山4个水平中段、12个单元构成的采空区为例(图 1)，对采空区群结构进行离散化处理，形成离散振动力学模型, 如图 2所示。

图 2中，顶(底)板及间柱各等效成一个质量惯性元件，各质量惯性元件之间用无质量的弹性元件和代表能量损耗的阻尼元件连接，采用固定边界对围岩进行约束^{[4, 15]}。

根据牛顿第三定律及达朗贝尔原理^{[4, 15]}，由m×n个单元空区组成的采空区群动力平衡方程为

$ \boldsymbol{M}\{\ddot{x}\}+\boldsymbol{P C}\{\dot{x}\}+\boldsymbol{K}\{x\}=\boldsymbol{F} $

(1)

式中：M、K、P、C分别为结构质量矩阵、刚度矩阵、修正矩阵、阻尼矩阵，F为外载荷矩阵。

令Q=PC，则上式转化为

$ \boldsymbol{M}\{\ddot{x}\}+\boldsymbol{Q}\{\dot{x}\}+\boldsymbol{K}\{x\}=\boldsymbol{F} $

(2)

式中Q为修正阻尼矩阵。

由于采空区群的各要素结构组合和承载方式不同，对于相同的外部激励，各自的振动响应不同，最终造成的损伤程度也不尽相同^[16-19]。在外力作用下，采空区群内某区域发生损伤效应，其应变改变量Δε将有明显不同，因此，可以用Δε表征采空区群单元结构的损伤。为清晰阐明损伤模态识别法分析的基本原理，下面从式(2)出发，推导Δε^[19]。

为了作解耦变换，令

$ \left\{\begin{array}{l} \boldsymbol{F}=\boldsymbol{f {\mathrm{e}}}^{\mathrm{j} \omega t} \\ \{x\}=\{X\} \mathrm{e}^{\mathrm{j} \omega t} \end{array}\right. $

(3)

式中：ω为采空区群的自振频率，j为虚数单位，f和X分别为等效荷载系数和等效位移系数。

阻尼矩阵采用瑞利阻尼模型构建而成^[15]，将式(3)代入式(2)，经解耦变换可得

$ \{X\}=\boldsymbol{\varPhi}\{q\} $

(4)

式中：Φ为正则化主模态矩阵，{q}为广义坐标。

将式(2)进行傅里叶变换，可得采空区群动力平衡方程的频域形式:

$ \left(-\omega^2 \boldsymbol{M}_r+\boldsymbol{K}_r+\mathrm{j} \omega \boldsymbol{C}_r\right)\{q\}=\boldsymbol{\varPhi} \boldsymbol{f} $

(5)

式中M_r、K_r、C_r分别为采空区群的模态质量矩阵、模态刚度矩阵、模态阻尼矩阵。

将式(5)代入式(4)，可得

$ \{X\}=\boldsymbol{\varPhi} \boldsymbol{Y}_r \boldsymbol{\varPhi}^{\mathrm{T}} \boldsymbol{f} $

(6)

式中$ \boldsymbol{Y}_r=\left(-\omega^2 \boldsymbol{M}_r+\boldsymbol{K}_r+\mathrm{j} \omega \boldsymbol{C}_r\right)^{-1}$。

由弹性力学原理，应变与位移之间的关系为

$ \left[\begin{array}{ll} \varepsilon_x & \alpha_{y x} \\ \alpha_{x y} & \varepsilon_y \end{array}\right]=\left[\begin{array}{ll} \frac{\partial}{\partial x} & \frac{\partial}{\partial x} \\ \frac{\partial}{\partial y} & \frac{\partial}{\partial y} \end{array}\right]\left[\begin{array}{ll} X_u & \\ & X_v \end{array}\right] $

(7)

式中：ε_x、ε_y为正应变，γ_xy=α_xy+α_yx为剪切应变。

将式(6)代入式(7)，可得

$ \left[\begin{array}{cc} \varepsilon_x & \alpha_{y x} \\ \alpha_{x y} & \varepsilon_y \end{array}\right]=\left[\begin{array}{cc} \frac{\partial}{\partial x} & \frac{\partial}{\partial x} \\ \frac{\partial}{\partial y} & \frac{\partial}{\partial y} \end{array}\right]\left[\begin{array}{ll} \boldsymbol{\varPhi}_u & \\ & \boldsymbol{\varPhi}_v \end{array}\right] \boldsymbol{Y}_r\left[\begin{array}{ll} \boldsymbol{\varPhi}_u & \\ & \boldsymbol{\varPhi}_v \end{array}\right]^{\mathrm{T}} \boldsymbol{f} $

(8)

为了简化分析，这里只考虑正应变分量的影响^[11]，单独提取式(8)中的正应变分量:

$ \varepsilon=\left[\begin{array}{ll} \frac{\partial \boldsymbol{\varPhi}_u}{\partial x} & \\ & \frac{\partial \boldsymbol{\varPhi}_v}{\partial y} \end{array}\right] \boldsymbol{Y}_r\left[\begin{array}{ll} \boldsymbol{\varPhi}_u & \\ & \boldsymbol{\varPhi}_v \end{array}\right]^{\mathrm{T}} \boldsymbol{f} $

(9)

定义ψ为应变模态，则其表达式为

$ \boldsymbol{\varPsi}=\left[\begin{array}{ll} \boldsymbol{\varPsi}_x & \\ & \boldsymbol{\varPsi}_y \end{array}\right]=\left[\begin{array}{ll} \frac{\partial \boldsymbol{\varPhi}_u}{\partial x} & \\ & \frac{\partial \boldsymbol{\varPhi}_v}{\partial y} \end{array}\right] $

(10)

将式(10)代入式(9)，可得

$ \varepsilon=\boldsymbol{\varPsi} \boldsymbol{Y} \boldsymbol{\varPhi}^{\mathrm{T}} \boldsymbol{f} $

(11)

对式(11)求一阶微分，可得采空区群的应变改变量Δε, 即

$ \Delta \varepsilon=\left(\boldsymbol{\varPsi} \Delta \boldsymbol{Y}_r \boldsymbol{\varPhi}^{\mathrm{T}}+\Delta \boldsymbol{\varPsi} \boldsymbol{Y}_r \boldsymbol{\varPhi}^{\mathrm{T}}+\boldsymbol{\varPsi} \boldsymbol{Y}_r \Delta \boldsymbol{\varPhi}^{\mathrm{T}}\right) \boldsymbol{f} $

(12)

式中：$ \boldsymbol{Y}_r 、\psi, \boldsymbol{\varPhi}^{\mathrm{T}} 、\Delta \boldsymbol{Y}_r 、\Delta \boldsymbol{\psi} 、\Delta \boldsymbol{\varPhi}^{\mathrm{T}} \boldsymbol{f}$分别为自振频率相关项、应变模态、位移模态、自振频率相关项改变量、应变模态改变量、位移模态改变量、等效荷载系数。

由式(12)可以发现，影响Δε的因素有4项，分别是频率影响因素$\boldsymbol{\psi} \Delta \boldsymbol{Y}_r \boldsymbol{\varPhi}^{\mathrm{T}} $、应变模态影响因素$\Delta\boldsymbol{\psi} \boldsymbol{Y}_r \boldsymbol{\varPhi}^{\mathrm{T}} $、位移模态影响因素$\boldsymbol{\psi} \boldsymbol{Y}_r \Delta \boldsymbol{\varPhi}^{\mathrm{T}} $、荷载影响因素f。

1.3 相关影响因素分析

下面分别对Δε的相关影响因素进行分析：

1) 频率($ \boldsymbol{\psi} \Delta \boldsymbol{Y}_r \boldsymbol{\varPhi}^{\mathrm{T}}$)。频率影响因素为ψ、ΔY_r和Φ^T三者乘积。其中，ψ、Φ^T为定值；Δ Y_r的变化将引起Δε的变化，但两者的位置坐标没有对应关系，只是在整体上有一定的关联。因此，Δε和Δ Y_r之间存在一种在整体上相互映射的关系。

2) 应变模态($ \Delta \boldsymbol{\psi} \boldsymbol{Y}_r \boldsymbol{\varPhi}^{\mathrm{T}}$)。应变模态影响因素为Δψ、Y_r和Φ^T三者乘积。其中，Y_r、Φ^T为定值；Δ ψ的变化将引起Δε的变化，且两者的位置坐标有对应关系。因此，Δε和Δψ之间存在一种在任意单元区域上相互映射的关系。

3) 位移模态($ \boldsymbol{\psi} \boldsymbol{Y}_r \Delta \boldsymbol{\varPhi}^{\mathrm{T}}$)。位移模态影响因素为ψ、Y_r和ΔΦ^T三者乘积。其中，Y_r、ψ为定值；Δ Φ^T变化将引起Δε的变化，但两者的位置坐标没有对应关系，对于结构体的无限阶振型，无法从整体上反映关联。因此，Δε和ΔΦ^T没有直接关联。

4) 外荷载(f)。Δε与f没有直接关联^[20-21]。

综上所述，采空区群的频率影响因素$\boldsymbol{\psi} \Delta \boldsymbol{Y}_r \boldsymbol{\varPhi}^{\mathrm{T}} $能够反映整体结构的损伤情况，应变模态影响因素$ \Delta \boldsymbol{\psi} \boldsymbol{Y}_r \boldsymbol{\varPhi}^{\mathrm{T}}$能够反映采空区群内单元结构的损伤状况。针对这两个因素，构建合理的甄别指标即可甄别出采空区群中的薄弱单元。

1.4 甄别指标构建

在甄别空区群中薄弱单元时，首先应分析是否存在薄弱单元，即初步判断空区群内是否存在损伤单元；其次判断存在的位置及损伤程度。

1) 自振频率甄别指标I_M(k)。由1.3节可知，ΔY_r可以反映采空区群整体损伤情况。由于ΔY_r过于复杂，且由式(6)可知，ΔY_r只与自振频率有关，因此可用结构损伤前后的同阶自振频率差来代替ΔY_r。令

$ I_M(k)=\omega_N(k)-\omega_{D N}(k) $

(13)

式中：I_M(k)为第k阶自振频率差，k=1，2，…，n；ω_N(k)、ω_DN(k)分别为采空区原始结构、损伤结构的第k阶频率。

为精确判断薄弱单元的存在，选择I_M(k)作为甄别指标，可反映损伤前后空区群的变化状况。若损伤后空区群的自振频率发生明显变化，则可初步推断空区群内部存在一个或多个较高损伤程度的空区单元，即可能存在薄弱单元，且I_M(k)越大，损伤程度越大。

2) 应变模态甄别指标I_N(x)。由1.3节可知，$ \Delta \boldsymbol{\psi} \boldsymbol{Y}_r \boldsymbol{\varPhi}^{\mathrm{T}}$可以反映空区群内任意空区单元，或空区单元组成结构(顶板、矿柱)的损伤情况。由于仅在空区群内同一位置才能体现Δε越大Δψ越大的关系，不同位置处Δε和Δψ之间并没有直接关系，很可能出现损伤严重处Δψ较小，损伤轻微处Δψ较大的现象，特别是在应变模态节点处，存在无论损伤多严重Δψ始终为零的问题。

因此，不能用应变模态改变量Δψ作为直接甄别指标，需要对其进行无量纲化修正。本文考虑利用叠加多阶模态来解决单阶模态检测节点的不足问题^[22]。为提高叠加效果，首先对各阶应变模态取绝对值，避免正负值抵消，再进行无量纲化处理、叠加：

1) 原始结构。对原始结构，有

$ \boldsymbol{\varPsi}_N(x)=\sum\limits_{j=1}^N \frac{\left|\boldsymbol{\varPsi}_j(x)\right|}{\max \left|\boldsymbol{\varPsi}_1(x), \cdots, \boldsymbol{\varPsi}_N(x)\right|} $

(14)

式中：ψ_N(x) 为无量纲化后原始结构的前N阶叠加应变模态，x为结构单元的位置坐标。

2) 损伤结构。对损伤结构进行计算时，无量纲化因子仍取同阶无损应变模态的最大值，即

$ \begin{aligned} \boldsymbol{\varPsi}_{D N}(x)= & \sum\limits_{j=1}^N \frac{\left|\boldsymbol{\varPsi}_{D j}(x)\right|}{\max \left|\boldsymbol{\varPsi}_{D 1}(x), \cdots, \boldsymbol{\varPsi}_{D N}(x)\right|}= \\ & \frac{\boldsymbol{\varPsi}_N(x)}{1-D(x)} \end{aligned} $

(15)

式中：ψ_DN(x)为无量纲化后损伤结构的前N阶叠加应变模态，D(x)(≥0)表示结构的损伤程度。

将式(15)与式(14)相减，得

$ \Delta \boldsymbol{\varPsi}_N(x)=\boldsymbol{\varPsi}_{D N}(x)-\boldsymbol{\varPsi}_N(x)=\frac{D(x) \boldsymbol{\varPsi}_N(x)}{1-D(x)} $

(16)

式中Δψ_DN(x)为无量纲化后损伤结构的前N阶叠加应变模态差。

为进一步消除原始模态影响，用式(16)除以式(15)可得到应变模态甄别指标I_N(x)，即

$ I_N(x)=\frac{\Delta \boldsymbol{\varPsi}_N(x)}{\boldsymbol{\varPsi}_N(x)} $

(17)

由式(17)可以发现，I_N(x)由N阶模态差叠加而来，相比于仅使用单阶模态差，其损伤识别的灵敏性更高，且基本消除了模态节点的影响。同时，选择I_N(x)来分析任意空区单元或空区单元组成结构(顶板、矿柱)在损伤前后的变化情况，可进一步定位识别局部区域的薄弱单元，并判断损伤程度。对于不同位置的单元区域，I_N(x)越大，则该区域发生损伤的可能性越大；对于相同位置的单元区域，I_N(x)越大，该区域的损伤程度越大。

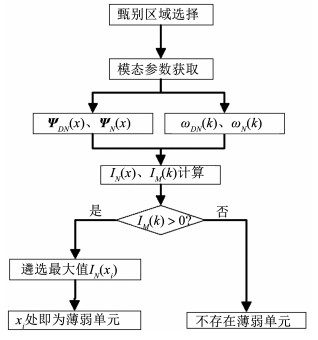
1.5 甄别流程

综上分析，下面给出采空区群内薄弱单元损伤模态识别法的甄别流程(图 3)包括：1)甄别区域选择，根据矿山实际工程需要，选择甄别区域^[23]；2)模态参数获取，分别获取原始结构和损伤结构的各阶模态参数值；3)指标计算，将模态参数代入式(13)、(17)计算出甄别指标；4)结果确定。

2 工程概况

为了验证损伤模态识别法的可行性，以广东省某地下石灰石矿多层采空区群为例，进行计算甄别分析。广东省某地下石灰石矿山利用空场房柱法进行开采，嗣后不进行充填，地下形成大面积采空区，空区面积约为31.33万立方米。经多年开采，现已形成+190 m、+160 m、+130 m、+100 m、+70 m、+40 m、+10 m、-20 m等8个水平中段，各中段高度为30 m，石灰岩体优势节理方向80° < 70°。由于长期受爆破扰动影响，上部中段采空区群顶板、间柱受到不同程度的损伤，部分区域存在顶板垮落、矿柱剪切破坏等现象，因此如何精准甄别上部老采空区群内部的薄弱单元，有的放矢进行安全监管，是矿山亟待解决的难题。

依据矿山地质资料和实测井下井上地形图，利用矿业软件Surpac，构建矿区三维可视化模型(图 4)，涉及矿区所有巷道和空区。以+130 m、+100 m、+70 m、+40 m四个中段采空群为研究对象，选取该区域每中段含有的3个单元采空区进行甄别计算，数量为4×3个(图 4)。已知各单元采空区的几何参数分别为跨度20 m、间柱宽10 m、高15 m、顶板厚15 m。

分别从不同巷道侧壁钻芯取样，按照《工程岩体试验方法标准GB/T 50266—2013》^[24]要求，加工成标准试样，进行岩石力学试验。由于侧壁为爆破后扰动区域，岩样抗压抗拉强度值均小于未扰动岩体值，计算结果将更接近采空区真实赋存环境。矿岩力学参数见表 1。

3 模态参数获取

模态参数获取是损伤模态识别法的关键环节，这里采用数值模拟和现场测量两种方法获取模态参数，在计算过程中，二者相互补充。

3.1 数值模拟获取

数值模拟是现有技术条件下分析复杂工程体稳定性的有效方法，采用数值模拟方法是获取地下空间结构体模态参数的有效途径。

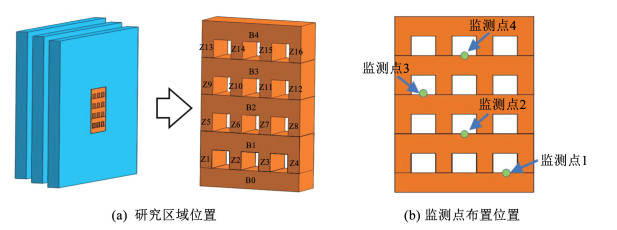
利用有限元软件Ansys，在图 4的基础上，构建4行3列12单元采空区群数值模型(图 5)。模型长为400 m、宽为30 m、高为520 m，单元类型设定为solid45。经离散化处理后，共包含350 278个计算单元，研究区域的网格单元编号为1~3 120。依下而上顶(底)板编号分别为B0、B1、B2、B3、B4，自左至右矿柱编号分别为Z1、Z2、…、Z16(图 5)。模型四周为固定边界条件约束，采用线弹性体模型描述本构关系。

在数值模拟方法中，模态参数的获取以模型数值计算为依据，实质是求解有限数量自由度的无阻尼线弹性运动方程。在设置好模型材料参数后，本文通过Ansys有限元分析软件的模态分析功能，可直接获取数值模型的模态参数值。

3.2 现场测量获取

本次试验的模态测量设备是中科院成都中科爆破测振仪TC-4850，该仪器采用六通道并行采集数据，采样率为1~50 ksps，频响为5~500 Hz，量程为0.001~35.4 cm/s，分辨率为0.01 cm/s，读数精度为0.1%，A/D为16Bit，感应器与岩体之间采用刚性固定^[4]。

为了尽可能精确测量采空区群的模态参数，避免人为因素干扰，自振频率和应变模态测量均安排在人员设备全部撤离时间段进行，监测点附近无车辆行驶振动或机械振动，无噪声。每次测量布置4个监测点，全部布设在+160 m、+130 m、+100 m、+70 m水平中段运输巷道底板(图 5)，每个监测点同时布设3台拾振器，分别记录南北、东西和垂直3个方向的地脉动信号。受限于地下采空区群空域分布及安全因素的影响，其他未布设监测点的区域采用数值模拟方法进行参数补充。

4 算例甄别

数值模拟方法与现场测量方法相比，具有低成本、范围广等优势，可高效获取多种不同工况条件下工程体的模态参数，以便进行后续的计算甄别分析。

4.1 损伤指标设定

相对损伤程度和损伤位置是薄弱单元甄别的关键要素，分别设定如下：

1) 相对损伤程度。复杂工程体中，通常利用降低网格单元区域抗弯刚度的方法来假定该区域发生损伤^[25]，因此，选择刚度折减法，通过改变网格单元抗弯刚度来假定网格单元的损伤值，损伤因子D_i由网格单元抗弯刚度的百分比系数来表示，即

$ D_i=\left[1-\frac{\left(E_D I\right)}{(E I)}\right] \times 100 \% $

(18)

式中：EI为原始结构单元的抗弯刚度，E_DI为损伤结构单元的抗弯刚度，i为损伤网格单元的编号。

2) 损伤位置。由于空区群数值模型内部网格单元众多，若对每一个网格单元分别进行损伤位置假定，耗时费力；若假定区域过小，则失去工程实际意义。

因此，本文随机从数值模型中，假定顶板B1和矿柱Z6为空区群的损伤位置。其中，B1的网格单元编号处于2 800~3 120之间，Z6的网格单元编号处于350~510之间，分别开展单体单元损伤(B1、Z6)及双体单元损伤(B1和Z6)两种算例的计算甄别分析。

4.2 损伤甄别

空区群的损伤甄别包含3个部分：损伤存在性判别、损伤单元级定位和损伤程度判定。

4.2.1 单体单元损伤甄别

与原始状态相比，设定空区群中顶板B1的损伤程度分别为0%、5%、…、55%、60%，同理，设定矿柱Z6损伤程度也为0%、5%、…、55%、60%，经正交组合，共计可得26种工况，进行单体单元损伤计算甄别分析。

1) 损伤存在性判别。先将数值模型进行岩体力学参数赋值(表 1)，再进行模态分析得到模态参数，分别将26种损伤工况条件下空区群的前四阶自振频率值代入式(13)，经计算得到空区群的I_M (图 6)。由图 6可以发现，无论是B1或是Z6发生损伤，空区群的自振频率都明显小于原始状态值(I_M>0)；随着损伤程度增加，空区群的自振频率值也越来越小。由1.4节分析结果，即可初步推断该空区群存在损伤。

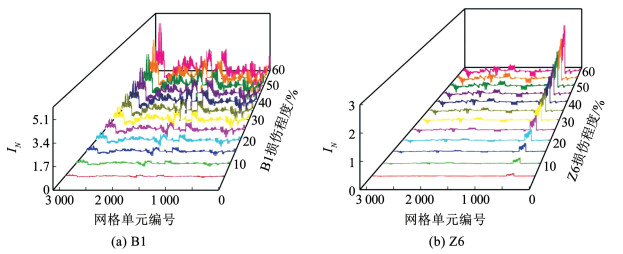
2) 损伤单元级定位及损伤程度判定。为进一步确定损伤位置，判断损伤程度，需计算比较敏感的应变模态甄别指标。提取26种不同损伤工况条件下, 空区群所有网格单元的前四阶应变模态代入式(17)，经计算得到空区群网格单元的I_N(x)分布(图 7)。由图 7(a)可以发现，当Z6无损伤，B1损伤程度增大时，各网格单元的I_N值也相应增大，当B1损伤程度为60%时，I_N值最大。网格单元编号处于2 800~3 120之间的I_N值明显出现凸起现象。由1.4节分析结果，即可判断该网格单元区间对应的区域为采空区群的薄弱单元，且IN峰值越大，损伤程度越大。由图 7(b)可以发现，当B1无损伤，Z6损伤程度增大时，各网格单元的IN值也相应增大，当Z6损伤程度为60%时，I_N值最大。网格单元编号处于350~510之间的I_N值明显出现凸起现象。由1.4节分析结果，即可判断该网格单元区间对应的区域为采空区群的薄弱单元，且I_N峰值越大，损伤程度越大。计算甄别结果确定的薄弱单元与假定工况中的薄弱单元相同，验证了损伤模态识别法对单体单元损伤识别的可靠性。

4.2.2 双体单元损伤甄别

设定B1和Z6为双体损伤单元，各自的损伤程度分别为15%、30%、45%、60%四级，共计16种工况进行双体单元损伤计算甄别分析。

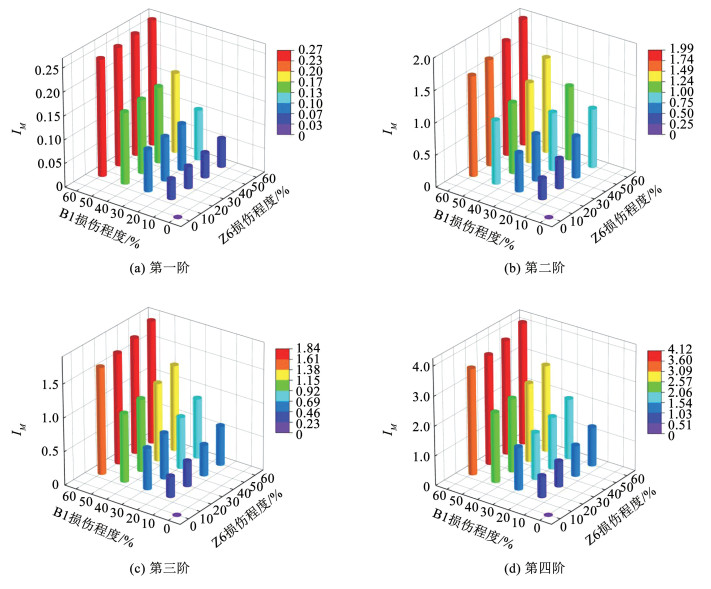
1) 损伤存在性判别。分别提取不同双体单元损伤工况条件下空区群的前四阶自振频率代入式(13)，经计算得到空区群的I_M(图 8)。由图 8可以发现，在B1和Z6同时损伤工况条件下，空区群的自振频率明显小于原始状态值。从总体趋势上来看，随着损伤程度增加，空区群的自振频率越来越小。由1.4节分析结果，即可初步判断该空区群存在损伤。

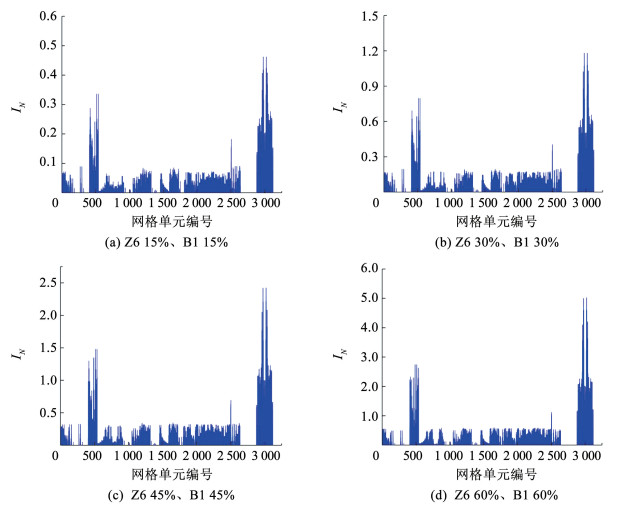
2) 损伤单元级定位及损伤程度判定。原理同上，受篇幅所限，分别提取双体单元(B1和Z6)同为15%、30%、45%、60%四种损伤工况条件下空区群结构单元的前四阶应变模态代入式(17)，经计算得到空区群网格单元的I_N(x)分布(图 9)。图 9揭示，双体单元在4种不同损伤工况条件下，I_N(x)分布曲线的形状几乎没有发生变化，仅峰值大小有所改变；随着损伤程度增加，各网格单元I_N值也相应增大。损伤程度分别为15%、30%、45%、60%四种损伤工况条件下，编号在2 800~3 120及350~510之间的网格单元区域I_N值均明显出现凸起现象。由1.4节分析结果，即可判断两个凸起区间的网格单元为采空区群的薄弱单元，且I_N峰值越大，损伤程度越大。

计算甄别结果确定的薄弱单元与假定工况中的薄弱单元相同，验证了损伤模态识别法对双体单元损伤识别的可靠性。

4.3 甄别计算效果评价 4.3.1 自振频率甄别指标评价

由4.2节分析可知，无论是单体或是双体单元损伤，I_M(k)均能有效判别空区群内是否存在损伤。

由图 6可以发现，仅B1损伤时，高阶I_M(k)比低阶更灵敏反映空区群损伤程度的变化状况，第四阶I_M(k)识别效果更优；仅Z6损伤时，第二、四阶I_M(k)相比于第一、三阶更灵敏反映损伤程度的变化，识别效果更优。

由图 8可以发现，空区群自振频率对B1的损伤程度变化相较于Z6更为敏感，经分析可知，B1区域的体积大于Z6区域，网格单元数量较多，同时也和其内部结构有关。此外，对于B1和Z6的双体单元损伤工况，第二、三、四阶的I_M(k)相较于第一阶的识别效果更好，其中第二阶I_M(k)识别效果更优。

4.3.2 应变模态甄别指标评价

由4.2节分析可知，无论是单体或是双体单元损伤，损伤区域的I_N(x)值均能准确甄别损伤位置及程度。

在图 7和图 9中，损伤区域对应的网格编号区间内I_N值明显出现大凸起，同时其他未损伤区域对应的网格单元也存在一些细小凸起。经进一步分析可知，个体单元损伤不仅会导致损伤区域的模态参数发生变化，其他未损伤区域也会受其影响，越临近损伤区域，所受影响程度越大。虽然这些细小凸起在一定程度上会微弱干扰损伤区域的甄别，但只需根据1.4节的方法寻找最大损伤区间，即可实现有效甄别。

5 区域工程体甄别验证

为了进一步检验该甄别方法的可靠性，利用3.2节中现场试验测量获得的模态参数进行计算识别，并将识别结果与现场实际工况进行对比。

1) 薄弱单元是否存在判别。将现场测量得到的自振频率参数代入式(13)，经计算得到研究区域各监测点的自振频率甄别指标I_M见表 2。从表 2可以看出，无论是哪个监测点，计算得到的I_M均明显大于0，采空区群的自振频率明显发生变化，采用1.4节的方法，即可初步判断该空区群存在薄弱单元。

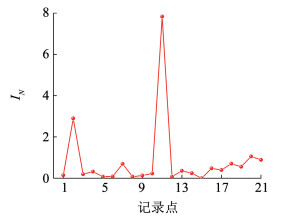
2) 薄弱单元计算圈定。将现场测量及补充获得的应变模态参数代入式(17)，经计算得到研究区域各单元体的应变模态甄别指标I_N(x)(图 10)。为了直观显示效果，将B0、B1、B2、B3、B4、Z1、Z2、…、Z16，按序编号为1、2、3、…、21。在图 10中，相比于其他单元体，应变模态指标分布曲线在记录点3(对应顶板B1)和记录点12(对应矿柱Z6)处明显出现大凸起。根据1.4节设定，可推断这两个区域岩体结构存在较大程度损伤，从而判断为所研究空区群区域的薄弱单元。

3) 现场勘察。研究区域的现场勘察结果表明，2020年9—10月份，顶板B1发生多次碎石脱落现象(图 11(a))，矿柱Z6发生局部滑移问题(图 11(b))，相对于其他顶板与矿柱，B1和Z6损伤程度较深，属于空区群的薄弱单元，与理论计算甄别结果相符，验证了理论方法识别的可行性。

6 讨论

1) 本文利用数值模拟方法获取采空区群模态参数，具有低成本、高效等特点，但这种方法对数值模型的精度有一定要求，不仅需客观建模，还需准确的岩体力学参数。

2) 无量纲化叠加方法处理应变模态甄别指标，可消除模态盲点带来的误差，减弱未损伤区域模态参数变化对薄弱单元甄别的干扰，完全消除这种干扰有待后续深入研究。

3) 目前，国内外尚未关注地下空区群单元的结构模态问题，本文为该领域探索性研究，现场模态试验结果难免会受到噪声、设备扰动等因素干扰。随着测试技术的发展，获取精度更高的模态参数并非难事^[26]。

4) 损伤模态识别法主要适用于围岩为石灰岩、大理岩、铁矿、铜矿等硬岩结构采空区群的薄弱单元甄别。对于铝土矿、煤矿等软岩采空区的甄别，有待后续深入研究。

7 结论

1) 为甄别复杂采空区群中的薄弱单元，以某地下石灰石矿山采空区群为工程实例，通过构建离散振动力学模型和应变改变量相关影响因素分析，创新地提出薄弱单元损伤模态识别法，给出甄别流程，并从算例计算和工程实际应用两方面验证其可靠性。

2) 自振频率和应变模态的甄别指标能准确识别采空区群中的薄弱单元。单体单元和双体单元损伤都会使采空区群的自振频率甄别指标I_M(k)值大于0，损伤区域的应变模态甄别指标I_N(x)值会明显出现凸起，随着损伤程度增大，I_M(k)值和I_N(x)峰值越来越大。

3) 仅顶板B1损伤时，高阶I_M(k)比低阶更灵敏反映损伤变化程度，第四阶指标识别效果更优；仅矿柱Z6损伤时，第二、四阶指标识别效果更优；B1和Z6共同损伤时，I_M(k)对B1损伤程度的变化相较于Z6更为敏感，第二阶指标识别效果更佳。

4) 现场勘察结果表明，研究区域采空区群内的顶板B1发生多次碎石脱落现象，矿柱Z6存在局部滑移问题，相对于其他顶板与矿柱，B1和Z6损伤程度较深，属于空区群的薄弱单元，勘察结果与理论计算甄别结果相符，验证了理论方法的可靠性。