2. 北京交通大学 交通运输学院,北京 100044
2. School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China
作为城轨系统中的重要组成部分,车辆基地对地铁的高效运营起着关键作用,其主要由停车库、检修库、办公生活设施等组成,它的规模主要取决于运用车数量[1]。对于同时配备多个车辆基地的城轨线路,车辆基地规模直接影响列车在发车阶段与回场阶段的行驶路径,进而影响其空驶里程。此外,在不同列车首发模式下,其空驶里程也存在差别。因此,从城轨车辆基地规划与运营组织协同考量的角度研究车辆基地规模的设计与分配方案,不仅有助于高效合理地利用各类资源,还可显著提高轨道交通路网的运营效率,从而取得良好的经济效益。
目前,国内外对于城轨车辆基地规模的研究主要考虑城轨车辆的检修体制以及规划设计阶段车辆基地的内部厂房布置等因素。文献[2]提出检修体制精细化、积极推进车辆基地资源共享等建议。文献[3]则提出可以通过利用社会资源进行城轨车辆的检修与维护,以优化其规模与布局。文献[4]的研究表明车辆基地功能布局不合理、列位总规模偏高等是导致车辆基地规模偏大的主要原因。文献[5-7]提出了不同的车辆基地集约化设计方法以优化车辆基地规模。部分研究关注与车辆基地规模、数量对列车运用的影响。文献[8]以长沙轨道交通2号线为例,提出停车库规模问题与运营列车数量的计算方法。文献[9-11]等研究了城轨首班车调配以及出场路径优化问题,在其所建立的模型中以车辆基地规模作为约束条件。
总体而言,基于城轨列车运用调度以分析车辆基地规模分配的研究仍为少数。且目前在实际规划设计中,车辆基地规模多凭借经验决定,难以保证车辆基地规模分配方案的质量。鉴于此,本文密切结合城轨运营组织的特点,考虑不同首发模式,面向不同列车运行阶段,以空驶里程为优化目标搭建混合整数线性规划模型以研究车辆基地的规模分配问题。本研究不仅提出了科学合理的城轨车辆基地规模分配确定方法,而且提供了城轨车辆基地规划决策理论支撑。
1 问题描述本文的研究对象是城市轨道交通中具有多个车辆基地、多个折返站的以及多条交路服务的复杂线路。正常情况下,较长的城轨线路会设置两个或两个以上的车辆基地,以保障日常的载客服务以及列车检修工作。城轨列车的空驶一般发生在以下3个阶段:1)运营前集中发车阶段,即在每日运营开始前,部分列车从车辆基地出发空驶至首发车站开始准备载客;2)高峰前加车阶段,在高峰期前将加开列车以提升运输能力,满足高峰期间的出行需求,列车从车辆基地出发空驶至首发车站;3)回场阶段,在运营结束后,列车在终点站完成清客,空驶返回车辆基地。
以包含9个车站、两个车辆基地、4个折返站、2条交路的简单线路为例进行问题描述,如图 1所示。S1~S9为车站编号,假设S1→S9的方向为上行,S9→S1的方向为下行。节点10~18表示上行站点,节点1~9表示下行站点。节点19、20则表示车辆基地,其出入线分别与站S1、S5相连。该线路具有2条交路,分别是S1~S9与S3~S7。为保证在运营期间两条交路上有足够数量的列车以满足不同交路上乘客出行需求,列车需要在运营前发车及高峰前加车阶段空驶至首发站,准备载客运营。首发站的选取与交路的设置以及不同的首发模式有关。根据文献[12-14],首发模式大致分为3类:大交路端点首发、多交路端点首发、均匀首发。3种首发模式的示意如图 2所示。在运营结束后,运营在不同交路的列车以交路端点站为终点站,在终点站完成清客后,空驶返回车辆基地。

|
图 1 假设线路示意图 Fig. 1 Diagram of the hypothetical line |

|
图 2 不同首发模式示意图 Fig. 2 Diagram of different departure modes |
对于给定线路,需要确定2个车辆基地的车辆规模,以明确其配属列车数,并指定列车的出场、回场路径,使总空驶里程最小。值得注意的是,车辆基地的配属列车一般包括运用车、检修车、备用车。其中检修车的数量可根据对应的检修制度计算;根据文献[15],初期和近期的备用车数量为运用车数量的10%,远期为6%。车辆基地规模主要由运用车数量决定[1]。在运用车数量固定的情况下,检修车与备用车的计算相对较为固定,因此本文以运用车列位数指代车辆基地规模。
2 面向空驶里程优化的车辆基地规模分配模型为实现车辆基地规模分配模型搭建,本节将第1节中的问题转化为车辆基地规模可变情况下的列车路径优化问题,建立以空驶里程为优化目标的混合整数线性规划模型。
2.1 模型假设为便于建模与描述,针对本文构建的城轨车辆基地规模分配模型作以下假设:1)在城轨线路实际运营中,一般由多个高峰时期。除早高峰外,其他阶段线路上列车已达到循环运行的状态,列车一般从车辆基地出发,直接进入正线运行,这部分里程为固定值,无优化空间,列车空驶里程可忽略不计,因此仅考虑早高峰阶段的列车空驶。2)在运营前发车阶段与高峰前加车阶段,车辆基地的发车能力与折返站的折返能力有限,因此发车作业与折返作业需要在规定的时间内完成。在回场阶段,由于列车为分散回场,因此该阶段回场与折返作业一般无时间限制。
2.2 车辆基地规模分配建模降低城轨企业运营成本,提高列车运用效率,减少列车空驶里程是城轨领域重要环节。因此,根据第1节所提出的问题,本文构建以空驶里程为目标的车辆基地规模分配模型:
| $ \begin{gathered} \min \sum\limits_r \sum\limits_i \sum\limits_j z_{r, i, j} \cdot G(i, j)+\sum\limits_i \sum\limits_j z_{r^{\prime}, i, j}^{\prime} \cdot \\ G^{\prime}(i, j)+\sum\limits_i \sum\limits_j z_{r^{\prime \prime}, i, j}^{\prime \prime} \cdot G^{\prime \prime}(i, j) \end{gathered} $ | (1) |
| $ \begin{gathered} \sum\limits_i z_{r, i, j}=\sum\limits_k z_{r, j, k}, \sum\limits_i z_{r^{\prime}, i, j}^{\prime}= \\ \sum\limits_k z_{r^{\prime}, j, k}^{\prime}, \sum\limits_i z_{r^{\prime \prime}, i, j}^{\prime \prime}=\sum\limits_k z_{r^{\prime \prime}, j, k}^{\prime \prime} \\ \forall r \in R, r^{\prime} \in R^{\prime}, r^{\prime \prime} \in R^{\prime \prime} ; i, j, k \in A \end{gathered} $ | (2) |
| $ \begin{gathered} \sum\limits_j z_{r, i, j} \leqslant 1, \sum\limits_j z_{r^{\prime}, i, j}^{\prime} \leqslant 1, \sum\limits_j z_{r^{\prime \prime}, i, j}^{\prime \prime} \leqslant 1 \\ \forall r \in R, r^{\prime} \in R^{\prime}, r^{\prime \prime} \in R^{\prime \prime} ; i, j \in A \end{gathered} $ | (3) |
| $ \begin{gathered} \sum\limits_r z_{r, i, v}=O_i, z_{r^{\prime}, i, v}=O_i^{\prime} \\ \forall r \in R, r^{\prime} \in R^{\prime}, i \in S, K(i, s)=1, K^{\prime}(i, s)=1 \end{gathered} $ | (4) |
| $ \begin{gathered} \sum\limits_{r^{\prime \prime}} z_{r^{\prime \prime}, v, i}^{\prime \prime}=D_i \\ \forall r^{\prime \prime} \in R^{\prime \prime}, i \in S, K^{\prime \prime}(v, i)=1 \end{gathered} $ | (5) |
| $ \begin{gathered} \sum\limits_r \sum\limits_i z_{r, i, j}=n_1, \sum\limits_r \sum\limits_i z_{r^{\prime}, i, j}^{\prime}=n_2 \\ \forall r \in R, r^{\prime} \in R^{\prime}, i \in P, j \in S \end{gathered} $ | (6) |
| $ \begin{gathered} \sum\limits_r z_{r, i, j} \leqslant C_{1, i}^{\prime}, \sum\limits_r z_{r, i, k} \leqslant C_{2, i}^{\prime} ; z_{r^{\prime}, i, j} \leqslant C_{1, i}^{\prime}, z_{r^{\prime}, i, k} \leqslant C_{2, i}^{\prime} \\ \forall r \in R, r^{\prime} \in R^{\prime}, i \in P, j \in\left\{1, 2, \cdots, N^{\prime}\right\}, k \in\left\{N^{\prime}+1, N^{\prime}+2, \cdots, 2 N^{\prime}\right\} \end{gathered} $ | (7) |
| $ \begin{gathered} \sum\limits_r z_{r, i, i+N^{\prime}}+\sum\limits_r z_{r, i+N^{\prime}, i} \leqslant \eta_i, z_{r^{\prime}, i, i+N^{\prime}}^{\prime}+z_{r^{\prime}, i+N^{\prime}, i}^{\prime} \leqslant \eta_i \\ \forall r \in R, r^{\prime} \in R^{\prime}, i \in P, j \in\left\{1, 2, \cdots, N^{\prime}\right\}, k \in\left\{N^{\prime}+1, N^{\prime}+2, \cdots, 2 N^{\prime}\right\} \end{gathered} $ | (8) |
| $ \begin{gathered} \sum\limits_j \sum\limits_r z_{r, i, j}+\sum\limits_j z_{r^{\prime}, i, j}^{\prime}=\sum\limits_j z_{r^{\prime \prime}, j, i}^{\prime} \\ \forall r \in R, r^{\prime} \in R^{\prime \prime}, r^{\prime} \in R^{\prime \prime}, i \in P, j \in S \end{gathered} $ | (9) |
式中:i、j、k线路上任意节点编号,节点种类包括站点、车辆基地与虚拟节点,当表示站点时,分上行站点与下行站点,若节点i表示某一站点的上行站点,则i+N′则表示该站点的下行站点;v表示虚拟节点;zr, i, j、z′r, i, j、z″r, i, j分别表示运营前发车阶段、高峰前加车阶段与运营后回场阶段的列车01变量,若r车连续经过i, j站点,则其值为1;G、G′、G″分别表示3个运营阶段的距离矩阵,例如在运营前发车阶段,节点i, j相邻且i可直达j,G(i, j)=d(节点间距),若站点i, j不相邻,则G(i, j)=M,i, j∈S;R、R′、R″分别表示不同运营阶段列车集合;K、K′、K″分别表示不同运营阶段邻接矩阵,例如在运营前发车阶段,若节点i, j相邻且i可直达j,K(i, j)=1,若站点i, j不相邻,则K(i, j)=0,i, j∈S;A表示线路所有节点集合,包括站点、车辆基地、虚拟节点;S、P、T分别表示线路站点集合、车辆基地集合与折返站集合;Oi、Oi′分别表示运营前发车阶段与高峰前加车阶段首发站i的发车列数,i∈S;n1、n2分别表示运营前发车阶段与高峰前加车阶段的列车数量;Di表示终点站i的到达列车数,i∈S;N、N′分别表示线路总列车数与总站点数;C′1, i、C′2, i分别表示车辆基地i的上下行发车能力,i∈P;ηi表示折返站i的折返能力,i∈T。
目标函数(1)由运营前发车阶段、高峰前加车阶段与回场阶段的空驶里程3部分组成;式(2)为路径连续性约束,同时引入虚拟节点v以保证列车路径的连通性;式(3)为路径唯一性约束;式(4)为运营前发车阶段与高峰前加车阶段的首发站列车数量约束,表示在规定的时间内需要空驶至首发站的列车数量;式(5)为终点站到站列车数量约束;式(6)则表示运营前发车阶段与高峰前加车阶段的发车数量;式(7)为车辆基地发车能力约束,影响车辆基地发车能力的主要因素为咽喉区列车通过能力[16];式(8)为折返站折返能力约束,折返能力取决于折返线的布置形式、车站作业控制方式和相关的作业时间标准等[17];式(9)为车辆基地规模守恒约束。
3 案例分析 3.1 案例描述以广州市城轨13号线远期规划阶段的线路为例,验证所提出模型的有效性。在规划阶段远期该线路全长59.3 km,设有34座车站。基于线路基本信息构建的有向网络图如图 3所示。

|
图 3 广州地铁13号线有向网络图 Fig. 3 Directed network of Guangzhou Metro Line 13 |
该线路共设置3个车辆基地以保障列车的正常运营,分别用节点69、70、71表示,与车站S2、S24、S33相连,其基本信息见表 1。默认车辆基地的出段线为上行方向、入段线为下行方向。由于地形与接轨方案的限制,车辆基地2仅与S24的上行站点相连,出入线共用一条线。
| 表 1 车辆基地基本信息 Tab. 1 Basic information of depots |
13号沿线共设置13个折返站,其中S1、S6、S13、S20、S26、S29、S30、S34默认为开启状态,折返距离为0.232 km,折返能力为26列/h。折返站S9、S17、S23、S24为渡线形式,在日常运营中,主要用于对故障列车的存放、检查与修理,避免影响全线列车的运行秩序[18];折返站S32则需承担不同线路的衔接功能,因此上述5个折返站默认为未开启状态。为满足该线路上不同车站区间的客流需求,提升列车运用效率,线路设置有两条交路:大交路S1~S34,小交路S6~S29。大小交路在运营前发车阶段与高峰前加车阶段的车底运用数量见表 2。
| 表 2 交路基本信息 Tab. 2 Basic information of routing schemes |
基于Python3.7编程,并结合CPLEX12.9求解第2节中的规模分配模型。求解运算在CPU为Inter Core i7-9700 3.00GHz,内存为16 GB的电脑上运行。对3.1节所示的案例,模型求解结果见表 3。可以看出,对于3种不同的首发模式,均可在12 s内快速获得最优解。其中,3个首发模式下车辆基地规模分配结果相同,多交路端点首发模式下车辆空驶里程最小。总体来看,3种模式下运营前发车阶段与高峰前加车阶段的空驶里程差异较为明显,但运营后回场阶段的空驶里程并无差异。对于3种首发模式,由于运营结束后到达终点站的列车数量不受首发模式的影响,因此列车在运营后回场阶段的空驶里程差异不大。车辆基地1与3的规模较大,其原因在于这两个车辆基地距离交路端点车站更近,因此在运营后回场阶段,多数列车可在较短的空驶里程条件下返回车辆基地。
| 表 3 模型求解结果 Tab. 3 Results of the model |
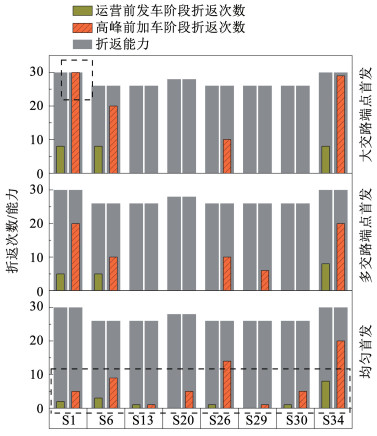
如图 4所示,在不同首发模式下,由于高峰前加车阶段所需列车数较多,在该阶段车辆基地1与3的发车数量达到发车能力的上限。这表明当前车辆基地规模受接轨方案与发车能力限制,且空驶里程仍存在优化空间。在运营前集中发车阶段与高峰前加车阶段,各个折返站的折返能力与列车折返次数如图 5所示。在大交路端点首发模式下,车站S1在高峰前加车阶段时折返次数达到上限,该折返站在此阶段占用率达到100%。在均匀首发模式下,各折返站的折返次数虽未达到上限,但均有一定数量的列车在车站折返,因此各折返站的使用率达到100%。

|
图 4 车辆基地发车能力与发车数量 Fig. 4 Capacity and number of departures from depots |
|
图 5 折返站折返能力与列车折返次数 Fig. 5 Capacity and times of turn-back stations |
在案例线路的远期规划阶段,车辆基地1、2、3的计划规模分别为34、8、33列。通过本文模型获得的规模分配结果分别为28、19、28列,与车辆基地计划规模存在一定差异,这是由于车辆基地1与3的发车能力较低,而在高峰前加车阶段所需列车数量较多,因此部分列车需要分配至车辆基地2以满足高峰前加车阶段的运营需求。但总体来看,规划阶段车辆基地计划规模的分配情况与模型计算结果的基本分配情况类似,即位于线路两端的车辆基地规模较大,位于线路中间的车辆基地规模较小,因此可验证模型合理性与有效性。
为验证利用本文模型可获得经济节约型的车辆基地规模分配结果,以案例实际车辆基地计划规模作为额外模型输入并计算空驶里程,并与本文模型结果对比分析。但由于车辆基地发车能力限制,在以案例实际车辆基地计划规模分配作为模型输入条件下,无法获得可行解。因此考虑不限制发车能力,对比分析空驶里程,结果如表 4所示。与实际车辆基地计划规模下的结果相比,本文提出的模型方法可以实现不同程度的空驶里程优化,在大交路端点首发、多交路端点首发与均匀首发模式下,空驶里程分别实现了18.11%、13.57%与3.58%的降低,进而节约列车运行成本,取得良好的经济效益,同时也可证明模型有效性。
| 表 4 与实际车辆基地计划规模对比(不限制发车能力) Tab. 4 Comparison with actual planned capacity of depot (without restriction on departure capacity) |
由3.2节中的描述可知,在研究案例背景下,车辆基地的收发车方向、发车能力以及折返站的开启方案的改变均可影响空驶里程,进而改变车辆基地规模分配方案,因此本文针对这3个方面进行敏感性分析。
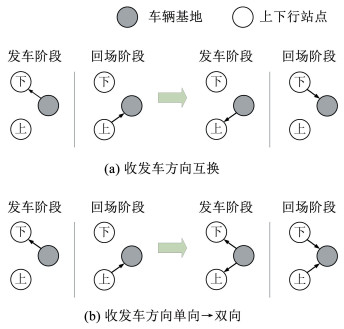
1) 车辆基地收发车方向。车辆基地1与3的出入线与其所在的车站上下行站点相连,因此考虑优化车辆基地1与3的收发车方向。对于双向连接的出入线,理论优化方案有以下两种:收发车方向互换;收发车方向单向变为双向,如图 6所示。考虑以上两种不同的收发车方向优化方法与默认的发车方向,共有9种组合方案,见表 5。不同发车方向配置方案下的模型结果如图 7所示。在大交路、多交路端点首发模式下,空驶里程对车辆基地的发车方向变化较为敏感。在这两种首发模式下,空驶里程的波动范围相对较大,空驶里程最大差值高达2 182.92 km与2 040.78 km,不同接轨方案下空驶里程数据标准差为655.35与613.87。而在均匀首发模式下,空驶里程波动范围相对较小,其最大差值仅为1 110.09 km,数据标准差仅为342.67。总体来说,在不同首发模式下,应用双向收发车可使空驶里程得到有效改善,原因在于双向收发车可使得列车行驶路径更为灵活,减少其不必要的折返。然而,在实际运营中,双向收发车相较于单向收发车意味着更高的运营成本,且可能会正线运行的列车造成影响,因此在不考虑双向收发车的情况下,发车方向最优配置方案为BA。
|
图 6 收发车方向优化 Fig. 6 Optimization of arrival and departure directions |
| 表 5 车辆基地1,3收发车方向 Tab. 5 Arrival and departure directions of Depots 1, 3 |

|
图 7 不同发车方向配置方案下模型结果 Fig. 7 Results under different departure direction scenarios |
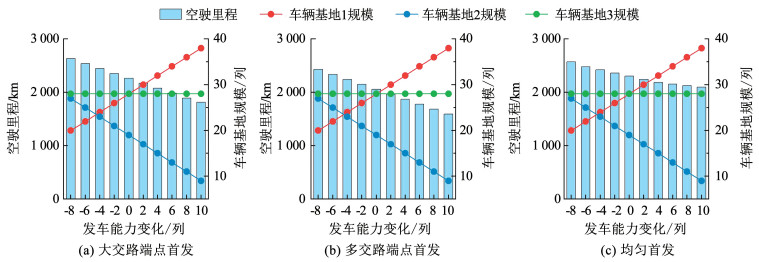
2) 发车能力。车辆基地发车能力是运营前发车阶段与高峰前加车阶段制约出场列车行车效率的主要因素。如图 8~10所示,使不同车辆基地的发车能力发生变化,车辆基地总的规模分配结果也并不相同。对于车辆基地1与车辆基地3,随着发车能力逐渐增加,空驶里程逐渐降低,车辆基地规模分配结果也随之变化;当发车能力增加到某一值时,空驶里程与规模分配保持稳定,不再变化。对于车辆基地2,发车能力的变化对空驶里程与车辆基地规模无影响作用。其原因在于车辆基地2本身的发车能力相对较高,且受其选址与接轨方案的限制,分配于其的列车数占比并不高,因此其发车能力在一定范围内调整并无影响。综上,在实际车辆基地规划建设与运营中,可考虑调整车辆基地1与3的发车能力与规模,以降低空驶里程与运营成本。
|
图 8 车辆基地1不同发车能力下的模型结果 Fig. 8 Results for Depot 1 under different departure capacity |

|
图 9 车辆基地2不同发车能力下的模型结果 Fig. 9 Results for Depot 2 under different departure capacity |

|
图 10 车辆基地3不同发车能力下的模型结果 Fig. 10 Results for Depot 3 under different departure capacity |
3) 折返站开启方案。由文献[13]的研究可知,开放未启用的折返站是缩短总空驶距离的有效措施。由3.1节中的案例描述可知,折返站S9、S17、S23、S24与S32默认为未开启状态。因此考虑开启以上折返站,折返距离与折返能力与其余折返站相同。如图 11所示,随着不同折返站的开启,总空驶里程也随之发生变化。其中,折返站S24开启时,总空驶里程最小。这是由于S24同时也是车辆基地接轨站,其开启折返功能可有效缩短部分列车在发车与回场时的行驶路径。在大交路、多交路端点首发模式下,不同折返站的开启对车辆基地规模分配并无影响;在均匀首发模式下,车辆基地规模分配发生一定变化,但变化程度相对较小。

|
图 11 不同折返站开启方案下的模型结果 Fig. 11 Results under different turn-back operation scenarios |
结合列车运营组织,考虑列车空驶里程研究城轨车辆基地规模分配是城轨线路规划阶段的重要决策,但目前该问题并未获得广泛关注。本文面向运营前发车阶段、高峰前加车阶段与运营结束后回场阶段3个阶段,以列车空驶里程最小为优化目标,建立了针对多车辆基地、多交路的城轨线路车辆基地规模分配模型。以广州地铁13号线远期规划为例验证模型的有效性。案例结果表明,所提出的方法可快速获得经济节约型的车辆基地的规模分配结果以及每日列车的总空驶里程,以辅助实际决策。同时,针对影响模型的3个因素(车辆基地收发车方向、发车能力以及折返站开启方案)进行敏感性分析,具有以下发现:
1) 在大交路、多交路端点首发模式下,空驶里程对车辆基地收发车方向的变化较为敏感;应用双向收发车可使得空驶里程得到明显改善;不考虑双向收发车时,车辆基地规模分配结果相对稳定。
2) 部分车辆基地发车能力的增加可使其规模也随之增加,列车总空驶里程下降。在实际车辆基地规划建设与运营中,可考虑调整车辆基地的发车能力与规模,以降低空驶里程与运营成本。
3) 总体而言,额外折返站的开启在一定程度可改善空驶里程,但对车辆基地规模分配结果影响较小。
本研究可为城轨车辆基地的规划决策提供一定的理论支撑。同时,本研究也具有一定的改进与拓展空间,在城轨资源共享背景下,同一个车辆基地往往承担着多条线路的列车检修工作,因此线网条件下的车辆基地规模分配对实际规划运营更具有参考价值。此外,从时刻表角度确定列车的行驶路径可获得更精细的空驶里程,以便于规模分配的讨论与分析。
| [1] |
陈福贵. 地铁不同场段分布对其规模分配和运营成本的影响[J]. 铁道标准设计, 2013(9): 37. CHEN Fugui. The influence caused by different metro yard and depot arrangements on its size distribution and operation cost[J]. Railway Standard Design, 2013(9): 37. DOI:10.13238/j.issn.1004-2954.2013.09.011 |
| [2] |
尚漾波, 叶霞飞. 城市轨道交通车辆段规模影响因素分析[J]. 中国科技论文, 2008(10): 731. SHANG Yangbo, YE Xiafei. Analysis on the influence factors of depot's scale in urban mass transit system[J]. China Sciencepaper, 2008(10): 731. |
| [3] |
郭欢, 陈峰. 城市轨道交通车辆基地的优化[J]. 城市轨道交通研究, 2010, 13(8): 73. GUO Huan, CHEN Feng. On the optimization of vehicle depot in urban rail transit[J]. Urban Mass Transit, 2010, 13(8): 73. DOI:10.3969/j.issn.1007-869X.2010.08.016 |
| [4] |
张道海, 江捷, 刘龙胜. 城市轨道交通车辆基地规模优化策略研究[J]. 城市轨道交通研究, 2014, 17(8): 69. ZHANG Daohai, JIANG Jie, LIU Longsheng. On the improved strategy for metro depot scale in China[J]. Urban Mass Transit, 2014, 17(8): 69. DOI:10.3969/j.issn.1007-869X.2014.08.017 |
| [5] |
史明红. 地铁车辆段的集约节能设计[J]. 都市快轨交通, 2011, 24(3): 40. SHI Minghong. Energy-saving design of a metro depot[J]. Urban Rapid Rail Transit, 2011, 24(3): 40. DOI:10.3969/j.issn.1672-6073.2011.03.011 |
| [6] |
张雄. 地铁车辆段设计规模的探讨[J]. 铁道工程学报, 1998(1): 99. ZAHNG Xiong. Exploration on design scale of car depot for subway[J]. Journal of Railway Engineering Society, 1998(1): 99. |
| [7] |
钱科元, 王孔明, 徐银光, 等. 悬挂式单轨车辆基地集约化设计[J]. 铁道标准设计, 2021, 65(12): 152. QIAN Keyuan, WANG Kongming, XU Yinguang, et al. Intensive design of suspended monorail depot[J]. Railway Standard Design, 2021, 65(12): 152. DOI:10.13238/j.issn.1004-2954.202010180002 |
| [8] |
宾松. 城市轨道交通车辆停放场规模优化研究[J]. 城市轨道交通研究, 2010, 13(6): 32. BIN Song. Optimization of urban rail transit car parking scale[J]. Urban Mass Transit, 2010, 13(6): 32. DOI:10.3969/j.issn.1007-869X.2010.06.010 |
| [9] |
钟庆伟, 赵军, 文超, 等. 城轨线路运营时段前车底空驶出场路径优化[J]. 铁道学报, 2018, 40(3): 31. ZHONG Qingwei, ZHAO Jun, WEN Chao, et al. Optimizing rolling stock deadhead routing problem before operation period of urban rail transit line[J]. Journal of the China Railway Society, 2018, 40(3): 31. DOI:10.3969/j.issn.1001-8360.2018.03.005 |
| [10] |
郑丽杰, 何世伟, 郭小乐. 城市轨道交通首班车车底调配及路径优化[J]. 交通信息与安全, 2019, 37(3): 118. ZHENG Lijie, HE Shiwei, GUO Xiaole. Optimization of rolling stock distribution and routing problem for the first train of urban rail transit[J]. Journal of Transport Information and Safety, 2019, 37(3): 118. DOI:10.3963/j.issn.1674-4861.2019.03.015 |
| [11] |
王典, 赵军, 钟庆伟, 等. 城轨线路车底空驶出场路径与时刻表综合优化[J]. 铁道学报, 2019, 41(8): 19. WANG Dian, ZHAO Jun, ZHONG Qingwei, et al. Integrated optimization of rolling stock deadhead routing and timetabling in urban rail transit line[J]. Journal of the China Railway Society, 2019, 41(8): 19. |
| [12] |
袁家伟. 基于大小交路方案的城市轨道交通列车时刻表与车底运用计划协同优化研究[D]. 北京: 北京交通大学, 2021 YUAN Jiawei. Integrated optimization of train timetable, rolling stock circulation plan and short-turning strategy for an urban rail transit line[D]. Beijing: Beijing Jiaotong University, 2021 |
| [13] |
许得杰. 城市轨道交通大小交路列车开行方案优化研究[D]. 北京: 北京交通大学, 2016 XU Dejie. Optimization for train plan of full-length and short-turn routing in urban rail transit[D]. Beijing: Beijing Jiaotong University, 2016. |
| [14] |
WANG Dian, D'ARIANO A, ZHAO Jun, et al. Integrated rolling stock deadhead routing and timetabling in urban rail transit lines[J]. European Journal of Operational Research, 2021, 298(2): 526. DOI:10.1016/j.ejor.2021.05.053 |
| [15] |
毛保华. 城市轨道交通规划与设计[M]. 3版. 北京: 人民交通出版社, 2006. MAO Baohua. Planning and design for urban rail transit[M]. 3rd ed. Beijing: China Communication Press, 2006. |
| [16] |
徐彰杰. 重庆轨道交通白居寺车辆段段内发车能力研究[J]. 都市快轨交通, 2021, 34(3): 65. XU Zhangjie. Capacity analysis of entrance/exit line from Bajusi depot of Chongqing rail transit[J]. Urban Rapid Rail Transit, 2021, 34(3): 65. DOI:10.3969/j.issn.1672-6073.2021.03.011 |
| [17] |
李英. 城市轨道交通折返线相关问题研究[J]. 城市轨道交通研究, 2003, 6(1): 28. LI Ying. A study on the turn-round track in urban mass transit[J]. Urban Mass Transit, 2003, 6(1): 28. DOI:10.3969/j.issn.1007-869X.2003.01.007 |
| [18] |
于春华. 城市轨道交通单渡线合理线间距的探讨[J]. 城市轨道交通研究, 2007, 10(4): 52. YU Chunhua. Right distance between tracks of single crossover in URT[J]. Urban Mass Transit, 2007, 10(4): 52. DOI:10.3969/j.issn.1007-869X.2007.04.017 |
 2023, Vol. 55
2023, Vol. 55


