2. 福建瑞森水泥制品发展有限公司,福建 漳平 364400
2. Fujian Ruisen Cement Products Development Co., Ltd., Zhangping 364400, Fujian, China
普通混凝土电杆存在自重大、抗拉强度较低、杆身易开裂、耐久性差、承载力低等问题[1-4]。难以满足电杆更多功能、更高强度的要求。针对普通混凝土电杆易开裂、受弯承载力低等问题。文献[5-8]开展了钢纤维混凝土电杆力学性能试验研究,表明一定量的钢纤维掺入并不会出现“结团”现象;电杆的抗裂度得到了提高,裂缝宽度也有减小的趋势。不过,这些方法对减小电杆自重、提高其耐久性方面仍有所不足。此外,在沿海地区,普通混凝土或钢纤维混凝土电杆会受到氯盐等介质腐蚀,常出现桩体过早开裂等问题,进而导致钢筋和纤维锈蚀等质量缺陷,影响结构的正常使用[9]。
为提高上述电杆使用性能,采用超高性能混凝土(ultra-high performance concrete,UHPC)[10-12]替代普通混凝土和纤维混凝土是另一种较具应用前景的选择。相比传统混凝土电杆,UHPC电杆不仅能提高其使用寿命以及耐久性能(高抗渗性、抗冻融性及抗腐蚀性),还可充分发挥电杆中高强钢筋抗拉性能和材料抗压强度高的优点[13-14]。然而,常规UHPC存在早期收缩和开裂等问题[15],并不能充分发挥其超高性能的特点。也有研究表明,加入一定量的粗骨料可以改善UHPC早收缩效果[16]、从而进一步优化其力学性能[17-19]。此外,文献[20]表明,UHPC输电杆需要添加一定量的粗骨料才能离心成型,但未给出具体配合比,并且该输电杆壁厚过大,将其应用在实际工程中的经济性不强。辽宁某企业已研制出薄壁UHPC输电杆[21],其电杆重量降低了一半,但成型方式为立式浇筑,成型效率低,且脱模工艺繁复,成本较高。为改进其成型工艺,文献[22]在常规UHPC材料的基础上优化其配合比,通过离心成型方式制出UHPC环形管构件。
综上所述,现有研究仅限于UHPC材料自身,很少涉及将新材料(UHPC)和新工艺(离心成型)相结合下的应用。为促进UHPC输电杆在国内的推广使用,了解基于离心成型的粗骨料UHPC电杆裂缝发展,以及承载力等力学性能较为重要。为此,本文在离心成型工艺基础上,制作了6根2.0 m含粗骨料的UHPC电杆,并进行了受弯试验研究,分析其不同钢纤维掺量和不同配筋率下的破坏模式、跨中变形、应变发展规律、刚度退化以及受弯承载力等力学性能,为基于离心成型含粗骨料的UHPC电杆设计和有关规范的制定提供参考。
1 试验 1.1 原材料UHPC中的主要材料水泥、硅灰、粗砂、中砂、细砂、减水剂、石灰石粉的配合比为1∶ 0.3∶ 0.71∶ 047∶ 0.24∶ 0.025∶ 0.15。水泥采用福建“红狮牌”P.O 52.5硅酸盐水泥。硅灰产于西宁铁合金厂,其SiO2质量分数不少于90%。石英砂分为3种不同粒径,包括粗粒径砂(1.25~0.63 mm)、中粒径砂(0.63~0.315 mm)、细粒径砂(0.315~0.16 mm)。减水剂采用聚羧酸类高效减水剂,减水率高达25%以上。石灰石粉主要成分为碳酸钙。另外,以粒径为5 mm的玄武岩碎石为粗骨料,掺量为800 kg/m3。钢纤维采用赣州大业金属纤维有限公司生产的直线型冷拔镀铜钢丝纤维,其公称粒径为0.2 mm,公称长度为13 mm,弹性模量为200 GPa,抗拉强度为2 850 MPa。
1.2 试件设计本试验预制并成功离心成型出6根含粗骨料的UHPC环形电杆。其设计长度均为2.0 m,外径均为300 mm、内径均为220 mm、壁厚均为40 mm,试件编号分别为U-1~U-6。此外,参考文献[23-24],将钢纤维掺量和配筋率作为UHPC电杆的基本参数。U1~U4电杆钢纤维掺量分别为0%、0.5%、1.0%、1.5%,沿环形截面均布置12根Φ10的纵向钢筋,配筋率为2.8%;U-5电杆的钢纤维掺量为1.0%,沿环形截面布置12根Φ8的纵向钢筋,配筋率为1.8%;U-6电杆的钢纤维掺量为1.0%,沿环形截面布置12根Φ12的纵向钢筋,配筋率为3.8%。同时,各电杆沿杆长方向每100 mm设置一道Φ6的横向箍筋。各电杆参数变化如图 1所示。

|
图 1 UHPC电杆截面 Fig. 1 UHPC transmission pole section |
最佳的离心制度是保证混凝土在离心阶段过程中尽可能排除多余水分,减少截面分层现象,从而达到最佳密实度。对于UHPC材料,由于高掺量减水剂的作用,以及离心振动下使其流动性较高,过长的拌和时间会造成UHPC组分离析。因此,普通混凝土输电杆或管桩的离心制度并不完全适用于UHPC构件。本次试验参照普通混凝土输电杆离心制度和UHPC混凝土离心特点,并经过多次调整离心速度、时间、离心加速度参数,确定了UHPC电杆离心制度,如表 1所示。
| 表 1 UHPC试件离心制度 Tab. 1 Centrifugal system of UHPC specimens |
由图 2(a)可知,对于掺加粗骨料UHPC电杆,离心后模边合缝处无漏浆、无环向和纵向裂缝,且输电杆合缝处的情况良好。外表面光滑透亮,无麻面、粘皮和蜂窝等现象,也未出现每米长度内麻面或粘皮总面积大于相同长度外表面积5%的情况。总体上满足《超高性能混凝土电杆》(T/CEC 143—2017)标准[24]的要求。由图 2(b)可知,离心成型的电杆壁厚均匀,无多余的净浆堆积,截面钢纤维分布均匀。说明骨料的掺加可明显改善钢纤维的分布形式,能防止钢纤维“跑偏”,减少钢纤维集中分布在最外层。

|
图 2 试件离心成型效果 Fig. 2 Centrifugal forming effect of specimens |
根据GB/T31387—2015《活性粉末混凝土》[25],本试验制作了100 mm×100 mm×100 mm的立方体试件,用于测试含粗骨料的UHPC立方体抗压强度fcu、劈裂抗拉强度ftk、抗折强度fcf和弹性模量Ec。另外,本试验也制作了基于离心成型的0.3 m环形试件,并将其沿截面均等分割为6份,分别对离心成型的含粗骨料的UHPC轴心抗压强度fc和劈裂抗拉强度ftk′进行测试,其力学性能指标如表 2所示。由表 2可知,随着钢纤维掺量由0%逐渐增加至1.5%,各试件的立方体抗压强度、轴心抗压强度、劈裂抗拉强度、抗折强度和弹性模量均有不同程度的提高。离心后的环形试件轴心抗压强度约为立方体抗压强度的75%;环形试件劈裂抗拉强度则为立方体试件的73%~82%,平均为76%。
| 表 2 含粗骨料的UHPC基本力学性能 Tab. 2 Basic mechanical properties of UHPC containing coarse aggregate |
此外,UHPC电杆分别采用Φ8、Φ10、Φ12的HRB400级纵向钢筋,其屈服强度fy分别为456.9 MPa、462.5 MPa、456.9 MPa;弹性模量E分别为200.3 GPa、201.5 GPa、202.1 GPa。
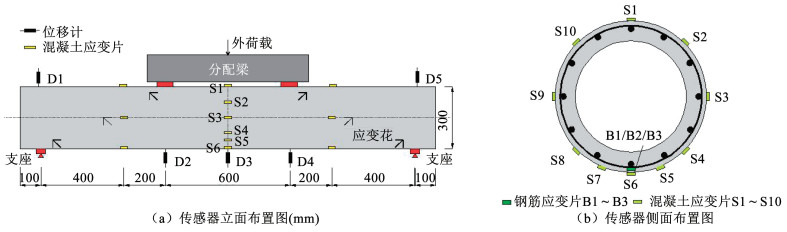
1.5 测点布置本文在试验中布置了两种传感器:位移计和应变片,具体布置情况如图 3所示。其中,在电杆的跨中、三分力点位置以及支座两端顶部安装了5个位移传感器,编号为D1~D5。在电杆跨中截面处沿环向布置了10片混凝土应变片。为防止试验因素导致构件底部应变片过早失效,对构件受拉区域测点进行了加密,编号分别为S1~S10。另外,在底部钢筋布置了3片钢筋应变片,编号为B1~B3。
|
图 3 传感器布置图 Fig. 3 Sensor layout |
本次试验中,由于没有可直接适用于UHPC电杆标准检验弯矩的规范。因此,本试验参照普通混凝土电杆规范进行加载。其加载方式是:根据普通混凝土输电杆极限承载力的计算方法初步估算出标准检验弯矩(约为承载力检验弯矩的50%),按照标准检验弯矩的5%得到加载步长。每两级加载之间静停3 min,观测并记录各项读数。当跨中环向裂缝出现时,每级加载步长取标准检验弯矩的2.5%。加载至试件裂缝宽度大于0.04 mm时,恢复原来的加载步长,随后加载至试件破坏,观测并记录各项读数。试验加载装置如图 4所示。

|
图 4 试验装置图 Fig. 4 Experimental device diagram |
为了更好地描述含粗骨料的UHPC电杆试验现象,此处仅给出典型试件U-3的破坏特征,如图 5所示。电杆在荷载作用下可分为弹性、裂缝开展和破坏3个受力阶段:

|
图 5 试件破坏形态 Fig. 5 Failure mode of specimen |
1) 弹性阶段。加载初期,构件处于弹性工作状态,未出现裂缝,仅电杆的竖向挠度缓慢增大。当荷载增加至极限承载力的16.9%时,构件在跨中截面底部出现第一条细微裂缝,裂缝宽度为0.04 mm。
2) 裂缝开展阶段。随着荷载的增加,不断有新的裂缝产生,当荷载增加至极限承载力的22.5%时,在纯弯区段新增6条细微裂缝,并均匀分布在跨中截面两侧。而已有的裂缝宽度和长度也逐渐发展,但已有裂缝的发展延伸则比较缓慢,主要是因为跨越裂缝的钢纤维参与抗拉工作并起到桥接作用,同时对裂缝的发展形成一定的阻碍。另外电杆沿全截面均匀配置的纵向钢筋对周围混凝土的约束作用较强,也进一步限制了裂缝的发展。当荷载增加至极限承载力的50.7%时,弯剪区段出现了由支点指向加载点的斜裂缝,此时跨中截面处主裂缝的最大宽度发展至0.29 mm。
3) 破坏阶段。继续加载至极限荷载的91.5%时,跨中底部受拉钢筋达到屈服应变,纯弯区不再产生新的环向主裂缝,弯剪区段也不再产生斜裂缝,仅是在原有裂缝的基础上发展。此时断裂截面钢纤维裸露,并没有出现混凝土脱落的现象。继续加载,跨中挠度和裂缝宽度急剧增大,并伴随有混凝土的断裂声及纤维的拉扯声。当荷载增加到极限承载力时,顶面受压区混凝土被压碎,裂缝宽度超过2 mm,构件宣告破坏。
此外,U-1~U-4电杆在纯弯区分别产生了14条、11条、10条和9条环向主裂缝,主裂缝沿环形截面呈现出非贯通的分布形态,沿杆长方向为间断分布,其裂缝长度由跨中向两侧逐渐减小。主裂缝间距为6~10 mm,分布较为均匀,钢纤维的掺入对电杆的主裂缝间距基本没有影响。而钢纤维含量最低的U-1电杆在主裂缝之间产生短细的次裂缝较少。随着钢纤维含量的提高,U-2~U-4电杆产生短细的次裂缝逐渐增多。由此说明,钢纤维的掺入在一定程度上阻碍裂缝的发展,而且钢纤维含量越多,电杆主裂缝数量越少,短细的次裂缝越多,其阻裂效果越明显,电杆的抗裂性能越强。
对于配筋率不同的电杆,U-5、U-3和U-6电杆产生的环向主裂缝数量相差不大,但U-5电杆环向主裂缝长度较长,最长可达61 cm,而U-3电杆最大主裂缝长度为42 cm、U-6构件则为31 cm。说明随着配筋率的提高,构件裂缝长度逐渐减小,较高的配筋率可以延缓裂缝开展。
图 6(a)为不同钢纤维含量的UHPC输电杆荷载-裂缝宽度曲线。由图可知,加载初期,构件未开裂,随着荷载增加,各构件裂缝宽度逐渐增大,但裂缝开展较慢。当最大裂缝宽度为0.4 mm时,各曲线出现了较为明显的拐点,此时曲线斜率变小,裂缝开展速率加快。比较U-1~U-4电杆各曲线可知,相同荷载下,钢纤维含量越多,裂缝宽度越小。如当荷载为225 kN时,U-1~U-4跨中截面裂缝最大宽度分别为0.67、0.37、0.32、0.28 mm。主要是因为跨越裂缝的钢纤维参与抗拉工作,同时也起到桥接作用,对裂缝的延伸形成阻碍。说明钢纤维可以起到良好的抗裂作用,钢纤维含量越多,其阻裂效果明显。尤其是钢纤维掺量为1.5%时,阻裂效果最好。

|
图 6 试件裂缝发展 Fig. 6 Crack development of specimens |
图 6(b)为不同配筋率的UHPC输电杆荷载-裂缝宽度曲线。由图可知,各电杆曲线斜率先增大后减小,裂缝先缓慢开展,随后开展速率加快。U-3和U-6电杆曲线趋势基本一致,而配筋率较小的U-5电杆出现了明显的拐点,随后斜率明显下降,裂缝急剧开展。主要原因是电杆纵向配筋率较小,钢纤维混凝土与钢筋的黏结力不足,截面一旦开裂后,部分钢纤维退出工作。说明较低的配筋率不能充分发挥两者的协同工作。当加载到210 kN时,U-5、U-3和U-6电杆的裂缝宽度分别为0.56、0.29、0.26 mm。由此说明,相同荷载下,较高的配筋率能减小裂缝开展速度,阻碍电杆裂缝发展。
2.2 荷载-跨中挠度图 7(a)为不同钢纤维掺量的UHPC电杆荷载-跨中挠度曲线。由图可知,加载前期,各电杆的曲线近似线性增长,此时为弹性变形阶段,曲线斜率较大。随着荷载增加,电杆跨中位移逐渐增大,各电杆曲线均有明显的拐点,随后曲线斜率均减小,变形增长速率加快。其中U-1电杆曲线斜率明显低于U2~U4电杆,这是因为U-1电杆跨裂缝的截面没有钢纤维参与工作,截面抗拉强度小。U-1~U-4电杆的最大承载力分别为297、374、390.5、423.5 kN,后三者比前者分别提高了25.9%、31.5%、42.6%。说明钢纤维掺量越高,电杆的承载能力也越强。另外,U-1~U-4电杆破坏时跨中挠度分别为17.6、33.82、32.79、32.48 mm,后三者比前者分别提高了92.2%、86.3%和84.5%,但U-2~U-4三者相差不大。由此说明,电杆中掺入钢纤维可显著提升其延性性能。由图还可知,当荷载达到360 kN时,U-2~U-4电杆跨中挠度为25.1、20.1、16.0 mm。由此说明,相同荷载下,随着钢纤维掺量增多,试件抵抗荷载变形的能力也越强。

|
图 7 荷载-跨中挠度曲线 Fig. 7 Load-midspan deflection relation curve |
图 7(b)为不同配筋率UHPC电杆荷载-跨中挠度曲线。由图可知,加载前期,各电杆的荷载-挠度曲线几乎重合,且呈线性关系,此时为弹性变形阶段,曲线斜率较大。随着荷载增加,各曲线出现拐点,构件进入裂缝开展阶段,此后,3根电杆的曲线斜率明显减小,变形增长速率加快。其中,U-5电杆荷载-挠度曲线明显低于U-3和U-6电杆,且极限荷载值和跨中挠度值均明显小于U-3、U-6电杆。而三者的最大荷载分别为258.5、390.5、423.5 kN,后两者比前者分别提高了51.1%和63.8%。说明配筋率的增大可显著提高UHPC电杆的承载能力。另外,U-5、U-3和U-6电杆破坏时的跨中挠度分别为21.37 mm、32.79 mm和34.02 mm,后两者比前者分别提高了53.4%、59.2%。这表明配筋率的增大也可提升UHPC电杆的延性性能。由图还可知,当荷载达到253kN时,U-5和U-6电杆跨中挠度分别为17.1、6.4 mm,后者比前者降低了1.67倍。由此说明,相同荷载下,随着配筋率的提高,电杆跨中位移逐渐减小,其抵抗荷载变形的能力也越强。
2.3 应变分析 2.3.1 混凝土压应变图 8(a)为不同钢纤维掺量的UHPC电杆混凝土荷载-压应变曲线。由图可知,加载初期,U-1~U-4的荷载-应变曲线大致呈线性增长,曲线基本重合且应变值较小。当构件进入裂缝开展阶段,荷载-应变曲线出现明显的转折点,各电杆的跨中截面应变均快速增长。其中U-1截面压应变增长最快,U-2~U-4应变增长较为缓慢。在相同荷载下(p=165 kN),U-1~U-4的压应变εc分别为1.538×10-3、0.85×10-3、0.768×10-3和0.58×10-3,后三者比前者分别降低了44.7%、50.1%、62.3%。由此说明,提高钢纤维掺量可以延缓电杆裂缝的开展速度,降低混凝土压应变值,且钢纤维掺量越高,效果越明显。

|
图 8 荷载-压应变曲线 Fig. 8 Load-compression strain curve |
图 8(b)为不同配筋率的U-3、U-5和U-6电杆荷载-压应变曲线。由图可知,在弹性阶段时,各电杆的应变曲线基本重合。随着裂缝开展,各电杆跨中截面应变出现了不同程度的增长。其中U-5截面应变增长最快,U-3和U-6应变增长相对缓慢。当荷载增加至170.5 kN时,各构件的压应变εc值分别为1.462×10-3、0.788×10-3和0.543×10-3,后两者比前者分别降低了46.1%和62.9%。由此说明UHPC电杆配筋率越大,其压应变值越小。较高的配筋率既能提高构件抗裂性能和抵抗变形的能力,又可发挥UHPC材料超高抗压强度的特点。
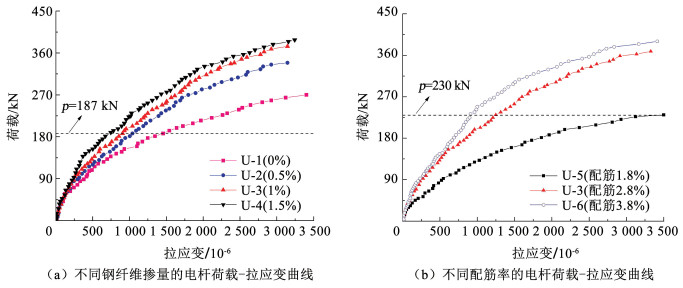
2.3.2 钢筋拉应变图 9(a)为不同钢纤维掺量的UHPC电杆跨中钢筋荷载-拉应变曲线。由图可知,加载初期,U-1~U-4的荷载-拉应变曲线大致呈线性增长,曲线基本重合且应变值较小。当构件进入裂缝开展阶段,荷载-应变曲线出现明显的转折点,各电杆的钢筋拉应变均快速增长。其中U-1钢筋拉应变增长最快,U-2~U-4应变增长较为缓慢,且在相同荷载下(p=187 kN),U-1~U-4的拉应变εt分别为1.447×10-3、1.03×10-3、0.892×10-3和0.739×10-3,后三者比前者分别降低了28.8%、38.4%和48.9%。说明钢纤维掺量较高的UHPC可以先承担一部分的荷载,此时钢筋承担的荷载就小,进而有效地阻碍钢筋应变的增长。
|
图 9 荷载-拉应变曲线 Fig. 9 Load-tensile strain curve |
图 9(b)为不同配筋率的UHPC输电杆跨中钢筋荷载-拉应变曲线。由图可知,加载初期,各电杆跨中截面应变均较小,应变发展随着荷载增加呈线性增长。在裂缝开展阶段时,曲线斜率减小,应变增长加快。其中,U-3和U-6钢筋荷载-拉应变曲线的斜率明显高于U-5电杆。当U-5跨中钢筋达到屈服应变3.5×10-3时,U-3和U-6应变分别为1.248×10-3、0.905×10-3。由此说明UHPC电杆配筋率越大,相同荷载下的钢筋拉应变值越小,较大的配筋率不仅能显著降低钢筋拉应变的增长速率,又能充分发挥与钢纤维阻裂和抗拉增韧作用。
2.4 刚度退化图 10(a)为不同钢纤维掺量的UHPC电杆抗弯刚度退化曲线。由图可知,曲线大致表现为:加载初期,构件刚度迅速下降;接着继续加载,刚度退化幅度逐渐变小,曲线逐渐平缓并趋于稳定地下降。在加载前期,各电杆刚度变化基本一致,而U-2~U-4电杆的初始刚度比U-1电杆分别提高了7.1%、7.1%和10.3%。加载后期U-1电杆的刚度退化幅度较大,而U-2~U-4电杆刚度相差不大。由此说明,掺加钢纤维的UHPC电杆截面抗弯刚度显著提高,其整体抗弯能力也相应增强。

|
图 10 刚度退化曲线 Fig. 10 Stiffness degradation curve |
图 10(b)为不同配筋率的UHPC电杆抗弯刚度退化曲线。由图可知,曲线大致表现为:加载初期,构件刚度迅速下降;当构件进入开裂阶段时,刚度退化幅度逐渐变小,并趋于稳定地下降。加载前期,U-3电杆下降幅度稍快,U-5和U-6电杆刚度退化曲线基本一致,并且U-6比U-3、U-5的初始刚度略大。加载后期,U-3和U-6电杆刚度退化曲线相差不大,而配筋率最小的U-5电杆曲线下降幅度最为明显。当荷载为70 kN·m时,U-5电杆的刚度为2 905 kN·m2,U-6为4 360 kN·m2,后者比前者提高了50.1%。说明配筋率的提高可减缓电杆截面刚度退化速率,且增强截面抗弯刚度和承载能力。
3 承载力计算本文较为系统地收集了管桩或电杆受弯承载力计算方法:
1) 文献[26]指出,电杆均未出现纵向受拉钢筋被拉断和受压区混凝土破坏的情形时,按矩形应力分布图的材料强度极限平衡条件来计算环形电杆的极限弯矩是偏于不安全的。从试验时的裂缝分布和发展分析,钢筋的矩形应力分布区较小,该矩形应力分布区约为受拉区的45%比较合适。因此,按式(1)~(4)计算,其受弯承载力计算值用Mfuc1表示。
| $ M_{\mathrm{fu}}=\alpha_1 f_{\mathrm{c}} A\left(r_1+r_2\right) \frac{\sin \alpha {\rm{ \mathsf{ π} }}}{2 {\rm{ \mathsf{ π} }}}+f_{\mathrm{y}} A_{\mathrm{s}} r_{\mathrm{s}} \frac{\sin \alpha {\rm{ \mathsf{ π} }}+\sin \alpha_{\mathrm{t}} {\rm{ \mathsf{ π} }}}{{\rm{ \mathsf{ π} }}} $ | (1) |
| $ \alpha_{\mathrm{t}} f_{\mathrm{y}} A_{\mathrm{s}}=\alpha_1 \alpha f_{\mathrm{c}} A+\alpha f_{\mathrm{y}} A_{\mathrm{s}} $ | (2) |
| $ \alpha_{\mathrm{t}}=0.45(1-\alpha) $ | (3) |
| $ \alpha=\frac{0.45 f_{\mathrm{y}} A_{\mathrm{s}}}{\alpha_1 f_{\mathrm{c}} A+1.45 f_{\mathrm{y}} A_{\mathrm{s}}} $ | (4) |
2) GB 50010—2010《混凝土结构设计规范》[27]第E.0.3条中,规定均匀配置纵向钢筋的环形截面受弯构件按式(1)、(2)、(5)、(6)计算混凝土电杆的受弯承载力,其受弯承载力计算值用Mfuc2表示。
| $ \alpha_{\mathrm{t}}=1-1.5 \alpha $ | (5) |
| $ \alpha=\frac{f_{\mathrm{y}} A_{\mathrm{s}}}{\alpha_1 f_{\mathrm{c}} A+2.5 f_{\mathrm{y}} A_{\mathrm{s}}} $ | (6) |
3) 文献[28]指出,当α较小时,实际受压区为环内弓形面积,由于环形截面的计算式是通过简化的等效矩形应力图形得出的,简化公式会低估截面的承载力。此时可按照圆形截面考虑,根据圆形截面的计算原理确定αt与α的关系,将将(5)、(6)修正为式(7)、(8),其受弯承载力计算值用Mfuc3表示。
| $ \alpha_{\mathrm{t}}=1.25-2 \alpha $ | (7) |
| $ \alpha=\frac{1.25 f_{\mathrm{y}} A_{\mathrm{s}}}{\alpha_1 f_{\mathrm{c}} A+3 f_{\mathrm{y}} A_{\mathrm{s}}} $ | (8) |
4) 文献[8]结合规范CECS 38—2004《纤维混凝土结构技术规程》[29],在原有受弯承载力计算公式的基础上,考虑钢纤维的阻裂与抗拉增韧作用,即在电杆正截面受拉部分引入了抗拉作用影响系数βte,进一步产生了钢纤维抗拉强度fte(如图 11所示),得到钢纤维混凝土电杆的受弯承载力计算公式,如(9)~(14)所示。其受弯承载力计算值用Mfuc4表示。

|
图 11 电杆截面应力分布图 Fig. 11 Stress distribution diagram of transmission pole section |
| $ \begin{aligned} M_{\mathrm{fu}}= & f_{\mathrm{c}} A\left(r_1+r_2\right) \frac{\sin \alpha {\rm{ \mathsf{ π} }}}{2 {\rm{ \mathsf{ π} }}}+f_{\mathrm{y}} A_{\mathrm{s}} r_{\mathrm{s}} \frac{\sin \alpha {\rm{ \mathsf{ π} }}+\sin \alpha_{\mathrm{t}} {\rm{ \mathsf{ π} }}}{{\rm{ \mathsf{ π} }}}+ \\ & f_{\mathrm{te}} A\left(r_1+r_2\right) \frac{\sin \alpha_{\mathrm{f}} {\rm{ \mathsf{ π} }}}{2 {\rm{ \mathsf{ π} }}} \end{aligned} $ | (9) |
| $ \alpha f_{\mathrm{c}} A+\alpha f_{\mathrm{y}} A_{\mathrm{s}}=\alpha_{\mathrm{t}} f_{\mathrm{y}} A_{\mathrm{s}}+\alpha_{\mathrm{f}} f_{\mathrm{te}} A $ | (10) |
| $ \alpha=\frac{f_{\mathrm{y}} A_{\mathrm{s}}+f_{\mathrm{te}} A}{f_{\mathrm{c}} A+2.5 f_{\mathrm{y}} A_{\mathrm{s}}+1.18 f_{\mathrm{te}} A} $ | (11) |
| $ \alpha_{\mathrm{t}}=1-1.5 \alpha $ | (12) |
| $ \alpha_{\mathrm{f}}=1-1.18 \alpha $ | (13) |
| $ f_{\mathrm{te}}=f_{\mathrm{t}} \beta_{\mathrm{te}} \lambda_{\mathrm{f}} $ | (14) |
5) 文献[30]通过对活性粉末混凝土(RPC)力学性能试验研究, 考虑了RPC较高的抗拉强度、韧性以及钢纤维对RPC抗拉强度的增强,进一步引入了混凝土抗拉强度增强系数βt,此系数是根据RPC中钢纤维掺量确定的,当钢纤维掺量为0.5%~3.0%时,分别对应βt的值为0.05~0.1,并将式(14)修正为式(15),其受弯承载力计算值用Mfuc5表示。
| $ f_{\mathrm{te}}=\left(1+\beta_{\mathrm{t}}\right) f_{\mathrm{t}} \beta_{\mathrm{te}} \lambda_{\mathrm{f}} $ | (15) |
式中:α1为受压区混凝土矩形应力图的应力值与混凝土轴心抗压强度设计值的比值;α为等效受压区混凝土截面面积与全截面面积比值;αt为受拉纵筋面积与全部纵筋面积的比值;αf为受拉区截面面积与全截面面积比值;fc为混凝土轴心抗压强度值,取试件离心后的轴心抗压强度实测值;fy取纵筋受拉或受压屈服强度实测值;ft为混凝土抗拉强度,取试件离心后的劈裂抗拉强度实测值;fte为受拉区钢纤维混凝土等效矩形应力图形的抗拉强度;βte为钢纤维对正截面受弯输电杆受拉区抗拉作用的影响系数,根据规范[29]选取;λf为钢纤维含量特征值,根据规范[29]选取;βt为混凝土抗拉强度增强系数;As为纵筋截面面积;A为UHPC输电杆截面面积;r1、r2分别为输电杆的外径和内径;rs为纵筋至输电杆圆心的半径。
本文采用上述公式分别对离心成型的UHPC输电杆正截面受弯承载力进行了计算,如表 3所示。由表 3可知,试验值Mfut分别为计算值Mfuc1、Mfuc2、Mfuc3、Mfuc4、Mfuc5的2.2~3.0倍、1.6~2.3倍、1.6~2.3倍、1.3~1.7倍、1.2~1.7倍。
| 表 3 受弯承载力计算值 Tab. 3 Calculation value of maximum bending moment of bending capacity |
结果表明,采用文献[26]计算值Mfuc1远小于试验值Mfut,说明普通混凝土环形构件承载力计算公式并不适用于UHPC电杆。而规范[27]和文献[28]在式(3)的基础上修正了αt受拉纵筋面积与全部纵筋面积的比值,进一步提高了电杆的受弯承载能力计算值,但与试验值相比,仍相差较大。
另外,文献[8]针对纤维混凝土考虑了钢纤维的阻裂与抗拉增强增韧作用,在电杆正截面受拉部分增添了钢纤维抗拉作用影响系数βte;在此基础上,文献[30]针对活性粉末混凝土(RPC)继续添加了钢纤维抗拉增强系数βt。其中Mfuc5略大于Mfuc4,两者的计算值与试验值Mfut较为接近,说明UHPC输电杆可以采用该方法进行承载力计算,且该公式计算偏于安全,但相对保守。进一步研究发现,当UHPC电杆的配筋率和钢纤维掺量越高时,其理论计算值与试验值越接近。
4 结论本文进行了6根基于离心成型的粗骨料UHPC输电杆受弯试验研究,分析比较了构件的破坏模式、荷载-挠度曲线、应变、刚度退化以及受弯承载力,得到了以下主要结论:
1) 含粗骨料的UHPC输电杆破坏方式可分为弹性阶段、裂缝开展阶段和破坏阶段,呈现出一定的延性破坏特征。电杆主要在弯剪区产生受拉破坏的环向主裂缝,以及在支座处产生的斜裂缝,而顶部混凝土产生受压破坏。
2) 钢纤维的掺入在一定程度上阻碍了裂缝的发展,电杆表面主裂缝数量较少,短细的次裂缝较多,而且钢纤维掺量越多,阻裂效果越明显,电杆的抗裂性能也越强。随着钢纤维含量由0%增至1.5%,电杆截面的抗弯刚度和承载能力显著提高,抵抗荷载变形的能力也越强。其正截面抗弯承载力由297 kN增至423.5 kN,提高了42.6%。
3) 随着配筋率由1.8%增至3.8%,电杆的主裂缝数量相差不大,但裂缝长度和宽度却明显减小。截面抗弯刚度和受弯承载力也大幅提高,其正截面承载力由258.5 kN也增至423.5 kN,提高了63.8%。配筋率的提高可增强UHPC电杆的抗裂性能和抵抗变形能力,截面应变和刚度退化速率也有所降低。较大的配筋率既可充分发挥钢纤维阻裂与抗拉增韧作用,也可发挥UHPC材料超高抗压强度的特点。
4) 采用普通混凝土电杆受弯承载力计算方法,其计算值与试验值偏差较大,不适用于UHPC电杆。采用钢纤维混凝土和活性粉末混凝土电杆受弯承载力计算方法与试验值较为接近,但偏于保守,不过随着UHPC电杆的配筋率和钢纤维掺量的提高,其理论计算值与试验值越接近。
| [1] |
SHIN D G, YOON K Y, LEE S H, et al. Ananalytical study on the ultimate strength of concrete poles[J]. Journal of Korean Society of Hazard Mitigation, 2007, 7(5): 19. |
| [2] |
刘思远, 夏开全, 陈宗平, 等. 在役钢筋混凝土电杆剩余承载能力试验研究[J]. 混凝土, 2010(4): 48. LIU Siyuan, XIA Kaiquan, CHEN Zongping, et al. Study on residual carrying capacity of existing reinforced concrete poles[J]. Concrete, 2010(4): 48. |
| [3] |
XIA K Q, WANG N, CHEN Z P. Experimental research on ultimate bending capacity of reinforced concrete poles in service period[J]. Advanced Materials Research, 2012, 368: 2468. |
| [4] |
MISZCZYK A, SZOCINSKI M, DAROWICKI K. Restoration and preservation of the reinforced concrete poles of fence at the formerauschwitz concentration and extermination camp[J]. Case Studies in Construction Materials, 2016, 4: 42. DOI:10.1016/j.cscm.2015.12.002 |
| [5] |
赵顺波, 高润东, 李长永, 等. 离心成型预应力钢纤维混凝土电杆设计试验研究[J]. 工程力学, 2006, 23(增刊1): 151. ZHAO Shunbo, GAO Rundong, LI Changyong, et al. Design and experimental study of prestressed sfrc pole fabricated by centrifugal shaping method[J]. Engineering Mechanics, 2006, 23(Sup.1): 151. |
| [6] |
赵顺波, 张吉红, 李凤兰. 离心成型钢纤维混凝土劈裂抗拉强度试验研究[J]. 应用基础与工程科学学报, 2009, 17(6): 867. ZHAO Shunbo, ZHANG Jihong, LI Fenglan. Experimental study on splitting-tensile strength of centrifugal shaping sfrc[J]. Journal of Basic Science and Engineering, 2009, 17(6): 867. |
| [7] |
高润东, 赵顺波, 张天光, 等. 离心成型钢筋钢纤维混凝土电杆受力性能试验研究[J]. 土木工程学报, 2005, 38(8): 43. GAO Rundong, ZHAO Shunbo, ZHANG Tianguang, et al. An experimental study on the behavior of steel fiber reinforced concrete pole fabricated by centrifugal shaping method[J]. China Civil Engineering Journal, 2005, 38(8): 43. |
| [8] |
李凤兰, 李晓克, 赵顺波, 等. 离心成型钢筋钢纤维混凝土电杆设计方法研究[J]. 应用基础与工程科学学报, 2007, 15(2): 190. LI Fenglan, LI Xiaoke, ZHAO Shunbo, et al. Design method for centrifugal shaping steel fiber reinforced concrete pole[J]. Journal of Basic Science and Engineering, 2007, 15(2): 190. |
| [9] |
金伟良, 赵羽习. 混凝土结构耐久性[M]. 2版. 北京: 科学出版社, 2014: 158. JIN Weiliang, ZHAO Yuxi. Durability of concrete structure[M]. 2nd ed. Beijing: Science Press, 2014: 158. |
| [10] |
WANG C, YANG C G, LIU F, et al. Preparation of ultra-high performance concrete with common technology and materials[J]. Cement and Concrete Composites, 2012, 34(4): 538. |
| [11] |
陈宝春, 季韬, 黄卿维, 等. 超高性能混凝土研究综述[J]. 建筑科学与工程学报, 2014, 31(3): 1. CHEN Baochun, JI Tao, HUANG Qingwei, et al. Review of research on ultra-high performance concrete[J]. Journal of Architecture and Civil Engineering, 2014, 31(3): 1. |
| [12] |
YU Z H, WU L S, YUAN Z, et al. Mechanical properties, durability and application of ultra-high-performance concrete containing coarse aggregate (UHPC-CA): a review[J]. Construction and Building Materials, 2022, 334: 127360. |
| [13] |
LUBBERS A R. Bond performance between ultra-high performance concrete and prestressing strands[D]. Columbus: Ohio University, 2003
|
| [14] |
王德弘, 鞠彦忠, 康孟新. 预应力等径活性粉末混凝土电杆的设计研究[J]. 混凝土与水泥制品, 2013(6): 25. WANG Dehong, JU Yanzhong, KANG Mengxin. Design research oh equal-diameter prestressed reactive powder concrete (RPC) pole[J]. China Concrete and Cement Products, 2013(6): 25. |
| [15] |
冯浩. 超高性能混凝土早期塑性收缩开裂的研究[D]. 长沙: 湖南大学, 2014 FENG Hao. Study on the early stage plastic shrinkage and cracking performance of ultra high performance concrete[D]. Changsha: Hunan University, 2014 |
| [16] |
黄政宇, 李仕根. 含粗骨料超高性能混凝土力学性能研究[J]. 湖南大学学报(自然科学版), 2018, 45(3): 47. HUANG Zhengyu, LI Shigen. Study on mechanical properties of ultra high performance concrete with coarse aggregate[J]. Journal of Hunan University (Natural Science Edition), 2018, 45(3): 47. |
| [17] |
黄维蓉, 杨玉柱, 刘延杰, 等. 含粗骨料超高性能混凝土的力学性能[J]. 硅酸盐学报, 2020, 48(11): 1747. HUANG Weirong, YANG Yuzhu, LIU Yanjie, et al. Mechanical properties of ultra-high performance concrete containing coarse aggregate[J]. Journal of the Chinese Ceramic Society, 2020, 48(11): 1747. |
| [18] |
周晓光, 王哲. 围压及粗骨料对超高强混凝土抗压性能的影响[J]. 哈尔滨工业大学学报, 2019, 51(12): 144. ZHOU Xiaoguang, WANG Zhe. Effect of confinement and coarse aggregate on compressive properties of ultra-high strength concrete[J]. Journal of Harbin Institute of Technology, 2019, 51(12): 144. |
| [19] |
LV Y J, ZHANG W H, WU F, et al. Static mechanical properties and mechanism of C200 ultra-high performance concrete (UHPC) containing coarse aggregates[J]. Science and Engineering of Composite Materials, 2020, 27(1): 186. |
| [20] |
ADAM T, MA J X. Development of an ultra-high performance concrete for precast spun concrete columns[C]//Presented at the 3rd International Symposium on UHPC and Nanotechnology for High Performance Construction Materials. Kassel: Kassel University Press, 2012: 841
|
| [21] |
鞍山远达电网工程有限公司. 超高性能混凝土(UHPC)电杆[EB/OL]. (2017-05-17). http://www.51sole.com/b2b/pd_8061188.htm AnshanYuanda Power Grid Engineering Co., Ltd. . Ultra high performance concrete (UHPC) poles[EB/OL]. (2017-05-17). http://www.51sole.com/b2b/pd_8061188.htm |
| [22] |
黄福云, 桂奎, 林潮, 等. 环形超高性能混凝土制品离心成型试验研究[J]. 混凝土与水泥制品, 2021(12): 34. HUANG Fuyun, GUI Kui, LIN Chao, et al. Experimental study on circular ultra-high performance concrete products using centrifugal forming[J]. China Concrete and Cement Products, 2021(12): 34. |
| [23] |
陈宝春, 林毅焌, 杨简, 等. 超高性能纤维增强混凝土中纤维作用综述[J]. 福州大学学报(自然科学版), 2020, 48(1): 58. CHEN Baochun, LIN Yiluo, YANG Jian, et al. Review on fiber function in ultra-high performance fiber reinforced concrete[J]. Journal of Fuzhou University (Natural Science Edition), 2020, 48(1): 58. |
| [24] |
中国电力企业联合会. 超高性能混凝土电杆: T/CEC 143—2017[S]. 北京: 中国电力出版社, 2017 China Electricity Council. Ultra-high performance concrete pole: T/CEC 143—2017[S]. Beijing: China Electric Power Press, 2017 |
| [25] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 活性粉末混凝土: GB/T 31387—2015[S]. 北京: 中国标准出版社, 2015 General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China. Reactive powder concrete: GB/T 31387—2015[S]. Beijing: Standards Press of China, 2015 |
| [26] |
汤关祚, 王清, 禹琦. 先张法预应力混凝土管桩抗裂弯矩和极限弯矩计算式的探讨[J]. 工业建筑, 2004(1): 57. TANG Guanzuo, WANG Qing, YU Qi. Discussion on calculating method of cracking resistance and ultimate bending moment of pretensioned spun concrete pipe[J]. Industrial Construction, 2004(1): 57. |
| [27] |
中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局. 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2015 Ministry of Housing and Urban-rural Development of the People's Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2015 |
| [28] |
曾庆响, 梁焕华, 肖芝兰, 等. PHC管桩的开裂弯矩和极限弯矩计算[J]. 工业建筑, 2010, 40(1): 68. ZENG Qingsheng, LIANG Huanhua, XIAO Zhilan, et al. Calculation methods of cracking moment and ultimate failure moment of prestressed high strength concrete pipe piles[J]. Industrial Construction, 2010, 40(1): 68. |
| [29] |
中国工程建设标准化协会. 纤维混凝土结构技术规程: CECS 38—2004[S]. 北京: 中国计划出版社, 2004 China Association for Engineering Construction. Technical specification for fiber reinforced concrete structures: CECS 38—2004[S]. Beijing: China Planning Press, 2004 |
| [30] |
王德弘, 鞠彦忠, 康孟新. 预应力活性粉末混凝土电杆的设计研究[J]. 广东电力, 2013, 26(4): 56. WANG Dehong, JU Yanzhong, KANG Mengxin. Study on design of prestessed reactive powder concrete pole[J]. Guangdong Electric Power, 2013, 26(4): 56. |
 2023, Vol. 55
2023, Vol. 55


