混凝土自锚式悬索桥在经济、美观等方面都有着较强的竞争能力,随着中国公路交通事业的迅速发展,混凝土自锚式悬索桥必将得到广泛应用[1]。但部分已建混凝土自锚式悬索桥,随着使用年限增加,出现不同程度的吊索倾斜、加劲梁线形偏离设计标高等现象,使得结构的实际受力状态与设计不吻合,影响桥梁的使用寿命。而造成这种现象的一个主要因素是设计阶段对混凝土自锚式悬索桥的徐变效应没有正确预计。
混凝土结构徐变效应的正装分析理论已较为成熟,有多种切实有效的计算方法和计算软件包;关于徐变倒退分析目前仍存在着很大困难,而混凝土徐变的倒退分析在结构的设计、施工、养护等各方面都具有重大的研究价值。因此,需要对混凝土徐变效应的倒退分析展开研究,找到一种更加精确的计算分析方法来分析成桥过程中混凝土结构的徐变效应。
1 徐变倒退分析方法混凝土徐变倒退分析最大的难点在于,徐变效应具有非线性、时变性以及不可逆性等,正是这些特点限制了混凝土徐变效应倒退分析的发展。倘若能够通过混凝土结构的某一目标状态倒退分析出该结构在加载龄期以及受载后任意时刻的内力状态,这对混凝土结构的设计、施工具有深远的影响,也是目前亟待解决的问题[2]。
1.1 混凝土应力条件不变时的徐变分析在混凝土徐变效应的研究当中,比较具有代表性的理论包括[3-4]:弹性徐变体理论、老化理论以及继续理论等等。这些理论广泛适用于各种工况下的结构徐变效应分析。在通常情况下,当混凝土应力条件不变时,徐变应变的计算公式可以表达为
| $ \varepsilon_c=\frac{\sigma_b}{E_b} \cdot \phi\left(t, t_0\right) $ | (1) |
式中Φ(t, t0)为加载龄期为t0时t时刻的徐变系数。
式(1)表示的是t0→t这一段时间内混凝土结构发生徐变应变,若采用倒退分析以时刻t为初始状态,加载龄期t0为最终状态,那么在t→t0这一段时间内混凝土结构发生的倒退徐变应变εc′应为
| $ \varepsilon_c^{\prime}=-\frac{\sigma_b}{E_b} \cdot \phi\left(t, t_0\right)=\frac{\sigma_b}{E_b} \cdot \phi\left(t_0, t\right) $ | (2) |
式中Φ(t0, t)=-Φ(t, t0)可称之为倒退徐变系数。
由于徐变倒退分析时是以时刻t结构的内力状态作为初始状态而时刻t0作为最终状态,故t0时刻混凝土结构所对应的弹性应变与徐变应变总和应为
| $ \begin{gathered} \varepsilon_{b\left(t_0\right)}=\varepsilon_{b(t)}+\frac{\sigma_b}{E_b} \cdot \phi\left(t_0, t\right)= \\ \frac{\sigma_b}{E_b}+\frac{\sigma_b}{E_b} \cdot\left[\phi\left(t, t_0\right)+\phi\left(t_0, t\right)\right]=\frac{\sigma_b}{E_b} \end{gathered} $ | (3) |
结合式(2)、(3)可知,在结构t时刻内力状态的基础上,以此为基础采用Φ(t0, t)=-Φ(t, t0)的倒退徐变系数对该结构进行分析可以倒推得到原加载龄期t0时刻结构的内力状态,且该内力状态与正装时的t0结构所处的状态相一致,如图 1所示。
|
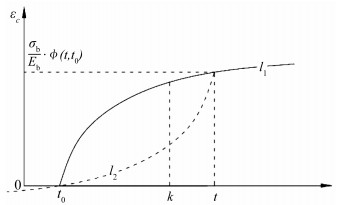
图 1 计算过程示意图 Fig. 1 Schematic diagram of the calculation process |
在图 1中,曲线l1为t0→t的徐变应变变化曲线,曲线l2为t→t0的倒退徐变应变变化曲线。正是由于结构的倒退徐变系数Φ(t0, t)=-Φ(t, t0),因此结构在t0与t这两点的徐变应变值必定相等,故可通过此方法以任意时刻t结构内力状态为基础进行倒退分析从而得到该结构在加载龄期t0时的内力状态。
采用本方法在计算过程中应特别注意,从图 1中可以非常直观地看出k时刻曲线l1与曲线l2并不相交,因此若以t时刻的混凝土状态为基础,计算任意其他时刻(k时刻)的结构状态时,只能通过t时刻的混凝土状态倒退分析得到加载龄期t0时刻混凝土的内力状态而后再以t0时刻的混凝土内力状态为基础得到k时刻的混凝土内力状态。换而言之,本文所述的这种徐变倒退分析法仅可通过时刻t的结构内力状态计算加载龄期t0时的内力状态,若还需对其他时刻的内力状态进行计算,则可在所求得的t0时刻混凝土内力状态的基础上进行正装计算即可得到结构在任意时刻的内力变形状态。
1.2 混凝土应力条件变化时的徐变分析在实际工程遇到超静定结构问题时,结构的徐变变形是随时间的发展而不断变化的。与此同时,受徐变效应影响结构所产生的次内力与截面的应力状态也会随时间的发展而改变。同样当混凝土应力条件变化时,在正装分析中以t0时刻荷载加载龄期为初始状态,在t时刻时因混凝土徐变而引起的徐变增量为
| $ \begin{gathered} \mathrm{d} \varepsilon_c=\mathrm{d} \sigma \cdot \frac{1}{E_b} \cdot \phi\left(t, t_0\right) \\ \mathrm{d} \sigma=\frac{\partial \sigma(\tau)}{\partial \tau} \mathrm{d} \tau \end{gathered} $ | (4) |
从加载龄期t0到观察时刻t,由不断变化的应力(应力梯度dσ)所产生的徐变应变为
| $ \begin{gathered} \varepsilon_c(t)=\frac{\sigma_{t_0}}{E_b} \phi\left(t, t_0\right)+ \\ \int\limits_{t_0}^t \frac{\partial \sigma}{\partial \tau} \cdot \frac{1}{E_b} \cdot[1+\phi(t, \tau)] \mathrm{d} \tau \end{gathered} $ | (5) |
式中:
式(5)表示的是t0→t这一段时间内混凝土结构发生徐变应变,在此基础上采用倒退分析以时刻t为初始状态,加载龄期为t0为最终状态,那么在t→t0这一段时间内混凝土的倒退徐变函数依然取Φ(t0, t)=-Φ(t, t0),在倒退徐变函数Φ(t0, t)的影响下t→t0这一时段内应力的梯度变为-∂σ(τ)/∂τ,故在这一时段产生的徐变应变εc(t0)应为
| $ \begin{aligned} \varepsilon_c\left(t_0\right)= & \frac{\sigma_t}{E_b} \phi\left(t_0, t\right)+\int\limits_t^{t_0}-\frac{\partial \sigma}{\partial \tau} \cdot \frac{1}{E_b} \cdot[(1+ \\ & \left.\left.\phi\left(t, t_0\right)\right)+\phi(\tau, t)\right] \mathrm{d} \tau \end{aligned} $ | (6) |
式中:
对式(6)进行化简,可得
| $ \begin{gathered} \varepsilon_c\left(t_0\right)=-\frac{\sigma_{\tau_0}}{E_b} \cdot \phi\left(t, t_0\right)- \\ \int\limits_{t_0}^t \frac{\partial \sigma}{\partial \tau} \cdot \frac{1}{E_b} \cdot[1+\phi(t, \tau)] \mathrm{d} \tau \end{gathered} $ | (7) |
通过式(5)与式(7)的对比,可以发现以观察时刻t作为结构计算初始状态,以倒退徐变系数Φ(t0, t)=-Φ(t, t0)进行t→t0的结构倒退徐变分析时,在这一时段内产生的徐变应变εc(t0)与该结构的正装分析(加载龄期t0→t时刻这一过程)产生的徐变应变εc(t)互为相反数,这说明在已知时刻t结构内力状态的基础上可以通过设置倒退徐变系数Φ(t0, t)=-Φ(t, t0)的方式倒退分析求得该结构在加载龄期时的初始内力状态,在混凝土结构加载龄期时的初始内力状态已知后可对其进行正装徐变分析,至此混凝土结构在所有时刻受到徐变效应影响的内力状态均可迎刃而解[5-6]。
值得注意的是,此处的倒退徐变系数只是混凝土徐变效应倒退分析时的一种计算手段,没有具体的物理意义。
2 徐变倒退分析验证 2.1 分析验证思路由于混凝土徐变效应是不可逆的,因此在对其进行倒退分析计算与验证时只能通过建立有限元模型分析计算的方式进行。
通过以下两个步骤对本文提出的混凝土徐变效应倒退分析计算方法进行验证:1)在已知的混凝土结构目标状态基础上,利用第1节提出的倒退分析计算方法,通过改变徐变系数的方式,计算分析得到该混凝土结构在加载龄期时的结构状态;2)对第1步中分析所得的结果进行混凝土徐变正装分析并提取该结构目标状态对应时刻的结构状态,与已知目标状态进行对比。
以倒退分析的计算结果作为基础进行正装分析,通过正装分析提取目标状态对应时刻的结构状态若与已知的结构目标状态一致,则说明混凝土徐变效应倒退分析计算方法与正装分析计算是闭合的,倒退分析所得的计算结果是准确、有效的[7-11]。
2.2 有限元模型建立以国内某一典型混凝土自锚式悬索桥作为工程实例。该桥位于抚顺市区东部,跨越浑河,道路等级为城市主干路,机动车道为双向6车道,两侧各有2.5 m宽人行道和3.5 m宽非机动车道,桥面总41 m宽。主桥为钢筋混凝土自锚式悬索桥,桥跨布置为:15 m+70 m+160 m+70 m+15 m,总计330 m。两主缆中心之间的相距26.5 m,顺桥向吊索间距5 m。
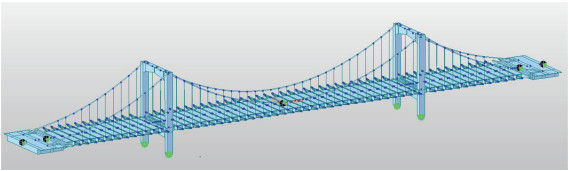
采用大型空间有限元计算程序MIDAS Civil,按照空间杆系对桥梁的各个构件进行离散和模拟。主要离散的构件有主缆、吊杆、加劲梁、普通钢筋混凝土索塔。本桥模型共计781个节点,672个单元,结构离散及加劲梁示意如图 2所示。
|
图 2 桥梁结构离散示意图 Fig. 2 Discrete schematic diagram of bridge structure |
建立有限元模型主要的目的就是为了验证本文所述徐变倒退计算分析的正确性,为此有限元模型计算分析步骤主要分为以下几步:1)根据结构混凝土计算初始状态的单元构件理论厚度得到相应混凝土单元的徐变系数以及倒退徐变系数;2)将倒退徐变系数施加在结构混凝土单元上通过进行施工阶段分析对混凝土徐变效应进行计算;3)将混凝土的徐变系数代入到步骤2中所得倒退分析的计算结果中,进行正装分析得到结构在考虑混凝土徐变效应后相应时间的内力状态并与结构的原内力状态进行对比,若结果吻合,则说明通过步骤2的计算方法是正确、有效的。
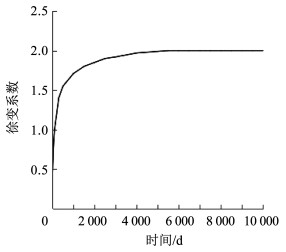
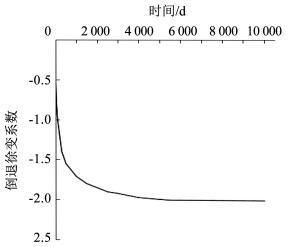
2.3 验证分析与结果提取 2.3.1 结构的计算参数根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》规定,计算得到加劲梁截面的构件理论厚度为34.25 cm。加劲梁采用C50混凝土,根据混凝土28 d立方体抗压标准强度(50 MPa)、环境年平均相对湿度(70%)、构件理论厚度(34.25)、水泥种类系数(5)、收缩时的混凝土龄期(3 d),可得加劲梁的徐变系数如图 3所示。加劲梁的倒退徐变系数如图 4所示。
|
图 3 加劲梁徐变系数 Fig. 3 Creep coefficient of stiffening beam |
|
图 4 加劲梁倒退徐变系数 Fig. 4 Retrogressive creep coefficient of stiffened beam |
设置徐变时间为720 d。利用已知状态倒退分析得到加载龄期(720 d前)的结构状态,再以此为基础进行正装徐变分析得到720 d后的结构状态,通过将正装所得结果与已知状态进行对比即可验证倒退分析所得结果的正确性。主梁变形(以结构加载龄期状态为基准)与吊索索力状态分别见表 1、2。
| 表 1 主梁变形(以结构加载龄期状态为基准) Tab. 1 Deformation of main beam (based on structural loading age state) |
| 表 2 吊索索力情况 Tab. 2 Sling cable force |
综合表 1与表 2中数据,在利用之前徐变倒退分析的结果基础上对该结构进行正装徐变分析,当时间设置与结构初始状态时间一致时(720 d)计算所得的内力状态与结构初始状态几乎没有差别,因此可以说明通过文中所述方法进行混凝土徐变倒退分析的计算结果是正确的,可以利用本文方法进行混凝土徐变倒退分析。
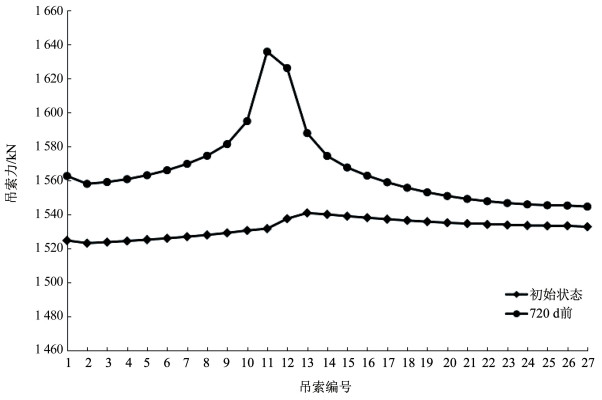
2.3.3 结果提取根据自锚式悬索桥各吊索所处的位置对各吊索进行编号,从加劲梁锚固段吊索开始往跨中吊索依次为1#~27#,提取结构在加载龄期时各吊索的索力并进行对比,如图 5所示。
|
图 5 吊索索力对比图 Fig. 5 Sling cable force comparison chart |
根据图 3可以得到,吊索在结构加载龄期(720 d前)时的索力大于模型初始计算状态的吊索力。吊索越接近桥塔其索力值变化越明显,受混凝土徐变效应的影响也就越明显,其中最大之处索力值变化了6.4%。在混凝土徐变效应的影响下,自锚式悬索桥结构中各吊索力会逐渐减小,吊索力趋于均匀分布,但在这一过程中,混凝土徐变效应仅会改变混凝土构件的内力、变形状态,而并不会直接改变吊索的无应力长度。
从结构整体的角度出发,混凝土徐变会使自锚式悬索桥结构中的吊索索力减小,从而传递给主缆的荷载减小,主缆的内力亦会随之而减小。由于自锚式悬索桥结构的恒载在混凝土徐变前后基本不发生变化,主缆内力的减小意味着加劲梁内力增大,导致其变形增大,影响结构受力。
3 成桥过程倒拆分析混凝土徐变倒退分析的最终目标是为了对结构的成桥过程进行倒退分析,通过倒退分析可以直接得到成桥过程中各施工阶段混凝土结构的状态,以便在施工过程中对结构进行监控。
在混凝土徐变效应倒退分析法的基础上,将混凝土徐变效应倒退分析与结构的施工顺序结合起来,每个施工工况逐一与施工工期相对应,在结构目标成桥状态的基础上严格按照倒拆顺序进行分析[12-14]。
以辽宁抚顺万新大桥主跨施工为例,考虑混凝土徐变效应其进行倒退分析,从而得到该自锚式悬索桥在体系转换过程中各施工工况相应吊索张拉力。将上述倒退分析结果与正装迭代分析的计算结果进行对比,若两者结果相吻合则说明本文所述的倒退分析计算与正装迭代计算闭合。
根据正装迭代计算,提取体系转换过程中各工况吊索张拉力见表 3。
| 表 3 吊索张拉力结果对比 Tab. 3 Comparison of sling tension results |
与此同时,主缆水平分力亦会随着结构体系转换的进行而逐渐增大。主缆水平分力可以反映出结构在体系转换过程中整体的受力情况,提取倒退分析中主缆水平分力的变化情况与正装迭代进行对比,如图 6所示。

|
图 6 主缆水平分力对比图 Fig. 6 Sling cable force comparison chart |
结合表 3以及图 6可以发现,在工况10至工况17这一区域内,主缆及吊索的内力迅速增大,正是在成桥过程的这一区域内结构的恒载逐步由支架转移到主缆上来,在工况17之后主缆受力趋于稳定,因此工况10至工况17是该自锚式悬索桥成桥过程控制的关键工况。综上所述,通过本文所述分析方法对结构进行施工阶段倒退分析,通过与正装迭代分析的计算结果进行对比,可以发现两者的计算结果是闭合。因此,可以通过本文所述方法对混凝土结构进行倒退分析指导成桥过程施工监控。
4 结论1) 分析了混凝土结构在常应力状态及变应力状态两种情况下混凝土徐变效应对其产生的影响,得到了加载龄期t0时结构状态与之后任意t时刻结构状态之间的关系。
2) 引入了倒退徐变系数的概念,利用倒退徐变系数可以实现混凝土自锚式悬索桥徐变的倒退分析,整个过程是一个“先退后进”的过程。
3) 有限元分析结果表明:在经历倒退正装后,加劲梁线形的最大误差在1 mm以内,吊索力误差均在0.1%以内;在此基础上将本文提出的倒退分析法用于结构的成桥过程分析,正装与倒退的分析计算结果是闭合的。
4) 通常情况下,混凝土结构具有刚度大、几何非线性程度较低等特点,本文提出的混凝土徐变倒退分析方法可较精确地预计徐变对混凝土结构内力和位移的影响,为混凝土徐变效应分析提供了一种新的研究思路。
| [1] |
张哲. 混凝土自锚式悬索桥[M]. 北京: 人民交通出版社, 2003. ZHANG Zhe. Concrete self-anchored suspension bridge[M]. Beijing: People's Communications Publishing House, 2003. |
| [2] |
张博恒. 混凝土斜拉桥前进与倒退分析不闭合问题研究[D]. 重庆: 重庆交通大学, 2018 ZHANG Boheng. Research on the non-close problem of forward and backward analysis of concrete cable-stayed bridge[D]. Chongqing: Chongqing Jiaotong University, 2018 |
| [3] |
项海帆. 高等桥梁结构理论[M]. 2版. 北京: 人民交通出版社, 2013. XIANG Haifan. Structural theory of higher bridges[M]. 2nd ed. Beijing: People's Transportation Press, 2013. |
| [4] |
黄新宇. 无应力状态法在混凝土斜拉桥施工控制中的研究[D]. 北京: 北京交通大学, 2017 HUANG Xinyu. The study of stress-free state method in the construction control of concrete cable-stayed bridge[D]. Beijing: Beijing Jiaotong University, 2017 |
| [5] |
ALAVI A H, HASNI H, LAJNEF N, et al. An intelligent structural damage detection approach based on self-powered wireless sensor data[J]. Automat Constr, 2016, 62: 24. DOI:10.1016/j.autcon.2015.10.001 |
| [6] |
毛昌时, 杜国华, 范立础. 混凝土斜拉桥徐变倒退分析[J]. 中国公路学报, 1995, 8(1): 42. MAO Changshi, DU Guohua, FAN Lichu. Analysis of the creep and retrogression of concrete cable-stayed bridges[J]. China Journal of Highway and Transport, 1995, 8(1): 42. |
| [7] |
苑仁安. 斜拉桥施工控制[D]. 成都: 西南交通大学, 2013 YUAN Ren'an. Cable-stayed bridge construction control[D]. Chengdu: Southwest Jiaotong University, 2013 |
| [8] |
黄新宇. 无应力状态法在混凝土斜拉桥施工控制中的研究[D]. 北京: 北京交通大学, 2017 HUANG Xinyu. The study of stress-free state method in the construction control of concrete cable-stayed bridge[D]. Beijing: Beijing Jiaotong University, 2017 |
| [9] |
吴会军. 抚顺万新大桥施工控制[D]. 大连: 大连理工大学, 2005 WU Huijun. Fushun Wanxin Bridge construction control[D]. Dalian: Dalian University of Technology, 2005 |
| [10] |
宋鑫, 邱文亮. 万新大桥主桥结构设计和施工控制[J]. 公路, 2005(4): 66. SONG Xin, QIU Wenliang. Structural design and construction control of the main bridge of Wanxin Bridge[J]. Highway, 2005(4): 66. |
| [11] |
FENG D M, FENG M Q. Experimental validation of cost-effective vision-based structural health monitoring[J]. Mech Syst Signal Pr, 2017, 88: 199. DOI:10.1016/j.ymssp.2016.11.021 |
| [12] |
FENG D M, FENG M Q. Vision-based multipoint displacement measurement for structural health monitoring[J]. Struct Control Hlth, 2016, 23(5): 876. DOI:10.1002/stc.1819 |
| [13] |
DENG Y, LIU Y, FENG D M. Monitoring damage evolution of steel strand using acoustic emission technique and rate process theory[J]. J Central South Univ, 2014, 21(9): 3692. DOI:10.1007/s11771-014-2352-2 |
| [14] |
MUTLIB N K, BAHAROM S B, EL-SHAFIE A, et al. Ultrasonic health monitoring in structural engineering: buildings and bridges[J]. Struct Control Health Monit, 2016, 23(3): 409. |
 2023, Vol. 55
2023, Vol. 55


