并网逆变器作为连接可再生能源与电网的接口,通常采用脉宽调制(pulse-width modulation, PWM)的工作方式,其在开关频率处产生的高频谐波对电网造成了谐波污染。为提高入网质量,衰减开关谐波并减小设备体积,在实际应用中常使用LCL型滤波器进行滤波[1]。然而,LCL滤波器在谐振频率处的谐振尖峰影响了系统的稳定性,为避免额外的功率损耗,系统大多采取有源阻尼进行谐振抑制。其中,以电容电流反馈法[2-5],电容电压反馈法[6-8]为代表的附加变量反馈法是主要的谐振抑制策略,但在数字控制及弱电网工况下,电网阻抗引起的谐振频率偏移与控制延时会改变有源阻尼特性,影响阻尼效果与系统稳定性[9-10];此外,该策略需较多的高精度传感器,提高了硬件成本。
为改善系统稳定性,同时避免增加额外传感器,单电流闭环控制得到了广泛研究。根据不同的电流反馈方式可将其分为网侧电流控制(grid current feedback, GCF)与逆变侧电流控制(inverter current feedback, ICF)[11]。文献[12]提出由于ICF系统存在固有的阻尼,在忽略数字控制延时下,相比GCF,ICF系统无需阻尼即可稳定且稳定性较高。文献[13]提出在考虑数字控制延时下,ICF与GCF系统在无阻尼时稳定的必要条件分别为谐振频率小于1/6采样频率(fs)与谐振频率大于1/6采样频率。此外,在弱电网工况下,电网阻抗会降低谐振频率,根据文献[14],随着谐振频率与采样频率比值的降低,ICF系统稳定性增强,GCF系统稳定性减弱。因此,在采样频率固定时,ICF系统更适用于弱电网工况。
然而,数字控制延时所产生的滞后环节使ICF系统稳定区间较小,需牺牲环路增益以保证系统稳定[15]。对此,文献[16]提出了一种延时调整方法改善系统稳定性,但该方法需精确控制代码执行时间,增加了系统的复杂程度;文献[17]提出基于牛顿插值法的延时补偿策略,但改变了系统在高频处的增益,衰减了系统的高频滤波能力;文献[18]通过提高控制器增益激起谐振以检测谐振频率,并利用陷波器直接抑制谐振尖峰,但该方法在电网阻抗变化时需频繁调用检测程序,降低了控制的实时性;文献[19]提出双二阶陷波器方法构造滞后补偿改良了系统的相位特性,但引入了额外的谐振尖峰,增加了并网电流的高频谐波含量。
针对ICF系统在数字控制下存在的问题,本文首先分析了控制延时与电网阻抗对ICF系统稳定性的影响。其次,为减小控制延时产生的相位滞后,利用陷波器的相位超前环节对相位进行补偿,从而避免相位在谐振频率处穿越-180°,增强了系统的稳定性与对弱电网的鲁棒性。同时,为提高系统对LCL参数变化的适应性,利用ANF算法对谐振频率进行估计,并根据估计结果调整陷波频率,扩大了谐振频率的稳定区间。最后,实验结果验证了所提方法的有效性。
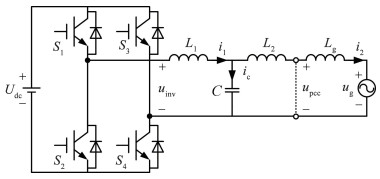
1 ICF控制的并网逆变器稳定性分析 1.1 数字控制延时对系统稳定性的影响图 1为弱电网下单相LCL并网逆变器的主电路结构,其中Udc为逆变器的直流侧输入电压,开关管S1~S4构成单相逆变桥,L1为逆变器侧电感,L2为电网侧电感,C为滤波电容,upcc为公共耦合点电压,ug为电网电压,Lg为电网阻抗。
|
图 1 弱电网下单相LCL并网逆变器的主电路 Fig. 1 Main circuit of single-phase LCL grid-connected inverter under the weak grid |
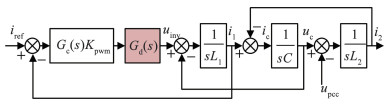
根据图 1得到数字控制下的并网逆变器控制框图,如图 2所示。其中,Gc(s)为电流控制器,Kpwm为逆变环节等效增益。
|
图 2 采用ICF策略的系统控制框图 Fig. 2 The control block of the system with ICF strategy |
为减小稳态误差,文中采用PR控制器,则Gc(s)的传递函数可表示为
| $ G_{\mathrm{c}}(s)=k_{\mathrm{p}}+\frac{2 k_{\mathrm{r}} \omega_{\mathrm{i}} s}{s^2+2 \omega_{\mathrm{i}} s+\omega_{\mathrm{o}}^2} $ | (1) |
式中: kp为比例系数,kr为谐振系数,ωi与ωo分别为谐振带宽与基波角频率。
Gd(s)由1拍的计算延时与0.5拍的零阶保持器构成,其在s域的等效传递函数由式(2)表示。式中,Ts为采样周期。
| $ G_{\mathrm{d}}(s)=\mathrm{e}^{-1.5 s T_{\mathrm{s}}} $ | (2) |
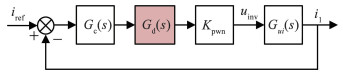
将图 2等效变换得到逆变侧电流i1的闭环控制框图,如图 3所示。其中,逆变器输出电压uinv到逆变侧电流i1的传递函数Gui(s)为
|
图 3 逆变侧电流的闭环控制框图 Fig. 3 The closed-loop of the inverter-side current control |
| $ G_{u i}(s)=\frac{i_1(s)}{u_{\text {inv }}(s)}=\frac{s^2\left(L_2+L_{\mathrm{g}}\right) C+1}{s^3 L_1\left(L_2+L_{\mathrm{g}}\right) C+s\left(L_1+L_2+L_{\mathrm{g}}\right)} $ | (3) |
系统的开环传递函数为
| $ G_{\mathrm{op}}(s)=\frac{G_{\mathrm{c}}(s) K_{\mathrm{pwm}} G_{\mathrm{d}}(s)\left(s^2\left(L_2+L_{\mathrm{g}}\right) C+1\right)}{s^3 L_1\left(L_2+L_{\mathrm{g}}\right) C+s\left(L_1+L_2+L_{\mathrm{g}}\right)} $ | (4) |
由式(3)可知,Gui(s)存在一对共轭零点与一对共轭极点。其中,共轭零点具有陷波作用,共轭极点具有谐振作用,定义Gui(s)固有的陷波频率与谐振频率分别为fn与fres:
| $ \left\{\begin{array}{l} f_{\mathrm{n}}=\frac{1}{2 {\rm{ \mathsf{ π} }}} \frac{1}{\sqrt{\left(L_2+L_{\mathrm{g}}\right) C}} \\ f_{\text {res }}=\frac{1}{2 {\rm{ \mathsf{ π} }}} \sqrt{\frac{L_1+L_2+L_{\mathrm{g}}}{L_1\left(L_2+L_{\mathrm{g}}\right) C}} \end{array}\right. $ | (5) |
当不考虑电流控制器Gc(s)与Kpwm对系统的影响时,令Gc(s)Kpwm=1。图 4为有无控制延时的开环系统Bode图,其中L1=3.6 mH,L2=1.6 mH,C=4.7 μF,采样频率fs=10 kHz。

|
图 4 有无控制延时的开环系统Bode图 Fig. 4 Bode plots of the open-loop system with and without the control delay |
由式(4)可知,开环系统不存在s右半平面极点,根据奈奎斯特稳定判据,当开环系统不存在s右半平面极点时:在幅值大于0 dB的区间内,若开环系统的相位曲线在(2n+1)π频率处的正、负穿越次数相等,则闭环系统稳定,其中n为任意整数。图 4表明,当无控制延时环节时,系统不产生(2n+1)π的相位穿越,该系统恒稳。而引入控制延时Gd(s)后,相位在谐振频率处穿越-180°,其对应的幅值为正无穷,系统不稳定。因此,在数字控制延时下,系统稳定的一个必要条件是避免开环系统相位在谐振频率处穿越-180°。
1.2 电网阻抗对数字控制系统的稳定性影响除控制延时之外,电网阻抗同样影响系统穿越-180°时的频率大小,图 5为电网阻抗增大时开环系统的Bode图。

|
图 5 电网阻抗增大时的开环系统Bode图 Fig. 5 Bode plots of the open-loop system with the increase of the grid impedance |
定义开环系统相位在f≥fres的区间内穿越-180°的频率为fcp,其对应的幅值裕度为GM。如图 5所示,当fres>1/6fs时,fcp=fres,GM < 0 dB,系统不稳定;当电网阻抗增大(Lg>2.6 mH)使fres < 1/6fs时,fcp=1/6fs且恒大于fres,GM>0 dB,系统稳定。当电网阻抗Lg继续增大时,GM随fres的减小而上升,系统稳定性增强。
当考虑Gc(s)Kpwm对开环系统的影响时:PR控制器Gc(s)在远离基频的频段近似为比例环节kp,令Kpwm=1,则Gc(s)Kpwm=kp。以Lg=3 mH为例:当不考虑Gc(s)Kpwm环节即kp=1时,GM=6.6 dB,系统稳定。而kp=5时,GM=-7.1 dB,系统失稳。实际上,当Lg=3 mH时,虽有fres < 1/6fs,但系统仅在kp < 2.5时稳定。由此说明,当无额外补偿器时,系统的稳定条件苛刻,对电路参数与控制器增益的选取要求较高。综上,对单电流环ICF系统在数字控制中的总结如下:1)在1.5拍的控制延时作用下,当未加入额外补偿环节时,系统仅在fres∈(0, 1/6fs)时稳定且环路增益需足够小, 这不仅限制了LCL参数的设计,同时导致系统带宽较低,动态性能较差。2)当所选取的电路参数与控制器参数使系统在电网阻抗Lg=0时稳定,则Lg增大时系统仍保持稳定且稳定性提升。3)通过设计相位补偿环节可减小控制延时产生的相位滞后,从而扩大谐振频率稳定区间并提高环路增益。
2 基于陷波器的超前补偿方案 2.1 陷波器与控制器的参数设计为减小数字控制延时对系统稳定性的影响,本文利用陷波器的超前环节对相位进行补偿,加入陷波器的控制框图如图 6所示。其中,Gtr(s)为陷波器的传递函数,表达式为

|
图 6 加入陷波器的系统控制框图 Fig. 6 The control block of the system with notch filter |
| $ G_{\mathrm{tr}}(s)=\frac{s^2+\omega_{\mathrm{tr}}^2}{s^2+2 \zeta \omega_{\mathrm{tr}} s+\omega_{\mathrm{tr}}^2} $ | (6) |
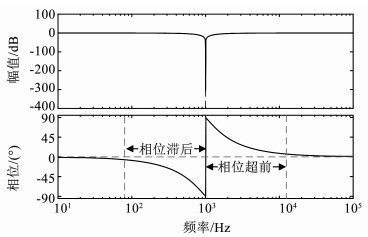
式中:ωtr=2πftr,ftr为陷波频率,ζ为陷波器的阻尼系数,图 7为Gtr(s)的Bode图(ζ=0.7, ftr=1 000 Hz)。
|
图 7 陷波器的频率特性 Fig. 7 Frequency characteristics diagram of the notch filter |
由陷波器的频率特性可知,陷波器在ftr两侧分别提供相角超前与滞后,且在全频段不提升系统的幅值增益,因此不影响系统对高频谐波的抑制能力。其相位φtr(f)可表示为
| $ \varphi_{\mathrm{tr}}(f)=-\arctan \frac{2 \zeta f_{\mathrm{tr}} f}{f_{\mathrm{tr}}^2-f^2} $ | (7) |
加入陷波器后,开环系统的相位为
| $ \varphi_{\mathrm{op}}(f)=\left\{\begin{array}{l} -3 {\rm{ \mathsf{ π} }} \frac{f}{f_{\mathrm{s}}}-\frac{{\rm{ \mathsf{ π} }}}{2}+\varphi_{\mathrm{tr}}(f), f <f_{\mathrm{n}} \\ -3 {\rm{ \mathsf{ π} }} \frac{f}{f_{\mathrm{s}}}+\frac{{\rm{ \mathsf{ π} }}}{2}+\varphi_{\mathrm{tr}}(f), f_{\mathrm{n}}<f <f_{\mathrm{res}} \\ -3 {\rm{ \mathsf{ π} }} \frac{f}{f_{\mathrm{s}}}-\frac{{\rm{ \mathsf{ π} }}}{2}+\varphi_{\mathrm{tr}}(f), f>f_{\mathrm{res}} \end{array}\right. $ | (8) |
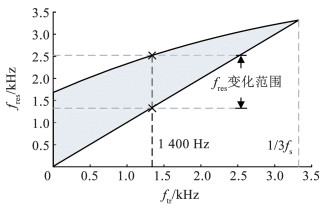
由于系统稳定的必要条件是φop在谐振频率fres处不产生-180°的穿越,φop在fres的相位需大于-180°。据此,谐振频率fres与陷波器频率ftr的可取区域由式(9)约束并可由图 8表示。
|
图 8 fres与ftr的可取区域 Fig. 8 The available area of fres and ftr |
| $ -3 {\rm{ \mathsf{ π} }} \frac{f_{\text {res }}}{f_{\mathrm{s}}}-\frac{{\rm{ \mathsf{ π} }}}{2}+\varphi_{\mathrm{tr}}\left(f_{\text {res }}, f_{\mathrm{tr}}\right)>-{\rm{ \mathsf{ π} }} $ | (9) |
由可取区域可知,当ftr的取值频段较低时,所对应的fres上限较低,导致环路的带宽下降且动态性能较差;当ftr的取值频段较高时,虽然fres上限提高,但可允许fres变化的区间减小,系统对电网阻抗的适应性下降。因此,为兼顾系统对弱电网的适应能力与动态性能,选取ftr=1 400 Hz,此时fres∈[1 400 Hz, 2 550 Hz]。考虑到LCL参数的波动对fres的影响,需在fres最大值处保留一定余量,故将fres的上限调整为2 200 Hz。定义L2+Lg=LT,当L1=3.6 mH,C=4.7 μF时,fres变化所对应的LT区间为[1.6 mH, 11.6 mH]。取L2=1.6 mH,则Lg的可变化区间为[0, 10 mH]。
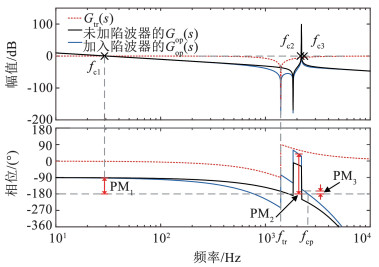
加入陷波器前后的开环系统Bode图如图 9所示(以kp=1为例)。其中,开环系统存在3个截止频率,一次截止频率fc1位于中频(fc1 < fn),其对应的相位裕度为PM1;二次截止频率fc2与三次截止频率fc3分别位于fres两侧(fn < fc2 < fres,fc3>fres),其对应的相位裕度分别为PM2、PM3。
|
图 9 加入陷波器前后的开环系统Bode图 Fig. 9 Bode plots of the open-loop system with and without notch filter |
当fres远离ftr时,陷波器的超前补偿作用减弱,存在PM2>PM1>PM3;当fres接近ftr时,陷波器的超前补偿作用增强,存在PM2>PM3>PM1。在大于fres的区间内,开环系统的幅值与相位单调递减,若GM>0 dB,则PM3>0。系统稳定的条件为PM1, 2, 3>0且GM>0,因此系统的稳定与否由GM与PM1主导。配置GM与PM需求解fc1与fcp,因滤波电容C在中低频段对系统的影响较小,且陷波频率ftr远离fc1,求解fc1时可忽略陷波器并将LCL滤波器近似为L滤波器,则fc1可表示为
| $ f_{\mathrm{c1}}=\frac{k_{\mathrm{p}}}{2 {\rm{ \mathsf{ π} }}\left(L_1+L_{\mathrm{T}}\right)} $ | (10) |
fc1所对应的相位裕度PM1为
| $ \mathrm{PM}_1=-3 {\rm{ \mathsf{ π} }} \frac{f_{\mathrm{c1}}}{f_{\mathrm{s}}}-\frac{{\rm{ \mathsf{ π} }}}{2}+\varphi_{\mathrm{tr}}\left(f_{\mathrm{c1}}\right)+{\rm{ \mathsf{ π} }} $ | (11) |
利用式(8)对fcp进行求解:
| $ -3 {\rm{ \mathsf{ π} }} \frac{f_{\mathrm{cp}}}{f_{\mathrm{s}}}-\frac{{\rm{ \mathsf{ π} }}}{2}+\varphi_{\mathrm{tr}}\left(f_{\mathrm{cp}}, f_{\mathrm{tr}}\right)=-{\rm{ \mathsf{ π} }} $ | (12) |
fcp所对应的幅值裕度GM为
| $ \mathrm{GM}=-20 \lg \left|\frac{k_{\mathrm{p}}\left(-\omega_{\mathrm{cp}}^3+\omega_{\mathrm{tr}}^2\right) \cdot G_{ui}\left(\mathrm{j} \omega_{\mathrm{cp}}\right)}{\sqrt{\left(\omega_{\mathrm{tr}}^2-\omega_{\mathrm{cp}}^2\right)^2+\left(2 \zeta \omega_{\mathrm{tr}} \omega_{\mathrm{cp}}\right)^2}}\right| $ | (13) |
式中ωcp=2πfcp。为保证系统具有一定的稳定裕度,设置约束条件为GM≥3 dB,PM1≥45°,结合式(10)~(13)得到LT变化时kp的可取区域,如图 10所示。为保证Lg在0~10 mH之间变化时系统恒稳,在LT=1.6 mH所对应的约束区间内选择kp,取kp=15。

|
图 10 LT变化时kp的可取区域 Fig. 10 The available area of kp when LT varies |
为验证加入陷波器的系统对电网阻抗与电路参数变化的鲁棒性,分别在弱电网下与LCL参数波动时对系统进行稳定性分析。
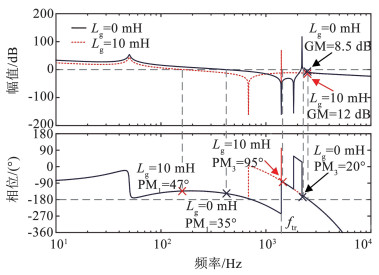
2.2.1 弱电网下的系统稳定性分析图 11为系统在弱电网(Lg=10 mH)与强电网(Lg=0 mH)下的开环Bode图。其中kp=15,同时,为减小稳态误差, 取PR控制器谐振系数kr=800。当Lg=0 mH时,PM1=35°,PM3=20°,GM=8.5 dB,系统稳定;当Lg=10 mH时,PM1=47°,PM3=95°,GM=12 dB,系统保持稳定且稳定裕度提升。由于Lg增大时谐振频率fres逐渐接近陷波频率ftr,陷波器的超前补偿作用增强;当Lg在0~10 mH之间变化时,PM1∈[35°, 47°],PM3∈[20°, 95°],GM∈[8.5 dB, 12 dB],系统恒稳。
|
图 11 开环系统在不同电网阻抗下的Bode图 Fig. 11 Bode plots of the open-loop system for different Lg |
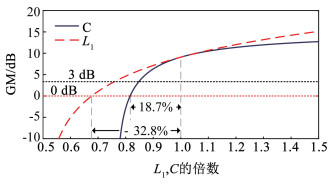
图 12为逆变侧电感L1与滤波电容C波动时GM的变化趋势。
|
图 12 L1与C波动时GM的变化趋势 Fig. 12 Curves of GM for the fluctuation of L1 and C |
当电路参数变化使fres远离初始谐振频率并向高频方向移动时,系统的稳定性由GM主导。由GM的变化趋势可知,L1与C正向波动对系统的稳定性有利,而L1与C负向波动则影响系统的稳定性,当L1的波动超出-32.8%(L1 < 2.42 mH)或C的波动超出-18.7%(C < 3.82 μF)时,幅值裕度GM < 0 dB,系统失稳。因此,为进一步提升系统对LCL参数波动的适应能力,本文引入ANF算法对谐振频率进行估计,并根据谐振频率估计值对陷波频率进行动态调整,从而提升系统在电路参数变化时的鲁棒性。
3 基于自适应陷波滤波器的改进控制方案 3.1 基于ANF算法的谐振频率估计设ANF的输入信号为u(t)=ksin ω0t,幅值k与频率ω0未知,根据文献[20],ANF算法的微分方程可表示为
| $ \left\{\begin{array}{l} \ddot{x}+2 \xi \dot{\theta} x+\theta^2 x=2 \xi \theta u(t) \\ \dot{\theta}=-\gamma x\left(\theta^2 u(t)-\dot{\theta} x\right) \end{array}\right. $ | (14) |
其中:ξ决定了ANF的阻尼系数,γ决定了自适应算法的收敛速度。式(14)具有唯一解为
| $ \boldsymbol{o}=\left(\begin{array}{l} x \\ \dot{x} \\ \theta \end{array}\right)=\left(\begin{array}{l} -k \cos \omega_0 t \\ k \omega_0 \sin \omega_0 t \\ \omega_0 \end{array}\right) $ | (15) |
为保证ANF稳定,幅值k与速度因子γ的取值应满足:
| $ \frac{k^2 \gamma}{2}<1 $ | (16) |
定义谐振频率的估计值

|
图 13 加入ANF算法的系统控制框图 Fig. 13 The control block of the system with ANF |
在系统稳定时,谐振频率fres处的谐波分量较低,i1h的幅值较小。当LCL参数波动幅度较大导致fres进入不稳定区域时,系统在fres附近发生震荡,此时执行ANF算法对谐振频率进行估计。
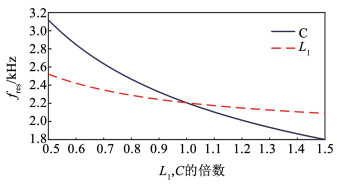
3.2 陷波频率的动态调整根据图 8,当fres∈(0, 1/3fs]时,每个fres均存在对应的ftr区间使系统稳定,因此可构造
|
图 14 L1与C波动时fres的变化趋势 Fig. 14 Curves of fres for the fluctuation of L1 and C |
|
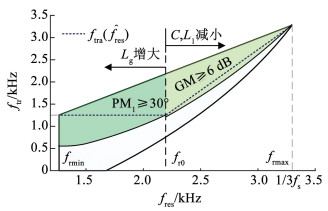
图 15 fres变化时陷波频率ftr的可取区域 Fig. 15 The available area of ftr when fres varies |
在ftr的可取区域内构造
| $ f_{\text {tra }}\left(\hat{f}_{\text {res }}\right)=\left\{\begin{array}{l} 1224, \hat{f}_{\text {res }} \leqslant f_{\text {r0 }} \\ 1.86 \hat{f}_{\text {res }}-2868, \hat{f}_{\text {res }}>f_{\text {r0 }} \end{array}\right. $ | (17) |
由
为验证ANF改进控制方案在弱电网工况及LCL参数波动下的鲁棒性,绘制其开环系统在电网阻抗及LCL参数变化下的Bode图,如图 16(a)与16(b)所示。

|
图 16 自适应后的开环系统在不同电网阻抗及滤波电容下的Bode图 Fig. 16 Bode plots of the open-loop system with ANF for different Lg and C |
在弱电网下,电网阻抗Lg是影响系统稳定性的主要因素,当Lg在0~10 mH之间变化时,fres≤fr0,自适应陷波器的陷波频率ftr保持1 224 Hz,此时PM1∈[31°, 46°],GM∈[6.5 dB, 11.3 dB],系统稳定且对弱电网的鲁棒性良好;在LCL参数波动下,根据图 14,滤波电容C的变化对谐振频率fres的影响较大,对系统的稳定性起主导作用。当C在4.7~2.4 μF之间变化时,根据
为验证所提补偿方法的可行性与有效性,搭建2 kW的单相并网逆变器。采用TMS320F28335芯片作为控制单元,并通过电网侧串联电感模拟弱电网工况,实验参数:直流电压Udc为200 V,电网电压ug为110 V,逆变器侧电感L1为3.6 mH,网侧电感L2为1.6 mH,滤波电容C为4.7~3.3 μF,电网阻抗Lg为0~4 mH,开关频率fsw为10 kHz,采样频率fs为10 kHz,比例系数kp为15,谐振系数kr为800,ANF速度因子γ为0.1,ANF阻尼因子ξ为0.2。
首先,将传统陷波方案、超前补偿陷波方案、ANF改进方案在不同的电网条件下进行对比。在传统陷波方案中,利用陷波器的陷波特性直接抑制谐振尖峰,其陷波频率位于初始谐振频率处:ftr=fr0=2 200 Hz;在超前补偿陷波方案与ANF改进方案中,利用陷波器的相位超前特性对系统相位进行补偿,其陷波频率分别设置为ftr=1 400 Hz与
图 17为电网阻抗Lg=0 mH时3种控制方案的实验波形。实验结果表明,在强电网的条件下,相比无补偿系统,3种控制方案均可保证系统稳定且并网电流质量良好,总谐波畸变率(total harmonic distortion, THD)小于3%。

|
图 17 不同陷波方案的实验结果,Lg=0 mH Fig. 17 The experimental results of different notch schemes for Lg=0 mH |
为验证系统在弱电网下的稳定性,增加电网阻抗进行对比实验。图 18为Lg=4 mH的实验结果,图中可见,采用超前补偿陷波方案与ANF改进方案的系统稳定,而采用传统陷波方案的系统失稳,其原因是在电网阻抗增大时,LCL的谐振频率向低频方向偏移,使传统陷波方案的陷波频率位于谐振频率右侧,此时陷波器的陷波作用失效,相位在谐振频率处重新穿越-180°,系统在谐振频率处震荡。而采用超前补偿陷波方案与ANF改进方案的陷波频率均位于谐振频率左侧,如Bode图 11与图 16(a)所示,因此电网阻抗的增加不对系统产生影响,所提方案对弱电网的鲁棒性良好。

|
图 18 不同陷波方案的实验结果,Lg=4 mH Fig. 18 The experimental results of different notch schemes for Lg=4 mH |
为验证超前补偿陷波方案与ANF改进方案对LCL参数波动的适应能力,在Lg=0 mH的条件下将滤波电容C的数值从4.7 μF降低至3.3 μF。如图 19(a)所示,其中,超前补偿陷波方案失稳,ANF改进方案稳定。其原因是降低滤波电容C导致谐振频率向高频段波动,陷波器的相位超前补偿作用下降,系统稳定裕度降低,如图 12所示。当滤波电容C的波动幅度较大时(C < 3.8 μF),超前补偿陷波方案的陷波频率位于稳定区间外,此时系统不稳定并在谐振频率附近震荡;相比之下,ANF改进方案可根据谐振频率调整陷波频率并使之位于稳定区间内,系统稳定,如Bode图 16(b)所示。

|
图 19 LCL参数变化后不同陷波方案的实验结果 Fig. 19 The experimental results of different notch schemes after the variation of the LCL parameter |
图 19(b)与图 19(c)分别为ANF算法的谐振频率估计结果与并网电流的THD分析结果。其中,实际的谐振频率集中在2 550~2 650 Hz,谐振频率的估计值为2 548~2 610 Hz,估计值与实际值基本相符,估计结果较准确。
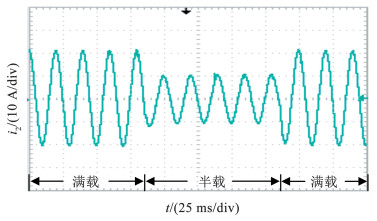
图 20为采用ANF改进方案的系统进行半满载切换的波形,由图可见,当电流参考值突变时,并网电流能快速跟随给定信号,系统的动态性能良好。
|
图 20 并网电流的动态实验结果 Fig. 20 Dynamic experimental results of the grid current |
本文对逆变侧电流反馈控制的LCL型并网逆变器进行了研究,分析了数字控制延时与弱电网对系统稳定性的影响,并提出了一种基于ANF算法的陷波超前补偿方法,得出以下结论:
1) 采用单逆变侧电流反馈的系统在数字控制下由于控制延时的相位滞后作用,当未加入额外的补偿环节时,仅在fres∈(0, 1/6fs)且环路增益较小的条件下稳定。
2) 提出利用陷波器的相位超前特性对系统相位进行补偿,并采用ANF算法对谐振频率进行估计,通过估计值调整陷波频率,将fres的稳定区间从(0, 1/6fs)扩大到(0, 1/3fs],在提高环路带宽的同时增强了系统的鲁棒性。
3) 该方法无需增加额外传感器,控制系统结构简单,易于参数整定。实验结果表明,相比于传统陷波方案,所提方法提高了系统对电网阻抗与LCL参数波动的适应能力,更适用于弱电网工况。
| [1] |
LISERRE M, BLAABJERG F, HANSEN S. Design and control of an LCL-filter-based three-phase active rectifier[J]. IEEE Transactions on Industry Applications, 2005, 41(5): 1281. DOI:10.1109/TIA.2005.853373 |
| [2] |
BAO C L, RUAN X B, WANG X H, et al. Step-by-step controller design for LCL-type grid-connected inverter with capacitor-current-feedback active-damping[J]. IEEE Transactions on Power Electronics, 2014, 29(3): 1239. DOI:10.1109/TPEL.2013.2262378 |
| [3] |
许津铭, 谢少军, 唐婷. 弱电网下LCL滤波并网逆变器自适应电流控制[J]. 中国电机工程学报, 2014, 34(24): 4031. XU Jinming, XIE Shaojun, TANG Ting. An adaptive current control for grid-connected LCL-filtered inverters in weak grid case[J]. Proceedings of the CSEE, 2014, 34(24): 4031. DOI:10.13334/j.0258-8013.pcsee.2014.24.006 |
| [4] |
PAN D H, RUAN X B, BAO C L, et al. Optimized controller design for LCL-type grid-connected inverter to achieve high robustness against grid-impedance variation[J]. IEEE Transactions on Industrial Electronics, 2015, 62(3): 1537. DOI:10.1109/TIE.2014.2341584 |
| [5] |
LI X, WU X, GENG Y, et al. Wide damping region for LCL-type grid-connected inverter with an improved capacitor-current-feedback method[J]. IEEE Transactions on Power Electronics, 2015, 30(9): 5247. DOI:10.1109/TPEL.2014.2364897 |
| [6] |
XIN Z, LOH P C, WANG X, et al. Highly accurate derivatives for LCL-filtered grid converter with capacitor voltage active damping[J]. IEEE Transactions on Power Electronics, 2016, 31(5): 3612. DOI:10.1109/TPEL.2015.2467313 |
| [7] |
RODRIGUEZ-DIAZ E, FREIJEDO F D, VASQUEZ J C, et al. Analysis and comparison of notch filter and capacitor voltage feedforward active damping techniques for LCL grid-connected converters[J]. IEEE Transactions on Power Electronics, 2019, 34(4): 3958. DOI:10.1109/TPEL.2018.2856634 |
| [8] |
FAIZ M T, KHAN M M, JIANMING X, et al. Capacitor voltage damping based on parallel feedforward compensation method for LCL-filter grid-connected inverter[J]. IEEE Transactions on Industry Applications, 2020, 56(1): 837. DOI:10.1109/TIA.2019.2951115 |
| [9] |
PAN D, RUAN X, BAO C, et al. Capacitor-current-feedback active damping with reduced computation delay for improving robustness of LCL-type grid-connected inverter[J]. IEEE Transactions on Power Electronics, 2014, 29(7): 3414. DOI:10.1109/TPEL.2013.2279206 |
| [10] |
YANG D, RUAN X, WU H. A real-time computation method with dual sampling mode to improve the current control performance of the LCL-type grid-connected inverter[J]. IEEE Transactions on Industrial Electronics, 2015, 62(7): 4563. DOI:10.1109/TIE.2014.2327575 |
| [11] |
许津铭, 谢少军, 张斌锋. 分布式发电系统中LCL滤波并网逆变器电流控制研究综述[J]. 中国电机工程学报, 2015, 35(16): 4153. XU Jinming, XIE Shaojun, ZHANG Binfeng. Overview of current control techniques for grid-connected inverters with LCL filters in distributed power generation systems[J]. Proceedings of the CSEE, 2015, 35(16): 4153. |
| [12] |
TANG Y, LOH P C, WANG P, et al. Exploring inherent damping characteristic of LCL-filters for three-phase grid-connected voltage source inverters[J]. IEEE Transactions on Power Electronics, 2012, 27(3): 1433. DOI:10.1109/TPEL.2011.2162342 |
| [13] |
WANG J, YAN J D, JIANG L, et al. Delay-dependent stability of single-loop controlled grid-connected inverters with LCL filters[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 743. DOI:10.1109/TPEL.2015.2401612 |
| [14] |
李军, 李玉玲, 陈国柱. 无阻尼LCL滤波器的并网变流器稳定性控制策略[J]. 电工技术学报, 2012, 27(4): 110. LI Jun, LI Yuzhen, CHEN Guozhu. A stability control strategy for PWM converter with undamped LCL-filter[J]. Transactions of China Electrotechnical Society, 2012, 27(4): 110. |
| [15] |
汪颖, 孙建风, 肖先勇, 等. 扩大等效虚拟阻尼正区间的逆变侧电流双环反馈控制方法[J]. 高电压技术, 2021, 47(11): 3981. WANG Ying, SUN Jianfeng, XIAO Xianyong, et al. Double loop feedback control method of inverter side current improved by extending the positive range of equivalent virtual damping[J]. High Voltage Engineering, 2021, 47(11): 3981. |
| [16] |
邹常跃, 刘邦银, 段善旭, 等. 并网逆变器中数字控制延时对系统稳定性的影响及其优化设计[J]. 中国电机工程学报, 2015, 35(2): 411. ZOU Changyue, LIU Bangyin, DUAN Shanxu, et al. Influence of delay on system stability and its optimization in grid-connected inventers[J]. Proceedings of the CSEE, 2015, 35(2): 411. |
| [17] |
贺诗明, 熊健. 基于牛顿插值的LCL型并网逆变器机侧电流反馈延时补偿策略[J]. 电网技术, 2020, 44(12): 4766. HE Shiming, XIONG Jian. A time delay compensation method based on Newton interpolation for inverter-side current feedback of LCL-type grid-tied Inverter[J]. Power System Technology, 2020, 44(12): 4766. |
| [18] |
PEÑA-ALZOLA R, LISERRE M, BLAABJERG F, et al. A self-commissioning notch filter for active damping in a three-phase LCL-filter-based grid-tie converter[J]. IEEE Transactions on Power Electronics, 2014, 29(12): 6754. |
| [19] |
AKHAVAN A, VASQUEZ J C, GUERRERO J M. A robust method for controlling grid-connected inverters in weak grids[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2021, 68(4): 1333. |
| [20] |
MOJIRI M, KARIMI-GHARTEMANI M, BAKHSHAI A. Time-domain signal analysis using adaptive notch filter[J]. IEEE Transactions on Signal Processing, 2007, 55(1): 85. |
 2023, Vol. 55
2023, Vol. 55


