执行器是过程工业控制系统中一个极为重要而不可或缺的组成部分,对执行器进行维修维护是保障其性能稳定的重要举措[1]。近年来,执行器设备的故障预测与健康管理技术越来越受到学术界和工业界的关注,包括基于模型的和基于数据的两大类,其中,利用数据驱动方法进行健康评估具有灵活性好和不依赖系统模型的优势,数据驱动方法分析系统的数据集,包括历史故障数据、统计数据和实时数据等,并加以应用算法对数据集进行求解推断。常用的数据驱动方法有主元分析、人工神经网络、支持向量机、模糊贝叶斯等[2-6]。基于上述研究成果,本项目组在传统的三组件式气动执行器上增加流量传感器、阀前压力传感器、阀后压力传感器和温度传感器,搭建一种自确认气动执行器结构模型[7]。由于气动执行器的某些故障为突发性故障,人工无法及时采取措施带来财产和人员上的损失[8],过度维护和不及时维修都会对执行机构造成不可逆的损坏。因而,一种直观量化自确认气动执行器性能变化的评估结果是必要的。基于此,本文尝试应用基于数据驱动的方法实现对自确认气动执行器健康状况的评估,该方法主要涉及特征提取、建立健康基准模型和健康状况可信度计算3个方面,从而实现建立一套比较完整的自确认气动执行器系统的健康状况评价体系。
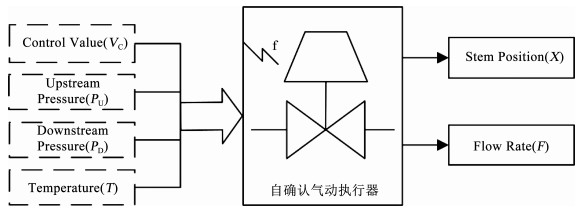
1 自确认气动执行器系统结构自确认气动执行器结构如图 1所示[9],由气动执行机构、调节阀和自确认单元组成,自确认单元接收工业自动化系统中的控制信号,依据采集的阀杆位置、流量、阀门前后的压力信号得到确认的定位器输出,通过气动执行机构实现对调节阀的控制,进而实现对介质流量的控制。

|
图 1 自确认气动执行器结构图 Fig. 1 Self-validating pneumatic actuator structure |
本文以气动执行器在卢布林糖厂的工业集成控制系统中的实际应用为背景,基于DAMADICS平台和DABLib模型,建立如图 2所示的模型,其中输入信号:阀位指令、阀前压力、阀后压力和介质温度,输出信号:阀杆位移和流量。
|
图 2 自确认气动执行器模型原理图 Fig. 2 General scheme of self-validating pneumatic actuator model |
DABLib是波兰华沙工业大学开发的基于MATLAB-SIMULINK的执行器模型库,该模型库在搭建的过程中充分了解了实际生产作业中气动执行器的结构特性,包括流体动力特性和热力学特性等等。通过不断的采集大量的实际数据进行分析验证,以保证所建立的仿真模型的真实性,从而能够有效的模拟出气动执行器的动作过程及输入输出信号,实现气动执行器19种典型故障模式的仿真[8]。
2 数据获取 2.1 关联向量机回归原理利用气动执行器正常工作时的的输入和输出数据建立训练样本集:{Xn, yn}n=1N,假设目标值yn所包含噪声εn满足均值为0,方差为σ2的高斯分布,则目标值yn=f(Xn; W)+εn,其条件概率分布模型可表示为
| $ f\left(\boldsymbol{X}_n ; \boldsymbol{W}\right)=\mathit{\boldsymbol{\varPhi}} \boldsymbol{W}=\sum\limits_{n=1}^N w_n K\left(\boldsymbol{X}, \boldsymbol{X}_n\right)+w_0 $ | (1) |
| $ p\left(y_n \mid \boldsymbol{X}_n, \boldsymbol{W}, \sigma^2\right)=N\left(f\left(\boldsymbol{X}_n ; \boldsymbol{W}\right), \sigma^2\right) $ | (2) |
式中:W=(ω0, ω1, ω2, …, ωn)T为模型的权值向量,K(X, Xn)为核函数,Φ为核映射矩阵。
给定一组新的待测试样本X*,则对应的预测目标值y*的预测概率模型为
| $ \begin{aligned} & p\left(y_* \mid \boldsymbol{y}, \sigma_{\mathrm{MP}}, \sigma_{\mathrm{MP}}^2\right)= \\ & \int p\left(y_* \mid \boldsymbol{W}, \sigma_{\mathrm{MP}}^2\right) p\left(\boldsymbol{W} \mid \boldsymbol{y}, \sigma_{\mathrm{MP}}, \sigma_{\mathrm{MP}}^2\right) \mathrm{d} \boldsymbol{W} \end{aligned} $ | (3) |
| $ \left\{\begin{array}{l} y_*=\boldsymbol{\mu}^{\mathrm{T}} \mathit{\boldsymbol{\varPhi} }\left(\boldsymbol{X}_*\right) \\ \sigma_*^2=\sigma_{\mathrm{MP}}^2+\mathit{\boldsymbol{\varPhi} }\left(\boldsymbol{X}_*\right)^{\mathrm{T}} \mathit{\Sigma} \mathit{\boldsymbol{\varPhi} }\left(\boldsymbol{X}_*\right) \\ \mathit{\boldsymbol{\varPhi} }\left(\boldsymbol{X}_*\right)=\left[1, K\left(\boldsymbol{X}_*, \boldsymbol{X}_1\right), \cdots, K\left(\boldsymbol{X}_*, \boldsymbol{X}_N\right)\right]^{\mathrm{T}} \end{array}\right. $ | (4) |
利用最大边缘似然函数方法将模型的求解转换为求解σMP和σMP2,详细的推导见文献[10]。
| $ \left\{\begin{array}{l} \alpha_i^{\text {new }}=\frac{r_i}{\mu_i^2} \\ \left(\sigma^2\right)^{\text {new }}=\frac{\left\|\boldsymbol{y}-\mathit{\boldsymbol{\varPhi}}{\boldsymbol{\mu}}\right\|^2}{N-\sum_{i=0}^N r_i} \\ r_i=1-\alpha_i N_{i i} \end{array}\right. $ | (5) |
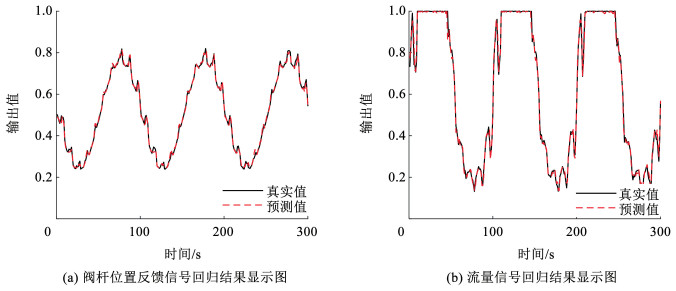
本文基于正常数据集,对阀杆位移反馈信号X和流量信号F根据其特点选择不同的核函数,前者采用高斯核函数:
|
图 3 利用最优核参数建立预测器的回归结果 Fig. 3 Regression results of RVM predictor based on kernel parameter |
| $ r_1=X-f_1\left(V_{\mathrm{C}}, \sqrt{P_{\mathrm{U}}-P_{\mathrm{D}}}, T\right) $ | (6) |
| $ r_2=F-f_2\left(V_{\mathrm{C}}, \sqrt{P_{\mathrm{U}}-P_{\mathrm{D}}}, T\right) $ | (7) |
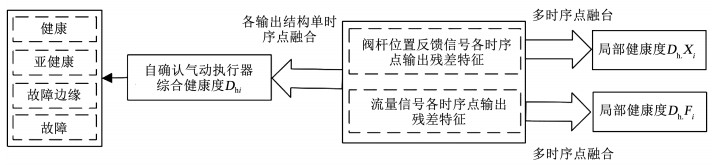
定义了健康状况可信度指标(简称健康度,health degree,Dh),取值在0~1之间,并根据健康度的量化结果,定义的4种健康状况见表 1。为了获得气动执行器各测量结构及执行器整体的健康状态信息,定义了局部健康度和综合健康度,其计算实现框图如图 4所示。
| 表 1 健康状况 Tab. 1 Health status levels |
|
图 4 自确认气动执行器的健康度计算框图 Fig. 4 Calculation diagram of health degree for self-validating pneumatic actuator |
局部健康度反映着单测量结构在不同时刻点具有的健康状态,通过对多时序点的残差特征状态进行信息融合获取,即
| $ D_{\text {h. } X_i}=f\left(X_{i-k+1}, X_{i-k+2}, \cdots, X_i\right) $ | (8) |
| $ D_{\mathrm{h} . F_i}=f\left(F_{i-k+1}, F_{i-k+2}, \cdots, F_i\right) $ | (9) |
综合健康度表示自确认气动执行器整体的健康水平,与某时刻点处所有测量结构的健康程度有关:
| $ D_{\mathrm{h} i}=g\left(X_i, F_i\right) $ | (10) |
式中:k表示时刻点序列长度,Xi和Fi分别表示阀杆位置反馈信号和流量信号各时序点输出残差特征。
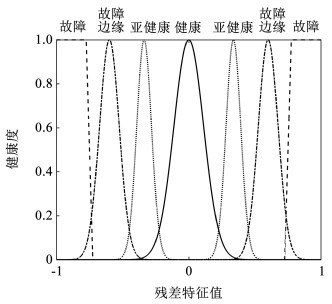
3.2 建立基准模型健康状况可信度表示执行器更为具体的健康信息,但是这种评估指标具有模糊性和不确定性。因此,将模糊集合理论[11-12]用于健康度的计算。以残差特征集作为评价自确认气动执行器健康状况评估系统的事件集,定义健康、亚健康、故障边缘、故障等4种评价指标,构成评价标准集。评价集合健康、亚健康及故障边缘的隶属度函数选用正态分布函数建立基准模型:
| $ y_{i j}^{(m)}=\left\{\begin{array}{l} 1, x_i^{(m)} \leqslant a_{11}, x_i^{(m)} \leqslant \mu_{i 1}^{(m)} \\ \frac{x_i^{(m)}-a_{21}}{a_{11}-a_{21}}, a_{11} \leqslant x_i^{(m)} \leqslant a_{21}, x_i^{(m)} \leqslant \mu_{i 1}^{(m)} \\ 0, x_i^{(m)} \geqslant a_{21}, x_i^{(m)} \leqslant \mu_{i 1}^{(m)} \end{array}\right. $ |
升半梯形基准模型为
| $ y_{i j}^{(m)}=\left\{\begin{array}{l} 0, x_i^{(m)} \leqslant a_{22}, x_i^{(m)} \geqslant \mu_{i 1}^{(m)} \\ \frac{x_i^{(m)}-a_{22}}{a_{12}-a_{22}}, a_{22} \leqslant x_i^{(m)} \leqslant a_{21}, x_i^{(m)} \geqslant \mu_{i 1}^{(m)} \\ 1, x_i^{(m)} \geqslant a_{12}, x_i^{(m)} \geqslant \mu_{i 1}^{(m)} \end{array}\right. $ |
式中:xi(m)为提取的残差特征值,μij(m)为最佳期望值,σij(m)为估计标准偏差,yij(m)为残差特征值对于评价集合j的隶属度,i=1, 2, …, I表示多时序点,j=1, 2, …, J代表评价指标集合,m=1, 2, …, M表示输出测量结构;当xi(m) < μi1(m)时,故障模糊集合隶属度函数为降半梯形函数,a11、a21为两个特征参数;当xi(m)>μi1(m)时,故障模糊集合隶属度函数为升半梯形函数,a12、a22为两个特征参数。图 5为所建立的基准模型曲线图。
|
图 5 隶属度函数曲线图 Fig. 5 Membership function curves |
依据基准模型分别构造局部健康度评价矩阵Li(m)和综合健康度评价矩阵Zi:
| $ \boldsymbol{L}_i^{(m)}=\left[\begin{array}{cccc} y_{(i-k+1) 1}^{(m)} & y_{(i-k+1) 2}^{(m)} & \cdots & y_{(i-k+1) J}^{(m)} \\ y_{(i-k+2) 1}^{(m)} & y_{(i-k+2) 2}^{(m)} & \cdots & y_{(i-k+2) J}^{(m)} \\ \vdots & \vdots & \vdots & \vdots \\ y_{i 1}^{(m)} & y_{i 2}^{(m)} & \cdots & y_{i J}^{(m)} \end{array}\right] $ | (11) |
| $ \boldsymbol{Z}_i=\left[\begin{array}{cccc} y_{i 1}^{(1)} & y_{i 2}^{(1)} & \cdots & y_{i J}^{(1)} \\ y_{i 1}^{(2)} & y_{i 2}^{(2)} & \cdots & y_{i J}^{(2)} \\ \vdots & \vdots & \vdots & \vdots \\ y_{i 1}^{(M)} & y_{i 2}^{(M)} & \cdots & y_{i J}^{(M)} \end{array}\right] $ | (12) |
基于对气动执行器残差特征的分析,在某时刻点处,执行机构的突发故障会使实际输出值偏离理想输出值,利用层次分析法[13-15]增强故障发生时刻点对于健康评估的影响,本文提出如下用于表征不同时刻点数据重要程度的权值确定原则:di(m)=|xi(m)-μi(m)|。定义标度值di(m)为时刻点i处输出结构m的实际测量值xi(m)与期望的最佳估计值μi(m)的偏差,偏差越大,表明越接近故障状态,对于健康状况评估影响程度越大。通过比较任意两两时刻点的影响程度,构造判断矩阵A(m):
| $ \boldsymbol{A}^{(m)}=\left[\begin{array}{cccccc} \frac{d_1^{(m)}}{d_1^{(m)}} & \frac{d_1^{(m)}}{d_2^{(m)}} & \cdots & \frac{d_1^{(m)}}{d_i^{(m)}} & \cdots & \frac{d_1^{(m)}}{d_k^{(m)}} \\ \frac{d_2^{(m)}}{d_1^{(m)}} & \frac{d_2^{(m)}}{d_2^{(m)}} & \cdots & \frac{d_2^{(m)}}{d_i^{(m)}} & \cdots & \frac{d_2^{(m)}}{d_k^{(m)}} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \frac{d_i^{(m)}}{d_1^{(m)}} & \frac{d_i^{(m)}}{d_2^{(m)}} & \cdots & \frac{d_i^{(m)}}{d_i^{(m)}} & \cdots & \frac{d_i^{(m)}}{d_k^{(m)}} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \frac{d_k^{(m)}}{d_1^{(m)}} & \frac{d_k^{(m)}}{d_2^{(m)}} & \cdots & \frac{d_k^{(m)}}{d_i^{(m)}} & \cdots & \frac{d_k^{(m)}}{d_k^{(m)}} \end{array}\right] $ | (13) |
求出判断矩阵的最大特征根λmax及特征向量αmax,并进行一致性检验。此时权值向量w(m)=αmax=[w(m)(1), w(m)(2), …, w(m)(k)],表示不同时刻点单输出结构健康状况中的相对重要性。
考虑到气动执行器自身结构原理以及不同输出结构之间的关系,本文通过引入灰色关联算法[16-17],用经过处理的关联度融合由层次分析法获得的各输出结构的权重向量,揭示数据之间更深层次的相关性。由式(14)计算灰色关联系数:
| $ \xi\left(w^{(m)}(t), w_0(t)\right)=\frac{\min \min +\rho \max \max }{\left|w_0(t)-w^{(m)}(t)\right|+\rho \max \max } $ | (14) |
关联度为
| $ e^{(m)}=\frac{\sum\limits_{t=1}^k \xi\left(w^{(m)}(t), w_0(t)\right)}{k} $ | (15) |
式中:w(m)被作为比较数列;w0为参考数列,
| $ \boldsymbol{G}=\boldsymbol{V} \boldsymbol{W}^* $ | (16) |
式中W*=[w(1), w(2), …w(m), …w(M)]T。
3.3.2 不同输出结构的权值分配本文采用熵值法[15]针对单时刻点不同输出结构对评判自确认气动执行器健康状况重要性建立权值分配模型。首先,依据基准模型构建评价矩阵Zi=(yij(m)),如式(12)所示,计算第j项指标下第m个测量结构的概率百分比:
| $ f_{i j}^{(m)}=\frac{y_{i j}^{(m)}}{\sum\limits_{j=1}^J y_{i j}^{(m)}} $ | (17) |
则第m个测量结构的熵值为
| $ \varpi_i^{(m)}=\frac{1-H_i^{(m)}}{m-\sum\limits_{m=1}^M H_i^{(m)}} $ | (18) |
式中:
通过建立权值模型和基准模型获得综合评价值:
| $ \boldsymbol{B}=\boldsymbol{W} \times \boldsymbol{R} $ | (19) |
式中B表示4种评价指标集合下的隶属参数值。
最后利用最小二乘支持向量机[18]建立隶属参数和健康度之间的映射关系:设训练数据集为{Bi, Dhi}i=1N,训练样本数为N,则最小二乘支持向量回归模型为
| $ D_{\mathrm{h}}(\boldsymbol{B})=\sum\limits_{i=1}^N \alpha_i K\left(\boldsymbol{B}, \boldsymbol{B}_i\right)+b $ | (20) |
式中αi、b由线性方程组求得。选取应用广泛的RBF函数作为核函数:K(B, Bi)=exp(-‖B-Bi‖2/σ2)。
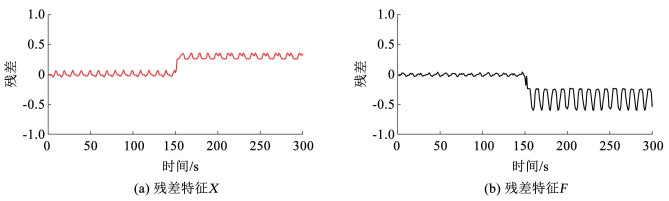
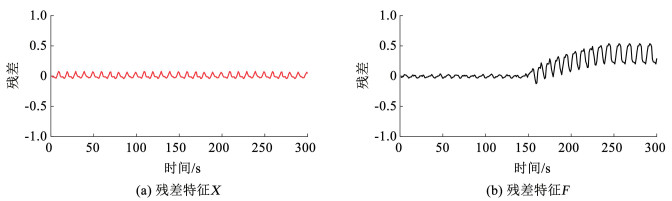
4 自确认气动执行器健康度评价实例执行器的不同故障类型数据(考虑了故障发生的不同强度)由DAMADICS故障仿真平台依据气动执行器结构以及工作原理,利用DABLib模型生成。利用自确认气动执行器正常工作数据,建立关联向量机预测模型并提取残差特征,利用健康状况可信度的计算方法对残差特征集测试样本进行处理,得到执行机构的局部健康度和综合健康度。图 6是无故障时的残差曲线图,图 7是故障f1时的残差曲线图,图 8是故障f2时的残差曲线图。

|
图 6 无故障仿真数据输出的残差特征 Fig. 6 Residual feature of simulated actuator data without failure |
|
图 7 故障f1仿真数据输出的残差特征 Fig. 7 Residual feature of simulated actuator data with fault f1 |
|
图 8 故障f2仿真数据输出的残差特征 Fig. 8 Residual feature of simulated actuator data with fault f2 |
以无故障、故障f1和故障f2为例,给出具体的健康状况可信度的计算过程。首先利用健康状况可信度对各时序点输出残差特征进行分析,选取时刻点序列长度为k=7,为了保证样本矩阵的实时更新,不断剔除第一个时刻点的历史数据,同时为了不改变序列长度,将下一时刻点处的测试数据补充到样本矩阵。测试样本见表 2。
| 表 2 测试样本数据 Tab. 2 Test sample data |
首先依据基准模型分别获得健康度评价矩阵LX和LF, 其次采用层次分析法建立权值分配模型,由式(13)分别得到判断矩阵AX和AF,最大特征值λmax.X=7, λmax.F=7,特征向量αmax.X和αmax.F,一致性指数CR=0 < 0.10,均满足一致性要求。因此将αmax.X和αmax.F归一化可得权值向量wX和wF,引入灰色关联算法,由式(14)和式(15)可得,关联系数ξX和ξF,关联度:eX=0.755 6,eF=0.770 3,将其归一化后得V = [0.495 2 0.504 8],则由式(16)计算可得G。
| $ \begin{array}{c} \boldsymbol{L}_X=\left[\begin{array}{llll} 0.9928 & 0.0693 & 0.0001 & 0 \\ 0.8671 & 0.1655 & 0.0006 & 0 \\ 0.8171 & 0.1996 & 0.0008 & 0 \\ 0.9192 & 0.1299 & 0.0003 & 0 \\ 0.4447 & 0.5116 & 0.0079 & 0 \\ 0.9714 & 0.0910 & 0.0001 & 0 \\ 0.8788 & 0.1576 & 0.0005 & 0 \end{array}\right] \\ \boldsymbol{L}_F=\left[\begin{array}{llll} 0.8895 & 0.1503 & 0.0004 & 0 \\ 0.9666 & 0.0949 & 0.0002 & 0 \\ 0.9820 & 0.0814 & 0.0001 & 0 \\ 0.4067 & 0.5525 & 0.0097 & 0 \\ 0.8958 & 0.1460 & 0.0004 & 0 \\ 0.9304 & 0.1221 & 0.0003 & 0 \\ 0.7606 & 0.2394 & 0.0013 & 0 \end{array}\right] \\ \boldsymbol{A}_X=\left[\begin{array}{ccccccc} 1 & 0.2257 & 0.1896 & 0.2936 & 0.0947 & 0.5000 & 0.2371 \\ 4.4314 & 1 & 0.8404 & 1.3012 & 0.4195 & 2.2156 & 1.0505 \\ 5.2732 & 1.1900 & 1 & 1.5484 & 0.4992 & 2.6365 & 1.2500 \\ 3.4055 & 0.7685 & 0.6458 & 1 & 0.3224 & 1.7027 & 0.8073 \\ 10.5653 & 2.3835 & 2.0030 & 3.1015 & 1 & 5.2809 & 2.5039 \\ 2.0001 & 0.4513 & 0.3793 & 0.5873 & 0.1894 & 1 & 0.4741 \\ 4.2184 & 0.9519 & 0.8000 & 1.2387 & 0.3994 & 2.1091 & 1 \end{array}\right] \\ \boldsymbol{A}_F=\left[\begin{array}{ccccccc} 1 & 1.8563 & 2.5357 & 0.3608 & 1.0319 & 1.2744 & 0.6541 \\ 0.5387 & 1 & 1.3660 & 0.1944 & 0.5559 & 0.6865 & 0.3534 \\ 0.3944 & 0.7321 & 1 & 0.1423 & 0.4069 & 0.5026 & 0.2580 \\ 2.7717 & 5.1451 & 7.0283 & 1 & 2.8601 & 3.5322 & 1.8130 \\ 0.9619 & 1.7989 & 2.4574 & 0.3496 & 1 & 1.2350 & 0.6339 \\ 0.7847 & 1.4566 & 1.9898 & 0.2831 & 0.8097 & 1 & 0.5133 \\ 1.5288 & 2.8378 & 3.8765 & 0.5516 & 1.5775 & 1.9482 & 1 \end{array}\right] \\ \boldsymbol{\alpha}_{\max . X}=\left[\begin{array}{lllllll} -0.0719 & -0.3187 & -0.3792 & -0.2449 & -0.7595 & -0.1438 & -0.3033 \end{array}\right] \\ \boldsymbol{\alpha}_{\text {max. } F}=\left[\begin{array}{lllllll} -0.2771 & -0.1493 & -0.1093 & -0.7681 & -0.2686 & -0.2175 & -0.4237 \end{array}\right] \\ \boldsymbol{w}_X=\left[\begin{array}{lllllll} 0.0324 & 0.1435 & 0.1707 & 0.1102 & 0.3419 & 0.0647 & 0.1366 \end{array}\right] \\ \boldsymbol{w}_F=\left[\begin{array}{lllllll} 0.1252 & 0.0674 & 0.0494 & 0.3470 & 0.1213 & 0.0982 & 0.1914 \end{array}\right] \\ \boldsymbol{\xi}_X=\left[\begin{array}{lllllll} 1 & 0.6467 & 0.5951 & 0.7231 & 0.3965 & 0.8626 & 0.6612 \end{array}\right] \\ \boldsymbol{\xi}_F=\left[\begin{array}{lllllll} 0.7462 & 0.9250 & 1 & 0.4282 & 0.7559 & 0.8202 & 0.6180 \end{array}\right] \\ \boldsymbol{G}=\left[\begin{array}{lllllllll} 0.0792 & 0.1051 & 0.1095 & 0.2298 & 0.2306 & 0.0817 & 0.1642 \end{array}\right] \end{array} $ |
由式(19)可得4个评价指标集下的隶属参数B:
| $ \begin{aligned} & \boldsymbol{B}_X=\left[\begin{array}{llll} 0.7966 & 0.2259 & 0.0022 & 0 \end{array}\right] \\ & \boldsymbol{B}_F=\left[\begin{array}{llll} 0.7804 & 0.2407 & 0.0027 & 0 \end{array}\right] \end{aligned} $ |
最后,由式(20)可得此时自确认气动执行器的健康状况可信度Dh:
| $ D_{\mathrm{h}}\left(\boldsymbol{B}_X\right)=0.8958, D_{\mathrm{h}}\left(\boldsymbol{B}_F\right)=0.8810 $ |
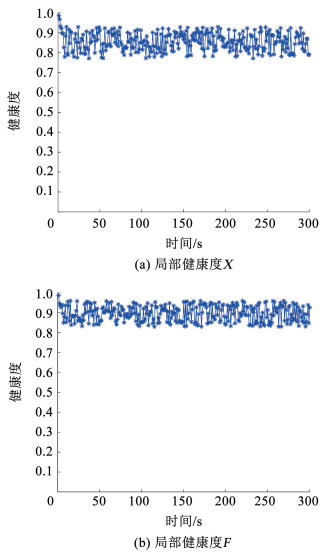
当气动执行器处于无故障状态时,利用健康状况可信度方法对各时序点输出残差特征分析,可得300 s测试样本序列的健康度结果,如图 9所示。由于前6次测量无法构成多时刻点序列,所以将其基准模型中获得的健康隶属度值直接作为其健康度值。
|
图 9 无故障时,局部健康度计算结果 Fig. 9 Calculation results of local health degree without failure |
同理,以第一组样本数据为例,利用熵值法求得
| $ \begin{aligned} \boldsymbol{Z}=\left[\begin{array}{llll} 0.9928 & 0.0693 & 0.0001 & 0 \\ 0.8903 & 0.1498 & 0.0004 & 0 \end{array}\right] \\ \boldsymbol{\varpi}=\left[\begin{array}{llll} 0.541 & 1 & 0.458 & 9 \end{array}\right] \\ \boldsymbol{B}=(0.9457, 0.1063, 0.0002, 0) \end{aligned} $ |
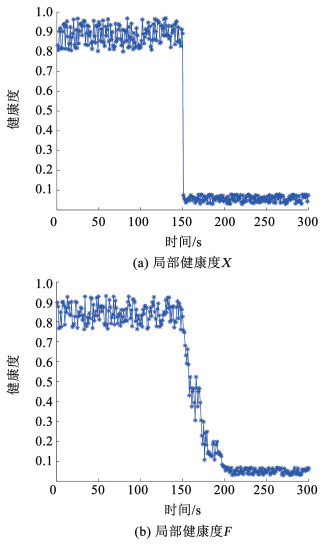
则Dh(B)=0.983 1。当执行机构发生故障时,为验证健康状况可信度方法的有效性,以突发故障f1和渐变性故障f2为例,在150 s时发生故障,通过对各时序点输出残差特征进行分析,其综合健康度结果如图 10所示。
|
图 10 发生故障时,综合健康度计算结果 Fig. 10 Calculation results of comprehensive health degree under failure |
由图 9可知,所有时刻点的健康度值均大于0.7,自确认气动执行器处于健康状态。由图 10(a)可知,在150 s时,健康度值小于0.1,处于故障状态。由图 10(b)可知,当发生渐变性故障时,健康度值逐渐变小。由此可见,在执行机构正常工作的基础上,当执行器工作异常时,其实验结果与实验条件一致,均能如实跟随执行机构的性能变化,表明此方法可用于计算健康状况可信度。
5 结论针对自确认气动执行器健康状况问题,提出了一种定量评价指标——健康状况可信度,可以直观地给出执行机构的健康状态信息。将关联向量机回归原理用于获取残差特征集,并采用模糊数据融合理论以及灰色关联算法融合层次分析法和熵值法用于健康度的计算,最后利用最小二乘支持向量机建立了隶属参数和健康状况可信度的映射关系,既考虑了单测量结构对执行器健康状况的影响,又考虑了不同输出结构之间影响程度的差异。研究结果表明,所提方法能够跟踪整个运行到故障过程中正常样本集的动态,给出定量的、合理的评价,并能及时采取措施进行维修和保养,减少系统性能退化失效的速率和发生故障的概率,实现了自确认气动执行器的健康状况评估。但是对于预测执行机构未来的健康水平还需要进一步完善和深化研究。
| [1] |
刘庆树. 浅谈气动执行器的工作原理与维护[J]. 新型工业化, 2020, 10(3): 53. LIU Qingshu. Preliminary analysis on the working principle and maintenance of metso pneumatic actuator[J]. The Journal of New Industrialization, 2020, 10(3): 53. |
| [2] |
ZHANG Lianlian, QIAO Fei, WANG Junkai, et al. Equipment health assessment based on improved incremental support vector data description[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(5): 3205. DOI:10.1109/TSMC.2019.2919468 |
| [3] |
曹宇. 基于支持向量机的变电站蓄电池健康度评估[J]. 电气传动自动化, 2021, 43(1): 1. CAO Yu. Health evaluation of storage battery in substation based on support vector machine[J]. Electric Drive Automation, 2021, 43(1): 1. |
| [4] |
MA Ning, YANG Fan, TAO Laifa, et al. State-of-health assessment for aero-engine based on density-distance clustering and fuzzy Bayesian risk[J]. IEEE Access, 2021, 9: 9996. DOI:10.1109/ACCESS.2021.3050792 |
| [5] |
LIU Kuijian, FENG Yunwen, XUE Xiaofeng. Fault diagnosis of hydraulic retraction system based on multi-source signals feature fusion and health assessment for the actuator[J]. Journal of Intelligent and Fuzzy Systems, 2018, 34(6): 3635. DOI:10.3233/JIFS-169539 |
| [6] |
王印松, 吴军超. 一种基于PCA和贝叶斯分类的气动调节阀故障诊断方法[J]. 中国测试, 2019, 45(12): 112. WANG Yinsong, WU Junchao. A fault diagnosis method for pneumatic regulating valve based on PCA and Bayesian classification[J]. China Measurement & Testing Technology, 2019, 45(12): 112. |
| [7] |
YANG J C, CLARKE D W. The self-validating actuator[J]. Control Engineering Practice, 1999, 7(2): 249. DOI:10.1016/S0967-0661(98)00148-8 |
| [8] |
MICHAL B, RON P, MICHAL S. Introduction to the DAMADICS actuator FDI benchmark problem[J]. Control Engineering Practice, 2006, 14(6): 577. DOI:10.1016/j.conengprac.2005.06.015 |
| [9] |
冯志刚, 杨佳琪. 自确认气动执行器的故障诊断算法研究[J]. 传感技术学报, 2022, 35(6): 785. FENG Zhigang, YANG Jiaqi. Research on fault diagnosis algorithm of self-validating pneumatic actuator[J]. Chinese Journal of Sensors and Actuators, 2022, 35(6): 785. |
| [10] |
王茹. 基于关联向量机的气动执行器故障诊断算法研究[D]. 沈阳: 沈阳航空航天大学, 2015 WANG Ru. Pneumatic actuator fault diagnosis based on relevance vector machine[D]. Shenyang: Shenyang Aerospace University, 2015 |
| [11] |
ZHANG Yongjie, CAO Kang, LIANG Ke, et al. Study on the evaluation model of serialized civil aircraft commonality index based on fuzzy set theory[J]. Journal of Intelligent & Fuzzy Systems, 2021, 40(6): 11539. |
| [12] |
周璐, 冯玉光, 顾均元. 基于模糊理论的导弹质量评估[J]. 兵工自动化, 2020, 39(8): 60. ZHOU Lu, FENG Yuguang, GU Junyuan. Missile quality assessment based on fuzzy theory[J]. Ordnance Industry Automation, 2020, 39(8): 60. |
| [13] |
XUE Wangyu, LI Xiu, HUANG Biqing. Health diagnosis of nuclear power plant[J]. International Journal of Advanced Robotic Systems, 2019, 16(5): 1. |
| [14] |
LIU Yan, ECKERT C M, EARL C. A review of fuzzy AHP methods for decision-making with subjective judgements[J]. Expert Systems with Applications, 2020, 161(15): 1. |
| [15] |
陈嘉杨, 张洪彦, 王敏. AHP-熵权法在综合传动装置健康状态综合评估中的应用[J]. 车辆与动力技术, 2017(1): 38. CHEN Jiayang, ZHANG Hongyan, WANG Min. Application of the AHP-entropy method on health status assessment of the integrated transmission device[J]. Vehicle & Power Technology, 2017(1): 38. DOI:10.16599/j.cnki.1009-4687.2017.01.009 |
| [16] |
TUSONGJIANG K, GAO Wensheng, LU Guojun, et al. Fault diagnosis model of power transformer based on improved grey relation method with combined weight[C]//Institution of Engineering and Technology 12th IET International Conference on AC and DC Power Transmission. Beijing: Institution of Engineering and Technology, 2016: 1
|
| [17] |
曹慧玲, 黄乐腾, 康力平. 基于AHP及灰色关联分析法的发动机健康评估研究[J]. 数学的实践与认识, 2015, 45(2): 122. CAO Huiling, HUANG Leteng, KANG Liping. To study on health assessment of aero-engine based on AHP and GRA[J]. Journal of Mathematics in Practice and Theory, 2015, 45(2): 122. |
| [18] |
ZHOU Shuisheng. Sparse LSSVM in primal using Cholesky factorization for large-scale problems[J]. IEEE Transactions on Neural Networks and Learning Systems, 2016, 27(4): 783. |
 2023, Vol. 55
2023, Vol. 55


