临近空间飞行器是指在20~100 km的临近空间区域内飞行并完成特定任务的飞行器。目前临近空间飞行器所能实现的机动性是很有限的[1]。飞行任务的多元化对临近空间飞行器的机动性提出了更高的要求。引入推力矢量技术可直接改变推力大小和方向,增加三轴方向运动的灵活性,是提升飞行器机动能力的重要技术方案。然而,复杂机动飞行环境以及推力矢量引入的不确定,为机动飞行控制带来挑战。因此,为实现临近空间飞行器机动飞行任务,解决机动飞行姿态跟踪稳定控制问题至关重要。
针对机动飞行的实现方法和不确定影响下控制系统设计问题,相关学者进行了广泛研究。文献[2]针对机动飞行下参数不确定鲁棒控制问题,设计了间断滑模控制律和超螺旋连续控制律。文献[3]针对先进飞机大迎角过失速飞行,提出基于最小参数学习径向基函数(RBF)网络和动态表面控制(DSC)的控制方法,估计非定常空气动力学引起的不确定。文献[4]提出了一种利用推力矢量技术实现战斗机大迎角跟踪和超机动动作的解耦控制方案,设计扩展状态观测器对干扰不确定性进行估计。文献[5]基于动态逆控制和高阶鲁棒自适应积分滑模控制设计控制器,实现大迎角机动飞行,并设计非线性函数对不确定自适应逼近。文献[6]针对V/STOL飞机短距起飞优化问题,提出了二次预置多推力偏转方案,并提出线性自抗扰反演控制方法,实现对爬升角不确定系统的有效控制。文献[7]研究了高超声速再入飞行器气动/反作用喷射复合姿态控制问题,利用在线数据神经学习和扰动观测器构造了预定义时间终端滑模控制器,对系统动力学不确定实现有效逼近。对于不确定影响下的机动飞行控制有多种有效的解决办法,但均基于不确定存在确定常数界的假设[8]。然而,在机动飞行环境中气动特性随状态量变化剧烈,由于难以精确描述二者之间关系而往往将其作为不确定处理,使得系统不确定表现出与状态量的相关性。为应对机动飞行环境下随状态量变化的复杂不确定,研究了新型自适应滑模控制技术,增强系统鲁棒性,提高机动飞行控制性能。
另外,在现有气动舵面基础上引入矢量喷管使得执行机构冗余,通过控制分配技术将控制力矩映射到执行机构上,可以实现气动舵面和矢量喷管协调控制下的机动飞行。针对控制分配技术,文献[9]采用广义逆控制分配方法实现所有舵面有效偏转,同时用粒子群算法优化设计,得到分配效率最佳的广义逆矩阵。文献[10]以减少执行器供电效率,增加执行器可控性为目标设计重分布伪逆控制算法求解推力分配问题。文献[11]在考虑舵面位置和速率约束范围内采用链式递增分配策略,首先由气动舵面进行控制,当气动舵面达到饱和再采用推力矢量补充分配误差。文献[12]针对控制分配精度和计算效率问题,改进二次规划算法使用拉格朗日乘子法进行优化求解,在保留原计算精度的同时,减少迭代循环计算。目前控制分配算法优化求解已有较为突出的研究成果,但是大多数控制分配方法并未考虑控制分配过程的稳定性问题。考虑机动飞行环境未知且复杂,本文改进了控制分配结构,在机动飞行实现的基础上,保证分配环节的稳定性。
基于以上分析,为满足临近空间飞行器机动飞行的需求,实现机动飞行姿态稳定跟踪控制,本文结合推力矢量技术提出一种新型自适应滑模协调控制策略。具体工作可以归纳如下:1)引入推力矢量技术升级控制结构,增加了飞行器操纵性能,有效提升飞行器机动能力;2)设计新型自适应滑模控制器,放宽不确定有界性条件,有效应对状态依赖局部有界不确定影响,得到保证机动稳定飞行的期望控制力矩,解决了机动飞行中大范围不确定问题;3)改进传统开环控制分配方法,设计闭环最优控制分配策略,将期望控制力矩分配到执行器,并获得分配过程稳定充分必要条件,保证了气动舵面和矢量喷管对飞行姿态调整的协调性与控制系统整体稳定性。
1 面向控制的临近空间飞行器姿态模型 1.1 带推力矢量的控制模型临近空间飞行器六自由度动力学模型包括描述质心运动的三自由度平动方程和绕质心运动的三自由度转动方程,其中转动方程用于描述飞行器的姿态运动[13]。考虑到推力分量可提供三轴方向力矩而对姿态角速率产生直接控制作用(为简化模型,忽略推力分量对角度量的直接影响),同时考虑到忽略部分模型带来的模型不确定性及外界干扰等,带推力矢量的临近空间飞行器控制模型[11]可以写为
| $ \dot{\boldsymbol{\theta}}=\boldsymbol{f}_1(\theta)+\boldsymbol{R} \boldsymbol{\omega}+\mathit{\boldsymbol{\varDelta}}_1 $ | (1) |
| $ \dot{\boldsymbol{\omega}}=\boldsymbol{f}_2({\boldsymbol{\omega}})+\boldsymbol{Gu} +\mathit{\boldsymbol{\varDelta}}_2 $ | (2) |
式中:θ=[α β μ]T为角度向量,α、β、μ分别为攻角、侧滑角和航迹滚转角(由于推力矢量直接影响上述3个角度量,故本文把这3个量用做姿态角度控制的状态量);ω=[p q r]T为姿态角速率向量,p、q、r分别为滚转角速率、俯仰角速率和偏航角速率;u=[Ml Mm Mn]T为控制力矩向量,由气动舵面及推力矢量共同产生,其中
| $ M_l \approx \bar{q} S b C_l\left(h, M a, \alpha, \beta, \delta_r, \delta_a, p, r\right) $ | (3) |
| $ M_m \approx \bar{q} S \bar{c} C_m\left(h, M a, \alpha, \delta_c, \delta_a, p\right)+m_T $ | (4) |
| $ M_n \approx \bar{q} S b C_n\left(h, M a, \alpha, \beta, \delta_r, \delta_a, p, r\right)+n_T $ | (5) |
式中:q为动压,可通过q=0.5ρV2求解,其中ρ为空气密度;S为机翼面积;b为翼展;c为平均气动弦长;气动系数Cl、Cm、Cn分别是关于状态量和舵面偏转角度δa、δc、δr的函数[13];mT, nT为发动机推力产生的力矩;Δ1, Δ2为综合不确定。
f1(θ), f2(ω)的表达式分别为
| $ \boldsymbol{f}_1(\boldsymbol{\theta})=\left[\begin{array}{l} f_1(\alpha) \\ f_1(\beta) \\ f_1(\mu) \end{array}\right]=\left[\begin{array}{c} \frac{m g \cos \gamma \cos \mu-L}{m V \cos \beta} \\ \frac{Y \cos \beta+m g \cos \gamma \sin \mu}{m V} \\ \frac{L(\tan \gamma \sin \mu+\tan \beta)+Y \tan \gamma \cos \mu \cos \beta-m g \cos \gamma \cos \mu \tan \beta}{m V} \end{array}\right] $ | (6) |
| $ \boldsymbol{f}_2(\boldsymbol{\omega})=\left[\begin{array}{c} \frac{I_{x z}\left(I_{x x}-I_{y y}+I_{z z}\right)}{I_{x x} I_{z z}-I_{x z}^2} p q+\frac{I_{z z}\left(I_{y y}-I_{z z}\right)-I_{x z}^2}{I_{x x} I_{z z}-I_{x z}^2} q r \\ \frac{I_{z z}-I_{x x}}{I_{y y}} p r+\frac{I_{x z}}{I_{y y}}\left(r^2-p^2\right) \\ \frac{I_{x x}\left(I_{x x}-I_{y y}\right)+I_{x z}^2}{I_{x x} I_{z z}-I_{x z}^2} p q-\frac{I_{x z}\left(I_{x x}-I_{y y}+I_{z z}\right)}{I_{x x} I_{z z}-I_{x z}^2} q r \end{array}\right] $ | (7) |
式中:V为当前时刻飞行速度;γ为飞行航向角;m为飞行器质量;g为重力加速度;Iij(i=x, y, z, j=x, y, z)为转动惯量;升力L,侧力Y分别表示为
| $ L \approx \bar{q} S C_L\left(h, M a, \alpha, \delta_c, \delta_a\right) $ | (8) |
| $ Y \approx \bar{q} S C_Y\left(h, M a, \alpha, \beta, \delta_r, \delta_a\right) $ | (9) |
其中气动系数CL, CY是有关状态量和控制量的函数[14]。
R, G矩阵的具体表达如下:
| $ \boldsymbol{R}=\left[\begin{array}{ccc} -\cos \alpha \tan \beta & 1 & -\sin \alpha \tan \beta \\ \sin \alpha & 0 & -\cos \alpha \\ \cos \alpha \sec \beta & 0 & \sin \alpha \sec \beta \end{array}\right] $ | (10) |
| $ \boldsymbol{G}=\left[\begin{array}{ccc} \frac{I_{z z}}{I_{x x} I_{z z}-I_{x z}^2} & 0 & \frac{I_{x z}}{I_{x x} I_{z z}-I_{x z}^2} \\ 0 & \frac{1}{I_{y y}} & 0 \\ \frac{I_{x z}}{I_{x x} I_{z z}-I_{x z}^2} & 0 & \frac{I_{x x}}{I_{x x} I_{z z}-I_{x z}^2} \end{array}\right] $ | (11) |
假设1:在姿态系统中,综合不确定Δ1, Δ2包括建模不确定及未知干扰,表现出与状态量的线性关系,且存在正常数f1, f2, d1, d2,使得不等式‖Δ1‖≤f1‖θ‖+d1,‖Δ2‖≤f2‖ω‖+d2成立,即不确定被限制在与状态量相关的函数范围内。当f1, f2, d1, d2确定时,综合不确定Δ1, Δ2在状态量附近局部有限。
1.2 推力矢量模型引入推力矢量技术,能够通过推力矢量喷管的偏转对飞行器实现直接力控制,进而对飞行器纵向和侧向的姿态运动起到控制作用。本文建立简化发动机推力矢量模型,只考虑发动机产生的最大推力与油门开度的关系。发动机产生的最大推力表达为
| $ T \approx \bar{q}\left(C_T+C_T^{\varphi_T} \varphi_T\right) $ | (12) |
式中:φT为油门开度,CT, CTφT为推力系数[13]。
由于矢量喷管可以在一定范围内偏转,使得推力在喷管处产生沿机体三轴方向的推力分量,表示为
| $ \left\{\begin{array}{l} T_x=T \cos \delta_z \cos \delta_y \\ T_y=T \cos \delta_z \sin \delta_y \\ T_z=T \sin \delta_z \end{array}\right. $ | (13) |
式中:T为发动机产生的总推力;δz, δy分别为矢量喷管在z轴和y轴方向的偏转角度,偏转饱和限制为[-15°, 15°]。定义xT, yT, zT为发动机在机体轴上的位置,发动机推力矩表达为
| $ \left[\begin{array}{c} l_T \\ m_T \\ n_T \end{array}\right]=\left[\begin{array}{c} x_T \\ y_T \\ z_T \end{array}\right] \otimes\left[\begin{array}{c} T_x \\ T_y \\ T_z \end{array}\right] $ | (14) |
姿态控制目标:针对临近空间飞行器带有推力矢量的姿态控制模型(1)和模型(2),控制力矩u由气动舵面及推力矢量共同产生,考虑模型不确定、外界干扰等综合不确定Δ1, Δ2影响,设计基于闭环最优控制分配的新型自适应滑模控制器,并通过闭环控制方法,实现气动舵面和矢量喷管协调控制下姿态角θ对参考指令θd的稳定跟踪。
2 临近空间飞行器机动飞行姿态控制基于综合闭环最优控制分配的新型自适应滑模控制结构分为两部分:第一部分为新型自适应滑模控制器。将姿态控制系统划分为姿态角子系统和姿态角速率子系统,基于反步法设计新型自适应滑模控制器,应对机动飞行环境下复杂不确定影响,得到确保机动飞行中姿态稳定的期望控制力矩,提升系统鲁棒性。第二部分为闭环最优控制分配。将控制器设计得到的期望控制力矩按最优控制分配策略分配到执行器,并搭建闭环控制分配结构,以实际值与期望值之间的误差调整分配过程,确保控制分配环节稳定。最终依据获得的期望控制力矩与执行器协调控制,保证机动飞行环境下系统整体稳定性,实现了在复杂不确定影响下临近空间飞行器对机动飞行参考指令的稳定跟踪。整体控制结构如图 1所示。

|
图 1 带闭环控制分配的临近空间飞行器姿态控制系统结构图 Fig. 1 Block diagram for near space vehicle attitude control system with a closed-loop control allocation |
针对姿态角度子系统(1),定义角度跟踪误差e1=θ-θd,其中θd为姿态角参考指令。定义滑动变量s1(t)=e1(t)=θ(t)-θd(t),基于式(1),对s1(t)求导, 可得
| $ \dot{\boldsymbol{s}}_1(t)=\dot{\boldsymbol{\theta}}(t)-\dot{\boldsymbol{\theta}}_{\mathrm{d}}(t)=\boldsymbol{f}_1(\boldsymbol{\theta})+\boldsymbol{R} \boldsymbol{\omega}-\dot{\boldsymbol{\theta}}_{\mathrm{d}}+\mathit{\boldsymbol{\varDelta}}_1 $ | (15) |
满足假设1条件下,有
| $ \begin{gathered} \left\|\mathit{\boldsymbol{\varDelta}}_1\right\| \leqslant \bar{f}_1\|\boldsymbol{\theta}\|+\bar{d}_1 \leqslant \bar{f}_1\left\|\boldsymbol{\theta}_d+\boldsymbol{e}_1\right\|+\bar{d}_1 \leqslant \\ \bar{f}_1\left\|\boldsymbol{\theta}_d\right\|+\bar{f}_1\left\|\boldsymbol{e}_1\right\|+\bar{d}_1 \leqslant L_0^*+L_1^*\left\|\boldsymbol{e}_1\right\| \end{gathered} $ | (16) |
式中:L0*=f1‖θd‖+d1,L1*=f1为有限标量。由式(16)可知,综合不确定与角度跟踪误差相关,并限制在线性函数范围内。
定理1[8]:考虑满足假设1条件的姿态角子系统(1),综合不确定满足式(16),设计控制器为
| $ \begin{aligned} \boldsymbol{\omega}_{\mathrm{d}}(t)= & \boldsymbol{R}^{-1}\left(-\mathit{\boldsymbol{\varLambda}}_1 \boldsymbol{s}_1(t)-\rho_1(t) \operatorname{sgn}\left(\boldsymbol{s}_1(t)\right)-\right. \\ & \left.\boldsymbol{f}_1(\boldsymbol{\theta})+\dot{\boldsymbol{\theta}}_{\mathrm{d}}\right) \end{aligned} $ | (17) |
| $ \rho_1(t)=\hat{L}_0(t)+\hat{L}_1(t)\left\|\boldsymbol{e}_1\right\| $ | (18) |
式中Λ1为待设计的正定矩阵。自适应增益设计为
| $ \dot{\hat{L}}_0(t)=\left\|\boldsymbol{s}_1\right\|-a_0 \hat{L}_0(t) $ | (19) |
| $ \dot{\hat{L}}_1(t)=\left\|\boldsymbol{s}_1\right\|\left\|\boldsymbol{e}_1\right\|-a_1 \hat{L}_1(t) $ | (20) |
式中:
证明:由式(19)、(20)可得
| $ \begin{gathered} \hat{L}_i(t)=\underbrace{\exp \left(-a_i t\right) \hat{L}_i(0)}_{\geqslant 0}+ \\ \underbrace{\int_0^t \exp \left(-a_i(t-\tau)\left\|\boldsymbol{s}_1(\tau)\right\|\left\|\boldsymbol{e}_1\right\|^i\right) \mathrm{d} \tau}_{\geqslant 0} \Rightarrow \\ \hat{L}_i(t) \geqslant 0, \forall t \geqslant 0 \end{gathered} $ | (21) |
定义Lyapunov函数
| $ V_1=\frac{1}{2} \boldsymbol{s}_1^{\mathrm{T}} \boldsymbol{s}_1+\sum\limits_{i=0}^1 \frac{1}{2}\left(\hat{L}_i-L_i^*\right)^2 $ | (22) |
对式(22)求导,同时由式(21)
| $ \begin{gathered} \dot{V}_1=\boldsymbol{s}_1^{\mathrm{T}} \dot{\boldsymbol{s}}_1+\sum\limits_{i=0}^1\left(\hat{L}_i-L_i^*\right) \dot{\hat{L}}_i= \\ \boldsymbol{s}_1^{\mathrm{T}}\left(\boldsymbol{f}_1(\boldsymbol{\theta})+\boldsymbol{R} \boldsymbol{\omega}_{\mathrm{d}}-\dot{\boldsymbol{\theta}}_{\mathrm{d}}+\mathit{\boldsymbol{\varDelta}}_1\right)+\sum\limits_{i=0}^1\left(\hat{L}_i-L_i^*\right) \dot{\hat{L}}_i= \\ \boldsymbol{s}_1^{\mathrm{T}}\left(-\mathit{\boldsymbol{\varLambda}}_1 \boldsymbol{s}_1-\rho_1 \operatorname{sgn}\left(\boldsymbol{s}_1\right)+\mathit{\boldsymbol{\varDelta}}_1\right)+\sum\limits_{i=0}^1\left(\hat{L}_i-L_i^*\right) \dot{\hat{L}}_i \leqslant \\ -\boldsymbol{s}_1^{\mathrm{T}} \mathit{\boldsymbol{\varLambda}}_1 \boldsymbol{s}_1-\sum\limits_{i=0}^1\left\{\left(\hat{L}_i-L_i^*\right)\left(\left\|\boldsymbol{s}_1\right\|\left\|\boldsymbol{e}_1\right\|^i-\dot{\hat{L}}_i\right)\right\} \end{gathered} $ | (23) |
结合等式
| $ \begin{gathered} \left(\hat{L}_i-L_i^*\right) \dot{\hat{L}}_i=\left(\hat{L}_i-L_i^*\right)\left(\left\|\boldsymbol{s}_1\right\|\left\|\boldsymbol{e}_1\right\|^i-a_i \hat{L}_i\right)= \\ \left(\hat{L}_i-L_i^*\right)\left\|\boldsymbol{s}_1\right\|\left\|\boldsymbol{e}_1\right\|^i+a_i \hat{L}_i L_i^*-a_i \hat{L}_i^2 \end{gathered} $ | (24) |
得到
| $ \dot{V}_1 \leqslant-\boldsymbol{s}_1^{\mathrm{T}} \mathit{\boldsymbol{\varLambda}}_1 \boldsymbol{s}_1-\sum\limits_{i=0}^1\left(a_i \hat{L}_i L_i^*-a_i \hat{L}_i^2\right) $ | (25) |
基于不等式
| $ \begin{aligned} \hat{L}_i L_i^*-\hat{L}_i^2= & -\left(\frac{\hat{L}_i}{\sqrt{2}}-\frac{L_i^*}{\sqrt{2}}\right)^2-\frac{\hat{L}_i^2}{2}+\frac{L_i^{* 2}}{2} \leqslant \\ & -\left(\frac{\hat{L}_i}{\sqrt{2}}-\frac{L_i^*}{\sqrt{2}}\right)^2+\frac{L_i^{* 2}}{2} \end{aligned} $ | (26) |
式(25)进一步得到
| $ \begin{gathered} \dot{V}_1 \leqslant-\boldsymbol{s}_1^{\mathrm{T}} \mathit{\boldsymbol{\varLambda}}_1 \boldsymbol{s}_1-\sum\limits_{i=0}^1\left(\frac{a_i}{2}\left(\hat{L}_i-L_i^*\right)^2-\frac{a_i L_i^{* 2}}{2}\right) \leqslant \\ -\frac{\lambda_{\min }\left(\mathit{\boldsymbol{\varLambda}}_1\right)\left\|\boldsymbol{s}_1\right\|^2}{n}-\sum\limits_{i=0}^1\left(\frac{a_i}{2}\left(\hat{L}_i-L_i^{-}\right)^2-\frac{a_i L_i^{* 2}}{2}\right) \end{gathered} $ | (27) |
利用Lyapunov函数定义,可知
| $ V_1 \leqslant \frac{1}{2}\left\|\boldsymbol{s}_1\right\|^2+\sum\limits_{i=0}^1 \frac{1}{2}\left(\hat{L}_i-L_i^*\right)^2 $ | (28) |
由此,式(27)进一步得到
| $ \dot{V}_1 \leqslant-\vartheta_1 V_1+\frac{1}{2} \sum\limits_{i=0}^1 a_i L_i^{* 2} $ | (29) |
其中
定义0 < κ1 < ϑ1,式(29)写为
| $ \dot{V}_1 \leqslant-\kappa_1 V_1-\left(\vartheta_1-\kappa_1\right) V_1+\frac{1}{2} \sum\limits_{i=0}^1 a_i L_i^{* 2} $ | (30) |
定义
针对姿态角速率子系统(2),定义角速率跟踪误差e2=ω-ωd。定义滑动变量s2(t)=e2(t)=ω(t)-ωd(t),并对s2求导得到
| $ \dot{\boldsymbol{s}}_2=\dot{\boldsymbol{\omega}}-\dot{\boldsymbol{\omega}}_{\mathrm{d}}=\boldsymbol{f}_2(\boldsymbol{\omega})+\boldsymbol{G} \boldsymbol{u}-\dot{\boldsymbol{\omega}}_{\mathrm{d}}+\mathit{\boldsymbol{\varDelta}}_2 $ | (31) |
满足假设1条件下,有
| $ \begin{gathered} \left\|\mathit{\boldsymbol{\varDelta}}_2\right\| \leqslant \bar{f}_2\|\boldsymbol{\omega}\|+\bar{d}_2 \leqslant \bar{f}_2\left\|\omega_{\mathrm{d}}\right\|+ \\ \bar{f}_2\left\|\boldsymbol{e}_2\right\|+\bar{d}_2 \leqslant L_2^*+L_3^*\left\|\boldsymbol{e}_2\right\| \end{gathered} $ | (32) |
式中:L2*=f2‖ωd‖+d2,L3*=f2为有限标量。由式(32),综合不确定与系统角速率跟踪误差相关,并限制在跟踪误差相关线性函数范围内。
定理2[8]:考虑满足假设1条件的姿态角速率子系统(2),在式(32)不确定上界未知情况下,设计控制器:
| $ \boldsymbol{u}(t)=\boldsymbol{G}^{-1}\left(-\mathit{\boldsymbol{\varLambda}}_2 \boldsymbol{s}_2(t)-\rho_2(t) \operatorname{sgn}\left(\boldsymbol{s}_2(t)\right)-\boldsymbol{f}_2(\boldsymbol{\omega})+\dot{\boldsymbol{\omega}}_{\mathrm{d}}\right) $ | (33) |
| $ \rho_2(t)=\hat{L}_2(t)+\hat{L}_3(t)\left\|\boldsymbol{e}_2\right\| $ | (34) |
式中Λ2为待设计的正定矩阵。自适应增益设计为
| $ \dot{\hat{L}}_i(t)=\left\|\boldsymbol{s}_2\right\|\left\|\boldsymbol{e}_2\right\|^{(i-2)}-a_i \hat{L}_i(t) $ | (35) |
其中:
证明:选取Lyapunov函数
| $ V_2=\frac{1}{2} \boldsymbol{s}_2^{\mathrm{T}} \boldsymbol{s}_2+\sum\limits_{i=2}^3 \frac{1}{2}\left(\hat{L}_i-L_i^*\right)^2 $ | (36) |
对式(36)求导,推导过程与角速度环类似,由此得到
| $ \begin{gathered} \dot{V}_2=\boldsymbol{s}_2^{\mathrm{T}} \dot{\boldsymbol{s}}_2+\sum\limits_{i=2}^3\left(\hat{L}_i-L_i^*\right) \dot{\hat{L}}_i \leqslant \\ -\frac{\lambda_{\min }\left(\mathit{\boldsymbol{\varLambda}}_2\right)\left\|\boldsymbol{s}_2\right\|^2}{n}-\sum\limits_{i=2}^3\left(\frac{a_i}{2}\left(\hat{L}_i-L_i^*\right)^2-\frac{a_i L_i^{* 2}}{2}\right) \end{gathered} $ | (37) |
利用Lyapunov函数定义,式(37)可进一步简化为
| $ \dot{V}_2 \leqslant-\vartheta_2 V_2+\frac{1}{2} \sum\limits_{i=2}^3 a_i L_i^{* 2} $ | (38) |
其中
定义0 < κ2 < ϑ2,式(38)写为
| $ \dot{V}_2 \leqslant-\kappa_2 V_2-\left(\vartheta_2-\kappa_2\right) V_2+\frac{1}{2} \sum\limits_{i=2}^3 a_i L^{* 2} $ | (39) |
定义
综合姿态角速度和角速率子系统,选取整个闭环系统Lyapunov函数
| $ V_{12}=V_1+V_2 $ | (40) |
求导可得
| $ \dot{V}_{12}=\dot{V}_1+\dot{V}_2 \leqslant-\vartheta V+\frac{1}{2} \sum\limits_{i=0}^3 a_i L_i^{* 2} $ | (41) |
其中
| $ \dot{V}_{12} \leqslant-\kappa V-(\vartheta-\kappa) V+\frac{1}{2} \sum\limits_{i=0}^3 a_i L_i^{* 2} $ | (42) |
定义
满足假设1条件下的综合不确定表现出状态依赖特性(并不局限于假设1所述的线性关系)。在状态量(如姿态角速度)变化未知情况下,无法预先获得不确定的界,因此不确定存在确定常数界的假设不再成立;但由于二者之间存在一定的函数关系,而使得不确定被约束在该函数所包络的范围内,当状态量一定时,不确定表现出在该范围内的局部有限性。对于此类不确定,设计如式(17),式(33)新型自适应滑模控制器,可以放宽现有自适应滑模控制方法中不确定整体有界性假设,保证控制系统在复杂不确定影响下的收敛性。
2.2 执行器协调下的闭环最优控制分配在实际飞行中,以上得到的期望控制力矩作为中间量需要分配到执行器上,通过执行器偏转调整飞行姿态。矢量喷管的加入使得执行器冗余,因而分配方式并不唯一,求解最优分配方式对于减少执行器损耗、提升控制效率至关重要;另外控制分配是否为一个稳定的过程也并未可知。本节将期望控制量与实际输出量之间误差最小为优化目标,求解最优控制分配;并将执行器实际输出反馈到控制分配系统中搭建闭环结构,给出闭环控制结构稳定的充分必要条件,实现了气动舵面和矢量喷管作用下的多执行器稳定协调控制,确保机动飞行的可实现性与控制系统的整体稳定性。
控制力矩与舵面偏转角度呈一定的线性关系,表示为
| $ \boldsymbol{u}=\boldsymbol{B} \boldsymbol{\delta} $ | (43) |
式中:u=[Ml Mm Mn]T,δ=[δa δc δr δy δz]T,控制效率矩阵表示为
| $ \boldsymbol{B}=\left[\begin{array}{ccccc} \frac{\partial M_l}{\partial \delta_a} & \frac{\partial M_l}{\partial \delta_c} & \frac{\partial M_l}{\partial \delta_r} & \frac{\partial M_l}{\partial \delta_y} & \frac{\partial M_l}{\partial \delta_z} \\ \frac{\partial M_m}{\partial \delta_a} & \frac{\partial M_m}{\partial \delta_c} & \frac{\partial M_m}{\partial \delta_r} & \frac{\partial M_m}{\partial \delta_y} & \frac{\partial M_m}{\partial \delta_z} \\ \frac{\partial M_n}{\partial \delta_a} & \frac{\partial M_n}{\partial \delta_c} & \frac{\partial M_n}{\partial \delta_r} & \frac{\partial M_n}{\partial \delta_y} & \frac{\partial M_n}{\partial \delta_z} \end{array}\right] $ | (44) |
舵面偏转约束条件为
| $ \mathit{\boldsymbol{\varOmega}}_1=\left\{\boldsymbol{\delta}_i \in \mathbb{R}^m \mid \bar{\delta}_1 \leqslant \delta_i \leqslant \underline{\delta}_1, i=a, c, r\right\} $ | (45) |
| $ \mathit{\boldsymbol{\varOmega}}_2=\left\{\boldsymbol{\delta}_i \in \mathbb{R}^m \mid \bar{\delta}_2 \leqslant \delta_i \leqslant \underline{\delta}_2, i=y, z\right\} $ | (46) |
式中:δ1, δ1分别为气动舵面偏转角度的最大值和最小值;δ2, δ2分别为矢量喷管偏转角度的最大值和最小值。
针对上述问题和约束,最优控制分配算法可表述为有约束最优二次规划问题:
| $ J=\underset{\delta(t) \in \mathit{\Gamma }}{\operatorname{argmin}}\left\|\boldsymbol{R}_1 \boldsymbol{W}_1\left[\delta_{\mathrm{sf}}(t)-\boldsymbol{\delta}_{\mathrm{d}}(t)\right]\right\|^2 $ | (47) |
| $ \mathit{\Gamma }=\underset{\underline{\delta}(t) \leqslant \delta_{\mathrm{sf}}(t) \leqslant \bar{\delta}(t)}{\operatorname{argmin}}\left\|\boldsymbol{u}_{\mathrm{d}}(t)-\boldsymbol{B} \boldsymbol{\delta}_{\mathrm{sf}}(t)\right\| $ | (48) |
| $ \text { s. t. } \quad \boldsymbol{u}_{\mathrm{d}}(t)=\boldsymbol{B} \boldsymbol{\delta}_{\mathrm{sf}}(t) $ | (49) |
式中:W1为对角正权值矩阵;R1为增益矩阵,用于将实际值和期望值转化到同一限制区域内,方便有约束最优二次问题求解;u, δ分别表示控制力矩和实际执行器相关项,下标d, sf表示期望值和实际值。
通过数值求解方式对最优问题求解[15],得到
| $ \boldsymbol{\delta}_{\mathrm{sf}}(t)=\boldsymbol{E} \boldsymbol{\delta}_{\mathrm{d}}(t)+\boldsymbol{H} \boldsymbol{u}_{\mathrm{d}}(t) $ | (50) |
式中:W=R1W1,E=I-HB,H=W-1(BW-1)†,†表示伪逆算子,定义为A†=AT(AAT)-1。
式(47)为约束条件下的代价函数,代价函数取到最小值时则表明控制分配误差最小,若选择一个较大的加权矩阵W1,执行器输出便能快速收敛到期望输出。
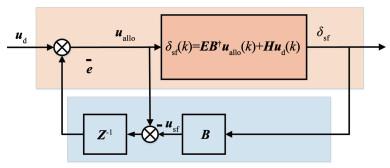
考虑临近空间飞行器机动飞行过程中复杂的环境特性,基于以上最优分配策略,进一步研究控制分配过程稳定性问题。为方便稳定性分析,首先对式(50)进行离散化表达,在此基础上将实际执行器力矩输出反馈到系统中搭建分配闭环。闭环最优控制分配结构如图 2所示,本文针对闭环输出进行分析。
|
图 2 闭环最优控制分配结构图 Fig. 2 Closed-loop optimal control allocation structure |
为便于分析闭环控制分配的稳定性,式(50)用离散模型描述为
| $ \begin{gathered} \boldsymbol{\delta}_{\mathrm{sf}}(k)=\boldsymbol{E} \boldsymbol{\delta}_{\text {allo }}(\boldsymbol{k})+\boldsymbol{H} \boldsymbol{u}_{\mathrm{d}}(k)= \\ \boldsymbol{E} \boldsymbol{B}^{\dagger} \boldsymbol{u}_{\text {allo }}(\boldsymbol{k})+\boldsymbol{H} \boldsymbol{u}_{\mathrm{d}}(\boldsymbol{k}) \end{gathered} $ | (51) |
由闭环结构分析可得
| $ \begin{gathered} \boldsymbol{u}_{\text {allo }}(k)=\boldsymbol{u}_{\mathrm{d}}(k)+\boldsymbol{e}(k-1)= \\ \boldsymbol{u}_{\mathrm{d}}(k)+\boldsymbol{u}_{\text {allo }}(k-1)-\boldsymbol{u}_{\mathrm{sf}}(k-1) \end{gathered} $ | (52) |
| $ \boldsymbol{u}_{\mathrm{sf}}(k)=\boldsymbol{B} \boldsymbol{\delta}_{\mathrm{sf}}(k) $ | (53) |
由式(51)~(53)可得
| $ \begin{aligned} \boldsymbol{E} \boldsymbol{B}^{\dagger} \boldsymbol{u}_{\mathrm{allo}}(k)= & \boldsymbol{E} \boldsymbol{B}^{\dagger} \boldsymbol{u}_{\mathrm{d}}(k)+\boldsymbol{E} \boldsymbol{B}^{\dagger} \boldsymbol{u}_{\mathrm{allo}}(k-1)- \\ & \boldsymbol{E} \boldsymbol{B}^{\dagger} \boldsymbol{B} \boldsymbol{\delta}_{\mathrm{sf}}(k-1) \end{aligned} $ | (54) |
定义EB†=K,由式(51)得到上一时刻Kuallo(k-1)表达式,代入式(52)中,得到
| $ \begin{aligned} \boldsymbol{K} \boldsymbol{u}_{\mathrm{allo}}(k)= & \boldsymbol{K} \boldsymbol{u}_{\mathrm{d}}(k)+\boldsymbol{\delta}_{\mathrm{sf}}(k-1)- \\ & \boldsymbol{H} \boldsymbol{u}_{\mathrm{d}}(k-1)-\boldsymbol{K} \boldsymbol{B} \boldsymbol{\delta}_{\mathrm{sf}}(k-1) \end{aligned} $ | (55) |
结合式(51),对上式进一步整理可得
| $ \begin{gathered} \boldsymbol{\delta}_{\mathrm{sf}}(k)-(\boldsymbol{I}-\boldsymbol{K} \boldsymbol{B}) \boldsymbol{\delta}_{\mathrm{sf}}(k-1)= \\ (\boldsymbol{K}+\boldsymbol{H}) \boldsymbol{u}_{\mathrm{d}}(k)-\boldsymbol{H} \boldsymbol{u}_{\mathrm{d}}(k-1) \end{gathered} $ | (56) |
通过Z变换可得
| $ \begin{gathered} \boldsymbol{\delta}_{\mathrm{sf}}(z)-z^{-1}(\boldsymbol{I}-\boldsymbol{K} \boldsymbol{B}) \boldsymbol{\delta}_{\mathrm{sf}}(z)= \\ (\boldsymbol{K}+\boldsymbol{H}) \boldsymbol{u}_{\mathrm{d}}(z)-z^{-1} \boldsymbol{H} \boldsymbol{u}_{\mathrm{d}}(z) \end{gathered} $ | (57) |
进一步整理,得到闭环控制分配系统执行器偏转角度输出为
| $ \left(\boldsymbol{I}-z^{-1}(\boldsymbol{I}-\boldsymbol{K} \boldsymbol{B})\right) \boldsymbol{\delta}_{\mathrm{sf}}(z)=\left(\boldsymbol{K}+\boldsymbol{H}-z^{-1} \boldsymbol{H}\right) \boldsymbol{u}_{\mathrm{d}}(z) $ | (58) |
定理3:对于闭环控制分配系统(58),保证其稳定的一个充分必要条件为:当且仅当K的特征值ki都在以(1, 0)为中心的单位圆内时,闭环控制分配系统(58)是稳定的。
证明:闭环控制分配系统的特征方程为
| $ \left|\boldsymbol{I}-z^{-1}(\boldsymbol{I}-\boldsymbol{K B})\right|=0 $ | (59) |
将式(59)变换为如下形式
| $ |z \boldsymbol{I}-(\boldsymbol{I}-\boldsymbol{K B})|=0 $ | (60) |
容易得到,式(59)的解为I-KB的特征值。若KB的特征值为λi, i=1, 2, …, m,则I-KB的特征值为1-λi, i=1, 2, …, m。所以闭环控制系统的特征根为ki=1-λi, i=1, 2, …, m。离散系统稳定的充分必要条件是所有特征根的范数小于1[16]。因此闭环控制系统稳定的充分必要条件为|ki|=|1-λi| < 1, i=1, 2, …, m。
闭环控制分配系统采用离散时间方法:一方面,计算机信号本质上是离散的,在实际工作环境中,控制分配环节采样周期与飞行器控制系统的采样周期保持一致;另一方面,采用离散时间方法便于对控制分配稳定性分析。所以采用Z变换理论对系统进行分析是合理的。
3 仿真与分析为了验证所提出的控制结构对提高临近空间飞行器机动性的可行性,以及所设计控制器应对状态依赖不确定的有效性,该部分将基于临近空间飞行器模型进行仿真验证分析。
仿真参数设置为:飞行器质量m=1.368 2×105 kg;角度初值为θ0=[α0 β0 μ0]T=[0° 0° 0°]T,姿态角速率初值为ω0=[p0 q0 r0]T=[0°·s-1 0°·s-1 0°·s-1]T。控制器参数设计为:Λ1=diag(20, 20, 20),Λ2=diag(5×105, 5×105, 5×105),a0=a1=500,a2=a3=2,L0=L1=0.1,L2=L3=0.01。假设飞行器当前处于平飞状态,速度V=8 Ma,且飞行过程中保持油门开度不变,即总推力大小不变T=8.422 5×105 N。
3.1 有/无推力矢量下飞行器姿态跟踪对比仿真结果本节中,设置参考指令分别为βc=0°,αc的初始值为0°,首先在第4秒时输入一个幅值为40°的阶跃信号,持续到第8秒结束;然后在第12秒时输入一个幅值为40°的负阶跃信号,持续到第16秒结束。μc的初始值为0°,先在第6秒时输入一个幅值为10°的阶跃信号,持续到第12秒结束。参考信号给定通过一阶滤波作平滑处理,避免突变。设置具有状态依赖的综合不确定为
| $ \begin{aligned} \mathit{\boldsymbol{\varDelta}}_1= & {[0.5 \alpha+0.55 \cos (0.1 t), 0.5 \beta+} \\ & 0.1 \sin (0.5 t), 0.5 \mu+0.55 \sin (0.05 t)] \end{aligned} $ | (61) |
| $ \begin{aligned} \mathit{\boldsymbol{\varDelta}}_2= & {[5 p+0.5 \sin (2 t), 3 q+0.1 \sin (2 t), r+} \\ & 0.2 \sin (2 t)] \end{aligned} $ | (62) |
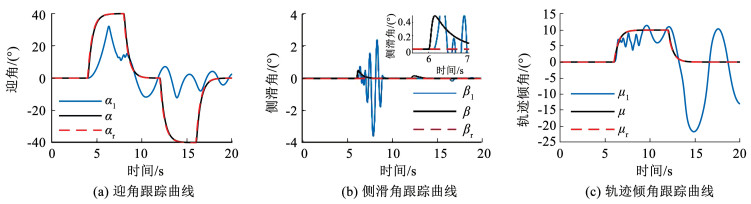
仿真结果如图 3~6所示。图 3为姿态角指令跟踪仿真结果,图中红色虚线为参考指令,蓝色实线、黑色实线分别为无推力矢量和引入推力矢量的实际姿态角。可以看出,无推力矢量下飞行器难以跟踪大范围变化的参考指令;加入推力矢量后,则可以实现对参考指令的跟踪,从而验证了加入推力矢量对于扩大飞行器姿态角变化范围的有效性。图 3(b)中,引入推力矢量后侧滑角在一定范围内偏离参考指令,这是由通道之间耦合影响造成的,属于跟踪误差的正常范围。图 4为闭环控制分配下执行器实际控制输出。黑色点划线表示在无推力矢量情况下,将控制力矩分配到气动舵面后的舵面实际偏转。从图中可知姿态角在跟踪±40°俯仰角,10°航迹倾角时,气动舵面偏转已经处于较为严重的饱和状态,此时由于舵面偏转所提供力矩不能达到期望值,使得姿态角无法跟踪参考指令(图 4黑色点划线)。加入推力矢量后,期望力矩按照所设计的闭环控制分配策略分配到气动舵面和矢量喷管(图 4蓝色实线),矢量喷管提供部分控制力矩,降低了气动舵面的饱和程度,从而放宽姿态角的限制,两部分执行机构共同作用达到期望的控制力矩,实现了大姿态角的跟踪控制。该仿真一方面验证了推力矢量的引入有助于临近空间飞行器实现机动飞行,另一方面验证了闭环控制分配策略在实现多执行机构控制分配中的有效性。
|
图 3 有/无推力矢量下临近空间飞行器飞行角度跟踪曲线 Fig. 3 Attitude angle tracking curve of near space vehicle with or without thrust vector |

|
图 4 闭环控制分配下姿态跟踪实际执行器偏转曲线 Fig. 4 The actual deflection of actuators of attitude tracking under closed-loop control allocation |

|
图 5 状态依赖不确定影响下机动飞行姿态角跟踪曲线(新型自适应滑模控制器) Fig. 5 Attitude angle tracking curve of maneuver flight under influence of state dependent uncertainty (novel adaptive sliding mode controller) |
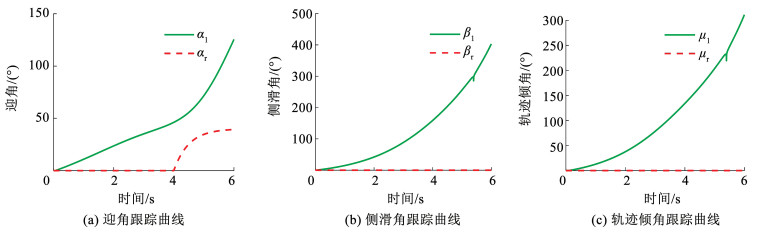
|
图 6 状态依赖不确定影响下机动飞行姿态角曲线(典型自适应滑模控制器) Fig. 6 Attitude angle tracking curve of maneuver flight under influence of state dependent uncertainty (typical adaptive sliding mode controller) |
本节在带有推力矢量情况下进行姿态角跟踪仿真验证,参考指令设置同3.1节,设置如式(62)状态依赖不确定。考虑相同不确定影响,对比所设计新型自适应滑模控制器与典型自适应滑模控制器的控制效果。典型自适应滑模控制器表达式为
| $ \boldsymbol{u}(t)=\boldsymbol{G}^{-1}\left(-K_2 \operatorname{sgn}\left(\boldsymbol{s}_2(t)\right)-\boldsymbol{f}_2(\boldsymbol{\omega})+\dot{\boldsymbol{\omega}}_{\mathrm{d}}\right) $ | (63) |
| $ \dot{K}_2(t)=\left\{\begin{array}{l} \bar{K}_2\left\|\boldsymbol{s}_2(t)\right\| \operatorname{sgn}\left(\left\|\boldsymbol{s}_2(t)\right\|\right)-\varpi_2, K_2(t)>\varepsilon_2 \\ \varepsilon_2, K_2(t)>\varepsilon_2 \end{array}\right. $ | (64) |
式中:K2为自适应增益,K2、
| $ \boldsymbol{\omega}_{\mathrm{d}}(t)=\boldsymbol{R}^{-1}\left(-K_1 \operatorname{sgn}\left(\boldsymbol{s}_1(t)\right)-\boldsymbol{f}_1(\boldsymbol{\theta})+\dot{\boldsymbol{\theta}}_{\mathrm{d}}\right) $ | (65) |
| $ \dot{K}_1(t)=\left\{\begin{array}{l} \bar{K}_1\left\|\boldsymbol{s}_1(t)\right\| \operatorname{sgn}\left(\left\|\boldsymbol{s}_1(t)\right\|\right)-\varpi_1, K_1(t)>\varepsilon_1 \\ \varepsilon_1, K_1(t)>\varepsilon_1 \end{array}\right. $ | (66) |
其中: K1为自适应增益,K1、

|
图 7 新型自适应滑模控制器自适应增益变化曲线 Fig. 7 Adaptive gain curve of novel adaptive sliding model control |
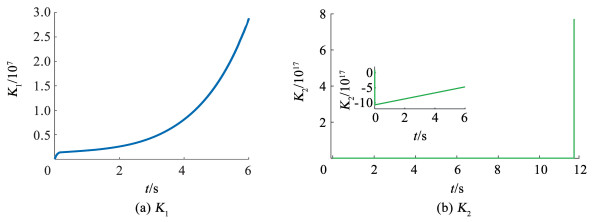
|
图 8 典型自适应滑模控制器自适应增益变化曲线 Fig. 8 Adaptive gain curve of typical adaptive sliding model control |
图 5为所设计控制器下姿态角跟踪仿真图,在状态依赖不确定影响下所设计控制器仍能对参考指令实现较好的跟踪。图 6为典型自适应控制器下姿态角跟踪仿真图,从图中看出第6秒时状态量已经发散,在11.7秒变化为无穷大,姿态角无法稳定。采用典型自适应滑模控制器实现对系统稳定控制需要满足不确定有界性假设,当综合不确定随状态量发生变化,使其难以得到确定上界,而不满足假设条件,从而无法使系统稳定。图 7为所设计控制器自适应增益变化曲线。从图中可知,在不确定上界未知且随状态量发生变化的情况下,自适应增益仍能相应调整,降低复杂不确定对姿态系统的影响,完成对姿态角的跟踪控制。图 8为典型自适应控制器中自适应增益曲线。在11.7秒时自适应增益变化为无穷大,难以自适应调整,而无法实现对姿态角的稳定跟踪。通过以上对比仿真,验证了所设计控制器在应对状态依赖不确定时的有效性,放宽了自适应滑模控制器设计中不确定有界性条件,能够更好应对机动飞行环境下复杂不确定。
4 结论1) 针对临近空间飞行器机动能力不足的问题,通过加入推力矢量控制技术,降低气动舵面饱和限制,从而扩大姿态角变化范围,提升临近空间飞行器机动性能。
2) 在控制器设计中,考虑复杂的机动飞行环境,设计新型自适应滑模控制器,应对状态依赖局部有限的不确定影响,放宽不确定有界性条件,最终证明姿态控制系统全局一致最终有界,保证了飞行姿态对机动飞行参考指令的稳定跟踪。
3) 在执行器协调控制中,考虑控制分配过程的稳定性问题,改进控制分配方法设计闭环最优控制分配,得到执行器偏转角度与期望控制力矩的直接关系,最终通过气动舵面和矢量喷管多执行器的协调控制,实现了对机动飞行姿态的精确稳定调整。
| [1] |
AN Hao, WU Qianqian, WANG Changhong. Differentiator based full-envelope adaptive control of air-breathing hypersonic vehicles[J]. Aerospace Science and Technology, 2018, 83(11): 312. |
| [2] |
IJAZ S, CHEN Fuyang, HAMAYUN M T, et al. Adaptive integral-sliding-mode control strategy for maneuvering control of F16 aircraft subject to aerodynamic uncertainty[J]. Applied Mathematics and Computation, 2021, 402(8): 126053. |
| [3] |
RAJ K, MUTHUKUMAR V, SINGH S N, et al. Finite-time sliding mode and super-twisting control of fighter aircraft[J]. Aerospace Science and Technology, 2018, 83(11): 487. |
| [4] |
刘俊杰, 陈增强, 孙明玮, 等. 自抗扰控制在推力矢量飞机大迎角机动中的应用[J]. 工程科学学报, 2019, 41(9): 1187. LIU Junjie, CHEN Zengqiang, SUN Mingwei, et al. Application of active disturbance rejection control in high-angle-of-attack maneuver for aircraft with thrust vector[J]. Chinese Journal of Engineering, 2019, 41(9): 1187. |
| [5] |
LIU Junjie, SUN Mingwei, CHEN Zengqiang, et al. High AOA decoupling control for aircraft based on ADRC[J]. Journal of Systems Engineering and Electronics, 2020, 31(2): 397. |
| [6] |
吴文海, 高阳, 王子健, 等. 基于LADRC的舰载V/STOL飞机短距起飞性能优化[J]. 航空学报, 2019, 40(6): 122772. WU Wenhai, GAO Yang, WANG Zijian, et al. Optimization of short take-off performance for carrier-based V/STOL aircraft via LADRC method[J]. Acta Aeronautica et Astronautica Sinica, 2019, 40(6): 122772. |
| [7] |
SHOU Yingxin, XU Bin, LIANG Xiaohui, et al. Aerodynamic/reaction-jet compound control of hypersonic reentry vehicle using sliding mode control and neural learning[J]. Aerospace Science and Technology, 2021(4): 106564. |
| [8] |
ROY S, BALDI S, FRIDMAN L M. On adaptive sliding mode control without a priori bounded uncertainty[J]. Automatica, 2020, 111(1): 108650. |
| [9] |
GUO Yiming, WU Mei, LUO Yu. Optimization of multi-effector aircraft control allocation based on generalized inverse[C]//2019 International Conference on Control, Automation and Information Sciences (ICCAIS). Chengdu: IEEE, 2019: 1
|
| [10] |
VAN BUI P, KIM Y B. A development of constrained control allocation for ship berthing by using autonomous tugboats[J]. International Journal of Control Automation & Systems, 2011, 9(6): 1205. |
| [11] |
LIU Junjie, SUN Mingwei, CHEN Zengqiang, et al. Super-twisting sliding mode control for aircraft at high angle of attack based on finite-time extended state observer[J]. Nonlinear Dynamics, 2020, 99(4): 2785. |
| [12] |
李岳明, 王小平, 张军军, 等. 基于改进二次规划算法的X舵智能水下机器人控制分配[J]. 上海交通大学学报, 2020, 54(5): 524. LI Yueming, WANG Xiaoping, ZHANG Junjun, et al. X-Rudder autonomous underwater vehicle control allocation based on improved quadratic programming algorithm[J]. Journal of Shanghai Jiao Tong University, 2020, 54(5): 524. |
| [13] |
BOLENDE M A, DOMAND B. Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle[J]. Journal of Spacecraft and Rockets, 2007, 44(2): 374. |
| [14] |
DOU Liqian, SU Peihua, ZONG Qun, et al. Fuzzy disturbance observer based dynamic surface control for air-breathing hypersonic vehicle with variable geometry inlets[J]. IET Control Theory and Applications, 2018, 12(1): 10. |
| [15] |
GOLUB G H, VANLOAN C F. Matrix computations[M]. Baltimore: Johns Hopkins Univ Press, 1986.
|
| [16] |
FRANKLIN G F, POWELL J D, WORKMAN M. Digital control of dynamic system[M]. 3rd ed. New York: Addison Wesley Longman, Inc., 1998.
|
 2023, Vol. 55
2023, Vol. 55


