刚体航天器姿态跟踪控制问题因其在空间任务中的重要作用得到了国内、外学者的广泛关注。针对航天器姿态控制系统的非线性特性，各种非线性控制方法已经在航天器姿态控制问题中得到了应用^[1-3]。但是，上述控制方法只能使航天器姿态误差渐近收敛，理论上完成收敛所需的时间是无穷大的，而工程应用中对姿态误差的收敛时间往往是有要求的，因而这些方法的实用性受到了一定限制。为增强控制器的实用性，有限时间控制是一种有效的方法^[4-6]。有限时间控制方法可以保证系统在不多于某确定值的时间内完成收敛，但此收敛时间上界与初始条件直接相关。相比之下，固定时间控制的收敛时间上界仅由控制器参数决定，与初始条件无关，可以使设计者在控制器设计期间摆脱初始条件的制约^[7-9]。文献[7]使用终端滑模控制方法，实现了刚体航天器的固定时间姿态跟踪控制。文献[8]使用神经网络对航天器所受的外部扰动力矩及自身建模不确定性进行近似逼近，并考虑执行机构饱和与故障的因素，提出了一种固定时间姿态控制方法。文献[9]则采用自适应方法对扰动项和系统建模不确定性进行补偿，考虑执行机构饱和与故障，设计了一个自适应航天器姿态控制器。传统固定时间控制方法的一个主要缺点是收敛时间上界往往与控制器的多个参数存在比较复杂的等式关系。给定要求的收敛时间以后，如何确定各个控制参数的值是一个比较困难的问题。

作为固定时间控制的一种特殊情况，预设时间控制^[9-12]的收敛时间上界显式存在于控制器参数当中，设计者可以根据实际需要很方便地对其进行设置。文献[13]针对战斗机空中加油时的姿态稳定问题设计了一种预设时间姿态控制方法，但是其控制律存在不连续性，易出现抖振现象。文献[14]基于一种新型性能函数，实现了航天器的预设时间预设精度姿态跟踪控制。文献[15]建立了一种准终端滑模面，在实现刚体航天器预设时间预设精度姿态跟踪控制的同时，保证了控制律的连续和非奇异。针对有界外部扰动力矩，文献[15]采用的处理方法是在控制律中添加鲁棒项予以补偿，这是一种比较保守的方法。

本文针对刚体航天器受有界外部扰动力矩的情形，首先设计了一个预设时间扰动观测器^[16-17]，用以对有界外部扰动力矩进行补偿，然后设计了一个预设时间准终端滑模面，最后基于上述观测器和滑模面构造了一个连续非奇异控制器。Lyapunov理论分析表明，本文提出的控制策略可以在已知外部扰动力矩上界的情况下实现刚体航天器的预设时间预设精度姿态跟踪控制，即保证航天器的姿态跟踪误差在预设的时间内收敛到预先指定的精度以内。

1 航天器建模与问题描述

描述航天器本体坐标系相对空间参考坐标系的方位的物理量称为姿态参数。姿态参数有多种描述形式，常用的有方向余弦矩阵、欧拉角、欧拉轴/角、欧拉四元数、罗德里格参数(Rodrigues parameters, RPs)以及修正罗德里格参数(Modified Rodrigues parameters, MRPs)。其中，修正罗德里格参数(MRPs)具有几何直观性好、不存在奇异性问题和范数约束等优点。故本文采用MRPs来描述航天器的姿态。在MRPs下，刚体航天器的姿态运动学和姿态动力学模型分别为：

$ \dot{{\boldsymbol{q}}}=\frac{1}{2}\left(\frac{1-{\boldsymbol{q}}^{{\mathrm{T}}} {\boldsymbol{q}}}{2} {\boldsymbol{I}}_3+{\boldsymbol{q}}^{\times}+{\boldsymbol{q}} {\boldsymbol{q}}^{{\mathrm{T}}}\right) {\boldsymbol{\omega}}={\boldsymbol{T}}({\boldsymbol{q}}) {\boldsymbol{\omega}} $

(1)

$ {\boldsymbol{J}} {\boldsymbol{\dot{\omega}}}=-{\boldsymbol{\omega}} ^{\times} {\boldsymbol{J \omega}} +{\boldsymbol{\tau}}+{\boldsymbol{d}} $

(2)

式中: ω为航天器的角速度，J为航天器的转动惯量矩阵，τ为所施加的控制力矩，d为外部扰动力矩，q即为航天器姿态的MRPs表示。对任一矢量a =[a₁ a₂ a₃]^T，a^×表示如下反对称矩阵：

$ {\boldsymbol{a}}^{\times}=\left[\begin{array}{ccc} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{array}\right] $

记航天器的目标姿态及相应目标角速度分别为q_d和ω_d，则姿态跟踪误差和角速度跟踪误差分别为：

$ {\boldsymbol{q}}_{{\mathrm{e}}}={\boldsymbol{q}} \otimes {\boldsymbol{q}}_{{\mathrm{d}}}^{-1}=\frac{{\boldsymbol{q}}_{{\mathrm{d}}}\left({\boldsymbol{q}}^{{\mathrm{T}}} {\boldsymbol{q}}-1\right)+{\boldsymbol{q}}\left(1-{\boldsymbol{q}}_{{\mathrm{d}}}^{{\mathrm{T}}} {\boldsymbol{q}}_{{\mathrm{d}}}\right)-2 {\boldsymbol{q}}_{{\mathrm{d}}}^{\times} {\boldsymbol{q}}}{1+{\boldsymbol{q}}_{{\mathrm{d}}}^{{\mathrm{T}}} {\boldsymbol{q}}_{{\mathrm{d}}} {\boldsymbol{q}}^{{\mathrm{T}}} {\boldsymbol{q}}+2 {\boldsymbol{q}}_{{\mathrm{d}}}^{{\mathrm{T}}} {\boldsymbol{q}}} $

(3)

$ {\boldsymbol{\omega}}_{{\mathrm{e}}}={\boldsymbol{\omega}}-{\boldsymbol{C}}_{{\mathrm{qe}}} {\boldsymbol{\omega}}_{{\mathrm{d}}} $

(4)

式中, ${\boldsymbol{C}}_{{\mathrm{qe}}}={\boldsymbol{I}}_3+\frac{8\left({\boldsymbol{q}}_{{\mathrm{e}}}^{\times}\right)^2-4\left(1-{\boldsymbol{q}}_{{\mathrm{e}}}^{{\mathrm{T}}} {\boldsymbol{q}}_{{\mathrm{e}}}\right) {\boldsymbol{q}}_{{\mathrm{e}}}^{\times}}{\left(1+{\boldsymbol{q}}_{{\mathrm{e}}}^{{\mathrm{T}}} {\boldsymbol{q}}_{{\mathrm{e}}}\right)^2}$为从目标体坐标系到本体坐标系的旋转矩阵。航天器相对目标姿态的相对运动方程即为：

$ \dot{{\boldsymbol{q}}}_{{\mathrm{e}}}={\boldsymbol{T}}\left({\boldsymbol{q}}_{{\mathrm{e}}}\right) {\boldsymbol{\omega}}_{{\mathrm{e}}}=\frac{1}{2}\left(\frac{1-{\boldsymbol{q}}_{{\mathrm{e}}}^{{\mathrm{T}}} {\boldsymbol{q}}_{{\mathrm{e}}}}{2} {\boldsymbol{I}}_3+{\boldsymbol{q}}_{{\mathrm{e}}}^{\times}+{\boldsymbol{q}}_{{\mathrm{e}}} {\boldsymbol{q}}_{{\mathrm{e}}}^{{\mathrm{T}}}\right) {\boldsymbol{\omega}}_{{\mathrm{e}}} $

(5)

$ \begin{aligned} {\boldsymbol{J}} \dot{{\boldsymbol{\omega}}}_{{\mathrm{e}}}= & -{\boldsymbol{\omega}}^{\times} {\boldsymbol{J}} {\boldsymbol{\omega}}+{\boldsymbol{\tau}}+{\boldsymbol{d}}-{\boldsymbol{J}} {\boldsymbol{C}}_{{\mathrm{qe}}} \dot{{\boldsymbol{\omega}}}_{{\mathrm{d}}}+{\boldsymbol{J}} {\boldsymbol{\omega}}_{{\mathrm{e}}}^{\times} {\boldsymbol{C}}_{{\mathrm{qe}}} {\boldsymbol{\omega}}_{{\mathrm{d}}}= \\ & {\boldsymbol{\tau}}+{\boldsymbol{f}}\left({\boldsymbol{q}}_{{\mathrm{e}}}, {\boldsymbol{\omega}}, {\boldsymbol{\omega}}_{{\mathrm{d}}}, \dot{{\boldsymbol{\omega}}}_{{\mathrm{d}}}\right)+{\boldsymbol{d}} \end{aligned} $

(6)

式中, f (q_e, ω, ω_d, $\dot{\boldsymbol{\omega}}_{\mathrm{d}}$)=- ω^× Jω-JC_qe $\dot{\boldsymbol{\omega}}_{\mathrm{d}}$+ Jω_e^× C_qe ω_d。

这里，运动学矩阵T(q_e)满足如下性质(在不至混淆的情况下，下文以T表示T(q_e))：

$ {\mathrm{det}}({\boldsymbol{T}})=\left(\frac{1+{\boldsymbol{q}}_{{\mathrm{e}}}^{{\mathrm{T}}} {\boldsymbol{q}}_{{\mathrm{e}}}}{4}\right)^3>0 $

(7)

$ \begin{aligned} & \dot{{\boldsymbol{T}}}=\frac{1}{2}\left(-\frac{1+{\boldsymbol{q}}_{{\mathrm{e}}}^{{\mathrm{T}}} {\boldsymbol{q}}_{{\mathrm{e}}}}{4} {\boldsymbol{q}}_{{\mathrm{e}}}^{{\mathrm{T}}} {\boldsymbol{\omega}}_{{\mathrm{e}}} {\boldsymbol{I}}_3+\right. \\ & \left.\left({\boldsymbol{T}} {\boldsymbol{\omega}}_{{\mathrm{e}}}\right)^{\times}+{\boldsymbol{T}} {\boldsymbol{\omega}}_{{\mathrm{e}}} {\boldsymbol{q}}_{{\mathrm{e}}}^{{\mathrm{T}}}+{\boldsymbol{q}}_{{\mathrm{e}}} {\boldsymbol{\omega}}_{{\mathrm{e}}}^{{\mathrm{T}}} {\boldsymbol{T}}^{{\mathrm{T}}}\right) \end{aligned} $

(8)

$ \dot{{\boldsymbol{T}}}^{-1}=-{\boldsymbol{T}}^{-1} \dot{{\boldsymbol{T}}} {\boldsymbol{T}}^{-1} $

(9)

现给出本文控制器设计过程所满足的假设。

假设 1   目标角速度及其时间导数ω_d、$\dot{\boldsymbol{\omega}}_{\mathrm{d}}$是一致最终有界的。

假设 2   外部扰动力矩是有界的，即存在正常数d_M使得外部扰动力矩满足‖ d ‖≤d_M，其中‖ · ‖表示向量的2范数。

本文的研究目标便是设计一个连续非奇异的控制律τ (t) 使得航天器在满足上述假设的外部扰动力矩作用下，其姿态跟踪误差仍能实现预设时间预设精度稳定，即对给定的预设时间常数T_p和预设精度常数ε_i(i=1, 2, 3)，当t≥T_p时，姿态跟踪误差的各分量满足|q_{e, i}|≤ε_i(i=1, 2, 3)。在本文的控制策略设计过程中会用到如下引理。

引理 1^[18]  假设某动态系统存在一个李雅普诺夫函数，满足:

$ \dot{V} \leqslant-\frac{\pi}{\eta T_{{\mathrm{p}}}}\left(V^{1-\frac{\eta}{2}}+V^{1+\frac{\eta}{2}}\right) $

(10)

式中0 < η < 1，则系统关于时间常数T_p是预设时间稳定的。

引理 2^[19]  设λ>0，x、r为n维列向量，其中x为状态空间中的单位向量，r的所有元素都为正。定义映射算子χ (λ, x)=[λ^r₁ x₁, …, λ^r_n x_n]^T，则此映射为一双射。同时对于其逆运算ϕ(y)= χ^-1(y)=(ϕ_λ(y), ϕ_x(y))(r一定)，ϕ_λ(y)和ϕ_x(y) 是无穷多阶连续可导的，且$\lim\limits _{\|{\boldsymbol{y}}\| \rightarrow 0} {\boldsymbol{\phi}}_\lambda({\boldsymbol{y}})=0$，$\lim\limits _{\|{\boldsymbol{y}}\| \rightarrow \infty} {\boldsymbol{\phi}}_\lambda({\boldsymbol{y}})=\infty$。

2 预设时间预设精度姿态跟踪控制器设计

本文考虑受有界外部扰动力矩的刚体航天器的预设时间姿态跟踪控制问题。首先，提出了一种预设时间扰动观测器，可以在预设的时间内保证对有界外部扰动力矩的估计误差收敛为零。然后，在此基础上设计了一个基于准终端滑模面的连续非奇异预设时间预设精度姿态跟踪控制器。

2.1 预设时间扰动观测器设计

为便于后续推导，首先构造中间变量：

$ {\boldsymbol{\xi}}(t)=\rho \int_0^t\left({\boldsymbol{\omega}}(l)^{\times} {\boldsymbol{J}} {\boldsymbol{\omega}}(l)-{\boldsymbol{\tau}}-{\boldsymbol{\xi}}(l)\right) d l+\rho {\boldsymbol{J}} {\boldsymbol{\omega}} $

(11)

式中ρ为一个大于零的常数。将式(11)求导并将式(2)代入可得

$ {\boldsymbol{\dot{\xi}}}=-\rho {\boldsymbol{\xi}}+\rho {\boldsymbol{d}} $

(12)

基于中间变量ξ，进一步构造辅助变量:

$ {\boldsymbol{s}}_0={\boldsymbol{z}}-{\boldsymbol{\xi}} $

(13)

式中z满足如下关系：

$ \begin{gathered} {\boldsymbol{\dot{z}}}=-\frac{\pi}{\eta \sigma T_{{\mathrm{p}} 1}}\left({\mathrm{sig}}\left({\boldsymbol{s}}_0\right)^{1-\eta}+{\mathrm{sig}}\left({\boldsymbol{s}}_0\right)^{1+\eta}\right)- \\ \rho d_{{\mathrm{M}}} {\mathrm{sign}}\left({\boldsymbol{s}}_0\right)-\rho\|{\boldsymbol{\xi}}\| {\mathrm{sign}}\left({\boldsymbol{s}}_0\right) \end{gathered} $

(14)

式中：0 < η < 1，$\sigma=\min \left\{2^{1-\frac{\eta}{2}}, 2^{1+\frac{\eta}{2}} / 3^{\frac{\eta}{2}}\right\}=2^{1-\frac{\eta}{2}}$，T_p1>0。对任一向量a =[a₁ a₂ … a_n]^T，符号sig(a)^α表示如下含义：

$ \begin{aligned} {\mathrm{sig}}({\boldsymbol{a}})^\alpha= & {\left[{\mathrm{sign}}\left(a_1\right)\left|a_1\right|^\alpha {\mathrm{sign}}\left(a_2\right)\left|a_2\right|^\alpha\right.} \\ & \left.\cdots {\mathrm{sign}}\left(a_n\right)\left|a_n\right|^\alpha\right]^{{\mathrm{T}}} \end{aligned} $

式中sign(·)为符号函数。

定理  1   取扰动力矩的估计值为

$ \begin{aligned} \hat{{\boldsymbol{d}}}= & -\frac{\pi}{\eta \sigma T_{{\mathrm{p}} 1}}\left({\mathrm{sig}}\left({\boldsymbol{s}}_0\right)^{1-\eta}+{\mathrm{sig}}\left({\boldsymbol{s}}_0\right)^{1+\eta}\right)- \\ & \rho d_{{\mathrm{M}}} \tanh \left(K {\boldsymbol{s}}_0\right)-\rho\|\xi\| \tanh \left(K {\boldsymbol{s}}_0\right)+\xi \end{aligned} $

(15)

式中K>0。则当t≥T_p1时，扰动力矩估计误差$\tilde{\boldsymbol{d}}$ = $\hat{\boldsymbol{d}}$ - d =0。

证明   由式(12)~(14)可得：

$ \begin{aligned} & \dot{{\boldsymbol{s}}}_0=\dot{{\boldsymbol{z}}}-\dot{{\boldsymbol{\xi}}}= \\ & -\frac{\pi}{\eta \sigma T_{{\mathrm{p}} 1}}\left({\mathrm{sig}}\left({\boldsymbol{s}}_0\right)^{1-\eta}+{\mathrm{sig}}\left({\boldsymbol{s}}_0\right)^{1+\eta}\right)- \\ & \rho d_{{\mathrm{M}}} {\mathrm{sign}}\left({\boldsymbol{s}}_0\right)-\rho\|{\boldsymbol{\xi}}\| {\mathrm{sign}}\left({\boldsymbol{s}}_0\right)+\rho {\boldsymbol{\xi}}-\rho {\boldsymbol{d}} \\ & \end{aligned} $

(16)

定义李雅普诺夫函数$V_0=\frac{1}{2} {\boldsymbol{s}}_0^{\mathrm{T}} {\boldsymbol{s}}_0$，则

$ \begin{aligned} \dot{V}_0= & {\boldsymbol{s}}_0^{{\mathrm{T}}} {\boldsymbol{\dot{s}}}_0={\boldsymbol{s}}_0^{{\mathrm{T}}}\left(-\frac{\pi}{\eta \sigma T_{{\mathrm{p}} 1}}\left({\mathrm{sig}}\left({\boldsymbol{s}}_0\right)^{1-\eta}+{\mathrm{sig}}\left({\boldsymbol{s}}_0\right)^{1+\eta}\right)-\right. \\ & \left.\rho d_{{\mathrm{M}}} {\mathrm{sign}}\left({\boldsymbol{s}}_0\right)-\rho\|{\boldsymbol{\xi}}\| {\mathrm{sign}}\left({\boldsymbol{s}}_0\right)+\rho {\boldsymbol{\xi}}-\rho {\boldsymbol{d}}\right) \leqslant \\ & {\boldsymbol{s}}_0^{{\mathrm{T}}}\left(-\frac{\pi}{\eta \sigma T_{{\mathrm{p}} 1}}\left({\mathrm{sig}}\left({\boldsymbol{s}}_0\right)^{1-\eta}+{\mathrm{sig}}\left({\boldsymbol{s}}_0\right)^{1+\eta}\right)\right) \leqslant \\ & -\frac{\pi}{\eta \sigma T_{{\mathrm{p}} 1}}\left(\left({\boldsymbol{s}}_0^{{\mathrm{T}}} {\boldsymbol{s}}_0\right)^{1-\frac{\eta}{2}}+3\left(\left(\frac{{\boldsymbol{s}}_0^{{\mathrm{T}}} {\boldsymbol{s}}_0}{3}\right)^{1+\frac{\eta}{2}}\right)=\right. \\ & -\frac{\pi}{\eta \sigma T_{{\mathrm{p}} 1}}\left(2^{1-\frac{\eta}{2}} V_0^{1-\frac{\eta}{2}}+\frac{2^{1+\frac{\eta}{2}}}{3^{\frac{\eta}{2}}} V_0^{1+\frac{\eta}{2}}\right) \leqslant \\ & -\frac{\pi}{\eta T_{{\mathrm{p}} 1}}\left(V_0^{1-\frac{\eta}{2}}+V_0^{1+\frac{\eta}{2}}\right) \end{aligned} $

(17)

由引理1，当t≥T_p1时，V₀=0，s₀= $\dot{\boldsymbol{s}}_0$=0，故此时系统满足如下关系：

$ \begin{aligned} \tilde{{\boldsymbol{d}}}= & \hat{{\boldsymbol{d}}}-{\boldsymbol{d}}=-\frac{\pi}{\eta \sigma T_{{\mathrm{p}} 1}}\left({\mathrm{sig}}\left({\boldsymbol{s}}_0\right)^{1-\eta}+{\mathrm{sig}}\left({\boldsymbol{s}}_0\right)^{1+\eta}\right)- \\ & \rho d_{{\mathrm{M}}} \tanh \left(K {\boldsymbol{s}}_0\right)-\rho\|\xi\| \tanh \left(K {\boldsymbol{s}}_0\right)+\xi-{\boldsymbol{d}}= \\ & \xi-{\boldsymbol{d}}=\dot{{\boldsymbol{s}}}_0 / \rho=0 \end{aligned} $

(18)

所以当t≥T_p1时，扰动力矩估计误差收敛到零，定理1得证。

注   从数学角度考虑，若s₀≡0，由式(14)可知$\dot{\boldsymbol{z}} \equiv \dot{\boldsymbol{s}}_0 \equiv 0$，这意味着ξ应为常值，显然这一点是无法保证的。与此同时，假设s₀的某分量由0变化到某非零值Δ，由式(16)可知实际上其在到达Δ之前就已经向0“折返”了，故s₀无法由零变化到任意非零值。根据这两点分析可以判断，收敛以后的s₀各分量其实是在0的一个无穷小邻域内“振荡”的。故上述推导过程中所用到的当t≥T_p1时$\boldsymbol{s}_0=\dot{\boldsymbol{s}}_0=0$其实是一个近似的结论，本文所设计的扰动观测器是一个近似的观测器。但是仿真结果表明其对有界外部扰动力矩的追踪效果是非常好的。

2.2 连续非奇异预设时间姿态跟踪控制器设计

首先，构造一个(准)终端滑模面:

$ {\boldsymbol{s}}={\boldsymbol{\omega}}_{{\mathrm{e}}}+{\boldsymbol{\varpi}} $

(19)

式中，${\boldsymbol{\varpi}}=\frac{\pi}{\sigma^{\prime} \eta T_{{\mathrm{p}} 2}} {\boldsymbol{T}}^{-1}\left({\boldsymbol{\varphi}}\left({\boldsymbol{q}}_{{\mathrm{e}}}\right)+\operatorname{sig}\left({\boldsymbol{q}}_{{\mathrm{e}}}\right)^{1+\eta}\right)$，其中:

$ {\boldsymbol{\varphi}}\left(q_{{\mathrm{e}}, i}\right)= \begin{cases}{\mathrm{sig}}\left(q_{{\mathrm{e}}, i}\right)^{1-\eta}, & \left|q_{{\mathrm{e}}, i}\right|>\varepsilon_i \\ k_1 {\mathrm{sign}}\left(q_{{\mathrm{e}}, i}\right) q_{{\mathrm{e}}, i}^2+k_2 q_{{\mathrm{e}}, i}, & 0 \leqslant\left|q_{{\mathrm{e}}, i}\right| \leqslant \varepsilon_i\end{cases} $

式中：k_{1, i}=-ηε_i^-1-η，k_{2, i}=(1+η)ε_i^-η，ε_i(i=1, 2, 3)分别为对姿态误差的3个分量所预设的收敛精度。显然，此滑模面及其一阶导数均是连续非奇异的。

定理  2   如果s =0，则当t≥T_p2时，|q_{e, i}|≤ε_i(i=1, 2, 3)，即经过预设的时间T_p2以后姿态跟踪误差将保持在指定的精度ε_i(i=1, 2, 3)以内。

证明   由定义(19), 当s =0时误差角速度的值为

$ {\boldsymbol{\omega}}_{{\mathrm{e}}}=-\frac{\pi}{\sigma^{\prime} \eta T_{{\mathrm{p}} 2}} {\boldsymbol{T}}^{-1}\left({\boldsymbol{\varphi}}\left({\boldsymbol{q}}_{{\mathrm{e}}}\right)+{\mathrm{sig}}\left({\boldsymbol{q}}_{{\mathrm{e}}}\right)^{1+\eta}\right) $

(20)

将式(20)代入式(5)可得

$ \dot{{\boldsymbol{q}}}_{{\mathrm{e}}}={\boldsymbol{T}} {\boldsymbol{\omega}}_{{\mathrm{e}}}=-\frac{{\boldsymbol{\pi}}}{\sigma^{\prime} \eta T_{{\mathrm{p}} 2}}\left({\boldsymbol{\varphi}}\left({\boldsymbol{q}}_{{\mathrm{e}}}\right)+{\mathrm{sig}}\left({\boldsymbol{q}}_{{\mathrm{e}}}\right)^{1+\eta}\right) $

(21)

取李雅普诺夫函数:

$ V_{1, i}=\frac{1}{2} q_{{\mathrm{e}}, i}^2 $

(22)

则有

$ \begin{aligned} \dot{V}_{1, i}= & q_{{\mathrm{e}}, i} \dot{q}_{{\mathrm{e}}, i}= \\ & -\frac{\pi}{\sigma^{\prime} \eta T_{{\mathrm{p}} 2}}\left(q_{{\mathrm{e}}, i} \varphi_1\left(q_{{\mathrm{e}}}\right)+\left|q_{{\mathrm{e}}, i}\right|^{2+\eta}\right) \end{aligned} $

(23)

当|q_{e, i}|>ε_i时，有

$ \begin{aligned} \dot{V}_{1, i}= & -\frac{\pi}{\sigma^{\prime} \eta T_{{\mathrm{p}} 2}}\left(\left|q_{{\mathrm{e}}, i}\right|^{2-\eta}+\left|q_{{\mathrm{e}}, i}\right|^{2+\eta}\right)= \\ & -\frac{\pi}{\sigma^{\prime} \eta T_{{\mathrm{p}} 2}}\left(2^{1-\frac{\eta}{2}} V_{1, i}^{1-\frac{\eta}{2}}+2^{1+\frac{\eta}{2}} V_{1, i}^{1+\frac{\eta}{2}}\right) \leqslant \\ & -\frac{\pi}{\eta T_{{\mathrm{p}} 2}}\left(V_{1, i}^{1-\frac{\eta}{2}}+V_{1, i}^{1+\frac{\eta}{2}}\right) \end{aligned} $

(24)

由引理1，在预设时间T_p2以内，姿态跟踪误差可以收敛至|q_{e, i}|≤ε_i(i=1, 2, 3)，定理2得证。

下面设计控制器, 使滑模面收敛为零。定义李雅普诺夫函数$V_2=\frac{1}{2} {\boldsymbol{s}}^{\mathrm{T}} {\boldsymbol{J}} {\boldsymbol{s}}$，并设计控制器如下：

$ {\boldsymbol{\tau}}=-{\boldsymbol{J}} \dot{{\boldsymbol{\varpi}}}-{\boldsymbol{f}}-\frac{\pi}{2 \eta T_{{\mathrm{p}} 3}}\left(V_2^{-\frac{\eta}{2}}+V_2^{\frac{\eta}{2}}\right) {\boldsymbol{J}} {\boldsymbol{s}}-\hat{{\boldsymbol{d}}} $

(25)

定理  3   控制律(25)是连续的；且当$\hat{\boldsymbol{d}}$ = d时，该控制律可在预设时间T_p3内使滑模面s收敛到0。

证明  关于第1点，由式(15)可见$\hat{\boldsymbol{d}}$是连续的，故只需证明$V_2^{-\frac{\eta}{2}} {\boldsymbol{Js}}$在s →0时的极限存在。由引理2，当r₁=r₂=…=r_n=1时，对任意s ≠0，存在唯一的正数λ和单位向量s ∈R³，使得s =λs。故

$ \begin{aligned} \lim _{{\boldsymbol{s}} \rightarrow 0} V_2^{-\frac{\eta}{2}} {\boldsymbol{J}} {\boldsymbol{s}}= & \lim _{{\boldsymbol{s}} \rightarrow 0}\left(\frac{1}{2} {\boldsymbol{s}}^{{\mathrm{T}}} {\boldsymbol{J}}{\boldsymbol{s}}\right)^{-\frac{\eta}{2}} {\boldsymbol{J}} {\boldsymbol{s}}= \\ & \lim _{\lambda \rightarrow 0}\left(\frac{1}{2}(\lambda \overline{{\boldsymbol{s}}})^{{\mathrm{T}}} {\boldsymbol{J}}(\lambda \overline{{\boldsymbol{s}}})\right)^{-\frac{\eta}{2}} {\boldsymbol{J}}(\lambda \overline{{\boldsymbol{s}}})= \\ & \lim _{\lambda \rightarrow 0} \lambda^{1-\eta}\left(\frac{1}{2} \overline{{\boldsymbol{s}}}^{{\mathrm{T}}} {\boldsymbol{J}}\overline{{\boldsymbol{s}}}\right)^{-\frac{\eta}{2}} {\boldsymbol{J}} \overline{{\boldsymbol{s}}}=0 \end{aligned} $

(26)

极限存在，连续性结论得证；同时，由式(6)、式(19)和式(25)可得

$ \begin{aligned} \dot{{\boldsymbol{J}} {\boldsymbol{s}}}= & {\boldsymbol{J}} \dot{{\boldsymbol{\omega}}}_{{\mathrm{e}}}+{\boldsymbol{J}} \dot{{\boldsymbol{\varpi}}}={\boldsymbol{\tau}}+{\boldsymbol{f}}+{\boldsymbol{d}}+{\boldsymbol{J}} \dot{{\boldsymbol{\varpi}}}= \\ & -\frac{\pi}{2 \eta T_{{\mathrm{p}} 3}}\left(V_2^{-\frac{\eta}{2}}+V_2^{\frac{\eta}{2}}\right) {\boldsymbol{J}} {\boldsymbol{s}}-\hat{{\boldsymbol{d}}}+{\boldsymbol{d}}= \\ & -\frac{\pi}{2 \eta T_{{\mathrm{p}} 3}}\left(V_2^{-\frac{\eta}{2}}+V_2^{\frac{\eta}{2}}\right) {\boldsymbol{J}} {\boldsymbol{s}} \end{aligned} $

(27)

所以:

$ \begin{aligned} \dot{V}_2= & {\boldsymbol{s}}^{{\mathrm{T}}} {\boldsymbol{J}} \dot{{\boldsymbol{s}}}=-\frac{\pi}{2 \eta T_{{\mathrm{p}} 3}}\left(V_2^{-\frac{\eta}{2}}+V_2^{\frac{\eta}{2}}\right) {\boldsymbol{s}}^{{\mathrm{T}}} {\boldsymbol{J}} {\boldsymbol{s}}= \\ & -\frac{\pi}{\eta T_{{\mathrm{p}} 3}}\left(V_2^{1-\frac{\eta}{2}}+V_2^{1+\frac{\eta}{2}}\right) \end{aligned} $

(28)

由引理1，在$\hat{{\boldsymbol{d}}}={\boldsymbol{d}}$的条件下，经过预设时间T_p3后，V₂=0，s =0，结论得证。

综上所述，根据定理1~定理3，在任意初始条件下，本文所设计的观测器及控制器可以保证系统的姿态跟踪误差在T_p1+T_p2+T_p3时间内收敛到|q_{e, i}|≤ε_i(i=1, 2, 3)范围以内。

3 仿真分析

为检验上述控制策略的性能，本文通过数值仿真对其进行了验证。航天器的转动惯量矩阵取为

$ {\boldsymbol{J}}_0=\left[\begin{array}{rrr} 20.0 & 1.2 & 0.9 \\ 1.2 & 17.0 & 1.4 \\ 0.9 & 1.4 & 15.0 \end{array}\right] {\mathrm{kg}} \cdot {\mathrm{m}}^2 $

(29)

目标姿态轨线取为

$ {\boldsymbol{q}}_{{\mathrm{d}}}=0.2[\cos (0.1 t) \sin (0.1 t) \sqrt{3}]^{{\mathrm{T}}} $

外部扰动力矩设为

$ {\boldsymbol{d}}=0.03[\sin (t / 4) \cos (t / 6) \sin (t / 5)]^{{\mathrm{T}}} {\mathrm{Nm}} $

控制器参数选择如下：T_p1=T_p2=30 s，T_p3=40 s，ρ=3，K=1，ε₁=ε₂=ε₃=0.000 5，η=0.3。

初始时刻姿态设为

$ {\boldsymbol{q}}(0)=\left[\begin{array}{lll} 1.0 & -2.0 & -1.5 \end{array}\right]^{{\mathrm{T}}} $

初始时刻角速度设为

$ {\boldsymbol{\omega}}(0)=\left[\begin{array}{lllll} 0.000 \; 5 & 0.000\;5 & -0.000 \; 5 \end{array}\right]^{{\mathrm{T}}} {\mathrm{rad}} / {\mathrm{s}} $

z的初始值取z (0)=[0 0 0]^T。以下两种仿真方案均满足上述条件。

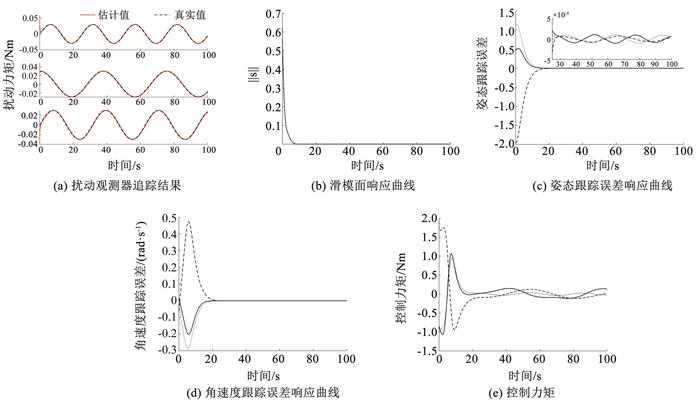
Case  Ⅰ   在上述条件下，仿真结果如图 1所示。图 1(a)所示为扰动观测器对有界外部扰动力矩的追踪结果，可以看出，观测器在5 s的时间内实现了对外部扰动力矩的高精度追踪，收敛后的观测器对扰动力矩的估计值相比其真实值略有时延。图 1(b)所示为滑模面(19)的响应曲线，可见滑模面在10 s的时间内收敛到零。图 1(c)、1(d)分别为姿态跟踪误差和角速度跟踪误差的响应曲线。可以看出，在25 s以后本体航天器的姿态值实现了对期望轨线的跟踪收敛，且跟踪误差远远小于控制器中预设的精度要求(|q_{e, i}|≤ε_i(i=1, 2, 3))。图 1(e)所示为在此控制策略下完成姿态跟踪任务所需的控制力矩，可以看出其是连续的，本文所设计的控制策略很好地避免了抖振现象，定理1~定理3中的有关结论得到了验证。

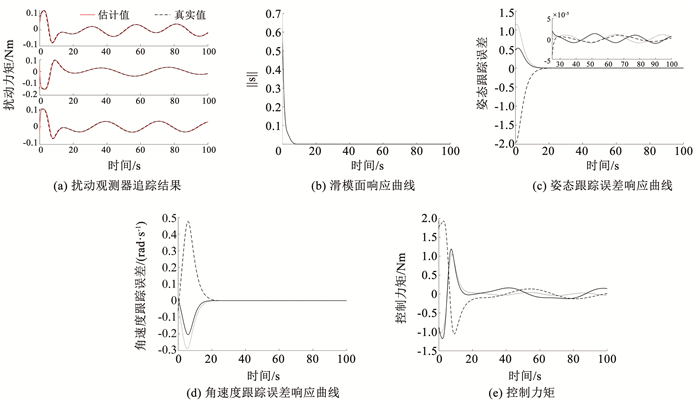
Case  Ⅱ    本方案考虑航天器系统的建模不确定性，假设航天器的转动惯量存在建模不确定性，其真实值为J = J₀+ΔJ，其中不确定项为ΔJ =0.1 J₀。将此时的真实转动惯量代入动力学方程, 可得

$ \left({\boldsymbol{J}}_0+\Delta {\boldsymbol{J}}\right) \dot{{\boldsymbol{\omega}}}=-{\boldsymbol{\omega}}^{\times}\left({\boldsymbol{J}}_0+\Delta {\boldsymbol{J}}\right) {\boldsymbol{\omega}}+{\boldsymbol{u}}+{\boldsymbol{d}} $

(30)

进一步整理有

$ {\boldsymbol{J}}_0 {\boldsymbol{ \dot{\omega}}}=-{\boldsymbol{\omega }}^{\times} {\boldsymbol{J}}_0 {\boldsymbol{\omega }}+{\boldsymbol{ u}}+{\boldsymbol{d }}-\Delta {\boldsymbol{J}} {\boldsymbol{ \dot{\omega}}}-{\boldsymbol{ \omega}}^{\times} \Delta {\boldsymbol{J}} {\boldsymbol{\omega }} $

(31)

故此时$\bar{{\boldsymbol{ d}}}={\boldsymbol{ d}}-\Delta {\boldsymbol{ J \dot{\omega}}}-{\boldsymbol{ \omega}}^{\times} \Delta {\boldsymbol{J \omega }}$即为系统所受的总扰动。对此情形进行数值仿真，结果如图 2所示。由图 2(a)可以看出，在系统转动惯量存在建模不确定性的情况下，本文所设计的扰动观测器仍然可以对系统所受的总扰动力矩实现比较精确的估计。图 2(b)~图 2(e)所示分别为仿真方案Ⅱ下滑模面、姿态跟踪误差、角速度跟踪误差以及相应的控制力矩的响应曲线。可以看出，此情形下系统状态的演化过程与情形Ⅰ相差无几，观测器在t≥5 s时可以实现对总扰动力矩的高精度追踪，滑模面在t≥10 s时收敛为零，姿态、角速度跟踪误差在t≥25 s时完成收敛，且控制力矩无抖振现象。仿真结果证明本文提出的控制策略对系统的建模不确定性有着比较好的鲁棒性。

从仿真结果可以看出，无论是观测器、滑模面、还是跟踪误差，它们的收敛时间都远远小于控制器中所预设的值，主要原因包括以下两方面: 1)观测器和姿态误差的收敛证明过程均进行过放缩，故实际收敛速度会快于预设值。蕴含在这些放缩处理中的鲁棒性也足够抵消掉扰动观测器估计值相对扰动真实值的微弱误差甚至是转动惯量建模不确定性带来的影响; 2)由文献[18]是对引理1的推导过程可以看出，在满足不等式(10)的条件下，系统的实际收敛时间为$t_{\mathrm{s}} \leqslant \frac{2}{\pi} T_{\mathrm{p}}$arctan(V(0))，当初始条件V(0)比较小时，收敛时间会远远小于T_p。

4 结论

1) 针对受有界外部扰动力矩的刚体航天器的姿态跟踪控制问题，提出了一种预设时间预设精度姿态跟踪控制策略。首先设计了一个预设时间扰动观测器，然后在利用此观测器的估计值对扰动力矩进行补偿的基础上使用终端滑模控制方法设计了一个姿态跟踪控制律。

2) 理论分析表明，本文所设计的观测器可以在外部扰动力矩上界已知的情况下对其进行精确估计；所提控制律可以保证姿态跟踪误差在预设的时间内收敛到指定的精度以内，并且其自身是连续非奇异的。

3) 数值仿真结果表明，本文所设计的观测器和控制器在实际应用中表现出的收敛速度和精度可能会远远优于预设值，并且其对系统的建模不确定性具有比较出色的鲁棒性，有关结果对工程应用有一定的参考价值。