2. 北京空间飞行器总体设计部,北京 100094;
3. 中国卫星网络集团有限公司,河北 雄安新区 071703
2. Beijing Institute of Spacecraft System Engineering, Beijing 100094, China;
3. China Satellite Network Group Co., Ltd, Xiong'an New Area 071703, Hebei, China
空间碎片和微流星体(Micro-meteoroid & orbital debris,M/OD)对航天器在轨安全运行形成了严重威胁,航天器一旦被M/OD撞击,功能将降级或失效,特别是对于载人航天器,密封舱结构被击穿将威胁航天员安全,直接影响任务成败。
中国载人空间站任务正在稳步推进,某载人航天器在轨寿命超过10年,密封舱选用玄武岩/芳纶纤维布填充式防护结构[1],提高航天员长期在轨驻留安全性。M/OD超高速撞击下,载人航天器密封舱结构撞击极限和穿孔孔径,是影响在轨任务风险评估的重要参数。目前工程任务上,保守认为密封舱一旦被击穿将直接导致航天器失效或航天员伤亡,导致防护结构过设计[2]。为掌握防护结构易损特性,准确获取密封舱结构易损性模型,本文以某大型载人航天器的在轨安全性评估为背景,开展了密封舱防护结构超高速撞击试验,对填充式防护结构防护屏、填充层和舱壁结构损伤特性进行分析,并采用遗传算法和多元线性/非线性回归方法,建立了适用于中国玄武岩/芳纶纤维填充式防护结构的撞击极限经验方程和穿孔经验方程,为在轨撞击失效风险精准评估的奠定基础。
1 填充式防护结构撞击试验 1.1 填充式防护结构载人航天器密封舱填充式防护结构由防护屏、填充层、舱壁结构组成,防护屏布置在最外侧,填充层由玄武岩纤维布和芳纶纤维布组成,靠近舱壁侧表面包覆双面镀铝聚酯膜热控多层,靠近防护屏侧包覆防原子氧膜,防护结构如图 1所示[3-4]。

|
图 1 某载人航天器填充式防护结构示意 Fig. 1 Schematic diagram of stuffed Whipple shield |
玄武岩/芳纶纤维填充式防护结构试验件各层板平面尺寸为20 cm×20 cm,层板之间通过套筒和螺钉连接。SW1防护屏选用5A06铝合金,SW2和SW3防护屏选用3A12铝合金,舱壁结构全部选用5A06铝合金,填充层全部由3层玄武岩纤维布和3层芳纶纤维布组成,总面密度0.38 g/cm2;观察屏为0.1 cm厚5A06铝合金板,位于舱壁结构后侧5 cm处,如图 2所示,结构参数见表 1。弹丸选用2A12铝合金标准球形弹丸[4]。

|
图 2 填充式防护结构撞击试验件 Fig. 2 A typical sample for stuffed Whipple shield used in impact tests |
| 表 1 3类防护结构试验件参数 Tab. 1 Parameters of stuffed Whipple shields for the Cinese large spacecraft |
利用中国空气动力研究与发展中心超高速空气动力学研究所FD-18A(配置0.76 cm口径二级轻气炮)和FD-18C(配置1.6 cm口径二级轻气炮)超高速撞击靶,如图 3所示。共计完成25次撞击试验,其中成功22次,结果见表 2。试验中,防护效果以舱壁结构是否穿孔、剥落作为评价判据:若舱壁未穿孔、无剥落,则防护有效;若舱壁穿孔、剥落或出现裂纹,则防护失效[5-7]。

|
图 3 超高速撞击靶 Fig. 3 Hypervelocity impact targets |
| 表 2 3类试验件撞击试验结果 Tab. 2 Test results for stuffed Whipple shields |
表中SW1试验件撞击试验8次,失效3次,有效防护5次;SW2撞击7次,失效3次,有效防护4次;SW3撞击7次,失效5次,有效防护2次。
利用中值定理,得到3类试验件在3.0、6.5 km/s两个名义撞击速度的撞击极限直径见表 3,其中SW1和SW2试验件在名义撞击速度为3.0 km/s时,舱壁结构的撞击极限直径都为0.412 5 cm,在6.5 km/s撞击工况下,SW1防护性能优于SW2,说明高速撞击,防护性能与防护屏厚度tb、防护间距S2对弹丸的破碎、撞击能量的分散效应正相关。SW3在全速区防护性能均为最优,应用在撞击风险最大的区域。
| 表 3 3类试验件撞击极限直径 Tab. 3 Ballistic limit diameters stuffed Whipple shields |
弹丸与防护结构撞击后,布置在防护结构最外侧的防护屏全部被弹丸贯穿,不同弹丸尺寸下防护屏穿孔孔径如图 4所示,相同速度下,随着弹丸直径增加,防护屏穿孔孔径增大。以SW1试验件为例,直径0.825 cm、撞击速度为6.536 km/s弹丸,SW1-16防护屏穿孔直径达到1.206 cm,直径增大到0.850 cm、撞击速度为6.326 km/s的弹丸,防护屏(SW1-12)穿孔直径增大到1.236 cm,如图 5所示。

|
图 4 3类防护穿孔孔径 Fig. 4 Hole size of three types of bumpers |

|
图 5 不同撞击速度下防护屏损伤特性比较 Fig. 5 Comparison of damage characteristics of bumper under different impact velocity |
弹丸穿孔后防护屏正反面都形成瓣形凸缘,主要原因是撞击过程中,防护屏材料在剪切破坏的同时,冲击压缩波扰动大量产热使防护屏材料熔化,熔化材料在撞击剪切力作用下沿撞击方向高速飞溅,未来得及飞溅材料则附着于穿孔周边,形成瓣形凸缘。
2.2 填充层损伤特性弹丸或碎片云穿过防护屏撞击填充后,填充层玄武岩纤维模和芳纶纤维均产生了较高程度的断裂、烧蚀和熔化,这是由于玄武岩纤维模量较高,在碎片云撞击作用下,表现为脆性断裂,且随着撞击速度提高,弹丸材料破碎更加充分和均匀,碎片云的能量分布更均匀,玄武岩纤维断裂截面趋于规则,如图 6所示。芳纶纤维穿孔近似为圆形,且伴有严重热烧蚀,但纤维断口不规则,主要是由于试验采用芳纶纤维具有较大韧性以及较低的玻璃化温度,在撞击作用下,产生了较大的拉伸变形和热塑性变形,进而对碎片云撞击能量进行充分吸收。

|
图 6 不同撞击速度下填充层损伤特性比较 Fig. 6 Comparison of damage characteristics of filling layers under different impact velocity |
舱壁结构撞击损伤特征包括穿孔、裂纹、花瓣形裂纹穿孔或成坑,其中成坑、裂纹对应较低的弹丸直径或撞击速度,随着弹丸撞击能量增加,舱壁结构会进一步发生穿孔;而当裂纹长度小于舱壁结构临界裂纹长度时,则会产生花瓣形裂纹穿孔,在密封舱内部压力作用下裂纹会进一步扩展,因此花瓣形裂纹穿孔是一种更为严重的穿孔失效。名义撞击速度6.5 km/s时,中心区域被碳化,沿中心孔径向向外损伤程度逐渐减轻,说明弹丸经过防护屏和填充层后产生了破碎,如图 7所示;原因是在高速、高温碎片云撞击到填充层后,玄武岩和芳纶纤维布发生碳化烧蚀与熔化、气化的碎片云一起撞击到舱壁结构,最终在舱壁结构形成碳化烧蚀区域。

|
图 7 不同撞击速度下舱壁结构超高速撞击损伤特性比较 Fig. 7 Comparison of damage characteristics of rear wall structures under different impact velocity |
6.5 km/s名义撞击速度下,弹丸直径从0.825 cm增大到0.850 cm后,舱壁结构损伤从微裂纹变成了花瓣形裂纹穿孔,说明弹丸经历防护屏和填充层破碎和分散后,沿主撞击方向的碎片云动能是引起舱壁结构发生花瓣形裂纹穿孔损伤的主要因素。
3 撞击极限方程撞击极限方程是航天器在轨风险评估的重要依据,也是开展舱壁结构穿孔方程研究的重要参数。NASA Christiansen方程主要是基于ESA和NASA试验数据拟合而来,在弹道区和气化区与其试验数据吻合较好[8-9],破碎区则通过弹道区和气化区在撞击速度阈值“拐点”处撞击极限直径线性插值得到。但由于防护结构材料屈服强度等参数差异,NASA Christiansen方程撞击极限曲线与3类试验件撞击试验结果吻合较差,无法准确应用于中国填充式防护结构撞击极限预示,具体表现在弹道区撞击极限直径预示结果远低于试验结果,而在气化区预示结果远高于试验结果。
本文保持NASA Christiansen方程形式不变,利用遗传算法和多元线性回归方法,基于3类试验件撞击试验结果对NASA Christiansen方程系数进行修正,得到了适用于中国某大型载人航天器玄武岩/芳纶纤维填充式防护结构撞击极限方程。
3.1 NASA Christiansen方程2013年,针对国际空间站应用需求,Christiansen等[9-10]针对Nextel/Kevlar填充材料,完成了大量的地面试验,基于试验数据并参照Whipple防护结构撞击极限方程形式,提出了应用于国际空间站的Nextel/Kevlar填充式防护结构的撞击极限方程:
1) 当V≤2.6/(cos θ)0.50时,即
| $ \begin{aligned} d_{{\mathrm{c}}}= & 2.350 \times\left(t_{{\mathrm{w}}}(\sigma / 275.8)^{0.5}+0.37 m_{{\mathrm{b}}}\right) \times \\ & \rho_{{\mathrm{P}}}^{-0.5} \times V^{-2 / 3} \times(\cos \theta)^{-4 / 3} \end{aligned} $ | (1) |
2) 当V≥6.5/(cos θ)0.75时,即
| $ \begin{aligned} d_{{\mathrm{c}}}= & 0.600 \times\left(t_{{\mathrm{w}}} \times \rho_{{\mathrm{w}}}\right)^{1 / 3} \times \rho_{{\mathrm{P}}}^{-1 / 3} \times(\sigma / 275.8)^{1 / 6} \times \\ & S^{2 / 3} \times V^{-1 / 3} \times(\cos \theta)^{-0.75} \end{aligned} $ | (2) |
3) 当2.6/(cos θ)0.50 < V < 6.5/(cos θ)0.75时,即
| $ \begin{aligned} d_{{\mathrm{c}}}= & 1.243 \times\left(t_{{\mathrm{w}}}(\sigma / 275.8)^{0.50}+0.37 m_{{\mathrm{b}}}\right) \times \rho_{{\mathrm{P}}}^{-0.50} \times \\ & (\cos \theta)^{-1} \times \frac{6.5 /(\cos \theta)^{0.75}-V}{6.5 /(\cos \theta)^{0.75}-2.6 /(\cos \theta)^{0.50}}+ \\ & 0.321 \times\left(t_{{\mathrm{w}}} \rho_{{\mathrm{w}}}\right)^{1 / 3} \times \rho_{{\mathrm{P}}}^{-1 / 3} \times(\sigma / 275.8)^{1 / 6} \times S^{2 / 3} \times \\ & (\cos \theta)^{-0.25} \times \frac{V-2.6 /(\cos \theta)^{0.50}}{6.5 /(\cos \theta)^{0.75}-2.6 /(\cos \theta)^{0.50}} \end{aligned} $ | (3) |
式中:dc为撞击极限直径,cm;tw为舱壁结构厚度,cm;σ为舱壁结构屈服强度,MPa;mb为防护屏和填充层总面密度,g/cm2;ρP为弹丸密度,g/cm3;V为弹丸撞击速度,km/s,θ为弹丸撞击角度,(°);ρw为舱壁结构密度,g/cm3;S为防护屏与舱壁结构间距,cm。2.35(g1/2cm-3/2km-2/3s-2/3),275.8(MPa),0.37(g-1cm3),0.6(km1/3s-1/3),1.243(g1/2cm-3/2),6.5(km/s),2.6(km/s)为量纲一的常数,其余为量纲一的常数。
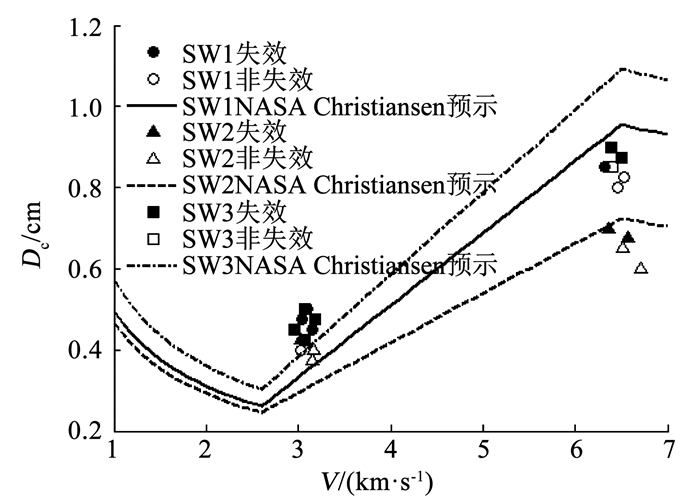
利用NASA Christiansen方程对3类试验件撞击极限进行预示,如图 8所示。
|
图 8 NASA Christiansen方程预示结果与试验结果比较 Fig. 8 Comparison of NASA Christiansen equation predictions and the test results |
定义总体预测率Ptotal为
| $ P_{\text {total }}={\text { 成功预测数/试验总数 }} $ | (4) |
定义安全预测率Psafe为
| $ P_{\text {safe }}=({\text { 试验末失效数 }} \cup {\text { 成功预测数 }}) / {\text { 试验总数 }} $ | (5) |
NASA Christiansen方程对22组试验结果成功预测了13组,则得到总体预测率Ptotal为59.1%;安全预测率Psafe为81.8%,说明NASA Christiansen方程对中国填充式防护结构具有一定的预测效果,但预测正确率偏低,直接应用将导致密封舱穿孔孔径预示出现更大的偏差,进而影响后续风险评估准确性;特别是名义撞击速度3.0 km/s附近预示结果偏于保守,如对于SW1,在撞击速度为3.0 km/s时,防护结构的撞击极限预示直径仅为0.380 cm,试验结果却达到0.450 cm;名义撞击速度6.5 km/s预示结果却偏于激进,如对于SW1,6.3 km/s撞击速度下,预示防护结构撞击极限直径为1.070 cm,试验结果却只有0.850 cm,分析认为,这主要是由于铝合金材料强度特性以及填充层材料差异导致[11]。
3.2 方程修正NASA Christiansen方程无法对中国填充式防护结构试验结果进行准确预示,影响因素很多,但主要由于防护屏、舱壁结构铝合金结构材料屈服强度以及填充层材料的差异导致。因此,以下对弹道区舱壁结构材料屈服强度系数、填充层材料的等效面密度修正系数以及气化区舱壁结构厚度与密度乘积系数、防护间距系数进行修正。
定义a1为舱壁结构材料屈服强度修正系数,a2为填充层材料等效面密度修正系数,且令
| $ T_1=a_1 \times t_{{\mathrm{w}}}(\sigma / 275.8)^{0.50}+a_2 \times 0.37 m_{{\mathrm{b}}} $ | (6) |
则式(1)改写为
| $ d_{{\mathrm{c}}}=2.35 \times T_1 \times \rho_{{\mathrm{P}}}^{-0.50} \times V^{-2 / 3} \times(\cos \theta)^{-4 / 3} $ | (7) |
定义a3为舱壁结构厚度与密度乘积修正系数,a4为防护间距修正系数,且令
| $ T_2=\left(t_{{\mathrm{w}}} \rho_{{\mathrm{w}}}\right)^{a_3} \times S^{a_4} $ | (8) |
则式(2)改写为
| $ \begin{aligned} d_{{\mathrm{c}}}= & 0.600 \times \rho_{{\mathrm{P}}}^{-1 / 3} \times(\sigma / 275.8)^{1 / 6} \times T_2 \times \\ & V^{-1 / 3} \times(\cos \theta)^{-0.50} \end{aligned} $ | (9) |
利用式(7)、(9)在2.6/(cos θ)0.50和6.5/(cos θ)0.75撞击极限值,对2.6/(cos θ)0.50 < V < 6.5/(cos θ)0.75速区内方程进行线性插值,得到破碎区方程:
| $ \begin{aligned} d_{{\mathrm{c}}}= & 2.350 \times\left(2.6 /(\cos \theta)^{0.50}\right)^{-2 / 3} \times T_1 \times \rho_{{\mathrm{P}}}^{-0.50} \times \\ & (\cos \theta)^{-1.00} \times \frac{6.5 /(\cos \theta)^{0.75}-V}{6.5 /(\cos \theta)^{0.75}-2.6 /(\cos \theta)^{0.50}}+ \\ & 0.600 \times T_2 \times\left(6.5 /(\cos \theta)^{0.57}\right)^{-1 / 3} \times \rho_{{\mathrm{P}}}^{-1 / 3} \times \\ & (\sigma / 275.8)^{1 / 6} \times(\cos \theta)^{-0.25} \times \\ & \frac{V-2.6 /(\cos \theta)^{0.50}}{6.5 /(\cos \theta)^{0.75}-2.6 /(\cos \theta)^{0.50}} \end{aligned} $ | (10) |
定义给定速度下预示结果与试验结果误差最小为目标函数,则T1和T2求解问题在数学上描述为:
| $ {\text { Find: }} X=\left\{T_1, T_2\right\} $ | (11) |
| $ {\text { Min: OBF }}=\sum\limits_{i=1}^2\left(d_{{\rm{c}}_{\text {pre }}}\left(T_i\right)-d_{{\rm{c}}_{\text {test }}}\left(V_i\right)\right)^2 $ | (12) |
式中:dcpre为利用修正的撞击极限方程预测直径,dctest为撞击试验撞击极限直径,见表 3。利用遗传算法[12],求解方程(12),得到3类试验件的T1和T2值见表 4,由于SW1和SW2在3.0 km/s撞击速度下撞击极限直径一致,因此T1和T2值都为0.330。
| 表 4 3类试验件参数值 Tab. 4 Parameters for three types of stuffed Whipple shields |
利用求得T1、T2结果,带入到方程(6)、(8),并采用文献[13]方法构建多元线性回归方程,分别如式(13)、(14)所示,其中mb=0.38 g/cm2,σ=160 MPa,其余防护结构参数见表 1。
| $ \left[\begin{array}{cc} t_{{\mathrm{w}}} \times(\sigma / 275.8)^{0.50} & 0.37 \times m_{{\mathrm{b}}} \\ t_{{\mathrm{w}}} \times(\sigma / 275.8)^{0.50} & 0.37 \times m_{{\mathrm{b}}} \\ t_{{\mathrm{w}}} \times(\sigma / 275.8)^{0.50} & 0.37 \times m_{{\mathrm{b}}} \end{array}\right]\left[\begin{array}{ll} a_1 & a_2 \end{array}\right]^{{\mathrm{T}}}=\left[\begin{array}{l} 0.330 \\ 0.330 \\ 0.342 \end{array}\right] $ | (13) |
| $ \left[\begin{array}{ll} \lg \left(t_{{\mathrm{w}}} \times \rho_{{\mathrm{w}}}\right) & \lg (S) \\ \lg \left(t_{{\mathrm{w}}} \times \rho_{{\mathrm{w}}}\right) & \lg (S) \\ \lg \left(t_{{\mathrm{w}}} \times \rho_{{\mathrm{w}}}\right) & \lg (S) \end{array}\right]\left[\begin{array}{ll} a_3 & a_4 \end{array}\right]^{{\mathrm{T}}}=\left[\begin{array}{l} \lg (4.280) \\ \lg (3.196) \\ \lg (4.360) \end{array}\right] $ | (14) |
得到不同防护结构的待定系数见表 5。
| 表 5 修正的撞击极限方程系数 Tab. 5 Coefficients for modified impact limit equation |
a1<1.00、a2>1.00、a3<1/3、a4<2/3,修正过程中弱化了防护屏、弹丸密度以及防护间距的影响、但填充层影响有所强化,说明试验用防护结构填充层发挥了更强的防护作用。利用修正的撞击极限方程系数,对3类防护结构撞击极限进行预示,如图 9所示,修正的撞击极限方程与试验结果吻合性较好,对22组撞击试验结果的总体预测率和安全预测率全部为100%,能够准确预示防护结构的撞击极限能力。与文献[6]比较,本文得到的撞击极限方程预示精度更高、更具有普适性,准确反映3类防护结构的易损特性。

|
图 9 修正撞击极限方程预示及与试验结果比较 Fig. 9 Comparison of modified impact limit equation predictions and the test results |
根据图 9撞击极限曲线,撞击速度在破碎区和气化区内3类试验件防护能力从高到低依次为SW3、SW1和SW2,而在弹道区,SW2和SW1撞击极限方程相同,与试验结果一致。
4 密封舱结构穿孔孔径对于空间站等超大型载人航天器,即使密封舱结构被击穿,并不一定会导致航天器失效或航天器伤亡,还与穿孔孔径大小、密封舱内压力体制、航天员耐受能力等因素密切相关,M/OD撞击下密封舱舱壁穿孔孔径是开展航天员低压和缺氧失效等两类密封舱穿孔失效模式下灾难性失效评估的重要基础。当前针对填充式防护结构的舱壁穿孔方程发展还不够完善,国际空间站选用的Burch方程和S/W等两类经验方程为针对Whipple防护结构开发,未考虑填充层材料影响,对穿孔孔径预示精度低。此外,Burch方程未考虑舱壁厚度的影响且只适用于法向撞击速度是防护屏材料声速的0.6~1.3倍,而S/W方程未考虑防护屏厚度、防护间距、舱壁结构厚度等防护结构尺寸的影响[14-15]。
1997年,Schonberg等[15]综合考虑了多种防护结构,提出了通用型W-S经验方程,本文选用该经验方程区域1(在该区域内穿孔直径和裂纹长度主要取决于作用在充压结构上的碎片云载荷,碎片与防护结构撞击破碎分裂,破碎程度、碎片云分布以及穿孔直径都随撞击粒子直径的增加而增大,直到粒子直径增加到某一值,无法再被外部的防护结构破碎)内方程对舱壁结构穿孔孔径进行预示,弹丸直径dP范围为tb~20tb,如图 10所示。

|
图 10 W-S方程穿孔孔径预示(V=3.0 km/s,0°撞击角) Fig. 10 Hole size prediction with W-S equation (V=3.0 km/s, 0° impact angle) |
根据方程形式,在区域1内,穿孔孔径随弹丸直径指数增长,但图 10预示结果远大于实际穿孔孔径,因此,选择对方程中指数系数Ch对应的两个参数FT和FP进行修正,其余参数保持与文献[15]一致。
采用修正后的填充式防护结构撞击极限方程和撞击试验穿孔数据,利用非线性回归方程得到适用于大型载人航天器填充式防护结构在不同碎片直径、撞击速度下,舱壁穿孔孔径方程:
| $ D_{{\mathrm{h}}}=A_{{\mathrm{h}}}\left(\frac{V_{{\mathrm{P}}}}{6.5}\right) \cos ^{B_{{\mathrm{h}}}} \theta\left(1-{\mathrm{e}}^{\left(-C_{{\mathrm{h}}}\left(\frac{d {\mathrm{P}}}{d_{{\mathrm{c}}}}-1\right)\right)}\right) $ | (15) |
其中:
Bh=-0.5(VB-11)(1-ρIBAD/0.79),若Bh<0则Bh=0
Ch=2max(FT, FP)
FT=0.478/tw,若FT<1,则FT=1
FP=
| $ \begin{aligned} & A_{{\mathrm{h}}}=3 F_{{\mathrm{S}}} \max \left(F_{{\mathrm{T}}}, F_{{\mathrm{P}}}\right) \\ & V_{{\mathrm{B}}}= \begin{cases}6.5 {\mathrm{~km}} / {\mathrm{s}}, & V<6.5 {\mathrm{~km}} / {\mathrm{s}} \\ V_{{\mathrm{P}}}, & 6.5 {\mathrm{~km}} / {\mathrm{s}} \leqslant V \leqslant 11.0 {\mathrm{~km}} / {\mathrm{s}} \\ 11.0 {\mathrm{~km}} / {\mathrm{s}}, & V>11.0 {\mathrm{~km}} / {\mathrm{s}}\end{cases} \end{aligned} $ |
θ>65°,则θ=65°;FS=S/11.43
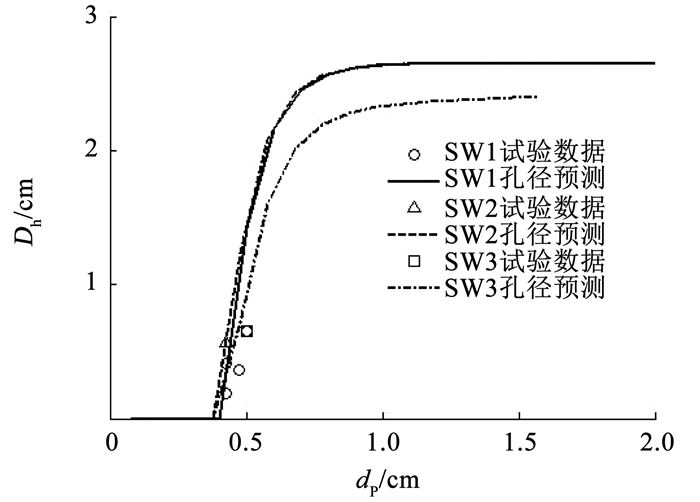
式中:Dh为舱壁穿孔直径,ρIBAD、ρwAD分别为填充层和舱壁面密度,其余参数定义与前文一致。使用修正后经验方程对3类防护结构进行穿孔孔径预示,得到3.0 km/s撞击速度、0°撞击角下密封舱穿孔孔径预示如图 11所示。与图 10对比可以看出,修正后的W-S穿孔经验方程,可以更准确预示载人航天器穿孔直径。
|
图 11 修正W-S方程穿孔孔径预示(V=3.0 km/s,0°撞击角) Fig. 11 Hole size prediction with modified W-S equation (V=3.0 km/s, 0° impact angle) |
1) 相同撞击速度下,防护屏穿孔孔径与弹丸直径正相关。
2) 玄武岩/芳纶纤维填充层对弹丸和碎片云有较强破碎作用和能量分散作用,降低对密封舱结构损伤。
3) 沿主撞击方向碎片云能量是引起舱壁结构花瓣形裂纹穿孔的主要因素。
4) 修正后的NASA Christiansen方程、W-S穿孔方程,预示精度更高、适用性更强。
| [1] |
闫军, 郑世贵, 于伟, 等. 空间站的碎片防护设计与实践[J]. 空间碎片研究, 2021, 21(2): 1. YAN Jun, ZHENG Shigui, YU Wei, et al. Space debris protection design for the space station[J]. Space Debris Research, 2021, 21(2): 1. DOI:10.19963/j.cnki.2096-4099.2021.02.001 |
| [2] |
武江凯, 田蕾, 邓凯文, 等. MMOD撞击下航天器风险评估系统的发展与启示[J]. 航天器环境工程, 2020, 37(6): 531. WU Jiangkai, TIAN Lei, DENG Kaiwen, et al. Development of risk assessment system for spacecraft under MMOD impact and the enlightenment[J]. Spacecraft Environment Engineering, 2020, 37(6): 531. DOI:10.12126/see.2020.06.001 |
| [3] |
闫军, 郑世贵. 填充式防护结构填充层撞击特性研究[J]. 载人航天, 2013, 19(1): 10. YAN Jun, ZHENG Shigui. A research on middle layer impact characteristic of stuffed Whipple Shields[J]. Manned Spaceflight, 2013, 19(1): 10. DOI:10.16329/j.cnki.zrht.2013.01.011 |
| [4] |
ZHENG Shigui, YAN Jun, GONG Weiwei. Impact characterization of stuffed Whipple for China Space Station[C]//FLOHRER, T, SCHMITZ, F. Proceedings of the 7th European Conference on Space Debris. Darmstadt: ESA Space Debris Office, 2017
|
| [5] |
郑世贵, 张帅, 宫伟伟. 空间站填充式防护结构撞击特性研究[J]. 空间碎片研究, 2018, 18(1): 41. ZHENG Shigui, ZHANG Shuai, GONG Weiwei. Impact Characterization of Stuffed Whipple for Space Station[J]. Space Debris Research, 2018, 18(1): 41. |
| [6] |
ZHENG Shigui, YAN Jun, SHAN Li, et al. Research on shield for space station from meteoroid and orbital debris[C]//Proceedings of the 64th International Astronautical Congress. Beijing, China: IAC-13, 2013: 2130
|
| [7] |
PUTZAR R, ZHENG Shigui, AN Jing, et al. A stuffed Whipple shield for the Chinese space station[J]. International Journal of Impact Engineering, 2019, 132: 103304. DOI:10.1016/j.ijimpeng.2019.05.018 |
| [8] |
ARNOLD J, CHRISTIANSEN E L, DAVIS A, et al. Handbook for designing MMOD protection: NASA/TM-2009-214785[R]. Houston, TX: NASA Johnson Space Center, 2009
|
| [9] |
RYAN S, LUNAR U, CHRISTIANSEN E L. Micrometeoroid and orbital debris (MMOD) shield ballistic limit analysis program: TM-2009-214789[R]. Houston, TX: NASA Johnson Space Center, 2013
|
| [10] |
CHRISTIANSEN E L, CREWS J L, WILLIAMSEN J E, et al. Enhanced meteoroid and orbital debris shielding[J]. International Journal of Impact Engineering, 1995, 17(1/2/3): 217. DOI:10.1016/0734-743X(95)99848-L |
| [11] |
贾古寨, 哈跃, 庞宝君, 等. 玄武岩/Kevlar纤维布填充防护结构撞击极限及损伤特性[J]. 爆炸与冲击, 2016, 36(4): 433. JIA Guzhai, HA Yue, PANG Baojun, et al. Ballistic limit and damage properties of basalt/Kevlar stuffed shield[J]. Explosion and Shock Waves, 2016, 36(4): 433. DOI:10.11883/1001-1455(2016)04-0433-08 |
| [12] |
冯宪彬, 丁蕊. 改进型遗传算法及其应用[M]. 北京: 冶金工业出版社, 2016. FENG Xianbin, DING Rui. Improved genetic algorithm and its application[M]. Beijing: Metallurgical Industry Press, 2016. |
| [13] |
邵军. 数理统计[M]. 2版. 北京: 高等教育出版社, 2018. SHAO Jun. Mathematical statistics[M]. 2nd ed. Beijing: Higher Education Press, 2018. |
| [14] |
ELFER N C. Stuctural damage prediction and analysis for hypervelocity impacts: Handbook: NASA-CR-4706[R]. Alabama: NASA Marshall Space Flight Center, 1996: 65
|
| [15] |
SCHONBERG W P, WILLIAMSEN J E. Empirical hole size and crack length models for dual-wall systems under hypervelocity projectile impact[J]. International Journal of Impact Engineering, 1997, 20(6/7/8/9/10): 711. DOI:10.1016/S0734-743X(97)87457-X |
 2023, Vol. 55
2023, Vol. 55


