2. 非定常空气动力学与流动控制工信部重点实验室(南京航空航天大学),南京 210016
2. Key Laboratory of Unsteady Aerodynamics and Flow Control (Nanjing University of Aeronautics and Astronautics), Ministry of Industry and Information Technology, Nanjing 210016, China
间断Galerkin(Discontinuous Galerkin method, DG)有限元方法源于20世纪70年代求解中子输运方程[1]。后期流行的Runge-Kutta DG(RKDG)有限元方法[2-3],是结合求解非线性守恒律方程(组)提出的。该方法的主要特点是能够构造任意阶精度的格式(基于非结构网格等),但相较于传统的低阶精度格式,同一网格上控制方程的求解,因高阶近似而涉及的未知量更多,消耗的计算量也就更多,影响到实际复杂工程问题的推广应用[4-5]。因此,很有必要提高算法的计算效率。实现算法的并行化是可考虑的可行途径。
现代图形处理器(GPU)通常拥有数以百计或千计的计算核,浮点运算能力强劲,适合并行地处理数据密集且规模大的运算[6-8]。DG有限元方法具有很好的局部紧致性,构造的高阶格式不需要非常宽的模板(stencil),因此,十分适合算法的GPU并行化[9]。早在2009年,Klöckner等[9]就把Nodal DG有限元方法GPU化,求解了三维Maxwell方程。之后,Siebenborn等[10]又发展用于求解三维Euler方程。Karakus等[11]则拓展用于求解二维不可压Navier Stokes方程。与上述基于Nodal DG有限元方法不同,Xia等[12]基于Modal DG有限元方法,实现了三维Euler方程GPU并行加速。Fuhry等[13]则结合求解二维Euler方程,依据单元或单元边界构建所需的线程结构,开展了算法GPU并行化的深入研究,其并行化效率能与Nodal DG GPU算法求解线性问题[9]相当。Gao等[14]进一步结合Navier Stokes方程,发展用于求解二维层流流动。不难看出,上述工作大多关注的是数据存储、线程结构和核函数构建等具体的GPU化问题,尚未涉及网格拓扑存在的单元不规则分布(非结构等)对并行效率的影响问题。就低阶精度格式的GPU并行化而言,这种影响不仅存在且是负面的,可采用单元[15]或点重排[16-17]等技术加以改善。因此有理由结合高阶精度DG格式,对此类问题加以深入研究。
本文结合求解Navier Stokes方程,选用Modal DG有限元方法,先构建出对应的RKDG算法,然后移植到GPU架构,发展出GPU加速的RKDG并行算法。该算法在结构网格上涉及的数据依赖区结构有序,但在非结构网格上,数据依赖区杂乱无序,影响到数据访存效率。为此,本文针对性地提出一种适合高阶DG有限元算法架构(任意阶)的单元分层排序方法,致力于改善并行效率。具体基于初始网格拓扑,创建单元或单元边界对应的分层结构,逐层重排,汇总形成适合GPU对齐合并访问(coalesced access)的数据存储结构。结合RKDG GPU算法的算例验证,展示出算法本身的GPU加速效果。同时,分析了网格拓扑对并行效率的影响,算例证实所提排序方法有助于进一步提升GPU并行化效率。
1 RKDG有限元并行算法 1.1 流动控制方程二维守恒形式可压缩Navier-Stokes方程为
| $ \frac{\partial {\boldsymbol{U}}}{\partial t}+\nabla \cdot\left({\boldsymbol{F}}_{{\mathrm{i}}}-{\boldsymbol{F}}_{{\mathrm{v}}}\right)=0 $ | (1) |
其中守恒变量U、无黏通量Fi=(fi, gi) 和黏性通量Fv=(fv, gv),可分别写为:
| $ \begin{gathered} {\boldsymbol{U}}=\left(\begin{array}{l} \rho \\ \rho u \\ \rho v \\ \rho E \end{array}\right), {\boldsymbol{f}}_{{\mathrm{i}}}=\left(\begin{array}{l} \rho u \\ \rho u^2+p \\ \rho u v \\ u(\rho E+p) \end{array}\right), {\boldsymbol{g}}_{{\mathrm{i}}}=\left(\begin{array}{l} \rho v \\ \rho v u \\ \rho v^2+p \\ v(\rho E+p) \end{array}\right), \\ {\boldsymbol{f}}_{{\mathrm{v}}}=\left(\begin{array}{l} 0 \\ \tau_{x x} \\ \tau_{x y} \\ u \tau_{x x}+v \tau_{x y}-q_x \end{array}\right), {\boldsymbol{g}}_{{\mathrm{v}}}=\left(\begin{array}{l} 0 \\ \tau_{y x} \\ \tau_{y y} \\ u \tau_{y x}+v \tau_{y y}-q_y \end{array}\right) \end{gathered} $ |
式中:密度ρ、单位质量总能E、压强p与沿坐标x和y方向的速度分量u和v,满足如下状态方程:
| $ E=\frac{1}{\gamma-1} \frac{p}{\rho}+\frac{1}{2}\left(u^2+v^2\right) $ | (2) |
式中γ为流体的比热比,对于空气而言,γ=1.4。黏性通量项中,即:
| $ \tau_{i j}=\mu\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)-\frac{2}{3} \mu \frac{\partial u_k}{\partial x_k} \delta_{i j}, q_j=-\frac{\mu c_P}{Pr} \frac{\partial T}{\partial x_j} $ | (3) |
式中:i、j分别为x或y方向,δij为Kronecker德尔塔函数,T为温度,cP为质量定压热容,Pr为普朗特数,μ为黏性系数,可由Sutherland公式计算确定。
1.2 间断Galerkin有限元离散采用间断Galerkin有限元方法,将计算域Ω划分为Nc个互不重叠单元Ωi的集合。定义有限元空间:
| $ {\boldsymbol{V}}_{{\mathrm{h}}}^p=\left\{v_{{\mathrm{h}}} \in\left[L_2(\varOmega)\right]^m:\left.{\boldsymbol{v}}_{{\mathrm{h}}}\right|_{\Omega_i} \in\left[{\boldsymbol{V}}_p^m\right] \forall \varOmega_i \in \varOmega\right\} $ | (4) |
式中:Vpm为单元Ωi上最高次数不超过p阶的多项式m维函数的集合,m为守恒变量的个数。对式(1)两端乘以测试函数vk,并在任一单元Ωi上进行分部积分,得到如下空间离散形式:
| $ \begin{gathered} \int_{\varOmega_i} {\boldsymbol{v}}_k \frac{\partial U_h}{\partial t} {\mathrm{~d}} \varOmega=-\int_{\partial \varOmega_i} {\boldsymbol{v}}_k\left(\widetilde{{\boldsymbol{F}}}_{{\mathrm{i}}}-\widetilde{{\boldsymbol{F}}}_{{\mathrm{v}}}\right) \cdot {\boldsymbol{n}} {\mathrm{d}} {\boldsymbol{\sigma}}+ \\ \int_{\varOmega_i} \nabla v_k \cdot\left({\boldsymbol{F}}_{{\mathrm{i}}}-{\boldsymbol{F}}_{{\mathrm{v}}}\right) {\mathrm{d}} \varOmega \end{gathered} $ | (5) |
这里间断有限元边界上不唯一的通量已用唯一的数值通量
| $ \begin{aligned} \int_{\varOmega_i} {\boldsymbol{v}}_k \frac{\partial {\boldsymbol{U}}_h}{\partial t} {\mathrm{~d}} \varOmega= & -\int_{\partial \varOmega_i} {\boldsymbol{v}}_k\left(\widetilde{{\boldsymbol{F}}}_{{\mathrm{i}}}\left({\boldsymbol{U}}_h^{+}, {\boldsymbol{U}}_h^{-}\right)-\widetilde{{\boldsymbol{F}}}_{{\mathrm{v}}}\right) \cdot {\boldsymbol{n}} {\mathrm{d}} {\boldsymbol{\sigma}}+ \\ & \int_{\varOmega_i} \nabla {\boldsymbol{v}}_k \cdot\left({\boldsymbol{F}}_{{\mathrm{i}}}\left({\boldsymbol{U}}_h\right)-{\boldsymbol{F}}_{{\mathrm{v}}}\left({\boldsymbol{U}}_h, \nabla {\boldsymbol{U}}_h+{\boldsymbol{R}}\right)\right) {\mathrm{d}} \varOmega \end{aligned} $ | (6) |
式中:(·)+、(·)-分别对应边界左、右单元,n为边界外法向,R =∑re,re为局部提升算子。无黏数值通量
| $ \widetilde{{\boldsymbol{F}}}_{{\mathrm{v}}}=\frac{1}{2}\left({\boldsymbol{F}}_{{\mathrm{v}}}\left({\boldsymbol{U}}_h^{+}, \nabla {\boldsymbol{U}}_h^{+}+\eta {\boldsymbol{r}}_e^{+}\right)+{\boldsymbol{F}}_{{\mathrm{v}}}\left({\boldsymbol{U}}_h^{-}, \nabla {\boldsymbol{U}}_h^{-}+\eta {\boldsymbol{r}}_e^{-}\right)\right) $ | (7) |
有关re和η的具体求解过程详见文献[18]。单元上的近似解Uh可表示为
| $ {\boldsymbol{U}}_h=\sum\limits_{k=1}^{N_p} \widetilde{{\boldsymbol{U}}}_{i, k}(t) {\boldsymbol{v}}_k({\boldsymbol{x}}) $ | (8) |
那么,式(6)可转化为与待求的单元上解系数
| $ {\boldsymbol{M}} \frac{\partial \widetilde{{\boldsymbol{U}}}}{\partial t}={\mathrm{RHS}} $ | (9) |
式中:M为块对角矩阵,每一块对应一个单元,
| $ \begin{aligned} & \widetilde{U}^{(1)}=\widetilde{{\boldsymbol{U}}}^n+\Delta t {\boldsymbol{M}}^{-1} \operatorname{RHS}\left(\widetilde{{\boldsymbol{U}}}^n\right) \\ & \widetilde{{\boldsymbol{U}}}^{(2)}=\frac{3}{4} \widetilde{{\boldsymbol{U}}}^n+\frac{1}{4}\left[\widetilde{{\boldsymbol{U}}}^{(1)}+\Delta t {\boldsymbol{M}}^{-1} \operatorname{RHS}\left(\widetilde{{\boldsymbol{U}}}^{(1)}\right)\right] \\ & \widetilde{{\boldsymbol{U}}}^{n+1}=\frac{1}{3} \widetilde{{\boldsymbol{U}}}^n+\frac{2}{3}\left[\widetilde{{\boldsymbol{U}}}^{(2)}+\Delta t {\boldsymbol{M}}^{-1} \operatorname{RHS}\left(\widetilde{{\boldsymbol{U}}}^{(2)}\right)\right] \end{aligned} $ | (10) |
可以看出,上述构建的RKDG算法,相较于传统的低阶方法,相同网格上待求的未知量与Np成正比,耗费的计算量往往难以承受[21]。因此有必要对算法进行并行化加速。
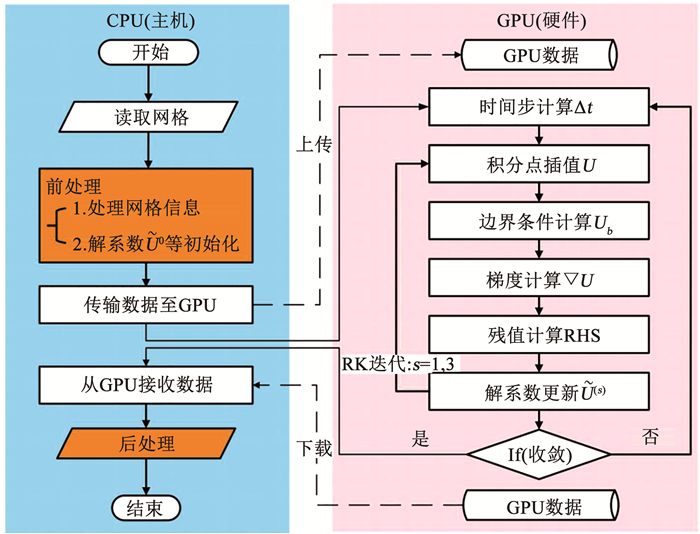
1.3 基于GPU的RKDG算法采用NVIDIA公司发布的CUDA C编程语言,对RKDG算法进行GPU并行化。这一过程也可理解为算法的CPU程序移植到GPU上。GPU内嵌平台大多拥有数以百计乃至千计的CUDA核(core),适合并行地处理数据密集且规模大的运算,但在涉及逻辑判断和分支结构等的计算时表现不佳[6]。为此,可结合算法任务归类,与CPU协同运行。如图 1所示,本文把前、后处理等保留在CPU,而把最耗时的部分(迭代运算等)移植到GPU。一旦GPU上指派的任务计算完成,就再把结果传回CPU。可以看出,每一步迭代运算由计算时间步、积分点插值、解系数更新等子任务构成。每一个子任务对应一个由用户开发的核函数(kernel)。要实现算法的GPU化,就必须对各类子任务创建核函数。可以看到,就RKDG方法而言,待创建的核函数主要与高斯积分相关。
|
图 1 算法的GPU并行化架构 Fig. 1 General framework of GPU computing |
在GPU上运行一个并行任务(调用一个核函数),是基于Grid-Block-Thread线程结构进行的。所有的线程(thread)被组织成若干个线程块(block),再由Block汇聚成对应的线程网格(grid)。在线程结构中,块中线程号(threadIdx.x)、线程块号(blockIdx.x)是内置给定的,而线程块维度(blockDim.x)可由用户调节确定[6]。此外,内嵌的各类存储器,访存速度不一,其合理利用问题也是核函数创建时所必须考虑的。按访存速度的快慢排列,GPU上的存储器主要有寄存器、常数存储器、共享存储器和全局存储器。全局存储器容量最大,适合存放算法产生的主要数据。共享存储器适合存储线程块中线程之间共享的数据,但容量相对不大。具有缓存加速等特点的常数存储器容量十分有限,适合存放规模不大且使用频繁的常量。寄存器在线程块中的数目有限,但访存速度最快,是需要考虑最大限度利用的对象。
如前述,DG方法主要涉及单元和边界等积分计算。本文根据DG方法局部紧致的特点,沿用Fuhry等[13]的做法,对每一计算子任务,依据单元或单元边界构建所需的线程结构,使得任一单元积分(或边界积分)都有对应的一个线程负责其积分运算。依据这一原则,本文已对算法涉及的相关积分运算构建了对应的核函数。以残值计算为例(见式(6)右端项),本文构建了单元积分核函数k_surf和单元边界积分核函数k_line。k_surf仅依赖于单元内部信息,积分运算可简单直接。比较而言,k_line涉及关联单元,相对复杂。这里结合k_line的伪代码,就核函数构建给出实例说明。
同一单元所有边界积分一体计算,逐单元更新残值,可按单元循环进行。这种方式计算量依单元密集,适合GPU合并访问。但由于边界左、右单元数值通量(

|
图 2 k_line核函数伪代码 Fig. 2 Pseudocode of the k_line kernel |
对于算法涉及的诸如龙格-库塔时间推进等其他计算子任务,创建对应的核函数相对简单,但为了节省GPU内存,可从算法层面压缩物理量的存储,个别物理量可考虑用到时直接计算不再存储,本文不再一一赘述。可以看出,与线程结构相关的核函数,其创建还必须注意数据结构与存储问题,这些因素与GPU访存效率密切相关。
1.3.2 数据结构与存储问题如前述,本文算法涉及的线程结构是依据单元或单元边界构建的,线程运行相对独立,因此上述开发的核函数仅涉及全局存储器、常数存储器和寄存器。具体来说,常数存储器用于存放参考单元基函数相关的物理量,寄存器用于处理循环重复利用(访存频率高)的数据(如k_line中的残值项处理),而全局存储器则用于存放计算产生的大容量数据。必须指出,减少算法对最慢的全局存储器的访存次数,有助于提升整体计算效率。通常可通过合并访问优化大容量数据的访存效率[22]。要做到这一点,就要结合算法构建合适的数据结构。为尽可能地满足合并访问的优化要求,本文把通常的多维数组映射到连续的一维数组,要求相同物理特征的变量依单元或单元边界编号连续存放。不失一般性,如果算法涉及的物理量为如下二维数组:
| $ {\boldsymbol{a}}(i, j)=\left[\begin{array}{cccc} a_1^{(1)} & a_1^{(2)} & \cdots & a_1^{(N)} \\ a_2^{(1)} & a_2^{(2)} & \cdots & a_2^{(N)} \\ \vdots & \vdots & \ddots & \vdots \\ a_m^{(1)} & a_m^{(2)} & \cdots & a_m^{(N)} \end{array}\right], i=1, \cdots, m, j=1, \cdots, N $ | (11) |
式中:m为变量维度(如守恒变量等),N为单元数或单元边界数。把二维数组a映射到一维数组A,可直接表示为
| $ \begin{aligned} {\boldsymbol{A}}= & \left(a_1^{(1)}, a_1^{(2)}, \cdots, a_1^{(N)}, a_2^{(1)}, a_2^{(2)}, \cdots, a_2^{(N)}, \cdots,\right. \\ & \left.a_m^{(1)}, a_m^{(2)}, \cdots, a_m^{(N)}\right) \end{aligned} $ | (12) |
对于高阶DG算法特有的总体对角块质量矩阵(见式(9)),每一对角块相当于一个单元上的二维数组(Np×Np),可按上述原则,先把所有对角块映射成一维数组,再按单元顺序排列形成最终的整体一维数组。可以看出,这样的数据结构是依赖于网格拓扑中单元或边排列顺序的,还不能确保算法依赖区信息的连续提取,进而影响到所谓的GPU合并访问。
2 重排加速技术如果并发的32个线程(线程束[22])访存的数据处在同一数据段,则只需要一次数据传输即可完成访存,否则需要多次传输。研究表明,访存效率一般与传输次数成反比[17]。将线程束需访问的数据集中置于尽可能少的数据段,可有效减少数据传输次数。可以看出,上述算法GPU化构建的核函数,单元相关的积分运算,是依赖于自身及其关联单元(相邻共边单元)的。对于依据单元编号构建的数据结构,提高访存效率的关键在于同一线程束访存单元的编号应尽可能接近或集中。这一点在复杂计算域非结构网格生成时,通常是难以顾及的。可以预见,在结构网格上,因单元排序的结构化,数据依赖单元相对集中,有助于线程束所需数据合并访问,访存效率会相对较高。
本文面向实用性强的非结构网格,借鉴无网格点云分层排序思想[17],针对性地提出一种单元分层排序方法,力求获得层化结构,提升计算效率。具体基于任意初始网格单元拓扑,创建单元或单元边界对应的分层结构,逐层重排,汇总形成适合GPU对齐合并访问的单元排序。方法的具体实施过程可从图 3、4排序实例看出。

|
图 3 排序方法实施实例 Fig. 3 An example for implementation of reordering |

|
图 4 排序前、后单元编号顺序 Fig. 4 Element orders before and after reordering |
图 3(a)为任意初始非结构网格,其单元初始顺序已用中心点连线示意。运用所提排序方法,先依据初始层创建对应的分层结构。初始层依附于计算域边界(如
经过单元分层排序后,邻近单元编号虽已相近,但基于边界积分的线程束,其依赖的关联单元是横跨不同层的,不利于合并访问。为此,在单元重排的基础上,还需要进行边排序。与单元排序类似,利用计算域边界
上述重排加速技术是基于任意非结构网格提出的,可作为一般网格生成后处理应用。本文将结合Delaunay网格生成,给出排序算法加速效果算例分析。
3 算例与分析本文用上述RKDG GPU算法,先对具有解析解的库埃特(Couette)流动问题进行了数值模拟,验证了所提算法所能达到的精度,并就网格拓扑对GPU并行效率影响问题,给出了结构与非结构网格比较分析;接着,给出了NACA0012翼型及圆柱绕流的算例,展示出基于结构或非结构网格排序对算法并行效率的影响;最后,给出了多段翼型绕流算例,展示算法处理复杂气动外形的能力。为定量分析,算法的T(每步迭代计算耗时)在CPU和GPU上分别记为TCPU和TGPU,单元重排后记为TGPU+,那么GPU加速比和重排加速比可分别定义为TCPU/TGPU和TGPU/TGPU+。本文仿照传统做法[17],T统一取为1 000次Runge-Kutta迭代的平均值(单一时间步计算耗时)。所有算例均在Windows工作平台上采用双精度计算。该平台配备了英特尔i5-3450 CPU和英伟达GTX TITAN GPU,其相关参数已在表 1中列出。
| 表 1 i5-3450 CPU和GTX TITAN GPU的参数 Tab. 1 Specifications of i5-3450 CPU and GTX TITAN GPU |
选用经典库埃特模型化流动[23]对发展的算法进行考核计算。该流动是两块无限长平行平板间的层流流动,下面的平板水平放置且固定不动,上面的平板则以速度U水平向右运动。假定黏性系数μ为常数,板间距为2,则该流动有如下形式的解析解:
| $ \begin{aligned} & u=\frac{y}{2} U, v=0, p=p_{\infty}, \\ & T=T_0+\frac{y}{2}\left(T_1-T_0\right)+\frac{Pr U^2}{2 c_P} \frac{y}{2}\left(1-\frac{y}{2}\right), \rho=\frac{p}{R T} \end{aligned} $ | (13) |
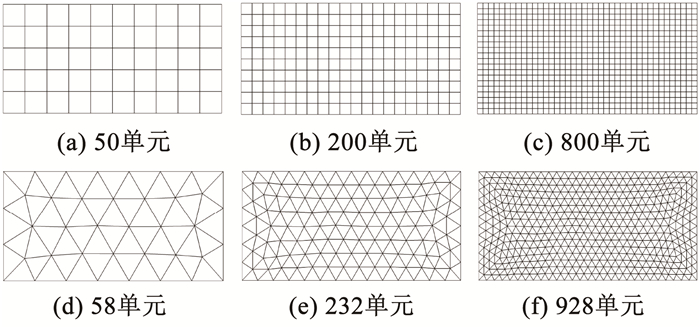
沿用文献[23]的参数设置,U=1,下壁面温度T0=0.80,上壁面温度T1=0.85和马赫数Ma1=0.1, 黏性系数μ=0.001时的雷诺数Re=100。用结构或非结构网格离散计算域(0≤x≤4,0≤y≤2),并用精确的解析解施加所需的边界条件。为了验证算法计算精度所能达到的阶数,两种计算网格均按比例进行了剖分加密(如图 5所示),并用密度的绝对误差(数值解与解析解的差值)的L2范数指示计算误差,进行了不同阶数算法的测试。测试结果已在表 2中列出。可从表 2中看出,数值解逼近的阶数在密网格上更符合预期。比较而言,结构网格优于非结构网格,高阶格式如预期比低阶格式更精确(表现为L2误差更小)。
|
图 5 渐次加密的结构((a)~(c))与非结构((d)~(f))网格 Fig. 5 Successively refined meshes (structured: (a) to (c); unstructured: (d) to (f)) |
| 表 2 RKDG GPU算法不同阶精度测试结果 Tab. 2 Test results of RKDG GPU algorithms with different orders |
接着,基于结构与非结构网格,构建了非结构区域占比约为0%、33%、67%和100%的一组网格(对应图 6中网格G到J),用于测试网格不规则程度对GPU加速的影响。注意,为排除网格单元类型的影响,结构和非结构区域均统一用三角形单元离散。表 3列出了这一测试结果。从表 3中可看出,发展的不同阶精度算法都能实现期望的GPU加速,加速比最高可达58.46;加速比大小是与非结构区域占比相关的,占比越高则加速比越小,体现出网格不规则程度对GPU加速的不利影响。

|
图 6 网格构建示意 Fig. 6 Schematic diagram of mesh construction |
| 表 3 算法不同阶精度加速特性测试结果 Tab. 3 GPU speedups of algorithms with different orders |
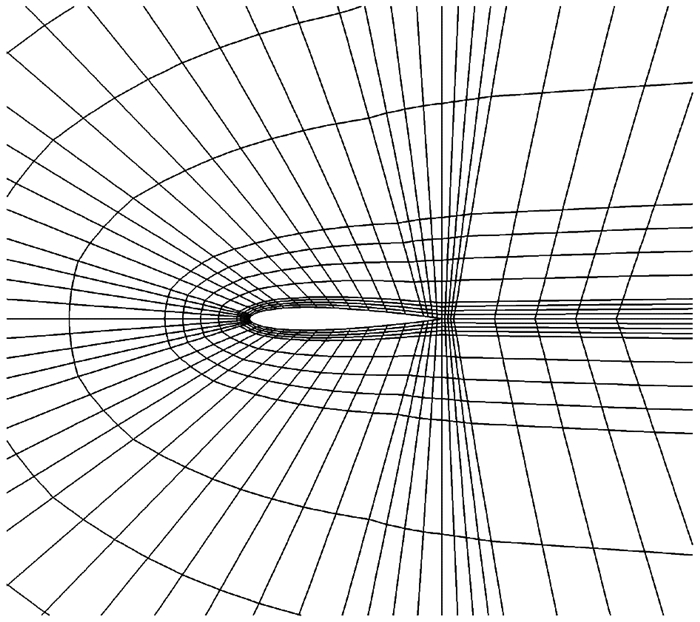
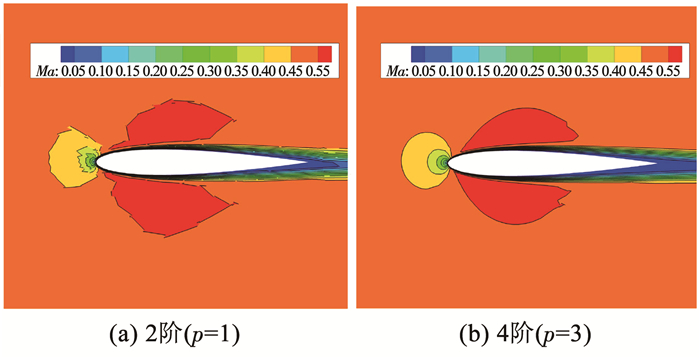
NACA0012翼型亚声速黏性绕流[24]经常被用来考核发展的高阶算法。本文先用2阶、3阶和4阶算法对该绕流进行了数值模拟。计算网格由2 240个四边形单元构成[24],翼型表面仅有41个点(如图 7所示)。计算来流马赫数为0.5,攻角为1°,雷诺数为5 000。随同文献计算结果[25],表 4给出了计算得到的阻力系数。可以注意到,随着算法阶数的提高,得到的阻力系数能与文献5阶结果接近,对应的马赫数等值线也变得清晰光滑(如图 8所示)。
|
图 7 NACA0012翼型计算网格 Fig. 7 Mesh for NACA0012 airfoil |
| 表 4 阻力系数计算结果 Tab. 4 Computed drag coefficients |
|
图 8 马赫数云图(2阶与4阶) Fig. 8 Mach contours (second order and fourth order) |
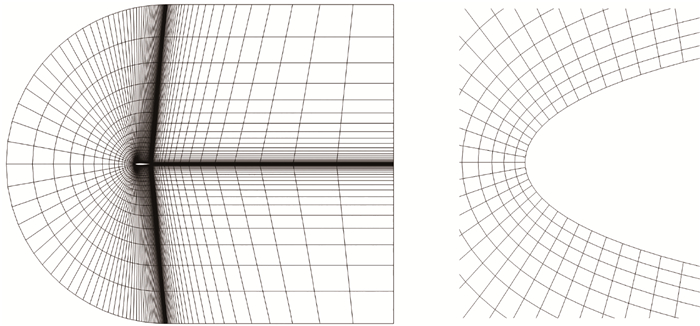
接着,本文依据如图 9所示的初始网格,构建了一套渐次加密的结构网格网格规模依次为170×30、340×60、680×120和1 360×240,进行了算法加速性能的测试。大体上,在同一阶数下,加速比随着网格规模增大而提高(表 5第6列),最大加速比可达67.47。表 5同时列出了重排加速比,如预期,接近于1且几乎不随网格变化,表明网格的结构化已很适合GPU对齐合并访问,无需进一步重排加速。
|
图 9 初始结构网格(170×30) Fig. 9 Initial structured mesh (170×30) |
| 表 5 不同阶算法NACA0012翼型绕流加速特性测试结果 Tab. 5 Speedups of algorithms with different orders for flow over NACA0012 airfoil |
圆柱绕流卡门涡街[26]常用来考核高阶算法的低耗散性。计算来流马赫数为0.2,雷诺数为100。计算网格由整体非结构网格(20 376个三角形单元)和局部结构网格(圆柱附近,1 560个四边形单元)混合构成(如图 10所示)。本文先用不同阶数的算法对该绕流进行了数值模拟。总体上,阶数不同的算法都能捕捉到卡门涡街,阶数越高则涡结构越清晰,表现为涡量等值线越光滑(如图 11所示)。图 12给出了对应的升、阻力系数周期解,表 6则列出了对应的斯特哈尔数(Strouhal)。可从中看出,对应3阶和4阶的计算斯特哈尔数能与文献[26]计算和实验[27]结果接近。

|
图 10 圆柱绕流计算网格 Fig. 10 Hybrid mesh around a circle cylinder |

|
图 11 圆柱绕流涡量等值线 Fig. 11 Vorticity contours for flow over a circle cylinder |

|
图 12 计算得到的升、阻力系数周期解 Fig. 12 Periodic solutions of calculated lift and drag coefficients |
| 表 6 斯特哈尔数 Tab. 6 Strouhal values |
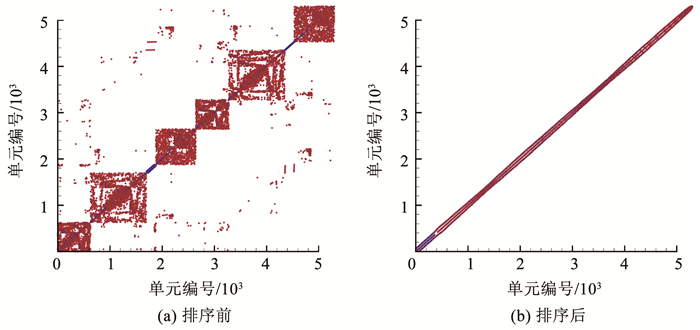
接着,对图 10所示的网格进行粗化和细化操作,由此形成一套渐次加密的结构与非结构混合网格(单元数分别为5 300、21 936和79 428),进行算法加速特性测试。图 13给出了本算例单元关联点阵图,图 13中纵、横向坐标都为单元编号,点代表两单元关联。从图 13中可以看出,本例初始网格对应点阵无序散布,重排后,关联单元编号已十分接近,表现为点阵向主对角集中,呈清晰的条带状,展示出所提重排算法对网格排序的影响。大体上,在同一阶数下,所有加速比随着网格规模增大而提高,GPU加速比最大可达45.68(表 7第6列),最大重排加速比达1.28(表 7第7列),实现了近30%的进一步GPU加速。表明整体非结构化的混合网格,是与上述结构网格算例不同的,有必要进一步结合重排加速。
|
图 13 结构与非结构混合网格单元关联点阵图 Fig. 13 Elemental correlation matrix for hybrid meshes |
| 表 7 圆柱绕流不同阶数算法GPU加速特性测试结果 Tab. 7 GPU speedups of algorithms with different orders for flow over a cycle cylinder |
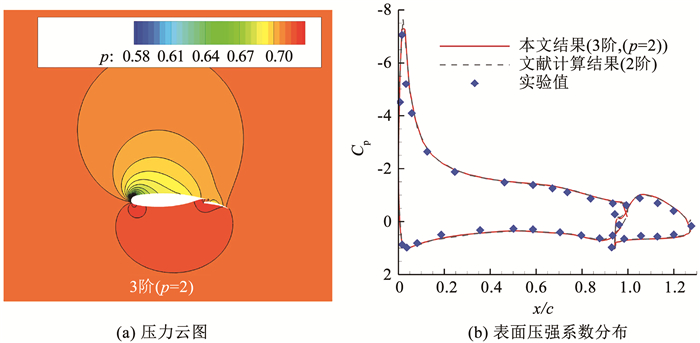
为了展示发展的算法处理复杂气动外形绕流的能力,这里给出了NLR7301多段翼型[28]亚声速无黏绕流算例,来流条件为马赫数0.187和攻角6°。计算网格为一套渐次加密的非结构网格,单元数依次分别为5 030、19 850、78 370和314 704。两段翼型和远场边界在初始网格(如图 14所示)中,表面网格点数相同,均取为65个点。本文先基于初始网格,用发展的3阶RKDG GPU算法对该绕流问题进行了数值模拟。计算得到的压力云图和表面压强系数分布已在图 15中给出,图中同时给出了文献[28]计算结果和实验结果[29]供比较。接着,以主翼、襟翼和远场边界作为重排算法的起始边界,进行了不同分层方向对重排加速比的影响测试,大体上影响不大(见表 8)。

|
图 14 NLR7301翼型绕流的计算网格 Fig. 14 Computational mesh for flow over a NLR7301 airfoil |
|
图 15 NLR7301翼型绕流的计算结果 Fig. 15 Results for flow over a NLR7301 airfoil |
| 表 8 不同起始边界对重排加速比的影响 Tab. 8 Effects of reordering with different starting boundaries |
不失一般性,表 9列出了以主翼作为起始边界的测试结果,表中结果再次证实,对于非结构网格,GPU加速比和重排加速比都随着网格规模增大而提高,这在一定程度上表明,对于涉及大规模非结构网格的数值模拟问题,算法的GPU化和重排加速是很有必要的。
| 表 9 计算耗时和加速比(NLR7301多段翼型,3阶格式(p=2)) Tab. 9 Consuming time and speedups (NLR7301 multi-airfoil, third order (p=2)) |
1) 算法涉及的线程结构是依据单元和单元边界构建的,使得阶数不同的算法可采用统一的程序结构,线程资源能得以有效利用。
2) 算法结构网格上结构有序的数据依赖区,已能较好满足GPU对齐合并访问的要求,无需重排加速。
3) 算法在非结构等混合网格上,数据依赖区非结构,重排加速是很有必要的。重排后的网格,层化结构明显,有助于GPU对齐合并访问,使得算法赢得GPU加速基础上的进一步重排加速。
4) 网格规模大的数值模拟问题更能赢得大的GPU加速。
5) 算法是依据任意类型有限元单元设计的,适合涉及非结构等各类混合网格的复杂气动外形数值模拟问题。
| [1] |
REED W H, HILL T R. Triangle mesh methods for the neutron transport equation: LA-UR-73-479[R]. Los Alamos: Los Alamos Scientific Laboratory, 1973
|
| [2] |
COCKBURN B, HOU Chiwang, SHU C W. The Runge-Kutta local projection discontinuous Galerkin finiteelement method for conservation Laws. Ⅳ: The multidimensional case[J]. Mathematics of Computation, 1990, 54(190): 545. DOI:10.2307/2008501 |
| [3] |
COCKBURN B, SHU Chiwang. The Runge-Kutta discontinuous galerkin method for conservation laws V: Multidimensional systems[J]. Journal of Computational Physics, 1998, 141(2): 199. DOI:10.1006/jcph.1998.5892 |
| [4] |
蔚喜军, 周铁. 流体力学方程的间断有限元方法[J]. 计算物理, 2005, 22(2): 108. YU Xijun, ZHOU Tie. Discontinuous finite element methods for solving hydrodynamic equations[J]. Chinese Journal of Computational Physics, 2005, 22(2): 108. DOI:10.19596/j.cnki.1001-246x.2005.02.001 |
| [5] |
龚小权, 贾洪印, 陈江涛, 等. 基于雅可比矩阵精确计算的GMRES隐式方法在间断Galerkin有限元中的应用[J]. 空气动力学学报, 2019, 37(1): 121. GONG Xiaoquan, JIA Hongyin, CHEN Jiangtao, et al. Applications of GMRES based on exact calculations of Jacobian matrix in discontinuous Galerkin methods[J]. Acta Aerodynamic a Sinica, 2019, 37(1): 121. DOI:10.7638/kqdlxxb-2018.0189 |
| [6] |
ZHANG Jiale, CHEN Hongquan, CAO Cheng. A graphics processing unit-accelerated meshless method for two-dimensional compressible flows[J]. Engineering Applications of Computational Fluid Mechanics, 2017, 11(1): 526. DOI:10.1080/19942060.2017.1317027 |
| [7] |
ZIMMERMAN B J, WANG Z J. The efficient implementation of correction procedure via reconstruction with GPU computing[C]//Proceedings of the 21st AIAA Computational Fluid Dynamics Conference. Reston, Virginia: AIAA, 2013: AIAA2013-2692. DOI: 10.2514/6.2013-2692
|
| [8] |
SRIDHAR A, TISSAOUI Y, MARRAS S, et al. Large-eddy simulations with ClimateMachine v0.2.0: a new open-source code for atmospheric simulations on GPUs and CPUs[J]. Geoscientific Model Development, 2022, 15(15): 6259. DOI:10.5194/gmd-15-6259-2022 |
| [9] |
KLÖCKNER A, WARBURTON T, BRIDGE J, et al. Nodal discontinuous Galerkin methods on graphics processors[J]. Journal of Computational Physics, 2009, 228(21): 7863. DOI:10.1016/j.jcp.2009.06.041 |
| [10] |
SIEBENBORN M, SCHULZ V, SCHMIDT S. A curved-element unstructured discontinuous Galerkin method on GPUs for the Euler equations[J]. Computing and Visualization in Science, 2012, 15(2): 61. DOI:10.1007/s00791-013-0197-0 |
| [11] |
KARAKUS A, CHALMERS N, ŚWIRYDOWICZ K, et al. A GPU accelerated discontinuous Galerkin incompressible flow solver[J]. Journal of Computational Physics, 2019, 390: 380. DOI:10.1016/j.jcp.2019.04.010 |
| [12] |
XIA Yidong, LUO Lixiang, LUO Hong, et al. OpenACC-based GPU acceleration of a 3-D unstructured discontinuous Galerkin method[C]//Proceedings of the 52nd Aerospace Sciences Meeting. Reston, Virginia: AIAA, 2014: AIAA2014-1129. DOI: 10.2514/6.2014-1129
|
| [13] |
FUHRY M, GIULIANI A, KRIVODONOVA L. Discontinuous Galerkin methods on graphics processing units for nonlinear hyperbolic conservation laws[J]. International Journal for Numerical Methods in Fluids, 2014, 76(12): 982. DOI:10.1002/fld.3963 |
| [14] |
GAO Huanqin, CHEN Hongquan, ZHANG Jiale, et al. A GPU-accelerated discontinuous Galerkin method for solving two-dimensional laminar flows[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2022, 39(4): 450. DOI:10.16356/j.1005-1120.2022.04.007 |
| [15] |
LACASTA A, MORALES-HERNÁNDEZ M, MURILLO J, et al. An optimized GPU implementation of a 2D free surface simulation model on unstructured meshes[J]. Advances in Engineering Software, 2014, 78: 1. DOI:10.1016/j.advengsoft.2014.08.007 |
| [16] |
MA Z H, WANG H, PU S H. GPU computing of compressible flow problems by a meshless method with space-filling curves[J]. Journal of Computational Physics, 2014, 263: 113. DOI:10.1016/j.jcp.2014.01.023 |
| [17] |
CAO Cheng, CHEN Hongquan, ZHANG Jiale, et al. A multi-layered point reordering study of GPU-based meshless method for compressible flow simulations[J]. Journal of Computational Science, 2019, 33: 45. DOI:10.1016/j.jocs.2019.04.001 |
| [18] |
BASSI F, CRIVELLINI A, REBAY S, et al. Discontinuous Galerkin solution of the Reynolds-averaged Navier-Stokes and k-ω turbulence model equations[J]. Computers & Fluids, 2005, 34(4/5): 507. DOI:10.1016/j.compfluid.2003.08.004 |
| [19] |
ZHANG Fan, CHENG Jian. A bound-preserving and positivity-preserving finite volume WENO scheme for solving five-equation model of two-medium flows[J]. Communications in Nonlinear Science and Numerical Simulation, 2022, 114: 106649. DOI:10.1016/j.cnsns.2022.106649 |
| [20] |
韩德超, 刘卫华, 司文朋. 三角网格间断有限元法弹性波模拟精度分析[J]. 石油地球物理勘探, 2021, 56(4): 758. HAN Dechao, LIU Weihua, SI Wenpeng. Analysis of elastic wave simulation accuracy with discontinuous Galerkin finite element method based on triangular meshes[J]. Oil Geophysical Prospecting, 2021, 56(4): 758. DOI:10.13810/j.cnki.issn.1000-7210.2021.04.009 |
| [21] |
夏轶栋, 伍贻兆, 吕宏强, 等. 高阶间断有限元法的并行计算研究[J]. 空气动力学学报, 2011, 29(5): 537. XIA Yidong, WU Yizhao, LV Hongqiang, et al. Parallel computation of a high-order discontinuous Galerkin method on unstructured grids[J]. Acta Aerodynamic a Sinica, 2011, 29(5): 537. DOI:10.3969/j.issn.0258-1825.2011.05.001 |
| [22] |
NVIDIA. CUDA C++ programming guide v11.7[Z/OL]. 2022-10-01. https://docs.nvidia.com/cuda/pdf/CUDA_C_Programming_Guide.pdf
|
| [23] |
CHENG Jian, LIU Tiegang, LUO Hong. A hybrid reconstructed discontinuous Galerkin method for compressible flows on arbitrary grids[J]. Computers & Fluids, 2016, 139: 68. DOI:10.1016/j.compfluid.2016.04.001 |
| [24] |
NASA. International Workshop on High-Order CFD Methods[Z/OL]. 2021-04-01. https://www1.grc.nasa.gov/research-and-engineering/hiocfd/
|
| [25] |
BALAN A, WOOPEN M, MAY G. Hp-adaptivity on anisotropic meshes for hybridized discontinuous Galerkin scheme[C]//Proceedings of the 22nd AIAA Computational Fluid Dynamics Conference. Reston, Virginia: AIAA, 2015: AIAA2015-2606. DOI: 10.2514/6.2015-2606
|
| [26] |
HENNINK A, TIBERGA M, LATHOUWERS D. A pressure-based solver for low-Mach number flow using a discontinuous Galerkin method[J]. Journal of Computational Physics, 2021, 425: 109877. DOI:10.1016/j.jcp.2020.109877 |
| [27] |
WANG Anbang, TRÁVNÍC EK Z, CHIA K C. On the relationship of effective Reynolds number and Strouhal number for the laminar vortex shedding of a heated circular cylinder[J]. Physics of Fluids, 2000, 12(6): 1401. DOI:10.1063/1.870391 |
| [28] |
张加乐. 面向求解三维复杂流动问题的GPU并行算法及其应用研究[D]. 南京: 南京航空航天大学, 2018 ZHANG Jiale. Research on GPU-accelerated numerical methods and their applications for three-dimensional complex flows[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2018. DOI: 10.27239/d.cnki.gnhhu.2018.000193 |
| [29] |
VAN DEN BERG B, OSKAM B. Boundary layer measurements on a two-dimensional wing with flap and a comparison with calculations: NLR MP 79034 U[R]. Netherlands: National Laboratorium Luchten Ruimtevoart, 1979
|
 2023, Vol. 55
2023, Vol. 55


